第3章 一次方程与方程组【章末复习】 课件(共47张PPT)
文档属性
| 名称 | 第3章 一次方程与方程组【章末复习】 课件(共47张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 22:03:07 | ||
图片预览











文档简介
(共47张PPT)
章末复习
第3章 一次方程与方程组
【2025-2026学年】2024沪科版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
第 3 章 一次方程与方程组 章末复习
复习目标:
系统梳理本章所学知识,构建知识网络,加深对一次方程与方程组相关概念的理解。
熟练掌握一元一次方程、二元一次方程组、三元一次方程组的解法,并能灵活运用解决实际问题。
总结解题规律和易错点,提高解题的准确性和效率。
知识网络构建
一次方程与方程组
├── 一元一次方程
│ ├── 概念:只含有一个未知数,未知数的次数都是1,等号两边都是整式的方程
│ ├── 解法步骤:去分母、去括号、移项、合并同类项、系数化为1
│ └── 应用:列方程解决实际问题(如行程、工程、利润等)
├── 二元一次方程组
│ ├── 概念:含有两个未知数,含有未知数的项的次数都是1的两个方程组成的方程组
│ ├── 解法:代入消元法、加减消元法
│ └── 应用:解决含两个未知量的实际问题(如比赛得分、调配、配比等)
└── 三元一次方程组
├── 概念:含有三个未知数,含有未知数的项的次数都是1的三个方程组成的方程组
├── 解法:消元(先转化为二元一次方程组,再转化为一元一次方程)
└── 应用:解决含三个未知量的实际问题
重点知识回顾
一、一元一次方程
等式的性质
性质 1:等式两边加(或减)同一个数(或式子),结果仍相等。如果\(a = b\),那么\(a\pm c = b\pm c\)。
性质 2:等式两边乘同一个数,或除以同一个不为 0 的数,结果仍相等。如果\(a = b\),那么\(ac = bc\);如果\(a = b\)(\(c\neq0\)),那么\(\frac{a}{c}=\frac{b}{c}\)。
解一元一次方程的注意事项
去分母时,不要漏乘不含分母的项。
去括号时,若括号前是负号,括号内各项要变号。
移项要变号。
系数化为 1 时,注意分子分母不要颠倒。
二、二元一次方程组
二元一次方程(组)的解
使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解(有无数组)。
二元一次方程组的两个方程的公共解,叫做二元一次方程组的解(有唯一解、无解或无数组解)。
解法对比
代入消元法:适用于有一个未知数的系数为 1 或 - 1 的方程组,将其变形为用含一个未知数的式子表示另一个未知数,再代入另一个方程。
加减消元法:适用于同一未知数的系数相等或互为相反数,或通过变形可使其满足该条件的方程组,通过相加或相减消去一个未知数。
三、三元一次方程组
解法核心:消元,即通过代入或加减消元法,逐步将三元转化为二元,再转化为一元。
步骤:消去一个未知数得到二元一次方程组→解二元一次方程组→回代求出第三个未知数→检验。
四、方程(组)的应用
解题步骤:审(审题,找等量关系)→设(设未知数)→列(列方程或方程组)→解(解方程或方程组)→验(检验解的合理性)→答(写出答案)。
常见题型:行程问题(相遇、追及、顺逆流)、工程问题、利润问题、比赛得分问题、调配问题、配比问题、配套问题等。
典型例题解析
例 1:解一元一次方程
解方程:\(\frac{2x - 1}{3}-\frac{5x + 1}{2}=1\)
解:去分母(两边同乘 6),得:\(2(2x - 1)-3(5x + 1)=6\)
去括号:\(4x - 2 - 15x - 3 = 6\)
移项:\(4x - 15x = 6 + 2 + 3\)
合并同类项:\(-11x = 11\)
系数化为 1:\(x=-1\)
例 2:解二元一次方程组
解方程组:\(\begin{cases}3x + 2y = 13& \\5x - 3y = 9& \end{cases}\)
解:①×3 + ②×2,消去\(y\):\(9x + 6y + 10x - 6y = 39 + 18\)\(19x = 57\),解得\(x = 3\)
把\(x = 3\)代入①:\(3 3 + 2y = 13\),解得\(y = 2\)
所以,方程组的解是\(\begin{cases}x = 3\\y = 2\end{cases}\)
例 3:解三元一次方程组
解方程组:\(\begin{cases}x + y + z = 12& \\x + 2y + 5z = 22& \\x = 4y& \end{cases}\)
解:把③代入①②,得:\(\begin{cases}4y + y + z = 12\\4y + 2y + 5z = 22\end{cases}\),化简为\(\begin{cases}5y + z = 12& \\6y + 5z = 22& ¤\end{cases}\)
④×5 - ⑤:\(25y + 5z - 6y - 5z = 60 - 22\)\(19y = 38\),解得\(y = 2\)
把\(y = 2\)代入③,得\(x = 8\)
把\(x = 8\),\(y = 2\)代入①,得\(z = 2\)
所以,方程组的解是\(\begin{cases}x = 8\\y = 2\\z = 2\end{cases}\)
例 4:方程(组)的应用
某商场购进甲、乙两种商品共 50 件,甲种商品进价每件 35 元,利润率是 20%;乙种商品进价每件 20 元,利润率是 15%,共获利 278 元。问甲、乙两种商品各购进多少件?
解:设购进甲种商品\(x\)件,乙种商品\(y\)件。
根据题意,得\(\begin{cases}x + y = 50\\35 20\%x + 20 15\%y = 278\end{cases}\)
化简第二个方程:\(7x + 3y = 278\)
由①得\(x = 50 - y\),代入②:\(7(50 - y)+3y = 278\)\(350 - 7y + 3y = 278\)\(-4y = -72\),解得\(y = 18\)
则\(x = 50 - 18 = 32\)
答:购进甲种商品 32 件,乙种商品 18 件。
易错点解析
去分母漏乘:解方程\(\frac{x}{2}-1=\frac{x - 1}{3}\)时,易漏乘常数项 1,正确去分母应为\(3x - 6 = 2(x - 1)\)。
解方程组时符号错误:用加减消元法解\(\begin{cases}2x - y = 5\\3x + y = 10\end{cases}\)时,相加后应为\(5x = 15\),而非\(-x = -5\)。
列方程时等量关系错误:行程问题中,相遇问题是 “路程和 = 总路程”,追及问题是 “路程差 = 初始距离”,易混淆两者关系。
忽略实际问题的解的合理性:如人数、物品数量等应为正整数,解出负数或小数时需检验是否符合题意。
复习题
解下列方程(组):
(1)\(4(x - 1)-3(2x + 1)=7\);
(2)\(\begin{cases}2x + y = 5\\x - 3y = 6\end{cases}\);
(3)\(\begin{cases}x + 2y - z = 3\\2x - y + z = 5\\3x + y - 2z = 4\end{cases}\)。
当\(k\)为何值时,方程\(2(x - 1)=k + x\)的解与方程\(\frac{x + 3}{2}=2x - 1\)的解相同?
某工厂计划生产 A、B 两种产品共 100 件,已知生产一件 A 产品需耗煤 3 吨、耗电 2 度;生产一件 B 产品需耗煤 2 吨、耗电 4 度。该工厂现有煤 300 吨,电 200 度。问 A、B 两种产品各生产多少件时,耗煤和耗电刚好都用完?
甲、乙两人从相距 36 千米的两地相向而行,若甲先出发 2 小时,则乙出发 2.5 小时后两人相遇;若乙先出发 2 小时,则甲出发 3 小时后两人相遇。求甲、乙两人的速度。
一个三位数,百位上的数字比十位上的数字大 1,个位上的数字比十位上的数字的 3 倍少 2,若将这个三位数的百位数字与个位数字对调,所得的新三位数与原三位数的和是 1171,求原三位数。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
等式的基本性质
1
性质1:等式的两边都加上(或减去)同一个整式,所得结果仍是等式. 即
如果 a=b,那么 a+c=b+c,a-c=b-c.
1
2
性质2:等式的两边都乘以(或除以)同一个数(除数不能为0),所得结果仍是等式. 即
如果 a=b,那么 ac=bc, (c≠0).
3
性质3:如果 a=b,那么 b=a.(对称性).
例如,由 -4=x,得 x=-4.
在解题过程中,根据等式的传递性,将一个量用与它相等的量代替,称为等量代换.
4
性质4:如果 a=b,b=c,那么 a=c.(传递性).
例如,x=3,又y=x,所以y=3.
一元一次方程
2
只含有一个未知数(元),未知数的次数是1,且等式两边都是整式的方程叫作一元一次方程.
使方程两边相等的未知数的值叫作方程的解. 一元方程的解也叫作根.
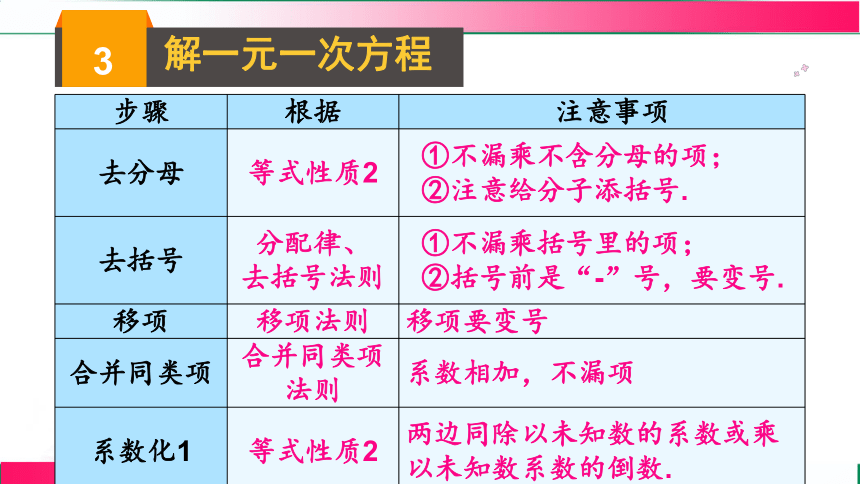
步骤 根据 注意事项
去分母 等式性质2 ①不漏乘不含分母的项;
②注意给分子添括号.
去括号 分配律、 去括号法则 ①不漏乘括号里的项;
②括号前是“-”号,要变号.
移项 移项法则 移项要变号
合并同类项 合并同类项法则 系数相加,不漏项
系数化1 等式性质2 两边同除以未知数的系数或乘以未知数系数的倒数.
解一元一次方程
3
弄清题意和题中的数量关系,用字母(如x,y)表示问题里的未知数;
分析题意,找出相等关系(可借助于示意图、表格等);
根据相等关系,列出需要的代数式,并列出方程;
解这个方程,求出未知数的值;
检查所得的值是否正确和符合实际情形,并写出答案(包括单位名称).
1
2
3
4
5
列方程解应用题的步骤
4
二元一次方程组
5
含有两个未知数的一次方程,叫作二元一次方程.
由两个一次方程组成,且含两个未知数的方程组叫作二元一次方程组.
使二元一次方程组中每个方程都成立的两个未知数的值,叫作二元一次方程组的解. 二元一次方程组的解必须同时满足方程组中的每一个方程.
解二元一次方程组的基本思路是消元.
解二元一次方程组的基本思路是什么?
代入消元法和加减消元法.
二元一次方程组有哪两种解法?
消去两个未知数中的一个.
解二元一次方程组中“代入”与“加减”的目的是什么?
用代入消元法解二元一次方程组的步骤:
①从方程组中选定一个系数比较简单的方程进行变形,用含有x(或y)的代数式表示y(或x);
②将变形后的方程代入另一个方程中,消去y(或x),得到一个关于x(或y)的一元一次方程;
③解这个一元一次方程,求出x(或y)的值;
④把x(或y)的值代入方程中,求y(或x)的值;
⑤用“{”联立两个未知数的值,得到方程组的解.
用加减法解二元一次方程组的一般步骤:
(1)如果某个未知数的系数的绝对值相等时,采用加减消去一个未知数.
(2)如果方程组中不存在某个未知数的系数绝对值相等,那么应选出一组系数求出它们的最小公倍数,然后将原方程组变形,使新方程组的这组系数的绝对值相等,再加减消元.
(3)对于较复杂的二元一次方程组,应先化简,再作如上加减消元的考虑.
由三个一次方程组成,且含三个未知数的方程组,叫作三元一次方程组.
三元一次方程组的解法:通过消元转化成解二元一次方程组的问题,再消元转化成解一元一次方程的问题.
三元一次方程组
6
联系:都是消元,转化为一元一次方程,最后求出方程组的解。
区别:未知数和方程的个数不同。
解三元一次方程组与解二元一次方程组有什么联系和区别?
解:x=6-2y的正整数解有
x = 4,
y = 1,
x = 2,
y = 2;
把
x = 4,
y = 1,
x = 2,
y = 2
分别代入方程x-y=9-3k,
得k=2或k=3.
[解析] 因为两个方程的解相同,先求出方程2x= 的解,再将其代入方程3(x+a)=a-5x 中得到关于a的一元一次方程,从而求出a的值.
解:将4x-y=5和3x+y=9组成方程组,得
4x-y=5,
3x+y=9,
x = 2,
y = 3.
解得
将x = 4,y = 3代入方程ax+ay=-1,
得2a+3b=-1,则(2a+3b)2017= -1.
解:设方程●x+●y=22中x,y的系数分别为a,b,方程3x-●y=8中y的系数为c,由题意,得方程组
4a+2b=22,
12-2c=8,
a+6b=22.
a = 4,
b = 3
c = 2.
解得
所以原方程组为
4x+3y=22,
3x-2y=8.
例5 某电视台在黄金时段的2分钟广告时间内,计划插播长度为15秒和30秒的两种广告. 15秒广告每播1次收费0.8万元,30秒广告每播1次收费1.5万元.若要求每种广告播放不少于2次.
(1)两种广告的播放次数有几种安排方式?
(2)电视台选择哪种方式播放收益较大?
解:(1)设15秒的广告播放x次,30秒的广告播放y次,则15x+30y=120.
又因为每种广告播放不少于2次,故该方程的解为
x=2,
y=3
x = 4,
y = 2.
或
故电视台有两种播放方式:15秒的广告播放2次,30秒的广告播放3次或15秒的广告播放4次,30秒的广告播放2次.
(2)当x=4,y=2时,
0.8×4+1.5×2=6.2(万元);
当x=2,y=3时,
0.8×2+1.5×3=6.1(万元).
所以,选择15秒的广告播放4次,30秒的广告播放2次收益较大.
整合1 方程(组)的相关概念及等式的基本性质
1.已知关于的方程 是一元一次方程,
则 ( )
C
A. B.2 C. D.
2.[2025年1月安庆期末]已知是关于, 的方程
的一个解,则 的值为( )
A
A.1 B. C.2 D.
3.[2025年1月滁州期末]下列各式中,正确的是( )
B
A.若,则
B.若,则
C.若,则
D.若,则
整合2 方程(组)的解法
4.(12分)解方程(组)
(1) ;
解: ,去分母,得
,去括号,得
,移项,得
,合并同类项,得
,两边同除以,得 .
(2)
解:整理,得,得 ,解得
.把代入②,得,解得 .所以原
方程组的解为
(3)
解:,得,解得.,得 ,解得
.将,代入③,得 .所以原方程组的解为
整合3 方程(组)的应用
5.某商场举办“迎元旦送大礼”促销活动,某品牌冰箱若按标
价的八折销售,每件可获利200元,其利润率为 ,若按
标价的八五折销售,每件可获利( )
D
A.475元 B.375元 C.562.5元 D.337.5元
6.[2025·天津模拟]甲地距乙地 ,有一段上坡路与
一段下坡路,一天李海同学保持上坡路每小时走 ,下坡
路每小时走的速度,从甲地到乙地共用了 .若设
李海同学上坡路用了,下坡路用了 ,可列出方程
组为_ ______________.
7.(8分) 数学文化 [2025年1月合肥期末] 我国传统数学名著
《九章算术》中记载:“今有牛五、羊二,直金十九两;牛
二、羊五,直金十六两.问牛、羊各直金几何?”译文:“5头
牛、2只羊,值19两银子;2头牛、5只羊,值16两银子.问每
头牛、每只羊分别值银子多少两?”根据以上译文,解答以
下两个问题:
(1)求每头牛、每只羊各值多少两银子;
解:设每头牛值两银子,每只羊值 两银子,根据题意,得
解得
答:每头牛值3两银子,每只羊值2两银子.
(2)若某商人准备用19两银子买牛和羊(要求:既有牛也有羊,
且银两须全部用完),请问商人有几种购买方法?列出所有
的购买方法.
设购买头牛,只羊,依题意有 ,所以
,因为,都是正整数,所以或 或
所以有三种购买方法:①购买1头牛,8只羊;②购买
3头牛,5只羊;③购买5头牛,2只羊.
整合4 两种数学思想
8.整体思想 已知关于,的二元一次方程组
的解互为相反数,则 的值为___.
1
9.分类讨论思想 甲、乙两人分别从、 两地同时出发,相
向而行,甲的速度是,乙的速度是甲的速度的 ,
出发后两人之间的距离为、两地之间距离的,则 、
两地之间的距离为____________ .
168或
由题意得:乙的速度为,设、
两地之间的距离为,①当甲、乙未相遇,出发 后两
人之间的距离为、两地之间距离的 时,则有:
,解得 .②当甲、乙已经相遇,
出发后两人之间的距离为、两地之间距离的 时,则
有:,解得 .
综上所述,、两地之间的距离为或 .
10.(8分)[2023·安徽中考]根据经营情况,公司对某商品在
甲、乙两地的销售单价进行了如下调整:甲地上涨 ,乙
地降价5元.已知销售单价调整前甲地比乙地少10元,调整后
甲地比乙地少1元,求调整前甲、乙两地该商品的销售单价.
解:设调整前甲、乙两地该商品的销售单价分别为元、 元,
根据题意得,
解得
答:调整前甲、乙两地该商品的销售单价分别为40元、50元.
11.(8分)[2024·安徽中考]乡村振兴战略实施以来,很多外
出人员返乡创业.某村有部分返乡青年承包了一些田地,采用
新技术种植, 两种农作物.种植这两种农作物每公顷所需
人数和投入资金如表:
农作物品种 每公顷所需人数 每公顷所需投入资金(万元)
4 8
3 9
已知农作物种植人员共24位,且每人只参与一种农作物种植,
投入资金共60万元.问, 这两种农作物的种植面积各多少
公顷?
解:设农作物的种植面积为公顷, 农作物的种植面积为
公顷,
由题意可得,解得
答:农作物的种植面积为3公顷, 农作物的种植面积为4
公顷.
谢谢观看!
章末复习
第3章 一次方程与方程组
【2025-2026学年】2024沪科版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
第 3 章 一次方程与方程组 章末复习
复习目标:
系统梳理本章所学知识,构建知识网络,加深对一次方程与方程组相关概念的理解。
熟练掌握一元一次方程、二元一次方程组、三元一次方程组的解法,并能灵活运用解决实际问题。
总结解题规律和易错点,提高解题的准确性和效率。
知识网络构建
一次方程与方程组
├── 一元一次方程
│ ├── 概念:只含有一个未知数,未知数的次数都是1,等号两边都是整式的方程
│ ├── 解法步骤:去分母、去括号、移项、合并同类项、系数化为1
│ └── 应用:列方程解决实际问题(如行程、工程、利润等)
├── 二元一次方程组
│ ├── 概念:含有两个未知数,含有未知数的项的次数都是1的两个方程组成的方程组
│ ├── 解法:代入消元法、加减消元法
│ └── 应用:解决含两个未知量的实际问题(如比赛得分、调配、配比等)
└── 三元一次方程组
├── 概念:含有三个未知数,含有未知数的项的次数都是1的三个方程组成的方程组
├── 解法:消元(先转化为二元一次方程组,再转化为一元一次方程)
└── 应用:解决含三个未知量的实际问题
重点知识回顾
一、一元一次方程
等式的性质
性质 1:等式两边加(或减)同一个数(或式子),结果仍相等。如果\(a = b\),那么\(a\pm c = b\pm c\)。
性质 2:等式两边乘同一个数,或除以同一个不为 0 的数,结果仍相等。如果\(a = b\),那么\(ac = bc\);如果\(a = b\)(\(c\neq0\)),那么\(\frac{a}{c}=\frac{b}{c}\)。
解一元一次方程的注意事项
去分母时,不要漏乘不含分母的项。
去括号时,若括号前是负号,括号内各项要变号。
移项要变号。
系数化为 1 时,注意分子分母不要颠倒。
二、二元一次方程组
二元一次方程(组)的解
使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解(有无数组)。
二元一次方程组的两个方程的公共解,叫做二元一次方程组的解(有唯一解、无解或无数组解)。
解法对比
代入消元法:适用于有一个未知数的系数为 1 或 - 1 的方程组,将其变形为用含一个未知数的式子表示另一个未知数,再代入另一个方程。
加减消元法:适用于同一未知数的系数相等或互为相反数,或通过变形可使其满足该条件的方程组,通过相加或相减消去一个未知数。
三、三元一次方程组
解法核心:消元,即通过代入或加减消元法,逐步将三元转化为二元,再转化为一元。
步骤:消去一个未知数得到二元一次方程组→解二元一次方程组→回代求出第三个未知数→检验。
四、方程(组)的应用
解题步骤:审(审题,找等量关系)→设(设未知数)→列(列方程或方程组)→解(解方程或方程组)→验(检验解的合理性)→答(写出答案)。
常见题型:行程问题(相遇、追及、顺逆流)、工程问题、利润问题、比赛得分问题、调配问题、配比问题、配套问题等。
典型例题解析
例 1:解一元一次方程
解方程:\(\frac{2x - 1}{3}-\frac{5x + 1}{2}=1\)
解:去分母(两边同乘 6),得:\(2(2x - 1)-3(5x + 1)=6\)
去括号:\(4x - 2 - 15x - 3 = 6\)
移项:\(4x - 15x = 6 + 2 + 3\)
合并同类项:\(-11x = 11\)
系数化为 1:\(x=-1\)
例 2:解二元一次方程组
解方程组:\(\begin{cases}3x + 2y = 13& \\5x - 3y = 9& \end{cases}\)
解:①×3 + ②×2,消去\(y\):\(9x + 6y + 10x - 6y = 39 + 18\)\(19x = 57\),解得\(x = 3\)
把\(x = 3\)代入①:\(3 3 + 2y = 13\),解得\(y = 2\)
所以,方程组的解是\(\begin{cases}x = 3\\y = 2\end{cases}\)
例 3:解三元一次方程组
解方程组:\(\begin{cases}x + y + z = 12& \\x + 2y + 5z = 22& \\x = 4y& \end{cases}\)
解:把③代入①②,得:\(\begin{cases}4y + y + z = 12\\4y + 2y + 5z = 22\end{cases}\),化简为\(\begin{cases}5y + z = 12& \\6y + 5z = 22& ¤\end{cases}\)
④×5 - ⑤:\(25y + 5z - 6y - 5z = 60 - 22\)\(19y = 38\),解得\(y = 2\)
把\(y = 2\)代入③,得\(x = 8\)
把\(x = 8\),\(y = 2\)代入①,得\(z = 2\)
所以,方程组的解是\(\begin{cases}x = 8\\y = 2\\z = 2\end{cases}\)
例 4:方程(组)的应用
某商场购进甲、乙两种商品共 50 件,甲种商品进价每件 35 元,利润率是 20%;乙种商品进价每件 20 元,利润率是 15%,共获利 278 元。问甲、乙两种商品各购进多少件?
解:设购进甲种商品\(x\)件,乙种商品\(y\)件。
根据题意,得\(\begin{cases}x + y = 50\\35 20\%x + 20 15\%y = 278\end{cases}\)
化简第二个方程:\(7x + 3y = 278\)
由①得\(x = 50 - y\),代入②:\(7(50 - y)+3y = 278\)\(350 - 7y + 3y = 278\)\(-4y = -72\),解得\(y = 18\)
则\(x = 50 - 18 = 32\)
答:购进甲种商品 32 件,乙种商品 18 件。
易错点解析
去分母漏乘:解方程\(\frac{x}{2}-1=\frac{x - 1}{3}\)时,易漏乘常数项 1,正确去分母应为\(3x - 6 = 2(x - 1)\)。
解方程组时符号错误:用加减消元法解\(\begin{cases}2x - y = 5\\3x + y = 10\end{cases}\)时,相加后应为\(5x = 15\),而非\(-x = -5\)。
列方程时等量关系错误:行程问题中,相遇问题是 “路程和 = 总路程”,追及问题是 “路程差 = 初始距离”,易混淆两者关系。
忽略实际问题的解的合理性:如人数、物品数量等应为正整数,解出负数或小数时需检验是否符合题意。
复习题
解下列方程(组):
(1)\(4(x - 1)-3(2x + 1)=7\);
(2)\(\begin{cases}2x + y = 5\\x - 3y = 6\end{cases}\);
(3)\(\begin{cases}x + 2y - z = 3\\2x - y + z = 5\\3x + y - 2z = 4\end{cases}\)。
当\(k\)为何值时,方程\(2(x - 1)=k + x\)的解与方程\(\frac{x + 3}{2}=2x - 1\)的解相同?
某工厂计划生产 A、B 两种产品共 100 件,已知生产一件 A 产品需耗煤 3 吨、耗电 2 度;生产一件 B 产品需耗煤 2 吨、耗电 4 度。该工厂现有煤 300 吨,电 200 度。问 A、B 两种产品各生产多少件时,耗煤和耗电刚好都用完?
甲、乙两人从相距 36 千米的两地相向而行,若甲先出发 2 小时,则乙出发 2.5 小时后两人相遇;若乙先出发 2 小时,则甲出发 3 小时后两人相遇。求甲、乙两人的速度。
一个三位数,百位上的数字比十位上的数字大 1,个位上的数字比十位上的数字的 3 倍少 2,若将这个三位数的百位数字与个位数字对调,所得的新三位数与原三位数的和是 1171,求原三位数。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
等式的基本性质
1
性质1:等式的两边都加上(或减去)同一个整式,所得结果仍是等式. 即
如果 a=b,那么 a+c=b+c,a-c=b-c.
1
2
性质2:等式的两边都乘以(或除以)同一个数(除数不能为0),所得结果仍是等式. 即
如果 a=b,那么 ac=bc, (c≠0).
3
性质3:如果 a=b,那么 b=a.(对称性).
例如,由 -4=x,得 x=-4.
在解题过程中,根据等式的传递性,将一个量用与它相等的量代替,称为等量代换.
4
性质4:如果 a=b,b=c,那么 a=c.(传递性).
例如,x=3,又y=x,所以y=3.
一元一次方程
2
只含有一个未知数(元),未知数的次数是1,且等式两边都是整式的方程叫作一元一次方程.
使方程两边相等的未知数的值叫作方程的解. 一元方程的解也叫作根.
步骤 根据 注意事项
去分母 等式性质2 ①不漏乘不含分母的项;
②注意给分子添括号.
去括号 分配律、 去括号法则 ①不漏乘括号里的项;
②括号前是“-”号,要变号.
移项 移项法则 移项要变号
合并同类项 合并同类项法则 系数相加,不漏项
系数化1 等式性质2 两边同除以未知数的系数或乘以未知数系数的倒数.
解一元一次方程
3
弄清题意和题中的数量关系,用字母(如x,y)表示问题里的未知数;
分析题意,找出相等关系(可借助于示意图、表格等);
根据相等关系,列出需要的代数式,并列出方程;
解这个方程,求出未知数的值;
检查所得的值是否正确和符合实际情形,并写出答案(包括单位名称).
1
2
3
4
5
列方程解应用题的步骤
4
二元一次方程组
5
含有两个未知数的一次方程,叫作二元一次方程.
由两个一次方程组成,且含两个未知数的方程组叫作二元一次方程组.
使二元一次方程组中每个方程都成立的两个未知数的值,叫作二元一次方程组的解. 二元一次方程组的解必须同时满足方程组中的每一个方程.
解二元一次方程组的基本思路是消元.
解二元一次方程组的基本思路是什么?
代入消元法和加减消元法.
二元一次方程组有哪两种解法?
消去两个未知数中的一个.
解二元一次方程组中“代入”与“加减”的目的是什么?
用代入消元法解二元一次方程组的步骤:
①从方程组中选定一个系数比较简单的方程进行变形,用含有x(或y)的代数式表示y(或x);
②将变形后的方程代入另一个方程中,消去y(或x),得到一个关于x(或y)的一元一次方程;
③解这个一元一次方程,求出x(或y)的值;
④把x(或y)的值代入方程中,求y(或x)的值;
⑤用“{”联立两个未知数的值,得到方程组的解.
用加减法解二元一次方程组的一般步骤:
(1)如果某个未知数的系数的绝对值相等时,采用加减消去一个未知数.
(2)如果方程组中不存在某个未知数的系数绝对值相等,那么应选出一组系数求出它们的最小公倍数,然后将原方程组变形,使新方程组的这组系数的绝对值相等,再加减消元.
(3)对于较复杂的二元一次方程组,应先化简,再作如上加减消元的考虑.
由三个一次方程组成,且含三个未知数的方程组,叫作三元一次方程组.
三元一次方程组的解法:通过消元转化成解二元一次方程组的问题,再消元转化成解一元一次方程的问题.
三元一次方程组
6
联系:都是消元,转化为一元一次方程,最后求出方程组的解。
区别:未知数和方程的个数不同。
解三元一次方程组与解二元一次方程组有什么联系和区别?
解:x=6-2y的正整数解有
x = 4,
y = 1,
x = 2,
y = 2;
把
x = 4,
y = 1,
x = 2,
y = 2
分别代入方程x-y=9-3k,
得k=2或k=3.
[解析] 因为两个方程的解相同,先求出方程2x= 的解,再将其代入方程3(x+a)=a-5x 中得到关于a的一元一次方程,从而求出a的值.
解:将4x-y=5和3x+y=9组成方程组,得
4x-y=5,
3x+y=9,
x = 2,
y = 3.
解得
将x = 4,y = 3代入方程ax+ay=-1,
得2a+3b=-1,则(2a+3b)2017= -1.
解:设方程●x+●y=22中x,y的系数分别为a,b,方程3x-●y=8中y的系数为c,由题意,得方程组
4a+2b=22,
12-2c=8,
a+6b=22.
a = 4,
b = 3
c = 2.
解得
所以原方程组为
4x+3y=22,
3x-2y=8.
例5 某电视台在黄金时段的2分钟广告时间内,计划插播长度为15秒和30秒的两种广告. 15秒广告每播1次收费0.8万元,30秒广告每播1次收费1.5万元.若要求每种广告播放不少于2次.
(1)两种广告的播放次数有几种安排方式?
(2)电视台选择哪种方式播放收益较大?
解:(1)设15秒的广告播放x次,30秒的广告播放y次,则15x+30y=120.
又因为每种广告播放不少于2次,故该方程的解为
x=2,
y=3
x = 4,
y = 2.
或
故电视台有两种播放方式:15秒的广告播放2次,30秒的广告播放3次或15秒的广告播放4次,30秒的广告播放2次.
(2)当x=4,y=2时,
0.8×4+1.5×2=6.2(万元);
当x=2,y=3时,
0.8×2+1.5×3=6.1(万元).
所以,选择15秒的广告播放4次,30秒的广告播放2次收益较大.
整合1 方程(组)的相关概念及等式的基本性质
1.已知关于的方程 是一元一次方程,
则 ( )
C
A. B.2 C. D.
2.[2025年1月安庆期末]已知是关于, 的方程
的一个解,则 的值为( )
A
A.1 B. C.2 D.
3.[2025年1月滁州期末]下列各式中,正确的是( )
B
A.若,则
B.若,则
C.若,则
D.若,则
整合2 方程(组)的解法
4.(12分)解方程(组)
(1) ;
解: ,去分母,得
,去括号,得
,移项,得
,合并同类项,得
,两边同除以,得 .
(2)
解:整理,得,得 ,解得
.把代入②,得,解得 .所以原
方程组的解为
(3)
解:,得,解得.,得 ,解得
.将,代入③,得 .所以原方程组的解为
整合3 方程(组)的应用
5.某商场举办“迎元旦送大礼”促销活动,某品牌冰箱若按标
价的八折销售,每件可获利200元,其利润率为 ,若按
标价的八五折销售,每件可获利( )
D
A.475元 B.375元 C.562.5元 D.337.5元
6.[2025·天津模拟]甲地距乙地 ,有一段上坡路与
一段下坡路,一天李海同学保持上坡路每小时走 ,下坡
路每小时走的速度,从甲地到乙地共用了 .若设
李海同学上坡路用了,下坡路用了 ,可列出方程
组为_ ______________.
7.(8分) 数学文化 [2025年1月合肥期末] 我国传统数学名著
《九章算术》中记载:“今有牛五、羊二,直金十九两;牛
二、羊五,直金十六两.问牛、羊各直金几何?”译文:“5头
牛、2只羊,值19两银子;2头牛、5只羊,值16两银子.问每
头牛、每只羊分别值银子多少两?”根据以上译文,解答以
下两个问题:
(1)求每头牛、每只羊各值多少两银子;
解:设每头牛值两银子,每只羊值 两银子,根据题意,得
解得
答:每头牛值3两银子,每只羊值2两银子.
(2)若某商人准备用19两银子买牛和羊(要求:既有牛也有羊,
且银两须全部用完),请问商人有几种购买方法?列出所有
的购买方法.
设购买头牛,只羊,依题意有 ,所以
,因为,都是正整数,所以或 或
所以有三种购买方法:①购买1头牛,8只羊;②购买
3头牛,5只羊;③购买5头牛,2只羊.
整合4 两种数学思想
8.整体思想 已知关于,的二元一次方程组
的解互为相反数,则 的值为___.
1
9.分类讨论思想 甲、乙两人分别从、 两地同时出发,相
向而行,甲的速度是,乙的速度是甲的速度的 ,
出发后两人之间的距离为、两地之间距离的,则 、
两地之间的距离为____________ .
168或
由题意得:乙的速度为,设、
两地之间的距离为,①当甲、乙未相遇,出发 后两
人之间的距离为、两地之间距离的 时,则有:
,解得 .②当甲、乙已经相遇,
出发后两人之间的距离为、两地之间距离的 时,则
有:,解得 .
综上所述,、两地之间的距离为或 .
10.(8分)[2023·安徽中考]根据经营情况,公司对某商品在
甲、乙两地的销售单价进行了如下调整:甲地上涨 ,乙
地降价5元.已知销售单价调整前甲地比乙地少10元,调整后
甲地比乙地少1元,求调整前甲、乙两地该商品的销售单价.
解:设调整前甲、乙两地该商品的销售单价分别为元、 元,
根据题意得,
解得
答:调整前甲、乙两地该商品的销售单价分别为40元、50元.
11.(8分)[2024·安徽中考]乡村振兴战略实施以来,很多外
出人员返乡创业.某村有部分返乡青年承包了一些田地,采用
新技术种植, 两种农作物.种植这两种农作物每公顷所需
人数和投入资金如表:
农作物品种 每公顷所需人数 每公顷所需投入资金(万元)
4 8
3 9
已知农作物种植人员共24位,且每人只参与一种农作物种植,
投入资金共60万元.问, 这两种农作物的种植面积各多少
公顷?
解:设农作物的种植面积为公顷, 农作物的种植面积为
公顷,
由题意可得,解得
答:农作物的种植面积为3公顷, 农作物的种植面积为4
公顷.
谢谢观看!
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
