2.3.2 多项式 课件(共44张PPT)
文档属性
| 名称 | 2.3.2 多项式 课件(共44张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 00:00:00 | ||
图片预览











文档简介
(共44张PPT)
2.3.2.多项式
第2章 整式及其加减
【华东师大版·2024】数学 七年级上册
授课教师:********
班 级:********
时 间:********
幻灯片 1:封面
标题:2.3.2 多项式
幻灯片 2:学习目标
理解多项式的概念,能准确判断一个代数式是否为多项式。
掌握多项式的项、常数项、次数等概念,能正确确定多项式的项数和次数。
区分单项式和多项式,明确它们之间的联系与区别。
通过实例分析,加深对多项式的认识,提升数学理解能力。
幻灯片 3:情境引入
展示代数式:
2x + 3y、a - 2ab + b 、3m - 2m + 5、-x + 1
提问:这些代数式与我们上节课学习的单项式有什么不同?它们是由什么组成的呢?
引入:这些代数式都是由几个单项式相加组成的,它们被称为多项式。本节课我们就来学习多项式的相关知识。
幻灯片 4:多项式的定义
定义:几个单项式的和叫做多项式。
注意事项:
多项式是由单项式通过加法连接而成的,减法可以看作是加上一个负数,因此多项式中也可以含有减法运算。例如,a - b 可以看作 a + (-b),是多项式。
多项式中不能含有字母作分母的项,因为这样的项不是单项式。例如,x + \(\frac{1}{y}\)不是多项式,因为\(\frac{1}{y}\)不是单项式。
示例:
是多项式的有:x + 2y、3a - 5、m + m - m + 1(都是单项式的和)。
不是多项式的有:\(\frac{x}{y}\) + 1(含有非单项式的项)、ab ÷ c(除法运算且字母在分母)。
幻灯片 5:多项式的项与常数项
项:在多项式中,每个单项式叫做多项式的项。例如,多项式 3x - 2x + 5 中的项分别是 3x 、-2x、5。
注意:多项式的项包括它前面的符号,如 3x - 2x + 5 中,-2x 的符号 “-” 是项的一部分。
常数项:多项式中不含字母的项叫做常数项。例如,多项式 a - 3a + 7 中的常数项是 7。
项数:一个多项式含有几项,就叫做几项式。例如,2x + y 是二项式,m - 2m + 3 是三项式。
示例:
多项式 4a - 1 的项是 4a、-1,项数是 2(二项式),常数项是 - 1。
多项式 x y + 2xy - 3x + 4 的项是 x y、2xy、-3x、4,项数是 4(四项式),常数项是 4。
幻灯片 6:多项式的次数
定义:多项式里,次数最高项的次数,叫做这个多项式的次数。
注意事项:
多项式的次数不是所有项的次数之和,而是由次数最高的项的次数决定的。
确定多项式次数时,需先找出每一项的次数,再从中找出最高次数作为多项式的次数。
示例:
多项式 2x + 3x - 5x + 1 中,各项的次数依次是 3、2、1、0,次数最高项是 2x (次数 3),所以这个多项式的次数是 3,称为三次四项式。
多项式 a b - 3ab + 2a - b 中,各项的次数依次是 3(2 + 1)、3(1 + 2)、1、1,次数最高项是 a b 和 - 3ab (次数 3),所以这个多项式的次数是 3,称为三次四项式。
多项式 5y + 3 的各项次数是 1、0,最高次数是 1,称为一次二项式。
幻灯片 7:整式的概念
整式:单项式和多项式统称为整式。
对比:
类别
定义
示例
单项式
数与字母的积,单独的数或字母
3x、-5、a b
多项式
几个单项式的和
2x + y、a - 3a + 1
整式
单项式和多项式的统称
上述单项式和多项式都是整式
注意:含有字母作分母的代数式不是整式,如\(\frac{1}{x}\)、\(\frac{x + 1}{y}\)都不是整式。
幻灯片 8:例题 1—— 判断是否为多项式及相关概念
题目:判断下列代数式是不是多项式,若是,指出它的项、项数、常数项和次数,并说明它是几次几项式。
(1)3x - 2x + 1
(2)x + \(\frac{1}{x}\)
(3)-a b + 2a b - ab + 3
解答过程:
(1)3x - 2x + 1 是由单项式 3x 、-2x、1 组成的和,是多项式。
项:3x 、-2x、1;项数:3;常数项:1。
各项次数:2、1、0;最高次数是 2。
结论:是二次三项式。
(2)x + \(\frac{1}{x}\)中,\(\frac{1}{x}\)不是单项式,所以不是多项式。
(3)-a b + 2a b - ab + 3 是由单项式 - a b、2a b 、-ab、3 组成的和,是多项式。
项:-a b、2a b 、-ab、3;项数:4;常数项:3。
各项次数:4(3 + 1)、4(2 + 2)、2(1 + 1)、0;最高次数是 4。
结论:是四次四项式。
结论:(1)是多项式,二次三项式;(2)不是多项式;(3)是多项式,四次四项式。
幻灯片 9:例题 2—— 根据条件写多项式
题目:写出一个二次三项式,使它的项分别为 x 、-2x、3。
解答过程:二次三项式是指次数为 2、项数为 3 的多项式。已知项为 x (次数 2)、-2x(次数 1)、3(次数 0),将它们相加即可。
结论:x - 2x + 3(答案唯一,按给定项组合)。
幻灯片 10:例题 3—— 确定多项式的次数和项数
题目:已知多项式 3x - 2x + 5(m、n 为正整数)是三次二项式,求 m、n 的值。
解答过程:
因为多项式是二项式,所以原式中只能有两项,即其中一项的系数为 0。观察多项式,常数项 5 不能为 0,所以只能是 - 2x 的系数为 0,但系数 - 2≠0,因此只能是 3x 与 - 2x 或 5 合并后为两项。
又因为是三次多项式,所以最高次数为 3。
情况一:若 3x 是最高次项,则 n + 1 = 3,n = 2;此时多项式为二项式,说明 - 2x 与 5 中有一项不存在,即 m 不符合正整数或与其他项合并,但 m 为正整数,所以只能是 - 2x 的次数与其他项相同并合并,或 5 被合并,但 5 是常数项,所以只能是 - 2x 不存在,不成立。实际应为项数为 2,所以有一项缺失,即 - 2x 的系数为 0 不成立,因此只能是 5 与另一项合并,不可能,故另一种情况:
情况二:-2x 是最高次项,则 m = 3;此时多项式为二项式,所以 3x 的系数为 0 不成立,只能是 3x 与 5 合并,不可能,或 3x 的次数低于 m 且项数为 2,即 3x 不存在,不成立。正确思路:二项式即有两项,所以其中一项为 0,只能是 3x 或 - 2x 为 0,但系数非 0,所以只能是两项中有一项与另一项为同类项合并,这里不涉及同类项,因此应为 n + 1 = 3 且 m 使得 - 2x 不存在,即 m 不是正整数,矛盾。重新分析:三次二项式,即有两项,最高次 3。所以可能:
3x 和 - 2x 中有一项为三次,另一项与常数项合并为一项,即另一项为常数项(次数 0)。所以:
若 3x 是三次项,n + 1 = 3→n=2;则 - 2x 必须是常数项,即 m=0,但 m 为正整数,不成立。
若 - 2x 是三次项,m=3;则 3x 必须是常数项,即 n + 1=0→n=-1,不是正整数,不成立。
另一可能:常数项 5 与其中一项合并,即 3x 或 - 2x 是常数项。3x 是常数项则 n + 1=0→n=-1(舍);-2x 是常数项则 m=0(舍)。因此,正确应为多项式只有两项,即 3x + 5(-2x 不存在),此时最高次 n + 1=3→n=2,m 不存在,不成立。实际正确解法:题目可能为 “三次二项式”,即项数 2,次数 3。所以两项分别为三次项和另一项(可为常数项或低于三次的项)。因此:
当 3x 是三次项,n + 1=3→n=2;此时另一项为 - 2x ,要使项数为 2,必须存在,所以 m 可为任意正整数,但次数≤3,且多项式为二项式,成立,此时 m 可以是 1、2、3(但 m=3 时也是三次项,仍为二项式)。
当 - 2x 是三次项,m=3;另一项 3x 次数≤3,n + 1≤3→n≤2(n 正整数),项数为 2,成立。
综上,n=2,m 为任意正整数(次数≤3)或 m=3,n 为正整数(次数≤3)。结合题意,最可能 n=2,m=0(舍),正确应为 n=2,m=1 或 2;或 m=3,n=1 或 2。简化:n + 1=3→n=2,m=1(二项式:3x - 2x + 5 是三项式,错误)。哦,原多项式是 3x - 2x + 5,是三项式,要成为二项式,必须有两项合并为一项,即同类项。所以 3x 与 - 2x 是同类项,即 n + 1 = m,合并后为一项,此时多项式为二项式。最高次为 3,所以 m = n + 1 = 3→m=3,n=2。
结论:m=3,n=2。
幻灯片 11:课堂练习 1
题目:下列代数式中,哪些是多项式?
(1)a + b
(2)\(\frac{1}{x}\) + y
(3)3x - 2x
(4)-5m + 1
(5)\(\frac{a + b}{3}\)(可看作\(\frac{1}{3}a + \frac{1}{3}b\))
答案:(1)、(3)、(4)、(5)是多项式;(2)不是多项式。
幻灯片 12:课堂练习 2
题目:指出下列多项式的项、项数、常数项和次数,并说明是几次几项式。
(1)x - 2x + 5x - 1
(2)2a b + ab - 3ab + 4
(3)3y + 1
答案:
(1)项:x 、-2x 、5x、-1;项数 4;常数项 - 1;次数 3;三次四项式。
(2)项:2a b、ab 、-3ab、4;项数 4;常数项 4;次数 3;三次四项式。
(3)项:3y、1;项数 2;常数项 1;次数 1;一次二项式。
幻灯片 13:课堂练习 3
题目:写出一个四次三项式,含有字母 x 和 y,且常数项为 - 5。
答案:答案不唯一,如 x + 2xy - 5、x y - 3y - 5 等。
幻灯片 14:单项式与多项式的对比
区别与联系
单项式
多项式
定义
数与字母的积,单独的数或字母
几个单项式的和
项数
1 项
2 项及以上
次数
所有字母指数的和(单独的数为 0)
次数最高项的次数
系数
有系数(数字因数)
无整体系数,各项有各自系数
联系
多项式由单项式组成,单项式和多项式统称为整式
幻灯片 15:易错点分析
常见错误:
对多项式的定义理解不清,把含有字母作分母的代数式当作多项式。例如,认为 x + \(\frac{1}{x}\)是多项式,实际上\(\frac{1}{x}\)不是单项式,所以它不是多项式。
确定多项式的项时,忽略项前面的符号。例如,多项式 3x - 2y 中的项错误地认为是 3x、2y,正确应为 3x、-2y。
计算多项式的次数时,误将所有项的次数相加,或者把常数项的次数算入。例如,认为多项式 x + 2x + 3 的次数是 2 + 1 + 0 = 3,正确应为最高次项 x 的次数 2。
混淆多项式的项数和次数,例如,把 “三次四项式” 说成 “四项三次式”。
对整式的概念理解错误,认为所有代数式都是整式,忽略了含有字母作分母的代数式不是整式。
规避方法:
牢记多项式是 “几个单项式的和”,确保每个组成部分都是单项式。
确定多项式的项时,严格包含项前面的符号。
计算多项式次数时,只关注各项的次数,找出最高次数作为多项式的次数,与项数无关。
明确 “几次几项式” 的表述顺序:先次数后项数。
区分整式与非整式,整式只包括单项式和多项式,排除含有字母作分母的代数式。
幻灯片 16:课堂小结
多项式的定义:几个单项式的和,可含减法(看作加负数)。
相关概念:
项(含符号)、常数项(不含字母的项)、项数(含几项)。
次数:次数最高项的次数,称为几次几项式。
与单项式的关系:统称为整式,多项式由单项式组成。
判断与确定:能准确判断多项式,正确指出其项、项数、常数项和次数。
幻灯片 17:布置作业
基础作业:教材课后练习题第 1、2 题(判断多项式,指出项、次数等)。
提升作业:已知一个多项式是二次三项式,它的各项系数之和为 0,且含有两项 x 和 - 2x,写出这个多项式。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
学习目标
1.理解多项式、整式的概念,能准确识别多项式、整式.
2.理解多项式的项、常数项和次数.
复习回顾
判断下列各代数式是不是单项式,如果不是,请说明理由;如果是,请指出它们的系数和次数:
(1)3a2;(2)x﹣7;(3)-a2b3;(4)﹣πx2y;
(5)2a+3b;(6) ;(7) .
列代数式:
(1)若三角形的三条边长分别为a 、b、c,则这个三角形的周长为_________;
(2)某班有男生x人,女生21人,这个班的学生一共有________人;
(3)图中阴影部分的面积为_________.
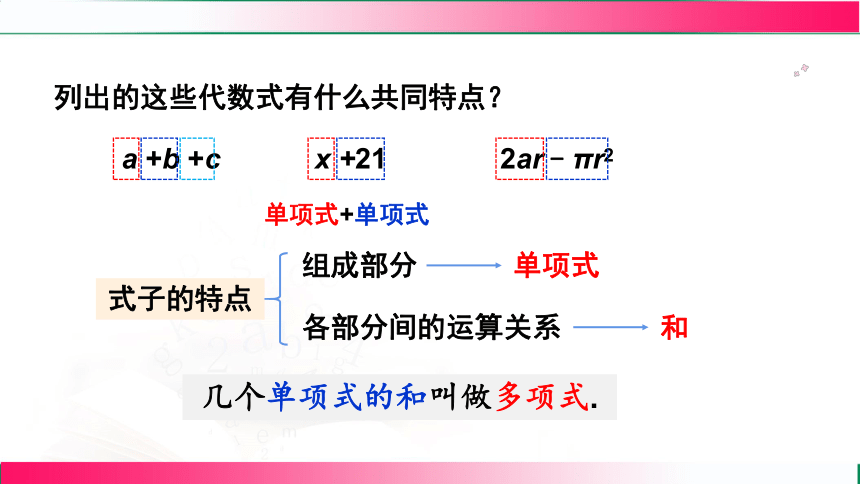
a+b+c
x+21
2ar-πr2
探索新知
你发现这些式子和上节课所学的单项式有什么不同
a +b +c
列出的这些代数式有什么共同特点?
x +21
2ar﹣πr2
单项式+单项式
式子的特点
组成部分
单项式
各部分间的运算关系
和
几个单项式的和叫做多项式.
判断:下列代数式哪些是多项式?
xy,-6, , , , ,m2-2m+1,-p2q
注意:(1)一个式子是多项式需具备两个条件:
①式子中含有运算符号“+”或“﹣”;
②分母中不含字母.
(2)多项式是由单项式组成的,但不能说多项式包含单项式,它们是两个不同的概念.
定义:几个单项式的和叫做多项式.
3x2﹣2x +5
每个单项式叫做多项式的项.
不含字母的项叫做常数项.
注意:多项式的每一项都是单项式,且每一项都包括它的正负号.
多项式的项数
3x2﹣2x +5
2次
1次
0次
多项式的次数
多项式中,次数最高项的次数,就是这个多项式的次数.
最高次数项的次数是2,
二次三项式
注意:多项式的次数不是所有项的次数之和.
指出下列多项式的项和次数:
(1)a3-a2b+ab2-b3;
(2)3n4-2n2+1.
例2
解:(1)多项式a3-a2b+ab2-b3的项有a3、-a2b、ab2 、-b3,次数是3.
(2)多项式3n4-2n2+1的项有3n4、-2n2 、1,次数是4.
多项式的每一项都包括它的正负号.
指出下列多项式是几次几项式:
(1)x3-x+1;
(2)x3-2x2y2+3y2.
例3
解:(1)x3-x+1是三次三项式.
(2)x3-2x2y2+3y2是四次三项式.
补充例题
指出下列多项式的项和次数,并说出它是几次几项式.
(1)x5-2+2x2-5x;
(2) .
解:(1)多项式x5-2+2x2-5x的项有x5、-2、2x2 、-5x,次数是5.它是五次四项式.
(2)多项式 的项有 、 、-xy、1,次数是7.它是七次四项式.
整式
定义:单项式与多项式统称为整式.
思考:你能说出单项式、多项式、整式三者之间的关系吗?
单项式
多项式
注意:所有单项式和多项式都是整式;
反之,一个整式,它要么是单项式,要么是多项式.
1.指出下列多项式是几次几项式:
1. 2x+1+3x2
2. 4x4+1
3. 2x2-3xy+y2
4. 4x3+2x-3y2
二次三项式
四次二项式
二次三项式
三次三项式
课堂练习
【选自教材P98 练习】
2.指出下列多项式的项和次数,并说明其是几次几项式.
(1) ;
(2)-4x4-x2+x-4.
解:(1)多项式 的项有 、-2xy、-3,次数是3.它是三次三项式.
(2)多项式-4x4-x2+x-4的项有-4x4、-x2、x、-4,次数是4.它是四次四项式.
3.在代数式 ,3a,a-y+ , ,xyz, ,
中有( )
A.5个整式
B.4个单项式,3个多项式
C.6个整式,4个单项式
D.6个整式,单项式与多项式个数相同
D
4.指出下列各式中哪些是单项式?哪些是多项式?哪些是整式?
x2+y2,-x, ,10,6xy+1, , ,2x2-x-5, ,a7
单项式:
多项式:
整式:
x2+y2
-x
10
6xy+1
2x2-x-5
a7
-x
10
a7
x2+y2
6xy+1
2x2-x-5
5.若关于x的多项式-5x3+(m-1)x2+(2+n)x-1不含二次项和一次项,求m、n的值.
解:因为多项式-5x3+(m-1)x2+(2+n)x-1不含二次项和一次项,所以m-1=0,2+n=0,所以m=1,n=-2.
知识点1 多项式的概念
1.下列式子是多项式的是( )
D
A. B. C. D.
返回
2.在式子,,,, 中,多项式有___个.
2
返回
知识点2 多项式的项和次数
3.多项式 的各项分别是( )
D
A.,,1 B., ,1
C.,, D.,,
返回
4.[2025新乡期末]多项式 的次数是( )
C
A.2 B.1 C.6 D.3
返回
5.下列关于多项式 的说法,正确的是( )
C
A.次数是3 B.次数最高的项是
C.二次项系数是 D.常数项是5
返回
6.如图,某同学笔记本上的多项式未记录完整,若要补充完整这个多项
式,横线上不能填写的是( )
C
A. B. C. D.
返回
7.[教材习题变式][2025太原月考]请写出一个含有字母, 且
常数项为 的五次三项式:__________________________.
(答案不唯一)
返回
8.当___时,是关于 的一次多项式.
1
返回
9.(8分)[2025吉林期中]已知 是六次四
项式,且 的次数与它相同.
(1)求, 的值;
解:因为 是六次四项式,
所以,解得 ,
因为 的次数也是6,
所以,所以 .
(2)请写出多项式的各项,并求出各项的系数和.
解:该多项式为 ,
所以多项式的各项为,,, ,各项的系数和为
.
返回
知识点3 整式
10.[2025信阳期末]在代数式,,,,, 中,是整
式的有( )
B
A.5个 B.4个 C.3个 D.2个
返回
11.把下列代数式的序号分别填入下表适当的位置:, ,
,,,,, .
整式 单项式 __________
多项式 ______
非整式 ______
①④⑤⑦
③⑥
②⑧
返回
12.如果一个多项式是七次多项式,那么它任何一项的次数( )
D
A.都小于7 B.都等于7 C.都不小于7 D.都不大于7
返回
13. 多项式是关于,的九次二项式,则 的值
为____.
返回
14.已知多项式是关于 的三次三项式,则
___.
8
返回
15.已知关于的多项式 不
含项和项,则 ____.
返回
16.(8分) 已知是关于 ,
的六次多项式,求 的值,并写出该多项式.下面是小亮给出的解法:
解:因为多项式的最高次项为,
所以,
解得
则原多项式为
(1)小亮的解法在第____步出错;
①
(2)请你给出正确的解法.
解:易知该多项式的最高次项为,所以,解得 .
所以原多项式为 .
返回
17.(8分)列多项式,并指出它们的项和次数.
(1)目前,在地球上生存的动物约有150万种,其
中无脊椎动物约有 万种,则脊椎动物约有多少万
种?
解:脊椎动物约有万种,的项分别是150, ,次
数是1.
(2)如图所示的是某古城墙及门洞的示意图,其中门洞的下部是长方
形,上部是半圆,则它的面积是多少?
解:它的面积是,的项分别是, ,次
数是2.
返回
18.(4分) 游戏规则:(1)抽卡片,每人每次抽取4
张卡片,如果抽到白色卡片,那么加上卡片上整式最高次项的系数;如
果抽到灰色卡片,那么减去卡片上整式的常数项;(2)比较两人所抽
取4张卡片的计算结果,结果大的为胜者.
小玉抽到了如图①的4张卡片:
小明抽到了如图②的4张卡片:
他们两人谁获胜了?
解:由题意,得小玉所抽取4张卡片的计算结果是
,小明所抽取4张卡片的计算结果是
.
因为 ,所以小明获胜.
返回
19.(8分)已知关于的整式 .
(1)若此整式是二次多项式,求 的值;
解:因为关于的整式是二次多项式,所以, ,
,解得,所以的值是 .
(2)若此整式是二项式,求 的值.
解:因为关于的整式是二项式,所以有以下3种情况: ,
,,解得;, ,且
,此情况无解;,,,解得 .
所以的值是 或0.
返回
课堂小结
整式
单项式
数与字母的乘积组成的代数式叫做单项式
单项式的系数
单项式的次数
多项式
几个单项式的和叫做多项式
单项式的系数
单项式的次数
谢谢观看!
2.3.2.多项式
第2章 整式及其加减
【华东师大版·2024】数学 七年级上册
授课教师:********
班 级:********
时 间:********
幻灯片 1:封面
标题:2.3.2 多项式
幻灯片 2:学习目标
理解多项式的概念,能准确判断一个代数式是否为多项式。
掌握多项式的项、常数项、次数等概念,能正确确定多项式的项数和次数。
区分单项式和多项式,明确它们之间的联系与区别。
通过实例分析,加深对多项式的认识,提升数学理解能力。
幻灯片 3:情境引入
展示代数式:
2x + 3y、a - 2ab + b 、3m - 2m + 5、-x + 1
提问:这些代数式与我们上节课学习的单项式有什么不同?它们是由什么组成的呢?
引入:这些代数式都是由几个单项式相加组成的,它们被称为多项式。本节课我们就来学习多项式的相关知识。
幻灯片 4:多项式的定义
定义:几个单项式的和叫做多项式。
注意事项:
多项式是由单项式通过加法连接而成的,减法可以看作是加上一个负数,因此多项式中也可以含有减法运算。例如,a - b 可以看作 a + (-b),是多项式。
多项式中不能含有字母作分母的项,因为这样的项不是单项式。例如,x + \(\frac{1}{y}\)不是多项式,因为\(\frac{1}{y}\)不是单项式。
示例:
是多项式的有:x + 2y、3a - 5、m + m - m + 1(都是单项式的和)。
不是多项式的有:\(\frac{x}{y}\) + 1(含有非单项式的项)、ab ÷ c(除法运算且字母在分母)。
幻灯片 5:多项式的项与常数项
项:在多项式中,每个单项式叫做多项式的项。例如,多项式 3x - 2x + 5 中的项分别是 3x 、-2x、5。
注意:多项式的项包括它前面的符号,如 3x - 2x + 5 中,-2x 的符号 “-” 是项的一部分。
常数项:多项式中不含字母的项叫做常数项。例如,多项式 a - 3a + 7 中的常数项是 7。
项数:一个多项式含有几项,就叫做几项式。例如,2x + y 是二项式,m - 2m + 3 是三项式。
示例:
多项式 4a - 1 的项是 4a、-1,项数是 2(二项式),常数项是 - 1。
多项式 x y + 2xy - 3x + 4 的项是 x y、2xy、-3x、4,项数是 4(四项式),常数项是 4。
幻灯片 6:多项式的次数
定义:多项式里,次数最高项的次数,叫做这个多项式的次数。
注意事项:
多项式的次数不是所有项的次数之和,而是由次数最高的项的次数决定的。
确定多项式次数时,需先找出每一项的次数,再从中找出最高次数作为多项式的次数。
示例:
多项式 2x + 3x - 5x + 1 中,各项的次数依次是 3、2、1、0,次数最高项是 2x (次数 3),所以这个多项式的次数是 3,称为三次四项式。
多项式 a b - 3ab + 2a - b 中,各项的次数依次是 3(2 + 1)、3(1 + 2)、1、1,次数最高项是 a b 和 - 3ab (次数 3),所以这个多项式的次数是 3,称为三次四项式。
多项式 5y + 3 的各项次数是 1、0,最高次数是 1,称为一次二项式。
幻灯片 7:整式的概念
整式:单项式和多项式统称为整式。
对比:
类别
定义
示例
单项式
数与字母的积,单独的数或字母
3x、-5、a b
多项式
几个单项式的和
2x + y、a - 3a + 1
整式
单项式和多项式的统称
上述单项式和多项式都是整式
注意:含有字母作分母的代数式不是整式,如\(\frac{1}{x}\)、\(\frac{x + 1}{y}\)都不是整式。
幻灯片 8:例题 1—— 判断是否为多项式及相关概念
题目:判断下列代数式是不是多项式,若是,指出它的项、项数、常数项和次数,并说明它是几次几项式。
(1)3x - 2x + 1
(2)x + \(\frac{1}{x}\)
(3)-a b + 2a b - ab + 3
解答过程:
(1)3x - 2x + 1 是由单项式 3x 、-2x、1 组成的和,是多项式。
项:3x 、-2x、1;项数:3;常数项:1。
各项次数:2、1、0;最高次数是 2。
结论:是二次三项式。
(2)x + \(\frac{1}{x}\)中,\(\frac{1}{x}\)不是单项式,所以不是多项式。
(3)-a b + 2a b - ab + 3 是由单项式 - a b、2a b 、-ab、3 组成的和,是多项式。
项:-a b、2a b 、-ab、3;项数:4;常数项:3。
各项次数:4(3 + 1)、4(2 + 2)、2(1 + 1)、0;最高次数是 4。
结论:是四次四项式。
结论:(1)是多项式,二次三项式;(2)不是多项式;(3)是多项式,四次四项式。
幻灯片 9:例题 2—— 根据条件写多项式
题目:写出一个二次三项式,使它的项分别为 x 、-2x、3。
解答过程:二次三项式是指次数为 2、项数为 3 的多项式。已知项为 x (次数 2)、-2x(次数 1)、3(次数 0),将它们相加即可。
结论:x - 2x + 3(答案唯一,按给定项组合)。
幻灯片 10:例题 3—— 确定多项式的次数和项数
题目:已知多项式 3x - 2x + 5(m、n 为正整数)是三次二项式,求 m、n 的值。
解答过程:
因为多项式是二项式,所以原式中只能有两项,即其中一项的系数为 0。观察多项式,常数项 5 不能为 0,所以只能是 - 2x 的系数为 0,但系数 - 2≠0,因此只能是 3x 与 - 2x 或 5 合并后为两项。
又因为是三次多项式,所以最高次数为 3。
情况一:若 3x 是最高次项,则 n + 1 = 3,n = 2;此时多项式为二项式,说明 - 2x 与 5 中有一项不存在,即 m 不符合正整数或与其他项合并,但 m 为正整数,所以只能是 - 2x 的次数与其他项相同并合并,或 5 被合并,但 5 是常数项,所以只能是 - 2x 不存在,不成立。实际应为项数为 2,所以有一项缺失,即 - 2x 的系数为 0 不成立,因此只能是 5 与另一项合并,不可能,故另一种情况:
情况二:-2x 是最高次项,则 m = 3;此时多项式为二项式,所以 3x 的系数为 0 不成立,只能是 3x 与 5 合并,不可能,或 3x 的次数低于 m 且项数为 2,即 3x 不存在,不成立。正确思路:二项式即有两项,所以其中一项为 0,只能是 3x 或 - 2x 为 0,但系数非 0,所以只能是两项中有一项与另一项为同类项合并,这里不涉及同类项,因此应为 n + 1 = 3 且 m 使得 - 2x 不存在,即 m 不是正整数,矛盾。重新分析:三次二项式,即有两项,最高次 3。所以可能:
3x 和 - 2x 中有一项为三次,另一项与常数项合并为一项,即另一项为常数项(次数 0)。所以:
若 3x 是三次项,n + 1 = 3→n=2;则 - 2x 必须是常数项,即 m=0,但 m 为正整数,不成立。
若 - 2x 是三次项,m=3;则 3x 必须是常数项,即 n + 1=0→n=-1,不是正整数,不成立。
另一可能:常数项 5 与其中一项合并,即 3x 或 - 2x 是常数项。3x 是常数项则 n + 1=0→n=-1(舍);-2x 是常数项则 m=0(舍)。因此,正确应为多项式只有两项,即 3x + 5(-2x 不存在),此时最高次 n + 1=3→n=2,m 不存在,不成立。实际正确解法:题目可能为 “三次二项式”,即项数 2,次数 3。所以两项分别为三次项和另一项(可为常数项或低于三次的项)。因此:
当 3x 是三次项,n + 1=3→n=2;此时另一项为 - 2x ,要使项数为 2,必须存在,所以 m 可为任意正整数,但次数≤3,且多项式为二项式,成立,此时 m 可以是 1、2、3(但 m=3 时也是三次项,仍为二项式)。
当 - 2x 是三次项,m=3;另一项 3x 次数≤3,n + 1≤3→n≤2(n 正整数),项数为 2,成立。
综上,n=2,m 为任意正整数(次数≤3)或 m=3,n 为正整数(次数≤3)。结合题意,最可能 n=2,m=0(舍),正确应为 n=2,m=1 或 2;或 m=3,n=1 或 2。简化:n + 1=3→n=2,m=1(二项式:3x - 2x + 5 是三项式,错误)。哦,原多项式是 3x - 2x + 5,是三项式,要成为二项式,必须有两项合并为一项,即同类项。所以 3x 与 - 2x 是同类项,即 n + 1 = m,合并后为一项,此时多项式为二项式。最高次为 3,所以 m = n + 1 = 3→m=3,n=2。
结论:m=3,n=2。
幻灯片 11:课堂练习 1
题目:下列代数式中,哪些是多项式?
(1)a + b
(2)\(\frac{1}{x}\) + y
(3)3x - 2x
(4)-5m + 1
(5)\(\frac{a + b}{3}\)(可看作\(\frac{1}{3}a + \frac{1}{3}b\))
答案:(1)、(3)、(4)、(5)是多项式;(2)不是多项式。
幻灯片 12:课堂练习 2
题目:指出下列多项式的项、项数、常数项和次数,并说明是几次几项式。
(1)x - 2x + 5x - 1
(2)2a b + ab - 3ab + 4
(3)3y + 1
答案:
(1)项:x 、-2x 、5x、-1;项数 4;常数项 - 1;次数 3;三次四项式。
(2)项:2a b、ab 、-3ab、4;项数 4;常数项 4;次数 3;三次四项式。
(3)项:3y、1;项数 2;常数项 1;次数 1;一次二项式。
幻灯片 13:课堂练习 3
题目:写出一个四次三项式,含有字母 x 和 y,且常数项为 - 5。
答案:答案不唯一,如 x + 2xy - 5、x y - 3y - 5 等。
幻灯片 14:单项式与多项式的对比
区别与联系
单项式
多项式
定义
数与字母的积,单独的数或字母
几个单项式的和
项数
1 项
2 项及以上
次数
所有字母指数的和(单独的数为 0)
次数最高项的次数
系数
有系数(数字因数)
无整体系数,各项有各自系数
联系
多项式由单项式组成,单项式和多项式统称为整式
幻灯片 15:易错点分析
常见错误:
对多项式的定义理解不清,把含有字母作分母的代数式当作多项式。例如,认为 x + \(\frac{1}{x}\)是多项式,实际上\(\frac{1}{x}\)不是单项式,所以它不是多项式。
确定多项式的项时,忽略项前面的符号。例如,多项式 3x - 2y 中的项错误地认为是 3x、2y,正确应为 3x、-2y。
计算多项式的次数时,误将所有项的次数相加,或者把常数项的次数算入。例如,认为多项式 x + 2x + 3 的次数是 2 + 1 + 0 = 3,正确应为最高次项 x 的次数 2。
混淆多项式的项数和次数,例如,把 “三次四项式” 说成 “四项三次式”。
对整式的概念理解错误,认为所有代数式都是整式,忽略了含有字母作分母的代数式不是整式。
规避方法:
牢记多项式是 “几个单项式的和”,确保每个组成部分都是单项式。
确定多项式的项时,严格包含项前面的符号。
计算多项式次数时,只关注各项的次数,找出最高次数作为多项式的次数,与项数无关。
明确 “几次几项式” 的表述顺序:先次数后项数。
区分整式与非整式,整式只包括单项式和多项式,排除含有字母作分母的代数式。
幻灯片 16:课堂小结
多项式的定义:几个单项式的和,可含减法(看作加负数)。
相关概念:
项(含符号)、常数项(不含字母的项)、项数(含几项)。
次数:次数最高项的次数,称为几次几项式。
与单项式的关系:统称为整式,多项式由单项式组成。
判断与确定:能准确判断多项式,正确指出其项、项数、常数项和次数。
幻灯片 17:布置作业
基础作业:教材课后练习题第 1、2 题(判断多项式,指出项、次数等)。
提升作业:已知一个多项式是二次三项式,它的各项系数之和为 0,且含有两项 x 和 - 2x,写出这个多项式。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
学习目标
1.理解多项式、整式的概念,能准确识别多项式、整式.
2.理解多项式的项、常数项和次数.
复习回顾
判断下列各代数式是不是单项式,如果不是,请说明理由;如果是,请指出它们的系数和次数:
(1)3a2;(2)x﹣7;(3)-a2b3;(4)﹣πx2y;
(5)2a+3b;(6) ;(7) .
列代数式:
(1)若三角形的三条边长分别为a 、b、c,则这个三角形的周长为_________;
(2)某班有男生x人,女生21人,这个班的学生一共有________人;
(3)图中阴影部分的面积为_________.
a+b+c
x+21
2ar-πr2
探索新知
你发现这些式子和上节课所学的单项式有什么不同
a +b +c
列出的这些代数式有什么共同特点?
x +21
2ar﹣πr2
单项式+单项式
式子的特点
组成部分
单项式
各部分间的运算关系
和
几个单项式的和叫做多项式.
判断:下列代数式哪些是多项式?
xy,-6, , , , ,m2-2m+1,-p2q
注意:(1)一个式子是多项式需具备两个条件:
①式子中含有运算符号“+”或“﹣”;
②分母中不含字母.
(2)多项式是由单项式组成的,但不能说多项式包含单项式,它们是两个不同的概念.
定义:几个单项式的和叫做多项式.
3x2﹣2x +5
每个单项式叫做多项式的项.
不含字母的项叫做常数项.
注意:多项式的每一项都是单项式,且每一项都包括它的正负号.
多项式的项数
3x2﹣2x +5
2次
1次
0次
多项式的次数
多项式中,次数最高项的次数,就是这个多项式的次数.
最高次数项的次数是2,
二次三项式
注意:多项式的次数不是所有项的次数之和.
指出下列多项式的项和次数:
(1)a3-a2b+ab2-b3;
(2)3n4-2n2+1.
例2
解:(1)多项式a3-a2b+ab2-b3的项有a3、-a2b、ab2 、-b3,次数是3.
(2)多项式3n4-2n2+1的项有3n4、-2n2 、1,次数是4.
多项式的每一项都包括它的正负号.
指出下列多项式是几次几项式:
(1)x3-x+1;
(2)x3-2x2y2+3y2.
例3
解:(1)x3-x+1是三次三项式.
(2)x3-2x2y2+3y2是四次三项式.
补充例题
指出下列多项式的项和次数,并说出它是几次几项式.
(1)x5-2+2x2-5x;
(2) .
解:(1)多项式x5-2+2x2-5x的项有x5、-2、2x2 、-5x,次数是5.它是五次四项式.
(2)多项式 的项有 、 、-xy、1,次数是7.它是七次四项式.
整式
定义:单项式与多项式统称为整式.
思考:你能说出单项式、多项式、整式三者之间的关系吗?
单项式
多项式
注意:所有单项式和多项式都是整式;
反之,一个整式,它要么是单项式,要么是多项式.
1.指出下列多项式是几次几项式:
1. 2x+1+3x2
2. 4x4+1
3. 2x2-3xy+y2
4. 4x3+2x-3y2
二次三项式
四次二项式
二次三项式
三次三项式
课堂练习
【选自教材P98 练习】
2.指出下列多项式的项和次数,并说明其是几次几项式.
(1) ;
(2)-4x4-x2+x-4.
解:(1)多项式 的项有 、-2xy、-3,次数是3.它是三次三项式.
(2)多项式-4x4-x2+x-4的项有-4x4、-x2、x、-4,次数是4.它是四次四项式.
3.在代数式 ,3a,a-y+ , ,xyz, ,
中有( )
A.5个整式
B.4个单项式,3个多项式
C.6个整式,4个单项式
D.6个整式,单项式与多项式个数相同
D
4.指出下列各式中哪些是单项式?哪些是多项式?哪些是整式?
x2+y2,-x, ,10,6xy+1, , ,2x2-x-5, ,a7
单项式:
多项式:
整式:
x2+y2
-x
10
6xy+1
2x2-x-5
a7
-x
10
a7
x2+y2
6xy+1
2x2-x-5
5.若关于x的多项式-5x3+(m-1)x2+(2+n)x-1不含二次项和一次项,求m、n的值.
解:因为多项式-5x3+(m-1)x2+(2+n)x-1不含二次项和一次项,所以m-1=0,2+n=0,所以m=1,n=-2.
知识点1 多项式的概念
1.下列式子是多项式的是( )
D
A. B. C. D.
返回
2.在式子,,,, 中,多项式有___个.
2
返回
知识点2 多项式的项和次数
3.多项式 的各项分别是( )
D
A.,,1 B., ,1
C.,, D.,,
返回
4.[2025新乡期末]多项式 的次数是( )
C
A.2 B.1 C.6 D.3
返回
5.下列关于多项式 的说法,正确的是( )
C
A.次数是3 B.次数最高的项是
C.二次项系数是 D.常数项是5
返回
6.如图,某同学笔记本上的多项式未记录完整,若要补充完整这个多项
式,横线上不能填写的是( )
C
A. B. C. D.
返回
7.[教材习题变式][2025太原月考]请写出一个含有字母, 且
常数项为 的五次三项式:__________________________.
(答案不唯一)
返回
8.当___时,是关于 的一次多项式.
1
返回
9.(8分)[2025吉林期中]已知 是六次四
项式,且 的次数与它相同.
(1)求, 的值;
解:因为 是六次四项式,
所以,解得 ,
因为 的次数也是6,
所以,所以 .
(2)请写出多项式的各项,并求出各项的系数和.
解:该多项式为 ,
所以多项式的各项为,,, ,各项的系数和为
.
返回
知识点3 整式
10.[2025信阳期末]在代数式,,,,, 中,是整
式的有( )
B
A.5个 B.4个 C.3个 D.2个
返回
11.把下列代数式的序号分别填入下表适当的位置:, ,
,,,,, .
整式 单项式 __________
多项式 ______
非整式 ______
①④⑤⑦
③⑥
②⑧
返回
12.如果一个多项式是七次多项式,那么它任何一项的次数( )
D
A.都小于7 B.都等于7 C.都不小于7 D.都不大于7
返回
13. 多项式是关于,的九次二项式,则 的值
为____.
返回
14.已知多项式是关于 的三次三项式,则
___.
8
返回
15.已知关于的多项式 不
含项和项,则 ____.
返回
16.(8分) 已知是关于 ,
的六次多项式,求 的值,并写出该多项式.下面是小亮给出的解法:
解:因为多项式的最高次项为,
所以,
解得
则原多项式为
(1)小亮的解法在第____步出错;
①
(2)请你给出正确的解法.
解:易知该多项式的最高次项为,所以,解得 .
所以原多项式为 .
返回
17.(8分)列多项式,并指出它们的项和次数.
(1)目前,在地球上生存的动物约有150万种,其
中无脊椎动物约有 万种,则脊椎动物约有多少万
种?
解:脊椎动物约有万种,的项分别是150, ,次
数是1.
(2)如图所示的是某古城墙及门洞的示意图,其中门洞的下部是长方
形,上部是半圆,则它的面积是多少?
解:它的面积是,的项分别是, ,次
数是2.
返回
18.(4分) 游戏规则:(1)抽卡片,每人每次抽取4
张卡片,如果抽到白色卡片,那么加上卡片上整式最高次项的系数;如
果抽到灰色卡片,那么减去卡片上整式的常数项;(2)比较两人所抽
取4张卡片的计算结果,结果大的为胜者.
小玉抽到了如图①的4张卡片:
小明抽到了如图②的4张卡片:
他们两人谁获胜了?
解:由题意,得小玉所抽取4张卡片的计算结果是
,小明所抽取4张卡片的计算结果是
.
因为 ,所以小明获胜.
返回
19.(8分)已知关于的整式 .
(1)若此整式是二次多项式,求 的值;
解:因为关于的整式是二次多项式,所以, ,
,解得,所以的值是 .
(2)若此整式是二项式,求 的值.
解:因为关于的整式是二项式,所以有以下3种情况: ,
,,解得;, ,且
,此情况无解;,,,解得 .
所以的值是 或0.
返回
课堂小结
整式
单项式
数与字母的乘积组成的代数式叫做单项式
单项式的系数
单项式的次数
多项式
几个单项式的和叫做多项式
单项式的系数
单项式的次数
谢谢观看!
同课章节目录
