3.2.1.1 由立体图形到视图 课件(共24张PPT)
文档属性
| 名称 | 3.2.1.1 由立体图形到视图 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 05:23:19 | ||
图片预览








文档简介
(共24张PPT)
3.2.1.1 由立体图形到视图
第3章 图形的初步认识
【华东师大版·2024】数学 七年级上册
授课教师:********
班 级:********
时 间:********
幻灯片 1:封面
标题:3.2.1.1 由立体图形到视图
副标题:从不同方向 “看” 立体图形
幻灯片 2:学习目标
理解视图的概念,知道主视图、俯视图、左视图的定义。
能说出从正面、上面、左面观察立体图形所得到的平面图形(视图)。
会画出正方体、长方体、圆柱、圆锥、球等简单立体图形的三视图,培养空间想象能力。
幻灯片 3:情境引入 —— 为什么需要视图?
问题:当我们描述一个立体图形时,只用语言可能很难让别人准确想象出它的形状。比如,如何向没见过魔方的人描述它的样子?
展示图片:建筑设计图、机械零件图(包含多个不同方向的平面图形)。
引入:为了更清晰地表达立体图形的形状,人们通常从不同方向观察立体图形,得到相应的平面图形,这些平面图形就是视图。本节课我们就来学习如何从立体图形得到视图。
幻灯片 4:视图的概念
定义:从某一方向观察一个立体图形时,所看到的平面图形叫做这个立体图形的一个视图。
常见的三种视图:
主视图:从立体图形的正面(正前方)观察所得到的平面图形。
俯视图:从立体图形的上面(正上方)观察所得到的平面图形。
左视图:从立体图形的左面(正左方)观察所得到的平面图形。
说明:通常将主视图、俯视图、左视图称为一个立体图形的三视图,它们共同反映了立体图形的形状和大小。
幻灯片 5:正方体的三视图
立体图形:正方体(各面都是正方形,棱长相等)。
观察与绘制:
主视图:从正面看,看到的是一个正方形(与正方体的一个面全等)。
俯视图:从上面看,看到的是一个正方形(与正方体的一个面全等)。
左视图:从左面看,看到的是一个正方形(与正方体的一个面全等)。
特征:正方体的三视图都是大小相同的正方形。
示意图:
主视图 俯视图 左视图
□ □ □
幻灯片 6:长方体的三视图
立体图形:长方体(长、宽、高不全相等,相对的面全等)。
观察与绘制:
假设长方体的长为 a、宽为 b、高为 c(a≠b≠c)。
主视图:从正面看,看到的是一个长方形(长为 a,宽为 c)。
俯视图:从上面看,看到的是一个长方形(长为 a,宽为 b)。
左视图:从左面看,看到的是一个长方形(长为 b,宽为 c)。
特征:长方体的三视图都是长方形(特殊情况下,若有两面相等,可能出现正方形,如长 = 宽≠高时,主视图和俯视图是正方形)。
示意图:
主视图 俯视图 左视图
(长×高) (长×宽) (宽×高)
幻灯片 7:圆柱的三视图
立体图形:圆柱(两个底面是大小相同的圆,侧面是曲面)。
观察与绘制:
假设圆柱的底面半径为 r,高为 h。
主视图:从正面看,看到的是一个长方形(长为圆柱的高 h,宽为底面直径 2r)。
俯视图:从上面看,看到的是一个圆(与底面圆大小相同,半径为 r)。
左视图:从左面看,看到的是一个长方形(与主视图完全相同,长为 h,宽为 2r)。
特征:主视图和左视图是全等的长方形,俯视图是圆。
示意图:
主视图 俯视图 左视图
○
(高×直径) (底面圆) (高×直径)
幻灯片 8:圆锥的三视图
立体图形:圆锥(底面是圆,侧面是曲面,有一个顶点)。
观察与绘制:
假设圆锥的底面半径为 r,高为 h。
主视图:从正面看,看到的是一个等腰三角形(底边为底面直径 2r,高为圆锥的高 h)。
俯视图:从上面看,看到的是一个圆(与底面圆大小相同,半径为 r),圆心处通常用一个点表示顶点的投影。
左视图:从左面看,看到的是一个等腰三角形(与主视图完全相同,底边为 2r,高为 h)。
特征:主视图和左视图是全等的等腰三角形,俯视图是带中心点的圆。
示意图:
主视图 俯视图 左视图
△ ○· △
(等腰三角形) (带点圆) (等腰三角形)
幻灯片 9:球的三视图
立体图形:球(由曲面围成,从任何方向看都是圆)。
观察与绘制:
主视图:从正面看,看到的是一个圆(半径与球的半径相等)。
俯视图:从上面看,看到的是一个圆(与主视图的圆大小相同)。
左视图:从左面看,看到的是一个圆(与主视图、俯视图的圆大小相同)。
特征:三视图都是全等的圆。
示意图:
主视图 俯视图 左视图
○ ○ ○
(球的截面圆) (球的截面圆) (球的截面圆)
幻灯片 10:简单组合体的三视图(基础)
示例:由两个正方体上下叠放组成的组合体(下面正方体棱长为 a,上面正方体棱长为 a,且放在下面正方体的正中央)。
观察与绘制:
主视图:从正面看,看到的是两个上下相连的正方形(每个正方形棱长为 a)。
俯视图:从上面看,看到的是一个正方形(与下面正方体的俯视图相同,棱长为 a,因为上面的正方体在正中央,投影被下面的正方块完全覆盖)。
左视图:从左面看,看到的是两个上下相连的正方形(与主视图相同)。
示意图:
主视图 俯视图 左视图
□ □ □
□ □ □
幻灯片 11:画三视图的注意事项
观察方向:必须从 “正前方”“正上方”“正左方” 观察,视线要与被观察的面垂直,确保看到的是平面图形。
大小对应:视图的大小要与立体图形的尺寸相对应,如圆柱的主视图长方形的宽等于底面直径,高等于圆柱的高。
细节呈现:圆锥的俯视图要画出中心点,组合体的视图要体现各部分的位置关系(如叠放、并排等)。
虚实线问题:对于初学者,先掌握简单立体图形的三视图(无遮挡部分),暂不涉及复杂图形的虚实线(后续会学习:被遮挡部分的轮廓线用虚线表示)。
幻灯片 12:例题 1—— 判断简单立体图形的视图
题目:如图所示的圆柱,它的主视图是( )
A. 圆 B. 长方形 C. 三角形 D. 正方形
解答过程:圆柱的主视图是长方形,所以选 B。
结论:B
幻灯片 13:例题 2—— 画出正方体的三视图
题目:已知一个正方体的棱长为 2cm,画出它的三视图。
解答过程:
主视图:从正面看,是一个边长为 2cm 的正方形。
俯视图:从上面看,是一个边长为 2cm 的正方形。
左视图:从左面看,是一个边长为 2cm 的正方形。
示意图:
主视图 俯视图 左视图
□ □ □
(边长2cm) (边长2cm) (边长2cm)
幻灯片 14:课堂练习 1—— 说出下列立体图形的三视图形状
题目:
(1)长方体(长 3cm,宽 2cm,高 4cm):主视图是______,俯视图是______,左视图是______。
(2)圆锥:主视图是______,俯视图是______,左视图是______。
(3)球:主视图是______,俯视图是______,左视图是______。
答案:
(1)长方形(4cm×3cm),长方形(3cm×2cm),长方形(4cm×2cm)
(2)等腰三角形,带点的圆,等腰三角形
(3)圆,圆,圆
幻灯片 15:课堂练习 2—— 判断对错
题目:
(1)圆柱的主视图和俯视图都是长方形。(×,俯视图是圆)
(2)圆锥的左视图是等腰三角形。(√)
(3)球的三视图都是大小相同的圆。(√)
(4)正方体的三视图都是正方形,且大小不同。(×,大小相同)
幻灯片 16:易错点分析
常见错误:
混淆圆柱和圆锥的主视图,把圆锥的主视图画成三角形(正确,但容易忘记是等腰三角形),或把圆柱的主视图画成正方形(只有特殊圆柱才是,一般是长方形)。
画圆锥的俯视图时,遗漏中心点(中心点表示顶点的投影,不可省略)。
认为球的三视图大小不同,实际上球从任何方向看都是等大的圆。
观察组合体时,无法判断各部分的位置关系对视图的影响,如两个正方体并排摆放,俯视图应是两个相连的正方形,而不是一个。
规避方法:
牢记每种立体图形三视图的典型特征,结合实物观察加深印象,如拿一个易拉罐(圆柱)从不同方向观察,验证主视图和俯视图的形状。
画圆锥俯视图时,刻意提醒自己加上中心点,形成习惯。
理解球的对称性,无论从哪个方向观察,看到的圆的大小都与球的半径相关,因此三视图全等。
观察组合体时,先分解成简单立体图形,再逐一分析每个部分在视图中的位置和形状,最后组合起来。
幻灯片 17:课堂小结
视图的定义:从某一方向观察立体图形得到的平面图形,主要包括主视图(正面)、俯视图(上面)、左视图(左面)。
常见立体图形的三视图:
正方体:三个全等的正方形。
长方体:三个长方形(可能有正方形)。
圆柱:主视图和左视图是长方形,俯视图是圆。
圆锥:主视图和左视图是等腰三角形,俯视图是带点的圆。
球:三个全等的圆。
关键能力:通过观察立体图形,想象出不同方向的视图,是从三维到二维的转化,需要多观察、多练习来培养空间观念。
幻灯片 18:布置作业
基础作业:
教材课后练习题第 1、2 题(说出立体图形的三视图形状,画出正方体、圆柱的三视图)。
观察家里的茶叶罐(圆柱)、篮球(球),分别画出它们的三视图。
提升作业:
一个圆锥的底面直径是 6cm,高是 4cm,画出它的三视图,并标注相关尺寸(主视图等腰三角形的底边和高,俯视图圆的直径)。
用两个相同的小正方体并排摆放(左右排列),画出这个组合体的三视图。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
情境导入
工人在建造房子之前,首先要看房子的图纸.但在平面上画空间的物体不是一件简单的事,因为必须把它画得从各个角度都能看得很清楚.
为了解决这个问题,可以采用三视图法.
视图来自投影.
窗框的影子
皮影
人和骆驼的影子
手影
故宫日晷
不同时刻影子的长度
物体的投影
投影线
投影面
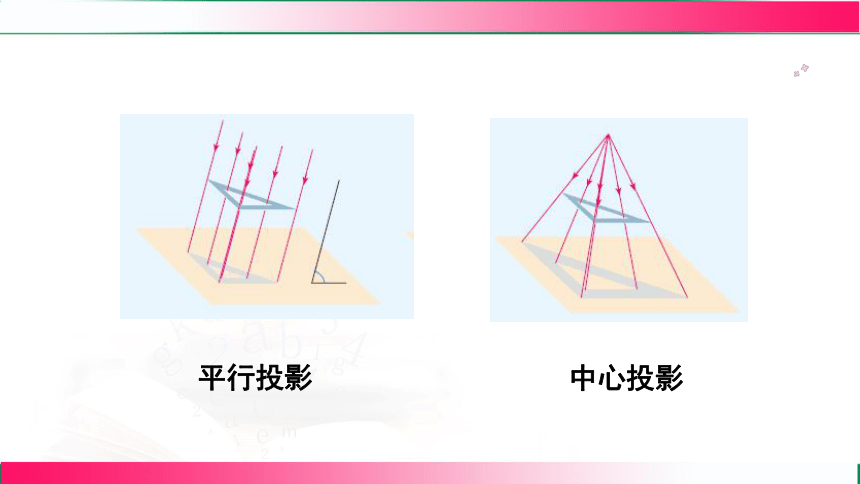
由平行光线形成的投影,叫做平行投影.物体在太阳光线照射下形成的影子就是平行投影.
由一点发出的光线形成的投影,叫做中心投影.
中心投影
平行投影
正投影
随堂练习
1. 举例说明生活中平行投影和中心投影的例子.
【教材P129 练习 第1题】
2. 路灯下,高矮相同的两个人的影子一定一样长吗?什么时候可能会一样长?试说明你的理由.
高矮相同的两个人的影子不一定一样长,影子的长度和位置有关.两人与路灯的距离相等时,可能会一样长.
【教材P129 练习 第2题】
知识点1 平行投影、中心投影
1.平行投影的光源可以是( )
B
A.手电筒 B.太阳 C.路灯 D.台灯
返回
2.[2025成都期末]下列各种现象属于中心投影的是( )
B
A.中午用来乘凉的树影 B.舞台上演员的影子
C.早晨升旗时旗杆的影子 D.阳光下人的影子
返回
3.[2025汉中期末]下列四幅图中,表示同一时刻两棵小树在月光下的
影子的是( )
A
A. B. C. D.
返回
4. 宋代诗人释惠明所作《手影戏》中写道:“三尺生绡作
戏台,全凭十指逞诙谐.有时明月灯窗下,一笑还从掌握来.”如图,“手
影戏”中的手影属于__________(填“中心投影”或“平行投影”)
中心投影
返回
知识点2 正投影
5.一个正五棱柱如下图摆放,光线由上到下照射此正五棱柱时的正投影
是( )
B
A. B. C. D.
返回
6. 一个正方形木框在地面上形成的正投影不可能是
( )
D
A.线段 B.长方形 C.正方形 D.梯形
返回
(第7题)
7.[2025焦作期末]如图,小亮夜晚从路灯下的 处走
到 处的过程中,他的影子( )
B
A.逐渐变短 B.先变短后变长
C.先变长后变短 D.逐渐变长
返回
8.艺术字母、、、的投影效果如图,与字母 属于同一种投影的是
字母______.
和
(第8题)
返回
9.如图是大树的影子随太阳转动情况(上午8时至下午5时之间),按时
间先后顺序排列是____________.(填序号)
②④①③⑤
返回
10.(4分)如图,两幅图中竹竿的影子是在太阳光下形成的,还是在灯
光下形成的?请你画出两幅图中小树的影子.
解:图①是在灯光下形成的,图②
是在太阳光下形成的.小树的影子如
图所示.
返回
课堂小结
中心投影
平行投影
谢谢观看!
3.2.1.1 由立体图形到视图
第3章 图形的初步认识
【华东师大版·2024】数学 七年级上册
授课教师:********
班 级:********
时 间:********
幻灯片 1:封面
标题:3.2.1.1 由立体图形到视图
副标题:从不同方向 “看” 立体图形
幻灯片 2:学习目标
理解视图的概念,知道主视图、俯视图、左视图的定义。
能说出从正面、上面、左面观察立体图形所得到的平面图形(视图)。
会画出正方体、长方体、圆柱、圆锥、球等简单立体图形的三视图,培养空间想象能力。
幻灯片 3:情境引入 —— 为什么需要视图?
问题:当我们描述一个立体图形时,只用语言可能很难让别人准确想象出它的形状。比如,如何向没见过魔方的人描述它的样子?
展示图片:建筑设计图、机械零件图(包含多个不同方向的平面图形)。
引入:为了更清晰地表达立体图形的形状,人们通常从不同方向观察立体图形,得到相应的平面图形,这些平面图形就是视图。本节课我们就来学习如何从立体图形得到视图。
幻灯片 4:视图的概念
定义:从某一方向观察一个立体图形时,所看到的平面图形叫做这个立体图形的一个视图。
常见的三种视图:
主视图:从立体图形的正面(正前方)观察所得到的平面图形。
俯视图:从立体图形的上面(正上方)观察所得到的平面图形。
左视图:从立体图形的左面(正左方)观察所得到的平面图形。
说明:通常将主视图、俯视图、左视图称为一个立体图形的三视图,它们共同反映了立体图形的形状和大小。
幻灯片 5:正方体的三视图
立体图形:正方体(各面都是正方形,棱长相等)。
观察与绘制:
主视图:从正面看,看到的是一个正方形(与正方体的一个面全等)。
俯视图:从上面看,看到的是一个正方形(与正方体的一个面全等)。
左视图:从左面看,看到的是一个正方形(与正方体的一个面全等)。
特征:正方体的三视图都是大小相同的正方形。
示意图:
主视图 俯视图 左视图
□ □ □
幻灯片 6:长方体的三视图
立体图形:长方体(长、宽、高不全相等,相对的面全等)。
观察与绘制:
假设长方体的长为 a、宽为 b、高为 c(a≠b≠c)。
主视图:从正面看,看到的是一个长方形(长为 a,宽为 c)。
俯视图:从上面看,看到的是一个长方形(长为 a,宽为 b)。
左视图:从左面看,看到的是一个长方形(长为 b,宽为 c)。
特征:长方体的三视图都是长方形(特殊情况下,若有两面相等,可能出现正方形,如长 = 宽≠高时,主视图和俯视图是正方形)。
示意图:
主视图 俯视图 左视图
(长×高) (长×宽) (宽×高)
幻灯片 7:圆柱的三视图
立体图形:圆柱(两个底面是大小相同的圆,侧面是曲面)。
观察与绘制:
假设圆柱的底面半径为 r,高为 h。
主视图:从正面看,看到的是一个长方形(长为圆柱的高 h,宽为底面直径 2r)。
俯视图:从上面看,看到的是一个圆(与底面圆大小相同,半径为 r)。
左视图:从左面看,看到的是一个长方形(与主视图完全相同,长为 h,宽为 2r)。
特征:主视图和左视图是全等的长方形,俯视图是圆。
示意图:
主视图 俯视图 左视图
○
(高×直径) (底面圆) (高×直径)
幻灯片 8:圆锥的三视图
立体图形:圆锥(底面是圆,侧面是曲面,有一个顶点)。
观察与绘制:
假设圆锥的底面半径为 r,高为 h。
主视图:从正面看,看到的是一个等腰三角形(底边为底面直径 2r,高为圆锥的高 h)。
俯视图:从上面看,看到的是一个圆(与底面圆大小相同,半径为 r),圆心处通常用一个点表示顶点的投影。
左视图:从左面看,看到的是一个等腰三角形(与主视图完全相同,底边为 2r,高为 h)。
特征:主视图和左视图是全等的等腰三角形,俯视图是带中心点的圆。
示意图:
主视图 俯视图 左视图
△ ○· △
(等腰三角形) (带点圆) (等腰三角形)
幻灯片 9:球的三视图
立体图形:球(由曲面围成,从任何方向看都是圆)。
观察与绘制:
主视图:从正面看,看到的是一个圆(半径与球的半径相等)。
俯视图:从上面看,看到的是一个圆(与主视图的圆大小相同)。
左视图:从左面看,看到的是一个圆(与主视图、俯视图的圆大小相同)。
特征:三视图都是全等的圆。
示意图:
主视图 俯视图 左视图
○ ○ ○
(球的截面圆) (球的截面圆) (球的截面圆)
幻灯片 10:简单组合体的三视图(基础)
示例:由两个正方体上下叠放组成的组合体(下面正方体棱长为 a,上面正方体棱长为 a,且放在下面正方体的正中央)。
观察与绘制:
主视图:从正面看,看到的是两个上下相连的正方形(每个正方形棱长为 a)。
俯视图:从上面看,看到的是一个正方形(与下面正方体的俯视图相同,棱长为 a,因为上面的正方体在正中央,投影被下面的正方块完全覆盖)。
左视图:从左面看,看到的是两个上下相连的正方形(与主视图相同)。
示意图:
主视图 俯视图 左视图
□ □ □
□ □ □
幻灯片 11:画三视图的注意事项
观察方向:必须从 “正前方”“正上方”“正左方” 观察,视线要与被观察的面垂直,确保看到的是平面图形。
大小对应:视图的大小要与立体图形的尺寸相对应,如圆柱的主视图长方形的宽等于底面直径,高等于圆柱的高。
细节呈现:圆锥的俯视图要画出中心点,组合体的视图要体现各部分的位置关系(如叠放、并排等)。
虚实线问题:对于初学者,先掌握简单立体图形的三视图(无遮挡部分),暂不涉及复杂图形的虚实线(后续会学习:被遮挡部分的轮廓线用虚线表示)。
幻灯片 12:例题 1—— 判断简单立体图形的视图
题目:如图所示的圆柱,它的主视图是( )
A. 圆 B. 长方形 C. 三角形 D. 正方形
解答过程:圆柱的主视图是长方形,所以选 B。
结论:B
幻灯片 13:例题 2—— 画出正方体的三视图
题目:已知一个正方体的棱长为 2cm,画出它的三视图。
解答过程:
主视图:从正面看,是一个边长为 2cm 的正方形。
俯视图:从上面看,是一个边长为 2cm 的正方形。
左视图:从左面看,是一个边长为 2cm 的正方形。
示意图:
主视图 俯视图 左视图
□ □ □
(边长2cm) (边长2cm) (边长2cm)
幻灯片 14:课堂练习 1—— 说出下列立体图形的三视图形状
题目:
(1)长方体(长 3cm,宽 2cm,高 4cm):主视图是______,俯视图是______,左视图是______。
(2)圆锥:主视图是______,俯视图是______,左视图是______。
(3)球:主视图是______,俯视图是______,左视图是______。
答案:
(1)长方形(4cm×3cm),长方形(3cm×2cm),长方形(4cm×2cm)
(2)等腰三角形,带点的圆,等腰三角形
(3)圆,圆,圆
幻灯片 15:课堂练习 2—— 判断对错
题目:
(1)圆柱的主视图和俯视图都是长方形。(×,俯视图是圆)
(2)圆锥的左视图是等腰三角形。(√)
(3)球的三视图都是大小相同的圆。(√)
(4)正方体的三视图都是正方形,且大小不同。(×,大小相同)
幻灯片 16:易错点分析
常见错误:
混淆圆柱和圆锥的主视图,把圆锥的主视图画成三角形(正确,但容易忘记是等腰三角形),或把圆柱的主视图画成正方形(只有特殊圆柱才是,一般是长方形)。
画圆锥的俯视图时,遗漏中心点(中心点表示顶点的投影,不可省略)。
认为球的三视图大小不同,实际上球从任何方向看都是等大的圆。
观察组合体时,无法判断各部分的位置关系对视图的影响,如两个正方体并排摆放,俯视图应是两个相连的正方形,而不是一个。
规避方法:
牢记每种立体图形三视图的典型特征,结合实物观察加深印象,如拿一个易拉罐(圆柱)从不同方向观察,验证主视图和俯视图的形状。
画圆锥俯视图时,刻意提醒自己加上中心点,形成习惯。
理解球的对称性,无论从哪个方向观察,看到的圆的大小都与球的半径相关,因此三视图全等。
观察组合体时,先分解成简单立体图形,再逐一分析每个部分在视图中的位置和形状,最后组合起来。
幻灯片 17:课堂小结
视图的定义:从某一方向观察立体图形得到的平面图形,主要包括主视图(正面)、俯视图(上面)、左视图(左面)。
常见立体图形的三视图:
正方体:三个全等的正方形。
长方体:三个长方形(可能有正方形)。
圆柱:主视图和左视图是长方形,俯视图是圆。
圆锥:主视图和左视图是等腰三角形,俯视图是带点的圆。
球:三个全等的圆。
关键能力:通过观察立体图形,想象出不同方向的视图,是从三维到二维的转化,需要多观察、多练习来培养空间观念。
幻灯片 18:布置作业
基础作业:
教材课后练习题第 1、2 题(说出立体图形的三视图形状,画出正方体、圆柱的三视图)。
观察家里的茶叶罐(圆柱)、篮球(球),分别画出它们的三视图。
提升作业:
一个圆锥的底面直径是 6cm,高是 4cm,画出它的三视图,并标注相关尺寸(主视图等腰三角形的底边和高,俯视图圆的直径)。
用两个相同的小正方体并排摆放(左右排列),画出这个组合体的三视图。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
情境导入
工人在建造房子之前,首先要看房子的图纸.但在平面上画空间的物体不是一件简单的事,因为必须把它画得从各个角度都能看得很清楚.
为了解决这个问题,可以采用三视图法.
视图来自投影.
窗框的影子
皮影
人和骆驼的影子
手影
故宫日晷
不同时刻影子的长度
物体的投影
投影线
投影面
由平行光线形成的投影,叫做平行投影.物体在太阳光线照射下形成的影子就是平行投影.
由一点发出的光线形成的投影,叫做中心投影.
中心投影
平行投影
正投影
随堂练习
1. 举例说明生活中平行投影和中心投影的例子.
【教材P129 练习 第1题】
2. 路灯下,高矮相同的两个人的影子一定一样长吗?什么时候可能会一样长?试说明你的理由.
高矮相同的两个人的影子不一定一样长,影子的长度和位置有关.两人与路灯的距离相等时,可能会一样长.
【教材P129 练习 第2题】
知识点1 平行投影、中心投影
1.平行投影的光源可以是( )
B
A.手电筒 B.太阳 C.路灯 D.台灯
返回
2.[2025成都期末]下列各种现象属于中心投影的是( )
B
A.中午用来乘凉的树影 B.舞台上演员的影子
C.早晨升旗时旗杆的影子 D.阳光下人的影子
返回
3.[2025汉中期末]下列四幅图中,表示同一时刻两棵小树在月光下的
影子的是( )
A
A. B. C. D.
返回
4. 宋代诗人释惠明所作《手影戏》中写道:“三尺生绡作
戏台,全凭十指逞诙谐.有时明月灯窗下,一笑还从掌握来.”如图,“手
影戏”中的手影属于__________(填“中心投影”或“平行投影”)
中心投影
返回
知识点2 正投影
5.一个正五棱柱如下图摆放,光线由上到下照射此正五棱柱时的正投影
是( )
B
A. B. C. D.
返回
6. 一个正方形木框在地面上形成的正投影不可能是
( )
D
A.线段 B.长方形 C.正方形 D.梯形
返回
(第7题)
7.[2025焦作期末]如图,小亮夜晚从路灯下的 处走
到 处的过程中,他的影子( )
B
A.逐渐变短 B.先变短后变长
C.先变长后变短 D.逐渐变长
返回
8.艺术字母、、、的投影效果如图,与字母 属于同一种投影的是
字母______.
和
(第8题)
返回
9.如图是大树的影子随太阳转动情况(上午8时至下午5时之间),按时
间先后顺序排列是____________.(填序号)
②④①③⑤
返回
10.(4分)如图,两幅图中竹竿的影子是在太阳光下形成的,还是在灯
光下形成的?请你画出两幅图中小树的影子.
解:图①是在灯光下形成的,图②
是在太阳光下形成的.小树的影子如
图所示.
返回
课堂小结
中心投影
平行投影
谢谢观看!
同课章节目录
