3.2.1.2 由立体图形到视图 课件(共41张PPT)
文档属性
| 名称 | 3.2.1.2 由立体图形到视图 课件(共41张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 00:00:00 | ||
图片预览



文档简介
(共41张PPT)
3.2.1.2由立体图形到视图
第3章 图形的初步认识
【华东师大版·2024】数学 七年级上册
授课教师:********
班 级:********
时 间:********
幻灯片 1:封面
标题:3.2.1.2 由立体图形到视图
副标题:复杂立体图形的视图探究
幻灯片 2:学习目标
能画出棱柱、棱锥等立体图形的三视图。
掌握简单组合体三视图的绘制方法,能分析组合体各部分对视图的影响。
进一步提升空间想象能力,能根据立体图形的特征准确判断视图形状。
幻灯片 3:复习回顾
三种基本视图:主视图(正面)、俯视图(上面)、左视图(左面)。
简单立体图形的三视图:
正方体:三个全等的正方形。
圆柱:主视图和左视图为长方形,俯视图为圆。
圆锥:主视图和左视图为等腰三角形,俯视图为带点的圆。
球:三个全等的圆。
引入:本节课我们将学习棱柱、棱锥及组合体的三视图绘制。
幻灯片 4:三棱柱的三视图
立体图形:三棱柱(两个底面是全等的三角形,侧面是三个长方形)。
观察与绘制:
底面为等边三角形,棱长为 a,高为 h。
主视图:从正面看,看到的是一个长方形(长为 h,宽为底面三角形的边长 a)。
俯视图:从上面看,看到的是一个三角形(与底面三角形全等)。
左视图:从左面看,看到的是一个长方形(长为 h,宽为底面三角形的高)。
特征:主视图和左视图为长方形(形状可能不同),俯视图为三角形。
示意图:
主视图 俯视图 左视图
△
(高×边长) (底面三角形) (高×底高)
幻灯片 5:四棱锥的三视图
立体图形:四棱锥(底面是正方形,侧面是四个等腰三角形,有一个顶点)。
观察与绘制:
底面边长为 a,高为 h。
主视图:从正面看,看到的是一个等腰三角形(底边为 a,高为 h)。
俯视图:从上面看,看到的是一个正方形(与底面全等),正方形中心有一个点(顶点的投影)。
左视图:从左面看,看到的是一个等腰三角形(与主视图全等)。
特征:主视图和左视图为全等的等腰三角形,俯视图为带中心点的正方形。
示意图:
主视图 俯视图 左视图
△ □· △
(等腰三角形) (带点正方形) (等腰三角形)
幻灯片 6:组合体视图 —— 叠加型
示例:一个正方体上方叠放一个圆锥(圆锥底面与正方体顶面中心重合)。
观察与绘制:
主视图:下方是正方形(正方体的主视图),上方是等腰三角形(圆锥的主视图),三角形底边与正方形上边长重合。
俯视图:中间是带点的圆(圆锥的俯视图),外围是正方形(正方体的俯视图),圆的直径小于正方形边长。
左视图:与主视图对称,下方是正方形,上方是等腰三角形。
示意图:
主视图 俯视图 左视图
△ □ △
□ ○· □
幻灯片 7:组合体视图 —— 拼接型
示例:一个圆柱体与一个长方体并排拼接(圆柱体的底面与长方体的侧面相切)。
观察与绘制:
主视图:左侧是长方形(长方体的主视图),右侧是长方形(圆柱体的主视图),两个长方形的高相等,紧密相连。
俯视图:左侧是长方形(长方体的俯视图),右侧是圆(圆柱体的俯视图),圆与长方形的一侧相切。
左视图:是一个长方形(长方体的左视图与圆柱体的左视图叠加,整体为一个长方形)。
示意图:
主视图 俯视图 左视图
○
幻灯片 8:绘制复杂立体图形视图的步骤
分解图形:将复杂立体图形或组合体分解为简单的基本立体图形(如正方体、圆柱、棱锥等)。
分析各部分视图:分别确定每个基本立体图形的三视图形状和位置。
组合视图:根据各部分的相对位置(如叠加、拼接、嵌套等),将各部分的视图组合起来,注意重叠部分的呈现。
检查修正:对照立体图形,检查三视图是否准确反映了各部分的形状和位置关系,修正错误之处。
幻灯片 9:例题 1—— 绘制三棱柱的三视图
题目:已知一个三棱柱的底面是直角三角形,两条直角边分别为 3cm、4cm,三棱柱的高为 5cm,画出它的三视图。
解答过程:
分解图形:该三棱柱由两个直角三角形底面和三个长方形侧面组成。
主视图:从正面看,看到的是一个长方形,长为三棱柱的高 5cm,宽为底面直角三角形的斜边 5cm(根据勾股定理计算)。
俯视图:从上面看,看到的是一个直角三角形(与底面全等),直角边分别为 3cm、4cm。
左视图:从左面看,看到的是一个长方形,长为 5cm,宽为 4cm(底面直角三角形的一条直角边)。
示意图:
主视图 俯视图 左视图
直角△
(5cm×5cm) (3cm×4cm) (5cm×4cm)
幻灯片 10:例题 2—— 绘制组合体的三视图
题目:一个由正方体和四棱锥组成的组合体,正方体棱长为 2cm,四棱锥底面与正方体顶面全等,高为 3cm,画出该组合体的三视图。
解答过程:
分解图形:由棱长 2cm 的正方体和底面为 2cm×2cm 正方形、高 3cm 的四棱锥组成,四棱锥位于正方体上方中心。
主视图:下方是边长 2cm 的正方形(正方体主视图),上方是等腰三角形(四棱锥主视图),三角形底边 2cm,高 3cm,底边与正方形上边长重合。
俯视图:是一个边长 2cm 的正方形(正方体俯视图),正方形中心有一个点(四棱锥顶点的投影)。
左视图:与主视图对称,下方是正方形,上方是等腰三角形。
示意图:
主视图 俯视图 左视图
△ □· △
□ □ □
幻灯片 11:视图中的虚实线初步认识
引入:当立体图形存在被遮挡的部分时,在视图中被遮挡部分的轮廓线需要用虚线表示。
示例:一个正方体前方有一个小正方体(部分遮挡)。
主视图:前方小正方体的轮廓线用实线表示,后方被遮挡的正方体部分轮廓线用虚线表示。
说明:虚实线的使用能更准确地反映立体图形的空间结构,后续会详细学习,此处仅作初步了解。
幻灯片 12:课堂练习 1—— 绘制棱锥的三视图
题目:一个三棱锥的底面是等边三角形(边长为 4cm),高为 3cm,画出它的三视图。
答案:
主视图:等腰三角形(底边 4cm,高 3cm)。
俯视图:等边三角形(边长 4cm),中心有一个点。
左视图:与主视图全等的等腰三角形。
幻灯片 13:课堂练习 2—— 绘制组合体的三视图
题目:两个相同的长方体(长 3cm、宽 2cm、高 1cm)上下叠放(上部长方体的底面中心与下部长方体的顶面中心重合),画出该组合体的三视图。
答案:
主视图:两个上下相连的长方形(长 3cm,宽 1cm),总高 2cm。
俯视图:一个长方形(3cm×2cm)。
左视图:两个上下相连的长方形(长 2cm,宽 1cm),总高 2cm。
幻灯片 14:易错点分析
常见错误:
绘制棱柱、棱锥的俯视图时,忽略底面的形状特征,如将三棱柱的俯视图画成三角形却未体现其是特定三角形(如直角三角形)。
组合体视图中,各部分的位置关系体现错误,如叠加的两个立体图形,视图中未体现上下对齐或左右相切的关系。
对有遮挡的立体图形,不知道用虚线表示被遮挡部分,导致视图不能准确反映立体图形结构。
规避方法:
绘制棱柱、棱锥的视图前,先明确底面的具体形状和尺寸,确保俯视图与底面特征一致。
分析组合体时,用实物模型或画图的方式确定各部分的相对位置,再绘制视图。
初步了解虚实线的作用,遇到有遮挡的情况,尝试用虚线标注被遮挡部分的轮廓。
幻灯片 15:课堂小结
复杂立体图形的三视图:
三棱柱:主视图和左视图为长方形,俯视图为三角形。
四棱锥:主视图和左视图为等腰三角形,俯视图为带点的正方形。
组合体视图绘制:先分解为基本立体图形,再结合位置关系组合视图。
关键:准确把握立体图形的结构特征和各部分的位置关系,是绘制正确视图的前提。
幻灯片 16:布置作业
基础作业:
画出一个五棱柱(底面是正五边形,棱长为 3cm,高为 5cm)的三视图。
观察生活中的一个复杂物品(如带盖子的盒子),尝试画出它的三视图。
提升作业:
一个组合体由一个圆柱体(底面半径 2cm,高 4cm)和一个圆锥体(底面半径 2cm,高 3cm)组成,圆锥体底面与圆柱体顶面重合,画出该组合体的三视图。
思考:一个有遮挡的组合体,如何用虚实线准确表示其视图?
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
情境导入
视图可以看作平行光线下物体的正投影,它是一种特殊的平行投影.
视图
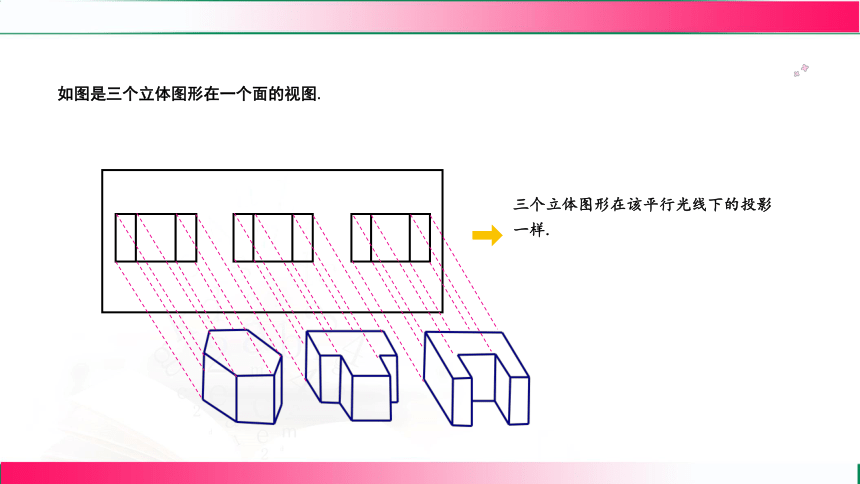
如图是三个立体图形在一个面的视图.
三个立体图形在该平行光线下的投影一样.
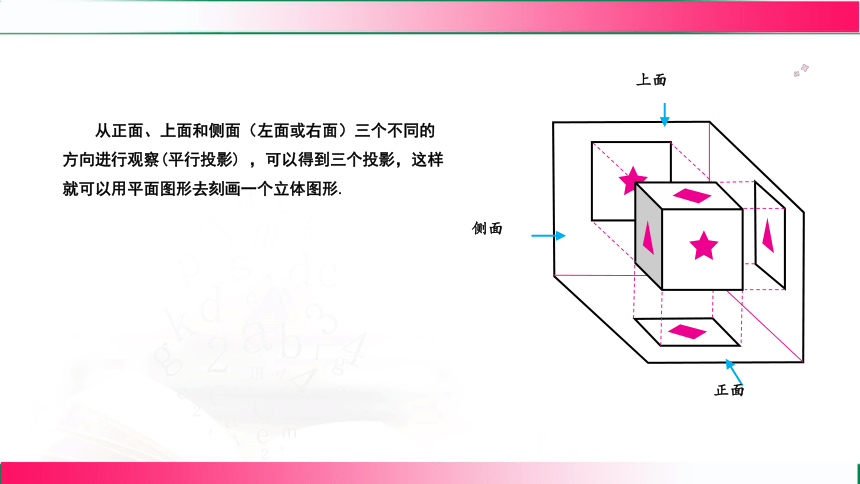
从正面、上面和侧面(左面或右面)三个不同的方向进行观察(平行投影) ,可以得到三个投影,这样就可以用平面图形去刻画一个立体图形.
正面
侧面
上面
正面
侧面
上面
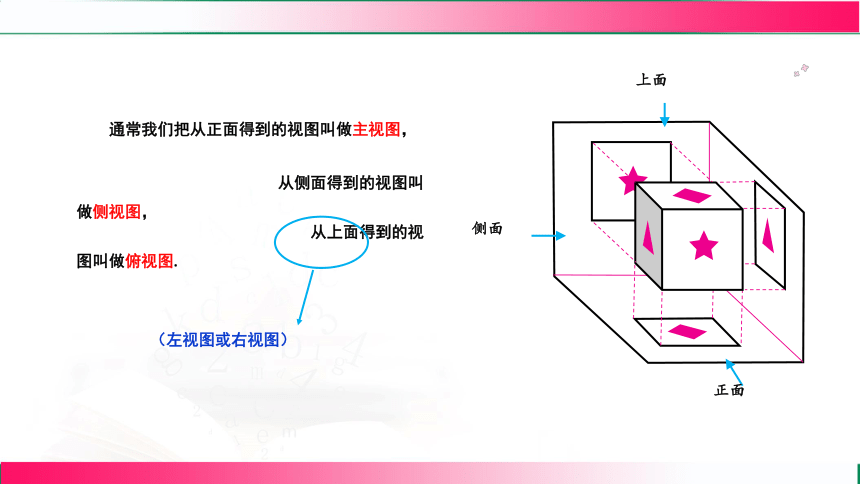
通常我们把从正面得到的视图叫做主视图,
从侧面得到的视图叫做侧视图,
从上面得到的视图叫做俯视图.
(左视图或右视图)
正面
侧面
上面
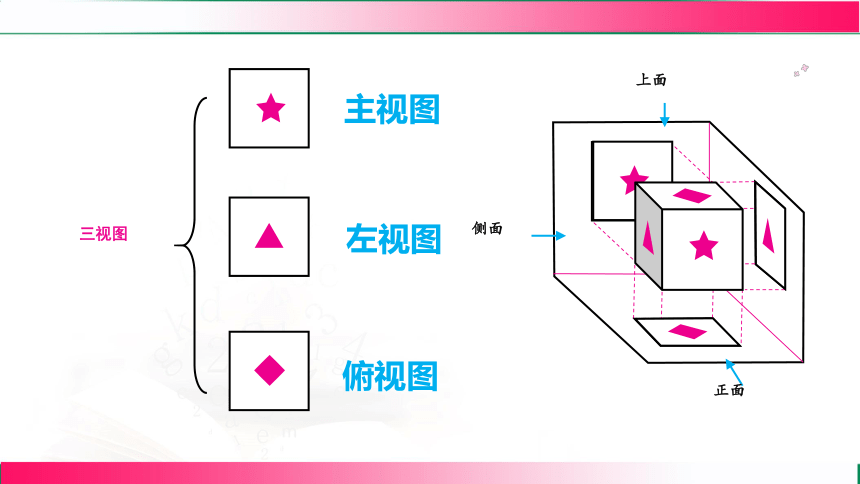
主视图
左视图
俯视图
三视图
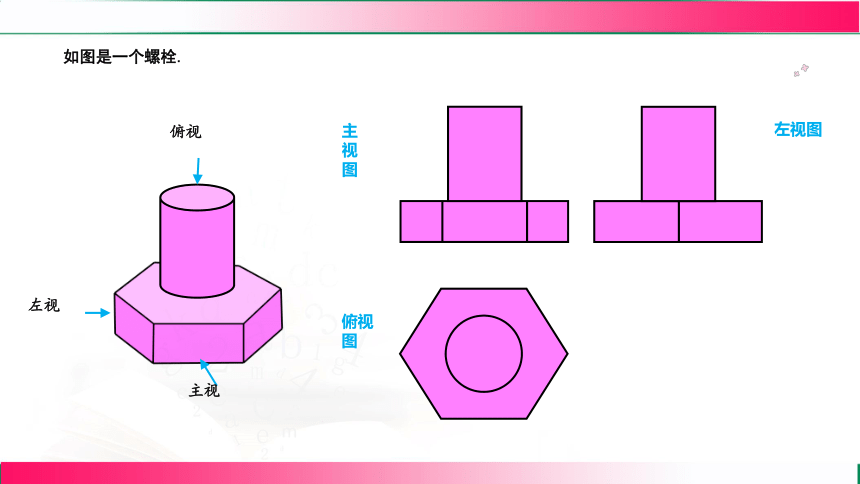
如图是一个螺栓.
主视
主视图
左视图
左视
俯视
俯视图
主视图
左视图
俯视图
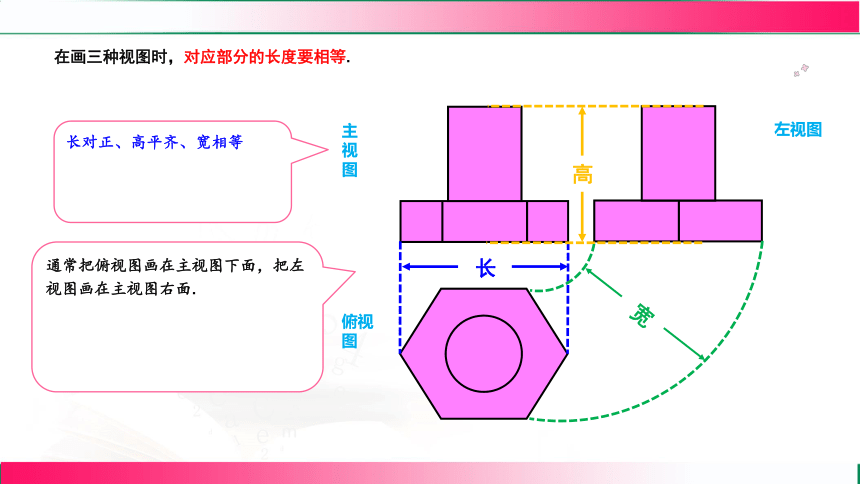
在画三种视图时,对应部分的长度要相等.
长
宽
高
长对正、高平齐、宽相等
通常把俯视图画在主视图下面,把左视图画在主视图右面.
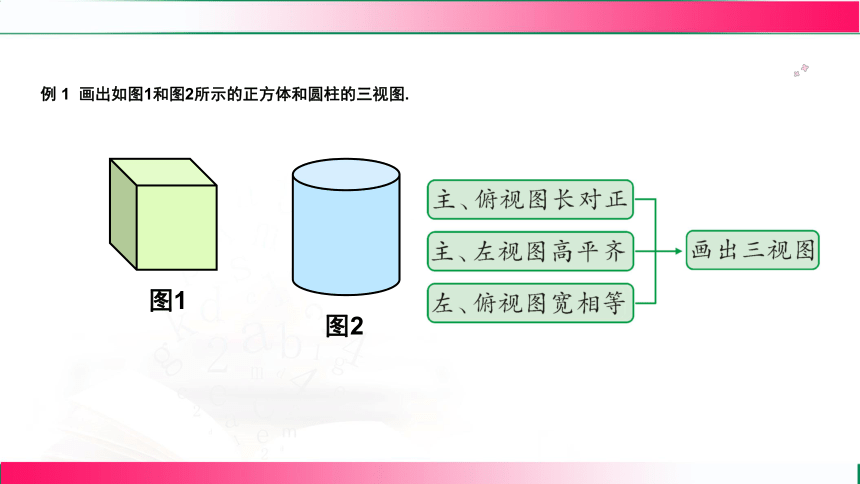
例 1 画出如图1和图2所示的正方体和圆柱的三视图.
图1
图2
主视图
左视图
俯视图
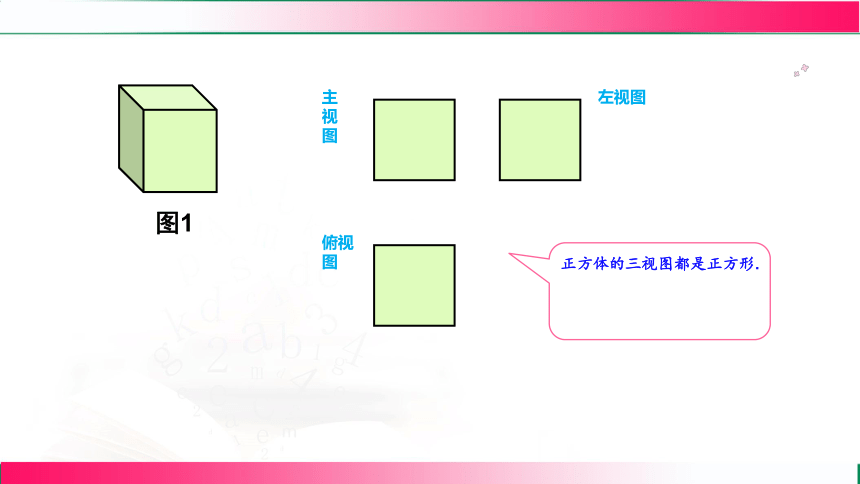
图1
正方体的三视图都是正方形.
主视图
左视图
俯视图
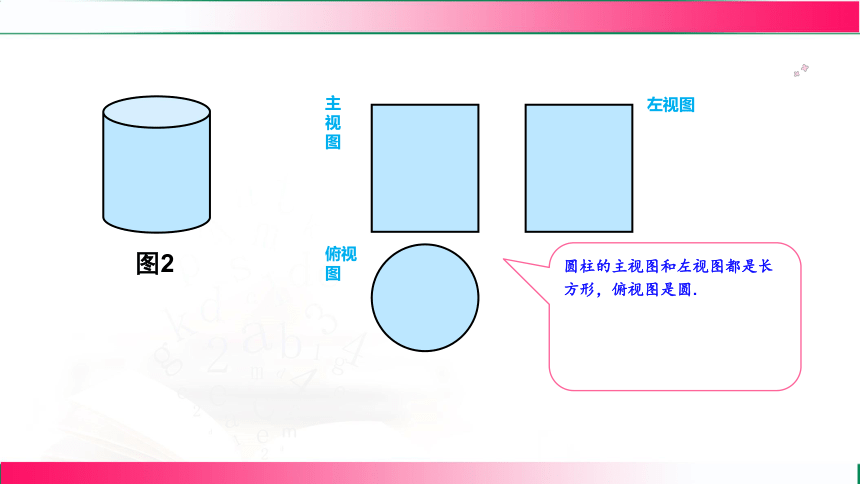
圆柱的主视图和左视图都是长方形,俯视图是圆.
图2
例 2 画出如图所示的圆锥的三视图.
主视图
左视图
俯视图
随堂练习
1. 画出下列立体图形的三视图.
【教材P132 练习 第1题】
主视图
左视图
俯视图
主视图
左视图
俯视图
2. 图中右边是由四个相同的小长方体堆成的物体,试指出左边三个平面图形分别是这个物体的三视图中的哪个视图.
( )
( )
( )
主视图
俯视图
左视图
【教材P132 练习 第2题】
知识点1 简单几何体的视图
(第1题)
1.[2024河南中考]信阳毛尖是中国十大名茶之一,如图
是信阳毛尖茶叶的包装盒,它的主视图为( )
A
A. B. C. D.
返回
(第2题)
2. 中国古代数学著作《九章算术》中,将
两底面是直角三角形,且侧棱垂直于底面的三棱柱称为
“堑堵”.将一个“堑堵”按如图方式摆放,它的左视图为
( )
B
A. B. C. D.
返回
3.[2024吉林中考]葫芦在我国古代被看作吉祥之物.如图是一个工艺葫
芦的示意图,关于它的三视图说法正确的是( )
A
A.主视图与左视图相同
B.主视图与俯视图相同
C.左视图与俯视图相同
D.主视图、左视图与俯视图都相同
返回
4.下列几何体中,其俯视图是四边形的是( )
D
A. B. C. D.
返回
5.如图摆放的几何体中,三视图不可能出现三角形的是( )
C
A. B. C. D.
返回
6.三视图都是同一平面图形的几何体有____、________.(写出两种)
球
正方体
返回
知识点2 简单组合体的视图
7.[2024德州中考]如图所示几何体的左视图为( )
C
A. B. C. D.
返回
8.[2024浙江中考]如图,5个相同正方体搭成的几何体主视图为( )
B
(第8题)
A. B. C. D.
返回
(第9题)
9.[2024东营中考]某几何体的俯视图如图所示,下列几何
体(箭头所示为正面)的俯视图与其相同的是( )
C
A. B. C. D.
返回
10.(4分)[2025晋中期中]请在方格内画出如图所示几何体的三视图.
解:如图所示.
返回
11.打印机是一种可以“打印”出真实物体的设备.如图是 打印的
一个积木模型,它的俯视图是( )
D
(第11题)
A. B. C. D.
返回
12.如图是一个正方体被截去一角后得到的几何体,它的主视图是( )
B
(第12题)
A. B. C. D.
返回
(第13题)
13.如图的几何体由6个大小相同的小正方体搭成,若拿
走其中1个小正方体,则下列说法不正确的是( )
C
A.拿走小正方体①,俯视图不变
B.拿走小正方体④,主视图不变
C.拿走小正方体②,左视图不变
D.拿走小正方体③或⑤,左视图不变
返回
14.[2024威海中考]下列几何体都是由四个大小相同的小正方体搭成
的.其中主视图、左视图和俯视图完全相同的是( )
D
A. B. C. D.
返回
15.如图,用三个大小不等的正方体拼成一个几何体,该几何体的主视
图、左视图和俯视图的面积分别为,,,则,, 的大小
关系是_____________.(用“ ”连接)
(第15题)
返回
16.(8分)如图①所示的组合体,它的下面是一个长方体,上面是一个
圆柱.
(1)图②和图③是它的两个视图,在横线上补全两种
视图的名称(填“主”“左”或“俯”);
左
俯
(2)根据两个视图中的尺寸,计算这个组合体的体积.(结果保留 )
解: .
答:这个组合体的体积是 .
返回
17.(12分)如图是由10个完全相同的棱长为 的小正方体组成的几何体.
(1)依次画出这个几何体的主视图、俯视图和左视图;
解:如图所示.
(2)若在这个几何体上再添加一些相同的小正方体,并保持其俯视图
和左视图不变,最多可以再添加___个小正方体;
4
(3)若在这个几何体的表面(包括底面)喷上黄漆,求这个几何体喷
漆的面积.
解: .
答:这个几何体喷漆的面积为 .
返回
课堂小结
长对正、高平齐、宽相等
主视
主视图
左视图
左视
俯视
俯视图
画三视图时看不见的轮廓线应画成虚线,不能漏掉.
谢谢观看!
3.2.1.2由立体图形到视图
第3章 图形的初步认识
【华东师大版·2024】数学 七年级上册
授课教师:********
班 级:********
时 间:********
幻灯片 1:封面
标题:3.2.1.2 由立体图形到视图
副标题:复杂立体图形的视图探究
幻灯片 2:学习目标
能画出棱柱、棱锥等立体图形的三视图。
掌握简单组合体三视图的绘制方法,能分析组合体各部分对视图的影响。
进一步提升空间想象能力,能根据立体图形的特征准确判断视图形状。
幻灯片 3:复习回顾
三种基本视图:主视图(正面)、俯视图(上面)、左视图(左面)。
简单立体图形的三视图:
正方体:三个全等的正方形。
圆柱:主视图和左视图为长方形,俯视图为圆。
圆锥:主视图和左视图为等腰三角形,俯视图为带点的圆。
球:三个全等的圆。
引入:本节课我们将学习棱柱、棱锥及组合体的三视图绘制。
幻灯片 4:三棱柱的三视图
立体图形:三棱柱(两个底面是全等的三角形,侧面是三个长方形)。
观察与绘制:
底面为等边三角形,棱长为 a,高为 h。
主视图:从正面看,看到的是一个长方形(长为 h,宽为底面三角形的边长 a)。
俯视图:从上面看,看到的是一个三角形(与底面三角形全等)。
左视图:从左面看,看到的是一个长方形(长为 h,宽为底面三角形的高)。
特征:主视图和左视图为长方形(形状可能不同),俯视图为三角形。
示意图:
主视图 俯视图 左视图
△
(高×边长) (底面三角形) (高×底高)
幻灯片 5:四棱锥的三视图
立体图形:四棱锥(底面是正方形,侧面是四个等腰三角形,有一个顶点)。
观察与绘制:
底面边长为 a,高为 h。
主视图:从正面看,看到的是一个等腰三角形(底边为 a,高为 h)。
俯视图:从上面看,看到的是一个正方形(与底面全等),正方形中心有一个点(顶点的投影)。
左视图:从左面看,看到的是一个等腰三角形(与主视图全等)。
特征:主视图和左视图为全等的等腰三角形,俯视图为带中心点的正方形。
示意图:
主视图 俯视图 左视图
△ □· △
(等腰三角形) (带点正方形) (等腰三角形)
幻灯片 6:组合体视图 —— 叠加型
示例:一个正方体上方叠放一个圆锥(圆锥底面与正方体顶面中心重合)。
观察与绘制:
主视图:下方是正方形(正方体的主视图),上方是等腰三角形(圆锥的主视图),三角形底边与正方形上边长重合。
俯视图:中间是带点的圆(圆锥的俯视图),外围是正方形(正方体的俯视图),圆的直径小于正方形边长。
左视图:与主视图对称,下方是正方形,上方是等腰三角形。
示意图:
主视图 俯视图 左视图
△ □ △
□ ○· □
幻灯片 7:组合体视图 —— 拼接型
示例:一个圆柱体与一个长方体并排拼接(圆柱体的底面与长方体的侧面相切)。
观察与绘制:
主视图:左侧是长方形(长方体的主视图),右侧是长方形(圆柱体的主视图),两个长方形的高相等,紧密相连。
俯视图:左侧是长方形(长方体的俯视图),右侧是圆(圆柱体的俯视图),圆与长方形的一侧相切。
左视图:是一个长方形(长方体的左视图与圆柱体的左视图叠加,整体为一个长方形)。
示意图:
主视图 俯视图 左视图
○
幻灯片 8:绘制复杂立体图形视图的步骤
分解图形:将复杂立体图形或组合体分解为简单的基本立体图形(如正方体、圆柱、棱锥等)。
分析各部分视图:分别确定每个基本立体图形的三视图形状和位置。
组合视图:根据各部分的相对位置(如叠加、拼接、嵌套等),将各部分的视图组合起来,注意重叠部分的呈现。
检查修正:对照立体图形,检查三视图是否准确反映了各部分的形状和位置关系,修正错误之处。
幻灯片 9:例题 1—— 绘制三棱柱的三视图
题目:已知一个三棱柱的底面是直角三角形,两条直角边分别为 3cm、4cm,三棱柱的高为 5cm,画出它的三视图。
解答过程:
分解图形:该三棱柱由两个直角三角形底面和三个长方形侧面组成。
主视图:从正面看,看到的是一个长方形,长为三棱柱的高 5cm,宽为底面直角三角形的斜边 5cm(根据勾股定理计算)。
俯视图:从上面看,看到的是一个直角三角形(与底面全等),直角边分别为 3cm、4cm。
左视图:从左面看,看到的是一个长方形,长为 5cm,宽为 4cm(底面直角三角形的一条直角边)。
示意图:
主视图 俯视图 左视图
直角△
(5cm×5cm) (3cm×4cm) (5cm×4cm)
幻灯片 10:例题 2—— 绘制组合体的三视图
题目:一个由正方体和四棱锥组成的组合体,正方体棱长为 2cm,四棱锥底面与正方体顶面全等,高为 3cm,画出该组合体的三视图。
解答过程:
分解图形:由棱长 2cm 的正方体和底面为 2cm×2cm 正方形、高 3cm 的四棱锥组成,四棱锥位于正方体上方中心。
主视图:下方是边长 2cm 的正方形(正方体主视图),上方是等腰三角形(四棱锥主视图),三角形底边 2cm,高 3cm,底边与正方形上边长重合。
俯视图:是一个边长 2cm 的正方形(正方体俯视图),正方形中心有一个点(四棱锥顶点的投影)。
左视图:与主视图对称,下方是正方形,上方是等腰三角形。
示意图:
主视图 俯视图 左视图
△ □· △
□ □ □
幻灯片 11:视图中的虚实线初步认识
引入:当立体图形存在被遮挡的部分时,在视图中被遮挡部分的轮廓线需要用虚线表示。
示例:一个正方体前方有一个小正方体(部分遮挡)。
主视图:前方小正方体的轮廓线用实线表示,后方被遮挡的正方体部分轮廓线用虚线表示。
说明:虚实线的使用能更准确地反映立体图形的空间结构,后续会详细学习,此处仅作初步了解。
幻灯片 12:课堂练习 1—— 绘制棱锥的三视图
题目:一个三棱锥的底面是等边三角形(边长为 4cm),高为 3cm,画出它的三视图。
答案:
主视图:等腰三角形(底边 4cm,高 3cm)。
俯视图:等边三角形(边长 4cm),中心有一个点。
左视图:与主视图全等的等腰三角形。
幻灯片 13:课堂练习 2—— 绘制组合体的三视图
题目:两个相同的长方体(长 3cm、宽 2cm、高 1cm)上下叠放(上部长方体的底面中心与下部长方体的顶面中心重合),画出该组合体的三视图。
答案:
主视图:两个上下相连的长方形(长 3cm,宽 1cm),总高 2cm。
俯视图:一个长方形(3cm×2cm)。
左视图:两个上下相连的长方形(长 2cm,宽 1cm),总高 2cm。
幻灯片 14:易错点分析
常见错误:
绘制棱柱、棱锥的俯视图时,忽略底面的形状特征,如将三棱柱的俯视图画成三角形却未体现其是特定三角形(如直角三角形)。
组合体视图中,各部分的位置关系体现错误,如叠加的两个立体图形,视图中未体现上下对齐或左右相切的关系。
对有遮挡的立体图形,不知道用虚线表示被遮挡部分,导致视图不能准确反映立体图形结构。
规避方法:
绘制棱柱、棱锥的视图前,先明确底面的具体形状和尺寸,确保俯视图与底面特征一致。
分析组合体时,用实物模型或画图的方式确定各部分的相对位置,再绘制视图。
初步了解虚实线的作用,遇到有遮挡的情况,尝试用虚线标注被遮挡部分的轮廓。
幻灯片 15:课堂小结
复杂立体图形的三视图:
三棱柱:主视图和左视图为长方形,俯视图为三角形。
四棱锥:主视图和左视图为等腰三角形,俯视图为带点的正方形。
组合体视图绘制:先分解为基本立体图形,再结合位置关系组合视图。
关键:准确把握立体图形的结构特征和各部分的位置关系,是绘制正确视图的前提。
幻灯片 16:布置作业
基础作业:
画出一个五棱柱(底面是正五边形,棱长为 3cm,高为 5cm)的三视图。
观察生活中的一个复杂物品(如带盖子的盒子),尝试画出它的三视图。
提升作业:
一个组合体由一个圆柱体(底面半径 2cm,高 4cm)和一个圆锥体(底面半径 2cm,高 3cm)组成,圆锥体底面与圆柱体顶面重合,画出该组合体的三视图。
思考:一个有遮挡的组合体,如何用虚实线准确表示其视图?
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
情境导入
视图可以看作平行光线下物体的正投影,它是一种特殊的平行投影.
视图
如图是三个立体图形在一个面的视图.
三个立体图形在该平行光线下的投影一样.
从正面、上面和侧面(左面或右面)三个不同的方向进行观察(平行投影) ,可以得到三个投影,这样就可以用平面图形去刻画一个立体图形.
正面
侧面
上面
正面
侧面
上面
通常我们把从正面得到的视图叫做主视图,
从侧面得到的视图叫做侧视图,
从上面得到的视图叫做俯视图.
(左视图或右视图)
正面
侧面
上面
主视图
左视图
俯视图
三视图
如图是一个螺栓.
主视
主视图
左视图
左视
俯视
俯视图
主视图
左视图
俯视图
在画三种视图时,对应部分的长度要相等.
长
宽
高
长对正、高平齐、宽相等
通常把俯视图画在主视图下面,把左视图画在主视图右面.
例 1 画出如图1和图2所示的正方体和圆柱的三视图.
图1
图2
主视图
左视图
俯视图
图1
正方体的三视图都是正方形.
主视图
左视图
俯视图
圆柱的主视图和左视图都是长方形,俯视图是圆.
图2
例 2 画出如图所示的圆锥的三视图.
主视图
左视图
俯视图
随堂练习
1. 画出下列立体图形的三视图.
【教材P132 练习 第1题】
主视图
左视图
俯视图
主视图
左视图
俯视图
2. 图中右边是由四个相同的小长方体堆成的物体,试指出左边三个平面图形分别是这个物体的三视图中的哪个视图.
( )
( )
( )
主视图
俯视图
左视图
【教材P132 练习 第2题】
知识点1 简单几何体的视图
(第1题)
1.[2024河南中考]信阳毛尖是中国十大名茶之一,如图
是信阳毛尖茶叶的包装盒,它的主视图为( )
A
A. B. C. D.
返回
(第2题)
2. 中国古代数学著作《九章算术》中,将
两底面是直角三角形,且侧棱垂直于底面的三棱柱称为
“堑堵”.将一个“堑堵”按如图方式摆放,它的左视图为
( )
B
A. B. C. D.
返回
3.[2024吉林中考]葫芦在我国古代被看作吉祥之物.如图是一个工艺葫
芦的示意图,关于它的三视图说法正确的是( )
A
A.主视图与左视图相同
B.主视图与俯视图相同
C.左视图与俯视图相同
D.主视图、左视图与俯视图都相同
返回
4.下列几何体中,其俯视图是四边形的是( )
D
A. B. C. D.
返回
5.如图摆放的几何体中,三视图不可能出现三角形的是( )
C
A. B. C. D.
返回
6.三视图都是同一平面图形的几何体有____、________.(写出两种)
球
正方体
返回
知识点2 简单组合体的视图
7.[2024德州中考]如图所示几何体的左视图为( )
C
A. B. C. D.
返回
8.[2024浙江中考]如图,5个相同正方体搭成的几何体主视图为( )
B
(第8题)
A. B. C. D.
返回
(第9题)
9.[2024东营中考]某几何体的俯视图如图所示,下列几何
体(箭头所示为正面)的俯视图与其相同的是( )
C
A. B. C. D.
返回
10.(4分)[2025晋中期中]请在方格内画出如图所示几何体的三视图.
解:如图所示.
返回
11.打印机是一种可以“打印”出真实物体的设备.如图是 打印的
一个积木模型,它的俯视图是( )
D
(第11题)
A. B. C. D.
返回
12.如图是一个正方体被截去一角后得到的几何体,它的主视图是( )
B
(第12题)
A. B. C. D.
返回
(第13题)
13.如图的几何体由6个大小相同的小正方体搭成,若拿
走其中1个小正方体,则下列说法不正确的是( )
C
A.拿走小正方体①,俯视图不变
B.拿走小正方体④,主视图不变
C.拿走小正方体②,左视图不变
D.拿走小正方体③或⑤,左视图不变
返回
14.[2024威海中考]下列几何体都是由四个大小相同的小正方体搭成
的.其中主视图、左视图和俯视图完全相同的是( )
D
A. B. C. D.
返回
15.如图,用三个大小不等的正方体拼成一个几何体,该几何体的主视
图、左视图和俯视图的面积分别为,,,则,, 的大小
关系是_____________.(用“ ”连接)
(第15题)
返回
16.(8分)如图①所示的组合体,它的下面是一个长方体,上面是一个
圆柱.
(1)图②和图③是它的两个视图,在横线上补全两种
视图的名称(填“主”“左”或“俯”);
左
俯
(2)根据两个视图中的尺寸,计算这个组合体的体积.(结果保留 )
解: .
答:这个组合体的体积是 .
返回
17.(12分)如图是由10个完全相同的棱长为 的小正方体组成的几何体.
(1)依次画出这个几何体的主视图、俯视图和左视图;
解:如图所示.
(2)若在这个几何体上再添加一些相同的小正方体,并保持其俯视图
和左视图不变,最多可以再添加___个小正方体;
4
(3)若在这个几何体的表面(包括底面)喷上黄漆,求这个几何体喷
漆的面积.
解: .
答:这个几何体喷漆的面积为 .
返回
课堂小结
长对正、高平齐、宽相等
主视
主视图
左视图
左视
俯视
俯视图
画三视图时看不见的轮廓线应画成虚线,不能漏掉.
谢谢观看!
同课章节目录
