3.2.2 由视图到立体图形 课件(共39张PPT)
文档属性
| 名称 | 3.2.2 由视图到立体图形 课件(共39张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 05:22:23 | ||
图片预览




文档简介
(共39张PPT)
3.2.2 由视图到立体图形
第3章 图形的初步认识
【华东师大版·2024】数学 七年级上册
授课教师:********
班 级:********
时 间:********
幻灯片 1:封面
标题:3.2.2 由视图**:从平面图形还原三维结构
幻灯片 2:学习目标
理解由三视图还原立体图形的原理,知道三视图与立体图形的对应关系。
能根据正方体、长方体、圆柱、圆锥、球等简单立体图形的三视图,还原出相应的立体图形。
掌握由三视图还原简单组合体的基本方法,提升空间想象能力和逆向思维能力。
幻灯片 3:情境引入 —— 视图的 “逆向工程”
展示图片:一个机械零件的三视图(主视图、俯视图、左视图)。
提问:工程师拿到这样的三视图,如何知道这个零件的立体形状?
引入:由视图还原立体图形,是从平面图形到立体图形的逆向过程,需要我们结合三视图的特征,想象立体图形的形状。本节课我们就来学习如何由视图得到立体图形。
幻灯片 4:由三视图还原立体图形的原理
对应关系:
主视图反映立体图形的正面形状和高度、长度。
俯视图反映立体图形的上面形状和长度、宽度。
左视图反映立体图形的左面形状和高度、宽度。
关键原则:
“长对正”:主视图和俯视图的长度相等,且左右对齐。
“高平齐”:主视图和左视图的高度相等,且上下对齐。
“宽相等”:俯视图和左视图的宽度相等,且前后对应。
示例:一个长方体的三视图都是长方形,主视图的长和高、俯视图的长和宽、左视图的高和宽分别对应长方体的长、宽、高,根据这三个视图的尺寸可确定长方体的形状。
幻灯片 5:由简单视图还原基本立体图形
球:
三视图特征:三个全等的圆。
还原方法:若三视图都是大小相同的圆,则对应的立体图形一定是球。
示意图:三个等大的○→球。
正方体:
三视图特征:三个全等的正方形。
还原方法:三视图都是相同的正方形,说明立体图形各棱长相等,是正方体。
示意图:三个等大的□→正方体。
圆柱:
三视图特征:主视图和左视图是全等的长方形,俯视图是圆。
还原方法:根据长方形的长(圆柱的高)和宽(底面直径)、圆的直径,可确定圆柱的形状和尺寸。
示意图:两个全等的 和一个○→圆柱。
圆锥:
三视图特征:主视图和左视图是全等的等腰三角形,俯视图是带中心点的圆。
还原方法:等腰三角形的底边(底面直径)和高(圆锥的高)、圆的直径(与底边相等)共同确定圆锥的形状。
示意图:两个全等的△和一个带点的○→圆锥。
幻灯片 6:由三视图还原棱柱
三棱柱:
三视图特征:主视图和左视图是长方形(可能不同),俯视图是三角形。
还原方法:
由俯视图的三角形确定底面是三角形(如直角三角形、等边三角形)。
由主视图和左视图的长方形的高度确定三棱柱的高,长方形的宽度对应底面三角形的相关边长(如边长、高)。
示例:俯视图是直角三角形(直角边 3cm、4cm),主视图是长 5cm、宽 5cm 的长方形,左视图是长 5cm、宽 4cm 的长方形→还原为底面是直角三角形(直角边 3cm、4cm)、高 5cm 的三棱柱。
四棱柱(长方体):
三视图特征:三个长方形(可能有正方形)。
还原方法:根据三个长方形的长、宽、高,确定长方体的长、宽、高(主视图的长 = 俯视图的长,主视图的高 = 左视图的高,俯视图的宽 = 左视图的宽)。
示例:主视图 3cm×2cm,俯视图 3cm×1cm,左视图 2cm×1cm→还原为长 3cm、宽 1cm、高 2cm 的长方体。
幻灯片 7:由三视图还原棱锥
四棱锥:
三视图特征:主视图和左视图是全等的等腰三角形,俯视图是带中心点的正方形。
还原方法:
由俯视图的正方形确定底面是正方形,中心点是顶点的投影。
由等腰三角形的底边(正方形的边长)和高(四棱锥的高)确定棱锥的形状。
示例:俯视图是边长 2cm 的正方形(带中心点),主视图和左视图是底边 2cm、高 3cm 的等腰三角形→还原为底面边长 2cm、高 3cm 的四棱锥。
三棱锥:
三视图特征:主视图和左视图是等腰三角形(可能不同),俯视图是带中心点的三角形。
还原方法:结合俯视图的三角形形状和主、左视图等腰三角形的尺寸,确定三棱锥的底面和高。
示例:俯视图是等边三角形(边长 4cm,带中心点),主视图和左视图是底边 4cm、高 3cm 的等腰三角形→还原为底面是等边三角形(边长 4cm)、高 3cm 的三棱锥。
幻灯片 8:由组合视图还原组合体
步骤:
分别分析主视图、俯视图、左视图,确定组合体由哪些基本立体图形组成。
根据三视图的位置关系,确定各基本立体图形的相对位置(如叠加、拼接、嵌套等)。
综合三个视图的信息,想象并还原组合体的整体形状。
示例 1:叠加型组合体:
三视图特征:主视图下方是正方形,上方是等腰三角形;俯视图是带点的圆和外围正方形;左视图与主视图对称。
还原过程:
主视图下方正方形和俯视图外围正方形对应正方体。
主视图上方等腰三角形和俯视图中间带点的圆对应圆锥。
结合位置关系(上方、中心重合)→ 正方体上方叠放圆锥的组合体。
示例 2:拼接型组合体:
三视图特征:主视图是两个相连的长方形;俯视图是长方形和旁边的圆;左视图是一个长方形。
还原过程:
主视图左侧长方形、俯视图左侧长方形对应长方体。
主视图右侧长方形、俯视图右侧圆对应圆柱。
结合位置关系(并排、侧面相切)→ 长方体与圆柱并排拼接的组合体。
幻灯片 9:例题 1—— 由三视图还原基本立体图形
题目:已知一个立体图形的三视图如下:主视图是长方形,俯视图是圆,左视图是长方形,且主视图和左视图全等。这个立体图形是什么?
解答过程:
主视图和左视图是全等的长方形,俯视图是圆,符合圆柱的三视图特征。
因为主视图和左视图全等,说明圆柱的高等于底面直径(特殊圆柱)。
结论:这个立体图形是圆柱(高等于底面直径)。
幻灯片 10:例题 2—— 由三视图还原组合体
题目:一个立体图形的三视图如下:主视图是下方正方形、上方等腰三角形;俯视图是正方形(中心有一点);左视图与主视图相同。这个组合体由哪些立体图形组成?
解答过程:
主视图下方正方形和俯视图正方形对应正方体(或长方体)。
主视图上方等腰三角形和俯视图中心的点对应四棱锥(底面与正方体顶面全等)。
结合位置关系(四棱锥在正方体上方,底面重合)。
结论:由正方体和四棱锥组成,四棱锥位于正方体上方。
幻灯片 11:例题 3—— 根据视图还原并判断尺寸
题目:一个立体图形的三视图中,主视图是长 5cm、宽 3cm 的长方形,俯视图是长 5cm、宽 2cm 的长方形,左视图是长 3cm、宽 2cm 的长方形。这个立体图形是什么?它的长、宽、高分别是多少?
解答过程:
三视图都是长方形,符合长方体的三视图特征。
根据 “长对正、高平齐、宽相等”:
长 = 主视图的长 = 俯视图的长 = 5cm。
高 = 主视图的宽 = 左视图的长 = 3cm。
宽 = 俯视图的宽 = 左视图的宽 = 2cm。
结论:这个立体图形是长方体,长、宽、高分别是 5cm、2cm、3cm。
幻灯片 12:课堂练习 1—— 由三视图还原立体图形
题目:说出下列三视图对应的立体图形名称:
(1)三视图都是圆→(球)
(2)三视图都是正方形→(正方体)
(3)主视图和左视图是等腰三角形,俯视图是带点的正方形→(四棱锥)
(4)主视图是长方形,俯视图是三角形,左视图是长方形→(三棱柱)
幻灯片 13:课堂练习 2—— 由组合视图还原组合体
题目:一个立体图形的三视图如下:主视图是正方形上方有一个三角形;俯视图是正方形内有一个圆(圆在正方形中心);左视图与主视图相同。这个组合体是什么?
答案:正方体上方叠放一个圆锥(圆锥底面与正方体顶面中心重合,且圆锥底面直径等于正方体棱长)。
幻灯片 14:课堂练习 3—— 根据视图判断尺寸
题目:一个圆锥的三视图中,主视图是等腰三角形,底边为 6cm,高为 4cm。这个圆锥的底面半径和高分别是多少?
答案:底面半径是 3cm(底边 6cm 为直径),高是 4cm(与主视图的高一致)。
幻灯片 15:易错点分析
常见错误:
仅根据一个视图就确定立体图形的形状,如看到主视图是三角形就认为是圆锥,忽略俯视图是否为圆(也可能是棱锥)。
还原组合体时,无法正确判断各部分的相对位置,如将叠加的组合体还原成拼接的,或位置偏移。
忽略 “长对正、高平齐、宽相等” 的原则,导致还原的立体图形尺寸与视图不符,如长方体的长、宽、高对应错误。
规避方法:
还原立体图形时,必须结合三个视图的特征综合判断,不能仅凭一个视图下结论,如三角形主视图可能对应圆锥或棱锥,需结合俯视图(圆对应圆锥,多边形对应棱锥)。
分析组合体的三视图时,用 “分部分、找对应” 的方法,先确定各部分对应的基本立体图形,再根据视图的对齐关系确定位置。
牢记 “长对正、高平齐、宽相等” 的原则,在还原立体图形时,对照三视图的尺寸,确保长、宽、高对应正确。
幻灯片 16:课堂小结
由视图到立体图形的过程:结合三视图的特征,利用 “长对正、高平齐、宽相等” 的原则,想象并还原立体图形。
基本立体图形的还原:根据球、正方体、圆柱、圆锥、棱柱、棱锥的三视图特征直接还原。
组合体的还原:先分解视图为基本部分,确定对应基本立体图形,再结合位置关系还原整体。
核心能力:空间想象能力是关键,通过多观察、多练习,逐步提高由平面图形想象立体图形的能力。
幻灯片 17:布置作业
基础作业:
教材课后练习题第 1、2 题(根据三视图说出立体图形名称,还原简单立体图形)。
一个立体图形的三视图都是正方形,它是什么立体图形?棱长为 5cm 时,画出它的三视图。
提升作业:
已知一个组合体的三视图:主视图是两个上下相连的正方形;俯视图是两个左右相连的正方形;左视图是两个上下相连的正方形。这个组合体是什么?画出它的立体图形草图。
观察一个常见物品(如墨水瓶),画出它的三视图,再根据三视图向家人描述这个物品的形状。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
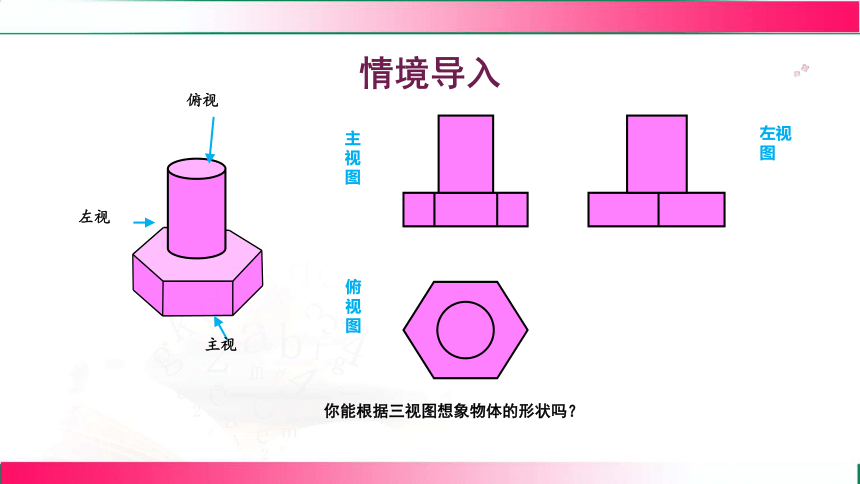
情境导入
你能根据三视图想象物体的形状吗?
主视
主视图
左视图
左视
俯视
俯视图
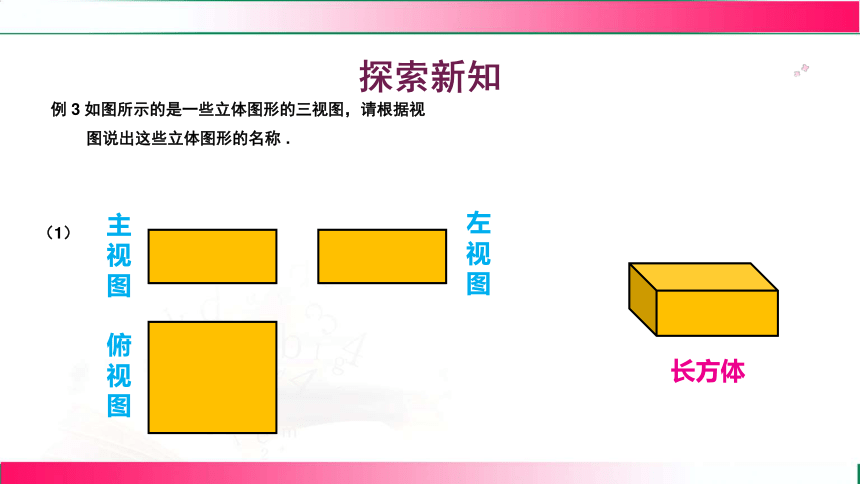
探索新知
例 3 如图所示的是一些立体图形的三视图,请根据视
图说出这些立体图形的名称 .
主视图
左视图
俯视图
长方体
(1)
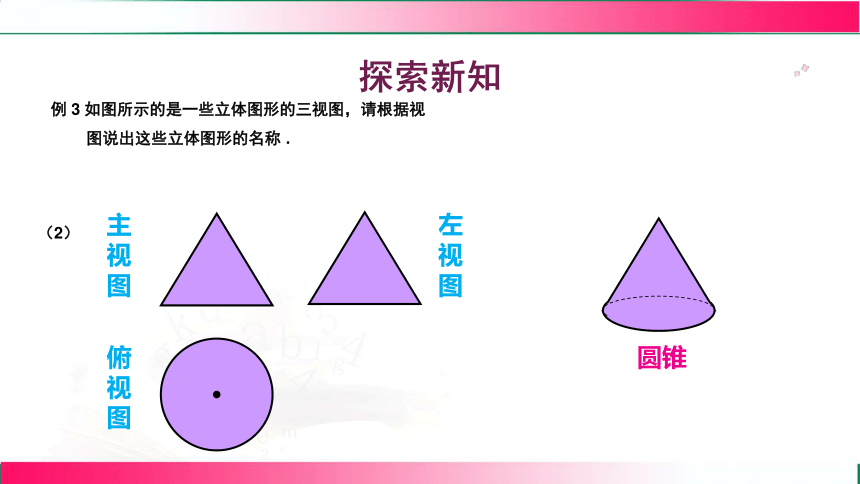
探索新知
圆锥
(2)
主视图
左视图
俯视图
例 3 如图所示的是一些立体图形的三视图,请根据视
图说出这些立体图形的名称 .
由三视图描述几何体(或实物原型),一般先根据各视图想象从各个方向看到的几何体形状,然后综合起来确定几何体(或实物原型)的形状,再根据三视图“长对正、高平齐、宽相等”的关系,确定轮廓线的位置,以及各个方向的尺寸.
确定立体图形
根据主视图可以想象原物体的正面
根据左视图可以想象原物体的左侧面
根据俯视图可以想象原物体的上面
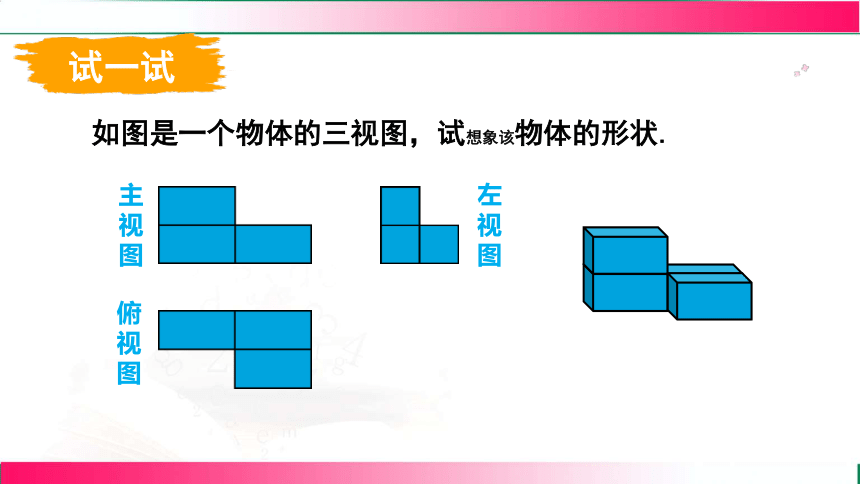
试一试
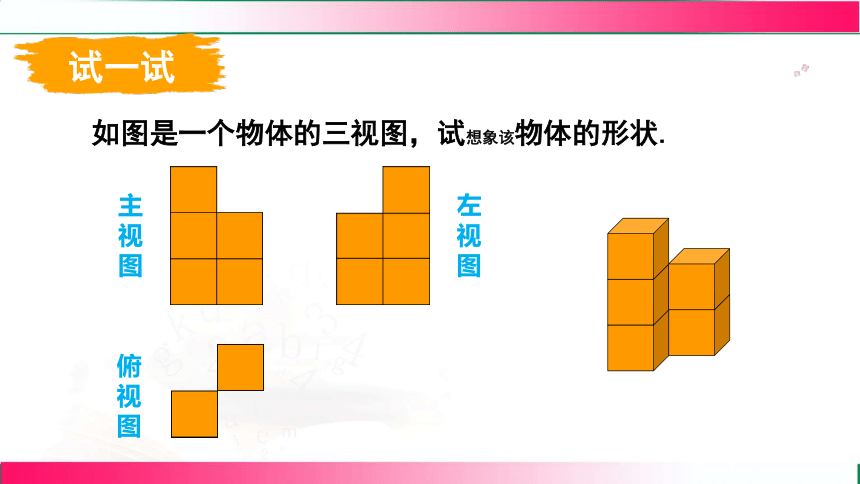
如图是一个物体的三视图,试想象该物体的形状.
主视图
左视图
俯视图
试一试
主视图
左视图
俯视图
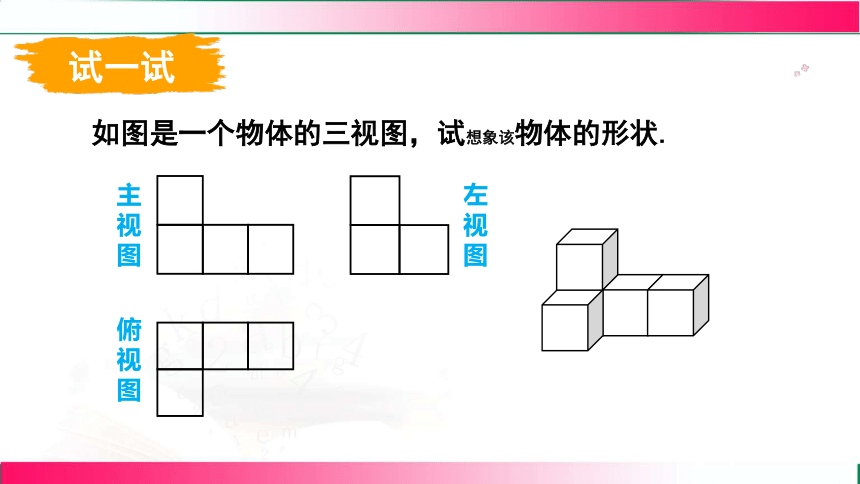
如图是一个物体的三视图,试想象该物体的形状.
试一试
主视图
左视图
俯视图
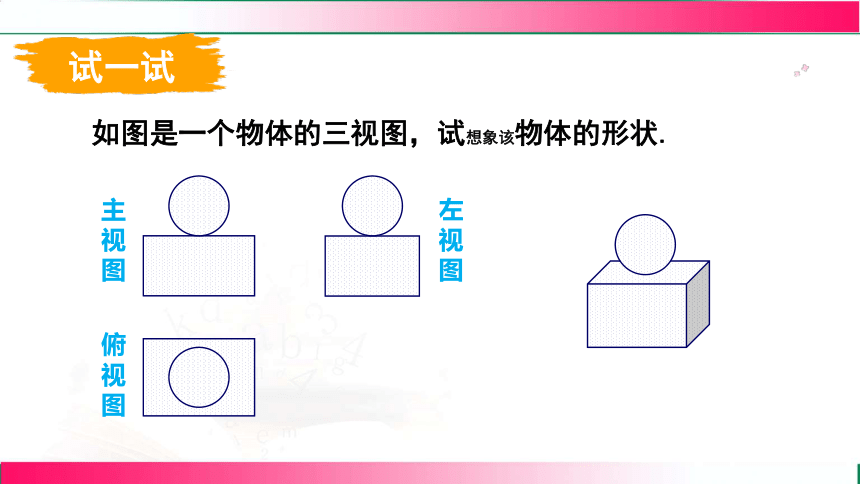
如图是一个物体的三视图,试想象该物体的形状.
试一试
主视图
左视图
俯视图
如图是一个物体的三视图,试想象该物体的形状.
3
2
1
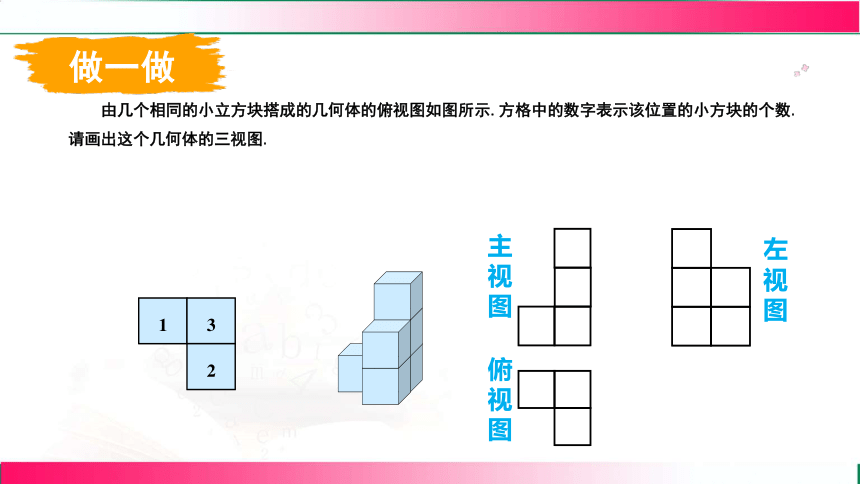
做一做
由几个相同的小立方块搭成的几何体的俯视图如图所示.方格中的数字表示该位置的小方块的个数.请画出这个几何体的三视图.
主视图
左视图
俯视图
在一个仓库里堆积着正方体的货箱若干,要搬运这些箱子很困难,可是仓库管理员要落实一下箱子的数量,于是就想出一个办法:将这堆货物的三种视图画了出来,你能根据三视图,帮他清点一下数量吗?
主视图
左视图
俯视图
1
1
1
2
2
1
8个
用小立方块搭一个几何体,使得它的主视图,俯视图如图所示,这样的几何体只有一种吗?它最少有多少个小立方块?最多需要多少个立方块?摆一摆,试一试.
主视图
俯视图
2
3
1
1
1
最少8个
2
3
3
1
1
最多10个
随堂练习
1. 如图是一个立体图形的三视图,请说出这个立体图形的名称,并画出它的大致形状.
主视图
左视图
俯视图
【教材P134 练习 第1题】
长方体
2. 试说出几个俯视图为一个圆的物体 .
【教材P134 练习 第2题】
球
竖立的圆柱
知识点1 由三视图确定简单的几何体
1.[2024南通中考]如图是一个几何体的三视图,该几何体是( )
D
(第1题)
A.球 B.棱柱 C.圆柱 D.圆锥
返回
2.一个立体图形的三视图如图所示,该立体图形是( )
B
(第2题)
A.三棱锥 B.三棱柱 C.四棱柱 D.四棱锥
返回
3.一个几何体的主视图、左视图、俯视图都是长方形,这个几何体可能
是( )
A
A.长方体 B.四棱锥 C.三棱锥 D.圆柱
返回
(第4题)
4.如图是某物体对应几何体的三视图,则最符合该三视
图的物体应是( )
C
A. B. C. D.
返回
5.(4分)[教材P练习T 变式]某几何体的主视图、左视图和俯视
图分别如图所示,求该几何体的表面积.
解:由三视图可知,该几何体是一个圆柱,且圆柱的底面直径为2,高
为3,
所以 .
返回
知识点2 由三视图确定简单的组合体
6.某几何体的三视图如图所示,该几何体是( )
A
(第6题)
A. B. C. D.
返回
(第7题)
7.如图是由一些完全相同的小正方体搭成的几何体的
三视图.这个几何体是( )
A
A. B. C. D.
返回
8.[2024安徽中考]某几何体的三视图如图所示,则该几何体为( )
D
A. B. C. D.
返回
9.(8分)[教材 “试一试”变式]如图是由若干个相同的小正方体组
成的一个立体图形的三视图.
(1)该立体图形共有___层;
2
(2)该立体图形中共有多少个小正方体?
解:综合三个视图可知,从下到上第1层有4个小正方体,第2层有1个小
正方体,所以立体图形中小正方体共有 (个).
返回
10.一个几何体的主视图和左视图如图所示,则这个几何体是( )
C
(第10题)
A. B. C. D.
返回
11.如图是一个几何体的左视图和俯视图,则该几何体是( )
B
(第11题)
A. B. C. D.
返回
12.在一张桌子上摆放着一些形状、大小都相同的碟子,从3个方向看到
的图形如图所示,则这个桌子上的碟子总个数是( )
B
A.11 B.12 C.13 D.14
返回
13.如图①,一个平台上已经放了三个棱长为1的正方体,要得到一个几
何体,其主视图和左视图如图②所示,平台上至少还需再放___个这样
的正方体.
2
返回
14.(8分)[2025洛阳期末]由若干大小相同的小正方体搭成的几何体
的俯视图如图,正方形中的数字表示在该位置的小正方体个数.
(1)在方格中画出该几何体的主视图和左视图;
解:如图所示.
(2)若拿掉部分小正方体,但保持左视图和俯视图不变,最多可拿掉
___个小正方体.
3
[解析] 点拨:若使得其左视图和俯视图保持不变,则可以拿走第一列的
3个小正方体或者第二列最后面的3个小正方体.
返回
15.(8分)[2025郑州期末]一个几何体的三视图如图所示.
(1)请描述这个几何体的形状;
解:该几何体的上半部分是半圆柱,下半部分是圆柱.(描述准确即可)
(2)计算这个几何体的体积.
解:这个几何体的体积是
.
返回
16.(12分) 用多个相同的小立方块搭一个几何体,
使它的主视图和俯视图如图所示,俯视图中小正方形中字母和数字表示
该位置小立方块的个数,请解答下列问题:
(1)___,___, ___;
3
1
1
(2)这个几何体至少由____个小立方块搭成,最多由____个小立方块搭成;
11
12
[解析] 点拨:由主视图得, 中有一个等于2时,小立方块个数最少,
最少个数为;当 时,小立方块
个数最多,最多个数为 .
(3)若, ,请画出该几何体的左视图.
解:如图所示.
返回
课堂小结
确定立体图形
根据主视图可以想象原物体的正面
根据左视图可以想象原物体的左侧面
根据俯视图可以想象原物体的上面
谢谢观看!
3.2.2 由视图到立体图形
第3章 图形的初步认识
【华东师大版·2024】数学 七年级上册
授课教师:********
班 级:********
时 间:********
幻灯片 1:封面
标题:3.2.2 由视图**:从平面图形还原三维结构
幻灯片 2:学习目标
理解由三视图还原立体图形的原理,知道三视图与立体图形的对应关系。
能根据正方体、长方体、圆柱、圆锥、球等简单立体图形的三视图,还原出相应的立体图形。
掌握由三视图还原简单组合体的基本方法,提升空间想象能力和逆向思维能力。
幻灯片 3:情境引入 —— 视图的 “逆向工程”
展示图片:一个机械零件的三视图(主视图、俯视图、左视图)。
提问:工程师拿到这样的三视图,如何知道这个零件的立体形状?
引入:由视图还原立体图形,是从平面图形到立体图形的逆向过程,需要我们结合三视图的特征,想象立体图形的形状。本节课我们就来学习如何由视图得到立体图形。
幻灯片 4:由三视图还原立体图形的原理
对应关系:
主视图反映立体图形的正面形状和高度、长度。
俯视图反映立体图形的上面形状和长度、宽度。
左视图反映立体图形的左面形状和高度、宽度。
关键原则:
“长对正”:主视图和俯视图的长度相等,且左右对齐。
“高平齐”:主视图和左视图的高度相等,且上下对齐。
“宽相等”:俯视图和左视图的宽度相等,且前后对应。
示例:一个长方体的三视图都是长方形,主视图的长和高、俯视图的长和宽、左视图的高和宽分别对应长方体的长、宽、高,根据这三个视图的尺寸可确定长方体的形状。
幻灯片 5:由简单视图还原基本立体图形
球:
三视图特征:三个全等的圆。
还原方法:若三视图都是大小相同的圆,则对应的立体图形一定是球。
示意图:三个等大的○→球。
正方体:
三视图特征:三个全等的正方形。
还原方法:三视图都是相同的正方形,说明立体图形各棱长相等,是正方体。
示意图:三个等大的□→正方体。
圆柱:
三视图特征:主视图和左视图是全等的长方形,俯视图是圆。
还原方法:根据长方形的长(圆柱的高)和宽(底面直径)、圆的直径,可确定圆柱的形状和尺寸。
示意图:两个全等的 和一个○→圆柱。
圆锥:
三视图特征:主视图和左视图是全等的等腰三角形,俯视图是带中心点的圆。
还原方法:等腰三角形的底边(底面直径)和高(圆锥的高)、圆的直径(与底边相等)共同确定圆锥的形状。
示意图:两个全等的△和一个带点的○→圆锥。
幻灯片 6:由三视图还原棱柱
三棱柱:
三视图特征:主视图和左视图是长方形(可能不同),俯视图是三角形。
还原方法:
由俯视图的三角形确定底面是三角形(如直角三角形、等边三角形)。
由主视图和左视图的长方形的高度确定三棱柱的高,长方形的宽度对应底面三角形的相关边长(如边长、高)。
示例:俯视图是直角三角形(直角边 3cm、4cm),主视图是长 5cm、宽 5cm 的长方形,左视图是长 5cm、宽 4cm 的长方形→还原为底面是直角三角形(直角边 3cm、4cm)、高 5cm 的三棱柱。
四棱柱(长方体):
三视图特征:三个长方形(可能有正方形)。
还原方法:根据三个长方形的长、宽、高,确定长方体的长、宽、高(主视图的长 = 俯视图的长,主视图的高 = 左视图的高,俯视图的宽 = 左视图的宽)。
示例:主视图 3cm×2cm,俯视图 3cm×1cm,左视图 2cm×1cm→还原为长 3cm、宽 1cm、高 2cm 的长方体。
幻灯片 7:由三视图还原棱锥
四棱锥:
三视图特征:主视图和左视图是全等的等腰三角形,俯视图是带中心点的正方形。
还原方法:
由俯视图的正方形确定底面是正方形,中心点是顶点的投影。
由等腰三角形的底边(正方形的边长)和高(四棱锥的高)确定棱锥的形状。
示例:俯视图是边长 2cm 的正方形(带中心点),主视图和左视图是底边 2cm、高 3cm 的等腰三角形→还原为底面边长 2cm、高 3cm 的四棱锥。
三棱锥:
三视图特征:主视图和左视图是等腰三角形(可能不同),俯视图是带中心点的三角形。
还原方法:结合俯视图的三角形形状和主、左视图等腰三角形的尺寸,确定三棱锥的底面和高。
示例:俯视图是等边三角形(边长 4cm,带中心点),主视图和左视图是底边 4cm、高 3cm 的等腰三角形→还原为底面是等边三角形(边长 4cm)、高 3cm 的三棱锥。
幻灯片 8:由组合视图还原组合体
步骤:
分别分析主视图、俯视图、左视图,确定组合体由哪些基本立体图形组成。
根据三视图的位置关系,确定各基本立体图形的相对位置(如叠加、拼接、嵌套等)。
综合三个视图的信息,想象并还原组合体的整体形状。
示例 1:叠加型组合体:
三视图特征:主视图下方是正方形,上方是等腰三角形;俯视图是带点的圆和外围正方形;左视图与主视图对称。
还原过程:
主视图下方正方形和俯视图外围正方形对应正方体。
主视图上方等腰三角形和俯视图中间带点的圆对应圆锥。
结合位置关系(上方、中心重合)→ 正方体上方叠放圆锥的组合体。
示例 2:拼接型组合体:
三视图特征:主视图是两个相连的长方形;俯视图是长方形和旁边的圆;左视图是一个长方形。
还原过程:
主视图左侧长方形、俯视图左侧长方形对应长方体。
主视图右侧长方形、俯视图右侧圆对应圆柱。
结合位置关系(并排、侧面相切)→ 长方体与圆柱并排拼接的组合体。
幻灯片 9:例题 1—— 由三视图还原基本立体图形
题目:已知一个立体图形的三视图如下:主视图是长方形,俯视图是圆,左视图是长方形,且主视图和左视图全等。这个立体图形是什么?
解答过程:
主视图和左视图是全等的长方形,俯视图是圆,符合圆柱的三视图特征。
因为主视图和左视图全等,说明圆柱的高等于底面直径(特殊圆柱)。
结论:这个立体图形是圆柱(高等于底面直径)。
幻灯片 10:例题 2—— 由三视图还原组合体
题目:一个立体图形的三视图如下:主视图是下方正方形、上方等腰三角形;俯视图是正方形(中心有一点);左视图与主视图相同。这个组合体由哪些立体图形组成?
解答过程:
主视图下方正方形和俯视图正方形对应正方体(或长方体)。
主视图上方等腰三角形和俯视图中心的点对应四棱锥(底面与正方体顶面全等)。
结合位置关系(四棱锥在正方体上方,底面重合)。
结论:由正方体和四棱锥组成,四棱锥位于正方体上方。
幻灯片 11:例题 3—— 根据视图还原并判断尺寸
题目:一个立体图形的三视图中,主视图是长 5cm、宽 3cm 的长方形,俯视图是长 5cm、宽 2cm 的长方形,左视图是长 3cm、宽 2cm 的长方形。这个立体图形是什么?它的长、宽、高分别是多少?
解答过程:
三视图都是长方形,符合长方体的三视图特征。
根据 “长对正、高平齐、宽相等”:
长 = 主视图的长 = 俯视图的长 = 5cm。
高 = 主视图的宽 = 左视图的长 = 3cm。
宽 = 俯视图的宽 = 左视图的宽 = 2cm。
结论:这个立体图形是长方体,长、宽、高分别是 5cm、2cm、3cm。
幻灯片 12:课堂练习 1—— 由三视图还原立体图形
题目:说出下列三视图对应的立体图形名称:
(1)三视图都是圆→(球)
(2)三视图都是正方形→(正方体)
(3)主视图和左视图是等腰三角形,俯视图是带点的正方形→(四棱锥)
(4)主视图是长方形,俯视图是三角形,左视图是长方形→(三棱柱)
幻灯片 13:课堂练习 2—— 由组合视图还原组合体
题目:一个立体图形的三视图如下:主视图是正方形上方有一个三角形;俯视图是正方形内有一个圆(圆在正方形中心);左视图与主视图相同。这个组合体是什么?
答案:正方体上方叠放一个圆锥(圆锥底面与正方体顶面中心重合,且圆锥底面直径等于正方体棱长)。
幻灯片 14:课堂练习 3—— 根据视图判断尺寸
题目:一个圆锥的三视图中,主视图是等腰三角形,底边为 6cm,高为 4cm。这个圆锥的底面半径和高分别是多少?
答案:底面半径是 3cm(底边 6cm 为直径),高是 4cm(与主视图的高一致)。
幻灯片 15:易错点分析
常见错误:
仅根据一个视图就确定立体图形的形状,如看到主视图是三角形就认为是圆锥,忽略俯视图是否为圆(也可能是棱锥)。
还原组合体时,无法正确判断各部分的相对位置,如将叠加的组合体还原成拼接的,或位置偏移。
忽略 “长对正、高平齐、宽相等” 的原则,导致还原的立体图形尺寸与视图不符,如长方体的长、宽、高对应错误。
规避方法:
还原立体图形时,必须结合三个视图的特征综合判断,不能仅凭一个视图下结论,如三角形主视图可能对应圆锥或棱锥,需结合俯视图(圆对应圆锥,多边形对应棱锥)。
分析组合体的三视图时,用 “分部分、找对应” 的方法,先确定各部分对应的基本立体图形,再根据视图的对齐关系确定位置。
牢记 “长对正、高平齐、宽相等” 的原则,在还原立体图形时,对照三视图的尺寸,确保长、宽、高对应正确。
幻灯片 16:课堂小结
由视图到立体图形的过程:结合三视图的特征,利用 “长对正、高平齐、宽相等” 的原则,想象并还原立体图形。
基本立体图形的还原:根据球、正方体、圆柱、圆锥、棱柱、棱锥的三视图特征直接还原。
组合体的还原:先分解视图为基本部分,确定对应基本立体图形,再结合位置关系还原整体。
核心能力:空间想象能力是关键,通过多观察、多练习,逐步提高由平面图形想象立体图形的能力。
幻灯片 17:布置作业
基础作业:
教材课后练习题第 1、2 题(根据三视图说出立体图形名称,还原简单立体图形)。
一个立体图形的三视图都是正方形,它是什么立体图形?棱长为 5cm 时,画出它的三视图。
提升作业:
已知一个组合体的三视图:主视图是两个上下相连的正方形;俯视图是两个左右相连的正方形;左视图是两个上下相连的正方形。这个组合体是什么?画出它的立体图形草图。
观察一个常见物品(如墨水瓶),画出它的三视图,再根据三视图向家人描述这个物品的形状。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
情境导入
你能根据三视图想象物体的形状吗?
主视
主视图
左视图
左视
俯视
俯视图
探索新知
例 3 如图所示的是一些立体图形的三视图,请根据视
图说出这些立体图形的名称 .
主视图
左视图
俯视图
长方体
(1)
探索新知
圆锥
(2)
主视图
左视图
俯视图
例 3 如图所示的是一些立体图形的三视图,请根据视
图说出这些立体图形的名称 .
由三视图描述几何体(或实物原型),一般先根据各视图想象从各个方向看到的几何体形状,然后综合起来确定几何体(或实物原型)的形状,再根据三视图“长对正、高平齐、宽相等”的关系,确定轮廓线的位置,以及各个方向的尺寸.
确定立体图形
根据主视图可以想象原物体的正面
根据左视图可以想象原物体的左侧面
根据俯视图可以想象原物体的上面
试一试
如图是一个物体的三视图,试想象该物体的形状.
主视图
左视图
俯视图
试一试
主视图
左视图
俯视图
如图是一个物体的三视图,试想象该物体的形状.
试一试
主视图
左视图
俯视图
如图是一个物体的三视图,试想象该物体的形状.
试一试
主视图
左视图
俯视图
如图是一个物体的三视图,试想象该物体的形状.
3
2
1
做一做
由几个相同的小立方块搭成的几何体的俯视图如图所示.方格中的数字表示该位置的小方块的个数.请画出这个几何体的三视图.
主视图
左视图
俯视图
在一个仓库里堆积着正方体的货箱若干,要搬运这些箱子很困难,可是仓库管理员要落实一下箱子的数量,于是就想出一个办法:将这堆货物的三种视图画了出来,你能根据三视图,帮他清点一下数量吗?
主视图
左视图
俯视图
1
1
1
2
2
1
8个
用小立方块搭一个几何体,使得它的主视图,俯视图如图所示,这样的几何体只有一种吗?它最少有多少个小立方块?最多需要多少个立方块?摆一摆,试一试.
主视图
俯视图
2
3
1
1
1
最少8个
2
3
3
1
1
最多10个
随堂练习
1. 如图是一个立体图形的三视图,请说出这个立体图形的名称,并画出它的大致形状.
主视图
左视图
俯视图
【教材P134 练习 第1题】
长方体
2. 试说出几个俯视图为一个圆的物体 .
【教材P134 练习 第2题】
球
竖立的圆柱
知识点1 由三视图确定简单的几何体
1.[2024南通中考]如图是一个几何体的三视图,该几何体是( )
D
(第1题)
A.球 B.棱柱 C.圆柱 D.圆锥
返回
2.一个立体图形的三视图如图所示,该立体图形是( )
B
(第2题)
A.三棱锥 B.三棱柱 C.四棱柱 D.四棱锥
返回
3.一个几何体的主视图、左视图、俯视图都是长方形,这个几何体可能
是( )
A
A.长方体 B.四棱锥 C.三棱锥 D.圆柱
返回
(第4题)
4.如图是某物体对应几何体的三视图,则最符合该三视
图的物体应是( )
C
A. B. C. D.
返回
5.(4分)[教材P练习T 变式]某几何体的主视图、左视图和俯视
图分别如图所示,求该几何体的表面积.
解:由三视图可知,该几何体是一个圆柱,且圆柱的底面直径为2,高
为3,
所以 .
返回
知识点2 由三视图确定简单的组合体
6.某几何体的三视图如图所示,该几何体是( )
A
(第6题)
A. B. C. D.
返回
(第7题)
7.如图是由一些完全相同的小正方体搭成的几何体的
三视图.这个几何体是( )
A
A. B. C. D.
返回
8.[2024安徽中考]某几何体的三视图如图所示,则该几何体为( )
D
A. B. C. D.
返回
9.(8分)[教材 “试一试”变式]如图是由若干个相同的小正方体组
成的一个立体图形的三视图.
(1)该立体图形共有___层;
2
(2)该立体图形中共有多少个小正方体?
解:综合三个视图可知,从下到上第1层有4个小正方体,第2层有1个小
正方体,所以立体图形中小正方体共有 (个).
返回
10.一个几何体的主视图和左视图如图所示,则这个几何体是( )
C
(第10题)
A. B. C. D.
返回
11.如图是一个几何体的左视图和俯视图,则该几何体是( )
B
(第11题)
A. B. C. D.
返回
12.在一张桌子上摆放着一些形状、大小都相同的碟子,从3个方向看到
的图形如图所示,则这个桌子上的碟子总个数是( )
B
A.11 B.12 C.13 D.14
返回
13.如图①,一个平台上已经放了三个棱长为1的正方体,要得到一个几
何体,其主视图和左视图如图②所示,平台上至少还需再放___个这样
的正方体.
2
返回
14.(8分)[2025洛阳期末]由若干大小相同的小正方体搭成的几何体
的俯视图如图,正方形中的数字表示在该位置的小正方体个数.
(1)在方格中画出该几何体的主视图和左视图;
解:如图所示.
(2)若拿掉部分小正方体,但保持左视图和俯视图不变,最多可拿掉
___个小正方体.
3
[解析] 点拨:若使得其左视图和俯视图保持不变,则可以拿走第一列的
3个小正方体或者第二列最后面的3个小正方体.
返回
15.(8分)[2025郑州期末]一个几何体的三视图如图所示.
(1)请描述这个几何体的形状;
解:该几何体的上半部分是半圆柱,下半部分是圆柱.(描述准确即可)
(2)计算这个几何体的体积.
解:这个几何体的体积是
.
返回
16.(12分) 用多个相同的小立方块搭一个几何体,
使它的主视图和俯视图如图所示,俯视图中小正方形中字母和数字表示
该位置小立方块的个数,请解答下列问题:
(1)___,___, ___;
3
1
1
(2)这个几何体至少由____个小立方块搭成,最多由____个小立方块搭成;
11
12
[解析] 点拨:由主视图得, 中有一个等于2时,小立方块个数最少,
最少个数为;当 时,小立方块
个数最多,最多个数为 .
(3)若, ,请画出该几何体的左视图.
解:如图所示.
返回
课堂小结
确定立体图形
根据主视图可以想象原物体的正面
根据左视图可以想象原物体的左侧面
根据俯视图可以想象原物体的上面
谢谢观看!
同课章节目录
