3.5.2 线段的长短比较 课件(共39张PPT)
文档属性
| 名称 | 3.5.2 线段的长短比较 课件(共39张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 05:21:02 | ||
图片预览










文档简介
(共39张PPT)
3.5.2 线段的长短比较
第3章 图形的初步认识
【华东师大版·2024】数学 七年级上册
授课教师:********
班 级:********
时 间:********
幻灯片 1:封面
标题:3.5.2 线段的长短比较
副标题:掌握比较方法,理解线段性质
幻灯片 2:学习目标
掌握线段长短比较的两种基本方法:叠合法和度量法。
理解线段中点的概念,能运用中点的性质解决简单问题。
结合实例感受线段长短比较在生活中的应用,培养几何操作和推理能力。
幻灯片 3:情境引入 —— 生活中的线段长短比较
展示图片:两根不同长度的铅笔、两条不同长度的绳子、地图上两条不同的路线(线段形式)。
提问:如何知道这些物体的长度谁长谁短?比如,怎样比较两根铅笔的长短?
引入:在生活中,我们经常需要比较线段的长短,比如选择较短的路线、裁剪合适长度的材料等。本节课我们就来学习线段长短比较的方法。
幻灯片 4:线段长短比较的方法 —— 叠合法
概念:把两条线段的一个端点重合,另一个端点落在同一条直线上,根据另一个端点的位置关系来比较线段的长短。
操作步骤:
将线段 AB 和线段 CD 的一个端点 A 与 C 重合。
使线段 AB 和线段 CD 落在同一条直线上,且点 B 和点 D 在 A(C)的同侧。
观察另一个端点的位置:
若点 B 与点 D 重合,则 AB = CD(如图 1)。
若点 B 在线段 CD 上,则 AB < CD(如图 2)。
若点 B 在线段 CD 的延长线上,则 AB > CD(如图 3)。
注意事项:
两条线段必须在同一条直线上,且端点方向一致。
重合的端点必须对齐,确保比较的准确性。
生活实例:比较两根铅笔的长短时,将一端对齐,看另一端的位置;比较两根绳子的长短时,将一端重合,拉直后看另一端的位置。
幻灯片 5:线段长短比较的方法 —— 度量法
概念:用刻度尺测量出两条线段的长度,再根据长度数值的大小来比较线段的长短。
操作步骤:
用刻度尺的 0 刻度线对准线段的一个端点(如线段 AB 的端点 A)。
读取线段另一个端点对应的刻度值(如端点 B 对应的刻度为 5cm,则 AB = 5cm)。
用同样的方法测量出线段 CD 的长度(如 3cm)。
比较两个数值的大小:5cm > 3cm,所以 AB > CD。
注意事项:
测量时刻度尺要与线段重合,确保刻度线与线段平行。
读数时视线要与刻度尺垂直,避免读数误差。
单位:常用的长度单位有厘米(cm)、毫米(mm)、米(m)等,测量时要注明单位。
幻灯片 6:两种比较方法的对比
方法
操作要点
优点
适用场景
叠合法
重合一个端点,使线段在同一直线,观察另一个端点位置
直观,无需测量工具
可直接操作的实物线段(如绳子、铅笔)
度量法
用刻度尺测量长度,比较数值大小
精确,能得到具体长度
需要知道具体长度的情况(如工程图纸、地图)
联系:两种方法都能比较出线段的长短,在实际应用中可根据需求选择合适的方法。
幻灯片 7:线段的基本性质 —— 两点之间线段最短
性质内容:两点之间的所有连线中,线段最短。简单说成:两点之间,线段最短。
理解:连接两点的线有很多种(如折线、曲线、线段),其中线段的长度是最短的。
两点间的距离:两点之间线段的长度,叫做这两点间的距离(距离是一个数值,有单位)。
生活应用:
从 A 地到 B 地,走直路(线段)比走弯路(折线或曲线)更近。
架设电线时,尽可能沿着线段架设,可节省材料。
跳远时,测量的是起跳点到落地点之间的线段长度,而不是身体划过的曲线长度。
幻灯片 8:线段中点的概念
定义:把一条线段分成两条相等线段的点,叫做这条线段的中点。
几何表示:若点 M 是线段 AB 的中点,则 AM = MB = \(\frac{1}{2}\)AB,或 AB = 2AM = 2MB。
图形表示:在线段 AB 上标出点 M,用符号 “=” 标注 AM 和 MB,表明两者长度相等。
说明:一个线段只有一个中点,中点一定在线段上。
幻灯片 9:线段中点的应用
示例:已知线段 AB = 8cm,点 C 是 AB 的中点,求 AC 和 BC 的长度。
解答:因为点 C 是 AB 的中点,所以 AC = BC = \(\frac{1}{2}\)AB = \(\frac{1}{2}\)×8 = 4cm。
结论:AC = 4cm,BC = 4cm。
幻灯片 10:例题 1—— 用叠合法比较线段长短
题目:如图,已知线段 AB 和线段 CD,用叠合法比较它们的长短。
解答过程:
将点 A 与点 C 重合,使线段 AB 和 CD 在同一直线上,点 B 和点 D 在点 A(C)的同侧。
观察发现点 B 在线段 CD 的延长线上,因此 AB > CD。
结论:AB > CD。
幻灯片 11:例题 2—— 用度量法比较线段长短
题目:测量下图中线段 EF 和线段 GH 的长度,并比较它们的长短。
解答过程:
用刻度尺测量得 EF = 3.5cm,GH = 4.2cm。
因为 3.5cm < 4.2cm,所以 EF < GH。
结论:EF < GH。
幻灯片 12:例题 3—— 线段中点的综合应用
题目:已知线段 AB = 10cm,点 M 是 AB 的中点,点 N 是 AM 的中点,求线段 MN 和 BN 的长度。
解答过程:
因为点 M 是 AB 的中点,所以 AM = \(\frac{1}{2}\)AB = \(\frac{1}{2}\)×10 = 5cm。
因为点 N 是 AM 的中点,所以 AN = MN = \(\frac{1}{2}\)AM = \(\frac{1}{2}\)×5 = 2.5cm。
BN = BA + AN = 10 + 2.5 = 12.5cm?(错误,应为 BN = BM + MN = 5 + 2.5 = 7.5cm,修正:BN = AB - AN = 10 - 2.5 = 7.5cm 或 BN = BM + MN = 5 + 2.5 = 7.5cm)。
结论:MN = 2.5cm,BN = 7.5cm。
幻灯片 13:课堂练习 1—— 比较线段长短
题目:
(1)用叠合法比较下图中线段 a 和线段 b 的长短。
(2)用刻度尺测量线段 c 和线段 d 的长度,比较它们的长短。
答案:(1)根据实际操作,a > b(或 a < b 或 a = b,以实际图形为准);(2)测量后比较,如 c = 2.8cm,d = 3.1cm,则 c < d。
幻灯片 14:课堂练习 2—— 线段中点的应用
题目:已知线段 PQ = 6cm,点 R 是 PQ 的中点,点 S 是 QR 的中点,求 PS 的长度。
解答过程:
QR = \(\frac{1}{2}\)PQ = 3cm,QS = \(\frac{1}{2}\)QR = 1.5cm,PS = PQ - QS = 6 - 1.5 = 4.5cm。
答案:4.5cm。
幻灯片 15:课堂练习 3—— 两点之间线段最短的应用
题目:在一个平面内有 A、B 两点,你能找到一点 C,使 AC + BC 的长度最短吗?为什么?
答案:当点 C 在线段 AB 上时,AC + BC = AB,此时长度最短,因为两点之间线段最短,若 C 在其他位置,AC + BC 会大于 AB。
幻灯片 16:易错点分析
常见错误:
用叠合法比较线段长短时,没有将两条线段的一个端点重合,或没有使它们在同一直线上,导致比较结果错误。
对线段中点的概念理解错误,认为中点可以在线段的延长线上,实际上中点一定在线段上。
混淆 “线段” 和 “距离” 的概念,如说 “两点之间线段最短” 是正确的,但说 “两点之间距离最短” 是错误的,因为距离是长度,是数值,应说 “两点之间线段的长度最短”。
规避方法:
用叠合法比较时,严格按照 “重合端点、同一直线、同侧观察” 的步骤操作,确保比较的规范性。
牢记线段中点的定义,中点是将线段分成两条相等线段的点,必然在线段上,可通过画图强化这一认知。
明确线段是图形,距离是线段的长度(数值),区分两者的概念,避免表述错误。
幻灯片 17:课堂小结
线段长短比较方法:叠合法(重合端点,观察位置)和度量法(测量长度,比较数值)。
线段的基本性质:两点之间线段最短,两点间的距离是线段的长度。
线段中点:将线段分成两条相等线段的点,满足 AM = MB = \(\frac{1}{2}\)AB。
幻灯片 18:布置作业
基础作业:
教材课后练习题第 1、2 题(用两种方法比较线段长短,应用中点性质计算)。
画一条长 5cm 的线段 AB,找出它的中点 C,并测量 AC 和 BC 的长度。
提升作业:
已知线段 AB = 12cm,点 D 在 AB 的延长线上,且 BD = 4cm,点 E 是 AD 的中点,求 AE 的长度。
举例说明生活中应用 “两点之间线段最短” 的 3 个实例,并简要分析。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
情境导入
记得你和同学是怎样比较个子高矮的吗?
探索新知
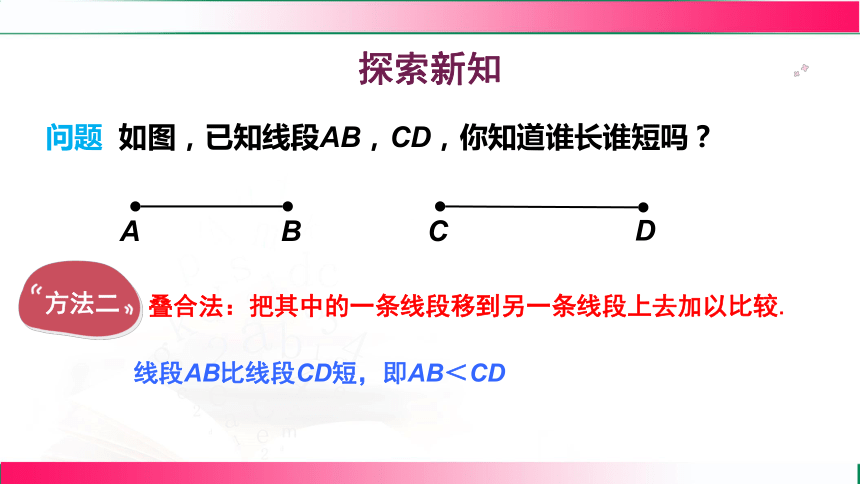
问题 如图,已知线段AB,CD,你知道谁长谁短吗?
A
B
C
D
度量法:用刻度尺量出有关线段的长度,再比较大小.
方法一
线段AB比线段CD短,记为:
AB<CD(或CD>AB)
A
探索新知
问题 如图,已知线段AB,CD,你知道谁长谁短吗?
B
C
D
叠合法:把其中的一条线段移到另一条线段上去加以比较.
方法二
线段AB比线段CD短,即AB<CD
①B点在线段CD的内部时,AB < CD.
②点B、点D点重合时,AB=CD.
图①
图②
图③
③当点B在线段CD的延长线上时,AB >CD.
用叠合法比较线段的长短时,有什么需要注意的吗?
两条线段要放在同一条直线上.
一个端点重合,另一个端点要放在公共端点的同侧.
图①
图②
图③
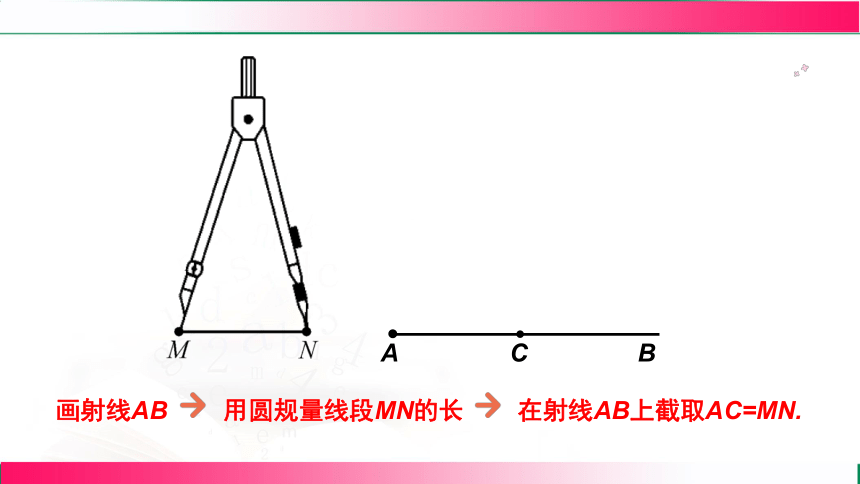
如图,MN为已知线段,你能用直尺和圆规准确地作一条与MN相等的线段吗?
做一做
画射线AB
用圆规量线段MN的长
在射线AB上截取AC=MN.
A
B
C
把一条线段分成两条相等线段的点,叫做这条线段的中点.
如图,AB = 6cm,点C是线段AB的中点,点D是线段CB的中点,那么AD有多长呢?
A、B、C、D四点在同一条直线上,
随堂练习
1. 根据所示图形填空:
(1)AB+BC=( );
(2)AD= ( ) +CD;
(3)CD=AD- ( );
(4)BD=CD+ ( ) =AD- ( );
(5)AC-AB+CD= ( ) =BC+ ( ).
A
B
C
D
AC
AC
AC
BC
AB
BD
CD
【教材P150 练习 第1题】
2. 如图,已知点C是线段AD的中点,AC = 1.5 cm,
BC= 2.2 cm,那么AD=( )cm,BD=( ) cm.
A
B
C
D
3
BD = BC-CD
0.7
【教材P150 练习 第2题】
3.请通过直接观察,分别比较下列三组图形中线段a、b的长短.再用刻度尺量一量,看看你的观察结果是否正确.
(1)
a
b
(2)
b
a
a = b
a = b
【教材P150 练习 第3题】
(3)
a
b
a = b
3.请通过直接观察,分别比较下列三组图形中线段a、b的长短.再用刻度尺量一量,看看你的观察结果是否正确.
【教材P150 练习 第3题】
4.已知线段MN和线段OP,用直尺和圆规作一条
线段AB,使AB =MN +OP.(不写作法,保留作图痕迹)
M
N
O
P
A
B
【教材P150 练习 第4题】
知识点1 线段的长短比较
1.[2025朔州期末]如图,用一支角度固定的圆规比较线段, 的长短,
则( )
A
(第1题)
A. B.
C. D.无法确定
返回
2. 体育课上,小明在点 处投了四次铅球,铅球分别落在
图中,,, 四点,则表示他最好成绩的点是___.
返回
知识点2 线段的尺规作图
3.(8分)如图,已知线段,, ,用直尺和圆规作图
(保留作图痕迹),并用字母表示出所作线段.
(1)作一条线段,使它等于 ;
解:如图①,线段 即为所求.
(2)作一条线段,使它等于 .
解:如图②,线段 即为所求.
返回
知识点3 线段的和与差
4.[教材P150练习T1变式]如图所示,完成填空.
(1) ____;
(2)____ ;
(3)____ ____;
(4)____ .
返回
5. 线段,是直线上的一点,,则
______________.
或
返回
6.如图,已知,,,则 的长是___.
3
返回
知识点4 线段的中点
7.如图,已知是的中点,下面结论中不是根据“是 的中点”推
出来的是( )
B
A. B.
C. D.
返回
8.[2025成都期末]如图,点为线段的中点,点在线段 上,如
果,,那么线段 的长是( )
B
A.2 B.3 C.4 D.5
返回
9.[2025西安期末]如图,,是线段上两点,若 ,
,点为的中点,则___ .
6
返回
10.(4分)如图,已知线段,为线段上一点,是
的中点,是的中点.若,求 的长.
解:因为是的中点,且, ,
所以, ,
又因为是的中点,所以 ,
所以 .
返回
11.如图,,则线段与线段 的长短关系是( )
B
A. B. C. D.无法比较
返回
12.下图中能表示线段 的是( )
B
A.
B.
C.
D.
返回
13.如图,点是的中点,点是的中点, .则
___ .
5
返回
14. 已知:,,是同一直线上的三点,为 的中点,若
,,则 的长为_______.
1或11
[解析] 点拨:分两种情况讨论:
(1)当点在线段 上时,如图①所示,
因为,为的中点,所以 .
因为,所以 ;
(2)当点在线段 的延长线上时,如图②所示,
因为,为 的中点,
所以 .
因为 ,
所以 .
综上所述, 的长为1或11.
返回
15.(8分)[2025开封期末]如图,已知线段 ,请用尺规按下列要求
步骤作图(保留作图痕迹,不写作法)
(1)延长线段到,使;延长线段到,使 ;
解:如图所示.
(2)若,点为的中点,为的中点,求线段 的长.
解:因为 ,
所以 ,
所以 .
因为为 的中点,
所以 .
因为为 的中点,
所以 ,
所以 .
返回
16.(8分)如图,已知数轴上,两点所表示的数分别为和8,点
表示原点.
(1)求线段 的长.
解:因为,两点所表示的数分别为和8,所以, ,
所以 .
(2)若为射线上的一点(点不与,两点重合),为 的中
点,为的中点,当点在射线上运动时, 的长度是否发生改变
若不变,请你求出线段 的长度;若改变,请说明理由.
解:线段 的长度不发生改变.分下面两种情况:
①当点在, 两点之间运动时,
如图a. .
②当点在点 的左侧运动时,如图b.
.
综上所述,线段 的长度不发生改变,其长度为5.
返回
课堂小结
画一条线段等于已知线段.
两条线段的和与差仍是线段.
线段的中点定义及相关计算.
线段的大小比较
谢谢观看!
3.5.2 线段的长短比较
第3章 图形的初步认识
【华东师大版·2024】数学 七年级上册
授课教师:********
班 级:********
时 间:********
幻灯片 1:封面
标题:3.5.2 线段的长短比较
副标题:掌握比较方法,理解线段性质
幻灯片 2:学习目标
掌握线段长短比较的两种基本方法:叠合法和度量法。
理解线段中点的概念,能运用中点的性质解决简单问题。
结合实例感受线段长短比较在生活中的应用,培养几何操作和推理能力。
幻灯片 3:情境引入 —— 生活中的线段长短比较
展示图片:两根不同长度的铅笔、两条不同长度的绳子、地图上两条不同的路线(线段形式)。
提问:如何知道这些物体的长度谁长谁短?比如,怎样比较两根铅笔的长短?
引入:在生活中,我们经常需要比较线段的长短,比如选择较短的路线、裁剪合适长度的材料等。本节课我们就来学习线段长短比较的方法。
幻灯片 4:线段长短比较的方法 —— 叠合法
概念:把两条线段的一个端点重合,另一个端点落在同一条直线上,根据另一个端点的位置关系来比较线段的长短。
操作步骤:
将线段 AB 和线段 CD 的一个端点 A 与 C 重合。
使线段 AB 和线段 CD 落在同一条直线上,且点 B 和点 D 在 A(C)的同侧。
观察另一个端点的位置:
若点 B 与点 D 重合,则 AB = CD(如图 1)。
若点 B 在线段 CD 上,则 AB < CD(如图 2)。
若点 B 在线段 CD 的延长线上,则 AB > CD(如图 3)。
注意事项:
两条线段必须在同一条直线上,且端点方向一致。
重合的端点必须对齐,确保比较的准确性。
生活实例:比较两根铅笔的长短时,将一端对齐,看另一端的位置;比较两根绳子的长短时,将一端重合,拉直后看另一端的位置。
幻灯片 5:线段长短比较的方法 —— 度量法
概念:用刻度尺测量出两条线段的长度,再根据长度数值的大小来比较线段的长短。
操作步骤:
用刻度尺的 0 刻度线对准线段的一个端点(如线段 AB 的端点 A)。
读取线段另一个端点对应的刻度值(如端点 B 对应的刻度为 5cm,则 AB = 5cm)。
用同样的方法测量出线段 CD 的长度(如 3cm)。
比较两个数值的大小:5cm > 3cm,所以 AB > CD。
注意事项:
测量时刻度尺要与线段重合,确保刻度线与线段平行。
读数时视线要与刻度尺垂直,避免读数误差。
单位:常用的长度单位有厘米(cm)、毫米(mm)、米(m)等,测量时要注明单位。
幻灯片 6:两种比较方法的对比
方法
操作要点
优点
适用场景
叠合法
重合一个端点,使线段在同一直线,观察另一个端点位置
直观,无需测量工具
可直接操作的实物线段(如绳子、铅笔)
度量法
用刻度尺测量长度,比较数值大小
精确,能得到具体长度
需要知道具体长度的情况(如工程图纸、地图)
联系:两种方法都能比较出线段的长短,在实际应用中可根据需求选择合适的方法。
幻灯片 7:线段的基本性质 —— 两点之间线段最短
性质内容:两点之间的所有连线中,线段最短。简单说成:两点之间,线段最短。
理解:连接两点的线有很多种(如折线、曲线、线段),其中线段的长度是最短的。
两点间的距离:两点之间线段的长度,叫做这两点间的距离(距离是一个数值,有单位)。
生活应用:
从 A 地到 B 地,走直路(线段)比走弯路(折线或曲线)更近。
架设电线时,尽可能沿着线段架设,可节省材料。
跳远时,测量的是起跳点到落地点之间的线段长度,而不是身体划过的曲线长度。
幻灯片 8:线段中点的概念
定义:把一条线段分成两条相等线段的点,叫做这条线段的中点。
几何表示:若点 M 是线段 AB 的中点,则 AM = MB = \(\frac{1}{2}\)AB,或 AB = 2AM = 2MB。
图形表示:在线段 AB 上标出点 M,用符号 “=” 标注 AM 和 MB,表明两者长度相等。
说明:一个线段只有一个中点,中点一定在线段上。
幻灯片 9:线段中点的应用
示例:已知线段 AB = 8cm,点 C 是 AB 的中点,求 AC 和 BC 的长度。
解答:因为点 C 是 AB 的中点,所以 AC = BC = \(\frac{1}{2}\)AB = \(\frac{1}{2}\)×8 = 4cm。
结论:AC = 4cm,BC = 4cm。
幻灯片 10:例题 1—— 用叠合法比较线段长短
题目:如图,已知线段 AB 和线段 CD,用叠合法比较它们的长短。
解答过程:
将点 A 与点 C 重合,使线段 AB 和 CD 在同一直线上,点 B 和点 D 在点 A(C)的同侧。
观察发现点 B 在线段 CD 的延长线上,因此 AB > CD。
结论:AB > CD。
幻灯片 11:例题 2—— 用度量法比较线段长短
题目:测量下图中线段 EF 和线段 GH 的长度,并比较它们的长短。
解答过程:
用刻度尺测量得 EF = 3.5cm,GH = 4.2cm。
因为 3.5cm < 4.2cm,所以 EF < GH。
结论:EF < GH。
幻灯片 12:例题 3—— 线段中点的综合应用
题目:已知线段 AB = 10cm,点 M 是 AB 的中点,点 N 是 AM 的中点,求线段 MN 和 BN 的长度。
解答过程:
因为点 M 是 AB 的中点,所以 AM = \(\frac{1}{2}\)AB = \(\frac{1}{2}\)×10 = 5cm。
因为点 N 是 AM 的中点,所以 AN = MN = \(\frac{1}{2}\)AM = \(\frac{1}{2}\)×5 = 2.5cm。
BN = BA + AN = 10 + 2.5 = 12.5cm?(错误,应为 BN = BM + MN = 5 + 2.5 = 7.5cm,修正:BN = AB - AN = 10 - 2.5 = 7.5cm 或 BN = BM + MN = 5 + 2.5 = 7.5cm)。
结论:MN = 2.5cm,BN = 7.5cm。
幻灯片 13:课堂练习 1—— 比较线段长短
题目:
(1)用叠合法比较下图中线段 a 和线段 b 的长短。
(2)用刻度尺测量线段 c 和线段 d 的长度,比较它们的长短。
答案:(1)根据实际操作,a > b(或 a < b 或 a = b,以实际图形为准);(2)测量后比较,如 c = 2.8cm,d = 3.1cm,则 c < d。
幻灯片 14:课堂练习 2—— 线段中点的应用
题目:已知线段 PQ = 6cm,点 R 是 PQ 的中点,点 S 是 QR 的中点,求 PS 的长度。
解答过程:
QR = \(\frac{1}{2}\)PQ = 3cm,QS = \(\frac{1}{2}\)QR = 1.5cm,PS = PQ - QS = 6 - 1.5 = 4.5cm。
答案:4.5cm。
幻灯片 15:课堂练习 3—— 两点之间线段最短的应用
题目:在一个平面内有 A、B 两点,你能找到一点 C,使 AC + BC 的长度最短吗?为什么?
答案:当点 C 在线段 AB 上时,AC + BC = AB,此时长度最短,因为两点之间线段最短,若 C 在其他位置,AC + BC 会大于 AB。
幻灯片 16:易错点分析
常见错误:
用叠合法比较线段长短时,没有将两条线段的一个端点重合,或没有使它们在同一直线上,导致比较结果错误。
对线段中点的概念理解错误,认为中点可以在线段的延长线上,实际上中点一定在线段上。
混淆 “线段” 和 “距离” 的概念,如说 “两点之间线段最短” 是正确的,但说 “两点之间距离最短” 是错误的,因为距离是长度,是数值,应说 “两点之间线段的长度最短”。
规避方法:
用叠合法比较时,严格按照 “重合端点、同一直线、同侧观察” 的步骤操作,确保比较的规范性。
牢记线段中点的定义,中点是将线段分成两条相等线段的点,必然在线段上,可通过画图强化这一认知。
明确线段是图形,距离是线段的长度(数值),区分两者的概念,避免表述错误。
幻灯片 17:课堂小结
线段长短比较方法:叠合法(重合端点,观察位置)和度量法(测量长度,比较数值)。
线段的基本性质:两点之间线段最短,两点间的距离是线段的长度。
线段中点:将线段分成两条相等线段的点,满足 AM = MB = \(\frac{1}{2}\)AB。
幻灯片 18:布置作业
基础作业:
教材课后练习题第 1、2 题(用两种方法比较线段长短,应用中点性质计算)。
画一条长 5cm 的线段 AB,找出它的中点 C,并测量 AC 和 BC 的长度。
提升作业:
已知线段 AB = 12cm,点 D 在 AB 的延长线上,且 BD = 4cm,点 E 是 AD 的中点,求 AE 的长度。
举例说明生活中应用 “两点之间线段最短” 的 3 个实例,并简要分析。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
情境导入
记得你和同学是怎样比较个子高矮的吗?
探索新知
问题 如图,已知线段AB,CD,你知道谁长谁短吗?
A
B
C
D
度量法:用刻度尺量出有关线段的长度,再比较大小.
方法一
线段AB比线段CD短,记为:
AB<CD(或CD>AB)
A
探索新知
问题 如图,已知线段AB,CD,你知道谁长谁短吗?
B
C
D
叠合法:把其中的一条线段移到另一条线段上去加以比较.
方法二
线段AB比线段CD短,即AB<CD
①B点在线段CD的内部时,AB < CD.
②点B、点D点重合时,AB=CD.
图①
图②
图③
③当点B在线段CD的延长线上时,AB >CD.
用叠合法比较线段的长短时,有什么需要注意的吗?
两条线段要放在同一条直线上.
一个端点重合,另一个端点要放在公共端点的同侧.
图①
图②
图③
如图,MN为已知线段,你能用直尺和圆规准确地作一条与MN相等的线段吗?
做一做
画射线AB
用圆规量线段MN的长
在射线AB上截取AC=MN.
A
B
C
把一条线段分成两条相等线段的点,叫做这条线段的中点.
如图,AB = 6cm,点C是线段AB的中点,点D是线段CB的中点,那么AD有多长呢?
A、B、C、D四点在同一条直线上,
随堂练习
1. 根据所示图形填空:
(1)AB+BC=( );
(2)AD= ( ) +CD;
(3)CD=AD- ( );
(4)BD=CD+ ( ) =AD- ( );
(5)AC-AB+CD= ( ) =BC+ ( ).
A
B
C
D
AC
AC
AC
BC
AB
BD
CD
【教材P150 练习 第1题】
2. 如图,已知点C是线段AD的中点,AC = 1.5 cm,
BC= 2.2 cm,那么AD=( )cm,BD=( ) cm.
A
B
C
D
3
BD = BC-CD
0.7
【教材P150 练习 第2题】
3.请通过直接观察,分别比较下列三组图形中线段a、b的长短.再用刻度尺量一量,看看你的观察结果是否正确.
(1)
a
b
(2)
b
a
a = b
a = b
【教材P150 练习 第3题】
(3)
a
b
a = b
3.请通过直接观察,分别比较下列三组图形中线段a、b的长短.再用刻度尺量一量,看看你的观察结果是否正确.
【教材P150 练习 第3题】
4.已知线段MN和线段OP,用直尺和圆规作一条
线段AB,使AB =MN +OP.(不写作法,保留作图痕迹)
M
N
O
P
A
B
【教材P150 练习 第4题】
知识点1 线段的长短比较
1.[2025朔州期末]如图,用一支角度固定的圆规比较线段, 的长短,
则( )
A
(第1题)
A. B.
C. D.无法确定
返回
2. 体育课上,小明在点 处投了四次铅球,铅球分别落在
图中,,, 四点,则表示他最好成绩的点是___.
返回
知识点2 线段的尺规作图
3.(8分)如图,已知线段,, ,用直尺和圆规作图
(保留作图痕迹),并用字母表示出所作线段.
(1)作一条线段,使它等于 ;
解:如图①,线段 即为所求.
(2)作一条线段,使它等于 .
解:如图②,线段 即为所求.
返回
知识点3 线段的和与差
4.[教材P150练习T1变式]如图所示,完成填空.
(1) ____;
(2)____ ;
(3)____ ____;
(4)____ .
返回
5. 线段,是直线上的一点,,则
______________.
或
返回
6.如图,已知,,,则 的长是___.
3
返回
知识点4 线段的中点
7.如图,已知是的中点,下面结论中不是根据“是 的中点”推
出来的是( )
B
A. B.
C. D.
返回
8.[2025成都期末]如图,点为线段的中点,点在线段 上,如
果,,那么线段 的长是( )
B
A.2 B.3 C.4 D.5
返回
9.[2025西安期末]如图,,是线段上两点,若 ,
,点为的中点,则___ .
6
返回
10.(4分)如图,已知线段,为线段上一点,是
的中点,是的中点.若,求 的长.
解:因为是的中点,且, ,
所以, ,
又因为是的中点,所以 ,
所以 .
返回
11.如图,,则线段与线段 的长短关系是( )
B
A. B. C. D.无法比较
返回
12.下图中能表示线段 的是( )
B
A.
B.
C.
D.
返回
13.如图,点是的中点,点是的中点, .则
___ .
5
返回
14. 已知:,,是同一直线上的三点,为 的中点,若
,,则 的长为_______.
1或11
[解析] 点拨:分两种情况讨论:
(1)当点在线段 上时,如图①所示,
因为,为的中点,所以 .
因为,所以 ;
(2)当点在线段 的延长线上时,如图②所示,
因为,为 的中点,
所以 .
因为 ,
所以 .
综上所述, 的长为1或11.
返回
15.(8分)[2025开封期末]如图,已知线段 ,请用尺规按下列要求
步骤作图(保留作图痕迹,不写作法)
(1)延长线段到,使;延长线段到,使 ;
解:如图所示.
(2)若,点为的中点,为的中点,求线段 的长.
解:因为 ,
所以 ,
所以 .
因为为 的中点,
所以 .
因为为 的中点,
所以 ,
所以 .
返回
16.(8分)如图,已知数轴上,两点所表示的数分别为和8,点
表示原点.
(1)求线段 的长.
解:因为,两点所表示的数分别为和8,所以, ,
所以 .
(2)若为射线上的一点(点不与,两点重合),为 的中
点,为的中点,当点在射线上运动时, 的长度是否发生改变
若不变,请你求出线段 的长度;若改变,请说明理由.
解:线段 的长度不发生改变.分下面两种情况:
①当点在, 两点之间运动时,
如图a. .
②当点在点 的左侧运动时,如图b.
.
综上所述,线段 的长度不发生改变,其长度为5.
返回
课堂小结
画一条线段等于已知线段.
两条线段的和与差仍是线段.
线段的中点定义及相关计算.
线段的大小比较
谢谢观看!
同课章节目录
