3.6.3 余角和补角 课件(共38张PPT)
文档属性
| 名称 | 3.6.3 余角和补角 课件(共38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 9.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 05:19:57 | ||
图片预览







文档简介
(共38张PPT)
3.6.3 余角和补角
第3章 图形的初步认识
【华东师大版·2024】数学 七年级上册
授课教师:********
班 级:********
时 间:********
幻灯片 1:封面
标题:3.6.3 余角和补角
副标题:理解余角与补角的概念,掌握其性质
幻灯片 2:学习目标
理解余角和补角的定义,能准确判断两个角是否互为余角或补角。
掌握余角和补角的性质(同角或等角的余角相等,同角或等角的补角相等),并能运用性质解决问题。
能进行余角和补角的计算,培养逻辑推理和运算能力。
幻灯片 3:情境引入 —— 特殊的角的关系
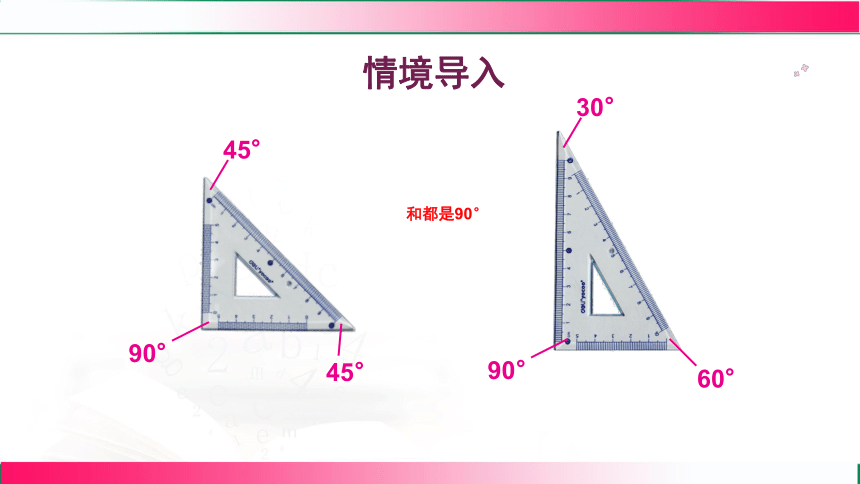
展示图片:一副直角三角尺(其中一个三角尺的两个锐角分别为 30° 和 60°,另一个为 45° 和 45°)。
提问:观察这两个三角尺,每个三角尺的两个锐角之和是多少度?平角是 180°,如果一个角是 120°,那么另一个角是多少度时,它们的和是 180°?
引入:在角的运算中,有两种特殊的角的关系非常重要,那就是余角和补角。本节课我们就来学习余角和补角。
幻灯片 4:余角的定义
定义:如果两个角的和等于 90°(直角),就说这两个角互为余角,简称互余。其中一个角是另一个角的余角。
几何表示:若∠1 + ∠2 = 90°,则∠1 与∠2 互为余角,即∠1 是∠2 的余角,∠2 也是∠1 的余角。
示例:∠A = 30°,∠B = 60°,因为 30° + 60° = 90°,所以∠A 与∠B 互为余角。
说明:
互为余角的两个角只与它们的度数之和有关,与位置无关。
一个角的余角可以有多个,但它们的度数都相等(因为 90° 减去这个角的度数是固定的)。
幻灯片 5:补角的定义
定义:如果两个角的和等于 180°(平角),就说这两个角互为补角,简称互补。其中一个角是另一个角的补角。
几何表示:若∠3 + ∠4 = 180°,则∠3 与∠4 互为补角,即∠3 是∠4 的补角,∠4 也是∠3 的补角。
示例:∠C = 110°,∠D = 70°,因为 110° + 70° = 180°,所以∠C 与∠D 互为补角。
说明:
互为补角的两个角同样只与度数之和有关,与位置无关。
一个角的补角也可以有多个,且度数相等(180° 减去这个角的度数是固定的)。
幻灯片 6:余角和补角的性质
性质 1(余角):同角或等角的余角相等。
几何表示:
若∠1 + ∠2 = 90°,∠1 + ∠3 = 90°,则∠2 = ∠3(同角的余角相等)。
若∠1 + ∠2 = 90°,∠3 + ∠4 = 90°,且∠1 = ∠3,则∠2 = ∠4(等角的余角相等)。
性质 2(补角):同角或等角的补角相等。
几何表示:
若∠1 + ∠2 = 180°,∠1 + ∠3 = 180°,则∠2 = ∠3(同角的补角相等)。
若∠1 + ∠2 = 180°,∠3 + ∠4 = 180°,且∠1 = ∠3,则∠2 = ∠4(等角的补角相等)。
示例:若∠α = 50°,则∠α 的余角是 40°;若∠β = 50°,则∠β 的余角也是 40°,体现等角的余角相等。
幻灯片 7:余角和补角的计算
求一个角的余角:若已知角为 x°,则它的余角为(90 - x)°(x° < 90°)。
求一个角的补角:若已知角为 x°,则它的补角为(180 - x)°(x° < 180°)。
示例:
60° 的余角是 90° - 60° = 30°。
120° 的补角是 180° - 120° = 60°。
幻灯片 8:例题 1—— 判断互余或互补
题目:判断下列各组角是否互为余角或补角:
(1)∠1 = 30°,∠2 = 60°
(2)∠3 = 100°,∠4 = 80°
(3)∠5 = 75°,∠6 = 25°
解答过程:
(1)∠1 + ∠2 = 30° + 60° = 90°,所以∠1 与∠2 互为余角。
(2)∠3 + ∠4 = 100° + 80° = 180°,所以∠3 与∠4 互为补角。
(3)∠5 + ∠6 = 75° + 25° = 100°,既不互余也不互补。
结论:(1)互为余角;(2)互为补角;(3)都不是。
幻灯片 9:例题 2—— 求角的余角或补角
题目:
(1)求 58° 角的余角和补角。
(2)一个角的补角是它的 3 倍,求这个角的度数。
解答过程:
(1)余角:90° - 58° = 32°;补角:180° - 58° = 122°。
(2)设这个角的度数为 x°,则它的补角为(180 - x)°,根据题意得 180 - x = 3x,解得 x = 45。
结论:(1)余角 32°,补角 122°;(2)这个角是 45°。
幻灯片 10:例题 3—— 余角和补角性质的应用
题目:已知∠A 与∠B 互为余角,∠A 与∠C 互为补角,且∠B = 25°,求∠C 的度数。
解答过程:
因为∠A 与∠B 互为余角,所以∠A = 90° - ∠B = 90° - 25° = 65°。
因为∠A 与∠C 互为补角,所以∠C = 180° - ∠A = 180° - 65° = 115°。
结论:∠C = 115°。
幻灯片 11:课堂练习 1—— 基本计算
题目:
(1)70° 的余角是( )°,补角是( )°。
(2)一个角的余角是 35°,这个角是( )°,它的补角是( )°。
答案:(1)20,110;(2)55,125。
幻灯片 12:课堂练习 2—— 性质应用
题目:已知∠1 与∠2 互为余角,∠3 与∠4 互为余角,且∠1 = ∠3,求证∠2 = ∠4。
证明过程:
因为∠1 与∠2 互为余角,所以∠1 + ∠2 = 90°,即∠2 = 90° - ∠1。
因为∠3 与∠4 互为余角,所以∠3 + ∠4 = 90°,即∠4 = 90° - ∠3。
又因为∠1 = ∠3,所以∠2 = ∠4。
幻灯片 13:课堂练习 3—— 综合应用
题目:一个角的补角比它的余角的 3 倍多 10°,求这个角的度数。
解答过程:
设这个角的度数为 x°,则它的补角为(180 - x)°,余角为(90 - x)°。
根据题意得:180 - x = 3(90 - x) + 10。
解方程:180 - x = 270 - 3x + 10,2x = 100,x = 50。
答案:这个角是 50°。
幻灯片 14:易错点分析
常见错误:
对余角和补角的定义理解不透彻,认为只有两个锐角才能互余,实际上只要两角之和为 90° 就互余,与角的类型无关(但钝角没有余角)。
混淆余角和补角的性质,在应用时出现逻辑错误,如错误认为 “同角的余角与补角相等”。
计算一个角的余角或补角时,忽略角的度数范围,如求 100° 的余角,而 100° 大于 90°,没有余角。
规避方法:
牢记余角和补角的定义,重点关注两角之和是否为 90° 或 180°,而非角的具体类型。
区分余角和补角的性质,通过几何表示和实例理解 “同角或等角的余角相等” 与 “同角或等角的补角相等” 的不同适用场景。
计算前先判断角是否有对应的余角或补角:锐角(小于 90°)才有余角,锐角、直角、钝角(小于 180°)才有补角。
幻灯片 15:课堂小结
余角和补角的定义:
互余:两角之和为 90°。
互补:两角之和为 180°。
性质:
同角或等角的余角相等。
同角或等角的补角相等。
计算:
余角 = 90° - 已知角(已知角 < 90°)。
补角 = 180° - 已知角(已知角 < 180°)。
幻灯片 16:布置作业
基础作业:
教材课后练习题第 1、2 题(判断互余互补、计算余角补角)。
一个角的度数是 36°,求它的余角和补角的度数。
提升作业:
已知∠α 和∠β 互为补角,且∠α 比∠β 大 30°,求∠α 和∠β 的度数。
如图,点 O 在直线 AB 上,OC 是∠AOD 的平分线,∠DOB = 90°,求证∠COD 与∠BOD 互余。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
情境导入
45°
45°
30°
60°
90°
90°
和都是90°
探索新知
1
2
α
β
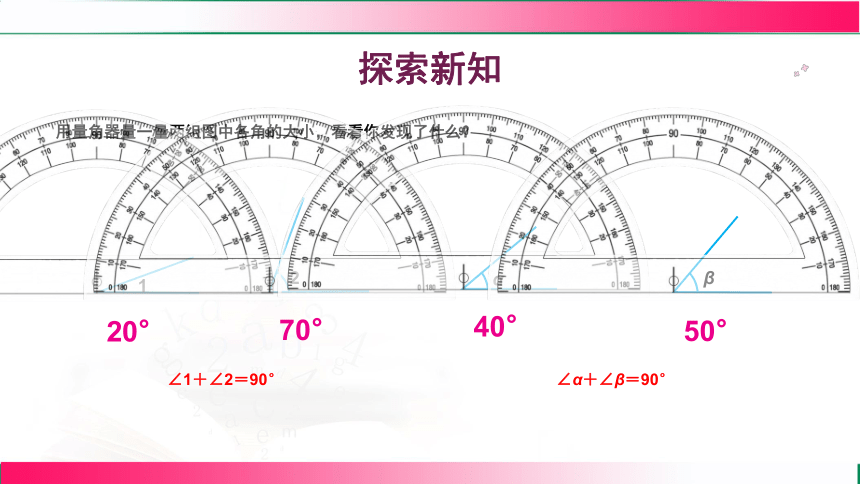
用量角器量一量两组图中各角的大小,看看你发现了什么?
20°
70°
40°
50°
∠1+∠2=90°
∠α+∠β=90°
1
2
α
β
两个角的和等于90°(直角),就说这两个角互为余角.
简称互余.
1
2
α
β
如果∠1+∠2=90°,那么∠1是∠2的余角,∠2也是∠1的余角.
两个角的和等于90°(直角),就说这两个角互为余角.
1
2
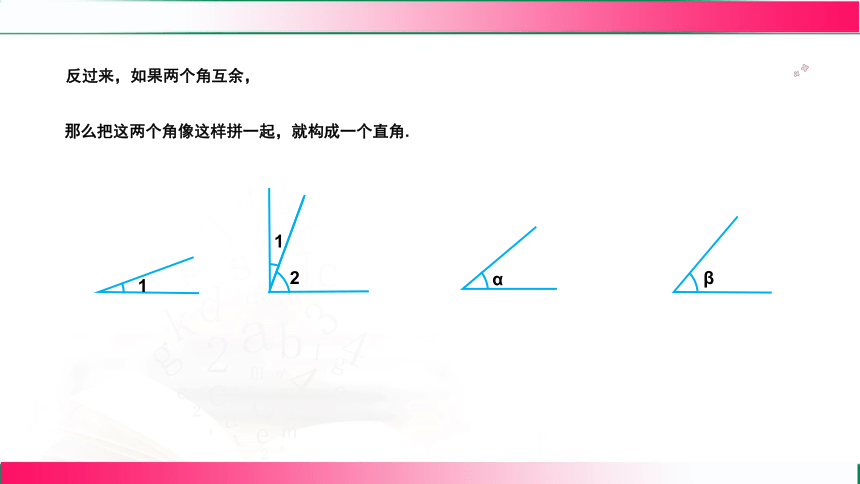
反过来,如果两个角互余,
1
那么把这两个角像这样拼一起,就构成一个直角.
α
β
3
4
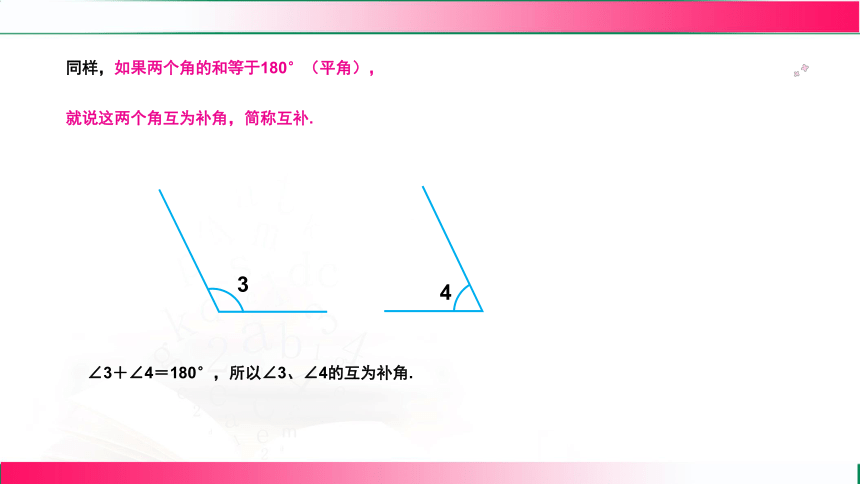
同样,如果两个角的和等于180°(平角),
就说这两个角互为补角,简称互补.
∠3+∠4=180°,所以∠3、∠4的互为补角.
1
2
3
4
想想看,如果∠1与∠2互余,∠3与∠4互余,∠2 =∠4,那么∠1和∠3有什么关系?相等角的补角又有什么关系?
∠1=∠3
归纳总结
同角或等角的余角相等;同角或等角的补角相等.
例3 已知∠α=50°17′,求∠α的余角和补角.
∠α的余角=90°-50°17′=39°43′
∠α的补角=180°-50°17′=129°43′
随堂练习
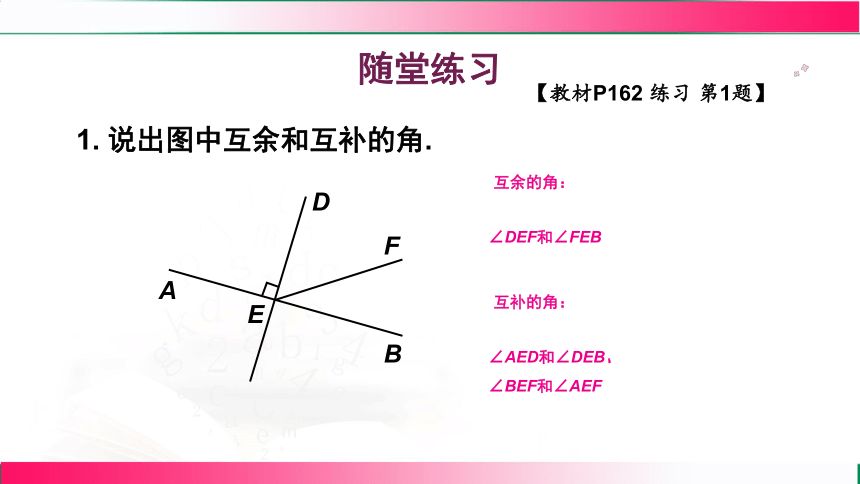
1. 说出图中互余和互补的角.
E
A
B
F
D
∠AED和∠DEB、
∠BEF和∠AEF
互补的角:
∠DEF和∠FEB
互余的角:
【教材P162 练习 第1题】
2.如图,有两堵围墙,有人想测量地面上所形成的∠AOB的度数,但人又不能进入围墙,只能站在墙外,请问该如何测量?
延长AO,测量∠AOB的补角即可.
提示:也可延长BO.
【教材P162 练习 第2题】
3 如图,已知∠AOB,利用尺规作图作一个角等于该角
补角.
B
O
A
C
∠COB是∠AOB是的补角
【教材P162 练习 第3题】
知识点1 余角和补角的定义
1.若 ,则 的补角为( )
D
A. B. C. D.
返回
2.若,则 的余角为( )
A
A. B. C. D.
返回
3.[2025成都期末]若两个角互补,则( )
D
A.这两个角都是锐角
B.这两个角都是钝角
C.这两个角一定一个是锐角,一个是钝角
D.以上答案都不对
返回
4.[教材P162练习T1变式]如图,,, 三点在同一条直线上,
.
(1) 的余角是_______,补角是_______;
(2)若 ,则 ______.
返回
5.若一个角的余角的3倍比这个角的补角多 ,则这个角的度数为_____.
返回
6.(8分)[教材P162练习T3变式]如图, , 平分
, .
(1)与互余吗?与 互补吗?试说明理由.
解:与互余.与 互补.理由如下:
因为 ,平分 ,
所以 .
又因为,所以 ,
所以 ,即与 互余.
因为 ,
所以与 互补.
(2)利用尺规作图,作一个角等于 的补角.(不写作法,保留作图痕迹)
解:如图, 即为所求.
返回
知识点2 余角和补角的性质
7. 若 , ,则与 的大小关系
是_________,理由是________________;若 ,且
, ,则与 的大小关系是______
___,理由是________________.
同角的余角相等
等角的补角相等
返回
(第8题)
8.[2025周口期末]如图,将一副三角板的直角
顶点重合摆放在桌面上,若 ,则
等于( )
B
A. B. C. D.
(第9题)
9.如图,直线,相交于点, ,那么
______.
返回
10.(8分)如图, , .
(1)的余角为______________; 的补角为______________.
,
,
(2)与有怎样的数量关系,为什么?与 有怎
样的数量关系,为什么?
解:因为, , ,
所以 .
因为 .
所以 ,
.
又因为 ,
所以 .
返回
11.[2025莆田期末]如图,将一副三角板按不同位置摆放,其中 和
不一定相等的是( )
D
A. B. C. D.
返回
(第12题)
12.如图,射线的方向为南偏东 ,且 平分
,则射线 的方向为( )
B
A.南偏西 B.南偏西 C.南偏西 D.西偏南
返回
13.已知两个角的度数比是,差是 ,则这两个角的关系是( )
B
A.互余 B.互补
C.既不互余也不互补 D.不能确定
返回
14.[2025长春期末]如果 和 互补,且 ,下列表示
的余角的式子中不正确的是( )
C
A. B. C. D.
返回
(第15题)
15.如图,点在直线上, ,
下列说法错误的是( )
D
A.与相等 B.与 互余
C.与互补 D.与 互补
返回
16.(8分)[2025驻马店期末]如图,是直线上一点, 为任意一
条射线,平分,平分 .
(1)图中的补角是_______________; 的余角是_________
______.
,
,
(2)与 具有怎样的数量关系?说明理由.
解: .理由:
因为平分,平分,所以 ,
,所以
,
即与的数量关系是 .
返回
17.(8分)如图,,, 三点在同一直线
上,与 互补.
(1)若 ,求 的度数;
解:因为,,三点在同一直线上,所以 ,
所以与 互补.
又因为与 互补,
所以 .
(2)已知平分,若射线在的内部,且满足 与
互余,试探究与 之间有怎样的数量关系,并说明理由.
解: .理由:
设 ,
因为平分 ,
所以 .
因为与 互余,
所以 ,
所以 .
由(1)易得 ,
所以 ,
所以 ,
所以 .
返回
课堂小结
互 余 互 补
数量 关系
对 应 图 形
性 质
∠1+∠2=90°
∠3+∠4=180°
同角或等角的余角相等
同角或等角的补角相等
谢谢观看!
3.6.3 余角和补角
第3章 图形的初步认识
【华东师大版·2024】数学 七年级上册
授课教师:********
班 级:********
时 间:********
幻灯片 1:封面
标题:3.6.3 余角和补角
副标题:理解余角与补角的概念,掌握其性质
幻灯片 2:学习目标
理解余角和补角的定义,能准确判断两个角是否互为余角或补角。
掌握余角和补角的性质(同角或等角的余角相等,同角或等角的补角相等),并能运用性质解决问题。
能进行余角和补角的计算,培养逻辑推理和运算能力。
幻灯片 3:情境引入 —— 特殊的角的关系
展示图片:一副直角三角尺(其中一个三角尺的两个锐角分别为 30° 和 60°,另一个为 45° 和 45°)。
提问:观察这两个三角尺,每个三角尺的两个锐角之和是多少度?平角是 180°,如果一个角是 120°,那么另一个角是多少度时,它们的和是 180°?
引入:在角的运算中,有两种特殊的角的关系非常重要,那就是余角和补角。本节课我们就来学习余角和补角。
幻灯片 4:余角的定义
定义:如果两个角的和等于 90°(直角),就说这两个角互为余角,简称互余。其中一个角是另一个角的余角。
几何表示:若∠1 + ∠2 = 90°,则∠1 与∠2 互为余角,即∠1 是∠2 的余角,∠2 也是∠1 的余角。
示例:∠A = 30°,∠B = 60°,因为 30° + 60° = 90°,所以∠A 与∠B 互为余角。
说明:
互为余角的两个角只与它们的度数之和有关,与位置无关。
一个角的余角可以有多个,但它们的度数都相等(因为 90° 减去这个角的度数是固定的)。
幻灯片 5:补角的定义
定义:如果两个角的和等于 180°(平角),就说这两个角互为补角,简称互补。其中一个角是另一个角的补角。
几何表示:若∠3 + ∠4 = 180°,则∠3 与∠4 互为补角,即∠3 是∠4 的补角,∠4 也是∠3 的补角。
示例:∠C = 110°,∠D = 70°,因为 110° + 70° = 180°,所以∠C 与∠D 互为补角。
说明:
互为补角的两个角同样只与度数之和有关,与位置无关。
一个角的补角也可以有多个,且度数相等(180° 减去这个角的度数是固定的)。
幻灯片 6:余角和补角的性质
性质 1(余角):同角或等角的余角相等。
几何表示:
若∠1 + ∠2 = 90°,∠1 + ∠3 = 90°,则∠2 = ∠3(同角的余角相等)。
若∠1 + ∠2 = 90°,∠3 + ∠4 = 90°,且∠1 = ∠3,则∠2 = ∠4(等角的余角相等)。
性质 2(补角):同角或等角的补角相等。
几何表示:
若∠1 + ∠2 = 180°,∠1 + ∠3 = 180°,则∠2 = ∠3(同角的补角相等)。
若∠1 + ∠2 = 180°,∠3 + ∠4 = 180°,且∠1 = ∠3,则∠2 = ∠4(等角的补角相等)。
示例:若∠α = 50°,则∠α 的余角是 40°;若∠β = 50°,则∠β 的余角也是 40°,体现等角的余角相等。
幻灯片 7:余角和补角的计算
求一个角的余角:若已知角为 x°,则它的余角为(90 - x)°(x° < 90°)。
求一个角的补角:若已知角为 x°,则它的补角为(180 - x)°(x° < 180°)。
示例:
60° 的余角是 90° - 60° = 30°。
120° 的补角是 180° - 120° = 60°。
幻灯片 8:例题 1—— 判断互余或互补
题目:判断下列各组角是否互为余角或补角:
(1)∠1 = 30°,∠2 = 60°
(2)∠3 = 100°,∠4 = 80°
(3)∠5 = 75°,∠6 = 25°
解答过程:
(1)∠1 + ∠2 = 30° + 60° = 90°,所以∠1 与∠2 互为余角。
(2)∠3 + ∠4 = 100° + 80° = 180°,所以∠3 与∠4 互为补角。
(3)∠5 + ∠6 = 75° + 25° = 100°,既不互余也不互补。
结论:(1)互为余角;(2)互为补角;(3)都不是。
幻灯片 9:例题 2—— 求角的余角或补角
题目:
(1)求 58° 角的余角和补角。
(2)一个角的补角是它的 3 倍,求这个角的度数。
解答过程:
(1)余角:90° - 58° = 32°;补角:180° - 58° = 122°。
(2)设这个角的度数为 x°,则它的补角为(180 - x)°,根据题意得 180 - x = 3x,解得 x = 45。
结论:(1)余角 32°,补角 122°;(2)这个角是 45°。
幻灯片 10:例题 3—— 余角和补角性质的应用
题目:已知∠A 与∠B 互为余角,∠A 与∠C 互为补角,且∠B = 25°,求∠C 的度数。
解答过程:
因为∠A 与∠B 互为余角,所以∠A = 90° - ∠B = 90° - 25° = 65°。
因为∠A 与∠C 互为补角,所以∠C = 180° - ∠A = 180° - 65° = 115°。
结论:∠C = 115°。
幻灯片 11:课堂练习 1—— 基本计算
题目:
(1)70° 的余角是( )°,补角是( )°。
(2)一个角的余角是 35°,这个角是( )°,它的补角是( )°。
答案:(1)20,110;(2)55,125。
幻灯片 12:课堂练习 2—— 性质应用
题目:已知∠1 与∠2 互为余角,∠3 与∠4 互为余角,且∠1 = ∠3,求证∠2 = ∠4。
证明过程:
因为∠1 与∠2 互为余角,所以∠1 + ∠2 = 90°,即∠2 = 90° - ∠1。
因为∠3 与∠4 互为余角,所以∠3 + ∠4 = 90°,即∠4 = 90° - ∠3。
又因为∠1 = ∠3,所以∠2 = ∠4。
幻灯片 13:课堂练习 3—— 综合应用
题目:一个角的补角比它的余角的 3 倍多 10°,求这个角的度数。
解答过程:
设这个角的度数为 x°,则它的补角为(180 - x)°,余角为(90 - x)°。
根据题意得:180 - x = 3(90 - x) + 10。
解方程:180 - x = 270 - 3x + 10,2x = 100,x = 50。
答案:这个角是 50°。
幻灯片 14:易错点分析
常见错误:
对余角和补角的定义理解不透彻,认为只有两个锐角才能互余,实际上只要两角之和为 90° 就互余,与角的类型无关(但钝角没有余角)。
混淆余角和补角的性质,在应用时出现逻辑错误,如错误认为 “同角的余角与补角相等”。
计算一个角的余角或补角时,忽略角的度数范围,如求 100° 的余角,而 100° 大于 90°,没有余角。
规避方法:
牢记余角和补角的定义,重点关注两角之和是否为 90° 或 180°,而非角的具体类型。
区分余角和补角的性质,通过几何表示和实例理解 “同角或等角的余角相等” 与 “同角或等角的补角相等” 的不同适用场景。
计算前先判断角是否有对应的余角或补角:锐角(小于 90°)才有余角,锐角、直角、钝角(小于 180°)才有补角。
幻灯片 15:课堂小结
余角和补角的定义:
互余:两角之和为 90°。
互补:两角之和为 180°。
性质:
同角或等角的余角相等。
同角或等角的补角相等。
计算:
余角 = 90° - 已知角(已知角 < 90°)。
补角 = 180° - 已知角(已知角 < 180°)。
幻灯片 16:布置作业
基础作业:
教材课后练习题第 1、2 题(判断互余互补、计算余角补角)。
一个角的度数是 36°,求它的余角和补角的度数。
提升作业:
已知∠α 和∠β 互为补角,且∠α 比∠β 大 30°,求∠α 和∠β 的度数。
如图,点 O 在直线 AB 上,OC 是∠AOD 的平分线,∠DOB = 90°,求证∠COD 与∠BOD 互余。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
情境导入
45°
45°
30°
60°
90°
90°
和都是90°
探索新知
1
2
α
β
用量角器量一量两组图中各角的大小,看看你发现了什么?
20°
70°
40°
50°
∠1+∠2=90°
∠α+∠β=90°
1
2
α
β
两个角的和等于90°(直角),就说这两个角互为余角.
简称互余.
1
2
α
β
如果∠1+∠2=90°,那么∠1是∠2的余角,∠2也是∠1的余角.
两个角的和等于90°(直角),就说这两个角互为余角.
1
2
反过来,如果两个角互余,
1
那么把这两个角像这样拼一起,就构成一个直角.
α
β
3
4
同样,如果两个角的和等于180°(平角),
就说这两个角互为补角,简称互补.
∠3+∠4=180°,所以∠3、∠4的互为补角.
1
2
3
4
想想看,如果∠1与∠2互余,∠3与∠4互余,∠2 =∠4,那么∠1和∠3有什么关系?相等角的补角又有什么关系?
∠1=∠3
归纳总结
同角或等角的余角相等;同角或等角的补角相等.
例3 已知∠α=50°17′,求∠α的余角和补角.
∠α的余角=90°-50°17′=39°43′
∠α的补角=180°-50°17′=129°43′
随堂练习
1. 说出图中互余和互补的角.
E
A
B
F
D
∠AED和∠DEB、
∠BEF和∠AEF
互补的角:
∠DEF和∠FEB
互余的角:
【教材P162 练习 第1题】
2.如图,有两堵围墙,有人想测量地面上所形成的∠AOB的度数,但人又不能进入围墙,只能站在墙外,请问该如何测量?
延长AO,测量∠AOB的补角即可.
提示:也可延长BO.
【教材P162 练习 第2题】
3 如图,已知∠AOB,利用尺规作图作一个角等于该角
补角.
B
O
A
C
∠COB是∠AOB是的补角
【教材P162 练习 第3题】
知识点1 余角和补角的定义
1.若 ,则 的补角为( )
D
A. B. C. D.
返回
2.若,则 的余角为( )
A
A. B. C. D.
返回
3.[2025成都期末]若两个角互补,则( )
D
A.这两个角都是锐角
B.这两个角都是钝角
C.这两个角一定一个是锐角,一个是钝角
D.以上答案都不对
返回
4.[教材P162练习T1变式]如图,,, 三点在同一条直线上,
.
(1) 的余角是_______,补角是_______;
(2)若 ,则 ______.
返回
5.若一个角的余角的3倍比这个角的补角多 ,则这个角的度数为_____.
返回
6.(8分)[教材P162练习T3变式]如图, , 平分
, .
(1)与互余吗?与 互补吗?试说明理由.
解:与互余.与 互补.理由如下:
因为 ,平分 ,
所以 .
又因为,所以 ,
所以 ,即与 互余.
因为 ,
所以与 互补.
(2)利用尺规作图,作一个角等于 的补角.(不写作法,保留作图痕迹)
解:如图, 即为所求.
返回
知识点2 余角和补角的性质
7. 若 , ,则与 的大小关系
是_________,理由是________________;若 ,且
, ,则与 的大小关系是______
___,理由是________________.
同角的余角相等
等角的补角相等
返回
(第8题)
8.[2025周口期末]如图,将一副三角板的直角
顶点重合摆放在桌面上,若 ,则
等于( )
B
A. B. C. D.
(第9题)
9.如图,直线,相交于点, ,那么
______.
返回
10.(8分)如图, , .
(1)的余角为______________; 的补角为______________.
,
,
(2)与有怎样的数量关系,为什么?与 有怎
样的数量关系,为什么?
解:因为, , ,
所以 .
因为 .
所以 ,
.
又因为 ,
所以 .
返回
11.[2025莆田期末]如图,将一副三角板按不同位置摆放,其中 和
不一定相等的是( )
D
A. B. C. D.
返回
(第12题)
12.如图,射线的方向为南偏东 ,且 平分
,则射线 的方向为( )
B
A.南偏西 B.南偏西 C.南偏西 D.西偏南
返回
13.已知两个角的度数比是,差是 ,则这两个角的关系是( )
B
A.互余 B.互补
C.既不互余也不互补 D.不能确定
返回
14.[2025长春期末]如果 和 互补,且 ,下列表示
的余角的式子中不正确的是( )
C
A. B. C. D.
返回
(第15题)
15.如图,点在直线上, ,
下列说法错误的是( )
D
A.与相等 B.与 互余
C.与互补 D.与 互补
返回
16.(8分)[2025驻马店期末]如图,是直线上一点, 为任意一
条射线,平分,平分 .
(1)图中的补角是_______________; 的余角是_________
______.
,
,
(2)与 具有怎样的数量关系?说明理由.
解: .理由:
因为平分,平分,所以 ,
,所以
,
即与的数量关系是 .
返回
17.(8分)如图,,, 三点在同一直线
上,与 互补.
(1)若 ,求 的度数;
解:因为,,三点在同一直线上,所以 ,
所以与 互补.
又因为与 互补,
所以 .
(2)已知平分,若射线在的内部,且满足 与
互余,试探究与 之间有怎样的数量关系,并说明理由.
解: .理由:
设 ,
因为平分 ,
所以 .
因为与 互余,
所以 ,
所以 .
由(1)易得 ,
所以 ,
所以 ,
所以 .
返回
课堂小结
互 余 互 补
数量 关系
对 应 图 形
性 质
∠1+∠2=90°
∠3+∠4=180°
同角或等角的余角相等
同角或等角的补角相等
谢谢观看!
同课章节目录
