4.1.2 垂线 课件(共52张PPT)
文档属性
| 名称 | 4.1.2 垂线 课件(共52张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 10.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 00:00:00 | ||
图片预览







文档简介
(共52张PPT)
4.1.2 垂线
第4章 相交线和平行线
【华东师大版·2024】数学 七年级上册
授课教师:********
班 级:********
时 间:********
幻灯片 1:封面
标题:4.1.2 垂线
副标题:理解垂线的概念,掌握垂线的性质与画法
幻灯片 2:学习目标
理解垂线的概念,知道两条直线互相垂直的含义,能正确表示两条互相垂直的直线。
掌握垂线的性质(在同一平面内,过一点有且只有一条直线与已知直线垂直),并能运用该性质解决问题。
学会用三角尺或量角器画一条直线的垂线,培养动手操作能力。
理解点到直线的距离的概念,能测量点到直线的距离。
幻灯片 3:情境引入 —— 生活中的垂直现象
展示图片:墙角的两条相交直线(互相垂直)、黑板的相邻两边(互相垂直)、十字路口的两条道路(互相垂直)、单杠的横杠与竖杠(互相垂直)。
提问:这些相交的直线所形成的角有什么特点?它们的位置关系有什么特殊之处?
引入:像这样相交成直角的两条直线,它们的位置关系就是垂直。本节课我们就来学习垂线的相关知识。
幻灯片 4:垂线的概念
定义:如果两条直线相交成直角,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足。
图形表示:画出直线 AB 和 CD 相交于点 O,且∠AOC=90°,标注 “AB⊥CD,垂足为 O”。
符号表示:“⊥” 是垂直符号,直线 AB 与直线 CD 互相垂直,记作 “AB⊥CD”(或 “CD⊥AB”),读作 “AB 垂直于 CD”。如果垂足为 O,还可以记作 “AB⊥CD 于 O”。
说明:
两条直线互相垂直是它们相交的一种特殊情况,只有当相交的角是直角(90°)时,才称这两条直线互相垂直。
垂直是相互的,若直线 a 是直线 b 的垂线,则直线 b 也是直线 a 的垂线。
幻灯片 5:垂线的性质
性质 1:在同一平面内,过一点有且只有一条直线与已知直线垂直。
理解:“过一点” 可以是直线上的点,也可以是直线外的点;“有且只有” 意味着存在性(有一条)和唯一性(只有一条)。
图形展示:
过直线 l 上一点 P,画直线 l 的垂线,只能画出一条。
过直线 l 外一点 Q,画直线 l 的垂线,也只能画出一条。
生活实例:在地面上,过一点要挖一条与已知直线道路垂直的水渠,只能挖出一条。
性质 2:连接直线外一点与直线上各点的所有线段中,垂线段最短。简单说成:垂线段最短。
幻灯片 6:点到直线的距离
定义:从直线外一点到这条直线的垂线段的长度,叫做这点到这条直线的距离。
图形展示:画出直线 l 和直线外一点 P,过 P 作 l 的垂线,垂足为 O,线段 PO 就是垂线段,标注 “PO 的长度就是点 P 到直线 l 的距离”。
说明:
点到直线的距离是一个长度,是数量,而垂线段是一个图形,两者不能混淆。
测量点到直线的距离时,要先画出垂线段,再测量其长度。
生活应用:测量跳远成绩时,从落地点向起跳线画垂线段,垂线段的长度就是跳远成绩,这是利用了 “垂线段最短” 的性质。
幻灯片 7:垂线的画法
方法 1:用三角尺画垂线
过直线上一点画已知直线的垂线:
把三角尺的一条直角边与已知直线重合。
沿着已知直线移动三角尺,使三角尺的直角顶点与直线上的已知点重合。
沿着三角尺的另一条直角边画一条直线,这条直线就是已知直线的垂线(标出垂直符号)。
过直线外一点画已知直线的垂线:
把三角尺的一条直角边与已知直线重合。
沿着已知直线移动三角尺,使三角尺的另一条直角边经过直线外的已知点。
沿着三角尺的另一条直角边画一条直线,这条直线就是已知直线的垂线(标出垂直符号)。
方法 2:用量角器画垂线
在已知直线上取一点(或过直线外一点)作为垂足的大致位置。
把量角器的中心与该点重合,0° 刻度线与已知直线重合。
在量角器 90° 刻度线的位置处点一个点。
过该点和已知点画一条直线,这条直线就是已知直线的垂线(标出垂直符号)。
幻灯片 8:例题 1—— 判断垂直关系
题目:如图,直线 AB、CD、EF 相交于点 O,∠AOC=90°,请找出图中所有互相垂直的直线,并说明理由。
图形:三条直线相交于点 O,∠AOC=90°。
解答过程:
因为∠AOC=90°,且∠AOC 与∠BOD 是对顶角,所以∠BOD=90°(对顶角相等)。
又因为∠AOC 与∠BOC 互补,所以∠BOC=180°-90°=90°,同理∠AOD=90°。
因此,AB⊥CD(因为它们相交成直角)。
若∠AOE=90°,则 AB⊥EF,以此类推(根据图形中其他直角情况判断)。
结论:AB⊥CD。
幻灯片 9:例题 2—— 应用垂线性质画图
题目:如图,过点 P 画直线 l 的垂线,过点 Q 画直线 m 的垂线。
图形:直线 l 和直线 m,点 P 在直线 l 外,点 Q 在直线 m 上。
解答过程:
过点 P 画直线 l 的垂线:按照三角尺画法,画出直线 l 的垂线,垂足为 A,标注 “PA⊥l”。
过点 Q 画直线 m 的垂线:按照三角尺画法,画出直线 m 的垂线,垂足为 Q,标注 “DQ⊥m(D 为垂线上一点)”。
结论:如图所示(画出相应垂线)。
幻灯片 10:例题 3—— 点到直线的距离计算
题目:如图,在直线 l 上有 A、B、C 三点,点 P 在直线 l 外,且 PO⊥l,垂足为 O,PA=5cm,PB=3cm,PC=4cm,PO=2cm,求点 P 到直线 l 的距离。
图形:直线 l 上有 A、B、C、O 四点,PO⊥l,PO=2cm,PA、PB、PC 为连接 P 与 A、B、C 的线段。
解答过程:
因为 PO⊥l,垂足为 O,所以 PO 是点 P 到直线 l 的垂线段。
根据点到直线的距离的定义,点 P 到直线 l 的距离就是 PO 的长度。
已知 PO=2cm,所以点 P 到直线 l 的距离是 2cm。
结论:点 P 到直线 l 的距离是 2cm。
幻灯片 11:课堂练习 1—— 表示垂直关系
题目:如图,直线 a 与直线 b 相交于点 O,且∠1=90°,则直线 a 与直线 b 的位置关系是( ),记作( ),读作( ),垂足是( )。
答案:互相垂直;a⊥b(或 b⊥a);a 垂直于 b(或 b 垂直于 a);点 O
幻灯片 12:课堂练习 2—— 应用垂线性质
题目:在同一平面内,过直线 l 外一点 P,可以画( )条直线与直线 l 垂直;过直线 l 上一点 Q,可以画( )条直线与直线 l 垂直。
答案:1;1
幻灯片 13:课堂练习 3—— 点到直线的距离
题目:如图,要从 A 地向河流 l 修一条水渠,应怎样修才能使水渠最短?请画出示意图,并说明理由。
图形:点 A 在河流 l 的一侧。
解答过程:
过点 A 画河流 l 的垂线,垂足为 B,沿着 AB 修水渠最短。
理由是:连接直线外一点与直线上各点的所有线段中,垂线段最短。
答案:过点 A 作 l 的垂线,沿垂线段修水渠,理由是垂线段最短。
幻灯片 14:易错点分析
常见错误:
对垂线的概念理解不透彻,认为只要两条直线相交就互相垂直,忽略 “相交成直角” 这个关键条件。
混淆 “垂线段” 和 “点到直线的距离”,把垂线段本身当成距离,实际上距离是垂线段的长度。
画垂线时,未使三角尺的直角边与已知直线完全重合,导致画出的直线与已知直线不垂直。
忽略垂线性质中 “在同一平面内” 的前提,错误认为在空间中过一点也只有一条直线与已知直线垂直(实际上在空间中可以有无数条)。
规避方法:
牢记垂线的定义,判断两条直线是否垂直时,必须看它们相交是否成直角(90°)。
明确垂线段是图形,点到直线的距离是该图形的长度(数值),区分两者的概念。
画垂线时,严格按照操作步骤进行,确保三角尺的直角边与已知直线紧密重合,画图后可用量角器检查是否成 90°。
应用垂线性质时,注意其适用范围是 “在同一平面内”,这是小学和初中阶段主要研究的范围。
幻灯片 15:课堂小结
垂线的概念:两条直线相交成直角时互相垂直,其中一条是另一条的垂线,交点是垂足,用 “⊥” 表示。
垂线的性质:在同一平面内,过一点有且只有一条直线与已知直线垂直;垂线段最短。
点到直线的距离:直线外一点到这条直线的垂线段的长度。
垂线的画法:用三角尺或量角器,过一点画已知直线的垂线。
幻灯片 16:布置作业
基础作业:
教材课后练习题第 1、2、3 题(判断垂直关系、画垂线、计算点到直线的距离)。
画一条直线 l,在直线 l 外任取一点 P,过点 P 画直线 l 的垂线,并量出点 P 到直线 l 的距离。
提升作业:
如图,直线 AB⊥CD,垂足为 O,OE 平分∠AOD,求∠COE 的度数。
已知点 P 到直线 l 的距离是 3cm,画出满足条件的点 P 的轨迹。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
观察以上图片中直线,它们有什么特殊的位置关系?
情景引入
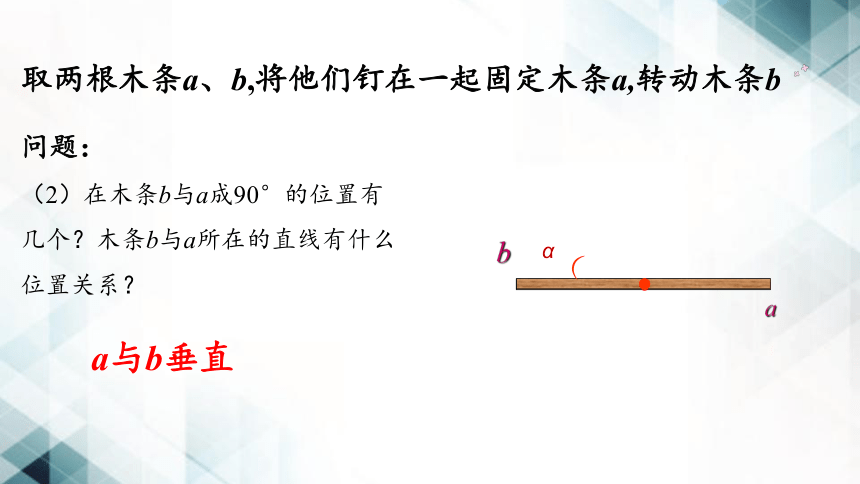
取两根木条a、b,将他们钉在一起固定木条a,转动木条b
a
b
)
α
垂线的概念
问题:
(1)在木条b转动的过程中,什么也随着改变
a与b所成的角也随之发生改变
取两根木条a、b,将他们钉在一起固定木条a,转动木条b
问题:
(2)在木条b与a成90°的位置有几个?木条b与a所在的直线有什么位置关系?
a
b
)
α
a与b垂直
定义:两条直线相交所构成的四个角中有一个为直角时,其他三个角也都成为直角,此时,这两条直线互相垂直.
记作:AB⊥CD或m⊥l
注意:两条线段互相垂直是指这两条线段所在的直线互相垂直.(如图2)
垂直的定义及表示方法
A
B
C
D
O
(2)
B
C
D
O
(1)
A
l
m
两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
记作:AB⊥CD于点O
A
B
C
D
O
符号语言:
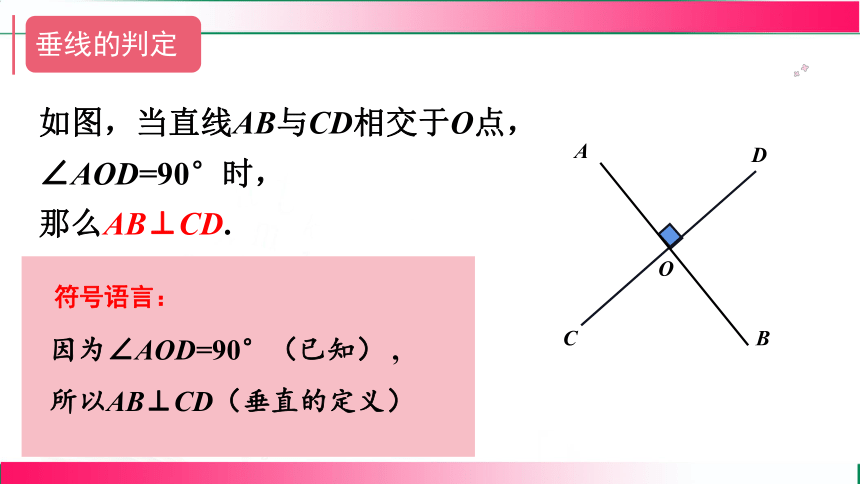
如图,当直线AB与CD相交于O点,∠AOD=90°时,
那么AB⊥CD.
因为∠AOD=90°(已知) ,
所以AB⊥CD(垂直的定义)
垂线的判定
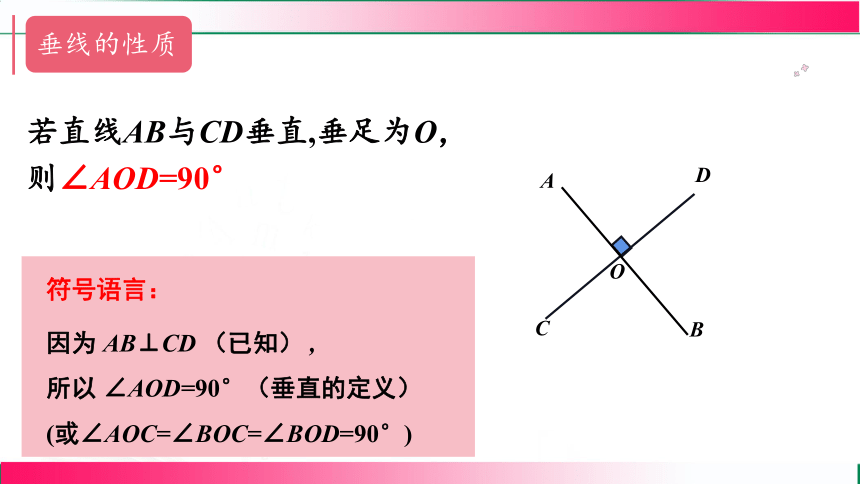
符号语言:
若直线AB与CD垂直,垂足为O,
则∠AOD=90°
因为 AB⊥CD (已知) ,
所以 ∠AOD=90°(垂直的定义)
(或∠AOC=∠BOC=∠BOD=90°)
A
B
C
D
O
垂线的性质
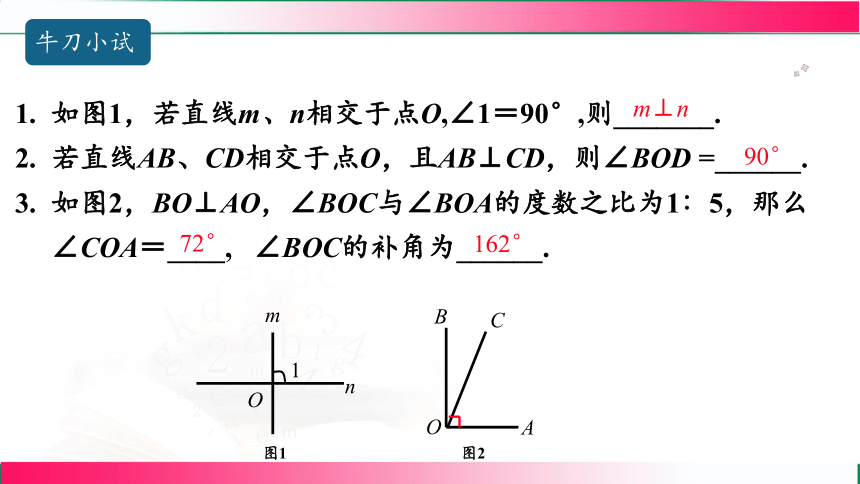
如图1,若直线m、n相交于点O,∠1=90°,则_______.
若直线AB、CD相交于点O,且AB⊥CD,则∠BOD =______.
如图2,BO⊥AO,∠BOC与∠BOA的度数之比为1∶5,那么∠COA=____, ∠BOC的补角为______.
O
m
n
1
B
C
A
O
m⊥n
90°
72°
162°
图1
图2
牛刀小试
4.日常生活中,我们经常可以看到线线互相垂直的图形,你能再举出一些例子么?
经过直线AB外一点P,按图中所示的两种方法,画出垂直于直线AB的直线,这样的垂线能画多少条呢?
垂线的画法及基本事实
试一试
P
B
A
(1)
(2)
P
A
B
B
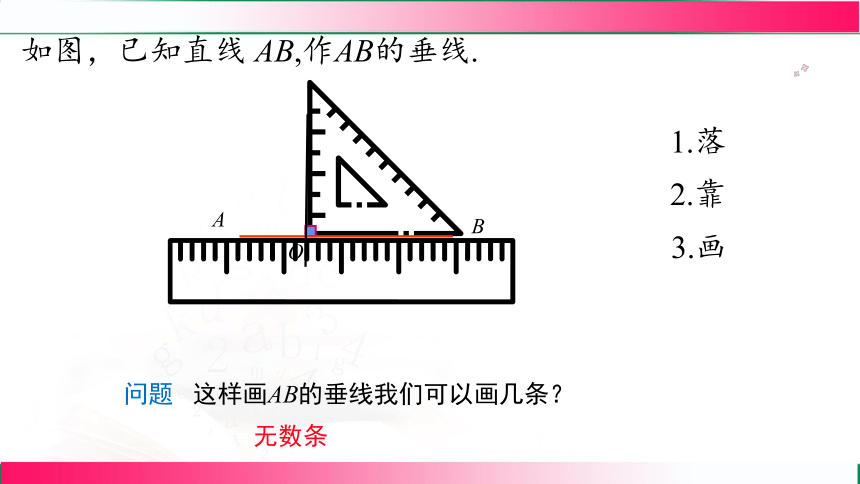
问题 这样画AB的垂线我们可以画几条?
O
如图,已知直线 AB,作AB的垂线.
无数条
1.落
2.靠
3.画
A
B
P
如图,已知直线 AB 和AB上的一点P ,过点P作AB的垂线.
问题 这样画l的垂线可以画几条?
一条
1.落
2.靠
3.移
4.画
A
B
P
如图,已知直线 AB 和AB外的一点P ,过点P作AB的垂线.
根据以上几种情况的操作,你能得出什么结论?
问题 这样画l的垂线可以画几条?
一条
1.落
2.靠
3.移
4.画
A
注意:
1.“过一点”中的点,可以在已知直线上,也可以在已知直线外;
2.“有且只有”中,“有”指存在性,“只有”指唯一性.
同一平面内,过一点有且只有一条直线与已知直线垂直.
垂线的性质
特殊的直线
如图,如果直线CD经过线段AB的中点O,并且CD⊥AB,我们可以得到AO=BO, CD⊥AB.
A
B
C
D
O
//
//
此时,我们将垂直并且平分一条线段的直线叫做这条线段的垂直平分线(图中直线CD即为线段AB的垂直平分线)
垂直平分线又可称为中垂线
如图①所示,已知钝角∠AOB,点 D 在射线 OB 上.
(1)画直线 DE⊥OB;
(2)画直线 DF⊥OA,垂足为 F.
解: (1)如图②所示,直线DE为所求作的直线.
(2)如图②所示,直线DF为所求作的直线.
牛刀小试
探究:在如图所示的方格图中,点A是直线l外一点,从A点向已知直线 l 画一条垂直的线段和几条不垂直的线段.
1.线段AB, AC, AD ,AE谁最短?
2.你能用一句话表示这个结论吗?
说一说:
连接直线外一点与直线上各点的所有线段中,垂线段最短
简述:垂线段最短.
线段AB的长度叫做点A到直线l的距离.
规定:
作图过程中我们可以发现其中最短的应该是线段AB,线段AB叫做点A到直线l的垂线段
从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
垂线段
思考:体育课上是怎样测量跳远成绩的?你知道其中的原因吗?
1.在灌溉时,要把河中的水引到农田P处,如何挖掘能使渠道最短?请画出图来,并说明理由.
m
垂线段最短
牛刀小试
如图,小海龟位于图中点 A 处,按下述口令移动:前进 3 格;向右转 90°,前进 5 格;向左转 90°,前进3 格;向左转 90°,前进 6 格;向右转 90°,后退 6 格;最后向右转 90°,前进 1 格. 用粗线将小海龟经过的路线描出来,看一看是什么图形.
做一做
1.如图,∠ABD = 90°,在下列各语句中填入适当的文字或数字: 【教材P175 练习 第1题】
(1)点 B 在直线______________上,点 D 在直线______外;
(2)直线_____与直线_____相交于点 A,点 D 是直线_____与直线_____的交点,也是直线_____与直线______的交点,又是直线_____与直线_____的交点;
(3)直线_____垂直于直线______,垂足为点_____;
(4)过点 D 有且只有_____条直线与直线 AC 垂直.
AC (或BD)
AC
AD
AC
AD
BD
AD
CD
BD
CD
BD
AC
B
一
随堂练习
如图所示的各个三角形中,分别过点 C 画出直线 AB 的垂线,并量出三角形顶点 C 到直线 AB 的距离.(精确到 1mm) 【教材P176 练习 第2题】
14 mm
23 mm
17 mm
(D)
3.在如图所示的方格图中,按下述要求画图并回答问题【教材P176 练习 第3题】
(1)过点C画线段AB的垂线,垂足为点D;
(2)量出点C到线段AB所在直线的距离(精确到1mm)
(3)画出线段AB的垂直平分线
C
A
B
D
4.如图, AC⊥BC,∠C=90°线段AC、BC、CD中最短的是( )
A. AC B. BC
C. CD D. 不能确定
D
A
B
C
C
知识点1 垂直的定义
1.如图所示,,且 ,则 的度数是( )
D
(第1题)
A. B. C. D.
返回
2.如图,直线,相交于点,下列条件能说明 的是( )
B
(第2题)
; ;
; .
A.①② B.①③ C.②④ D.①③④
返回
3.[2025南阳期末]如图,,直线经过点.若 ,
则 _____.
(第3题)
返回
知识点2 垂线的画法
4.下列选项中,过点画的垂线 ,三角板放法正确的是( )
C
A. B. C. D.
返回
5.(8分)利用三角板和直尺作图.
(1)如图①,过点分别画 ,
的垂线;
解:如图①所示,直线,,, 即为所求.
(2)如图②,过点画 的垂线.
解:如图②所示,直线 即为所求.
返回
知识点3 垂线的基本事实及线段的垂直平分线
6.在平面内作已知直线的垂线,可作( )
D
A.0条 B.1条 C.2条 D.无数条
返回
7.如图,若,,则与 ______,其理由是_______
_____________________________________________.
共线
同一
平面内,过一点有且只有一条直线与已知直线垂直
(第7题)
返回
8.在如图所示的方格图中,线段 的垂直平分线是四条直线中的直线___.
(第8题)
返回
知识点4 垂线段
(第9题)
9.如图,在同一平面内有直线及直线外一点 ,作
,垂足为,则点到直线 的距离是( )
A
A.线段的长度 B.线段 的长度
C.线段的长度 D.线段 的长度
返回
10. 运动会上,跳远运动员跳落到沙坑时的痕迹和测量跳
远成绩的方法如图所示,应选择其中的____(填序号)号线的长度作为
跳远成绩,这样测量的依据是____________.
③
垂线段最短
(第10题)
返回
11.(12分)如图,在直角三角形中, , ,
, .
(1)点到的距离是___ ;
(2)点到点的距离是____ ;
8
10
(3)画出表示点到的距离的线段,则____ .
4.8
解:如图所示
返回
12. 为直线外一点,,,为直线上三点, ,
,,则点到直线 的距离( )
D
A.是 B.是 C.小于 D.不大于
返回
13. 如图是光的反射规律示意图,是入射光线,
是反射光线,法线,是入射角, 是反射角,
.若,则 的度数为_____.
(第13题)
返回
14.[2025信阳期末]如图,已知直线和相交于点, ,
平分, ,则的度数为____ .
22
(第14题)
返回
15.(12分)[教材P练习T ]在如图所示
的方格纸中,按下列要求画图并回答问题:
(1)过点画线段的垂线,垂足为 ;
解:如图所示,即为 的垂线.
(2)量出点到线段所在直线的距离精确到 ;
解: .
(3)连结,画出一条直线,使该直线垂直并且平分线段 .
解:如图,直线 即为所求.
返回
16.(8分)如图,直线,相交于点, .
(1)若 , ,求 的度数.
解:因为,所以 .
因为 ,所以 .
因为 ,所以 .
(2)如果,那么与 互相垂直吗?请说明理由.
解: .理由如下:
因为 , ,
所以 ,即 ,所以 .
返回
17.(16分) 已知一个
角的两边与另一个角的两边分别垂直,
试探索这两个角之间的数量关系.
(1)如图①,,,
与 的数量关系是_________;
(2)如图②,,,与 的数量关系是__________
_______;
(3)由 得出结论:若一个角的两边与另一个角的两边分别垂直,
则这两个角____________;
相等或互补
(4)若两个角的两边互相垂直,且一个角比另一个角的3倍少 ,则
求这两个角的度数.
解:设另一个角的度数为 ,则这个角的度数为 ,
根据题意可得 或 ,解得
或 ,
当 时, ,
当 时, ,
所以这两个角的度数为 , 或 , .
返回
课堂小结
谢谢观看!
4.1.2 垂线
第4章 相交线和平行线
【华东师大版·2024】数学 七年级上册
授课教师:********
班 级:********
时 间:********
幻灯片 1:封面
标题:4.1.2 垂线
副标题:理解垂线的概念,掌握垂线的性质与画法
幻灯片 2:学习目标
理解垂线的概念,知道两条直线互相垂直的含义,能正确表示两条互相垂直的直线。
掌握垂线的性质(在同一平面内,过一点有且只有一条直线与已知直线垂直),并能运用该性质解决问题。
学会用三角尺或量角器画一条直线的垂线,培养动手操作能力。
理解点到直线的距离的概念,能测量点到直线的距离。
幻灯片 3:情境引入 —— 生活中的垂直现象
展示图片:墙角的两条相交直线(互相垂直)、黑板的相邻两边(互相垂直)、十字路口的两条道路(互相垂直)、单杠的横杠与竖杠(互相垂直)。
提问:这些相交的直线所形成的角有什么特点?它们的位置关系有什么特殊之处?
引入:像这样相交成直角的两条直线,它们的位置关系就是垂直。本节课我们就来学习垂线的相关知识。
幻灯片 4:垂线的概念
定义:如果两条直线相交成直角,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足。
图形表示:画出直线 AB 和 CD 相交于点 O,且∠AOC=90°,标注 “AB⊥CD,垂足为 O”。
符号表示:“⊥” 是垂直符号,直线 AB 与直线 CD 互相垂直,记作 “AB⊥CD”(或 “CD⊥AB”),读作 “AB 垂直于 CD”。如果垂足为 O,还可以记作 “AB⊥CD 于 O”。
说明:
两条直线互相垂直是它们相交的一种特殊情况,只有当相交的角是直角(90°)时,才称这两条直线互相垂直。
垂直是相互的,若直线 a 是直线 b 的垂线,则直线 b 也是直线 a 的垂线。
幻灯片 5:垂线的性质
性质 1:在同一平面内,过一点有且只有一条直线与已知直线垂直。
理解:“过一点” 可以是直线上的点,也可以是直线外的点;“有且只有” 意味着存在性(有一条)和唯一性(只有一条)。
图形展示:
过直线 l 上一点 P,画直线 l 的垂线,只能画出一条。
过直线 l 外一点 Q,画直线 l 的垂线,也只能画出一条。
生活实例:在地面上,过一点要挖一条与已知直线道路垂直的水渠,只能挖出一条。
性质 2:连接直线外一点与直线上各点的所有线段中,垂线段最短。简单说成:垂线段最短。
幻灯片 6:点到直线的距离
定义:从直线外一点到这条直线的垂线段的长度,叫做这点到这条直线的距离。
图形展示:画出直线 l 和直线外一点 P,过 P 作 l 的垂线,垂足为 O,线段 PO 就是垂线段,标注 “PO 的长度就是点 P 到直线 l 的距离”。
说明:
点到直线的距离是一个长度,是数量,而垂线段是一个图形,两者不能混淆。
测量点到直线的距离时,要先画出垂线段,再测量其长度。
生活应用:测量跳远成绩时,从落地点向起跳线画垂线段,垂线段的长度就是跳远成绩,这是利用了 “垂线段最短” 的性质。
幻灯片 7:垂线的画法
方法 1:用三角尺画垂线
过直线上一点画已知直线的垂线:
把三角尺的一条直角边与已知直线重合。
沿着已知直线移动三角尺,使三角尺的直角顶点与直线上的已知点重合。
沿着三角尺的另一条直角边画一条直线,这条直线就是已知直线的垂线(标出垂直符号)。
过直线外一点画已知直线的垂线:
把三角尺的一条直角边与已知直线重合。
沿着已知直线移动三角尺,使三角尺的另一条直角边经过直线外的已知点。
沿着三角尺的另一条直角边画一条直线,这条直线就是已知直线的垂线(标出垂直符号)。
方法 2:用量角器画垂线
在已知直线上取一点(或过直线外一点)作为垂足的大致位置。
把量角器的中心与该点重合,0° 刻度线与已知直线重合。
在量角器 90° 刻度线的位置处点一个点。
过该点和已知点画一条直线,这条直线就是已知直线的垂线(标出垂直符号)。
幻灯片 8:例题 1—— 判断垂直关系
题目:如图,直线 AB、CD、EF 相交于点 O,∠AOC=90°,请找出图中所有互相垂直的直线,并说明理由。
图形:三条直线相交于点 O,∠AOC=90°。
解答过程:
因为∠AOC=90°,且∠AOC 与∠BOD 是对顶角,所以∠BOD=90°(对顶角相等)。
又因为∠AOC 与∠BOC 互补,所以∠BOC=180°-90°=90°,同理∠AOD=90°。
因此,AB⊥CD(因为它们相交成直角)。
若∠AOE=90°,则 AB⊥EF,以此类推(根据图形中其他直角情况判断)。
结论:AB⊥CD。
幻灯片 9:例题 2—— 应用垂线性质画图
题目:如图,过点 P 画直线 l 的垂线,过点 Q 画直线 m 的垂线。
图形:直线 l 和直线 m,点 P 在直线 l 外,点 Q 在直线 m 上。
解答过程:
过点 P 画直线 l 的垂线:按照三角尺画法,画出直线 l 的垂线,垂足为 A,标注 “PA⊥l”。
过点 Q 画直线 m 的垂线:按照三角尺画法,画出直线 m 的垂线,垂足为 Q,标注 “DQ⊥m(D 为垂线上一点)”。
结论:如图所示(画出相应垂线)。
幻灯片 10:例题 3—— 点到直线的距离计算
题目:如图,在直线 l 上有 A、B、C 三点,点 P 在直线 l 外,且 PO⊥l,垂足为 O,PA=5cm,PB=3cm,PC=4cm,PO=2cm,求点 P 到直线 l 的距离。
图形:直线 l 上有 A、B、C、O 四点,PO⊥l,PO=2cm,PA、PB、PC 为连接 P 与 A、B、C 的线段。
解答过程:
因为 PO⊥l,垂足为 O,所以 PO 是点 P 到直线 l 的垂线段。
根据点到直线的距离的定义,点 P 到直线 l 的距离就是 PO 的长度。
已知 PO=2cm,所以点 P 到直线 l 的距离是 2cm。
结论:点 P 到直线 l 的距离是 2cm。
幻灯片 11:课堂练习 1—— 表示垂直关系
题目:如图,直线 a 与直线 b 相交于点 O,且∠1=90°,则直线 a 与直线 b 的位置关系是( ),记作( ),读作( ),垂足是( )。
答案:互相垂直;a⊥b(或 b⊥a);a 垂直于 b(或 b 垂直于 a);点 O
幻灯片 12:课堂练习 2—— 应用垂线性质
题目:在同一平面内,过直线 l 外一点 P,可以画( )条直线与直线 l 垂直;过直线 l 上一点 Q,可以画( )条直线与直线 l 垂直。
答案:1;1
幻灯片 13:课堂练习 3—— 点到直线的距离
题目:如图,要从 A 地向河流 l 修一条水渠,应怎样修才能使水渠最短?请画出示意图,并说明理由。
图形:点 A 在河流 l 的一侧。
解答过程:
过点 A 画河流 l 的垂线,垂足为 B,沿着 AB 修水渠最短。
理由是:连接直线外一点与直线上各点的所有线段中,垂线段最短。
答案:过点 A 作 l 的垂线,沿垂线段修水渠,理由是垂线段最短。
幻灯片 14:易错点分析
常见错误:
对垂线的概念理解不透彻,认为只要两条直线相交就互相垂直,忽略 “相交成直角” 这个关键条件。
混淆 “垂线段” 和 “点到直线的距离”,把垂线段本身当成距离,实际上距离是垂线段的长度。
画垂线时,未使三角尺的直角边与已知直线完全重合,导致画出的直线与已知直线不垂直。
忽略垂线性质中 “在同一平面内” 的前提,错误认为在空间中过一点也只有一条直线与已知直线垂直(实际上在空间中可以有无数条)。
规避方法:
牢记垂线的定义,判断两条直线是否垂直时,必须看它们相交是否成直角(90°)。
明确垂线段是图形,点到直线的距离是该图形的长度(数值),区分两者的概念。
画垂线时,严格按照操作步骤进行,确保三角尺的直角边与已知直线紧密重合,画图后可用量角器检查是否成 90°。
应用垂线性质时,注意其适用范围是 “在同一平面内”,这是小学和初中阶段主要研究的范围。
幻灯片 15:课堂小结
垂线的概念:两条直线相交成直角时互相垂直,其中一条是另一条的垂线,交点是垂足,用 “⊥” 表示。
垂线的性质:在同一平面内,过一点有且只有一条直线与已知直线垂直;垂线段最短。
点到直线的距离:直线外一点到这条直线的垂线段的长度。
垂线的画法:用三角尺或量角器,过一点画已知直线的垂线。
幻灯片 16:布置作业
基础作业:
教材课后练习题第 1、2、3 题(判断垂直关系、画垂线、计算点到直线的距离)。
画一条直线 l,在直线 l 外任取一点 P,过点 P 画直线 l 的垂线,并量出点 P 到直线 l 的距离。
提升作业:
如图,直线 AB⊥CD,垂足为 O,OE 平分∠AOD,求∠COE 的度数。
已知点 P 到直线 l 的距离是 3cm,画出满足条件的点 P 的轨迹。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
观察以上图片中直线,它们有什么特殊的位置关系?
情景引入
取两根木条a、b,将他们钉在一起固定木条a,转动木条b
a
b
)
α
垂线的概念
问题:
(1)在木条b转动的过程中,什么也随着改变
a与b所成的角也随之发生改变
取两根木条a、b,将他们钉在一起固定木条a,转动木条b
问题:
(2)在木条b与a成90°的位置有几个?木条b与a所在的直线有什么位置关系?
a
b
)
α
a与b垂直
定义:两条直线相交所构成的四个角中有一个为直角时,其他三个角也都成为直角,此时,这两条直线互相垂直.
记作:AB⊥CD或m⊥l
注意:两条线段互相垂直是指这两条线段所在的直线互相垂直.(如图2)
垂直的定义及表示方法
A
B
C
D
O
(2)
B
C
D
O
(1)
A
l
m
两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
记作:AB⊥CD于点O
A
B
C
D
O
符号语言:
如图,当直线AB与CD相交于O点,∠AOD=90°时,
那么AB⊥CD.
因为∠AOD=90°(已知) ,
所以AB⊥CD(垂直的定义)
垂线的判定
符号语言:
若直线AB与CD垂直,垂足为O,
则∠AOD=90°
因为 AB⊥CD (已知) ,
所以 ∠AOD=90°(垂直的定义)
(或∠AOC=∠BOC=∠BOD=90°)
A
B
C
D
O
垂线的性质
如图1,若直线m、n相交于点O,∠1=90°,则_______.
若直线AB、CD相交于点O,且AB⊥CD,则∠BOD =______.
如图2,BO⊥AO,∠BOC与∠BOA的度数之比为1∶5,那么∠COA=____, ∠BOC的补角为______.
O
m
n
1
B
C
A
O
m⊥n
90°
72°
162°
图1
图2
牛刀小试
4.日常生活中,我们经常可以看到线线互相垂直的图形,你能再举出一些例子么?
经过直线AB外一点P,按图中所示的两种方法,画出垂直于直线AB的直线,这样的垂线能画多少条呢?
垂线的画法及基本事实
试一试
P
B
A
(1)
(2)
P
A
B
B
问题 这样画AB的垂线我们可以画几条?
O
如图,已知直线 AB,作AB的垂线.
无数条
1.落
2.靠
3.画
A
B
P
如图,已知直线 AB 和AB上的一点P ,过点P作AB的垂线.
问题 这样画l的垂线可以画几条?
一条
1.落
2.靠
3.移
4.画
A
B
P
如图,已知直线 AB 和AB外的一点P ,过点P作AB的垂线.
根据以上几种情况的操作,你能得出什么结论?
问题 这样画l的垂线可以画几条?
一条
1.落
2.靠
3.移
4.画
A
注意:
1.“过一点”中的点,可以在已知直线上,也可以在已知直线外;
2.“有且只有”中,“有”指存在性,“只有”指唯一性.
同一平面内,过一点有且只有一条直线与已知直线垂直.
垂线的性质
特殊的直线
如图,如果直线CD经过线段AB的中点O,并且CD⊥AB,我们可以得到AO=BO, CD⊥AB.
A
B
C
D
O
//
//
此时,我们将垂直并且平分一条线段的直线叫做这条线段的垂直平分线(图中直线CD即为线段AB的垂直平分线)
垂直平分线又可称为中垂线
如图①所示,已知钝角∠AOB,点 D 在射线 OB 上.
(1)画直线 DE⊥OB;
(2)画直线 DF⊥OA,垂足为 F.
解: (1)如图②所示,直线DE为所求作的直线.
(2)如图②所示,直线DF为所求作的直线.
牛刀小试
探究:在如图所示的方格图中,点A是直线l外一点,从A点向已知直线 l 画一条垂直的线段和几条不垂直的线段.
1.线段AB, AC, AD ,AE谁最短?
2.你能用一句话表示这个结论吗?
说一说:
连接直线外一点与直线上各点的所有线段中,垂线段最短
简述:垂线段最短.
线段AB的长度叫做点A到直线l的距离.
规定:
作图过程中我们可以发现其中最短的应该是线段AB,线段AB叫做点A到直线l的垂线段
从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
垂线段
思考:体育课上是怎样测量跳远成绩的?你知道其中的原因吗?
1.在灌溉时,要把河中的水引到农田P处,如何挖掘能使渠道最短?请画出图来,并说明理由.
m
垂线段最短
牛刀小试
如图,小海龟位于图中点 A 处,按下述口令移动:前进 3 格;向右转 90°,前进 5 格;向左转 90°,前进3 格;向左转 90°,前进 6 格;向右转 90°,后退 6 格;最后向右转 90°,前进 1 格. 用粗线将小海龟经过的路线描出来,看一看是什么图形.
做一做
1.如图,∠ABD = 90°,在下列各语句中填入适当的文字或数字: 【教材P175 练习 第1题】
(1)点 B 在直线______________上,点 D 在直线______外;
(2)直线_____与直线_____相交于点 A,点 D 是直线_____与直线_____的交点,也是直线_____与直线______的交点,又是直线_____与直线_____的交点;
(3)直线_____垂直于直线______,垂足为点_____;
(4)过点 D 有且只有_____条直线与直线 AC 垂直.
AC (或BD)
AC
AD
AC
AD
BD
AD
CD
BD
CD
BD
AC
B
一
随堂练习
如图所示的各个三角形中,分别过点 C 画出直线 AB 的垂线,并量出三角形顶点 C 到直线 AB 的距离.(精确到 1mm) 【教材P176 练习 第2题】
14 mm
23 mm
17 mm
(D)
3.在如图所示的方格图中,按下述要求画图并回答问题【教材P176 练习 第3题】
(1)过点C画线段AB的垂线,垂足为点D;
(2)量出点C到线段AB所在直线的距离(精确到1mm)
(3)画出线段AB的垂直平分线
C
A
B
D
4.如图, AC⊥BC,∠C=90°线段AC、BC、CD中最短的是( )
A. AC B. BC
C. CD D. 不能确定
D
A
B
C
C
知识点1 垂直的定义
1.如图所示,,且 ,则 的度数是( )
D
(第1题)
A. B. C. D.
返回
2.如图,直线,相交于点,下列条件能说明 的是( )
B
(第2题)
; ;
; .
A.①② B.①③ C.②④ D.①③④
返回
3.[2025南阳期末]如图,,直线经过点.若 ,
则 _____.
(第3题)
返回
知识点2 垂线的画法
4.下列选项中,过点画的垂线 ,三角板放法正确的是( )
C
A. B. C. D.
返回
5.(8分)利用三角板和直尺作图.
(1)如图①,过点分别画 ,
的垂线;
解:如图①所示,直线,,, 即为所求.
(2)如图②,过点画 的垂线.
解:如图②所示,直线 即为所求.
返回
知识点3 垂线的基本事实及线段的垂直平分线
6.在平面内作已知直线的垂线,可作( )
D
A.0条 B.1条 C.2条 D.无数条
返回
7.如图,若,,则与 ______,其理由是_______
_____________________________________________.
共线
同一
平面内,过一点有且只有一条直线与已知直线垂直
(第7题)
返回
8.在如图所示的方格图中,线段 的垂直平分线是四条直线中的直线___.
(第8题)
返回
知识点4 垂线段
(第9题)
9.如图,在同一平面内有直线及直线外一点 ,作
,垂足为,则点到直线 的距离是( )
A
A.线段的长度 B.线段 的长度
C.线段的长度 D.线段 的长度
返回
10. 运动会上,跳远运动员跳落到沙坑时的痕迹和测量跳
远成绩的方法如图所示,应选择其中的____(填序号)号线的长度作为
跳远成绩,这样测量的依据是____________.
③
垂线段最短
(第10题)
返回
11.(12分)如图,在直角三角形中, , ,
, .
(1)点到的距离是___ ;
(2)点到点的距离是____ ;
8
10
(3)画出表示点到的距离的线段,则____ .
4.8
解:如图所示
返回
12. 为直线外一点,,,为直线上三点, ,
,,则点到直线 的距离( )
D
A.是 B.是 C.小于 D.不大于
返回
13. 如图是光的反射规律示意图,是入射光线,
是反射光线,法线,是入射角, 是反射角,
.若,则 的度数为_____.
(第13题)
返回
14.[2025信阳期末]如图,已知直线和相交于点, ,
平分, ,则的度数为____ .
22
(第14题)
返回
15.(12分)[教材P练习T ]在如图所示
的方格纸中,按下列要求画图并回答问题:
(1)过点画线段的垂线,垂足为 ;
解:如图所示,即为 的垂线.
(2)量出点到线段所在直线的距离精确到 ;
解: .
(3)连结,画出一条直线,使该直线垂直并且平分线段 .
解:如图,直线 即为所求.
返回
16.(8分)如图,直线,相交于点, .
(1)若 , ,求 的度数.
解:因为,所以 .
因为 ,所以 .
因为 ,所以 .
(2)如果,那么与 互相垂直吗?请说明理由.
解: .理由如下:
因为 , ,
所以 ,即 ,所以 .
返回
17.(16分) 已知一个
角的两边与另一个角的两边分别垂直,
试探索这两个角之间的数量关系.
(1)如图①,,,
与 的数量关系是_________;
(2)如图②,,,与 的数量关系是__________
_______;
(3)由 得出结论:若一个角的两边与另一个角的两边分别垂直,
则这两个角____________;
相等或互补
(4)若两个角的两边互相垂直,且一个角比另一个角的3倍少 ,则
求这两个角的度数.
解:设另一个角的度数为 ,则这个角的度数为 ,
根据题意可得 或 ,解得
或 ,
当 时, ,
当 时, ,
所以这两个角的度数为 , 或 , .
返回
课堂小结
谢谢观看!
同课章节目录
