4.2.1 平行线 课件(共42张PPT)
文档属性
| 名称 | 4.2.1 平行线 课件(共42张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 9.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 05:34:27 | ||
图片预览








文档简介
(共42张PPT)
4.2.1 平行线
第4章 相交线和平行线
【华东师大版·2024】数学 七年级上册
授课教师:********
班 级:********
时 间:********
幻灯片 1:封面
标题:4.2.1 平行线
副标题:认识同一平面内直线的特殊位置关系
幻灯片 2:学习目标
理解平行线的概念,知道在同一平面内两条直线的位置关系只有相交和平行两种。
掌握平行线的表示方法,能正确读写平行线。
学会用直尺和三角尺画平行线,培养动手操作能力。
掌握平行线的基本事实(经过直线外一点,有且只有一条直线与这条直线平行)及其推论(如果两条直线都与第三条直线平行,那么这两条直线也互相平行),并能运用它们解决简单问题。
幻灯片 3:情境引入 —— 生活中的平行线
展示图片:铁轨(两条铁轨可以看作平行线)、黑板的上下边缘、练习本上的横线、电梯的扶手、高速公路上的分隔线。
提问:这些图片中的直线有什么共同特点?它们与相交直线有什么不同?
引入:在同一平面内,两条直线除了相交之外,还有一种特殊的位置关系 —— 平行。本节课我们就来学习平行线的相关知识。
幻灯片 4:平行线的概念
定义:在同一平面内,不相交的两条直线叫做平行线。
关键词解析:
“在同一平面内”:这是平行线概念的前提,如果两条直线不在同一平面内,即使不相交,也不能称为平行线(如异面直线,小学阶段暂不涉及)。
“不相交”:两条直线没有公共点,这是平行线的核心特征。
反例说明:
两条相交的直线(有一个公共点)不是平行线。
不在同一平面内的两条不相交的直线(如正方体的一条棱和与它不相交的另一条棱)不是平行线。
图形展示:画出两条平行线 a 和 b,标注 “a 与 b 不相交”。
幻灯片 5:同一平面内两条直线的位置关系
分类:在同一平面内,两条直线的位置关系只有两种:
相交:两条直线有且只有一个公共点。
平行:两条直线没有公共点。
注意:“重合” 的两条直线通常看作一条直线,不视为独立的位置关系。
图示:用表格形式展示相交和平行的图形、特征对比:
位置关系
图形
公共点数量
相交
两条直线交叉,有一个交点
1 个
平行
两条直线不相交,无交点
0 个
幻灯片 6:平行线的表示方法
表示符号:平行用符号 “∥” 表示。
表示方法:
直线 a 与直线 b 平行,记作 “a∥b”,读作 “a 平行于 b”。
直线 AB 与直线 CD 平行,记作 “AB∥CD”,读作 “AB 平行于 CD”。
示例:在图中画出直线 l 和直线 m,标注 “l∥m”,并读作 “l 平行于 m”。
幻灯片 7:平行线的画法
工具:直尺和三角尺。
步骤(过直线外一点画已知直线的平行线):
放:把三角尺的一条直角边与已知直线重合。
靠:用直尺紧靠三角尺的另一条直角边。
推:沿着直尺移动三角尺,使三角尺与已知直线重合的直角边过直线外的已知点。
画:沿着三角尺的这条直角边画一条直线,这条直线就是已知直线的平行线。
图示:用动画分步展示画法,标注每一步的操作要点。
说明:过直线上一点画已知直线的平行线的方法类似,但此时画出的平行线与已知直线重合(通常视为同一条直线),因此一般研究过直线外一点画平行线。
幻灯片 8:平行线的基本事实
基本事实:经过直线外一点,有且只有一条直线与这条直线平行。
关键词解析:
“经过直线外一点”:强调点的位置在直线外,如果点在直线上,无法画出与该直线平行的直线(会重合)。
“有且只有一条”:“有” 表示存在性(至少有一条),“只有” 表示唯一性(最多有一条)。
图形展示:直线 l 外有一点 P,画出过 P 且与 l 平行的直线 a,说明这样的直线只有一条。
生活实例:经过直线外一点,只能画出一条直线与已知直线平行,如经过铁轨外一点,只能画出一条与铁轨平行的直线。
幻灯片 9:平行线基本事实的推论
推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
符号表示:如果 a∥b,b∥c,那么 a∥c。
图形展示:画出直线 a、b、c,其中 a∥b,b∥c,标注 “a∥c”。
说明:这个推论也称为平行线的传递性,它表明平行线具有传递关系。
实例:如果直线 a 平行于直线 b,直线 b 平行于直线 c,那么直线 a 一定平行于直线 c,就像如果甲和乙同岁,乙和丙同岁,那么甲和丙同岁一样。
幻灯片 10:例题 1—— 判断平行线
题目:如图,在同一平面内,直线 AB、CD、EF 中,哪两条直线是平行线?请说明理由。
图形:AB 与 CD 不相交,AB 与 EF 相交,CD 与 EF 相交。
解答过程:
根据平行线的定义,在同一平面内不相交的两条直线是平行线。
图中 AB 与 CD 不相交,因此 AB∥CD;AB 与 EF、CD 与 EF 都相交,不是平行线。
结论:AB∥CD。
幻灯片 11:例题 2—— 应用基本事实画图
题目:如图,点 P 在直线 l 外,点 Q 在直线 l 上,过点 P 画直线 l 的平行线,过点 Q 画直线 l 的平行线,能画出几条?
图形:直线 l,点 P 在 l 外,点 Q 在 l 上。
解答过程:
过点 P 画直线 l 的平行线,根据基本事实,能画出 1 条。
过点 Q 画直线 l 的平行线,由于点 Q 在 l 上,画出的直线与 l 重合,因此只能看作 1 条(即直线 l 本身)。
结论:过点 P 能画 1 条,过点 Q 能画 1 条(与 l 重合)。
幻灯片 12:例题 3—— 应用推论判断平行关系
题目:已知直线 a∥b,直线 c∥b,那么直线 a 与直线 c 的位置关系是什么?为什么?
解答过程:
根据平行线的推论,如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
因为 a∥b,c∥b,所以 a∥c。
结论:a∥c。
幻灯片 13:课堂练习 1—— 基本概念判断
题目:判断下列说法是否正确:
(1)在同一平面内,不相交的两条线段是平行线。
(2)过一点有且只有一条直线与已知直线平行。
(3)如果直线 m∥n,n∥p,那么 m∥p。
答案:(1)错误(线段有端点,不相交的线段所在直线可能相交);(2)错误(应是过直线外一点);(3)正确。
幻灯片 14:课堂练习 2—— 画图操作
题目:在如图所示的方格纸中,过点 A 画直线 BC 的平行线。
图形:方格纸中有直线 BC 和点 A。
解答提示:利用方格的边作为直尺,结合三角尺画出平行线。
答案:画出的平行线如图所示(根据实际画图结果)。
幻灯片 15:课堂练习 3—— 应用推论
题目:如图,直线 a、b、c 在同一平面内,a∥b,b 与 c 相交,那么 a 与 c 的位置关系是什么?
解答过程:
假设 a 与 c 不相交,即 a∥c,因为 a∥b,根据推论,b∥c,这与 “b 与 c 相交” 矛盾,因此 a 与 c 相交。
答案:相交。
幻灯片 16:易错点分析
常见错误:
忽略 “在同一平面内” 这个前提,认为空间中不相交的两条直线也是平行线,实际上它们可能是异面直线。
对平行线的基本事实理解错误,说成 “过一点有且只有一条直线与已知直线平行”,漏掉 “直线外” 这个关键条件,导致错误。
画平行线时,未用直尺紧靠三角尺,导致画出的直线与已知直线不平行。
规避方法:
牢记平行线概念中的 “在同一平面内”,这是小学和初中阶段研究平行线的重要前提。
背诵基本事实时,强调 “直线外一点”,明确点的位置不能在已知直线上。
画平行线时,严格按照 “放、靠、推、画” 的步骤操作,确保三角尺移动时不偏移,画图后可通过观察是否相交验证是否平行。
幻灯片 17:课堂小结
平行线的概念:在同一平面内,不相交的两条直线。
位置关系:同一平面内,两条直线要么相交,要么平行。
表示方法:用 “∥” 表示,如 a∥b。
画法:用直尺和三角尺,按 “放、靠、推、画” 步骤操作。
基本事实及推论:
经过直线外一点,有且只有一条直线与这条直线平行。
如果两条直线都与第三条直线平行,那么这两条直线也互相平行(a∥b,b∥c,则 a∥c)。
幻灯片 18:布置作业
基础作业:
教材课后练习题第 1、2 题(判断平行线、用符号表示平行线)。
过直线 l 外一点 P,画直线 l 的平行线,并用符号表示。
提升作业:
在同一平面内,有三条直线 a、b、c,若 a∥b,b 与 c 相交,那么 a 与 c 的位置关系是什么?请说明理由。
举例说明生活中平行线的应用,至少 3 个例子。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
掌握平行线的公理及推论.
学习目标
重点
理解平行线的定义
掌握平行线的画法
难点
两条直线相交(其中垂直是相交的特殊情形)
生活中两条直线除了相交以外,还有什么情形呢?
想一想
前面我们学的两条直线具有怎样位置关系?
情景引入
生活中两条直线除了相交以外,我们还可以看到下面情况的两条直线
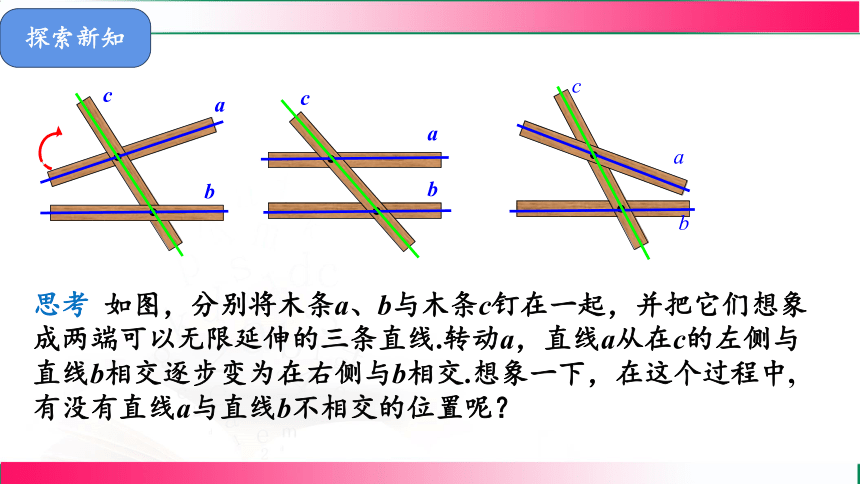
思考 如图,分别将木条a、b与木条c钉在一起,并把它们想象成两端可以无限延伸的三条直线.转动a,直线a从在c的左侧与直线b相交逐步变为在右侧与b相交.想象一下,在这个过程中,有没有直线a与直线b不相交的位置呢?
a
b
c
a
b
c
a
b
c
探索新知
在木条转动过程中,存在直线a与直线b不相交的情形,这时我们说直线a与b互相平行.记作a∥b.
在同一平面内不相交的两条直线叫做平行线.
注意:平行线的定义包含三层意思:
(1)“在同一平面内”是前提条件;
(2)“不相交”就是说两条直线没有交点;
(3)平行线指的是两条直线,而不是两条射线或两条线段.
a
b
c
平行线的概念
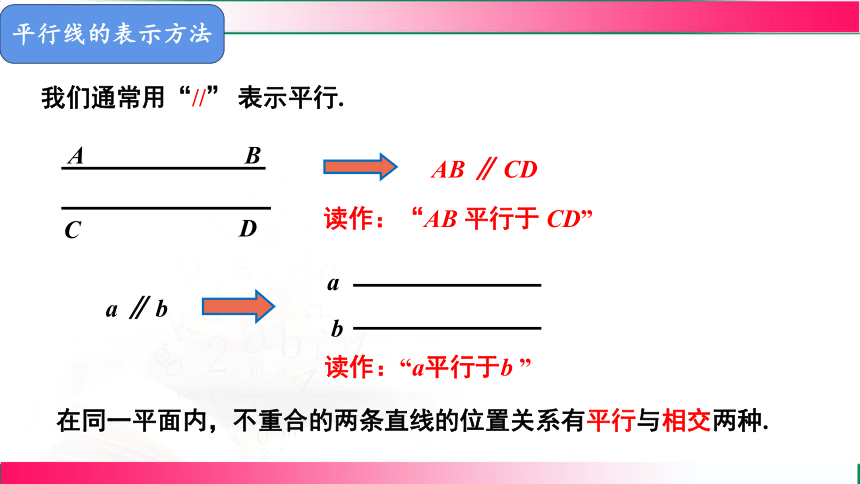
我们通常用“//” 表示平行.
C
B
A
D
a ∥ b
AB ∥ CD
a
b
读作:“AB 平行于 CD”
读作:“a平行于b ”
在同一平面内,不重合的两条直线的位置关系有平行与相交两种.
平行线的表示方法
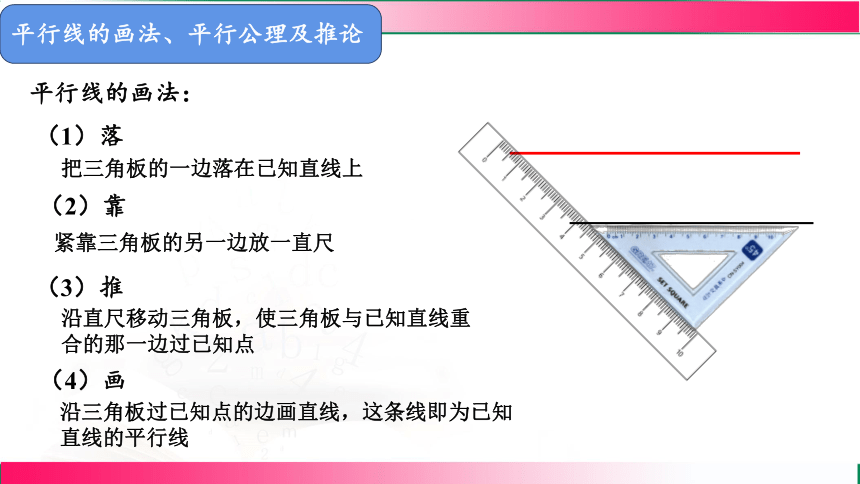
平行线的画法:
(1)落
(2)靠
(3)推
(4)画
平行线的画法、平行公理及推论
把三角板的一边落在已知直线上
紧靠三角板的另一边放一直尺
沿直尺移动三角板,使三角板与已知直线重合的那一边过已知点
沿三角板过已知点的边画直线,这条线即为已知直线的平行线
a
(3)经过点P能画出几条直线与直线a平行?
(4)过点D画一条直线与直线a平行,与(3)中所画的直线平行吗?
·
P
·
D
(1)经过点P 能画出几条直线?
无数条
1条
b
(2)与直线a平行的直线有几条?
无数条
平行
做一做
平行公理
过直线外一点有且只有一条直线与这条直线平行.
·
A
·
B
·
·
C
D
a
b
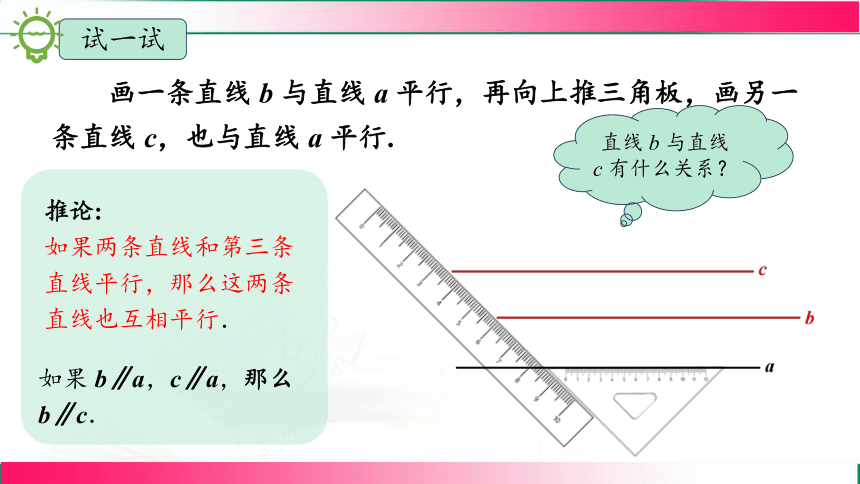
试一试
画一条直线 b 与直线 a 平行,再向上推三角板,画另一条直线 c,也与直线 a 平行.
如果 b∥a,c∥a,那么b∥c.
推论:
如果两条直线和第三条直线平行,那么这两条直线也互相平行.
直线 b 与直线 c 有什么关系?
几何语言表达:
c
b
a
平行公理的推论(平行线的传递性)
如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
∵ a//c , c//b (已知)
∴ a//b (如果两条直线都和第三条直线平行,那么这两条直线也互相平行).
1.下列说法正确的是( )
A.在同一平面内,不相交的两条射线是平行线
B.在同一平面内,不相交的两条线段是平行线
C.在同一平面内,两条不重合的直线的位置关系不是相交就是平行
D.不相交的两条直线是平行线
C
随堂及练
2. 下面说法中正确的有( )
①一条直线的平行线只有一条;
②因为 a∥ b,c∥ d,所以 a∥ d;
③过一点有且只有一条直线与已知直线平行.
A. 0 个 B. 1 个 C. 2 个 D. 3 个
A
3.使用直尺、量角器和三角板,在如图所示的某平面图上找出互相平行的道路和互相垂直的道路. 【教材P183 练习 第1题】
互相垂直的道路:
清华路与新民大街、新疆街、长庆路百汇路垂直
桂林路与新民大街、新疆街、长庆路百汇路垂直
互相平行的道路:
新民大街、新疆街、长庆路百汇路互相平行;
清华路与桂林路互相平行
4. 根据下列语句,利用所给三角形ABC 画出图形:【教材P184练习 第2题】
(1)过三角形ABC 的顶点 C,画出平行于 AB 的直线 MN;
(2)过三角形ABC 的边 AB 的中点 D,画出平行于 AC 的直线, 交 BC 于点 E .
如图所示
5.如图,两条直线a、b相交于点O,如果直线a∥直线c,那么直线b能与直线c平行么?为什么? 【教材P184练习 第3题】
a
b
c
直线b不能与直线c平行
因为过直线外一点有且只有一条直线与这条直线平行
O
知识点1 平行线及其表示
1.有下列生活实例:
①路口的斑马线;②天上的彩虹;③体操队的纵队; 米跑道线;⑤
平直的火车铁轨.
其中大致能看成平行线的有( )
D
A.1个 B.2个 C.3个 D.4个
返回
2.在同一平面内,不重合的两条直线的位置关系是( )
C
A.平行 B.相交 C.相交或平行 D.垂直
返回
3.[2025南阳期末]如图,已知四条直线,,,
中的一条与挡板另一侧的直线 平行,请判断该直线是
( )
B
A. B. C. D.
返回
知识点2 平行线的画法
4.如图,已知直线外一点,过
点画直线,使 ,借助直
尺和三角板有如下操作:①固定直
尺,并沿 方向移动三角板,使
C
A.①②③④ B.②④③① C.②④①③ D.④③②①
斜边经过点;②用三角板的斜边紧贴直线 ;③沿三角板斜边画直线
;④用直尺 紧靠三角板的一条直角边.
其正确操作顺序是( )
返回
5.(8分)如图,已知方格纸上有两条线段
, ,根据下列要求完成以下操作:
(1)过点作的平行线 ;
解:如图.
(2)连结,取中点,过点作的平行线与交于点 .
解:如图.
返回
知识点3 平行线的基本事实及其推论
6.过直线外一点作 的平行线,可以作( )
A
A.1条 B.2条 C.3条 D.4条
返回
7.[2025郑州开学考]如图,,过点画,则与
的位置关系是______,理由是____________________________________
_______________________.
平行
如果两条直线都和第三条直线平行,那
么这两条直线也互相平行
(第7题)
返回
8.如图,,,则,, 三点共线,理由是______________
_______________________________.
过直线外一点
有且只有一条直线与这条直线平行
(第8题)
返回
9.(8分)如图,点,分别是直线 外两点.
(1)过点画直线,过点画直线 ;
解:如图所示.
(2)与 有怎样的位置关系?为什么?
解: .理由如下∶
因为, ,
所以 .
返回
10.下列说法错误的是( )
A
A.若两条直线不垂直,则这两条直线平行
B.平行于同一条直线的两条直线平行
C.若,,,则
D.同一平面内,若一条直线与两条平行线中的一条相交,则它也和另一
条相交
返回
11. [2025太原月考]如图,若将一张长方形纸片沿图
示方向对折两次,则产生的折痕与折痕间的位置关系是( )
A
A.平行 B.垂直 C.平行或垂直 D.相交但不垂直
返回
(第12题)
12. 如图,经过直线外一点 的4条直线中,与
直线 相交的直线至少有( )
B
A.4条 B.3条 C.2条 D.1条
返回
13.[教材习题 变式]观察如图所示的长方体,回答下列问题.
(第13题)
(1)用符号表示两棱的位置关系:___ ,
___,___,___ .
//
//
(2)与 所在的直线不相交,它们______
平行线(填“是”或“不是”).由此可知,只有在
__________内,两条不相交的直线才是平行线.
不是
同一平面
返回
14.(12分)如图所示,在内有一点 .
(1)过画 ;
解:如图所示.
(2)过画 ;
解:如图所示.
(3)用量角器量一量与相交形成的角与 的大小有怎样关系?
解:如图,与相交的角有,,, ,
经测量, , ,所以 与
相交形成的角与 相等或互补.
返回
15.(4分)甲:同一平面内,互不重合的三条直线的交点有0个,因为
,如图①.
乙:同一平面内,互不重合的三条
直线的交点只有1个,因为,,
交于同一点 ,如图②.
以上说法谁对谁错?为什么?
解:甲、乙说法都错.
理由:除了两人说的,还有两种情况:
(1),与, 相交,如图①,此时有2个交点;
(2),,两两相交(不包括,, 交于一点的情
况),如图②,此时有3个交点.
所以同一平面内,互不重合的三条直线的交点有0个或1个
或2个或3个.
返回
平行线
定义
在同一平面内,不相交的两条直线叫做平行线
画法
一落;二靠;三移;四画
基本事实
过直线外一点有且只有一条直线与这条直线平行
推论
如果两条直线都与第三条直线平行,那么这两条直线也互相平行
课堂小结
谢谢观看!
4.2.1 平行线
第4章 相交线和平行线
【华东师大版·2024】数学 七年级上册
授课教师:********
班 级:********
时 间:********
幻灯片 1:封面
标题:4.2.1 平行线
副标题:认识同一平面内直线的特殊位置关系
幻灯片 2:学习目标
理解平行线的概念,知道在同一平面内两条直线的位置关系只有相交和平行两种。
掌握平行线的表示方法,能正确读写平行线。
学会用直尺和三角尺画平行线,培养动手操作能力。
掌握平行线的基本事实(经过直线外一点,有且只有一条直线与这条直线平行)及其推论(如果两条直线都与第三条直线平行,那么这两条直线也互相平行),并能运用它们解决简单问题。
幻灯片 3:情境引入 —— 生活中的平行线
展示图片:铁轨(两条铁轨可以看作平行线)、黑板的上下边缘、练习本上的横线、电梯的扶手、高速公路上的分隔线。
提问:这些图片中的直线有什么共同特点?它们与相交直线有什么不同?
引入:在同一平面内,两条直线除了相交之外,还有一种特殊的位置关系 —— 平行。本节课我们就来学习平行线的相关知识。
幻灯片 4:平行线的概念
定义:在同一平面内,不相交的两条直线叫做平行线。
关键词解析:
“在同一平面内”:这是平行线概念的前提,如果两条直线不在同一平面内,即使不相交,也不能称为平行线(如异面直线,小学阶段暂不涉及)。
“不相交”:两条直线没有公共点,这是平行线的核心特征。
反例说明:
两条相交的直线(有一个公共点)不是平行线。
不在同一平面内的两条不相交的直线(如正方体的一条棱和与它不相交的另一条棱)不是平行线。
图形展示:画出两条平行线 a 和 b,标注 “a 与 b 不相交”。
幻灯片 5:同一平面内两条直线的位置关系
分类:在同一平面内,两条直线的位置关系只有两种:
相交:两条直线有且只有一个公共点。
平行:两条直线没有公共点。
注意:“重合” 的两条直线通常看作一条直线,不视为独立的位置关系。
图示:用表格形式展示相交和平行的图形、特征对比:
位置关系
图形
公共点数量
相交
两条直线交叉,有一个交点
1 个
平行
两条直线不相交,无交点
0 个
幻灯片 6:平行线的表示方法
表示符号:平行用符号 “∥” 表示。
表示方法:
直线 a 与直线 b 平行,记作 “a∥b”,读作 “a 平行于 b”。
直线 AB 与直线 CD 平行,记作 “AB∥CD”,读作 “AB 平行于 CD”。
示例:在图中画出直线 l 和直线 m,标注 “l∥m”,并读作 “l 平行于 m”。
幻灯片 7:平行线的画法
工具:直尺和三角尺。
步骤(过直线外一点画已知直线的平行线):
放:把三角尺的一条直角边与已知直线重合。
靠:用直尺紧靠三角尺的另一条直角边。
推:沿着直尺移动三角尺,使三角尺与已知直线重合的直角边过直线外的已知点。
画:沿着三角尺的这条直角边画一条直线,这条直线就是已知直线的平行线。
图示:用动画分步展示画法,标注每一步的操作要点。
说明:过直线上一点画已知直线的平行线的方法类似,但此时画出的平行线与已知直线重合(通常视为同一条直线),因此一般研究过直线外一点画平行线。
幻灯片 8:平行线的基本事实
基本事实:经过直线外一点,有且只有一条直线与这条直线平行。
关键词解析:
“经过直线外一点”:强调点的位置在直线外,如果点在直线上,无法画出与该直线平行的直线(会重合)。
“有且只有一条”:“有” 表示存在性(至少有一条),“只有” 表示唯一性(最多有一条)。
图形展示:直线 l 外有一点 P,画出过 P 且与 l 平行的直线 a,说明这样的直线只有一条。
生活实例:经过直线外一点,只能画出一条直线与已知直线平行,如经过铁轨外一点,只能画出一条与铁轨平行的直线。
幻灯片 9:平行线基本事实的推论
推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
符号表示:如果 a∥b,b∥c,那么 a∥c。
图形展示:画出直线 a、b、c,其中 a∥b,b∥c,标注 “a∥c”。
说明:这个推论也称为平行线的传递性,它表明平行线具有传递关系。
实例:如果直线 a 平行于直线 b,直线 b 平行于直线 c,那么直线 a 一定平行于直线 c,就像如果甲和乙同岁,乙和丙同岁,那么甲和丙同岁一样。
幻灯片 10:例题 1—— 判断平行线
题目:如图,在同一平面内,直线 AB、CD、EF 中,哪两条直线是平行线?请说明理由。
图形:AB 与 CD 不相交,AB 与 EF 相交,CD 与 EF 相交。
解答过程:
根据平行线的定义,在同一平面内不相交的两条直线是平行线。
图中 AB 与 CD 不相交,因此 AB∥CD;AB 与 EF、CD 与 EF 都相交,不是平行线。
结论:AB∥CD。
幻灯片 11:例题 2—— 应用基本事实画图
题目:如图,点 P 在直线 l 外,点 Q 在直线 l 上,过点 P 画直线 l 的平行线,过点 Q 画直线 l 的平行线,能画出几条?
图形:直线 l,点 P 在 l 外,点 Q 在 l 上。
解答过程:
过点 P 画直线 l 的平行线,根据基本事实,能画出 1 条。
过点 Q 画直线 l 的平行线,由于点 Q 在 l 上,画出的直线与 l 重合,因此只能看作 1 条(即直线 l 本身)。
结论:过点 P 能画 1 条,过点 Q 能画 1 条(与 l 重合)。
幻灯片 12:例题 3—— 应用推论判断平行关系
题目:已知直线 a∥b,直线 c∥b,那么直线 a 与直线 c 的位置关系是什么?为什么?
解答过程:
根据平行线的推论,如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
因为 a∥b,c∥b,所以 a∥c。
结论:a∥c。
幻灯片 13:课堂练习 1—— 基本概念判断
题目:判断下列说法是否正确:
(1)在同一平面内,不相交的两条线段是平行线。
(2)过一点有且只有一条直线与已知直线平行。
(3)如果直线 m∥n,n∥p,那么 m∥p。
答案:(1)错误(线段有端点,不相交的线段所在直线可能相交);(2)错误(应是过直线外一点);(3)正确。
幻灯片 14:课堂练习 2—— 画图操作
题目:在如图所示的方格纸中,过点 A 画直线 BC 的平行线。
图形:方格纸中有直线 BC 和点 A。
解答提示:利用方格的边作为直尺,结合三角尺画出平行线。
答案:画出的平行线如图所示(根据实际画图结果)。
幻灯片 15:课堂练习 3—— 应用推论
题目:如图,直线 a、b、c 在同一平面内,a∥b,b 与 c 相交,那么 a 与 c 的位置关系是什么?
解答过程:
假设 a 与 c 不相交,即 a∥c,因为 a∥b,根据推论,b∥c,这与 “b 与 c 相交” 矛盾,因此 a 与 c 相交。
答案:相交。
幻灯片 16:易错点分析
常见错误:
忽略 “在同一平面内” 这个前提,认为空间中不相交的两条直线也是平行线,实际上它们可能是异面直线。
对平行线的基本事实理解错误,说成 “过一点有且只有一条直线与已知直线平行”,漏掉 “直线外” 这个关键条件,导致错误。
画平行线时,未用直尺紧靠三角尺,导致画出的直线与已知直线不平行。
规避方法:
牢记平行线概念中的 “在同一平面内”,这是小学和初中阶段研究平行线的重要前提。
背诵基本事实时,强调 “直线外一点”,明确点的位置不能在已知直线上。
画平行线时,严格按照 “放、靠、推、画” 的步骤操作,确保三角尺移动时不偏移,画图后可通过观察是否相交验证是否平行。
幻灯片 17:课堂小结
平行线的概念:在同一平面内,不相交的两条直线。
位置关系:同一平面内,两条直线要么相交,要么平行。
表示方法:用 “∥” 表示,如 a∥b。
画法:用直尺和三角尺,按 “放、靠、推、画” 步骤操作。
基本事实及推论:
经过直线外一点,有且只有一条直线与这条直线平行。
如果两条直线都与第三条直线平行,那么这两条直线也互相平行(a∥b,b∥c,则 a∥c)。
幻灯片 18:布置作业
基础作业:
教材课后练习题第 1、2 题(判断平行线、用符号表示平行线)。
过直线 l 外一点 P,画直线 l 的平行线,并用符号表示。
提升作业:
在同一平面内,有三条直线 a、b、c,若 a∥b,b 与 c 相交,那么 a 与 c 的位置关系是什么?请说明理由。
举例说明生活中平行线的应用,至少 3 个例子。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
掌握平行线的公理及推论.
学习目标
重点
理解平行线的定义
掌握平行线的画法
难点
两条直线相交(其中垂直是相交的特殊情形)
生活中两条直线除了相交以外,还有什么情形呢?
想一想
前面我们学的两条直线具有怎样位置关系?
情景引入
生活中两条直线除了相交以外,我们还可以看到下面情况的两条直线
思考 如图,分别将木条a、b与木条c钉在一起,并把它们想象成两端可以无限延伸的三条直线.转动a,直线a从在c的左侧与直线b相交逐步变为在右侧与b相交.想象一下,在这个过程中,有没有直线a与直线b不相交的位置呢?
a
b
c
a
b
c
a
b
c
探索新知
在木条转动过程中,存在直线a与直线b不相交的情形,这时我们说直线a与b互相平行.记作a∥b.
在同一平面内不相交的两条直线叫做平行线.
注意:平行线的定义包含三层意思:
(1)“在同一平面内”是前提条件;
(2)“不相交”就是说两条直线没有交点;
(3)平行线指的是两条直线,而不是两条射线或两条线段.
a
b
c
平行线的概念
我们通常用“//” 表示平行.
C
B
A
D
a ∥ b
AB ∥ CD
a
b
读作:“AB 平行于 CD”
读作:“a平行于b ”
在同一平面内,不重合的两条直线的位置关系有平行与相交两种.
平行线的表示方法
平行线的画法:
(1)落
(2)靠
(3)推
(4)画
平行线的画法、平行公理及推论
把三角板的一边落在已知直线上
紧靠三角板的另一边放一直尺
沿直尺移动三角板,使三角板与已知直线重合的那一边过已知点
沿三角板过已知点的边画直线,这条线即为已知直线的平行线
a
(3)经过点P能画出几条直线与直线a平行?
(4)过点D画一条直线与直线a平行,与(3)中所画的直线平行吗?
·
P
·
D
(1)经过点P 能画出几条直线?
无数条
1条
b
(2)与直线a平行的直线有几条?
无数条
平行
做一做
平行公理
过直线外一点有且只有一条直线与这条直线平行.
·
A
·
B
·
·
C
D
a
b
试一试
画一条直线 b 与直线 a 平行,再向上推三角板,画另一条直线 c,也与直线 a 平行.
如果 b∥a,c∥a,那么b∥c.
推论:
如果两条直线和第三条直线平行,那么这两条直线也互相平行.
直线 b 与直线 c 有什么关系?
几何语言表达:
c
b
a
平行公理的推论(平行线的传递性)
如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
∵ a//c , c//b (已知)
∴ a//b (如果两条直线都和第三条直线平行,那么这两条直线也互相平行).
1.下列说法正确的是( )
A.在同一平面内,不相交的两条射线是平行线
B.在同一平面内,不相交的两条线段是平行线
C.在同一平面内,两条不重合的直线的位置关系不是相交就是平行
D.不相交的两条直线是平行线
C
随堂及练
2. 下面说法中正确的有( )
①一条直线的平行线只有一条;
②因为 a∥ b,c∥ d,所以 a∥ d;
③过一点有且只有一条直线与已知直线平行.
A. 0 个 B. 1 个 C. 2 个 D. 3 个
A
3.使用直尺、量角器和三角板,在如图所示的某平面图上找出互相平行的道路和互相垂直的道路. 【教材P183 练习 第1题】
互相垂直的道路:
清华路与新民大街、新疆街、长庆路百汇路垂直
桂林路与新民大街、新疆街、长庆路百汇路垂直
互相平行的道路:
新民大街、新疆街、长庆路百汇路互相平行;
清华路与桂林路互相平行
4. 根据下列语句,利用所给三角形ABC 画出图形:【教材P184练习 第2题】
(1)过三角形ABC 的顶点 C,画出平行于 AB 的直线 MN;
(2)过三角形ABC 的边 AB 的中点 D,画出平行于 AC 的直线, 交 BC 于点 E .
如图所示
5.如图,两条直线a、b相交于点O,如果直线a∥直线c,那么直线b能与直线c平行么?为什么? 【教材P184练习 第3题】
a
b
c
直线b不能与直线c平行
因为过直线外一点有且只有一条直线与这条直线平行
O
知识点1 平行线及其表示
1.有下列生活实例:
①路口的斑马线;②天上的彩虹;③体操队的纵队; 米跑道线;⑤
平直的火车铁轨.
其中大致能看成平行线的有( )
D
A.1个 B.2个 C.3个 D.4个
返回
2.在同一平面内,不重合的两条直线的位置关系是( )
C
A.平行 B.相交 C.相交或平行 D.垂直
返回
3.[2025南阳期末]如图,已知四条直线,,,
中的一条与挡板另一侧的直线 平行,请判断该直线是
( )
B
A. B. C. D.
返回
知识点2 平行线的画法
4.如图,已知直线外一点,过
点画直线,使 ,借助直
尺和三角板有如下操作:①固定直
尺,并沿 方向移动三角板,使
C
A.①②③④ B.②④③① C.②④①③ D.④③②①
斜边经过点;②用三角板的斜边紧贴直线 ;③沿三角板斜边画直线
;④用直尺 紧靠三角板的一条直角边.
其正确操作顺序是( )
返回
5.(8分)如图,已知方格纸上有两条线段
, ,根据下列要求完成以下操作:
(1)过点作的平行线 ;
解:如图.
(2)连结,取中点,过点作的平行线与交于点 .
解:如图.
返回
知识点3 平行线的基本事实及其推论
6.过直线外一点作 的平行线,可以作( )
A
A.1条 B.2条 C.3条 D.4条
返回
7.[2025郑州开学考]如图,,过点画,则与
的位置关系是______,理由是____________________________________
_______________________.
平行
如果两条直线都和第三条直线平行,那
么这两条直线也互相平行
(第7题)
返回
8.如图,,,则,, 三点共线,理由是______________
_______________________________.
过直线外一点
有且只有一条直线与这条直线平行
(第8题)
返回
9.(8分)如图,点,分别是直线 外两点.
(1)过点画直线,过点画直线 ;
解:如图所示.
(2)与 有怎样的位置关系?为什么?
解: .理由如下∶
因为, ,
所以 .
返回
10.下列说法错误的是( )
A
A.若两条直线不垂直,则这两条直线平行
B.平行于同一条直线的两条直线平行
C.若,,,则
D.同一平面内,若一条直线与两条平行线中的一条相交,则它也和另一
条相交
返回
11. [2025太原月考]如图,若将一张长方形纸片沿图
示方向对折两次,则产生的折痕与折痕间的位置关系是( )
A
A.平行 B.垂直 C.平行或垂直 D.相交但不垂直
返回
(第12题)
12. 如图,经过直线外一点 的4条直线中,与
直线 相交的直线至少有( )
B
A.4条 B.3条 C.2条 D.1条
返回
13.[教材习题 变式]观察如图所示的长方体,回答下列问题.
(第13题)
(1)用符号表示两棱的位置关系:___ ,
___,___,___ .
//
//
(2)与 所在的直线不相交,它们______
平行线(填“是”或“不是”).由此可知,只有在
__________内,两条不相交的直线才是平行线.
不是
同一平面
返回
14.(12分)如图所示,在内有一点 .
(1)过画 ;
解:如图所示.
(2)过画 ;
解:如图所示.
(3)用量角器量一量与相交形成的角与 的大小有怎样关系?
解:如图,与相交的角有,,, ,
经测量, , ,所以 与
相交形成的角与 相等或互补.
返回
15.(4分)甲:同一平面内,互不重合的三条直线的交点有0个,因为
,如图①.
乙:同一平面内,互不重合的三条
直线的交点只有1个,因为,,
交于同一点 ,如图②.
以上说法谁对谁错?为什么?
解:甲、乙说法都错.
理由:除了两人说的,还有两种情况:
(1),与, 相交,如图①,此时有2个交点;
(2),,两两相交(不包括,, 交于一点的情
况),如图②,此时有3个交点.
所以同一平面内,互不重合的三条直线的交点有0个或1个
或2个或3个.
返回
平行线
定义
在同一平面内,不相交的两条直线叫做平行线
画法
一落;二靠;三移;四画
基本事实
过直线外一点有且只有一条直线与这条直线平行
推论
如果两条直线都与第三条直线平行,那么这两条直线也互相平行
课堂小结
谢谢观看!
同课章节目录
