4.2.3 平行线的性质 课件(共45张PPT)
文档属性
| 名称 | 4.2.3 平行线的性质 课件(共45张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 05:32:59 | ||
图片预览










文档简介
(共45张PPT)
4.2.3 平行线的性质
第4章 相交线和平行线
【华东师大版·2024】数学 七年级上册
授课教师:********
班 级:********
时 间:********
幻灯片 1:封面
标题:4.2.3 平行线的性质
副标题:探索平行线被截形成的角的关系
幻灯片 2:学习目标
掌握平行线的三条性质:两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补。
能运用平行线的性质解决角度计算和简单的推理问题。
区分平行线的性质与判定,理解它们之间的联系与区别,培养逻辑思维能力。
幻灯片 3:复习回顾 —— 平行线的判定
展示表格:
判定方法
条件
结论
方法 1
同位角相等
两直线平行
方法 2
内错角相等
两直线平行
方法 3
同旁内角互补
两直线平行
提问:这些判定方法中,条件和结论分别是什么?如果已知两直线平行,那么同位角、内错角、同旁内角会有什么关系呢?
引入:本节课我们将反过来研究 —— 当两条直线平行时,被第三条直线所截形成的同位角、内错角、同旁内角有什么性质。
幻灯片 4:平行线的性质 1—— 两直线平行,同位角相等
探究活动:
画出两条平行线 a、b,被第三条直线 c 所截,标注同位角∠1 和∠2。
用量角器测量∠1 和∠2 的度数,记录测量结果。
改变截线 c 的位置,再次测量同位角的度数,观察数据变化。
性质总结:两条平行线被第三条直线所截,同位角相等。简单说成:两直线平行,同位角相等。
符号表示:∵a∥b,∴∠1=∠2(∠1 与∠2 是同位角)。
图形展示:标注 a∥b,∠1=∠2,用箭头指示角的关系。
幻灯片 5:平行线的性质 2—— 两直线平行,内错角相等
推导过程:
已知:a∥b,c 是截线,∠1 与∠2 是内错角。
由 a∥b,得∠1=∠3(两直线平行,同位角相等)。
又∵∠3=∠2(对顶角相等),∴∠1=∠2(等量代换)。
性质总结:两条平行线被第三条直线所截,内错角相等。简单说成:两直线平行,内错角相等。
符号表示:∵a∥b,∴∠1=∠2(∠1 与∠2 是内错角)。
图形展示:标注 a∥b,∠1=∠2(内错角),展示推导逻辑链。
幻灯片 6:平行线的性质 3—— 两直线平行,同旁内角互补
推导过程:
已知:a∥b,c 是截线,∠1 与∠2 是同旁内角。
由 a∥b,得∠1=∠3(两直线平行,同位角相等)。
又∵∠3+∠2=180°(邻补角互补),∴∠1+∠2=180°(等量代换)。
性质总结:两条平行线被第三条直线所截,同旁内角互补。简单说成:两直线平行,同旁内角互补。
符号表示:∵a∥b,∴∠1+∠2=180°(∠1 与∠2 是同旁内角)。
图形展示:标注 a∥b,∠1+∠2=180°,用弧线标注角的和为平角。
幻灯片 7:平行线的性质与判定的区别与联系
区别:
类别
条件
结论
用途
判定
角的关系
直线平行
判定两直线是否平行
性质
直线平行
角的关系
由平行求角的度数或关系
联系:
两者都涉及同位角、内错角、同旁内角与平行线的关系。
判定是性质的逆过程,性质是判定的逆推理。
口诀记忆:“判定是由角定平行,性质是由平行定角”。
幻灯片 8:例题 1—— 利用同位角性质计算
题目:如图,a∥b,c 是截线,∠1=50°,求∠2 的度数。
图形:a∥b,∠1 与∠2 是同位角。
解答过程:
∵a∥b(已知),∴∠2=∠1(两直线平行,同位角相等)。
∵∠1=50°(已知),∴∠2=50°。
结论:∠2=50°。
幻灯片 9:例题 2—— 利用内错角性质推理
题目:如图,AB∥CD,BC 平分∠ABD,∠1=60°,求∠2 的度数。
图形:AB∥CD,BC 交 AB 于 B,交 CD 于 C,∠1 是∠ABC,∠2 是∠BCD。
解答过程:
∵AB∥CD(已知),∴∠2=∠1(两直线平行,内错角相等)。
∵BC 平分∠ABD(已知),∠1=60°,∴∠ABC=∠1=60°。
∴∠2=60°。
结论:∠2=60°。
幻灯片 10:例题 3—— 利用同旁内角性质综合计算
题目:如图,AD∥BC,∠B=50°,∠D=130°,AB 与 CD 平行吗?为什么?
图形:AD 是截线,分别交 AB、CD 于 A、D;BC 是截线,分别交 AB、CD 于 B、C。
解答过程:
∵AD∥BC(已知),∴∠A+∠B=180°(两直线平行,同旁内角互补)。
∵∠B=50°(已知),∴∠A=180°-50°=130°。
∵∠D=130°(已知),∴∠A=∠D。
∵∠A 与∠D 是 AB、CD 被 AD 所截的内错角,∴AB∥CD(内错角相等,两直线平行)。
结论:AB∥CD。
幻灯片 11:课堂练习 1—— 基础计算
题目:如图,l1∥l2,∠α=120°,则∠β=( )°。
图形:l1∥l2,∠α 与∠β 是同旁内角。
答案:60(∵l1∥l2,∴∠α+∠β=180°,∠β=60°)。
幻灯片 12:课堂练习 2—— 性质与判定综合
题目:如图,∠1=∠2,∠3=100°,求∠4 的度数。
图形:∠1 与∠2 是同位角(判定 a∥b),∠3 与∠4 是同旁内角(性质求角)。
解答过程:
∵∠1=∠2(已知),∴a∥b(同位角相等,两直线平行)。
∵a∥b(已证),∴∠3+∠4=180°(两直线平行,同旁内角互补)。
∵∠3=100°(已知),∴∠4=80°。
答案:80°。
幻灯片 13:课堂练习 3—— 实际应用
题目:一辆汽车在笔直的公路上行驶,两次拐弯后仍与原来的方向平行,若第一次拐弯的角度是 70°,则第二次拐弯的角度是多少?
图形:模拟公路拐弯,两次拐弯形成 “Z” 形或 “U” 形。
解答过程:
分两种情况:
两次拐弯方向相反(如先右拐 70°,再左拐 70°),第二次拐弯 70°。
两次拐弯方向相同(如先右拐 70°,再右拐 110°),第二次拐弯 110°。
答案:70° 或 110°。
幻灯片 14:易错点分析
常见错误:
混淆性质与判定,如将 “两直线平行,同位角相等” 说成 “同位角相等,两直线平行”。
忽略 “两直线平行” 的前提,直接使用性质,如对不平行的直线应用 “同位角相等”。
计算同旁内角时,误将 “互补” 当作 “相等”,导致结果错误。
规避方法:
做题时先明确是 “由平行求角”(用性质)还是 “由角定平行”(用判定),标注关键条件。
应用性质前,务必确认两条直线是否平行,无平行条件时不能使用。
记忆同旁内角性质时,结合 “平角 = 180°” 理解 “互补” 的含义,避免与内错角、同位角的 “相等” 混淆。
幻灯片 15:课堂小结
平行线的性质:
两直线平行,同位角相等。
两直线平行,内错角相等。
两直线平行,同旁内角互补。
与判定的区别:性质是 “平行→角的关系”,判定是 “角的关系→平行”。
应用要点:明确前提(两直线平行),选择对应性质,结合已知条件推理计算。
幻灯片 16:布置作业
基础作业:
教材课后练习题第 1、2、3 题(性质的直接应用)。
如图,AB∥CD,∠A=75°,∠C=40°,求∠E 的度数(提示:过 E 作平行线)。
提升作业:
已知:如图,∠1+∠2=180°,∠3=∠B,求证:∠AED=∠C。
总结平行线性质与判定在解题中的综合应用技巧,举例说明。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
学习目标
掌握平行线的性质,会运用两条直线是平行关系判
断角相等或互补;
能够根据平行线的性质进行简单的推理.
重点
难点
复习旧知
根据右图,填空:
①如果∠1=∠C,
那么__∥__( )
② 如果∠1=∠B
那么__∥__( )
③ 如果∠2+∠B=180°,那么__∥__( )
AB
CD
EC
BD
同位角相等,两直线平行
内错角相等,两直线平行
EC
BD
同旁内角互补,两直线平行
E
A
C
D
B
1
2
3
4
两直线平行
1.同位角相等
2.内错角相等
3.同旁内角互补
问:通过上题可知平行线的判定方法是什么?
思考:反过来如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢
复习旧知
新课探究
翻开你的数学练习横格本,每一页上都有许多互相平行的横线条,随意画一条斜线与这些横线条相交,找出其中任意一对同位角.观察或用量角器度量这对同位角,你有什么发现?
2
1
∠1=∠2
试一试
平行线的性质探究
活动 如图所示如果直线a与直线b平行,那么直线l与直线a、b分别交于点O与点P,其中的同位角∠1与∠2必定相等吗?
1
2
a
b
l
O
P
平行线的性质探究
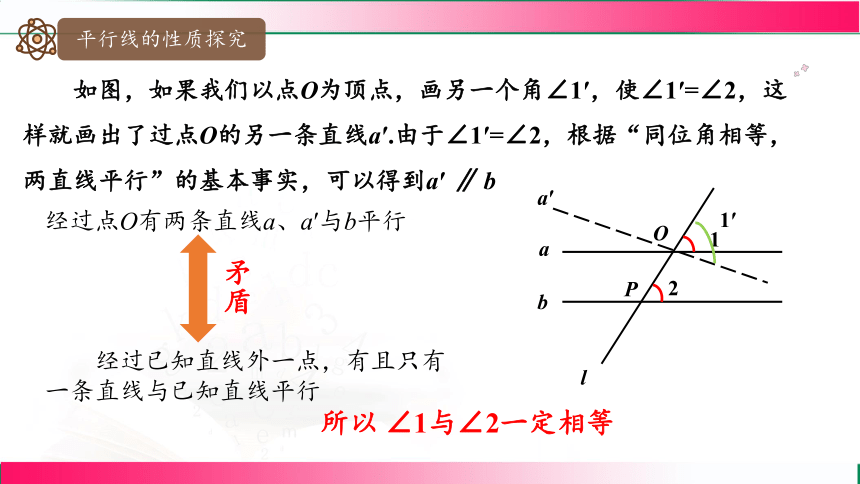
如图,如果我们以点O为顶点,画另一个角∠1′,使∠1′=∠2,这样就画出了过点O的另一条直线a′.由于∠1′=∠2,根据“同位角相等,两直线平行”的基本事实,可以得到a′ ∥ b
1
2
a
b
l
a′
1′
O
P
经过点O有两条直线a、a′与b平行
经过已知直线外一点,有且只有一条直线与已知直线平行
矛盾
所以 ∠1与∠2一定相等
平行线的性质1
两条平行直线被第三条直线所截,同位角相等.
简写成:两直线平行,同位角相等.
b
1
2
a
l
书写格式:
∵ a∥b(已知)
∴ ∠1=∠2
(两直线平行,同位角相等)
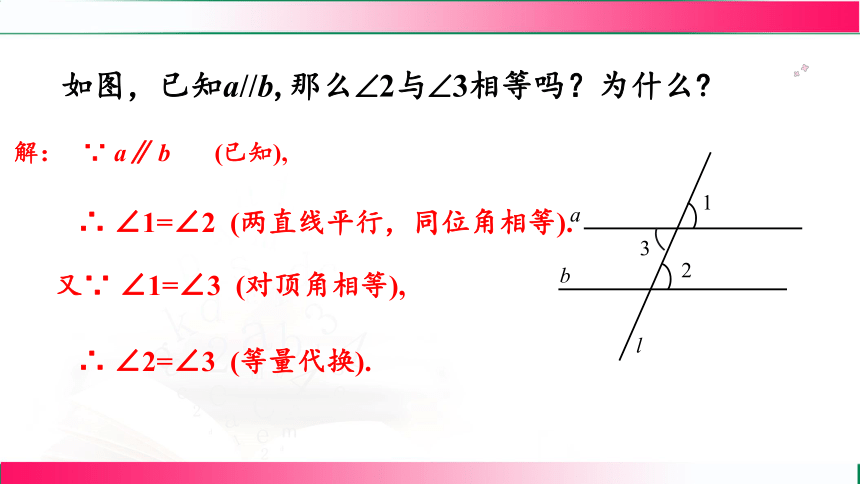
如图,已知a//b,那么 2与 3相等吗?为什么
b
1
2
a
l
3
解: ∵ a∥ b (已知),
∴ ∠1=∠2 (两直线平行,同位角相等).
又∵ ∠1=∠3 (对顶角相等),
∴ ∠2=∠3 (等量代换).
b
1
2
a
l
3
平行线的性质2
性质:两条平行直线被第三条直线所截,内错角相等.
简写成:两直线平行,内错角相等.
书写格式:
∵ a∥b(已知)
∴ ∠2=∠3
(两直线平行,内错角相等)
如图,已知a//b,那么 2与 4有什么关系呢?为什么
b
1
2
a
l
4
思 考
∴ 2+ 4=180°(等量代换).
解: ∵a//b (已知)
∴ 1= 2(两直线平行,同位角相等)
∵ 1+ 4=180°(邻补角的性质)
平行线的性质3
性质:两条平行直线被第三条直线所截,同旁内角互补.
简写成:两直线平行,同旁内角互补.
书写格式:
∵ a∥b(已知),
∴ ∠2+∠4=180 °
(两直线平行,同旁内角互补)
b
1
2
a
l
4
总结
平行线的性质:
1.两直线平行,同位角相等;
2.两直线平行,内错角相等;
3.两直线平行,同旁内角互补。
思考
平行线的性质与判定有什么区别呢?
线的关系
角的关系
两直线平行
线的关系
同位角相等
内错角相等
同旁内角互补
角的关系
判定
平行线的性质
平行线的判定
性质
例题分析
例4 如图,已知直线 a∥ b,∠1=50°,求∠2的度数.
∴∠2=50°(等量代换)
解:∵a∥ b(已知)
∴∠1=∠2(两直线平行,内错角相等)
∵∠1=50°(已知)
例5 如图,在四边形 ABCD 中 ,AB // CD,∠B = 60°,求∠C 的度数. 能否求得 ∠A 的度数?
根据题目的已知条件,无法求出 ∠A 的度数.
解:∵ AB// CD (已知)
∴ ∠B+∠C = 180°(两直线平行,同旁内角互补).
∵ ∠B = 60° (已知),
∴ ∠C = 180°-∠B = 120°(等式的性质).
例6 将如图所示的方格图中的图形向右平行移动 4 格,再向上平行移动 3 格,画出平行移动后的图形.
解:如图2所示的图形,即为原图形,以及原图形向右平行移动4格,再向上平行移动3格后的图形.
从图中可以看出,原图形中的每一个顶点及每一条边都向右平行移动了4格,再向上平行移动了3格.
图1
图2
随堂练习
1.根据题图,在下列解答中,填上适当的理由: 【教材P192 练习 第1题】
(1)∵AD // BC (已知),
∴ ∠1 = ∠B( );
(2)∵AB // CD (已知),
∴ ∠1 = ∠D( ).
两直线平行,同位角相等
两直线平行,内错角相等
2. 在下列解答中,填空:【教材P192 练习 第2题】
(1)∵AD // BC (已知),
∴( ) + ∠ABC = 180°
(两直线平行,同旁内角互补);
(2)∵ AB // CD (已知),
∴∠ABC + ( ) = 180°
(两直线平行,同旁内角互补).
∠BAD
∠BCD
3.如图,两条平行直线a、b被第三条直线c所截.若∠1=52°,
那么∠2=_______, ∠3=_______, ∠4=_______, 【教材P192 练习 第3题】
1
2
3
4
a
b
c
52°
128°
52°
4.如图,将方格图中的图形向右平行移动3格,再向下平行移动4格,画出平行移动后的图形. 【教材P192 练习 第4题】
5.如图,已知直线a∥ b,∠3 = 131°,求∠1、∠2的度数.
阅读下面的解答过程,并填空(理由或数学式). 【教材P192 练习 第5题】
解 ∵ ∠3=131°( )
又∵∠3=∠1 ( )
∴ ∠1=( )( )
∵a ∥ b( )
∴ ∠1+ ∠2=180°( )
∴ ∠2=( )(等式的性质).
a
b
1
3
2
已知
对顶角相等
131°
等量代换
已知
两直线平行,同旁内角互补
49°
知识点1 两直线平行,同位角相等
1.如图,直线,被直线所截,, ,则 等于( )
B
(第1题)
A. B. C. D.
返回
2.[2025安阳月考]如图,于点,, ,则
_____.
(第2题)
返回
3.如图,,, ,则 _____.
(第3题)
返回
知识点2 两直线平行,内错角相等
(第4题)
4.[2024河南中考]如图,乙地在甲地的北偏东
方向上,则 的度数为( )
B
A. B. C. D.
返回
(第5题)
5.[2024泸州中考]把一块含 角的直角三角板
按如图方式放置于两条平行线间,若 ,
则 ( )
B
A. B. C. D.
返回
知识点3 两直线平行,同旁内角互补
6.[2024湖北中考改编]如图,一条公路的两侧铺设了, 两条平
行管道,并有纵向管道连通.若 ,则 的度数是_____.
返回
7.如图,若,,则 _____.
(第7题)
返回
(第8题)
8.[2025长春期末]如图,若, ,
, ,则 的度数为
( )
B
A. B. C. D.
返回
9.如图,万岁山武侠城的两条小路 ,则
( )
C
(第9题)
A. B. C. D.
返回
知识点4 图形的平行移动
(第10题)
10.如图,若图形 经过平移与下方阴影部分拼成一
个长方形,则平移方式可以是( )
A
A.向右平移4个格,再向下平移4个格
B.向右平移6个格,再向下平移5个格
C.向右平移4个格,再向下平移3个格
D.向右平移5个格,再向下平移4个格
返回
11.[2024陕西中考]如图,, ,
,则 的度数为( )
B
A. B. C. D.
返回
(第12题)
12. 光线在不同介质中的传播速度是不同
的,因此当光线从水中射向空气时,要发生折射,由于
折射率相同,所以在水中平行的光线,在空气中也是平
行的.如图, , 的度数为( )
B
A. B. C. D.
返回
13.如图,将一长方形纸片沿折叠后,点,分别落在点、 的位
置,若 ,则 _____.
(第13题)
返回
14.某兴趣小组利用几何图形画出了螳螂的简笔画,如图,已知
,, ,则 _____.
返回
15.(4分)如图,画出方格纸中的图形向右平行移动3格,再向下平行
移动4格后的图形.
解:如图所示.
返回
16.(4分)如图,,,平分 ,
, ,求 的度数.
解:, ,
, .
, .
,
.
平分 ,
.
, .
返回
17.(8分) 如图①,, 是两个互相平行的镜面,
根据镜面反射规律:若一束光线照射到镜面上,反射光线为 ,
则一定有.光线是由 镜面反射得到.
(1)判断与 的位置关系,并说明理由;
解: .理由如下:
, ,
, ,
.
, ,
, .
(2)如图②,镜面上有一光源,发射的光线交反射光线于点 ,
若,猜想与 的数量关系,并说明理由.
解: .理由如下:
, .
, .
返回
课堂小结
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
性质
已知
结论
结论
已知
谢谢观看!
4.2.3 平行线的性质
第4章 相交线和平行线
【华东师大版·2024】数学 七年级上册
授课教师:********
班 级:********
时 间:********
幻灯片 1:封面
标题:4.2.3 平行线的性质
副标题:探索平行线被截形成的角的关系
幻灯片 2:学习目标
掌握平行线的三条性质:两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补。
能运用平行线的性质解决角度计算和简单的推理问题。
区分平行线的性质与判定,理解它们之间的联系与区别,培养逻辑思维能力。
幻灯片 3:复习回顾 —— 平行线的判定
展示表格:
判定方法
条件
结论
方法 1
同位角相等
两直线平行
方法 2
内错角相等
两直线平行
方法 3
同旁内角互补
两直线平行
提问:这些判定方法中,条件和结论分别是什么?如果已知两直线平行,那么同位角、内错角、同旁内角会有什么关系呢?
引入:本节课我们将反过来研究 —— 当两条直线平行时,被第三条直线所截形成的同位角、内错角、同旁内角有什么性质。
幻灯片 4:平行线的性质 1—— 两直线平行,同位角相等
探究活动:
画出两条平行线 a、b,被第三条直线 c 所截,标注同位角∠1 和∠2。
用量角器测量∠1 和∠2 的度数,记录测量结果。
改变截线 c 的位置,再次测量同位角的度数,观察数据变化。
性质总结:两条平行线被第三条直线所截,同位角相等。简单说成:两直线平行,同位角相等。
符号表示:∵a∥b,∴∠1=∠2(∠1 与∠2 是同位角)。
图形展示:标注 a∥b,∠1=∠2,用箭头指示角的关系。
幻灯片 5:平行线的性质 2—— 两直线平行,内错角相等
推导过程:
已知:a∥b,c 是截线,∠1 与∠2 是内错角。
由 a∥b,得∠1=∠3(两直线平行,同位角相等)。
又∵∠3=∠2(对顶角相等),∴∠1=∠2(等量代换)。
性质总结:两条平行线被第三条直线所截,内错角相等。简单说成:两直线平行,内错角相等。
符号表示:∵a∥b,∴∠1=∠2(∠1 与∠2 是内错角)。
图形展示:标注 a∥b,∠1=∠2(内错角),展示推导逻辑链。
幻灯片 6:平行线的性质 3—— 两直线平行,同旁内角互补
推导过程:
已知:a∥b,c 是截线,∠1 与∠2 是同旁内角。
由 a∥b,得∠1=∠3(两直线平行,同位角相等)。
又∵∠3+∠2=180°(邻补角互补),∴∠1+∠2=180°(等量代换)。
性质总结:两条平行线被第三条直线所截,同旁内角互补。简单说成:两直线平行,同旁内角互补。
符号表示:∵a∥b,∴∠1+∠2=180°(∠1 与∠2 是同旁内角)。
图形展示:标注 a∥b,∠1+∠2=180°,用弧线标注角的和为平角。
幻灯片 7:平行线的性质与判定的区别与联系
区别:
类别
条件
结论
用途
判定
角的关系
直线平行
判定两直线是否平行
性质
直线平行
角的关系
由平行求角的度数或关系
联系:
两者都涉及同位角、内错角、同旁内角与平行线的关系。
判定是性质的逆过程,性质是判定的逆推理。
口诀记忆:“判定是由角定平行,性质是由平行定角”。
幻灯片 8:例题 1—— 利用同位角性质计算
题目:如图,a∥b,c 是截线,∠1=50°,求∠2 的度数。
图形:a∥b,∠1 与∠2 是同位角。
解答过程:
∵a∥b(已知),∴∠2=∠1(两直线平行,同位角相等)。
∵∠1=50°(已知),∴∠2=50°。
结论:∠2=50°。
幻灯片 9:例题 2—— 利用内错角性质推理
题目:如图,AB∥CD,BC 平分∠ABD,∠1=60°,求∠2 的度数。
图形:AB∥CD,BC 交 AB 于 B,交 CD 于 C,∠1 是∠ABC,∠2 是∠BCD。
解答过程:
∵AB∥CD(已知),∴∠2=∠1(两直线平行,内错角相等)。
∵BC 平分∠ABD(已知),∠1=60°,∴∠ABC=∠1=60°。
∴∠2=60°。
结论:∠2=60°。
幻灯片 10:例题 3—— 利用同旁内角性质综合计算
题目:如图,AD∥BC,∠B=50°,∠D=130°,AB 与 CD 平行吗?为什么?
图形:AD 是截线,分别交 AB、CD 于 A、D;BC 是截线,分别交 AB、CD 于 B、C。
解答过程:
∵AD∥BC(已知),∴∠A+∠B=180°(两直线平行,同旁内角互补)。
∵∠B=50°(已知),∴∠A=180°-50°=130°。
∵∠D=130°(已知),∴∠A=∠D。
∵∠A 与∠D 是 AB、CD 被 AD 所截的内错角,∴AB∥CD(内错角相等,两直线平行)。
结论:AB∥CD。
幻灯片 11:课堂练习 1—— 基础计算
题目:如图,l1∥l2,∠α=120°,则∠β=( )°。
图形:l1∥l2,∠α 与∠β 是同旁内角。
答案:60(∵l1∥l2,∴∠α+∠β=180°,∠β=60°)。
幻灯片 12:课堂练习 2—— 性质与判定综合
题目:如图,∠1=∠2,∠3=100°,求∠4 的度数。
图形:∠1 与∠2 是同位角(判定 a∥b),∠3 与∠4 是同旁内角(性质求角)。
解答过程:
∵∠1=∠2(已知),∴a∥b(同位角相等,两直线平行)。
∵a∥b(已证),∴∠3+∠4=180°(两直线平行,同旁内角互补)。
∵∠3=100°(已知),∴∠4=80°。
答案:80°。
幻灯片 13:课堂练习 3—— 实际应用
题目:一辆汽车在笔直的公路上行驶,两次拐弯后仍与原来的方向平行,若第一次拐弯的角度是 70°,则第二次拐弯的角度是多少?
图形:模拟公路拐弯,两次拐弯形成 “Z” 形或 “U” 形。
解答过程:
分两种情况:
两次拐弯方向相反(如先右拐 70°,再左拐 70°),第二次拐弯 70°。
两次拐弯方向相同(如先右拐 70°,再右拐 110°),第二次拐弯 110°。
答案:70° 或 110°。
幻灯片 14:易错点分析
常见错误:
混淆性质与判定,如将 “两直线平行,同位角相等” 说成 “同位角相等,两直线平行”。
忽略 “两直线平行” 的前提,直接使用性质,如对不平行的直线应用 “同位角相等”。
计算同旁内角时,误将 “互补” 当作 “相等”,导致结果错误。
规避方法:
做题时先明确是 “由平行求角”(用性质)还是 “由角定平行”(用判定),标注关键条件。
应用性质前,务必确认两条直线是否平行,无平行条件时不能使用。
记忆同旁内角性质时,结合 “平角 = 180°” 理解 “互补” 的含义,避免与内错角、同位角的 “相等” 混淆。
幻灯片 15:课堂小结
平行线的性质:
两直线平行,同位角相等。
两直线平行,内错角相等。
两直线平行,同旁内角互补。
与判定的区别:性质是 “平行→角的关系”,判定是 “角的关系→平行”。
应用要点:明确前提(两直线平行),选择对应性质,结合已知条件推理计算。
幻灯片 16:布置作业
基础作业:
教材课后练习题第 1、2、3 题(性质的直接应用)。
如图,AB∥CD,∠A=75°,∠C=40°,求∠E 的度数(提示:过 E 作平行线)。
提升作业:
已知:如图,∠1+∠2=180°,∠3=∠B,求证:∠AED=∠C。
总结平行线性质与判定在解题中的综合应用技巧,举例说明。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
学习目标
掌握平行线的性质,会运用两条直线是平行关系判
断角相等或互补;
能够根据平行线的性质进行简单的推理.
重点
难点
复习旧知
根据右图,填空:
①如果∠1=∠C,
那么__∥__( )
② 如果∠1=∠B
那么__∥__( )
③ 如果∠2+∠B=180°,那么__∥__( )
AB
CD
EC
BD
同位角相等,两直线平行
内错角相等,两直线平行
EC
BD
同旁内角互补,两直线平行
E
A
C
D
B
1
2
3
4
两直线平行
1.同位角相等
2.内错角相等
3.同旁内角互补
问:通过上题可知平行线的判定方法是什么?
思考:反过来如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢
复习旧知
新课探究
翻开你的数学练习横格本,每一页上都有许多互相平行的横线条,随意画一条斜线与这些横线条相交,找出其中任意一对同位角.观察或用量角器度量这对同位角,你有什么发现?
2
1
∠1=∠2
试一试
平行线的性质探究
活动 如图所示如果直线a与直线b平行,那么直线l与直线a、b分别交于点O与点P,其中的同位角∠1与∠2必定相等吗?
1
2
a
b
l
O
P
平行线的性质探究
如图,如果我们以点O为顶点,画另一个角∠1′,使∠1′=∠2,这样就画出了过点O的另一条直线a′.由于∠1′=∠2,根据“同位角相等,两直线平行”的基本事实,可以得到a′ ∥ b
1
2
a
b
l
a′
1′
O
P
经过点O有两条直线a、a′与b平行
经过已知直线外一点,有且只有一条直线与已知直线平行
矛盾
所以 ∠1与∠2一定相等
平行线的性质1
两条平行直线被第三条直线所截,同位角相等.
简写成:两直线平行,同位角相等.
b
1
2
a
l
书写格式:
∵ a∥b(已知)
∴ ∠1=∠2
(两直线平行,同位角相等)
如图,已知a//b,那么 2与 3相等吗?为什么
b
1
2
a
l
3
解: ∵ a∥ b (已知),
∴ ∠1=∠2 (两直线平行,同位角相等).
又∵ ∠1=∠3 (对顶角相等),
∴ ∠2=∠3 (等量代换).
b
1
2
a
l
3
平行线的性质2
性质:两条平行直线被第三条直线所截,内错角相等.
简写成:两直线平行,内错角相等.
书写格式:
∵ a∥b(已知)
∴ ∠2=∠3
(两直线平行,内错角相等)
如图,已知a//b,那么 2与 4有什么关系呢?为什么
b
1
2
a
l
4
思 考
∴ 2+ 4=180°(等量代换).
解: ∵a//b (已知)
∴ 1= 2(两直线平行,同位角相等)
∵ 1+ 4=180°(邻补角的性质)
平行线的性质3
性质:两条平行直线被第三条直线所截,同旁内角互补.
简写成:两直线平行,同旁内角互补.
书写格式:
∵ a∥b(已知),
∴ ∠2+∠4=180 °
(两直线平行,同旁内角互补)
b
1
2
a
l
4
总结
平行线的性质:
1.两直线平行,同位角相等;
2.两直线平行,内错角相等;
3.两直线平行,同旁内角互补。
思考
平行线的性质与判定有什么区别呢?
线的关系
角的关系
两直线平行
线的关系
同位角相等
内错角相等
同旁内角互补
角的关系
判定
平行线的性质
平行线的判定
性质
例题分析
例4 如图,已知直线 a∥ b,∠1=50°,求∠2的度数.
∴∠2=50°(等量代换)
解:∵a∥ b(已知)
∴∠1=∠2(两直线平行,内错角相等)
∵∠1=50°(已知)
例5 如图,在四边形 ABCD 中 ,AB // CD,∠B = 60°,求∠C 的度数. 能否求得 ∠A 的度数?
根据题目的已知条件,无法求出 ∠A 的度数.
解:∵ AB// CD (已知)
∴ ∠B+∠C = 180°(两直线平行,同旁内角互补).
∵ ∠B = 60° (已知),
∴ ∠C = 180°-∠B = 120°(等式的性质).
例6 将如图所示的方格图中的图形向右平行移动 4 格,再向上平行移动 3 格,画出平行移动后的图形.
解:如图2所示的图形,即为原图形,以及原图形向右平行移动4格,再向上平行移动3格后的图形.
从图中可以看出,原图形中的每一个顶点及每一条边都向右平行移动了4格,再向上平行移动了3格.
图1
图2
随堂练习
1.根据题图,在下列解答中,填上适当的理由: 【教材P192 练习 第1题】
(1)∵AD // BC (已知),
∴ ∠1 = ∠B( );
(2)∵AB // CD (已知),
∴ ∠1 = ∠D( ).
两直线平行,同位角相等
两直线平行,内错角相等
2. 在下列解答中,填空:【教材P192 练习 第2题】
(1)∵AD // BC (已知),
∴( ) + ∠ABC = 180°
(两直线平行,同旁内角互补);
(2)∵ AB // CD (已知),
∴∠ABC + ( ) = 180°
(两直线平行,同旁内角互补).
∠BAD
∠BCD
3.如图,两条平行直线a、b被第三条直线c所截.若∠1=52°,
那么∠2=_______, ∠3=_______, ∠4=_______, 【教材P192 练习 第3题】
1
2
3
4
a
b
c
52°
128°
52°
4.如图,将方格图中的图形向右平行移动3格,再向下平行移动4格,画出平行移动后的图形. 【教材P192 练习 第4题】
5.如图,已知直线a∥ b,∠3 = 131°,求∠1、∠2的度数.
阅读下面的解答过程,并填空(理由或数学式). 【教材P192 练习 第5题】
解 ∵ ∠3=131°( )
又∵∠3=∠1 ( )
∴ ∠1=( )( )
∵a ∥ b( )
∴ ∠1+ ∠2=180°( )
∴ ∠2=( )(等式的性质).
a
b
1
3
2
已知
对顶角相等
131°
等量代换
已知
两直线平行,同旁内角互补
49°
知识点1 两直线平行,同位角相等
1.如图,直线,被直线所截,, ,则 等于( )
B
(第1题)
A. B. C. D.
返回
2.[2025安阳月考]如图,于点,, ,则
_____.
(第2题)
返回
3.如图,,, ,则 _____.
(第3题)
返回
知识点2 两直线平行,内错角相等
(第4题)
4.[2024河南中考]如图,乙地在甲地的北偏东
方向上,则 的度数为( )
B
A. B. C. D.
返回
(第5题)
5.[2024泸州中考]把一块含 角的直角三角板
按如图方式放置于两条平行线间,若 ,
则 ( )
B
A. B. C. D.
返回
知识点3 两直线平行,同旁内角互补
6.[2024湖北中考改编]如图,一条公路的两侧铺设了, 两条平
行管道,并有纵向管道连通.若 ,则 的度数是_____.
返回
7.如图,若,,则 _____.
(第7题)
返回
(第8题)
8.[2025长春期末]如图,若, ,
, ,则 的度数为
( )
B
A. B. C. D.
返回
9.如图,万岁山武侠城的两条小路 ,则
( )
C
(第9题)
A. B. C. D.
返回
知识点4 图形的平行移动
(第10题)
10.如图,若图形 经过平移与下方阴影部分拼成一
个长方形,则平移方式可以是( )
A
A.向右平移4个格,再向下平移4个格
B.向右平移6个格,再向下平移5个格
C.向右平移4个格,再向下平移3个格
D.向右平移5个格,再向下平移4个格
返回
11.[2024陕西中考]如图,, ,
,则 的度数为( )
B
A. B. C. D.
返回
(第12题)
12. 光线在不同介质中的传播速度是不同
的,因此当光线从水中射向空气时,要发生折射,由于
折射率相同,所以在水中平行的光线,在空气中也是平
行的.如图, , 的度数为( )
B
A. B. C. D.
返回
13.如图,将一长方形纸片沿折叠后,点,分别落在点、 的位
置,若 ,则 _____.
(第13题)
返回
14.某兴趣小组利用几何图形画出了螳螂的简笔画,如图,已知
,, ,则 _____.
返回
15.(4分)如图,画出方格纸中的图形向右平行移动3格,再向下平行
移动4格后的图形.
解:如图所示.
返回
16.(4分)如图,,,平分 ,
, ,求 的度数.
解:, ,
, .
, .
,
.
平分 ,
.
, .
返回
17.(8分) 如图①,, 是两个互相平行的镜面,
根据镜面反射规律:若一束光线照射到镜面上,反射光线为 ,
则一定有.光线是由 镜面反射得到.
(1)判断与 的位置关系,并说明理由;
解: .理由如下:
, ,
, ,
.
, ,
, .
(2)如图②,镜面上有一光源,发射的光线交反射光线于点 ,
若,猜想与 的数量关系,并说明理由.
解: .理由如下:
, .
, .
返回
课堂小结
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
性质
已知
结论
结论
已知
谢谢观看!
同课章节目录
