第1章 有理数【章末复习】 课件(共50张PPT)
文档属性
| 名称 | 第1章 有理数【章末复习】 课件(共50张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 05:32:20 | ||
图片预览










文档简介
(共50张PPT)
章末复习
第1章 有理数
【华东师大版·2024】数学 七年级上册
授课教师:********
班 级:********
时 间:********
幻灯片 1:封面
标题:第 1 章 有理数 章末复习
副标题:系统梳理知识,巩固提升能力
幻灯片 2:复习目标
梳理有理数的相关概念,包括正数、负数、数轴、相反数、绝对值、有理数的分类等,明确各概念之间的联系与区别。
熟练掌握有理数的各种运算(加、减、乘、除、乘方)及混合运算的顺序和法则,能准确、快速地进行计算。
理解科学记数法、近似数的概念,能正确表示和运用。
会使用计算器进行有理数的计算,提高运算效率。
能运用有理数的知识解决实际问题,体会数学与生活的联系。
幻灯片 3:知识框架图
有理数
├── 基本概念
│ ├── 正数与负数
│ ├── 有理数的分类(整数、分数)
│ ├── 数轴(三要素:原点、正方向、单位长度)
│ ├── 相反数(a的相反数是-a)
│ └── 绝对值(|a|≥0,正数的绝对值是本身,负数的是相反数,0的是0)
├── 运算
│ ├── 加法(法则:同号、异号、与0相加)
│ ├── 减法(法则:减去一个数等于加它的相反数)
│ ├── 乘法(法则:同号得正,异号得负,绝对值相乘;多个数相乘)
│ ├── 除法(法则:除以非0数等于乘它的倒数;同号得正,异号得负)
│ ├── 乘方(定义:n个相同因数的积;符号法则)
│ └── 混合运算(顺序:先乘方,再乘除,最后加减;同级从左到右;有括号先算括号内)
├── 扩展内容
│ ├── 科学记数法(a×10 ,1≤a<10,n是正整数)
│ └── 近似数(精确到哪一位;有效数字)
└── 工具使用:计算器(基本操作,进行各类运算)
幻灯片 4:要点回顾 —— 基本概念
正数与负数:大于 0 的数是正数,在正数前加 “-” 的数是负数,0 既不是正数也不是负数。它们可表示具有相反意义的量。
有理数的分类:
按定义:有理数分为整数(正整数、0、负整数)和分数(正分数、负分数)。
按性质:有理数分为正有理数(正整数、正分数)、0、负有理数(负整数、负分数)。
数轴:规定了原点、正方向、单位长度的直线。任何一个有理数都可以用数轴上的点表示。
相反数:只有符号不同的两个数互为相反数,0 的相反数是 0。在数轴上,互为相反数的两个数位于原点两侧,且到原点的距离相等。
绝对值:数轴上表示数 a 的点与原点的距离叫做 a 的绝对值,记作 | a|。互为相反数的两个数绝对值相等。
幻灯片 5:要点回顾 —— 运算(1)
加法法则:
同号两数相加,取相同的符号,并把绝对值相加。
异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值。
互为相反数的两数相加得 0;一个数与 0 相加,仍得这个数。
减法法则:a - b = a + (-b),即减去一个数等于加上这个数的相反数。
加减法统一:有理数的加减混合运算可统一成加法运算,写成省略加号和括号的形式。
幻灯片 6:要点回顾 —— 运算(2)
乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘。
任何数与 0 相乘,都得 0。
多个不为 0 的数相乘,负因数的个数是奇数时,积为负;是偶数时,积为正。
除法法则:
除以一个不等于 0 的数,等于乘这个数的倒数,即 a÷b = a×(1/b)(b≠0)。
两数相除,同号得正,异号得负,并把绝对值相除。0 除以任何一个不等于 0 的数,都得 0。
幻灯片 7:要点回顾 —— 运算(3)
乘方:
定义:求 n 个相同因数 a 的积的运算,记作 a ,其中 a 是底数,n 是指数,结果叫幂。
符号法则:正数的任何次幂都是正数;负数的奇次幂是负数,偶次幂是正数;0 的任何正整数次幂都是 0。
混合运算顺序:
先算乘方,再算乘除,最后算加减。
同级运算,从左到右依次进行。
如有括号,先算括号里面的(小括号→中括号→大括号)。
幻灯片 8:要点回顾 —— 扩展内容与工具
科学记数法:把一个大于 10 的数表示成 a×10 的形式(其中 1≤a<10,n 是正整数)。n 的值等于原数的整数位数减 1。
近似数:
精确到哪一位:看四舍五入到哪一位。
有效数字:从左边第一个非 0 数字起,到末位数字止的所有数字。
计算器:熟悉数字键、运算符号键、功能键(如 CE/C、x 、± 等)的使用,按运算顺序输入可进行各类计算。
幻灯片 9:例题 1—— 概念辨析
题目:下列说法正确的是( )
A. 有理数就是正数和负数 B. 互为相反数的两个数的绝对值相等
C. 数轴上原点两侧的数互为相反数 D. 绝对值等于本身的数是正数
解答过程:
A 选项错误,有理数包括正数、0 和负数。
B 选项正确,互为相反数的两个数到原点的距离相等,即绝对值相等。
C 选项错误,数轴上原点两侧且到原点距离相等的数才互为相反数。
D 选项错误,绝对值等于本身的数是正数和 0。
答案:B
幻灯片 10:例题 2—— 运算计算
题目:计算:
(1)\((-12) + 15 + (-8) + 7\)
(2)\((-3)^2\times(-\frac{2}{3}) - 4\div(-\frac{1}{2})\)
解答过程:
(1)运用加法交换律和结合律:\([(-12) + (-8)] + (15 + 7) = (-20) + 22 = 2\)。
(2)先算乘方:\(9\times(-\frac{2}{3}) - 4\times(-2) = -6 + 8 = 2\)。
答案:(1)2;(2)2。
幻灯片 11:例题 3—— 科学记数法与近似数
题目:
(1)用科学记数法表示 13000000。
(2)近似数 3.04×10 精确到哪一位?有几个有效数字?
解答过程:
(1)13000000 的整数位数是 8,n=7,所以表示为\(1.3\times10^7\)。
(2)3.04×10 =304000,4 在千位,所以精确到千位;有效数字是 3、0、4,共 3 个。
答案:(1)\(1.3\times10^7\);(2)千位,3 个。
幻灯片 12:例题 4—— 实际应用
题目:某检修小组乘汽车沿公路检修线路,约定前进为正,后退为负。某天自 A 地出发到收工时所走路线(单位:千米)为:+10,-3,+4,+2,-8,+13,-2,+12,+8,+5。
(1)收工时距 A 地多远?
(2)若每千米耗油 0.2 升,从 A 地出发到收工时共耗油多少升?
解答过程:
(1)将所有数相加:\((+10)+(-3)+(+4)+(+2)+(-8)+(+13)+(-2)+(+12)+(+8)+(+5)=41\)(千米)。
(2)先求总路程(各数绝对值之和):\(10 + 3 + 4 + 2 + 8 + 13 + 2 + 12 + 8 + 5 = 67\)(千米),耗油量:\(67\times0.2 = 13.4\)(升)。
答案:(1)41 千米;(2)13.4 升。
幻灯片 13:课堂练习 1—— 概念与运算
题目:
(1)-5 的相反数是______,绝对值是______。
(2)计算:\(-2^2 + (-3)\times(-4) - (-1)^3\)。
答案:(1)5,5;(2)\(-4 + 12 - (-1) = 9\)。
幻灯片 14:课堂练习 2—— 科学记数法与近似数
题目:
(1)将 5670000 用科学记数法表示为______。
(2)近似数 2.8 万精确到______位,有______个有效数字。
答案:(1)\(5.67\times10^6\);(2)千,2。
幻灯片 15:课堂练习 3—— 实际应用
题目:某商店一周的收入、支出情况如下表(收入为正):
日期
周一
周二
周三
周四
周五
周六
周日
收支(元)
+1500
-200
-300
+400
-500
+600
-100
这一周商店的总利润是多少元?
答案:\(1500 - 200 - 300 + 400 - 500 + 600 - 100 = 1400\)(元)。
幻灯片 16:易错点总结
概念类:
混淆相反数和倒数的概念。
对绝对值的性质理解不清,如认为 | a|=a 一定成立(忽略 a 为负数的情况)。
有理数分类时遗漏 0。
运算类:
符号错误,如异号两数相加、乘除时符号判断错误。
运算顺序错误,尤其是乘方与乘除、加减的顺序。
对\(-a^n\)与\((-a)^n\)区分不清,导致乘方计算错误。
其他:
科学记数法中 a 的范围错误或 n 的值计算错误。
近似数的精确度判断错误,尤其是带单位或用科学记数法表示的数。
幻灯片 17:总结与寄语
总结:本章主要学习了有理数的概念、运算及相关应用,核心是掌握各种运算的法则和顺序,理解相关概念的内涵。
寄语:有理数是初中数学的基础,希望同学们通过本次复习,查漏补缺,熟练运用所学知识解决问题,为后续学习打下坚实的基础。
幻灯片 18:作业布置
基础作业:完成章末复习题 A 组(巩固基础知识和基本运算)。
提升作业:完成章末复习题 B 组(综合运用知识解决复杂问题)。
拓展作业:结合生活实际,编一道运用有理数知识解决的应用题并解答。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
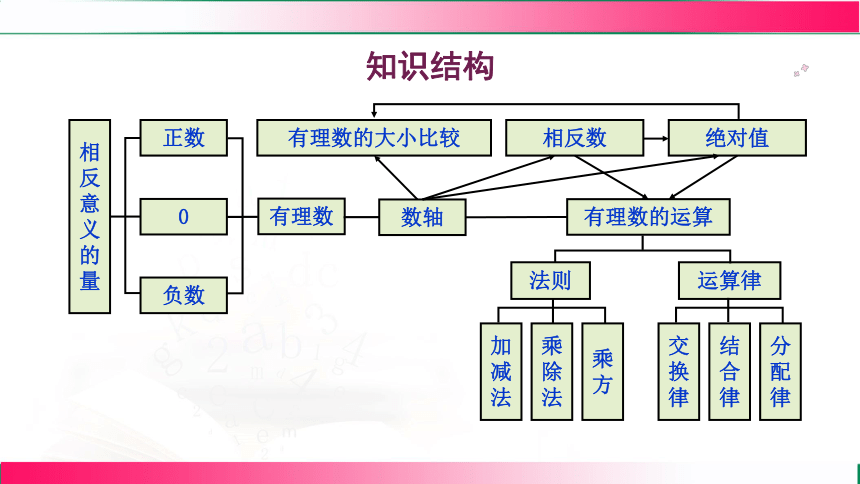
知识结构
有理数的运算
正数
负数
相反意义的量
0
有理数
数轴
有理数的大小比较
相反数
绝对值
加减法
乘除法
乘方
法则
运算律
交换律
结合律
分配律
有理数
相关概念
有理数
数轴
相反数
绝对值
倒数
概念:整数和分数统称为有理数
分类
整数
分数
正整数
0
负整数
正分数
负分数
规定了原点、正方向、单位长度的直线
只有正负号不同的两个数称互为相反数.
规定 0 的相反数是 0 .
乘积是 1 的两个数互为倒数
一个正数的绝对值是它本身
0 的绝对值是 0
一个负数的绝对值是它的相反数
怎样比较有理数的大小?
利用数轴比较
利用法则比较
利用绝对值比较
在数轴上表示的两个数,右边的数总比左边的数大
正数都大于0;负数都小于0;正数都大于负数
两个负数,绝对值大的反而小
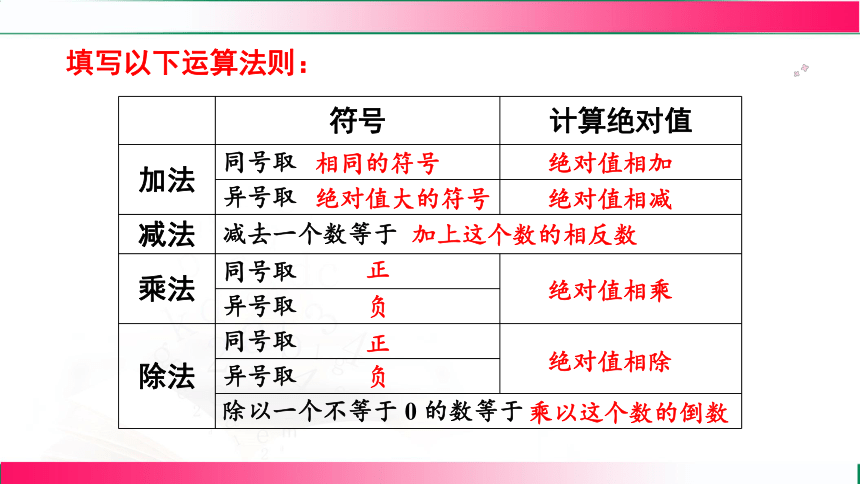
符号 计算绝对值
加法 同号取
异号取
减法 减去一个数等于 乘法 同号取
异号取 除法 同号取
异号取 除以一个不等于 0 的数等于 相同的符号
绝对值相加
负
绝对值相乘
绝对值大的符号
绝对值相减
正
正
绝对值相除
加上这个数的相反数
乘以这个数的倒数
负
填写以下运算法则:
交换律:a+b=b+a
结合律:(a+b)+c=a+(b+c)
加法
乘法
运算律
交换律:ab=ba
结合律:(ab)c=a(bc)
分配律:a(b+c)=ab+ac
有理数的运算律有哪些?
有理数的混合运算应按照怎样的顺序进行?
1.先做乘方,再做乘除,最后做加减;
2.同级运算,按照从左至右的顺序进行;
3.如果有括号,就先算小括号里的,再算中括号里的,然后算大括号里的.
计算:
20+(-2)×10 +1 =
(20-1)×0 ÷(2+8) =
(20-1)× +20+(-2)×10 =
1÷( -33÷9) =
做一做
1
0
科学记数法是什么?
取近似数的方法有哪些?
一个绝对值大于 10 的数可以记成 的形式,其中
n 是正整数.像这样的记数法叫做科学记数法.
四舍五入法、进一法、去尾法
释疑解惑
1.为什么要引入负数?举出实例说明正数和负数在表示相反意义的量时的作用.
现实生活中存在很多个有相反意义的量,如:向东5米与向西5米,零上2℃与零下2℃,收入100元与支出100元,低于海平面150米与高出海平面800米……用正数表示其中一种量,负数表示和它相反意义的量,这样既简单又明白.例如吐鲁番盆地的海拔高度为-154.31m,表示吐鲁番盆地的海拔高度是低于海平面154.31m.
2.数的范围从正整数、0和正分数扩充到有理数后,增加了哪些数?减法中哪些原来不能进行的运算可以进行了?
增加了负整数、负分数,解决了原来“小数不能减去大数”的问题,现在任何有理数都可以进行减法运算.
3.怎样用数轴表示有理数?数轴与普通直线有什么不同?怎样用数轴解释绝对值和相反数?
任何一个有理数都可以用数轴上的一个点表示,但数轴上的点不是都表示有理数,这一点,以后我们将要学习.数轴是一条特殊的直线,是规定了正方向、原点和单位长度的直线.原点、正方向、单位长度也称数轴的三要素,缺一不可.
数轴上与原点的距离相等的两个点所表示的数互为相反数.
4.有理数的加法与减法有什么关系?乘法与除法呢?
有理数的减法可以转化为加法,转化的桥梁是相反数,减去一个数等于加上这个数的相反数,同样,除法可以转化为乘法,转化的桥梁是倒数,除以一个数(不为0),等于乘这个数的倒数.有理数的混合运算都可以转化为加法与乘法.
随堂练习
例1 填空:
(1)在知识竞赛中,如果 +10分表示加10分,那么扣20分可表示成_______;
(2)某人转动转盘,如果沿逆时针转5圈记作 +5圈,那么沿顺时针转12圈可表示成_______;
(3)某次乒乓球质量检测中,一只乒乓球超出标准0.02g记作 +0.02g,那么 -0.03g表示_______________ .
-20分
-12圈
低于标准0.03g
例2 填空:
(1)若m,n互为相反数,则m+n =______;
(2)-2006的倒数是________;
(3)-(-3)= ______;
(4)-|-2|的倒数是_______.
0
3
例3 如图,数轴上两点所表示的两数( )
A.和为正数 B.和为负数
C.积为正数 D.积为负数
D
例4 下列四个运算中,结果最小的是( )
A.1+(-2) B.1-(-2)
C.1×(-2) D.1÷(-2)
C
例5 如果a<0,b>0,a+b<0,那么下列关系式中正确的是( )
A.a>b>-b>-a B.a>-a>b>-b
C.b>a>-b>-a D.-a>b>-b>a
D
-1
3
-2
-a>b
例7 神舟六号飞船,在平安飞行115小时23分后重返神州. 用科学记数法表示神舟六号飞船飞行的时间是______________秒 (精确到千位).
分析:a×10x中a的取值范围是1≤a<10,底数10的指数n等于所表示的整数位数减去1.
4.15×105
115×60×60+23×60=415380≈415000(秒)
例8 (-8)2014+(-8)2013能被下列数整除的是( )
A.3 B.5 C.7 D.9
C
=(-8)2013×[(-8)+1]
=(-8)2013×(-7)
核心知识巩固
一、基础考点演练
考点1 有理数及其分类
1.[2025安阳模拟]小东在妈妈的微信零钱明细中看到,收入2 000元
被记作元,则 元表示_____________.
支出1 600元
返回
2.有下列说法:①有理数的个数是无限的;②整数包括正整数和负整数;
③正有理数和负有理数统称有理数;④负分数是有理数.其中正确说法
的序号是______.
①④
返回
3.把下列各数填入相应的大括号内:
,,,,, ,
,0.
正分数集:{__________________…};
整数集:{________________…};
负有理数集:{_____________________…};
非负数集:{_____________________________…}.
,,
,,0
,,
,,,,0
返回
考点2 数轴、相反数、绝对值、倒数
4.下列说法中,正确的序号为______.
的相反数是;一定是负数; 既没有倒数也没有相反
数;④绝对值大于它本身的数是负数.
①④
返回
5.有理数,, 在数轴上的对应点的位置如图所示,这三个数中绝对
值最大的是___.
返回
6.填空:
(1) ___;
(2) ____;
(3) 的倒数是__;
(4) ____.
2
7.5
返回
7.已知是数轴上的一点,且点到原点的距离为1,把点 沿数轴向右
移动3个单位长度得到点,则点 表示的数是______.
4或2
返回
考点3 有理数的大小比较
8.下列四个数中,比 小的数是( )
D
A.0 B. C. D.
返回
9.[2025忻州期末]如果,, ,那么下列比较大小
中正确的是( )
D
A. B.
C. D.
返回
10.比较大小(填“ ”“”或“ ”)
(1)___ ;
(2)___ .
返回
11.(4分)某校举行一场文艺汇演,汇演中途设置了一个有奖问答环节,
题目在背景屏幕上显示如图,请回答图中的问题.
解:,,最小的正整数是1, 的最小
值是,0的相反数是0,比大的数是 .将这些数在数轴上表示出来,
如图.
所以 .
返回
考点4 有理数的运算
12.下列各组数中,结果相等的是( )
A
A.和 B.和 C.和 D.和
返回
13.数轴上,,三点表示的有理数分别为,,,若 ,
, ,则下列数轴符合题意的是( )
B
A. B.
C. D.
返回
14.已知,互为相反数,,, 互为倒数,则
的值为___.
0
返回
15.[2025郑州期末]若,则 内填的运算符号是___.
返回
16. 定义两种新运算“ ”和“”: ,
,则 _____.
返回
17.某种细菌在培养过程中,每半小时分裂一次(由一个分裂成两个).
经过 ,这种细菌由1个可分裂为____个.
64
返回
18.(12分)[2025南阳期末]计算:
(1) ;
解:原式 .
(2) ;
解:原式 .
(3) .
解:原式 .
返回
19.(12分)小亮家新换了一辆新能源汽车,他连续记录了一周每天行
驶的路程(如下表).以为标准,超过记为“ ”,不足
记为“-”,刚好 记为“0”.
星期 一 二 三 四 五 六 日
0
(1)小亮家本周行驶的路程最多的一天比最少的一天多____ .
(2)小亮家的汽车本周一共行驶了_____ .
50
400
[解析] 点拨: .
(3)已知汽油车每行驶 需用汽油7升,油价为7.5元/升,而新能
源汽车每行驶 耗电15度,每度电0.8元,换成新能源汽车后这一
周的行驶费用比原来节省多少钱?
解:汽油车的费用为 (元),
新能源汽车的费用为(元),
(元).
答:换成新能源汽车后这一周的行驶费用比原来节省162元.
返回
考点5 科学记数法与近似数
20.下列说法正确的是( )
D
A.近似数2.8和2.80表示的意义一样 B.6.7万精确到万位
C.0.680精确到百分位 D.300精确到个位
返回
21.北京数字经济算力中心日前已部署上架和调试的设备的算力为
是计算机系统算力的一种度量单位 ,整体投产后,
累计实现的算力将是日前已部署上架和调试的设备的算力的5倍,达到
,则 的值为_________.
返回
22.地球绕太阳公转的速度用科学记数法表示约为 ,则
原数是_________.
110 000
返回
23.一个小数“四舍五入”得到的近似数是 ,这个小数最小是_____,
最大是_____.
6.75
6.84
返回
二、思想方法演练
思想1 转化思想
24.若,均为有理数,且,则 _____.
返回
思想2 数形结合思想
25.(8分)如图,以 为1个单位长度用直尺画数轴时,数轴上的
点,,刚好对着直尺上的刻度2,8和10.设点,, 所表示的数
的和是,该数轴的原点为 .
(1)点到点之间有____个单位长度;若点表示的数是,则点
表示的数为____;
16
15
(2)若点,所表示的数互为相反数,直接写出此时数轴的原点 对
应直尺上的刻度,并求此时 的值.
思想3 分类讨论思想
解:因为点,所表示的数互为相反数,所以数轴的原点 对应直尺上
的刻度5.
此时点,,所表示的数分别是 ,6,10,因此
.
返回
26.有理数,,在数轴上对应点的位置如图所示,若 ,则下
列结论中正确的是( )
B
A. B. C. D.
返回
谢谢观看!
章末复习
第1章 有理数
【华东师大版·2024】数学 七年级上册
授课教师:********
班 级:********
时 间:********
幻灯片 1:封面
标题:第 1 章 有理数 章末复习
副标题:系统梳理知识,巩固提升能力
幻灯片 2:复习目标
梳理有理数的相关概念,包括正数、负数、数轴、相反数、绝对值、有理数的分类等,明确各概念之间的联系与区别。
熟练掌握有理数的各种运算(加、减、乘、除、乘方)及混合运算的顺序和法则,能准确、快速地进行计算。
理解科学记数法、近似数的概念,能正确表示和运用。
会使用计算器进行有理数的计算,提高运算效率。
能运用有理数的知识解决实际问题,体会数学与生活的联系。
幻灯片 3:知识框架图
有理数
├── 基本概念
│ ├── 正数与负数
│ ├── 有理数的分类(整数、分数)
│ ├── 数轴(三要素:原点、正方向、单位长度)
│ ├── 相反数(a的相反数是-a)
│ └── 绝对值(|a|≥0,正数的绝对值是本身,负数的是相反数,0的是0)
├── 运算
│ ├── 加法(法则:同号、异号、与0相加)
│ ├── 减法(法则:减去一个数等于加它的相反数)
│ ├── 乘法(法则:同号得正,异号得负,绝对值相乘;多个数相乘)
│ ├── 除法(法则:除以非0数等于乘它的倒数;同号得正,异号得负)
│ ├── 乘方(定义:n个相同因数的积;符号法则)
│ └── 混合运算(顺序:先乘方,再乘除,最后加减;同级从左到右;有括号先算括号内)
├── 扩展内容
│ ├── 科学记数法(a×10 ,1≤a<10,n是正整数)
│ └── 近似数(精确到哪一位;有效数字)
└── 工具使用:计算器(基本操作,进行各类运算)
幻灯片 4:要点回顾 —— 基本概念
正数与负数:大于 0 的数是正数,在正数前加 “-” 的数是负数,0 既不是正数也不是负数。它们可表示具有相反意义的量。
有理数的分类:
按定义:有理数分为整数(正整数、0、负整数)和分数(正分数、负分数)。
按性质:有理数分为正有理数(正整数、正分数)、0、负有理数(负整数、负分数)。
数轴:规定了原点、正方向、单位长度的直线。任何一个有理数都可以用数轴上的点表示。
相反数:只有符号不同的两个数互为相反数,0 的相反数是 0。在数轴上,互为相反数的两个数位于原点两侧,且到原点的距离相等。
绝对值:数轴上表示数 a 的点与原点的距离叫做 a 的绝对值,记作 | a|。互为相反数的两个数绝对值相等。
幻灯片 5:要点回顾 —— 运算(1)
加法法则:
同号两数相加,取相同的符号,并把绝对值相加。
异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值。
互为相反数的两数相加得 0;一个数与 0 相加,仍得这个数。
减法法则:a - b = a + (-b),即减去一个数等于加上这个数的相反数。
加减法统一:有理数的加减混合运算可统一成加法运算,写成省略加号和括号的形式。
幻灯片 6:要点回顾 —— 运算(2)
乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘。
任何数与 0 相乘,都得 0。
多个不为 0 的数相乘,负因数的个数是奇数时,积为负;是偶数时,积为正。
除法法则:
除以一个不等于 0 的数,等于乘这个数的倒数,即 a÷b = a×(1/b)(b≠0)。
两数相除,同号得正,异号得负,并把绝对值相除。0 除以任何一个不等于 0 的数,都得 0。
幻灯片 7:要点回顾 —— 运算(3)
乘方:
定义:求 n 个相同因数 a 的积的运算,记作 a ,其中 a 是底数,n 是指数,结果叫幂。
符号法则:正数的任何次幂都是正数;负数的奇次幂是负数,偶次幂是正数;0 的任何正整数次幂都是 0。
混合运算顺序:
先算乘方,再算乘除,最后算加减。
同级运算,从左到右依次进行。
如有括号,先算括号里面的(小括号→中括号→大括号)。
幻灯片 8:要点回顾 —— 扩展内容与工具
科学记数法:把一个大于 10 的数表示成 a×10 的形式(其中 1≤a<10,n 是正整数)。n 的值等于原数的整数位数减 1。
近似数:
精确到哪一位:看四舍五入到哪一位。
有效数字:从左边第一个非 0 数字起,到末位数字止的所有数字。
计算器:熟悉数字键、运算符号键、功能键(如 CE/C、x 、± 等)的使用,按运算顺序输入可进行各类计算。
幻灯片 9:例题 1—— 概念辨析
题目:下列说法正确的是( )
A. 有理数就是正数和负数 B. 互为相反数的两个数的绝对值相等
C. 数轴上原点两侧的数互为相反数 D. 绝对值等于本身的数是正数
解答过程:
A 选项错误,有理数包括正数、0 和负数。
B 选项正确,互为相反数的两个数到原点的距离相等,即绝对值相等。
C 选项错误,数轴上原点两侧且到原点距离相等的数才互为相反数。
D 选项错误,绝对值等于本身的数是正数和 0。
答案:B
幻灯片 10:例题 2—— 运算计算
题目:计算:
(1)\((-12) + 15 + (-8) + 7\)
(2)\((-3)^2\times(-\frac{2}{3}) - 4\div(-\frac{1}{2})\)
解答过程:
(1)运用加法交换律和结合律:\([(-12) + (-8)] + (15 + 7) = (-20) + 22 = 2\)。
(2)先算乘方:\(9\times(-\frac{2}{3}) - 4\times(-2) = -6 + 8 = 2\)。
答案:(1)2;(2)2。
幻灯片 11:例题 3—— 科学记数法与近似数
题目:
(1)用科学记数法表示 13000000。
(2)近似数 3.04×10 精确到哪一位?有几个有效数字?
解答过程:
(1)13000000 的整数位数是 8,n=7,所以表示为\(1.3\times10^7\)。
(2)3.04×10 =304000,4 在千位,所以精确到千位;有效数字是 3、0、4,共 3 个。
答案:(1)\(1.3\times10^7\);(2)千位,3 个。
幻灯片 12:例题 4—— 实际应用
题目:某检修小组乘汽车沿公路检修线路,约定前进为正,后退为负。某天自 A 地出发到收工时所走路线(单位:千米)为:+10,-3,+4,+2,-8,+13,-2,+12,+8,+5。
(1)收工时距 A 地多远?
(2)若每千米耗油 0.2 升,从 A 地出发到收工时共耗油多少升?
解答过程:
(1)将所有数相加:\((+10)+(-3)+(+4)+(+2)+(-8)+(+13)+(-2)+(+12)+(+8)+(+5)=41\)(千米)。
(2)先求总路程(各数绝对值之和):\(10 + 3 + 4 + 2 + 8 + 13 + 2 + 12 + 8 + 5 = 67\)(千米),耗油量:\(67\times0.2 = 13.4\)(升)。
答案:(1)41 千米;(2)13.4 升。
幻灯片 13:课堂练习 1—— 概念与运算
题目:
(1)-5 的相反数是______,绝对值是______。
(2)计算:\(-2^2 + (-3)\times(-4) - (-1)^3\)。
答案:(1)5,5;(2)\(-4 + 12 - (-1) = 9\)。
幻灯片 14:课堂练习 2—— 科学记数法与近似数
题目:
(1)将 5670000 用科学记数法表示为______。
(2)近似数 2.8 万精确到______位,有______个有效数字。
答案:(1)\(5.67\times10^6\);(2)千,2。
幻灯片 15:课堂练习 3—— 实际应用
题目:某商店一周的收入、支出情况如下表(收入为正):
日期
周一
周二
周三
周四
周五
周六
周日
收支(元)
+1500
-200
-300
+400
-500
+600
-100
这一周商店的总利润是多少元?
答案:\(1500 - 200 - 300 + 400 - 500 + 600 - 100 = 1400\)(元)。
幻灯片 16:易错点总结
概念类:
混淆相反数和倒数的概念。
对绝对值的性质理解不清,如认为 | a|=a 一定成立(忽略 a 为负数的情况)。
有理数分类时遗漏 0。
运算类:
符号错误,如异号两数相加、乘除时符号判断错误。
运算顺序错误,尤其是乘方与乘除、加减的顺序。
对\(-a^n\)与\((-a)^n\)区分不清,导致乘方计算错误。
其他:
科学记数法中 a 的范围错误或 n 的值计算错误。
近似数的精确度判断错误,尤其是带单位或用科学记数法表示的数。
幻灯片 17:总结与寄语
总结:本章主要学习了有理数的概念、运算及相关应用,核心是掌握各种运算的法则和顺序,理解相关概念的内涵。
寄语:有理数是初中数学的基础,希望同学们通过本次复习,查漏补缺,熟练运用所学知识解决问题,为后续学习打下坚实的基础。
幻灯片 18:作业布置
基础作业:完成章末复习题 A 组(巩固基础知识和基本运算)。
提升作业:完成章末复习题 B 组(综合运用知识解决复杂问题)。
拓展作业:结合生活实际,编一道运用有理数知识解决的应用题并解答。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识结构
有理数的运算
正数
负数
相反意义的量
0
有理数
数轴
有理数的大小比较
相反数
绝对值
加减法
乘除法
乘方
法则
运算律
交换律
结合律
分配律
有理数
相关概念
有理数
数轴
相反数
绝对值
倒数
概念:整数和分数统称为有理数
分类
整数
分数
正整数
0
负整数
正分数
负分数
规定了原点、正方向、单位长度的直线
只有正负号不同的两个数称互为相反数.
规定 0 的相反数是 0 .
乘积是 1 的两个数互为倒数
一个正数的绝对值是它本身
0 的绝对值是 0
一个负数的绝对值是它的相反数
怎样比较有理数的大小?
利用数轴比较
利用法则比较
利用绝对值比较
在数轴上表示的两个数,右边的数总比左边的数大
正数都大于0;负数都小于0;正数都大于负数
两个负数,绝对值大的反而小
符号 计算绝对值
加法 同号取
异号取
减法 减去一个数等于 乘法 同号取
异号取 除法 同号取
异号取 除以一个不等于 0 的数等于 相同的符号
绝对值相加
负
绝对值相乘
绝对值大的符号
绝对值相减
正
正
绝对值相除
加上这个数的相反数
乘以这个数的倒数
负
填写以下运算法则:
交换律:a+b=b+a
结合律:(a+b)+c=a+(b+c)
加法
乘法
运算律
交换律:ab=ba
结合律:(ab)c=a(bc)
分配律:a(b+c)=ab+ac
有理数的运算律有哪些?
有理数的混合运算应按照怎样的顺序进行?
1.先做乘方,再做乘除,最后做加减;
2.同级运算,按照从左至右的顺序进行;
3.如果有括号,就先算小括号里的,再算中括号里的,然后算大括号里的.
计算:
20+(-2)×10 +1 =
(20-1)×0 ÷(2+8) =
(20-1)× +20+(-2)×10 =
1÷( -33÷9) =
做一做
1
0
科学记数法是什么?
取近似数的方法有哪些?
一个绝对值大于 10 的数可以记成 的形式,其中
n 是正整数.像这样的记数法叫做科学记数法.
四舍五入法、进一法、去尾法
释疑解惑
1.为什么要引入负数?举出实例说明正数和负数在表示相反意义的量时的作用.
现实生活中存在很多个有相反意义的量,如:向东5米与向西5米,零上2℃与零下2℃,收入100元与支出100元,低于海平面150米与高出海平面800米……用正数表示其中一种量,负数表示和它相反意义的量,这样既简单又明白.例如吐鲁番盆地的海拔高度为-154.31m,表示吐鲁番盆地的海拔高度是低于海平面154.31m.
2.数的范围从正整数、0和正分数扩充到有理数后,增加了哪些数?减法中哪些原来不能进行的运算可以进行了?
增加了负整数、负分数,解决了原来“小数不能减去大数”的问题,现在任何有理数都可以进行减法运算.
3.怎样用数轴表示有理数?数轴与普通直线有什么不同?怎样用数轴解释绝对值和相反数?
任何一个有理数都可以用数轴上的一个点表示,但数轴上的点不是都表示有理数,这一点,以后我们将要学习.数轴是一条特殊的直线,是规定了正方向、原点和单位长度的直线.原点、正方向、单位长度也称数轴的三要素,缺一不可.
数轴上与原点的距离相等的两个点所表示的数互为相反数.
4.有理数的加法与减法有什么关系?乘法与除法呢?
有理数的减法可以转化为加法,转化的桥梁是相反数,减去一个数等于加上这个数的相反数,同样,除法可以转化为乘法,转化的桥梁是倒数,除以一个数(不为0),等于乘这个数的倒数.有理数的混合运算都可以转化为加法与乘法.
随堂练习
例1 填空:
(1)在知识竞赛中,如果 +10分表示加10分,那么扣20分可表示成_______;
(2)某人转动转盘,如果沿逆时针转5圈记作 +5圈,那么沿顺时针转12圈可表示成_______;
(3)某次乒乓球质量检测中,一只乒乓球超出标准0.02g记作 +0.02g,那么 -0.03g表示_______________ .
-20分
-12圈
低于标准0.03g
例2 填空:
(1)若m,n互为相反数,则m+n =______;
(2)-2006的倒数是________;
(3)-(-3)= ______;
(4)-|-2|的倒数是_______.
0
3
例3 如图,数轴上两点所表示的两数( )
A.和为正数 B.和为负数
C.积为正数 D.积为负数
D
例4 下列四个运算中,结果最小的是( )
A.1+(-2) B.1-(-2)
C.1×(-2) D.1÷(-2)
C
例5 如果a<0,b>0,a+b<0,那么下列关系式中正确的是( )
A.a>b>-b>-a B.a>-a>b>-b
C.b>a>-b>-a D.-a>b>-b>a
D
-1
3
-2
-a>b
例7 神舟六号飞船,在平安飞行115小时23分后重返神州. 用科学记数法表示神舟六号飞船飞行的时间是______________秒 (精确到千位).
分析:a×10x中a的取值范围是1≤a<10,底数10的指数n等于所表示的整数位数减去1.
4.15×105
115×60×60+23×60=415380≈415000(秒)
例8 (-8)2014+(-8)2013能被下列数整除的是( )
A.3 B.5 C.7 D.9
C
=(-8)2013×[(-8)+1]
=(-8)2013×(-7)
核心知识巩固
一、基础考点演练
考点1 有理数及其分类
1.[2025安阳模拟]小东在妈妈的微信零钱明细中看到,收入2 000元
被记作元,则 元表示_____________.
支出1 600元
返回
2.有下列说法:①有理数的个数是无限的;②整数包括正整数和负整数;
③正有理数和负有理数统称有理数;④负分数是有理数.其中正确说法
的序号是______.
①④
返回
3.把下列各数填入相应的大括号内:
,,,,, ,
,0.
正分数集:{__________________…};
整数集:{________________…};
负有理数集:{_____________________…};
非负数集:{_____________________________…}.
,,
,,0
,,
,,,,0
返回
考点2 数轴、相反数、绝对值、倒数
4.下列说法中,正确的序号为______.
的相反数是;一定是负数; 既没有倒数也没有相反
数;④绝对值大于它本身的数是负数.
①④
返回
5.有理数,, 在数轴上的对应点的位置如图所示,这三个数中绝对
值最大的是___.
返回
6.填空:
(1) ___;
(2) ____;
(3) 的倒数是__;
(4) ____.
2
7.5
返回
7.已知是数轴上的一点,且点到原点的距离为1,把点 沿数轴向右
移动3个单位长度得到点,则点 表示的数是______.
4或2
返回
考点3 有理数的大小比较
8.下列四个数中,比 小的数是( )
D
A.0 B. C. D.
返回
9.[2025忻州期末]如果,, ,那么下列比较大小
中正确的是( )
D
A. B.
C. D.
返回
10.比较大小(填“ ”“”或“ ”)
(1)___ ;
(2)___ .
返回
11.(4分)某校举行一场文艺汇演,汇演中途设置了一个有奖问答环节,
题目在背景屏幕上显示如图,请回答图中的问题.
解:,,最小的正整数是1, 的最小
值是,0的相反数是0,比大的数是 .将这些数在数轴上表示出来,
如图.
所以 .
返回
考点4 有理数的运算
12.下列各组数中,结果相等的是( )
A
A.和 B.和 C.和 D.和
返回
13.数轴上,,三点表示的有理数分别为,,,若 ,
, ,则下列数轴符合题意的是( )
B
A. B.
C. D.
返回
14.已知,互为相反数,,, 互为倒数,则
的值为___.
0
返回
15.[2025郑州期末]若,则 内填的运算符号是___.
返回
16. 定义两种新运算“ ”和“”: ,
,则 _____.
返回
17.某种细菌在培养过程中,每半小时分裂一次(由一个分裂成两个).
经过 ,这种细菌由1个可分裂为____个.
64
返回
18.(12分)[2025南阳期末]计算:
(1) ;
解:原式 .
(2) ;
解:原式 .
(3) .
解:原式 .
返回
19.(12分)小亮家新换了一辆新能源汽车,他连续记录了一周每天行
驶的路程(如下表).以为标准,超过记为“ ”,不足
记为“-”,刚好 记为“0”.
星期 一 二 三 四 五 六 日
0
(1)小亮家本周行驶的路程最多的一天比最少的一天多____ .
(2)小亮家的汽车本周一共行驶了_____ .
50
400
[解析] 点拨: .
(3)已知汽油车每行驶 需用汽油7升,油价为7.5元/升,而新能
源汽车每行驶 耗电15度,每度电0.8元,换成新能源汽车后这一
周的行驶费用比原来节省多少钱?
解:汽油车的费用为 (元),
新能源汽车的费用为(元),
(元).
答:换成新能源汽车后这一周的行驶费用比原来节省162元.
返回
考点5 科学记数法与近似数
20.下列说法正确的是( )
D
A.近似数2.8和2.80表示的意义一样 B.6.7万精确到万位
C.0.680精确到百分位 D.300精确到个位
返回
21.北京数字经济算力中心日前已部署上架和调试的设备的算力为
是计算机系统算力的一种度量单位 ,整体投产后,
累计实现的算力将是日前已部署上架和调试的设备的算力的5倍,达到
,则 的值为_________.
返回
22.地球绕太阳公转的速度用科学记数法表示约为 ,则
原数是_________.
110 000
返回
23.一个小数“四舍五入”得到的近似数是 ,这个小数最小是_____,
最大是_____.
6.75
6.84
返回
二、思想方法演练
思想1 转化思想
24.若,均为有理数,且,则 _____.
返回
思想2 数形结合思想
25.(8分)如图,以 为1个单位长度用直尺画数轴时,数轴上的
点,,刚好对着直尺上的刻度2,8和10.设点,, 所表示的数
的和是,该数轴的原点为 .
(1)点到点之间有____个单位长度;若点表示的数是,则点
表示的数为____;
16
15
(2)若点,所表示的数互为相反数,直接写出此时数轴的原点 对
应直尺上的刻度,并求此时 的值.
思想3 分类讨论思想
解:因为点,所表示的数互为相反数,所以数轴的原点 对应直尺上
的刻度5.
此时点,,所表示的数分别是 ,6,10,因此
.
返回
26.有理数,,在数轴上对应点的位置如图所示,若 ,则下
列结论中正确的是( )
B
A. B. C. D.
返回
谢谢观看!
同课章节目录
