第2章 整式及其加减【章末复习】 课件(共58张PPT)
文档属性
| 名称 | 第2章 整式及其加减【章末复习】 课件(共58张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 00:00:00 | ||
图片预览








文档简介
(共58张PPT)
章末复习
第2章 整式及其加减
【华东师大版·2024】数学 七年级上册
授课教师:********
班 级:********
时 间:********
幻灯片 1:封面
标题:第 2 章 整式及其加减 章末复习
副标题:梳理知识脉络,巩固基础技能
幻灯片 2:复习目标
梳理本章所学知识,构建整式及其加减的知识体系。
巩固整式、单项式、多项式、同类项等基本概念,能准确辨析相关概念。
熟练掌握合并同类项、去括号和添括号法则,能正确进行整式的加减运算。
能运用整式及其加减解决简单的实际问题,提高综合运用知识的能力。
幻灯片 3:知识框架图
第2章 整式及其加减
├─ 整式的有关概念
│ ├─ 单项式:定义、系数、次数
│ ├─ 多项式:定义、项、常数项、次数、升幂/降幂排列
│ └─ 整式:单项式和多项式统称为整式
├─ 整式的加减运算
│ ├─ 同类项:定义、判断
│ ├─ 合并同类项:法则、步骤
│ ├─ 去括号和添括号:法则、应用
│ └─ 整式的加减:实质(合并同类项)、步骤
└─ 实际应用:用整式表示数量关系,通过整式加减解决问题
幻灯片 4:核心概念回顾(一)—— 整式的基本概念
单项式:
定义:由数与字母的积组成的代数式,单独的一个数或一个字母也是单项式。
系数:单项式中的数字因数(包括符号,1 或 - 1 可省略)。
次数:单项式中所有字母的指数的和(单独的数次数为 0)。
示例:-3x y 的系数是 - 3,次数是 3(2+1)。
多项式:
定义:几个单项式的和叫做多项式。
项:多项式中的每个单项式(含符号),不含字母的项叫常数项。
次数:多项式中次数最高项的次数,称为 “几次几项式”。
示例:2x - 5x + 1 是三次三项式,项为 2x 、-5x、1,常数项是 1。
整式:单项式和多项式统称为整式(不含字母作分母的代数式)。
幻灯片 5:核心概念回顾(二)—— 整式的运算相关概念
同类项:
定义:所含字母相同,并且相同字母的指数也相同的项(常数项都是同类项)。
判断依据:“两相同”(字母相同、相同字母指数相同),“两无关”(与系数、字母顺序无关)。
示例:3a b 与 - 5a b 是同类项,2x 与 3y 不是同类项。
合并同类项:
法则:同类项的系数相加,字母和字母的指数不变。
步骤:找出同类项→移动同类项→合并→整理结果。
示例:3x + 2x = (3+2)x = 5x ;4xy - 6xy = (4-6)xy = -2xy。
幻灯片 6:核心法则回顾 —— 去括号与添括号
去括号法则:
括号外是正数,去括号后符号不变:+(a + b) = a + b,+(a - b) = a - b。
括号外是负数,去括号后符号全变:-(a + b) = -a - b,-(a - b) = -a + b。
示例:2(x - y) - (3x + 1) = 2x - 2y - 3x - 1 = -x - 2y - 1。
添括号法则:
括号前是正数,括入项符号不变:a + b - c = +(a + b - c)。
括号前是负数,括入项符号全变:a - b + c = -(-a + b - c)。
示例:3x - 2y + z = 3x - (2y - z);5a + b - 1 = +(5a + b - 1)。
幻灯片 7:核心运算回顾 —— 整式的加减
实质:去括号后合并同类项。
步骤:
去括号(若有括号):根据去括号法则去掉括号。
合并同类项:将同类项的系数相加,字母和指数不变。
整理结果:按某一字母升幂或降幂排列(可选)。
示例:计算 (3x - 2x) + 2 (x + 3x - 1)
去括号:3x - 2x + 2x + 6x - 2
合并同类项:(3x + 2x ) + (-2x + 6x) - 2 = 5x + 4x - 2
幻灯片 8:例题 1—— 辨析整式相关概念
题目:下列说法正确的是( )
A. 单项式\(\frac{2}{3}\)xy 的系数是\(\frac{2}{3}\),次数是 2
B. 多项式 x + 2x - 1 是二次二项式
C. 0 不是整式
D. 3x y 与 - xy 是同类项
解答过程:
A 选项:\(\frac{2}{3}\)xy 的系数是\(\frac{2}{3}\),次数是 1+1=2,正确。
B 选项:多项式 x + 2x - 1 有 3 项,是二次三项式,错误。
C 选项:0 是单项式,属于整式,错误。
D 选项:3x y 与 - xy 中相同字母的指数不同(x 的指数 2 vs 1,y 的指数 1 vs 2),不是同类项,错误。
结论:选 A。
幻灯片 9:例题 2—— 整式的化简与求值
题目:先化简,再求值:3 (2a b - ab ) - 2 (ab + 3a b),其中 a = -1,b = 2。
解答过程:
化简:6a b - 3ab - 2ab - 6a b = (6a b - 6a b) + (-3ab - 2ab ) = -5ab 。
求值:当 a = -1,b = 2 时,-5×(-1)×2 = 5×4 = 20。
结论:化简结果为 - 5ab ,值为 20。
幻灯片 10:例题 3—— 整式加减的实际应用
题目:一个长方形的长为 (4x + 3y),宽比长短 (x - y),
(1)求长方形的宽(用含 x、y 的整式表示);
(2)求长方形的周长。
解答过程:
(1)宽 = (4x + 3y) - (x - y) = 4x + 3y - x + y = 3x + 4y。
(2)周长 = 2×(长 + 宽) = 2 [(4x + 3y) + (3x + 4y)] = 2 (7x + 7y) = 14x + 14y。
结论:(1)宽为 3x + 4y;(2)周长为 14x + 14y。
幻灯片 11:例题 4—— 整式的综合运算
题目:已知多项式 A = 2x - 3x + 1,B = -x + 2x - 5,求:
(1)A + 2B;
(2)当 x = -2 时,A + 2B 的值。
解答过程:
(1)A + 2B = (2x - 3x + 1) + 2(-x + 2x - 5) = 2x - 3x + 1 - 2x + 4x - 10 = (2x - 2x ) + (-3x + 4x) + (1 - 10) = x - 9。
(2)当 x = -2 时,x - 9 = -2 - 9 = -11。
结论:(1)A + 2B = x - 9;(2)值为 - 11。
幻灯片 12:易错题集锦与解析
易错点 1:单项式系数与次数判断错误
错误示例:认为单项式 - xy 的系数是 1,次数是 2。
解析:系数是 - 1(含符号),次数是 1+2=3,正确结果:系数 - 1,次数 3。
易错点 2:合并同类项时符号错误
错误示例:合并 3x - (2x - y) 时,得到 3x - 2x - y = x - y。
解析:去括号时括号外是负号,括号内各项符号应变号,正确结果:3x - 2x + y = x + y。
易错点 3:多项式次数判断错误
错误示例:认为多项式 x + 2x y - 1 的次数是 3。
解析:次数最高项是 2x y (次数 2+2=4),正确次数是 4。
幻灯片 13:针对性练习 1—— 概念辨析
题目:
(1)指出单项式 -\(\frac{5}{3}\)a b 的系数和次数;
(2)判断多项式 3x - 2x + 5x - 1 是几次几项式,常数项是多少。
答案:
(1)系数 -\(\frac{5}{3}\),次数 3;
(2)四次四项式,常数项是 - 1。
幻灯片 14:针对性练习 2—— 整式化简
题目:化简:
(1)5 (x - 2y) - 2 (3x - y);
(2)(a b - 2ab ) - 2 (a b - 1) + 3ab + 2。
答案:
(1)5x - 10y - 6x + 2y = -x - 8y;
(2)a b - 2ab - 2a b + 2 + 3ab + 2 = -a b + ab + 4。
幻灯片 15:针对性练习 3—— 综合应用
题目:已知 A = x + xy + y ,B = -3xy - x ,求:
(1)A - B;
(2)当 x = 1,y = -1 时,A - B 的值。
答案:
(1)A - B = (x + xy + y ) - (-3xy - x ) = x + xy + y + 3xy + x = 2x + 4xy + y ;
(2)当 x = 1,y = -1 时,2×1 + 4×1×(-1) + (-1) = 2 - 4 + 1 = -1。
幻灯片 16:本章总结
知识体系:从整式的基本概念(单项式、多项式)到运算(同类项合并、去括号、整式加减),形成完整的知识链。
核心方法:
概念辨析:抓住 “定义关键词”(如单项式的 “数与字母的积”)。
运算技巧:去括号 “符号先行”,合并同类项 “系数相加,字母不变”。
实际应用:先列整式表示数量关系,再通过运算解决问题。
学习建议:多练习基础题巩固概念,通过综合题提升应用能力,重视错题分析。
幻灯片 17:章末测试题(节选)
下列各式中,是单项式的是( )
A. x + y B. \(\frac{1}{x}\) C. -5 D. x + 2x
化简 3a - 2 (a - b) 的结果是( )
A. a + 2b B. a - 2b C. a + b D. a - b
已知单项式 3x y 与 - 2x y 是同类项,则 m + n = ______。
先化简,再求值:2 (x y + xy ) - 2 (x y - 1) - 3xy - 2,其中 x = -2,y = \(\frac{1}{2}\)。
一个多项式与 x - 2x + 1 的和是 3x - 2,求这个多项式。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
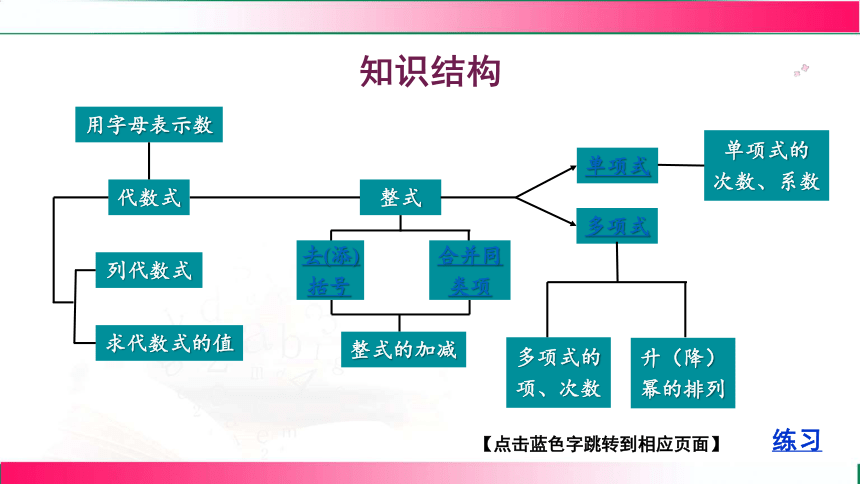
知识结构
代数式
列代数式
求代数式的值
多项式的项、次数
升(降)幂的排列
用字母表示数
整式
多项式
单项式
单项式的
次数、系数
去(添)括号
合并同类项
整式的加减
【点击蓝色字跳转到相应页面】
练习
定义:由________________组成的代数式叫做单项式.
单独________或_________也是单项式.
系数:单项式中的_________.
次数:一个单项式中的_____________________.
总结
单项式
数与字母的乘积
一个数
一个字母
数字因数
所有字母的指数的和
(1)当单项式的系数是1或-1时,“1”通常省略不写.
(2)当式子的分母中出现字母时不是单项式.
(3)圆周率π是常数,不要看成字母.
(4)当单项式的系数是带分数时,通常写成假分数.
(5)单项式的系数应包括它前面的符号.
(6)单项式的次数是指单项式中所有字母的指数的和,与数字的指数没有关系.
(7)单独的数字不含字母,规定它的次数是零次.
注意的问题
总结
多项式
定义:几个________________.
项:组成多项式中的_________________.
常数项:多项式中_________________________.
次数:_______________________________________.
升幂排列(或降幂排列):把一个多项式的各项按照某个字母的指数从小到大(或从大到小)的顺序排列起来.
单项式的和
每一个单项式
不含字母的项
多项式中,次数最高项的次数
注意的问题
(1)在确定多项式的项时,要连同它前面的符号.
(2)一个多项式中次数最高项的次数是几,就说这个多项式是几次多项式.
(3)在多项式中,每个单项式都是这个多项式的项,每一项都有系数,但对整个多项式来说,没有系数的概念,只有次数的概念.
同类项
同类项的定义:
_______________________________________________.
规定:几个常数项也是_________.
合并同类项概念:把多项式中的同类项合并成一项.
合并同类项法则:
(1)_______相加;
(2)_________________不变.
总结
所含字母相同,并且相同字母的指数都相等的项
同类项
系数
字母和字母的指数
口诀:只求系数和,字母指数不变样.
添括号法则:
所添括号前面是“+”号,括到括号里的各项都不改变正负号;
所添括号前面是“-”号,括到括号里的各项都改变正负号.
去括号法则:
括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都不改变正负号;
括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变正负号.
总结
去(添)括号
知识要点
1.用字母表示数,从数的研究过渡到代数式的研究,是数学发展的一次飞跃. 代数式及其运算,是进一步学习数学(方程、不等式、函数等)的基础,也是解决实际问题的工具.学习时要注意联系实际,体会从具体到抽象、从特殊到一般的思想方法.
2.整式包括单项式和多项式.多项式可以看作几个单项式的和,其中的每一个单项式是多项式的项.多项式的项(单项式)的系数包括正负号,在进行整式运算时不容忽视.
知识要点
3.整式的加减运算是本章学习的又一个重点.去括号和合并同类项是整式加减的基础.
4.去(添)括号时,要特别注意括号前面是“-”号的情形:去括号时,括号内的各项都改变正负号;添括号时,括到括号内的各项都改变正负号.
课堂练习
1.填空:
(1)如果a表示一个有理数,那么它的相反数是______;
(2)如果n表示一个自然数,那么它的后一个自然数是_______;
(3)一个正方形的边长是 a cm,把这个正方形的边长增加1cm后所得到的正方形的面积是_________;
(4)某商品原价是x元,提价10%后的价格是_________;
-a
n+1
(a+1)2cm2
1.1x 元
【选自教材P118复习题第1题】
A组
1.填空:
(5)如果一个两位数的十位数字是a,个位数字是b,那么这个两位数可表示为___________;
(6)如果甲、乙两人分别从相距 s km的A、B两地同时出发相向而行,他们的速度分别为 a km/h与 b km/h,那么他们从出发到相遇所需要的时间为________.
10a+b
h
【选自教材P118复习题第1题】
2.用代数式表示:
(1) a的3倍与b的平方的差;
(2)x与y平方的和;
(3)x 、y两数的平方和减去它们积的2倍;
(4)x的相反数与y的倒数的和.
3a-b2
x+y2
x2+y2-2xy
【选自教材P118复习题第2题】
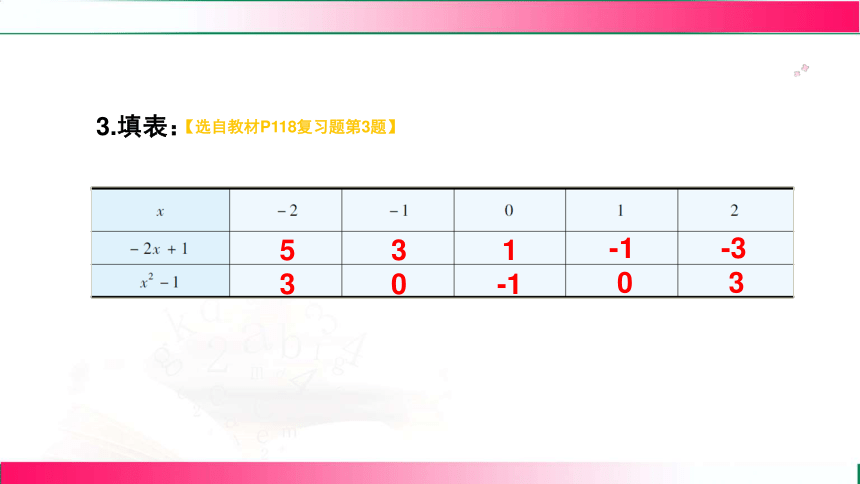
3.填表:
5
3
3
0
1
-1
-1
0
-3
3
【选自教材P118复习题第3题】
4.若某班同学在体育达标检测中,达标率为p,达标人数为n,则总人数为_________. 若p=88%,n=44,则这个班有______人.
50
【选自教材P119复习题第4题】
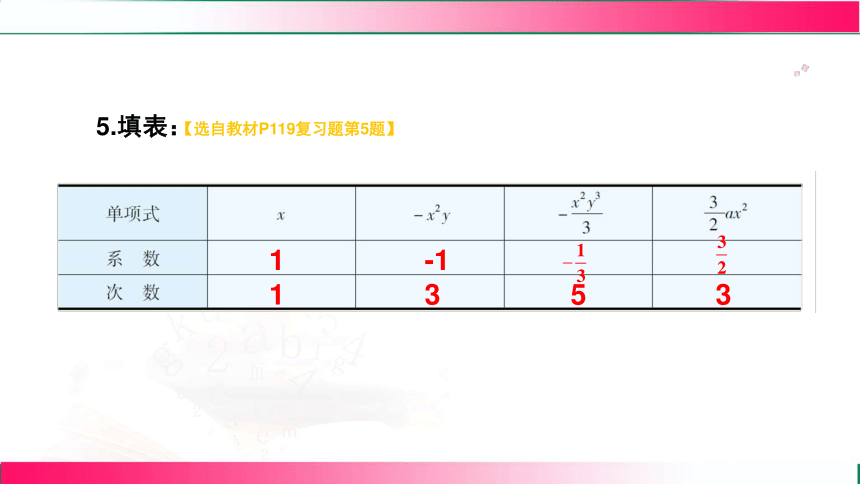
5.填表:
1
1
-1
3
5
3
【选自教材P119复习题第5题】
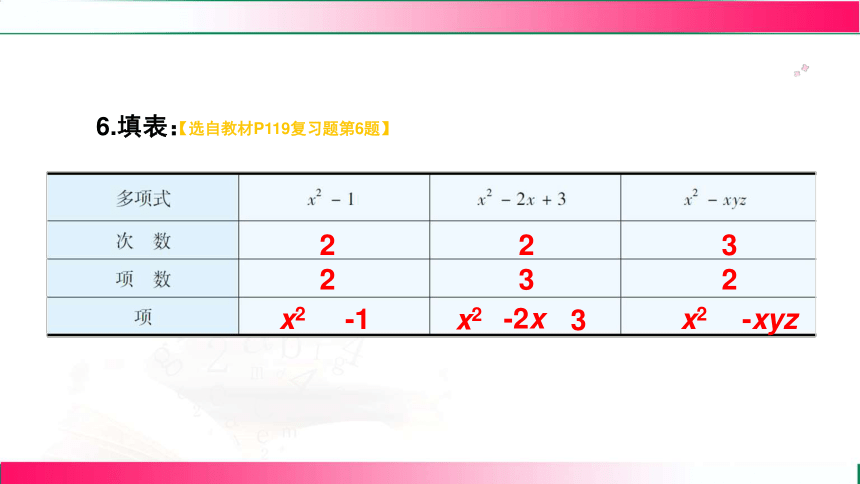
6.填表:
2
2
x2
-1
2
3
x2
-2x
3
3
2
x2
-xyz
【选自教材P119复习题第6题】
7.将下列多项式按x的降幂排列:
(1)3-2x2+x;
(2)-2xy+x2+y2;
(3)2x-1-x3;
(4)2x2y-3xy2-x3+2y3.
-2x2+x+3
x2-2xy+y2
-x3+2x-1
-x3+2x2y-3xy2+2y3
【选自教材P119复习题第7题】
8.合并同类项:
(1)2ax+3by-4ax+3by-2ax;
(2)-2x2+x-3+x2-3x;
(3)3x2y-xy2-2x2y+3xy2.
解 原式=2ax-2ax-4ax+3by+3by
=-4ax+6by
解 原式=-2x2+x2+x-3x-3
=-x2-2x-3
解 原式=3x2y-2x2y-xy2+3xy2
=x2y+2xy2
【选自教材P119复习题第8题】
9.填空(去括号或添括号):
(1)2a+3(b-c)=__________;
(2)2a-3(b-c)=__________;
(3)x2-xy+y2=x2-(_________);
(4)x2-xy+y2=x2+(_________);
2a+3b-3c
2a-3b+3c
xy-y2
-xy+y2
【选自教材P119复习题第9题】
10.化简:
(1) 3x+2x2-2-15x2+1-5x; (2)3x2+2xy-4y2-3xy+4y2-3x2;
(3)-7x2+(6x2-5xy)-(3y2+xy-x2); (4) (2x2-5x) - (3x+5-2x2).
解 原式=2x2-15x2-5x+3x-2+1
=-13x2-2x-1
解 原式=3x2-3x2+2xy-3xy-4y2+4y2
=-xy
解 原式=-7x2+6x2-5xy-3y2-xy+x2
=-7x2+6x2+x2-5xy-xy-3y2
=-6xy-3y2
解 原式=2x2-5x-3x-5+2x2
=4x2-8x-5
【选自教材P120复习题第10题】
11.先化简,再求值:
(1)3x3-[x3+(6x2-7x)]-2(x3-3x2-4x),其中x=-1.
解 3x3-[x3+(6x2-7x)]-2(x3-3x2-4x)
=3x3-[x3+6x2-7x]-2x3+6x2+8x
=3x3-x3-6x2+7x-2x3+6x2+8x
=3x3-x3-2x3-6x2+6x2+7x+8x
=15x
当x=-1时,原式=15×(-1)=-15
【选自教材P120复习题第11题】
11.先化简,再求值:
(2) ,其中x= ,y=2.
当x= ,y=2时,原式=22=4
【选自教材P120复习题第11题】
12. x表示一个两位数,y表示一个三位数,若把x放在y的右边组成一个五位数,则这个五位数可以表示为____________.
13.代数式x2+x+3的值为7,则代数式2x2+2x-3的值为_________.
100y+x
2x2+2x-3=2(x2+x+3)-9=14-9=5
5
【选自教材P120复习题第12题】
【选自教材P120复习题第13题】
B组
14.已知多项式A = 4x2- 4xy + y2,B = x2+ xy - 5y2,求:
(1) A - 3B; (2) 3A + B.
解 (1) A - 3B=4x2- 4xy + y2-3(x2+ xy - 5y2)
=4x2- 4xy + y2-3x2-3xy +15y2
=4x2-3x2- 4xy-3xy+y2+15y2
=x2-7xy+16y2
【选自教材P120复习题第14题】
解 (2)3A + B=3(4x2- 4xy + y2)+x2+ xy - 5y2
=12x2-12xy+3y2+x2+ xy - 5y2
=12x2+x2-12xy+xy+3y2-5y2
=13x2-11xy-2y2
14.已知多项式A = 4x2- 4xy + y2,B = x2+ xy - 5y2,求:
(1) A - 3B; (2) 3A + B.
15.把 x-y 看作一个整体,化简:
5(x-y)+2(x-y)-4(x-y); (2) 3(x-y)2-4(x-y)+7(x-y)-6(x-y)2.
解 原式=(5+2-4) (x-y)
=3(x-y)
解 原式=3(x-y)2-6(x-y)2-4(x-y)+7(x-y)
=-3(x-y)2+3(x-y)
【选自教材P120复习题第15题】
16.如图,若a-b=4,求长方形A与B的面积的差.
解 根据题意,两个长方形的面积的差为:
答:两个长方形的面积的差为8.
【选自教材P120复习题第16题】
5a-2b
6a-2b
4
3
4(5a-2b)-3(6a-2b)=20a-8b-18a+6b
=2a-2b=2(a-b)
当a-b=4时,原式=2×4=8
A
B
17.有这样一道题:“求(2x3-3x2y-2xy2)-(x3-2xy2+y3)+(-x3+3x2y-y3)的值,其中x= ,y=-1.”甲同学把“x= ”错抄成“x= ”,但他计算的结果却是正确的.这是怎么回事呢?
解 (2x3-3x2y-2xy2)-(x3-2xy2+y3)+(-x3+3x2y-y3)
=2x3-3x2y-2xy2-x3+2xy2-y3-x3+3x2y-y3
=2x3-x3-x3-3x2y+3x2y-2xy2+2xy2-y3-y3
=-2y3
化简后可知,原式的结果与x的值无关.
【选自教材P120复习题第17题】
核心知识巩固
一、基础考点演练
考点1 代数式
1.下列各式中,不是代数式的是( )
B
A.7 B. C. D.
返回
2.用代数式表示“ 的2倍与3的和”,下列表示正确的是( )
B
A. B. C. D.
返回
3.小明比小强大2岁,比小华小4岁.如果小强 岁,那么小华的年龄为
________岁.
返回
4.学习委员小明带了200元钱去文具店买学习用品,已知一支笔 元,一
个笔记本元,则代数式 表示的实
际意义是_______________________________________.
用200元购买3支笔和4个笔记本后剩余的钱
返回
考点2 代数式的值
5.当,,时,代数式 的值为____.
返回
6.[2025福州期末]根据一项科学研究,一个10岁至15岁的人每天所需
的睡眠时间可用公式计算出来,其中 代表人的岁数.根
据这个公式,一个12岁的未成年人每天所需的睡眠时间是____ .
9.8
返回
7.(4分)[2025郑州月考]已知,互为相反数,,互为倒数,
是绝对值最小的负整数,求 的值.
解:因为,互为相反数,,互为倒数, 是绝对值最小的负整数,
所以,, ,
所以原式 .
返回
考点3 整式
8.下列各式中,不是整式的是( )
C
A. B. C. D.0
返回
9.下列说法正确的是( )
A
A.单项式 的次数是5
B.的系数是
C.多项式 的常数项是2
D.多项式 是三次二项式
返回
10.若多项式是关于, 的四次三项式,则
的值为___.
9
返回
11.(16分)已知多项式 ,按要求解答下列问题:
(1)指出该多项式的项;
解:多项式各项依次为,,, .
(2)该多项式的次数是___,三次项的系数是____,常数项是____;
(3)按 的降幂排列:__________________________________________
______________________;
4
(或
)
(4)若 ,求该多项式的值.
解:由题意,得, ,
所以, .所以原式
.
返回
考点4 同类项及其合并
12.合并同类项, ____________.
返回
13.已知单项式与的和是单项式,则___, ___.
4
3
返回
考点5 去括号与添括号
14.下列变形中,正确的是( )
B
A. B.
C. D.
返回
15.(______________) (__________).
返回
考点6 整式的加减
16.下列计算结果正确的是( )
D
A. B.
C. D.
返回
17. 定义 为二阶行列式,规定它的运算法则为
,那么当时,二阶行列式 的值为
___.
4
返回
18.(8分)化简:
(1) ;
解:原式
.
(2) .
解:原式 .
返回
19.(8分)已知多项式: ,
.
(1)求多项式 ;
解:因为 ,
,
所以 ,
则 .
(2)若是的相反数,是的倒数,求 的值.
解:因为是的相反数,是的倒数,所以,,故 .
返回
考点7 整式加减运算的应用
20.把四张形状、大小完全相同的小长方形卡
片(如图①,卡片长为、宽为 )不重叠地
放在一个长为、宽为 的长方形中
(如图②),涂色部分表示长方形未被卡片覆
盖的部分,则图②中两块涂色部分的周长和是
( )
A
A. B. C. D.
返回
21.(8分)为满足学生的课外活动需要,学校决定添置一批某品牌的足
球和跳绳.已知足球每个定价为80元,跳绳每根定价为20元.现有, 两
家网店提供包邮服务,并提出了各自的优惠方案.具体如下:
A网店:足球和跳绳都按定价的 付款.
B网店:买一个足球送一根跳绳.
已知该校计划从上述网店中购买足球50个,跳绳根 .
(1)在网店购买需付款______________元,在 网店购买需付款
______________元;(用含 的式子表示)
(2)若只选择一家网店购买,当 时,请通过计算说明学校选哪
家网店比较合算.
解:当时,方案 (元),
方案 (元).
因为,所以选 网店购买较为划算.
返回
考点8 规律探究
22.观察按规律排列的一组数:,3,,7,,11, ,则第 个
数是( )
C
A. B.
C. D.
返回
23.[2025南阳期末]小茗同学用小木棍按如图方式进行排列.回答下列问题:
(1)第4个图形用____根小木棍;
(2)第 个图形需要_________根小木棍;
(3)第_____个图形需要2 027根小木棍.
22
405
返回
二、思想方法演练
思想1 分类讨论思想
24.按如图所示的程序计算,我们发
现第二次输出的结果为24,那么开
始输入 的值为____________.
53或96或58
[解析] 点拨:分两种情况:当开始输入 的值是奇数时,由题意得
或,解得 (不符合题意,舍去)或
;当开始输入的值是偶数时,由题意得 或
,解得或.综上所述, 的值为53或96或58.
返回
思想2 数形结合思想
25.已知有理数,在数轴上的位置如图所示,化简 的
结果是_____.
返回
思想3 方程思想
26.[2025成都期末]已知关于的整式 ,
,为常数.若整式的取值与无关,则 的
值为____.
返回
思想3 整体思想
27.(4分)已知,,求
的值.
解:
,
因为, ,所以原式
.
返回
谢谢观看!
章末复习
第2章 整式及其加减
【华东师大版·2024】数学 七年级上册
授课教师:********
班 级:********
时 间:********
幻灯片 1:封面
标题:第 2 章 整式及其加减 章末复习
副标题:梳理知识脉络,巩固基础技能
幻灯片 2:复习目标
梳理本章所学知识,构建整式及其加减的知识体系。
巩固整式、单项式、多项式、同类项等基本概念,能准确辨析相关概念。
熟练掌握合并同类项、去括号和添括号法则,能正确进行整式的加减运算。
能运用整式及其加减解决简单的实际问题,提高综合运用知识的能力。
幻灯片 3:知识框架图
第2章 整式及其加减
├─ 整式的有关概念
│ ├─ 单项式:定义、系数、次数
│ ├─ 多项式:定义、项、常数项、次数、升幂/降幂排列
│ └─ 整式:单项式和多项式统称为整式
├─ 整式的加减运算
│ ├─ 同类项:定义、判断
│ ├─ 合并同类项:法则、步骤
│ ├─ 去括号和添括号:法则、应用
│ └─ 整式的加减:实质(合并同类项)、步骤
└─ 实际应用:用整式表示数量关系,通过整式加减解决问题
幻灯片 4:核心概念回顾(一)—— 整式的基本概念
单项式:
定义:由数与字母的积组成的代数式,单独的一个数或一个字母也是单项式。
系数:单项式中的数字因数(包括符号,1 或 - 1 可省略)。
次数:单项式中所有字母的指数的和(单独的数次数为 0)。
示例:-3x y 的系数是 - 3,次数是 3(2+1)。
多项式:
定义:几个单项式的和叫做多项式。
项:多项式中的每个单项式(含符号),不含字母的项叫常数项。
次数:多项式中次数最高项的次数,称为 “几次几项式”。
示例:2x - 5x + 1 是三次三项式,项为 2x 、-5x、1,常数项是 1。
整式:单项式和多项式统称为整式(不含字母作分母的代数式)。
幻灯片 5:核心概念回顾(二)—— 整式的运算相关概念
同类项:
定义:所含字母相同,并且相同字母的指数也相同的项(常数项都是同类项)。
判断依据:“两相同”(字母相同、相同字母指数相同),“两无关”(与系数、字母顺序无关)。
示例:3a b 与 - 5a b 是同类项,2x 与 3y 不是同类项。
合并同类项:
法则:同类项的系数相加,字母和字母的指数不变。
步骤:找出同类项→移动同类项→合并→整理结果。
示例:3x + 2x = (3+2)x = 5x ;4xy - 6xy = (4-6)xy = -2xy。
幻灯片 6:核心法则回顾 —— 去括号与添括号
去括号法则:
括号外是正数,去括号后符号不变:+(a + b) = a + b,+(a - b) = a - b。
括号外是负数,去括号后符号全变:-(a + b) = -a - b,-(a - b) = -a + b。
示例:2(x - y) - (3x + 1) = 2x - 2y - 3x - 1 = -x - 2y - 1。
添括号法则:
括号前是正数,括入项符号不变:a + b - c = +(a + b - c)。
括号前是负数,括入项符号全变:a - b + c = -(-a + b - c)。
示例:3x - 2y + z = 3x - (2y - z);5a + b - 1 = +(5a + b - 1)。
幻灯片 7:核心运算回顾 —— 整式的加减
实质:去括号后合并同类项。
步骤:
去括号(若有括号):根据去括号法则去掉括号。
合并同类项:将同类项的系数相加,字母和指数不变。
整理结果:按某一字母升幂或降幂排列(可选)。
示例:计算 (3x - 2x) + 2 (x + 3x - 1)
去括号:3x - 2x + 2x + 6x - 2
合并同类项:(3x + 2x ) + (-2x + 6x) - 2 = 5x + 4x - 2
幻灯片 8:例题 1—— 辨析整式相关概念
题目:下列说法正确的是( )
A. 单项式\(\frac{2}{3}\)xy 的系数是\(\frac{2}{3}\),次数是 2
B. 多项式 x + 2x - 1 是二次二项式
C. 0 不是整式
D. 3x y 与 - xy 是同类项
解答过程:
A 选项:\(\frac{2}{3}\)xy 的系数是\(\frac{2}{3}\),次数是 1+1=2,正确。
B 选项:多项式 x + 2x - 1 有 3 项,是二次三项式,错误。
C 选项:0 是单项式,属于整式,错误。
D 选项:3x y 与 - xy 中相同字母的指数不同(x 的指数 2 vs 1,y 的指数 1 vs 2),不是同类项,错误。
结论:选 A。
幻灯片 9:例题 2—— 整式的化简与求值
题目:先化简,再求值:3 (2a b - ab ) - 2 (ab + 3a b),其中 a = -1,b = 2。
解答过程:
化简:6a b - 3ab - 2ab - 6a b = (6a b - 6a b) + (-3ab - 2ab ) = -5ab 。
求值:当 a = -1,b = 2 时,-5×(-1)×2 = 5×4 = 20。
结论:化简结果为 - 5ab ,值为 20。
幻灯片 10:例题 3—— 整式加减的实际应用
题目:一个长方形的长为 (4x + 3y),宽比长短 (x - y),
(1)求长方形的宽(用含 x、y 的整式表示);
(2)求长方形的周长。
解答过程:
(1)宽 = (4x + 3y) - (x - y) = 4x + 3y - x + y = 3x + 4y。
(2)周长 = 2×(长 + 宽) = 2 [(4x + 3y) + (3x + 4y)] = 2 (7x + 7y) = 14x + 14y。
结论:(1)宽为 3x + 4y;(2)周长为 14x + 14y。
幻灯片 11:例题 4—— 整式的综合运算
题目:已知多项式 A = 2x - 3x + 1,B = -x + 2x - 5,求:
(1)A + 2B;
(2)当 x = -2 时,A + 2B 的值。
解答过程:
(1)A + 2B = (2x - 3x + 1) + 2(-x + 2x - 5) = 2x - 3x + 1 - 2x + 4x - 10 = (2x - 2x ) + (-3x + 4x) + (1 - 10) = x - 9。
(2)当 x = -2 时,x - 9 = -2 - 9 = -11。
结论:(1)A + 2B = x - 9;(2)值为 - 11。
幻灯片 12:易错题集锦与解析
易错点 1:单项式系数与次数判断错误
错误示例:认为单项式 - xy 的系数是 1,次数是 2。
解析:系数是 - 1(含符号),次数是 1+2=3,正确结果:系数 - 1,次数 3。
易错点 2:合并同类项时符号错误
错误示例:合并 3x - (2x - y) 时,得到 3x - 2x - y = x - y。
解析:去括号时括号外是负号,括号内各项符号应变号,正确结果:3x - 2x + y = x + y。
易错点 3:多项式次数判断错误
错误示例:认为多项式 x + 2x y - 1 的次数是 3。
解析:次数最高项是 2x y (次数 2+2=4),正确次数是 4。
幻灯片 13:针对性练习 1—— 概念辨析
题目:
(1)指出单项式 -\(\frac{5}{3}\)a b 的系数和次数;
(2)判断多项式 3x - 2x + 5x - 1 是几次几项式,常数项是多少。
答案:
(1)系数 -\(\frac{5}{3}\),次数 3;
(2)四次四项式,常数项是 - 1。
幻灯片 14:针对性练习 2—— 整式化简
题目:化简:
(1)5 (x - 2y) - 2 (3x - y);
(2)(a b - 2ab ) - 2 (a b - 1) + 3ab + 2。
答案:
(1)5x - 10y - 6x + 2y = -x - 8y;
(2)a b - 2ab - 2a b + 2 + 3ab + 2 = -a b + ab + 4。
幻灯片 15:针对性练习 3—— 综合应用
题目:已知 A = x + xy + y ,B = -3xy - x ,求:
(1)A - B;
(2)当 x = 1,y = -1 时,A - B 的值。
答案:
(1)A - B = (x + xy + y ) - (-3xy - x ) = x + xy + y + 3xy + x = 2x + 4xy + y ;
(2)当 x = 1,y = -1 时,2×1 + 4×1×(-1) + (-1) = 2 - 4 + 1 = -1。
幻灯片 16:本章总结
知识体系:从整式的基本概念(单项式、多项式)到运算(同类项合并、去括号、整式加减),形成完整的知识链。
核心方法:
概念辨析:抓住 “定义关键词”(如单项式的 “数与字母的积”)。
运算技巧:去括号 “符号先行”,合并同类项 “系数相加,字母不变”。
实际应用:先列整式表示数量关系,再通过运算解决问题。
学习建议:多练习基础题巩固概念,通过综合题提升应用能力,重视错题分析。
幻灯片 17:章末测试题(节选)
下列各式中,是单项式的是( )
A. x + y B. \(\frac{1}{x}\) C. -5 D. x + 2x
化简 3a - 2 (a - b) 的结果是( )
A. a + 2b B. a - 2b C. a + b D. a - b
已知单项式 3x y 与 - 2x y 是同类项,则 m + n = ______。
先化简,再求值:2 (x y + xy ) - 2 (x y - 1) - 3xy - 2,其中 x = -2,y = \(\frac{1}{2}\)。
一个多项式与 x - 2x + 1 的和是 3x - 2,求这个多项式。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识结构
代数式
列代数式
求代数式的值
多项式的项、次数
升(降)幂的排列
用字母表示数
整式
多项式
单项式
单项式的
次数、系数
去(添)括号
合并同类项
整式的加减
【点击蓝色字跳转到相应页面】
练习
定义:由________________组成的代数式叫做单项式.
单独________或_________也是单项式.
系数:单项式中的_________.
次数:一个单项式中的_____________________.
总结
单项式
数与字母的乘积
一个数
一个字母
数字因数
所有字母的指数的和
(1)当单项式的系数是1或-1时,“1”通常省略不写.
(2)当式子的分母中出现字母时不是单项式.
(3)圆周率π是常数,不要看成字母.
(4)当单项式的系数是带分数时,通常写成假分数.
(5)单项式的系数应包括它前面的符号.
(6)单项式的次数是指单项式中所有字母的指数的和,与数字的指数没有关系.
(7)单独的数字不含字母,规定它的次数是零次.
注意的问题
总结
多项式
定义:几个________________.
项:组成多项式中的_________________.
常数项:多项式中_________________________.
次数:_______________________________________.
升幂排列(或降幂排列):把一个多项式的各项按照某个字母的指数从小到大(或从大到小)的顺序排列起来.
单项式的和
每一个单项式
不含字母的项
多项式中,次数最高项的次数
注意的问题
(1)在确定多项式的项时,要连同它前面的符号.
(2)一个多项式中次数最高项的次数是几,就说这个多项式是几次多项式.
(3)在多项式中,每个单项式都是这个多项式的项,每一项都有系数,但对整个多项式来说,没有系数的概念,只有次数的概念.
同类项
同类项的定义:
_______________________________________________.
规定:几个常数项也是_________.
合并同类项概念:把多项式中的同类项合并成一项.
合并同类项法则:
(1)_______相加;
(2)_________________不变.
总结
所含字母相同,并且相同字母的指数都相等的项
同类项
系数
字母和字母的指数
口诀:只求系数和,字母指数不变样.
添括号法则:
所添括号前面是“+”号,括到括号里的各项都不改变正负号;
所添括号前面是“-”号,括到括号里的各项都改变正负号.
去括号法则:
括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都不改变正负号;
括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变正负号.
总结
去(添)括号
知识要点
1.用字母表示数,从数的研究过渡到代数式的研究,是数学发展的一次飞跃. 代数式及其运算,是进一步学习数学(方程、不等式、函数等)的基础,也是解决实际问题的工具.学习时要注意联系实际,体会从具体到抽象、从特殊到一般的思想方法.
2.整式包括单项式和多项式.多项式可以看作几个单项式的和,其中的每一个单项式是多项式的项.多项式的项(单项式)的系数包括正负号,在进行整式运算时不容忽视.
知识要点
3.整式的加减运算是本章学习的又一个重点.去括号和合并同类项是整式加减的基础.
4.去(添)括号时,要特别注意括号前面是“-”号的情形:去括号时,括号内的各项都改变正负号;添括号时,括到括号内的各项都改变正负号.
课堂练习
1.填空:
(1)如果a表示一个有理数,那么它的相反数是______;
(2)如果n表示一个自然数,那么它的后一个自然数是_______;
(3)一个正方形的边长是 a cm,把这个正方形的边长增加1cm后所得到的正方形的面积是_________;
(4)某商品原价是x元,提价10%后的价格是_________;
-a
n+1
(a+1)2cm2
1.1x 元
【选自教材P118复习题第1题】
A组
1.填空:
(5)如果一个两位数的十位数字是a,个位数字是b,那么这个两位数可表示为___________;
(6)如果甲、乙两人分别从相距 s km的A、B两地同时出发相向而行,他们的速度分别为 a km/h与 b km/h,那么他们从出发到相遇所需要的时间为________.
10a+b
h
【选自教材P118复习题第1题】
2.用代数式表示:
(1) a的3倍与b的平方的差;
(2)x与y平方的和;
(3)x 、y两数的平方和减去它们积的2倍;
(4)x的相反数与y的倒数的和.
3a-b2
x+y2
x2+y2-2xy
【选自教材P118复习题第2题】
3.填表:
5
3
3
0
1
-1
-1
0
-3
3
【选自教材P118复习题第3题】
4.若某班同学在体育达标检测中,达标率为p,达标人数为n,则总人数为_________. 若p=88%,n=44,则这个班有______人.
50
【选自教材P119复习题第4题】
5.填表:
1
1
-1
3
5
3
【选自教材P119复习题第5题】
6.填表:
2
2
x2
-1
2
3
x2
-2x
3
3
2
x2
-xyz
【选自教材P119复习题第6题】
7.将下列多项式按x的降幂排列:
(1)3-2x2+x;
(2)-2xy+x2+y2;
(3)2x-1-x3;
(4)2x2y-3xy2-x3+2y3.
-2x2+x+3
x2-2xy+y2
-x3+2x-1
-x3+2x2y-3xy2+2y3
【选自教材P119复习题第7题】
8.合并同类项:
(1)2ax+3by-4ax+3by-2ax;
(2)-2x2+x-3+x2-3x;
(3)3x2y-xy2-2x2y+3xy2.
解 原式=2ax-2ax-4ax+3by+3by
=-4ax+6by
解 原式=-2x2+x2+x-3x-3
=-x2-2x-3
解 原式=3x2y-2x2y-xy2+3xy2
=x2y+2xy2
【选自教材P119复习题第8题】
9.填空(去括号或添括号):
(1)2a+3(b-c)=__________;
(2)2a-3(b-c)=__________;
(3)x2-xy+y2=x2-(_________);
(4)x2-xy+y2=x2+(_________);
2a+3b-3c
2a-3b+3c
xy-y2
-xy+y2
【选自教材P119复习题第9题】
10.化简:
(1) 3x+2x2-2-15x2+1-5x; (2)3x2+2xy-4y2-3xy+4y2-3x2;
(3)-7x2+(6x2-5xy)-(3y2+xy-x2); (4) (2x2-5x) - (3x+5-2x2).
解 原式=2x2-15x2-5x+3x-2+1
=-13x2-2x-1
解 原式=3x2-3x2+2xy-3xy-4y2+4y2
=-xy
解 原式=-7x2+6x2-5xy-3y2-xy+x2
=-7x2+6x2+x2-5xy-xy-3y2
=-6xy-3y2
解 原式=2x2-5x-3x-5+2x2
=4x2-8x-5
【选自教材P120复习题第10题】
11.先化简,再求值:
(1)3x3-[x3+(6x2-7x)]-2(x3-3x2-4x),其中x=-1.
解 3x3-[x3+(6x2-7x)]-2(x3-3x2-4x)
=3x3-[x3+6x2-7x]-2x3+6x2+8x
=3x3-x3-6x2+7x-2x3+6x2+8x
=3x3-x3-2x3-6x2+6x2+7x+8x
=15x
当x=-1时,原式=15×(-1)=-15
【选自教材P120复习题第11题】
11.先化简,再求值:
(2) ,其中x= ,y=2.
当x= ,y=2时,原式=22=4
【选自教材P120复习题第11题】
12. x表示一个两位数,y表示一个三位数,若把x放在y的右边组成一个五位数,则这个五位数可以表示为____________.
13.代数式x2+x+3的值为7,则代数式2x2+2x-3的值为_________.
100y+x
2x2+2x-3=2(x2+x+3)-9=14-9=5
5
【选自教材P120复习题第12题】
【选自教材P120复习题第13题】
B组
14.已知多项式A = 4x2- 4xy + y2,B = x2+ xy - 5y2,求:
(1) A - 3B; (2) 3A + B.
解 (1) A - 3B=4x2- 4xy + y2-3(x2+ xy - 5y2)
=4x2- 4xy + y2-3x2-3xy +15y2
=4x2-3x2- 4xy-3xy+y2+15y2
=x2-7xy+16y2
【选自教材P120复习题第14题】
解 (2)3A + B=3(4x2- 4xy + y2)+x2+ xy - 5y2
=12x2-12xy+3y2+x2+ xy - 5y2
=12x2+x2-12xy+xy+3y2-5y2
=13x2-11xy-2y2
14.已知多项式A = 4x2- 4xy + y2,B = x2+ xy - 5y2,求:
(1) A - 3B; (2) 3A + B.
15.把 x-y 看作一个整体,化简:
5(x-y)+2(x-y)-4(x-y); (2) 3(x-y)2-4(x-y)+7(x-y)-6(x-y)2.
解 原式=(5+2-4) (x-y)
=3(x-y)
解 原式=3(x-y)2-6(x-y)2-4(x-y)+7(x-y)
=-3(x-y)2+3(x-y)
【选自教材P120复习题第15题】
16.如图,若a-b=4,求长方形A与B的面积的差.
解 根据题意,两个长方形的面积的差为:
答:两个长方形的面积的差为8.
【选自教材P120复习题第16题】
5a-2b
6a-2b
4
3
4(5a-2b)-3(6a-2b)=20a-8b-18a+6b
=2a-2b=2(a-b)
当a-b=4时,原式=2×4=8
A
B
17.有这样一道题:“求(2x3-3x2y-2xy2)-(x3-2xy2+y3)+(-x3+3x2y-y3)的值,其中x= ,y=-1.”甲同学把“x= ”错抄成“x= ”,但他计算的结果却是正确的.这是怎么回事呢?
解 (2x3-3x2y-2xy2)-(x3-2xy2+y3)+(-x3+3x2y-y3)
=2x3-3x2y-2xy2-x3+2xy2-y3-x3+3x2y-y3
=2x3-x3-x3-3x2y+3x2y-2xy2+2xy2-y3-y3
=-2y3
化简后可知,原式的结果与x的值无关.
【选自教材P120复习题第17题】
核心知识巩固
一、基础考点演练
考点1 代数式
1.下列各式中,不是代数式的是( )
B
A.7 B. C. D.
返回
2.用代数式表示“ 的2倍与3的和”,下列表示正确的是( )
B
A. B. C. D.
返回
3.小明比小强大2岁,比小华小4岁.如果小强 岁,那么小华的年龄为
________岁.
返回
4.学习委员小明带了200元钱去文具店买学习用品,已知一支笔 元,一
个笔记本元,则代数式 表示的实
际意义是_______________________________________.
用200元购买3支笔和4个笔记本后剩余的钱
返回
考点2 代数式的值
5.当,,时,代数式 的值为____.
返回
6.[2025福州期末]根据一项科学研究,一个10岁至15岁的人每天所需
的睡眠时间可用公式计算出来,其中 代表人的岁数.根
据这个公式,一个12岁的未成年人每天所需的睡眠时间是____ .
9.8
返回
7.(4分)[2025郑州月考]已知,互为相反数,,互为倒数,
是绝对值最小的负整数,求 的值.
解:因为,互为相反数,,互为倒数, 是绝对值最小的负整数,
所以,, ,
所以原式 .
返回
考点3 整式
8.下列各式中,不是整式的是( )
C
A. B. C. D.0
返回
9.下列说法正确的是( )
A
A.单项式 的次数是5
B.的系数是
C.多项式 的常数项是2
D.多项式 是三次二项式
返回
10.若多项式是关于, 的四次三项式,则
的值为___.
9
返回
11.(16分)已知多项式 ,按要求解答下列问题:
(1)指出该多项式的项;
解:多项式各项依次为,,, .
(2)该多项式的次数是___,三次项的系数是____,常数项是____;
(3)按 的降幂排列:__________________________________________
______________________;
4
(或
)
(4)若 ,求该多项式的值.
解:由题意,得, ,
所以, .所以原式
.
返回
考点4 同类项及其合并
12.合并同类项, ____________.
返回
13.已知单项式与的和是单项式,则___, ___.
4
3
返回
考点5 去括号与添括号
14.下列变形中,正确的是( )
B
A. B.
C. D.
返回
15.(______________) (__________).
返回
考点6 整式的加减
16.下列计算结果正确的是( )
D
A. B.
C. D.
返回
17. 定义 为二阶行列式,规定它的运算法则为
,那么当时,二阶行列式 的值为
___.
4
返回
18.(8分)化简:
(1) ;
解:原式
.
(2) .
解:原式 .
返回
19.(8分)已知多项式: ,
.
(1)求多项式 ;
解:因为 ,
,
所以 ,
则 .
(2)若是的相反数,是的倒数,求 的值.
解:因为是的相反数,是的倒数,所以,,故 .
返回
考点7 整式加减运算的应用
20.把四张形状、大小完全相同的小长方形卡
片(如图①,卡片长为、宽为 )不重叠地
放在一个长为、宽为 的长方形中
(如图②),涂色部分表示长方形未被卡片覆
盖的部分,则图②中两块涂色部分的周长和是
( )
A
A. B. C. D.
返回
21.(8分)为满足学生的课外活动需要,学校决定添置一批某品牌的足
球和跳绳.已知足球每个定价为80元,跳绳每根定价为20元.现有, 两
家网店提供包邮服务,并提出了各自的优惠方案.具体如下:
A网店:足球和跳绳都按定价的 付款.
B网店:买一个足球送一根跳绳.
已知该校计划从上述网店中购买足球50个,跳绳根 .
(1)在网店购买需付款______________元,在 网店购买需付款
______________元;(用含 的式子表示)
(2)若只选择一家网店购买,当 时,请通过计算说明学校选哪
家网店比较合算.
解:当时,方案 (元),
方案 (元).
因为,所以选 网店购买较为划算.
返回
考点8 规律探究
22.观察按规律排列的一组数:,3,,7,,11, ,则第 个
数是( )
C
A. B.
C. D.
返回
23.[2025南阳期末]小茗同学用小木棍按如图方式进行排列.回答下列问题:
(1)第4个图形用____根小木棍;
(2)第 个图形需要_________根小木棍;
(3)第_____个图形需要2 027根小木棍.
22
405
返回
二、思想方法演练
思想1 分类讨论思想
24.按如图所示的程序计算,我们发
现第二次输出的结果为24,那么开
始输入 的值为____________.
53或96或58
[解析] 点拨:分两种情况:当开始输入 的值是奇数时,由题意得
或,解得 (不符合题意,舍去)或
;当开始输入的值是偶数时,由题意得 或
,解得或.综上所述, 的值为53或96或58.
返回
思想2 数形结合思想
25.已知有理数,在数轴上的位置如图所示,化简 的
结果是_____.
返回
思想3 方程思想
26.[2025成都期末]已知关于的整式 ,
,为常数.若整式的取值与无关,则 的
值为____.
返回
思想3 整体思想
27.(4分)已知,,求
的值.
解:
,
因为, ,所以原式
.
返回
谢谢观看!
同课章节目录
