1.4 有理数的大小 课件(共30张PPT)
文档属性
| 名称 | 1.4 有理数的大小 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 00:00:00 | ||
图片预览










文档简介
(共30张PPT)
1.4 有理数的大小
第一章 有理数
【2024新教材】2025-2026学年冀教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
第一页:标题页
1.4 有理数的大小
—— 掌握有理数大小比较的方法
(右下角添加授课教师姓名及日期:2025 年 7 月 30 日)
第二页:引入
我们已经学习了数轴、绝对值和相反数等知识,知道了有理数在数轴上的表示方法。那么,如何比较不同有理数的大小呢?比如,3 和 5 哪个大?-2 和 - 4 哪个大?-1 和 2 哪个大?这节课我们就来学习有理数的大小比较方法,解决这些问题。
第三页:利用数轴比较有理数的大小
基本法则:在数轴上表示的两个数,右边的数总比左边的数大。
实例分析:
在数轴上表示出 - 3、-1、0、2 这几个数,从左到右的顺序为 - 3、-1、0、2,所以它们的大小关系是 - 3 < -1 < 0 < 2。
结论延伸:
正数都在原点的右边,负数都在原点的左边,因此正数大于 0,负数小于 0,正数大于一切负数。
第四页:两个负数比较大小
方法:两个负数比较大小,绝对值大的反而小。
推导过程:
例如,比较 - 2 和 - 5 的大小。
先求出它们的绝对值:| -2 | = 2,| -5 | = 5。
因为 2 <5,即 | -2 | < | -5 |,所以根据 “绝对值大的反而小”,可得 - 2 > -5。
在数轴上,-2 在 - 5 的右边,也能说明 - 2 > -5,与上述结论一致。
第五页:有理数大小比较的步骤
区分数的类型:明确要比较的数是正数、0 还是负数。
直接比较的情况:
正数与正数比较:绝对值大的数大。
正数与 0 比较:正数大于 0。
正数与负数比较:正数大于负数。
负数与 0 比较:负数小于 0。
特殊情况(两个负数比较):
第一步:求出两个负数的绝对值。
第二步:比较两个绝对值的大小。
第三步:根据 “绝对值大的反而小” 得出结论。
第六页:例题解析(一)
例题 1:比较下列各组数的大小:
(1)3 和 7;(2)-3 和 - 7;(3)-2 和 0;(4)-1 和 3。
解:(1)3 和 7 都是正数,因为 3 < 7,所以 3 < 7。
(2)-3 和 - 7 都是负数,先求绝对值:| -3 | = 3,| -7 | = 7。因为 3 <7,所以 - 3> -7(绝对值大的反而小)。
(3)-2 是负数,0 既不是正数也不是负数,所以 - 2 < 0(负数小于 0)。
(4)-1 是负数,3 是正数,所以 - 1 < 3(负数小于正数)。
第七页:例题解析(二)
例题 2:将下列各数按从小到大的顺序排列:-5、2、-3、0、4、-1。
解:步骤一:区分类型,负数有 - 5、-3、-1;正数有 2、4;还有 0。
步骤二:比较负数的大小,先求绝对值:| -5 | = 5,| -3 | = 3,| -1 | = 1。因为 5 > 3 > 1,所以 - 5 < -3 < -1(绝对值大的反而小)。
步骤三:正数 2 < 4,且负数小于 0,0 小于正数。
所以,从小到大的顺序为:-5 < -3 < -1 < 0 < 2 < 4。
第八页:例题解析(三)
例题 3:比较下列各组数的大小:
(1)-0.5 和 - 0.3;(2)\(-\frac{3}{4}\)和\(-\frac{2}{3}\)。
解:(1)-0.5 和 - 0.3 都是负数,| -0.5 | = 0.5,| -0.3 | = 0.3。因为 0.5 > 0.3,所以 - 0.5 < -0.3。
(2)\(-\frac{3}{4}\)和\(-\frac{2}{3}\)都是负数,先通分再求绝对值:| \(-\frac{3}{4}\) | = \(\frac{3}{4}\) = \(\frac{9}{12}\),| \(-\frac{2}{3}\) | = \(\frac{2}{3}\) = \(\frac{8}{12}\)。因为\(\frac{9}{12}\) > \(\frac{8}{12}\),即 | \(-\frac{3}{4}\) | > | \(-\frac{2}{3}\) |,所以\(-\frac{3}{4}\) < \(-\frac{2}{3}\)。
第九页:课堂练习
填空题:
比较大小:-6 ______ -4;3 ______ -5;0 ______ -1;-0.8 ______ -0.7。
最大的负整数是______,最小的正整数是______。
在数 - 3、2、-1、0、5 中,最大的数是______,最小的数是______。
选择题:
下列各数中,比 - 2 小的数是( )
A. -3 B. -1 C. 0 D. 1
下列说法正确的是( )
A. 所有的正数都比负数大 B. 绝对值越大的数越大 C. 0 是最大的数 D. 负数都比正数大
把下列各数按从大到小的顺序排列:-2.5、3、-1、0、-4、1.5。
第十页:课堂小结
利用数轴比较有理数大小:数轴上右边的数总比左边的数大,由此可得正数大于 0,负数小于 0,正数大于一切负数。
两个负数比较大小:绝对值大的反而小,步骤是先求绝对值,再比较绝对值大小,最后得出结论。
有理数大小比较的关键是区分数的类型,针对不同类型的数采用相应的比较方法。
第十一页:作业布置
教材第 XX 页习题 1.4 第 1、2、3 题。
比较下列各组数的大小:
(1)-10 和 - 12;(2)7 和 - 9;(3)-0.6 和 - 0.5;(4)\(-\frac{5}{6}\)和\(-\frac{4}{5}\)。
将下列各数按从小到大的顺序排列:-3.2、5、0、-4、2.8、-1。
若 a 是正数,b 是负数,且 | a | < | b |,比较 a、b、-a、-b 的大小。
思考:有没有最大的有理数?有没有最小的有理数?有没有绝对值最大的有理数?为什么?
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.能借助数轴比较两个有理数的大小.
2.掌握用绝对值比较两个负数的大小的方法,并会比较两个负数的大小.
3.能通过比较有理数的大小解决实际生活中的问题.
学习目标
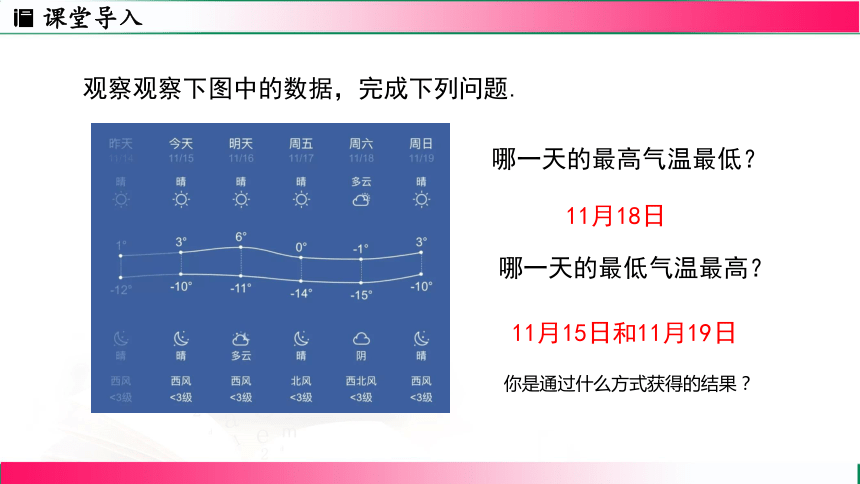
观察观察下图中的数据,完成下列问题.
哪一天的最高气温最低?
11月18日
哪一天的最低气温最高?
11月15日和11月19日
你是通过什么方式获得的结果?
课堂导入
探究 某地某一天中4个不同时刻的气温分别是
-3℃,-5℃,4℃,0℃.
1、请你按照由低到高的顺序把不同时刻的气温
排列出来.
-5℃,-3℃,0℃,4℃.
2、4个不同时刻的气温在温度计上对应的位置
有什么规律?
新知探究
知识点1 利用数轴比较有理数的大小
3、你能把有理数-3,-5,4,0在数轴上表示出来吗?
4、这些数的 大小与它们在数轴上所表示的点的位置有什么关
系?
从左向右越来越大
新知探究
知识点1 利用数轴比较有理数的大小
记住了吗?
有理数大小的比较方法1:
在数轴上表示的两个数,右边的数总比左边的数大.
-5 -4 -3 -2 -1 0 1 2 3 4 5
小 大
正数大于0,0大于负数,正数大于负数.
总 结
新知探究
知识点1 利用数轴比较有理数的大小
问题1 在数轴上表示数-3.5,-1,0,并将它们按从小到大的顺序用“<”号连接起来.
解:
把3.5,-1,0在数轴上表示出来,如下图所示:
将它们按从小到大的顺序排列为:
-1 <0 <3.5.
-5 -4 -3 -2 -1 0 1 2 3 4 5
●
●
●
新知探究
知识点1 利用数轴比较有理数的大小
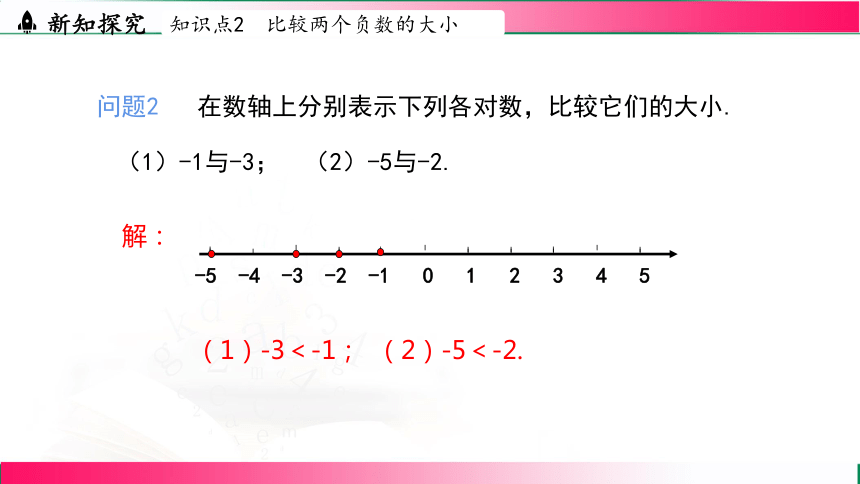
问题2 在数轴上分别表示下列各对数,比较它们的大小.
(1)-1与-3; (2)-5与-2.
-5 -4 -3 -2 -1 0 1 2 3 4 5
(1)-3<-1; (2)-5<-2.
解:
新知探究
知识点2 比较两个负数的大小
两个负数,绝对值大的反而小.
问题3 求出各对数的绝对值,并比较它们的大小.
|-1|=1;|-3|=3;
|-1|<|-3|
|-2|=2;|-5|=5;
|-2|<|-5|
-5<-2
-3<-1
对比
观察
总结
有理数大小的比较方法2:
新知探究
知识点2 比较两个负数的大小
解:
(1)0>-6,(0大于负数).
问题4 比较下列每组数的大小
(1)0与-6; (2)3和-4.4; (3) 和 .
(2)3>-4.4,(正数大于负数).
(3)因为
所以
新知探究
知识点2 比较两个负数的大小
1.下面有理数比较大小正确的是( )
A.0<-2 B.-5<3
C. -2<-3 D.1<- 4
B
随堂练习
2.如图,点A,B,C,D,E,F表示的数中,比点A表示的数大的有( )
A.5个 B.4个 C.3个 D.2个
C
随堂练习
4.比较下面各对数的大小,并说明理由:
>
<
>
<
3.在有理数0,│-(-3 )│,-│+1000│,-(-5)中最大的数是( )
A.0 B.-(-5) C.-│+1000│ D.│-(-3 )│
B
随堂练习
5.下列判断,正确的是( )
A.若a>b,则│a│>│b│ B.若│a│>│b│,则a>b
C.若a<b<0,则│a│<│b│ D.若a>b>0,则│a│>│b│
D
如a=1,b=-2
如a=-3,b=2
如a=-3,b=-2
6.将下列这些数用“<”连接
0,-3,|5|,-(-4),-|-5|
解:-|-5|< -3 <0< -(-4)<|5|
随堂练习
7. 下表记录了今年一月某日部分城市的最高气温:
城市 阜阳 安庆 淮北 合肥 芜湖
最高气温/℃ -5 2 -3 -1 4
(1)在数轴上表示这些城市最高气温的值;
(2)用“<”连接这些城市的最高气温.
解:(1)如图
(2)-5℃<-3℃<-1℃<2℃<4℃.
随堂练习
8.如果a是有理数,试比较|a|与-2a的大小.
[思路引导]由于不能确定a的正负,所以需分类讨论
解: 当a>0时,|a|>0,-2a<0,所以|a|>-2a;
当a=0时,|a|=0,-2a=0,所以|a|=-2a;
当a<0时,-2a>0,|a|=-a,
因为-2a>-a,所以|a|<-2a.
随堂练习
知识点1用数轴比较大小
1. 有理数 a , b 在数轴上对应点的位置如图所示,则 a , b
的大小关系为( B )
A. a > b B. a < b
C. a = b D. 无法确定
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2. 如图,比较大小:- m - n .
>
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
知识点2用法则比较大小
3. 在数轴上标出表示下列各数的点,并用“<”把这些数连
接起来.
-2.5, ,-2,+5,- .
【解】在数轴上表示各数如图所示.
用“<”将各数连接:-2.5<-2<- < <+5.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
4. 下列有理数比较大小正确的是( C )
A. 0<-1 B. 2<-1
C. 3>-2 D. -1>1
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
知识点3用绝对值比较大小
5. 下列说法正确的是( C )
A. 有理数中存在最大的数
B. 任何数都大于它的相反数
C. 最小的正整数是1
D. 两个数中,较大的那个数的绝对值较大
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
6. 绝对值小于3的负整数有 ,绝对值不大于2
的非负整数有 .
-2,-1
0,1,2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
7. 比较下列每组数的大小.
(1)- 与|-(-3)|;
【解】因为- =- ,|-(-3)|=3,
所以- <|-(-3)|.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(2)-(-0.5)与 .
【解】-(-0.5)=0.5, = =0.4.
因为0.5>0.4,所以-(-0.5)> .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
知识点4生活中有理数的大小比较
8. [新趋势·跨学科题] 几种气体的固化温度(标准大气压)
如下表:
气体 氧气 氮气 二氧化碳 氢气
固化温度/℃ -218 -209.8 -78.5 -259.1
其中固化温度最高的气体是( C )
A. 氧气 B. 氮气
C. 二氧化碳 D. 氢气
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
9. [新视角·结论开放题] 冰激凌保存温度是-18 ℃以下,请
写出一个适合冰激凌保存的温度: ℃.
-2(答案不唯一)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
易错点 对绝对值的几何意义理解不透彻而致错
10. 如图,数轴上点 A , B , C , D 分别对应数 a , b , c ,
d ,下列各式的值最小的是( C )
A. | a | B. | b |
C. | c | D. | d |
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
比较有理数的大小
利用数轴比较大小
利用法则比较大小
在数轴上表示的两个数,右边的数总比左边的数大.
正数大于0,负数小于0,正数大于负数.
两个负数,绝对值大的反而小.
课堂小结
谢谢观看!
1.4 有理数的大小
第一章 有理数
【2024新教材】2025-2026学年冀教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
第一页:标题页
1.4 有理数的大小
—— 掌握有理数大小比较的方法
(右下角添加授课教师姓名及日期:2025 年 7 月 30 日)
第二页:引入
我们已经学习了数轴、绝对值和相反数等知识,知道了有理数在数轴上的表示方法。那么,如何比较不同有理数的大小呢?比如,3 和 5 哪个大?-2 和 - 4 哪个大?-1 和 2 哪个大?这节课我们就来学习有理数的大小比较方法,解决这些问题。
第三页:利用数轴比较有理数的大小
基本法则:在数轴上表示的两个数,右边的数总比左边的数大。
实例分析:
在数轴上表示出 - 3、-1、0、2 这几个数,从左到右的顺序为 - 3、-1、0、2,所以它们的大小关系是 - 3 < -1 < 0 < 2。
结论延伸:
正数都在原点的右边,负数都在原点的左边,因此正数大于 0,负数小于 0,正数大于一切负数。
第四页:两个负数比较大小
方法:两个负数比较大小,绝对值大的反而小。
推导过程:
例如,比较 - 2 和 - 5 的大小。
先求出它们的绝对值:| -2 | = 2,| -5 | = 5。
因为 2 <5,即 | -2 | < | -5 |,所以根据 “绝对值大的反而小”,可得 - 2 > -5。
在数轴上,-2 在 - 5 的右边,也能说明 - 2 > -5,与上述结论一致。
第五页:有理数大小比较的步骤
区分数的类型:明确要比较的数是正数、0 还是负数。
直接比较的情况:
正数与正数比较:绝对值大的数大。
正数与 0 比较:正数大于 0。
正数与负数比较:正数大于负数。
负数与 0 比较:负数小于 0。
特殊情况(两个负数比较):
第一步:求出两个负数的绝对值。
第二步:比较两个绝对值的大小。
第三步:根据 “绝对值大的反而小” 得出结论。
第六页:例题解析(一)
例题 1:比较下列各组数的大小:
(1)3 和 7;(2)-3 和 - 7;(3)-2 和 0;(4)-1 和 3。
解:(1)3 和 7 都是正数,因为 3 < 7,所以 3 < 7。
(2)-3 和 - 7 都是负数,先求绝对值:| -3 | = 3,| -7 | = 7。因为 3 <7,所以 - 3> -7(绝对值大的反而小)。
(3)-2 是负数,0 既不是正数也不是负数,所以 - 2 < 0(负数小于 0)。
(4)-1 是负数,3 是正数,所以 - 1 < 3(负数小于正数)。
第七页:例题解析(二)
例题 2:将下列各数按从小到大的顺序排列:-5、2、-3、0、4、-1。
解:步骤一:区分类型,负数有 - 5、-3、-1;正数有 2、4;还有 0。
步骤二:比较负数的大小,先求绝对值:| -5 | = 5,| -3 | = 3,| -1 | = 1。因为 5 > 3 > 1,所以 - 5 < -3 < -1(绝对值大的反而小)。
步骤三:正数 2 < 4,且负数小于 0,0 小于正数。
所以,从小到大的顺序为:-5 < -3 < -1 < 0 < 2 < 4。
第八页:例题解析(三)
例题 3:比较下列各组数的大小:
(1)-0.5 和 - 0.3;(2)\(-\frac{3}{4}\)和\(-\frac{2}{3}\)。
解:(1)-0.5 和 - 0.3 都是负数,| -0.5 | = 0.5,| -0.3 | = 0.3。因为 0.5 > 0.3,所以 - 0.5 < -0.3。
(2)\(-\frac{3}{4}\)和\(-\frac{2}{3}\)都是负数,先通分再求绝对值:| \(-\frac{3}{4}\) | = \(\frac{3}{4}\) = \(\frac{9}{12}\),| \(-\frac{2}{3}\) | = \(\frac{2}{3}\) = \(\frac{8}{12}\)。因为\(\frac{9}{12}\) > \(\frac{8}{12}\),即 | \(-\frac{3}{4}\) | > | \(-\frac{2}{3}\) |,所以\(-\frac{3}{4}\) < \(-\frac{2}{3}\)。
第九页:课堂练习
填空题:
比较大小:-6 ______ -4;3 ______ -5;0 ______ -1;-0.8 ______ -0.7。
最大的负整数是______,最小的正整数是______。
在数 - 3、2、-1、0、5 中,最大的数是______,最小的数是______。
选择题:
下列各数中,比 - 2 小的数是( )
A. -3 B. -1 C. 0 D. 1
下列说法正确的是( )
A. 所有的正数都比负数大 B. 绝对值越大的数越大 C. 0 是最大的数 D. 负数都比正数大
把下列各数按从大到小的顺序排列:-2.5、3、-1、0、-4、1.5。
第十页:课堂小结
利用数轴比较有理数大小:数轴上右边的数总比左边的数大,由此可得正数大于 0,负数小于 0,正数大于一切负数。
两个负数比较大小:绝对值大的反而小,步骤是先求绝对值,再比较绝对值大小,最后得出结论。
有理数大小比较的关键是区分数的类型,针对不同类型的数采用相应的比较方法。
第十一页:作业布置
教材第 XX 页习题 1.4 第 1、2、3 题。
比较下列各组数的大小:
(1)-10 和 - 12;(2)7 和 - 9;(3)-0.6 和 - 0.5;(4)\(-\frac{5}{6}\)和\(-\frac{4}{5}\)。
将下列各数按从小到大的顺序排列:-3.2、5、0、-4、2.8、-1。
若 a 是正数,b 是负数,且 | a | < | b |,比较 a、b、-a、-b 的大小。
思考:有没有最大的有理数?有没有最小的有理数?有没有绝对值最大的有理数?为什么?
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.能借助数轴比较两个有理数的大小.
2.掌握用绝对值比较两个负数的大小的方法,并会比较两个负数的大小.
3.能通过比较有理数的大小解决实际生活中的问题.
学习目标
观察观察下图中的数据,完成下列问题.
哪一天的最高气温最低?
11月18日
哪一天的最低气温最高?
11月15日和11月19日
你是通过什么方式获得的结果?
课堂导入
探究 某地某一天中4个不同时刻的气温分别是
-3℃,-5℃,4℃,0℃.
1、请你按照由低到高的顺序把不同时刻的气温
排列出来.
-5℃,-3℃,0℃,4℃.
2、4个不同时刻的气温在温度计上对应的位置
有什么规律?
新知探究
知识点1 利用数轴比较有理数的大小
3、你能把有理数-3,-5,4,0在数轴上表示出来吗?
4、这些数的 大小与它们在数轴上所表示的点的位置有什么关
系?
从左向右越来越大
新知探究
知识点1 利用数轴比较有理数的大小
记住了吗?
有理数大小的比较方法1:
在数轴上表示的两个数,右边的数总比左边的数大.
-5 -4 -3 -2 -1 0 1 2 3 4 5
小 大
正数大于0,0大于负数,正数大于负数.
总 结
新知探究
知识点1 利用数轴比较有理数的大小
问题1 在数轴上表示数-3.5,-1,0,并将它们按从小到大的顺序用“<”号连接起来.
解:
把3.5,-1,0在数轴上表示出来,如下图所示:
将它们按从小到大的顺序排列为:
-1 <0 <3.5.
-5 -4 -3 -2 -1 0 1 2 3 4 5
●
●
●
新知探究
知识点1 利用数轴比较有理数的大小
问题2 在数轴上分别表示下列各对数,比较它们的大小.
(1)-1与-3; (2)-5与-2.
-5 -4 -3 -2 -1 0 1 2 3 4 5
(1)-3<-1; (2)-5<-2.
解:
新知探究
知识点2 比较两个负数的大小
两个负数,绝对值大的反而小.
问题3 求出各对数的绝对值,并比较它们的大小.
|-1|=1;|-3|=3;
|-1|<|-3|
|-2|=2;|-5|=5;
|-2|<|-5|
-5<-2
-3<-1
对比
观察
总结
有理数大小的比较方法2:
新知探究
知识点2 比较两个负数的大小
解:
(1)0>-6,(0大于负数).
问题4 比较下列每组数的大小
(1)0与-6; (2)3和-4.4; (3) 和 .
(2)3>-4.4,(正数大于负数).
(3)因为
所以
新知探究
知识点2 比较两个负数的大小
1.下面有理数比较大小正确的是( )
A.0<-2 B.-5<3
C. -2<-3 D.1<- 4
B
随堂练习
2.如图,点A,B,C,D,E,F表示的数中,比点A表示的数大的有( )
A.5个 B.4个 C.3个 D.2个
C
随堂练习
4.比较下面各对数的大小,并说明理由:
>
<
>
<
3.在有理数0,│-(-3 )│,-│+1000│,-(-5)中最大的数是( )
A.0 B.-(-5) C.-│+1000│ D.│-(-3 )│
B
随堂练习
5.下列判断,正确的是( )
A.若a>b,则│a│>│b│ B.若│a│>│b│,则a>b
C.若a<b<0,则│a│<│b│ D.若a>b>0,则│a│>│b│
D
如a=1,b=-2
如a=-3,b=2
如a=-3,b=-2
6.将下列这些数用“<”连接
0,-3,|5|,-(-4),-|-5|
解:-|-5|< -3 <0< -(-4)<|5|
随堂练习
7. 下表记录了今年一月某日部分城市的最高气温:
城市 阜阳 安庆 淮北 合肥 芜湖
最高气温/℃ -5 2 -3 -1 4
(1)在数轴上表示这些城市最高气温的值;
(2)用“<”连接这些城市的最高气温.
解:(1)如图
(2)-5℃<-3℃<-1℃<2℃<4℃.
随堂练习
8.如果a是有理数,试比较|a|与-2a的大小.
[思路引导]由于不能确定a的正负,所以需分类讨论
解: 当a>0时,|a|>0,-2a<0,所以|a|>-2a;
当a=0时,|a|=0,-2a=0,所以|a|=-2a;
当a<0时,-2a>0,|a|=-a,
因为-2a>-a,所以|a|<-2a.
随堂练习
知识点1用数轴比较大小
1. 有理数 a , b 在数轴上对应点的位置如图所示,则 a , b
的大小关系为( B )
A. a > b B. a < b
C. a = b D. 无法确定
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2. 如图,比较大小:- m - n .
>
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
知识点2用法则比较大小
3. 在数轴上标出表示下列各数的点,并用“<”把这些数连
接起来.
-2.5, ,-2,+5,- .
【解】在数轴上表示各数如图所示.
用“<”将各数连接:-2.5<-2<- < <+5.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
4. 下列有理数比较大小正确的是( C )
A. 0<-1 B. 2<-1
C. 3>-2 D. -1>1
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
知识点3用绝对值比较大小
5. 下列说法正确的是( C )
A. 有理数中存在最大的数
B. 任何数都大于它的相反数
C. 最小的正整数是1
D. 两个数中,较大的那个数的绝对值较大
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
6. 绝对值小于3的负整数有 ,绝对值不大于2
的非负整数有 .
-2,-1
0,1,2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
7. 比较下列每组数的大小.
(1)- 与|-(-3)|;
【解】因为- =- ,|-(-3)|=3,
所以- <|-(-3)|.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(2)-(-0.5)与 .
【解】-(-0.5)=0.5, = =0.4.
因为0.5>0.4,所以-(-0.5)> .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
知识点4生活中有理数的大小比较
8. [新趋势·跨学科题] 几种气体的固化温度(标准大气压)
如下表:
气体 氧气 氮气 二氧化碳 氢气
固化温度/℃ -218 -209.8 -78.5 -259.1
其中固化温度最高的气体是( C )
A. 氧气 B. 氮气
C. 二氧化碳 D. 氢气
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
9. [新视角·结论开放题] 冰激凌保存温度是-18 ℃以下,请
写出一个适合冰激凌保存的温度: ℃.
-2(答案不唯一)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
易错点 对绝对值的几何意义理解不透彻而致错
10. 如图,数轴上点 A , B , C , D 分别对应数 a , b , c ,
d ,下列各式的值最小的是( C )
A. | a | B. | b |
C. | c | D. | d |
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
比较有理数的大小
利用数轴比较大小
利用法则比较大小
在数轴上表示的两个数,右边的数总比左边的数大.
正数大于0,负数小于0,正数大于负数.
两个负数,绝对值大的反而小.
课堂小结
谢谢观看!
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
