1.6 有理数的减法 课件(共23张PPT)
文档属性
| 名称 | 1.6 有理数的减法 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 00:00:00 | ||
图片预览





文档简介
(共23张PPT)
1.6 有理数的减法
第一章 有理数
【2024新教材】2025-2026学年冀教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
第一页:标题页
1.6 有理数的减法
—— 掌握有理数减法法则,实现加减运算转化
(右下角添加授课教师姓名及日期:2025 年 7 月 30 日)
第二页:引入
在生活中,我们常常需要解决类似这样的问题:某地白天的最高气温是\(5 \),夜间的最低气温是\(-3 \),那么白天的最高气温比夜间的最低气温高多少摄氏度呢?这就涉及到有理数的减法运算。有理数的减法和我们之前学过的加法有什么关系呢?这节课我们就来探究有理数的减法法则。
第三页:有理数减法法则的探究
问题 1:计算\(5 - (-3)\),这表示求\(5\)比\(-3\)多多少。
我们可以借助数轴来理解,从表示\(-3\)的点到表示\(5\)的点,需要向右移动\(8\)个单位长度,所以\(5 - (-3)=8\)。
而我们知道\(5+(+3)=8\),由此可以发现\(5 - (-3)=5+(+3)\)。
问题 2:计算\(3 - 5\),表示求\(3\)比\(5\)少多少。
从数轴上看,从表示\(5\)的点到表示\(3\)的点,需要向左移动\(2\)个单位长度,所以\(3 - 5=-2\)。
又因为\(3+(-5)=-2\),所以\(3 - 5=3+(-5)\)。
法则总结:
减去一个数,等于加上这个数的相反数。用字母表示为:\(a - b=a+(-b)\)。
第四页:有理数减法法则的解读
减法运算可以转化为加法运算,转化的关键是 “两变”:
改变运算符号:把减号变为加号。
改变减数的符号:把减数变为它的相反数。
被减数的符号不变,被减数本身也不变。
转化后就可以按照有理数的加法法则进行计算。
实例:
\(10 - 6=10+(-6)=4\)(其中\(6\)的相反数是\(-6\))
\((-8)-(-5)=(-8)+(+5)=-3\)(其中\(-5\)的相反数是\(+5\))
\(0 - 7=0+(-7)=-7\)(其中\(7\)的相反数是\(-7\))
第五页:例题解析(一)
例题 1:计算下列各题
(1)\((-3)-(-5)\);(2)\(0 - 7\);(3)\(7.2 - (-4.8)\);(4)\(-3\frac{1}{2}-5\frac{1}{4}\)。
解:(1)\((-3)-(-5)\)
根据减法法则,转化为加法:\((-3)+(+5)\)
按照加法法则计算:\((-3)+(+5)=2\)
(2)\(0 - 7\)
转化为加法:\(0+(-7)\)
计算得:\(-7\)
(3)\(7.2 - (-4.8)\)
转化为加法:\(7.2+(+4.8)\)
计算得:\(12\)
(4)\(-3\frac{1}{2}-5\frac{1}{4}\)
转化为加法:\(-3\frac{1}{2}+(-5\frac{1}{4})\)
通分计算:\(-3\frac{2}{4}-5\frac{1}{4}=-8\frac{3}{4}\)
第六页:例题解析(二)
例题 2:计算\((-20)-(-5)-(-5)-(-12)\)
解:按照减法法则,将所有的减法转化为加法:\(\begin{align*}
&(-20)-(-5)-(-5)-(-12)\\
=&(-20)+(+5)+(+5)+(+12)
\end{align*}\)
利用加法交换律和结合律进行简便计算:\(\begin{align*}
=&(-20)+[(+5)+(+5)+(+12)]\\
=&(-20)+22\\
=&2
\end{align*}\)
第七页:有理数加减混合运算
有理数的加减混合运算可以统一成加法运算,即省略加号和括号的和的形式。
例如:\(3 - 5 + 7 - 9\)可以写成\(3+(-5)+(+7)+(-9)\),也可简化为\(3 - 5 + 7 - 9\)。
读法:
可以读作 “\(3\)减\(5\)加\(7\)减\(9\)”。
也可以读作 “\(3\)、\(-5\)、\(+7\)、\(-9\)的和”。
例题 3:把\((-8)-(-10)+(-6)-(+4)\)写成省略加号和括号的形式,并计算。
解:先转化为加法:\((-8)+(+10)+(-6)+(-4)\)
省略加号和括号:\(-8 + 10 - 6 - 4\)
计算:\(\begin{align*}
&-8 + 10 - 6 - 4\\
=&( -8 - 6 - 4)+10\\
=&-18 + 10\\
=&-8
\end{align*}\)
第八页:加减混合运算的技巧
统一成加法后运用运算律:将混合运算转化为加法后,利用加法交换律和结合律,把正数、负数分别结合相加,或把能凑整、互为相反数的数结合相加。
按 “和” 的意义读算式:有助于理解算式的本质,方便分组计算。
分步计算:对于复杂的混合运算,可以逐步转化和计算,避免出错。
例题 4:计算\(0.25+\frac{1}{12}-(-\frac{2}{3})-(-\frac{1}{4})+(-\frac{5}{12})\)
解:先转化为加法:\(0.25+\frac{1}{12}+\frac{2}{3}+\frac{1}{4}-\frac{5}{12}\)
把\(0.25\)化为\(\frac{1}{4}\),再分组结合:\(\begin{align*}
=&\left(\frac{1}{4}+\frac{1}{4}\right)+\left(\frac{1}{12}-\frac{5}{12}\right)+\frac{2}{3}\\
=&\frac{1}{2}+\left(-\frac{4}{12}\right)+\frac{2}{3}\\
=&\frac{1}{2}-\frac{1}{3}+\frac{2}{3}\\
=&\frac{1}{2}+\left(-\frac{1}{3}+\frac{2}{3}\right)\\
=&\frac{1}{2}+\frac{1}{3}\\
=&\frac{5}{6}
\end{align*}\)
第九页:实际应用举例
例题 5:某粮库一周内粮食进出库的记录如下(运进为正,运出为负,单位:吨):\(+30\)、\(-25\)、\(-10\)、\(+35\)、\(-20\)、\(-15\)、\(+20\)。
(1)这一周粮库的粮食是增多了还是减少了?增多或减少了多少吨?
(2)若粮库原有粮食\(1000\)吨,则一周后粮库还有多少吨粮食?
解:(1)计算一周内粮食进出库的总和:\(\begin{align*}
&30+(-25)+(-10)+35+(-20)+(-15)+20\\
=&(30 + 35 + 20)+[(-25)+(-10)+(-20)+(-15)]\\
=&85+(-70)\\
=&15
\end{align*}\)
结果为正,说明粮食增多了,增多了\(15\)吨。
(2)原有粮食\(1000\)吨,一周后有:\(1000 + 15=1015\)(吨)
第十页:课堂练习
填空题:
\(6 - 9=\);\((-4)-(-7)=\);\(0 - (-5)=\);\(-8 - 3=\)。
比\(-3\)小\(5\)的数是______;\(7\)比\(-2\)大______。
计算下列各题:
(1)\((-12)-(-18)+(-7)-15\)
(2)\(4.7 - (-8.9)-7.5+(-6)\)
(3)\(-\frac{1}{3}+\frac{3}{4}-\frac{5}{6}+\frac{1}{2}\)
(4)\(\vert -2 \vert - (-3)+1 - \vert 1 - 3 \vert\)
一天早晨的气温是\(-7 \),中午上升了\(11 \),半夜又下降了\(9 \),半夜的气温是多少?
第十一页:课堂小结
有理数减法法则:减去一个数,等于加上这个数的相反数,即\(a - b=a+(-b)\)。
减法运算的转化关键是 “两变”:变运算符号和变减数符号。
有理数加减混合运算可以统一成加法运算,省略加号和括号后可灵活运用加法运算律简化计算。
在解决实际问题时,要先明确正负数的意义,再通过有理数的加减运算求解。
第十二页:作业布置
教材第 XX 页习题 1.6 第 1、2、3、4 题。
计算下列各题:
(1)\(23 - (-76)-36 - (-105)\)
(2)\(-1.5 - (-4\frac{1}{4})+3.75 - (+8\frac{1}{2})\)
(3)\((-\frac{1}{2})+(-\frac{1}{6})-(-\frac{1}{4})-(+\frac{2}{3})\)
(4)\(\vert -3\frac{1}{2} \vert - \vert -\frac{1}{2} \vert + \vert -2 \vert\)
某潜水员先潜入水下\(61\)米,然后又上升\(32\)米,这时潜水员在水下多少米?
已知\(\vert a \vert=5\),\(\vert b \vert=3\),且\(a > b\),求\(a - b\)的值。
思考:若\(a\)、\(b\)为有理数,\(a - b\)一定小于\(a\)吗?举例说明。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.理解有理数减法法则,能熟练进行有理数的减法运算并解决简单的实际问题.
2.从有理数减法中体会加法和减法互为逆运算,以及减法可以转化为加法的转化思想.
学习目标
绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得0.
(3) 一个数与0相加,仍得这个数.
(1) 1 + 6 =
(2)(–2)+(–8) =
(3) (–9)+ 10 =
(4) 5 + (–9) =
(5) (–2.2)+ 2.2 =
(6) 6 + 0 =
(7) 0 + (–8) =
7
–10
1
–4
6
–8
同号两数相加,取相同的符号,并把绝对值相加.
0
计算
课堂导入
下表记录了石家庄2023年12月13日至12月17日每天的气温情况:
月/日 12/13 12/14 12/15 12/16 12/17
最高温度/℃ 8 10 10 5 8
最低温度/℃ 4 2 0 -5 -3
请问12月15日和16日两天的最大温差分别是多少?
解:10-0=10(℃);
5-(-5)=?
课堂导入
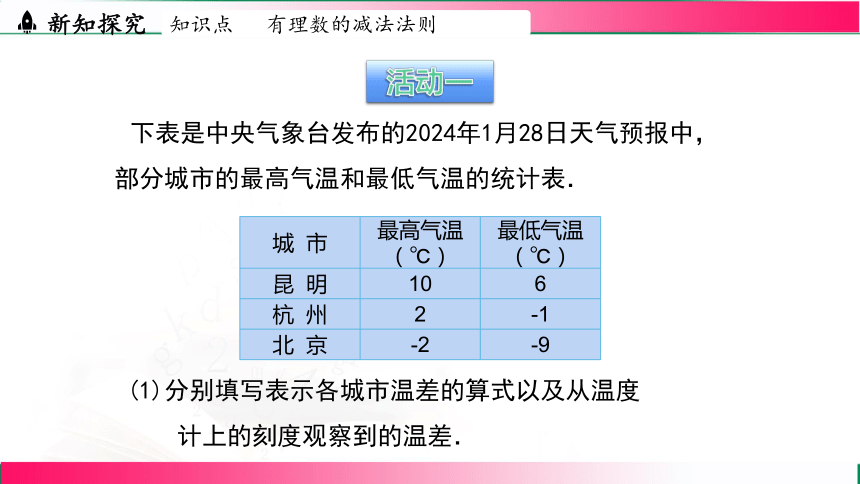
活动一
下表是中央气象台发布的2024年1月28日天气预报中,部分城市的最高气温和最低气温的统计表.
(1)分别填写表示各城市温差的算式以及从温度
计上的刻度观察到的温差.
城 市 最高气温(℃) 最低气温(℃)
昆 明 10 6
杭 州 2 -1
北 京 -2 -9
新知探究
知识点 有理数的减法法则
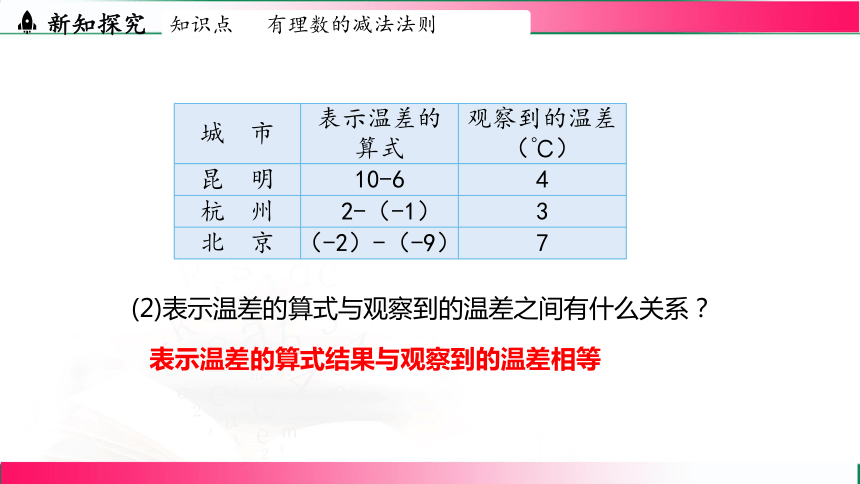
(2)表示温差的算式与观察到的温差之间有什么关系?
表示温差的算式结果与观察到的温差相等
城 市 表示温差的算式 观察到的温差(℃)
昆 明 10-6 4
杭 州 2-(-1) 3
北 京 (-2)-(-9) 7
新知探究
知识点 有理数的减法法则
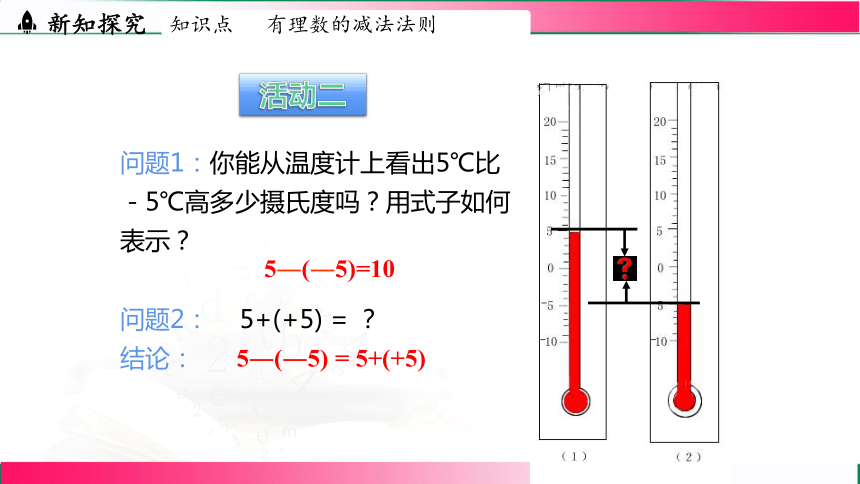
问题1:你能从温度计上看出5℃比-5℃高多少摄氏度吗?用式子如何表示?
问题2: 5+(+5) = ?
结论:
5―(―5)=10
5―(―5) = 5+(+5)
新知探究
知识点 有理数的减法法则
活动二
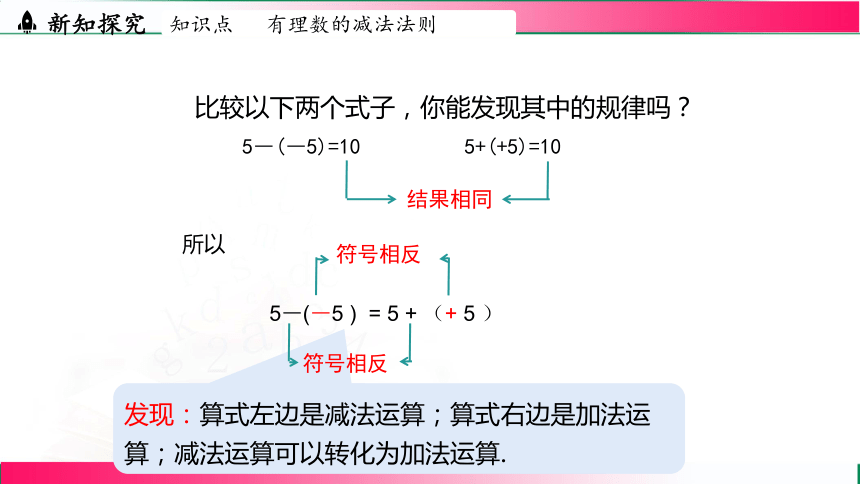
发现:算式左边是减法运算;算式右边是加法运算;减法运算可以转化为加法运算.
符号相反
所以
比较以下两个式子,你能发现其中的规律吗?
5―(―5)=10
5+(+5)=10
5―(―5 ) = 5 + (+ 5 )
结果相同
符号相反
新知探究
知识点 有理数的减法法则
有理数减法法则
减去一个数,等于加上这个数的相反数.
表达式为: a - b=a + (-b)
被减数不变
通过上面的探究可得结论
减号变加号
减数变其相反数
新知探究
知识点 有理数的减法法则
问题3 计算:
(1)6-(-8); (2)(-2)-3;
(3) (-2.8)-(-1.7); (4) 0-4;
(5) 5+(-3)-(-2);(6)(-5)-(-2.4)+(-1).
新知探究
知识点 有理数的减法法则
解:
(1)6-(-8)=6 +(+8)=14;
“-”变“+”
变为相反数
(2)(-2)-3=(-2)+(-3)=-5.
“-”变“+”
变为相反数
(3)(-2.8)-(-1.7)=(-2.8)+1.7=-1.1.
(4) 0-4=0+(-4)=-4.
(5) 5+(-3)-(-2)=5+(-3)+2=4.
(6)(-5)-(-2.4)+(-1)=(-5)+2.4+(-1)=-3.6.
新知探究
知识点 有理数的减法法则
问题4 壮壮家蔬菜大棚内的气温是24℃,此时棚外的气温是-13℃.棚内气温比棚外气温高多少摄氏度?
解:24-(-13)=24+13=37(℃)
答:棚内气温比棚外高37℃.
新知探究
知识点 有理数的减法法则
知识点1有理数的减法法则
1. [新考法·法则运用法]在下列括号内填上适当的数.
(1)(-8)-(-3)=(-8)+( 3 )=( -5 );
(2)(-3)-4=(-3)+( -4 )=( -7 );
(3)0-(-7.5)=0+( 7.5 )=( 7.5 ).
3
-5
-4
-7
7.5
7.5
1
2
3
4
5
6
7
8
9
2. [母题·2023·临沂·教材P29例(3)]计算(-7)-(-5)的结果
是( C )
A. -12 B. 12
C. -2 D. 2
C
1
2
3
4
5
6
7
8
9
3. [2023·陕西]计算:3-5=( B )
A. 2 B. -2
C. 8 D. -8
B
1
2
3
4
5
6
7
8
9
知识点2有理数减法的应用
4. 比0小1的数是( B )
A. 0 B. -1
C. 1 D. ±1
B
1
2
3
4
5
6
7
8
9
5. [2023·潍坊]有理数 a , b , c 在数轴上对应的点的位置如
图所示,下列判断正确的是( C )
A. - c < b
B. a >- c
C. | a - b |= b - a
D. | c - a |= a - c
1
2
3
4
5
6
7
8
9
由数轴可得, a < b <0< c ,| c |<| b |<|
a |,
所以- c > b , a <- c ,| a - b |= b - a ,| c
- a |= c - a .
故选C.
【点拨】
C
【答案】
1
2
3
4
5
6
7
8
9
6. [情境题·生活应用]圆圆想了解某地某天的天气情况,在某
气象网站查询到该地这天的最低气温为-6 ℃,最高气温
为2 ℃(如图),则该地这天的温差(最高气温与最低气温的
差)为( D )
A. -8 ℃ B. -4 ℃
C. 4 ℃ D. 8 ℃
D
【点拨】
温差为2-(-6)=2+6=8(℃).
1
2
3
4
5
6
7
8
9
易错点 将减法转化为加法时,因忽略符号而致错
7. 如果 a =0.5-(-1.5),则 a 的值的对应点落在如图所示
的数轴上的范围是( C )
A. ① B. ②
C. ③ D. 以上都不对
1
2
3
4
5
6
7
8
9
有理数的减法
应用
减去一个数,等于加上这个数的相反数.
减法运算
列式计算
计算步骤
先转换为加法
根据加法法则计算
法则
课堂小结
谢谢观看!
1.6 有理数的减法
第一章 有理数
【2024新教材】2025-2026学年冀教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
第一页:标题页
1.6 有理数的减法
—— 掌握有理数减法法则,实现加减运算转化
(右下角添加授课教师姓名及日期:2025 年 7 月 30 日)
第二页:引入
在生活中,我们常常需要解决类似这样的问题:某地白天的最高气温是\(5 \),夜间的最低气温是\(-3 \),那么白天的最高气温比夜间的最低气温高多少摄氏度呢?这就涉及到有理数的减法运算。有理数的减法和我们之前学过的加法有什么关系呢?这节课我们就来探究有理数的减法法则。
第三页:有理数减法法则的探究
问题 1:计算\(5 - (-3)\),这表示求\(5\)比\(-3\)多多少。
我们可以借助数轴来理解,从表示\(-3\)的点到表示\(5\)的点,需要向右移动\(8\)个单位长度,所以\(5 - (-3)=8\)。
而我们知道\(5+(+3)=8\),由此可以发现\(5 - (-3)=5+(+3)\)。
问题 2:计算\(3 - 5\),表示求\(3\)比\(5\)少多少。
从数轴上看,从表示\(5\)的点到表示\(3\)的点,需要向左移动\(2\)个单位长度,所以\(3 - 5=-2\)。
又因为\(3+(-5)=-2\),所以\(3 - 5=3+(-5)\)。
法则总结:
减去一个数,等于加上这个数的相反数。用字母表示为:\(a - b=a+(-b)\)。
第四页:有理数减法法则的解读
减法运算可以转化为加法运算,转化的关键是 “两变”:
改变运算符号:把减号变为加号。
改变减数的符号:把减数变为它的相反数。
被减数的符号不变,被减数本身也不变。
转化后就可以按照有理数的加法法则进行计算。
实例:
\(10 - 6=10+(-6)=4\)(其中\(6\)的相反数是\(-6\))
\((-8)-(-5)=(-8)+(+5)=-3\)(其中\(-5\)的相反数是\(+5\))
\(0 - 7=0+(-7)=-7\)(其中\(7\)的相反数是\(-7\))
第五页:例题解析(一)
例题 1:计算下列各题
(1)\((-3)-(-5)\);(2)\(0 - 7\);(3)\(7.2 - (-4.8)\);(4)\(-3\frac{1}{2}-5\frac{1}{4}\)。
解:(1)\((-3)-(-5)\)
根据减法法则,转化为加法:\((-3)+(+5)\)
按照加法法则计算:\((-3)+(+5)=2\)
(2)\(0 - 7\)
转化为加法:\(0+(-7)\)
计算得:\(-7\)
(3)\(7.2 - (-4.8)\)
转化为加法:\(7.2+(+4.8)\)
计算得:\(12\)
(4)\(-3\frac{1}{2}-5\frac{1}{4}\)
转化为加法:\(-3\frac{1}{2}+(-5\frac{1}{4})\)
通分计算:\(-3\frac{2}{4}-5\frac{1}{4}=-8\frac{3}{4}\)
第六页:例题解析(二)
例题 2:计算\((-20)-(-5)-(-5)-(-12)\)
解:按照减法法则,将所有的减法转化为加法:\(\begin{align*}
&(-20)-(-5)-(-5)-(-12)\\
=&(-20)+(+5)+(+5)+(+12)
\end{align*}\)
利用加法交换律和结合律进行简便计算:\(\begin{align*}
=&(-20)+[(+5)+(+5)+(+12)]\\
=&(-20)+22\\
=&2
\end{align*}\)
第七页:有理数加减混合运算
有理数的加减混合运算可以统一成加法运算,即省略加号和括号的和的形式。
例如:\(3 - 5 + 7 - 9\)可以写成\(3+(-5)+(+7)+(-9)\),也可简化为\(3 - 5 + 7 - 9\)。
读法:
可以读作 “\(3\)减\(5\)加\(7\)减\(9\)”。
也可以读作 “\(3\)、\(-5\)、\(+7\)、\(-9\)的和”。
例题 3:把\((-8)-(-10)+(-6)-(+4)\)写成省略加号和括号的形式,并计算。
解:先转化为加法:\((-8)+(+10)+(-6)+(-4)\)
省略加号和括号:\(-8 + 10 - 6 - 4\)
计算:\(\begin{align*}
&-8 + 10 - 6 - 4\\
=&( -8 - 6 - 4)+10\\
=&-18 + 10\\
=&-8
\end{align*}\)
第八页:加减混合运算的技巧
统一成加法后运用运算律:将混合运算转化为加法后,利用加法交换律和结合律,把正数、负数分别结合相加,或把能凑整、互为相反数的数结合相加。
按 “和” 的意义读算式:有助于理解算式的本质,方便分组计算。
分步计算:对于复杂的混合运算,可以逐步转化和计算,避免出错。
例题 4:计算\(0.25+\frac{1}{12}-(-\frac{2}{3})-(-\frac{1}{4})+(-\frac{5}{12})\)
解:先转化为加法:\(0.25+\frac{1}{12}+\frac{2}{3}+\frac{1}{4}-\frac{5}{12}\)
把\(0.25\)化为\(\frac{1}{4}\),再分组结合:\(\begin{align*}
=&\left(\frac{1}{4}+\frac{1}{4}\right)+\left(\frac{1}{12}-\frac{5}{12}\right)+\frac{2}{3}\\
=&\frac{1}{2}+\left(-\frac{4}{12}\right)+\frac{2}{3}\\
=&\frac{1}{2}-\frac{1}{3}+\frac{2}{3}\\
=&\frac{1}{2}+\left(-\frac{1}{3}+\frac{2}{3}\right)\\
=&\frac{1}{2}+\frac{1}{3}\\
=&\frac{5}{6}
\end{align*}\)
第九页:实际应用举例
例题 5:某粮库一周内粮食进出库的记录如下(运进为正,运出为负,单位:吨):\(+30\)、\(-25\)、\(-10\)、\(+35\)、\(-20\)、\(-15\)、\(+20\)。
(1)这一周粮库的粮食是增多了还是减少了?增多或减少了多少吨?
(2)若粮库原有粮食\(1000\)吨,则一周后粮库还有多少吨粮食?
解:(1)计算一周内粮食进出库的总和:\(\begin{align*}
&30+(-25)+(-10)+35+(-20)+(-15)+20\\
=&(30 + 35 + 20)+[(-25)+(-10)+(-20)+(-15)]\\
=&85+(-70)\\
=&15
\end{align*}\)
结果为正,说明粮食增多了,增多了\(15\)吨。
(2)原有粮食\(1000\)吨,一周后有:\(1000 + 15=1015\)(吨)
第十页:课堂练习
填空题:
\(6 - 9=\);\((-4)-(-7)=\);\(0 - (-5)=\);\(-8 - 3=\)。
比\(-3\)小\(5\)的数是______;\(7\)比\(-2\)大______。
计算下列各题:
(1)\((-12)-(-18)+(-7)-15\)
(2)\(4.7 - (-8.9)-7.5+(-6)\)
(3)\(-\frac{1}{3}+\frac{3}{4}-\frac{5}{6}+\frac{1}{2}\)
(4)\(\vert -2 \vert - (-3)+1 - \vert 1 - 3 \vert\)
一天早晨的气温是\(-7 \),中午上升了\(11 \),半夜又下降了\(9 \),半夜的气温是多少?
第十一页:课堂小结
有理数减法法则:减去一个数,等于加上这个数的相反数,即\(a - b=a+(-b)\)。
减法运算的转化关键是 “两变”:变运算符号和变减数符号。
有理数加减混合运算可以统一成加法运算,省略加号和括号后可灵活运用加法运算律简化计算。
在解决实际问题时,要先明确正负数的意义,再通过有理数的加减运算求解。
第十二页:作业布置
教材第 XX 页习题 1.6 第 1、2、3、4 题。
计算下列各题:
(1)\(23 - (-76)-36 - (-105)\)
(2)\(-1.5 - (-4\frac{1}{4})+3.75 - (+8\frac{1}{2})\)
(3)\((-\frac{1}{2})+(-\frac{1}{6})-(-\frac{1}{4})-(+\frac{2}{3})\)
(4)\(\vert -3\frac{1}{2} \vert - \vert -\frac{1}{2} \vert + \vert -2 \vert\)
某潜水员先潜入水下\(61\)米,然后又上升\(32\)米,这时潜水员在水下多少米?
已知\(\vert a \vert=5\),\(\vert b \vert=3\),且\(a > b\),求\(a - b\)的值。
思考:若\(a\)、\(b\)为有理数,\(a - b\)一定小于\(a\)吗?举例说明。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.理解有理数减法法则,能熟练进行有理数的减法运算并解决简单的实际问题.
2.从有理数减法中体会加法和减法互为逆运算,以及减法可以转化为加法的转化思想.
学习目标
绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得0.
(3) 一个数与0相加,仍得这个数.
(1) 1 + 6 =
(2)(–2)+(–8) =
(3) (–9)+ 10 =
(4) 5 + (–9) =
(5) (–2.2)+ 2.2 =
(6) 6 + 0 =
(7) 0 + (–8) =
7
–10
1
–4
6
–8
同号两数相加,取相同的符号,并把绝对值相加.
0
计算
课堂导入
下表记录了石家庄2023年12月13日至12月17日每天的气温情况:
月/日 12/13 12/14 12/15 12/16 12/17
最高温度/℃ 8 10 10 5 8
最低温度/℃ 4 2 0 -5 -3
请问12月15日和16日两天的最大温差分别是多少?
解:10-0=10(℃);
5-(-5)=?
课堂导入
活动一
下表是中央气象台发布的2024年1月28日天气预报中,部分城市的最高气温和最低气温的统计表.
(1)分别填写表示各城市温差的算式以及从温度
计上的刻度观察到的温差.
城 市 最高气温(℃) 最低气温(℃)
昆 明 10 6
杭 州 2 -1
北 京 -2 -9
新知探究
知识点 有理数的减法法则
(2)表示温差的算式与观察到的温差之间有什么关系?
表示温差的算式结果与观察到的温差相等
城 市 表示温差的算式 观察到的温差(℃)
昆 明 10-6 4
杭 州 2-(-1) 3
北 京 (-2)-(-9) 7
新知探究
知识点 有理数的减法法则
问题1:你能从温度计上看出5℃比-5℃高多少摄氏度吗?用式子如何表示?
问题2: 5+(+5) = ?
结论:
5―(―5)=10
5―(―5) = 5+(+5)
新知探究
知识点 有理数的减法法则
活动二
发现:算式左边是减法运算;算式右边是加法运算;减法运算可以转化为加法运算.
符号相反
所以
比较以下两个式子,你能发现其中的规律吗?
5―(―5)=10
5+(+5)=10
5―(―5 ) = 5 + (+ 5 )
结果相同
符号相反
新知探究
知识点 有理数的减法法则
有理数减法法则
减去一个数,等于加上这个数的相反数.
表达式为: a - b=a + (-b)
被减数不变
通过上面的探究可得结论
减号变加号
减数变其相反数
新知探究
知识点 有理数的减法法则
问题3 计算:
(1)6-(-8); (2)(-2)-3;
(3) (-2.8)-(-1.7); (4) 0-4;
(5) 5+(-3)-(-2);(6)(-5)-(-2.4)+(-1).
新知探究
知识点 有理数的减法法则
解:
(1)6-(-8)=6 +(+8)=14;
“-”变“+”
变为相反数
(2)(-2)-3=(-2)+(-3)=-5.
“-”变“+”
变为相反数
(3)(-2.8)-(-1.7)=(-2.8)+1.7=-1.1.
(4) 0-4=0+(-4)=-4.
(5) 5+(-3)-(-2)=5+(-3)+2=4.
(6)(-5)-(-2.4)+(-1)=(-5)+2.4+(-1)=-3.6.
新知探究
知识点 有理数的减法法则
问题4 壮壮家蔬菜大棚内的气温是24℃,此时棚外的气温是-13℃.棚内气温比棚外气温高多少摄氏度?
解:24-(-13)=24+13=37(℃)
答:棚内气温比棚外高37℃.
新知探究
知识点 有理数的减法法则
知识点1有理数的减法法则
1. [新考法·法则运用法]在下列括号内填上适当的数.
(1)(-8)-(-3)=(-8)+( 3 )=( -5 );
(2)(-3)-4=(-3)+( -4 )=( -7 );
(3)0-(-7.5)=0+( 7.5 )=( 7.5 ).
3
-5
-4
-7
7.5
7.5
1
2
3
4
5
6
7
8
9
2. [母题·2023·临沂·教材P29例(3)]计算(-7)-(-5)的结果
是( C )
A. -12 B. 12
C. -2 D. 2
C
1
2
3
4
5
6
7
8
9
3. [2023·陕西]计算:3-5=( B )
A. 2 B. -2
C. 8 D. -8
B
1
2
3
4
5
6
7
8
9
知识点2有理数减法的应用
4. 比0小1的数是( B )
A. 0 B. -1
C. 1 D. ±1
B
1
2
3
4
5
6
7
8
9
5. [2023·潍坊]有理数 a , b , c 在数轴上对应的点的位置如
图所示,下列判断正确的是( C )
A. - c < b
B. a >- c
C. | a - b |= b - a
D. | c - a |= a - c
1
2
3
4
5
6
7
8
9
由数轴可得, a < b <0< c ,| c |<| b |<|
a |,
所以- c > b , a <- c ,| a - b |= b - a ,| c
- a |= c - a .
故选C.
【点拨】
C
【答案】
1
2
3
4
5
6
7
8
9
6. [情境题·生活应用]圆圆想了解某地某天的天气情况,在某
气象网站查询到该地这天的最低气温为-6 ℃,最高气温
为2 ℃(如图),则该地这天的温差(最高气温与最低气温的
差)为( D )
A. -8 ℃ B. -4 ℃
C. 4 ℃ D. 8 ℃
D
【点拨】
温差为2-(-6)=2+6=8(℃).
1
2
3
4
5
6
7
8
9
易错点 将减法转化为加法时,因忽略符号而致错
7. 如果 a =0.5-(-1.5),则 a 的值的对应点落在如图所示
的数轴上的范围是( C )
A. ① B. ②
C. ③ D. 以上都不对
1
2
3
4
5
6
7
8
9
有理数的减法
应用
减去一个数,等于加上这个数的相反数.
减法运算
列式计算
计算步骤
先转换为加法
根据加法法则计算
法则
课堂小结
谢谢观看!
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
