1.8.2有理数的乘法运算律 课件(共32张PPT)
文档属性
| 名称 | 1.8.2有理数的乘法运算律 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 00:00:00 | ||
图片预览










文档简介
(共32张PPT)
1.8.2有理数的乘法运算律
第一章 有理数
【2024新教材】2025-2026学年冀教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
第一页:标题页
1.8.2 有理数的乘法运算律
—— 灵活运用运算律简化乘法运算
(右下角添加授课教师姓名及日期:2025 年 7 月 30 日)
第二页:复习回顾
上节课我们学习了有理数的乘法法则,知道两数相乘,同号得正,异号得负,并把绝对值相乘;任何数与 0 相乘都得 0。在有理数乘法中,同样存在一些运算律,它们可以帮助我们简化计算。这节课我们就来学习有理数的乘法运算律及其应用。
第三页:乘法交换律
定义:两个数相乘,交换因数的位置,积相等。
用字母表示为:\(a b = b a\)(可简写成\(ab=ba\))。
实例验证:
计算\((-3) 5\)和\(5 (-3)\):
\((-3) 5=-15\)
\(5 (-3)=-15\)
结果相等,说明\((-3) 5 = 5 (-3)\),验证了乘法交换律在有理数乘法中成立。
应用:在多个有理数相乘时,交换因数的位置,可将便于计算的因数放在一起,简化运算。
第四页:乘法结合律
定义:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积相等。
用字母表示为:\((a b) c = a (b c)\)(可简写成\((ab)c=a(bc)\))。
实例验证:
计算\([(-2) (-3)] 4\)和\((-2) [(-3) 4]\):
\([(-2) (-3)] 4=6 4 = 24\)
\((-2) [(-3) 4]=(-2) (-12)=24\)
结果相等,说明\([(-2) (-3)] 4=(-2) [(-3) 4]\),验证了乘法结合律在有理数乘法中成立。
应用:当三个或三个以上有理数相乘时,通过结合其中两个数,可使计算更简便(如结合能凑整的数)。
第五页:乘法分配律
定义:一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加。
用字母表示为:\(a (b + c)=a b + a c\)(可简写成\(a(b + c)=ab+ac\))。
实例验证:
计算\((-4) (3 + 5)\)和\((-4) 3+(-4) 5\):
\((-4) (3 + 5)=(-4) 8=-32\)
\((-4) 3+(-4) 5=-12+(-20)=-32\)
结果相等,说明\((-4) (3 + 5)=(-4) 3+(-4) 5\),验证了乘法分配律在有理数乘法中成立。
逆用:\(ab + ac=a(b + c)\),即两个积相加,若有相同的因数,可提取这个因数,简化计算。
第六页:例题解析(一)—— 运用交换律和结合律
例题 1:计算下列各题
(1)\((-10) (-\frac{1}{3}) (-0.1) 6\);(2)\((-4) (-7) (-25)\)。
解:(1)\((-10) (-\frac{1}{3}) (-0.1) 6\)
观察到\((-10)\)与\((-0.1)\)相乘、\((-\frac{1}{3})\)与\(6\)相乘可简化计算,运用交换律和结合律:\(\begin{align*}
=&[(-10) (-0.1)] [(-\frac{1}{3}) 6]\\
=&1 (-2)\\
=&-2
\end{align*}\)
(2)\((-4) (-7) (-25)\)
观察到\((-4)\)与\((-25)\)相乘可得到 100,运用交换律:\(\begin{align*}
=&(-4) (-25) (-7)\\
=&100 (-7)\\
=&-700
\end{align*}\)
第七页:例题解析(二)—— 运用分配律
例题 2:计算下列各题
(1)\((\frac{1}{4}-\frac{1}{2}+\frac{1}{6}) (-12)\);(2)\((-100) (0.7-\frac{3}{10}-\frac{4}{5}+0.03)\)。
解:(1)\((\frac{1}{4}-\frac{1}{2}+\frac{1}{6}) (-12)\)
运用分配律,将\(-12\)分别与括号内的每一项相乘:\(\begin{align*}
=&\frac{1}{4} (-12)-\frac{1}{2} (-12)+\frac{1}{6} (-12)\\
=&-3 + 6-2\\
=&1
\end{align*}\)
(2)\((-100) (0.7-\frac{3}{10}-\frac{4}{5}+0.03)\)
先将分数化为小数:\(\frac{3}{10}=0.3\),\(\frac{4}{5}=0.8\),再运用分配律:\(\begin{align*}
=&(-100) 0.7-(-100) 0.3-(-100) 0.8+(-100) 0.03\\
=&-70 + 30 + 80-3\\
=&37
\end{align*}\)
第八页:例题解析(三)—— 分配律的逆用
例题 3:计算\(3.14 (-4.5)+3.14 (-5.5)\)
解:观察到两项中都有相同的因数\(3.14\),逆用分配律:\(\begin{align*}
=&3.14 [(-4.5)+(-5.5)]\\
=&3.14 (-10)\\
=&-31.4
\end{align*}\)
例题 4:计算\(-99\frac{71}{72} 36\)
解:将带分数拆分为整数和分数的差,再运用分配律:\(\begin{align*}
=&-(100-\frac{1}{72}) 36\\
=&-100 36+\frac{1}{72} 36\\
=&-3600 + 0.5\\
=&-3599.5
\end{align*}\)
第九页:运用乘法运算律的注意事项
运用交换律和结合律时,要连同因数的符号一起交换或结合,避免符号错误。
例如:\((-2) (-3) (-4)=(-2) [(-3) (-4)]\),不能忽略每个因数的负号。
运用分配律时,要将括号外的数分别与括号内的每一项相乘,不能漏乘任何一项,且要注意符号的变化。
例如:\(a (b - c)=ab-ac\),不要误写成\(ab - c\)。
对于复杂的算式,要先观察数的特点,选择合适的运算律,以达到简化计算的目的。
多个有理数相乘时,可先根据负因数的个数确定积的符号,再运用运算律计算绝对值的乘积。
第十页:课堂练习
填空题:
\( (-5) 8 (-0.2)=\);\((\frac{1}{3}-\frac{1}{6}) 12=\)。
运用乘法分配律计算\(-3 (4 - 6)\),结果为______。
若\(a b = 0\),则\(a\)、\(b\)的关系是______。
计算下列各题:
(1)\((-8) (-12) (-0.125) (-\frac{1}{3})\)
(2)\((\frac{3}{4}-\frac{5}{6}+\frac{7}{12}) (-36)\)
(3)\(7 (-3.6)+7 (-6.4)\)
(4)\(99\frac{17}{18} (-9)\)
第十一页:课堂小结
有理数乘法的运算律包括:
乘法交换律:\(ab = ba\)
乘法结合律:\((ab)c=a(bc)\)
乘法分配律:\(a(b + c)=ab + ac\)(逆用:\(ab + ac=a(b + c)\))
运用这些运算律可以简化有理数乘法的计算,尤其是在多个数相乘或有括号的情况下。
运用运算律时要注意符号的处理,避免漏乘或符号错误,同时要根据数的特点灵活选择合适的运算律。
第十二页:作业布置
教材第 XX 页习题 1.8 第 4、5、6 题。
计算下列各题:
(1)\((-25) (-8) (-4) 125\)
(2)\((-\frac{1}{2}+\frac{2}{3}-\frac{1}{4}) (-24)\)
(3)\(1.25 (-3.2) (-0.8)\)
(4)\(6.8 (-5)+6.8 (-12)+6.8 17\)
(5)\(-101 190 + 101 (-10)\)
已知\(a = -3\),\(b = 4\),\(c = -5\),求\(a (b + c)\)和\(a b + a c\)的值,观察它们的关系,验证乘法分配律。
思考:如何运用乘法运算律计算\(1 + 2 + 3 + \cdots + 100\)?(提示:可利用乘法分配律的思想)
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.掌握有理数的乘法运算律,能灵活运用乘法运算律
简化运算.
2.能利用有理数的乘法解决简单的实际问题,形成
应用意识.
学习目标
3.小学时候大家学过乘法的那些运算律?
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数同0相乘,仍得0.
先确定积的符号; 再计算绝对值的积.
乘法交换律、乘法结合律、乘法对加法的分配律
1.有理数乘法法则是什么?
2.如何进行有理数的乘法运算?
回顾
课堂导入
1.填空:
(1) (-2)×4=_______ , 4×(-2)=________.
(2) [(-2)×(-3)×(-4)=_____×(-4)=______ ,
(-2)×[(-3)×(-4)]=(-2)×_____=_______.
问题1 在有理数的范围内,乘法的交换律和结合律是否仍然适用?
-8
-8
6
-24
12
-24
探究
乘法交换律仍然成立
乘法结合律仍然成立
新知探究
知识点 有理数乘法的运算律
一般地,有理数的乘法有以下运算律:
乘法交换律:ab=ba.
即,两个数相乘,交换因数的位置,积不变.
乘法结合律:(a×b)×c=a×(b×c).
即对于三个有理数相乘,可以先把前面两个数相乘,
再把结果与第三个数相乘;或者先把后两个数相乘,再
把第一个数与所得结果相乘,积不变.
归纳
新知探究
知识点 有理数乘法的运算律
问题2 计算
解:
运用交换律
运用结合律
新知探究
知识点 有理数乘法的运算律
问题3 在有理数的范围内,乘法对加法的分配律是否仍然适用?
填空
(1) (-6)×[4+(-9)]=(-6)×______=_______,
(-6)×4+(-6)×(-9)=____+____=_______;
(2) 5×[(-8)+(-3)]=5×_______=_________.
5×(-8)+5×(-3)=____+____=________.
-5
30
-24
54
30
-11
-55
-40
-15
-55
乘法对加法的分配律(简称分配律)
仍然成立
新知探究
知识点 有理数乘法的运算律
一般地,我们可以得出:
乘法对加法的分配律(简称分配律): a(b+c)=ab+ac.
即一个数与两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
归纳
新知探究
知识点 有理数乘法的运算律
问题4 计算
解:
新知探究
知识点 有理数乘法的运算律
1.计算:
(1)1×2×3×4= ,
(2)(-1)×2×3×4= ,
(3)(-1)×(-2)×3×4= ,
(4)(-1)×(-2)×(-3)×4= ,
(5)(-1)×(-2)×(-3)×(-4)= ,
24
-24
24
-24
24
探究
多个有理数相乘的符号法则
新知探究
知识点 有理数乘法的运算律
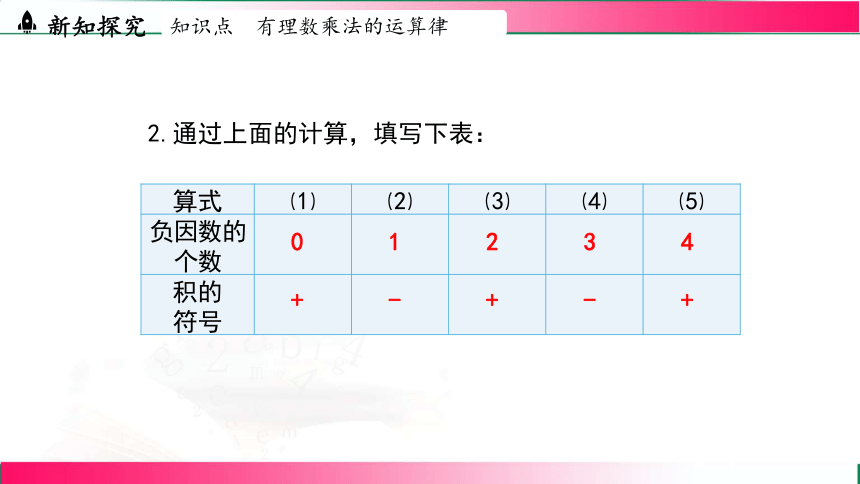
2.通过上面的计算,填写下表:
算式 ⑴ ⑵ ⑶ ⑷ ⑸
负因数的个数
积的 符号
0
+
1
-
2
+
3
-
4
+
新知探究
知识点 有理数乘法的运算律
3.根据表中填写的结果,探究几个不为0的数相乘时,积的符号与负因数个数之间有什么关系?
几个不为0的数相乘,积的符号由_____________ 决定.
当负因数有_____ 个时,积为负;
当负因数有_____ 个时,积为正.
几个数相乘,如果有一个因数为0,_________
负因数的个数
奇数
偶数
奇负偶正
积就为0.
新知探究
知识点 有理数乘法的运算律
问题5 计算
解:
先确定积的符号,再把绝对值相乘.
新知探究
知识点 有理数乘法的运算律
1.(-0.125)×15×(-8)×-0.8=[(-0.125)×(-8)]×15×-0.8的运算中用到了( )
A.乘法结合律 B.乘法交换律
C.分配律 D.乘法交换律和结合律
D
随堂练习
2.算式 -25×14+18×14-39×(-14)=(-25+18+39)×14是逆用了( )
A.加法交换律 B.乘法交换律
C.乘法结合律 D.乘法对加法的分配律
D
随堂练习
3.有2021个有理数相乘,如果积为0,那么这2021个有理数( )
A.全部为0 B.只有一个因数为0
C.至少有一个为0 D.有两个数互为相反数
C
随堂练习
4.下列计算(-55)×99+(-44)×99-99正确的是( )
A.原式=99×(-55-44)=-9 801
B.原式=99×(-55-44+1)=-9 702
C.原式=99×(-55-44-1)=-9 900
D.原式=99×(-55-44-99)=-19 602
C
随堂练习
5.计算
解:
随堂练习
随堂练习
6.计算:
(1) (2)
解:(1)原式
(2)原式
随堂练习
知识点1 乘法运算律
1. 在算式变形:1.25× ×(-8)=1.25×(-8)×
中,运用了( C )
A. 分配律 B. 乘法交换律和分配律
C. 乘法交换律 D. 分配律和乘法结合律
C
1
2
3
4
5
6
2. (-0.125)×15×(-8)× =[(-0.125)×(-8)]×
,运算中没有运用的运算律是( C )
A. 乘法交换律
B. 乘法结合律
C. 分配律
D. 乘法交换律和乘法结合律
C
1
2
3
4
5
6
知识点2 乘法运算律的应用
3. 计算71 ×(-8)最简单的方法是( C )
C
1
2
3
4
5
6
易错点 用分配律时易漏乘或弄错符号
4. (荣德原创题)用分配律计算(-3)× 的过程正
确的是( A )
1
2
3
4
5
6
【点拨】
利用分配律最易出现的两种错误是漏乘和计算过程中
出现符号错误.
A
【答案】
1
2
3
4
5
6
利用有理数的乘法运算律进行巧算
5. [2024·邢台信都区模拟]如图,请你参考老师的讲解,用运
算律简便计算:
(1)999×(-15);
【解】原式=(1 000-1)×(-15)=-15 000+15=-14 985.
1
2
3
4
5
6
(2)999×118 +999× -999×18 .
【解】原式=999×[118 +(- )-18 ]=999×100
=99 900.
【点拨】
对于分配律,可以正用,也可以逆用.
1
2
3
4
5
6
6. [新考法·阅读类比法]阅读材料,回答下列问题:
× = × =1;
× × × = × × × =
× =1×1=1.
根据以上信息,请求出下式的结果:
1
2
3
4
5
6
× × ×…× × ×
× ×…× .
【解】原式= × × ×…× × × × ×…× =
( × )× ×( × )×…× =
1×1×1×…×1=1.
1
2
3
4
5
6
有理数乘法的运算律
乘法的运算律
多个有理数相乘的符号法则
乘法的交换律
______________
乘法的结合律
__________________
乘法对加法的分配律
_________________
ab=ba.
(ab)c=a(bc).
a(b+c)=ab+bc.
有一个因数为0时,积就为0.
几个不等于0的数相乘,当负因数有____个时,积为__;当负因数有____个时,积为___.
奇数
负
偶数
正
谢谢观看!
1.8.2有理数的乘法运算律
第一章 有理数
【2024新教材】2025-2026学年冀教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
第一页:标题页
1.8.2 有理数的乘法运算律
—— 灵活运用运算律简化乘法运算
(右下角添加授课教师姓名及日期:2025 年 7 月 30 日)
第二页:复习回顾
上节课我们学习了有理数的乘法法则,知道两数相乘,同号得正,异号得负,并把绝对值相乘;任何数与 0 相乘都得 0。在有理数乘法中,同样存在一些运算律,它们可以帮助我们简化计算。这节课我们就来学习有理数的乘法运算律及其应用。
第三页:乘法交换律
定义:两个数相乘,交换因数的位置,积相等。
用字母表示为:\(a b = b a\)(可简写成\(ab=ba\))。
实例验证:
计算\((-3) 5\)和\(5 (-3)\):
\((-3) 5=-15\)
\(5 (-3)=-15\)
结果相等,说明\((-3) 5 = 5 (-3)\),验证了乘法交换律在有理数乘法中成立。
应用:在多个有理数相乘时,交换因数的位置,可将便于计算的因数放在一起,简化运算。
第四页:乘法结合律
定义:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积相等。
用字母表示为:\((a b) c = a (b c)\)(可简写成\((ab)c=a(bc)\))。
实例验证:
计算\([(-2) (-3)] 4\)和\((-2) [(-3) 4]\):
\([(-2) (-3)] 4=6 4 = 24\)
\((-2) [(-3) 4]=(-2) (-12)=24\)
结果相等,说明\([(-2) (-3)] 4=(-2) [(-3) 4]\),验证了乘法结合律在有理数乘法中成立。
应用:当三个或三个以上有理数相乘时,通过结合其中两个数,可使计算更简便(如结合能凑整的数)。
第五页:乘法分配律
定义:一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加。
用字母表示为:\(a (b + c)=a b + a c\)(可简写成\(a(b + c)=ab+ac\))。
实例验证:
计算\((-4) (3 + 5)\)和\((-4) 3+(-4) 5\):
\((-4) (3 + 5)=(-4) 8=-32\)
\((-4) 3+(-4) 5=-12+(-20)=-32\)
结果相等,说明\((-4) (3 + 5)=(-4) 3+(-4) 5\),验证了乘法分配律在有理数乘法中成立。
逆用:\(ab + ac=a(b + c)\),即两个积相加,若有相同的因数,可提取这个因数,简化计算。
第六页:例题解析(一)—— 运用交换律和结合律
例题 1:计算下列各题
(1)\((-10) (-\frac{1}{3}) (-0.1) 6\);(2)\((-4) (-7) (-25)\)。
解:(1)\((-10) (-\frac{1}{3}) (-0.1) 6\)
观察到\((-10)\)与\((-0.1)\)相乘、\((-\frac{1}{3})\)与\(6\)相乘可简化计算,运用交换律和结合律:\(\begin{align*}
=&[(-10) (-0.1)] [(-\frac{1}{3}) 6]\\
=&1 (-2)\\
=&-2
\end{align*}\)
(2)\((-4) (-7) (-25)\)
观察到\((-4)\)与\((-25)\)相乘可得到 100,运用交换律:\(\begin{align*}
=&(-4) (-25) (-7)\\
=&100 (-7)\\
=&-700
\end{align*}\)
第七页:例题解析(二)—— 运用分配律
例题 2:计算下列各题
(1)\((\frac{1}{4}-\frac{1}{2}+\frac{1}{6}) (-12)\);(2)\((-100) (0.7-\frac{3}{10}-\frac{4}{5}+0.03)\)。
解:(1)\((\frac{1}{4}-\frac{1}{2}+\frac{1}{6}) (-12)\)
运用分配律,将\(-12\)分别与括号内的每一项相乘:\(\begin{align*}
=&\frac{1}{4} (-12)-\frac{1}{2} (-12)+\frac{1}{6} (-12)\\
=&-3 + 6-2\\
=&1
\end{align*}\)
(2)\((-100) (0.7-\frac{3}{10}-\frac{4}{5}+0.03)\)
先将分数化为小数:\(\frac{3}{10}=0.3\),\(\frac{4}{5}=0.8\),再运用分配律:\(\begin{align*}
=&(-100) 0.7-(-100) 0.3-(-100) 0.8+(-100) 0.03\\
=&-70 + 30 + 80-3\\
=&37
\end{align*}\)
第八页:例题解析(三)—— 分配律的逆用
例题 3:计算\(3.14 (-4.5)+3.14 (-5.5)\)
解:观察到两项中都有相同的因数\(3.14\),逆用分配律:\(\begin{align*}
=&3.14 [(-4.5)+(-5.5)]\\
=&3.14 (-10)\\
=&-31.4
\end{align*}\)
例题 4:计算\(-99\frac{71}{72} 36\)
解:将带分数拆分为整数和分数的差,再运用分配律:\(\begin{align*}
=&-(100-\frac{1}{72}) 36\\
=&-100 36+\frac{1}{72} 36\\
=&-3600 + 0.5\\
=&-3599.5
\end{align*}\)
第九页:运用乘法运算律的注意事项
运用交换律和结合律时,要连同因数的符号一起交换或结合,避免符号错误。
例如:\((-2) (-3) (-4)=(-2) [(-3) (-4)]\),不能忽略每个因数的负号。
运用分配律时,要将括号外的数分别与括号内的每一项相乘,不能漏乘任何一项,且要注意符号的变化。
例如:\(a (b - c)=ab-ac\),不要误写成\(ab - c\)。
对于复杂的算式,要先观察数的特点,选择合适的运算律,以达到简化计算的目的。
多个有理数相乘时,可先根据负因数的个数确定积的符号,再运用运算律计算绝对值的乘积。
第十页:课堂练习
填空题:
\( (-5) 8 (-0.2)=\);\((\frac{1}{3}-\frac{1}{6}) 12=\)。
运用乘法分配律计算\(-3 (4 - 6)\),结果为______。
若\(a b = 0\),则\(a\)、\(b\)的关系是______。
计算下列各题:
(1)\((-8) (-12) (-0.125) (-\frac{1}{3})\)
(2)\((\frac{3}{4}-\frac{5}{6}+\frac{7}{12}) (-36)\)
(3)\(7 (-3.6)+7 (-6.4)\)
(4)\(99\frac{17}{18} (-9)\)
第十一页:课堂小结
有理数乘法的运算律包括:
乘法交换律:\(ab = ba\)
乘法结合律:\((ab)c=a(bc)\)
乘法分配律:\(a(b + c)=ab + ac\)(逆用:\(ab + ac=a(b + c)\))
运用这些运算律可以简化有理数乘法的计算,尤其是在多个数相乘或有括号的情况下。
运用运算律时要注意符号的处理,避免漏乘或符号错误,同时要根据数的特点灵活选择合适的运算律。
第十二页:作业布置
教材第 XX 页习题 1.8 第 4、5、6 题。
计算下列各题:
(1)\((-25) (-8) (-4) 125\)
(2)\((-\frac{1}{2}+\frac{2}{3}-\frac{1}{4}) (-24)\)
(3)\(1.25 (-3.2) (-0.8)\)
(4)\(6.8 (-5)+6.8 (-12)+6.8 17\)
(5)\(-101 190 + 101 (-10)\)
已知\(a = -3\),\(b = 4\),\(c = -5\),求\(a (b + c)\)和\(a b + a c\)的值,观察它们的关系,验证乘法分配律。
思考:如何运用乘法运算律计算\(1 + 2 + 3 + \cdots + 100\)?(提示:可利用乘法分配律的思想)
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.掌握有理数的乘法运算律,能灵活运用乘法运算律
简化运算.
2.能利用有理数的乘法解决简单的实际问题,形成
应用意识.
学习目标
3.小学时候大家学过乘法的那些运算律?
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数同0相乘,仍得0.
先确定积的符号; 再计算绝对值的积.
乘法交换律、乘法结合律、乘法对加法的分配律
1.有理数乘法法则是什么?
2.如何进行有理数的乘法运算?
回顾
课堂导入
1.填空:
(1) (-2)×4=_______ , 4×(-2)=________.
(2) [(-2)×(-3)×(-4)=_____×(-4)=______ ,
(-2)×[(-3)×(-4)]=(-2)×_____=_______.
问题1 在有理数的范围内,乘法的交换律和结合律是否仍然适用?
-8
-8
6
-24
12
-24
探究
乘法交换律仍然成立
乘法结合律仍然成立
新知探究
知识点 有理数乘法的运算律
一般地,有理数的乘法有以下运算律:
乘法交换律:ab=ba.
即,两个数相乘,交换因数的位置,积不变.
乘法结合律:(a×b)×c=a×(b×c).
即对于三个有理数相乘,可以先把前面两个数相乘,
再把结果与第三个数相乘;或者先把后两个数相乘,再
把第一个数与所得结果相乘,积不变.
归纳
新知探究
知识点 有理数乘法的运算律
问题2 计算
解:
运用交换律
运用结合律
新知探究
知识点 有理数乘法的运算律
问题3 在有理数的范围内,乘法对加法的分配律是否仍然适用?
填空
(1) (-6)×[4+(-9)]=(-6)×______=_______,
(-6)×4+(-6)×(-9)=____+____=_______;
(2) 5×[(-8)+(-3)]=5×_______=_________.
5×(-8)+5×(-3)=____+____=________.
-5
30
-24
54
30
-11
-55
-40
-15
-55
乘法对加法的分配律(简称分配律)
仍然成立
新知探究
知识点 有理数乘法的运算律
一般地,我们可以得出:
乘法对加法的分配律(简称分配律): a(b+c)=ab+ac.
即一个数与两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
归纳
新知探究
知识点 有理数乘法的运算律
问题4 计算
解:
新知探究
知识点 有理数乘法的运算律
1.计算:
(1)1×2×3×4= ,
(2)(-1)×2×3×4= ,
(3)(-1)×(-2)×3×4= ,
(4)(-1)×(-2)×(-3)×4= ,
(5)(-1)×(-2)×(-3)×(-4)= ,
24
-24
24
-24
24
探究
多个有理数相乘的符号法则
新知探究
知识点 有理数乘法的运算律
2.通过上面的计算,填写下表:
算式 ⑴ ⑵ ⑶ ⑷ ⑸
负因数的个数
积的 符号
0
+
1
-
2
+
3
-
4
+
新知探究
知识点 有理数乘法的运算律
3.根据表中填写的结果,探究几个不为0的数相乘时,积的符号与负因数个数之间有什么关系?
几个不为0的数相乘,积的符号由_____________ 决定.
当负因数有_____ 个时,积为负;
当负因数有_____ 个时,积为正.
几个数相乘,如果有一个因数为0,_________
负因数的个数
奇数
偶数
奇负偶正
积就为0.
新知探究
知识点 有理数乘法的运算律
问题5 计算
解:
先确定积的符号,再把绝对值相乘.
新知探究
知识点 有理数乘法的运算律
1.(-0.125)×15×(-8)×-0.8=[(-0.125)×(-8)]×15×-0.8的运算中用到了( )
A.乘法结合律 B.乘法交换律
C.分配律 D.乘法交换律和结合律
D
随堂练习
2.算式 -25×14+18×14-39×(-14)=(-25+18+39)×14是逆用了( )
A.加法交换律 B.乘法交换律
C.乘法结合律 D.乘法对加法的分配律
D
随堂练习
3.有2021个有理数相乘,如果积为0,那么这2021个有理数( )
A.全部为0 B.只有一个因数为0
C.至少有一个为0 D.有两个数互为相反数
C
随堂练习
4.下列计算(-55)×99+(-44)×99-99正确的是( )
A.原式=99×(-55-44)=-9 801
B.原式=99×(-55-44+1)=-9 702
C.原式=99×(-55-44-1)=-9 900
D.原式=99×(-55-44-99)=-19 602
C
随堂练习
5.计算
解:
随堂练习
随堂练习
6.计算:
(1) (2)
解:(1)原式
(2)原式
随堂练习
知识点1 乘法运算律
1. 在算式变形:1.25× ×(-8)=1.25×(-8)×
中,运用了( C )
A. 分配律 B. 乘法交换律和分配律
C. 乘法交换律 D. 分配律和乘法结合律
C
1
2
3
4
5
6
2. (-0.125)×15×(-8)× =[(-0.125)×(-8)]×
,运算中没有运用的运算律是( C )
A. 乘法交换律
B. 乘法结合律
C. 分配律
D. 乘法交换律和乘法结合律
C
1
2
3
4
5
6
知识点2 乘法运算律的应用
3. 计算71 ×(-8)最简单的方法是( C )
C
1
2
3
4
5
6
易错点 用分配律时易漏乘或弄错符号
4. (荣德原创题)用分配律计算(-3)× 的过程正
确的是( A )
1
2
3
4
5
6
【点拨】
利用分配律最易出现的两种错误是漏乘和计算过程中
出现符号错误.
A
【答案】
1
2
3
4
5
6
利用有理数的乘法运算律进行巧算
5. [2024·邢台信都区模拟]如图,请你参考老师的讲解,用运
算律简便计算:
(1)999×(-15);
【解】原式=(1 000-1)×(-15)=-15 000+15=-14 985.
1
2
3
4
5
6
(2)999×118 +999× -999×18 .
【解】原式=999×[118 +(- )-18 ]=999×100
=99 900.
【点拨】
对于分配律,可以正用,也可以逆用.
1
2
3
4
5
6
6. [新考法·阅读类比法]阅读材料,回答下列问题:
× = × =1;
× × × = × × × =
× =1×1=1.
根据以上信息,请求出下式的结果:
1
2
3
4
5
6
× × ×…× × ×
× ×…× .
【解】原式= × × ×…× × × × ×…× =
( × )× ×( × )×…× =
1×1×1×…×1=1.
1
2
3
4
5
6
有理数乘法的运算律
乘法的运算律
多个有理数相乘的符号法则
乘法的交换律
______________
乘法的结合律
__________________
乘法对加法的分配律
_________________
ab=ba.
(ab)c=a(bc).
a(b+c)=ab+bc.
有一个因数为0时,积就为0.
几个不等于0的数相乘,当负因数有____个时,积为__;当负因数有____个时,积为___.
奇数
负
偶数
正
谢谢观看!
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
