2.7.2余角和补角 课件(共34张PPT)
文档属性
| 名称 | 2.7.2余角和补角 课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 00:00:00 | ||
图片预览




文档简介
(共34张PPT)
2.7.2余角和补角
第二章 几何图形的初步认识
【2024新教材】2025-2026学年冀教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
第一页:标题页
2.7.2 余角和补角
—— 理解互余与互补的关系
(右下角添加授课教师姓名及日期)
第二页:引入
在角的世界里,有些角之间存在着特殊的数量关系,比如两个角的和是一个直角,或者两个角的和是一个平角。这些特殊的关系在我们解决几何问题时经常会用到,它们就是我们今天要学习的余角和补角。通过本节课的学习,我们将掌握余角和补角的定义、性质以及它们在实际计算中的应用。
第三页:余角的定义
定义:如果两个角的和等于\(90 °\)(直角),就说这两个角互为余角,简称互余。其中一个角叫做另一个角的余角。
数学表达式:若\(\angle 1 + \angle 2 = 90 °\),则\(\angle 1\)与\(\angle 2\)互为余角,即\(\angle 1\)是\(\angle 2\)的余角,\(\angle 2\)也是\(\angle 1\)的余角。
实例:
\(\angle A = 30 °\),\(\angle B = 60 °\),因为\(30 ° + 60 ° = 90 °\),所以\(\angle A\)与\(\angle B\)互为余角。
一个直角被分成两个角,这两个角互为余角。
注意:
互余是指两个角之间的关系,不能单独说一个角是余角。
两个角互余,只与它们的度数之和有关,与它们的位置无关。
第四页:补角的定义
定义:如果两个角的和等于\(180 °\)(平角),就说这两个角互为补角,简称互补。其中一个角叫做另一个角的补角。
数学表达式:若\(\angle 3 + \angle 4 = 180 °\),则\(\angle 3\)与\(\angle 4\)互为补角,即\(\angle 3\)是\(\angle 4\)的补角,\(\angle 4\)也是\(\angle 3\)的补角。
实例:
\(\angle C = 110 °\),\(\angle D = 70 °\),因为\(110 ° + 70 ° = 180 °\),所以\(\angle C\)与\(\angle D\)互为补角。
一个平角被分成两个角,这两个角互为补角。
注意:
互补同样是指两个角之间的关系,不能单独说一个角是补角。
两个角互补,只与它们的度数之和有关,与它们的位置无关。
第五页:余角和补角的性质
性质 1:同角(或等角)的余角相等。
若\(\angle 1 + \angle 2 = 90 °\),\(\angle 1 + \angle 3 = 90 °\),则\(\angle 2 = \angle 3\)(同角的余角相等)。
若\(\angle 1 + \angle 2 = 90 °\),\(\angle 3 + \angle 4 = 90 °\),且\(\angle 1 = \angle 3\),则\(\angle 2 = \angle 4\)(等角的余角相等)。
性质 2:同角(或等角)的补角相等。
若\(\angle 5 + \angle 6 = 180 °\),\(\angle 5 + \angle 7 = 180 °\),则\(\angle 6 = \angle 7\)(同角的补角相等)。
若\(\angle 5 + \angle 6 = 180 °\),\(\angle 7 + \angle 8 = 180 °\),且\(\angle 5 = \angle 7\),则\(\angle 6 = \angle 8\)(等角的补角相等)。
实例:
若\(\angle \alpha = 40 °\),则\(\angle \alpha\)的余角是\(50 °\),如果另一个角\(\angle \beta\)的余角也是\(50 °\),那么\(\angle \alpha = \angle \beta\),这体现了等角的余角相等。
若\(\angle \gamma = 120 °\),则\(\angle \gamma\)的补角是\(60 °\),如果\(\angle \delta\)的补角也是\(60 °\),那么\(\angle \gamma = \angle \delta\),这体现了等角的补角相等。
第六页:例题解析(一)—— 余角和补角的基本计算
例题 1:已知一个角的度数是\(35 °\),求它的余角和补角的度数。
解:这个角的余角的度数为\(90 ° - 35 ° = 55 °\)。
这个角的补角的度数为\(180 ° - 35 ° = 145 °\)。
例题 2:一个角的补角是它的 3 倍,求这个角的度数。
解:设这个角的度数为\(x\),则它的补角的度数为\(180 ° - x\)。
根据题意可得:\(180 ° - x = 3x\)
移项得:\(3x + x = 180 °\)
合并同类项得:\(4x = 180 °\)
解得:\(x = 45 °\)
所以这个角的度数是\(45 °\)。
第七页:例题解析(二)—— 余角和补角性质的应用
例题 3:已知\(\angle 1\)与\(\angle 2\)互为余角,\(\angle 3\)与\(\angle 4\)互为余角,且\(\angle 1 = \angle 3\),求证:\(\angle 2 = \angle 4\)。
证明:因为\(\angle 1\)与\(\angle 2\)互为余角,所以\(\angle 1 + \angle 2 = 90 °\),即\(\angle 2 = 90 ° - \angle 1\)。
因为\(\angle 3\)与\(\angle 4\)互为余角,所以\(\angle 3 + \angle 4 = 90 °\),即\(\angle 4 = 90 ° - \angle 3\)。
又因为\(\angle 1 = \angle 3\),所以\(90 ° - \angle 1 = 90 ° - \angle 3\),即\(\angle 2 = \angle 4\)。
例题 4:如图,点\(O\)在直线\(AB\)上,\(OC\)是射线,\(\angle AOC = 50 °\),求\(\angle BOC\)的余角的度数。
解:因为点\(O\)在直线\(AB\)上,所以\(\angle AOC + \angle BOC = 180 °\),则\(\angle BOC = 180 ° - 50 ° = 130 °\)。
设\(\angle BOC\)的余角为\(\angle x\),则\(\angle x + 130 ° = 90 °\),显然不成立,说明\(\angle BOC\)是钝角,没有余角?不,错误在于余角是指两个角的和为\(90 °\),所以\(\angle BOC\)的余角应该是\(90 ° - (180 ° - \angle AOC)\)?不,正确解法:\(\angle BOC = 130 °\),它的余角不存在,因为余角要求两个角的和为\(90 °\),而\(130 °>90 °\),所以此题应改为求\(\angle AOC\)的余角,\(\angle AOC = 50 °\),其余角为\(40 °\),或者题目中\(\angle AOC = 140 °\),则\(\angle BOC = 40 °\),其余角为\(50 °\),此处修正题目为\(\angle AOC = 40 °\),则\(\angle BOC = 140 °\),显然仍不对,正确例题应为:点\(O\)在直线\(AB\)上,\(OC\)是射线,\(\angle AOC = 40 °\),求\(\angle BOC\)的补角的度数,\(\angle BOC = 140 °\),补角为\(40 °\),但更合适的例题为:
例题 4:已知\(\angle \alpha\)与\(\angle \beta\)互为补角,\(\angle \alpha\)比\(\angle \beta\)大\(30 °\),求\(\angle \alpha\)和\(\angle \beta\)的度数。
解:设\(\angle \beta\)的度数为\(x\),则\(\angle \alpha\)的度数为\(x + 30 °\)。
因为\(\angle \alpha\)与\(\angle \beta\)互为补角,所以\(\angle \alpha + \angle \beta = 180 °\),即\((x + 30 °) + x = 180 °\)。
解得\(2x = 150 °\),\(x = 75 °\),则\(\angle \alpha = 75 ° + 30 ° = 105 °\)。
所以\(\angle \alpha = 105 °\),\(\angle \beta = 75 °\)。
第八页:课堂练习
填空题:
若\(\angle A = 25 °\),则它的余角是______°,补角是______°。
一个角的余角是\(40 °\),则这个角的度数是______°,它的补角是______°。
若\(\angle 1\)与\(\angle 2\)互为余角,\(\angle 2 = 35 °\),则\(\angle 1=\)______°。
选择题:
下列说法正确的是( )
A. 一个角的余角一定是锐角
B. 一个角的补角一定是钝角
C. 若\(\angle 1 + \angle 2 + \angle 3 = 90 °\),则\(\angle 1\)、\(\angle 2\)、\(\angle 3\)互为余角
D. 若\(\angle \alpha\)与\(\angle \beta\)互为补角,则\(\angle \alpha\)与\(\angle \beta\)一定有一个是锐角,一个是钝角
已知\(\angle \alpha = 50 °\),则\(\angle \alpha\)的余角的补角是( )
A. \(40 °\) B. \(140 °\) C. \(50 °\) D. \(130 °\)
解答题:
(1)一个角的余角比它的补角的\(\frac{1}{3}\)还小\(10 °\),求这个角的度数。
(2)已知\(\angle A\)与\(\angle B\)互为余角,且\(\angle A = 2\angle B\),求\(\angle A\)和\(\angle B\)的度数。
(3)如图,\(\angle AOB = 90 °\),\(\angle COD = 90 °\),求证:\(\angle AOC = \angle BOD\)。
第九页:课堂小结
余角的定义:两个角的和为\(90 °\),则这两个角互为余角。
补角的定义:两个角的和为\(180 °\),则这两个角互为补角。
余角和补角的性质:
同角(或等角)的余角相等。
同角(或等角)的补角相等。
在解决与余角和补角相关的问题时,要注意运用定义列出关系式,必要时通过设未知数建立方程求解,同时要灵活运用它们的性质简化计算和推理。
第十页:作业布置
教材第 XX 页相关习题第 1、2、3、4 题。
填空题:
若\(\angle \alpha\)的补角是\(130 °\),则\(\angle \alpha=\)______°,\(\angle \alpha\)的余角是______°。
已知\(\angle 1\)与\(\angle 2\)互为补角,且\(\angle 1 = 55 °\),则\(\angle 2=\)______°。
判断题(对的打 “√”,错的打 “×”):
锐角的补角一定是钝角。( )
一个角的余角一定小于这个角的补角。( )
若两个角互补,则这两个角一定是一个锐角和一个钝角。( )
解答题:
(1)已知一个角的补角是它的余角的 4 倍,求这个角的度数。
(2)已知\(\angle A\)与\(\angle B\)互为补角,\(\angle A\)的度数比\(\angle B\)的度数的 2 倍还多\(30 °\),求\(\angle A\)和\(\angle B\)的度数。
(3)如图,直线\(AB\)与\(CD\)相交于点\(O\),\(\angle AOC = 50 °\),求\(\angle BOD\)的余角的度数。
思考:如果两个角互为补角,那么它们的平分线所成的角是多少度?请画图并说明理由。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.了解两角互余和两角互补的定义.
2.通过探究了解“同角(或等角)的余角相等”“同角(或等角)的补角相等”并能利用这些性质进行角的计算,发展推理能力.
学习目标
O
A
B
要测量两堵墙所成的∠AOB的度数,但人不能进入围墙,如何测量
你能帮他解决这个问题吗?
课堂导入
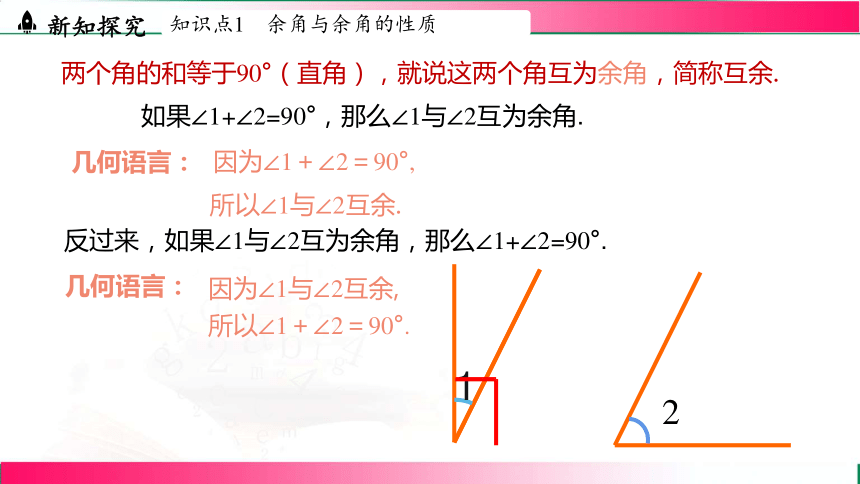
两个角的和等于90°(直角),就说这两个角互为余角,简称互余.
如果∠1+∠2=90°,那么∠1与∠2互为余角.
1
2
几何语言:
因为∠1+∠2=90°,
所以∠1与∠2互余.
反过来,如果∠1与∠2互为余角,那么∠1+∠2=90°.
几何语言:
所以∠1+∠2=90°.
因为∠1与∠2互余,
新知探究
知识点1 余角与余角的性质
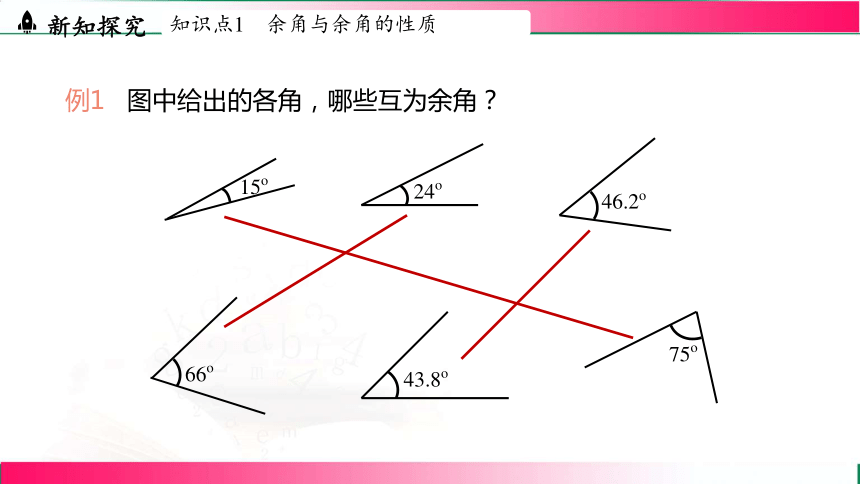
例1 图中给出的各角,哪些互为余角?
15o
24o
66o
75o
46.2o
43.8o
新知探究
知识点1 余角与余角的性质
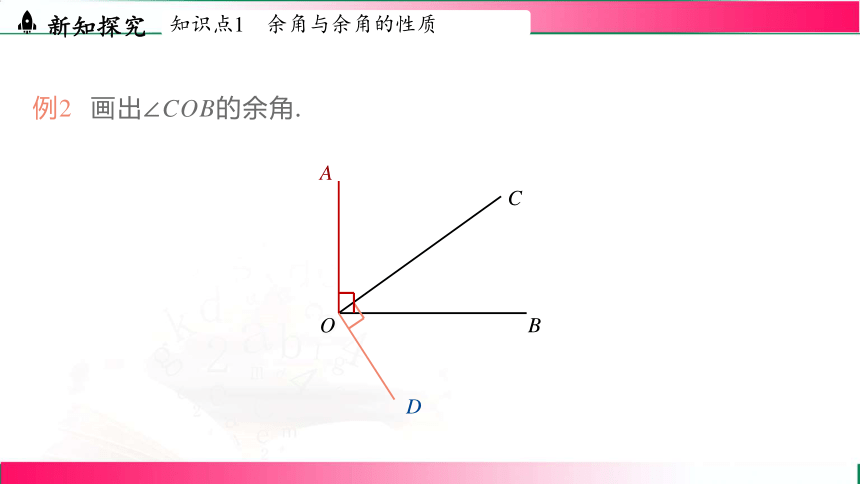
例2 画出∠COB的余角.
C
O
B
A
D
新知探究
知识点1 余角与余角的性质
(2)量一量: 用量角器量一下这两个角的度数;
根据图形回答下列问题:
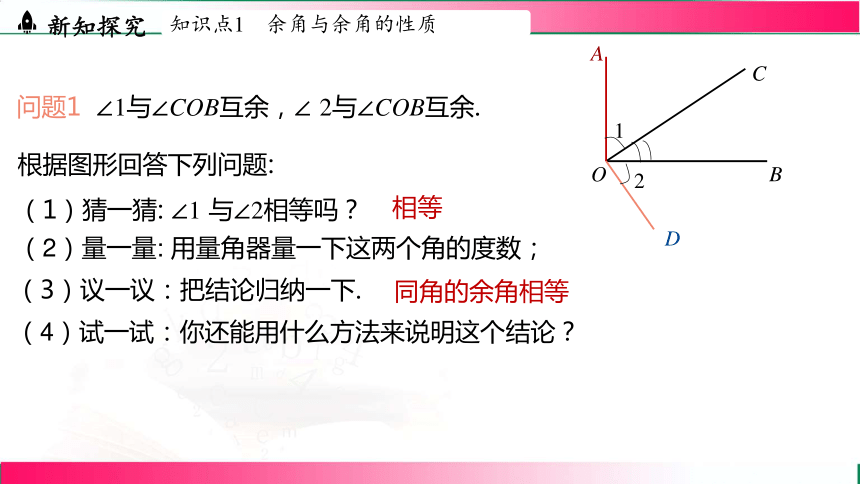
(1)猜一猜: ∠1 与∠2相等吗?
问题1 ∠1与∠COB互余,∠ 2与∠COB互余.
C
O
B
A
D
(3)议一议:把结论归纳一下.
(4)试一试:你还能用什么方法来说明这个结论?
相等
同角的余角相等
1
2
新知探究
知识点1 余角与余角的性质
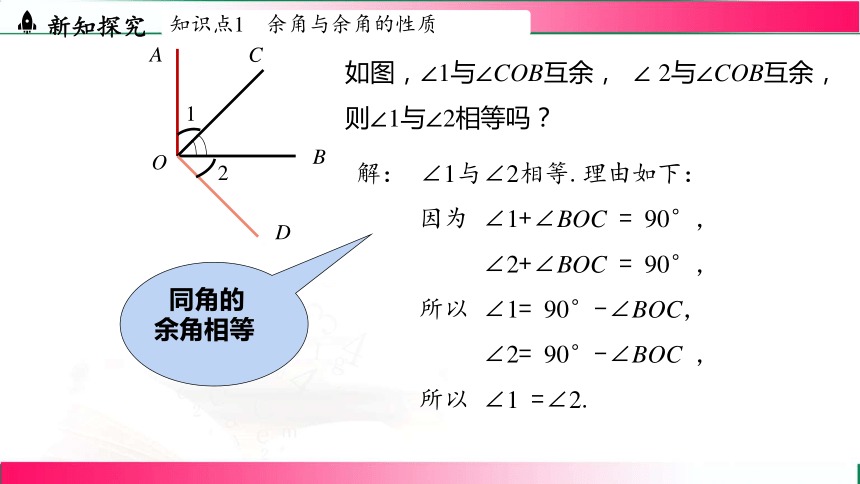
解: ∠1与∠2相等.理由如下:
因为 ∠1+∠BOC = 90°,
∠2+∠BOC = 90°,
所以 ∠1= 90°-∠BOC,
∠2= 90°-∠BOC ,
所以 ∠1 =∠2.
如图,∠1与∠COB互余, ∠ 2与∠COB互余,
则∠1与∠2相等吗?
A
O
B
D
C
1
2
同角的
余角相等
新知探究
知识点1 余角与余角的性质
问题2 如图,∠1与∠2互余,∠3与∠4互余,
如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
3
4
解: ∠2与∠4相等.理由如下:
因为∠1﹢∠2 = 90°, ∠3﹢∠4 = 90°,
所以∠2 = 90°-∠1,∠4 = 90°-∠3.
因为∠1 =∠3,
所以∠2 =∠4.
等角的余角相等
新知探究
知识点1 余角与余角的性质
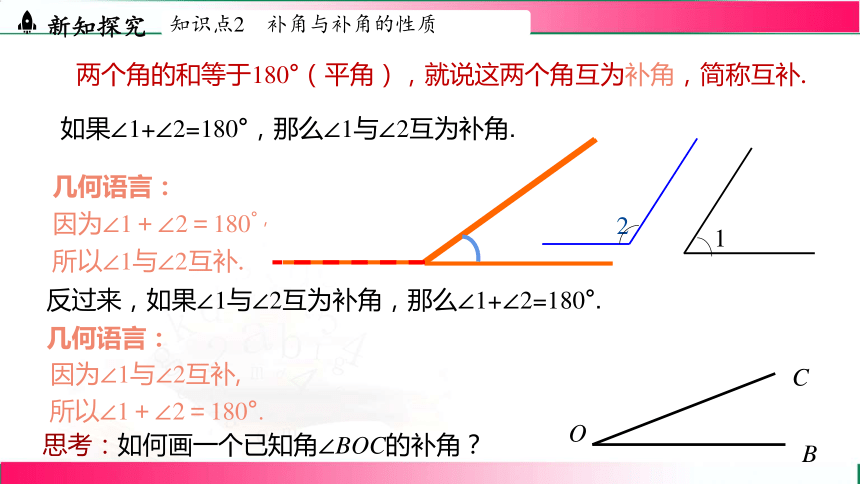
两个角的和等于180°(平角),就说这两个角互为补角,简称互补.
如果∠1+∠2=180°,那么∠1与∠2互为补角.
1
2
几何语言:
因为∠1+∠2=180°,
所以∠1与∠2互补.
思考:如何画一个已知角∠BOC的补角?
B
O
C
新知探究
知识点2 补角与补角的性质
反过来,如果∠1与∠2互为补角,那么∠1+∠2=180°.
几何语言:
因为∠1与∠2互补,
所以∠1+∠2=180°.
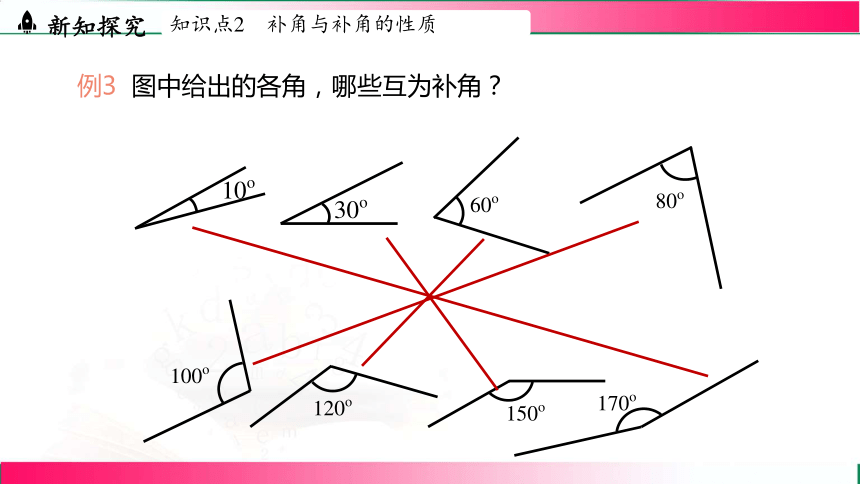
例3 图中给出的各角,哪些互为补角?
10o
30o
60o
80o
100o
120o
150o
170o
新知探究
知识点2 补角与补角的性质
问题3 如图,∠1是∠BOC 的补角, ∠2是∠BOC 的补角.∠1与∠2相等吗
解: ∠1与∠2相等.理由如下:
因为∠1+ ∠BOC = 180°,
∠2+ ∠BOC = 180°,
所以∠1=180°- ∠BOC ,
∠2=180°- ∠BOC,
所以∠1=∠2.
A
O
B
D
C
1
2
同角的补角相等
新知探究
知识点2 补角与补角的性质
问题4 如图,∠1与∠2互补,∠3与∠4互补,如果∠1=∠3,那么
∠2与∠4相等吗?为什么?
解:∠2与∠4相等.理由如下:
因为 ∠1﹢∠2 = 180°,∠3﹢∠4 = 180°,
所以 ∠2 = 180°-∠1, ∠4 = 180°-∠3.
因为 ∠1 =∠3,
所以 ∠2 =∠4.
等角的补角相等
1
2
4
3
新知探究
知识点2 补角与补角的性质
例4 如图,点A,O,B在同一直线上,射线 OD 和射线 OE 分别平分∠AOC 和∠BOC,图中哪些角互为余角?
解:因为点A,O,B在同一直线上,
所以 ∠AOC 和∠BOC互为补角.
O
A
B
C
D
E
又因为射线OD和射线OE分别平分∠AOC 和∠BOC,
所以∠COD+∠COE= ∠AOC+ ∠BOC
= (∠AOC+∠BOC ) = 90°.
所以∠COD和∠COE互为余角.
同理∠AOD和∠BOE,∠AOD和∠COE,∠COD和∠BOE也互为余角.
新知探究
知识点2 补角与补角的性质
例5 如图,直线AB与∠COD的两边OC,OD分别相交于点E,
F,∠1+∠2=180°.找出图中与∠2相等的角,并说明理由.
分析:已知∠1+∠2=180°,说明∠2是∠1的补角.根据同角
(或等角)的补角相等,找出图中∠1的其他补角和∠2的其他补角
的补角,便可确定与∠2相等的角.
新知探究
知识点2 补角与补角的性质
解:如图,因为∠1+∠3=180°,∠1+∠2=180°,
所以∠3=∠2.
因为∠1+∠4=180°,∠1+∠2=180°,
所以∠4=∠2.
因为∠2+∠5=180°,
∠6+∠5=180°,
所以∠2=∠6.
所以图中与∠2相等的角有∠3,∠4,∠6.
新知探究
知识点2 补角与补角的性质
例5 如图,直线AB与∠COD的两边OC,OD分别相交于点E,
F,∠1+∠2=180°.找出图中与∠2相等的角,并说明理由.
1.一个角的余角是它的2倍,这个角的度数是( )
A.30° B.45° C.60° D.75°
A
随堂练习
2.下列说法正确的是( )
A.一个角的补角一定大于它本身
B.一个角的余角一定小于它本身
C.一个钝角减去一个锐角的差一定是一个锐角
D.一个角的余角一定小于其补角
D
随堂练习
3. 如图,直线AB,CD交于点O,因为∠1+∠3=180°,∠2+∠3=180°,所以∠1=∠2的依据是( )
A.同角的余角相等
B.等角的余角相等
C.同角的补角相等
D.等角的补角相等
C
随堂练习
4. ∠1 与 ∠2 互余,∠1 = (6x + 8)°,∠2 = (4x-8)°,
则∠1= ,∠2= .
62°
28°
随堂练习
知识点1 余角和补角的定义
1. 若∠ A =40°,则∠ A 的余角的大小是( A )
A. 50° B. 60°
C. 140° D. 160°
A
1
2
3
4
5
6
7
8
9
10
11
2. 如果一个角的度数比它补角的2倍多30°,那么这个角的
度数是( C )
A. 50° B. 70°
C. 130° D. 160°
【点拨】
设这个角的度数是 x °.
根据题意,得 x =2(180- x )+30,
解得 x =130,即这个角的度数是130°.
C
1
2
3
4
5
6
7
8
9
10
11
3. 将一副三角尺按下列位置摆放,使∠α和∠β互余的摆放
方式是( A )
1
2
3
4
5
6
7
8
9
10
11
A. ∠α+∠β=180°-90°=90°,∠α与∠β互余;
B. 同角的余角相等,则∠α=∠β,但∠α与∠β不一定互
余;C. ∠α=∠β=180°-45°=135°,∠α与∠β不互
余;D. ∠α+∠β=180°,∠α与∠β不互余,故选A.
【点拨】
A
【答案】
1
2
3
4
5
6
7
8
9
10
11
知识点2 余角和补角的性质
4. 如图,直线 AB , CD 交于点 O ,因为∠1+∠3=180°,
∠2+∠3=180°,所以∠1=∠2.此判断的依据是
( C )
A. 同角的余角相等 B. 等角的余角相等
C. 同角的补角相等 D. 等角的补角相等
C
1
2
3
4
5
6
7
8
9
10
11
5. 如图,点 C , O , B 在同一条直线上,∠ AOB =90°,
∠1=∠2,则下列结论:①∠ EOD =90°;②∠3=
∠4;③∠2=∠3;④∠2+∠3=90°.其中正确的有
( C )
A. 1个 B. 2个
C. 3个 D. 4个
1
2
3
4
5
6
7
8
9
10
11
【点拨】
因为∠ AOB =90°,所以∠2+∠4=90°.又因
为∠1=∠2,所以∠1+∠4=90°,即∠ EOD =
90°,故①正确;因为∠ AOC =180°-∠ AOB =
90°,所以∠1+∠3=90°,所以∠3=∠4,故②正
确;因为∠ EOD =90°,所以∠2+∠3=180°-
90°=90°,∠2与∠3不一定相等,故③错误,④正
确.综上,正确的有3个,故选C.
C
【答案】
1
2
3
4
5
6
7
8
9
10
11
6. [情境题·2023·衢州·生活应用]如图是脊柱侧弯的检测示意
图,在体检时为方便测出Cobb角∠ O 的大小,需将∠ O
转化为与它相等的角(图中∠ CBO =∠ DAO =90°),则
图中与∠ O 相等的角是( B )
A. ∠ BEA B. ∠ DEB
C. ∠ ECA D. ∠ ADO
B
1
2
3
4
5
6
7
8
9
10
11
7. [2024·邯郸丛台区期末]如图,将三个大小不同的正方形的
一个顶点重合放置,则α,β,γ三个角的数量关系为
( C )
A. α+β+γ=90° B. α+β-γ=90°
C. α-β+γ=90° D. α+2β-γ=90°
1
2
3
4
5
6
7
8
9
10
11
【点拨】
如图,
由题意得α+∠1=∠1+β+∠2=∠2+γ=90°,
所以∠1=90°-α,∠2=90°-γ,
所以β=90°-∠1-∠2=90°-90°+α-90°+γ
=α+γ-90°,即α-β+γ=90°.故选C.
C
【答案】
1
2
3
4
5
6
7
8
9
10
11
易错点 对余角和补角的定义理解不透彻致错
8. [新考法·定义辨析法]下列说法中,正确的有 .(填
序号)
①钝角与锐角互补;
②锐角∠α的余角是90°-∠α;
③∠β的补角是180°-∠β;
④若∠1+∠2+∠3=90°,则∠1,∠2,∠3互余.
②③
1
2
3
4
5
6
7
8
9
10
11
同角或等角的
补角相等
同角或等角的
余角相等
互余 互补
两角间的数量关系
对应图形
性质
课堂小结
谢谢观看!
2.7.2余角和补角
第二章 几何图形的初步认识
【2024新教材】2025-2026学年冀教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
第一页:标题页
2.7.2 余角和补角
—— 理解互余与互补的关系
(右下角添加授课教师姓名及日期)
第二页:引入
在角的世界里,有些角之间存在着特殊的数量关系,比如两个角的和是一个直角,或者两个角的和是一个平角。这些特殊的关系在我们解决几何问题时经常会用到,它们就是我们今天要学习的余角和补角。通过本节课的学习,我们将掌握余角和补角的定义、性质以及它们在实际计算中的应用。
第三页:余角的定义
定义:如果两个角的和等于\(90 °\)(直角),就说这两个角互为余角,简称互余。其中一个角叫做另一个角的余角。
数学表达式:若\(\angle 1 + \angle 2 = 90 °\),则\(\angle 1\)与\(\angle 2\)互为余角,即\(\angle 1\)是\(\angle 2\)的余角,\(\angle 2\)也是\(\angle 1\)的余角。
实例:
\(\angle A = 30 °\),\(\angle B = 60 °\),因为\(30 ° + 60 ° = 90 °\),所以\(\angle A\)与\(\angle B\)互为余角。
一个直角被分成两个角,这两个角互为余角。
注意:
互余是指两个角之间的关系,不能单独说一个角是余角。
两个角互余,只与它们的度数之和有关,与它们的位置无关。
第四页:补角的定义
定义:如果两个角的和等于\(180 °\)(平角),就说这两个角互为补角,简称互补。其中一个角叫做另一个角的补角。
数学表达式:若\(\angle 3 + \angle 4 = 180 °\),则\(\angle 3\)与\(\angle 4\)互为补角,即\(\angle 3\)是\(\angle 4\)的补角,\(\angle 4\)也是\(\angle 3\)的补角。
实例:
\(\angle C = 110 °\),\(\angle D = 70 °\),因为\(110 ° + 70 ° = 180 °\),所以\(\angle C\)与\(\angle D\)互为补角。
一个平角被分成两个角,这两个角互为补角。
注意:
互补同样是指两个角之间的关系,不能单独说一个角是补角。
两个角互补,只与它们的度数之和有关,与它们的位置无关。
第五页:余角和补角的性质
性质 1:同角(或等角)的余角相等。
若\(\angle 1 + \angle 2 = 90 °\),\(\angle 1 + \angle 3 = 90 °\),则\(\angle 2 = \angle 3\)(同角的余角相等)。
若\(\angle 1 + \angle 2 = 90 °\),\(\angle 3 + \angle 4 = 90 °\),且\(\angle 1 = \angle 3\),则\(\angle 2 = \angle 4\)(等角的余角相等)。
性质 2:同角(或等角)的补角相等。
若\(\angle 5 + \angle 6 = 180 °\),\(\angle 5 + \angle 7 = 180 °\),则\(\angle 6 = \angle 7\)(同角的补角相等)。
若\(\angle 5 + \angle 6 = 180 °\),\(\angle 7 + \angle 8 = 180 °\),且\(\angle 5 = \angle 7\),则\(\angle 6 = \angle 8\)(等角的补角相等)。
实例:
若\(\angle \alpha = 40 °\),则\(\angle \alpha\)的余角是\(50 °\),如果另一个角\(\angle \beta\)的余角也是\(50 °\),那么\(\angle \alpha = \angle \beta\),这体现了等角的余角相等。
若\(\angle \gamma = 120 °\),则\(\angle \gamma\)的补角是\(60 °\),如果\(\angle \delta\)的补角也是\(60 °\),那么\(\angle \gamma = \angle \delta\),这体现了等角的补角相等。
第六页:例题解析(一)—— 余角和补角的基本计算
例题 1:已知一个角的度数是\(35 °\),求它的余角和补角的度数。
解:这个角的余角的度数为\(90 ° - 35 ° = 55 °\)。
这个角的补角的度数为\(180 ° - 35 ° = 145 °\)。
例题 2:一个角的补角是它的 3 倍,求这个角的度数。
解:设这个角的度数为\(x\),则它的补角的度数为\(180 ° - x\)。
根据题意可得:\(180 ° - x = 3x\)
移项得:\(3x + x = 180 °\)
合并同类项得:\(4x = 180 °\)
解得:\(x = 45 °\)
所以这个角的度数是\(45 °\)。
第七页:例题解析(二)—— 余角和补角性质的应用
例题 3:已知\(\angle 1\)与\(\angle 2\)互为余角,\(\angle 3\)与\(\angle 4\)互为余角,且\(\angle 1 = \angle 3\),求证:\(\angle 2 = \angle 4\)。
证明:因为\(\angle 1\)与\(\angle 2\)互为余角,所以\(\angle 1 + \angle 2 = 90 °\),即\(\angle 2 = 90 ° - \angle 1\)。
因为\(\angle 3\)与\(\angle 4\)互为余角,所以\(\angle 3 + \angle 4 = 90 °\),即\(\angle 4 = 90 ° - \angle 3\)。
又因为\(\angle 1 = \angle 3\),所以\(90 ° - \angle 1 = 90 ° - \angle 3\),即\(\angle 2 = \angle 4\)。
例题 4:如图,点\(O\)在直线\(AB\)上,\(OC\)是射线,\(\angle AOC = 50 °\),求\(\angle BOC\)的余角的度数。
解:因为点\(O\)在直线\(AB\)上,所以\(\angle AOC + \angle BOC = 180 °\),则\(\angle BOC = 180 ° - 50 ° = 130 °\)。
设\(\angle BOC\)的余角为\(\angle x\),则\(\angle x + 130 ° = 90 °\),显然不成立,说明\(\angle BOC\)是钝角,没有余角?不,错误在于余角是指两个角的和为\(90 °\),所以\(\angle BOC\)的余角应该是\(90 ° - (180 ° - \angle AOC)\)?不,正确解法:\(\angle BOC = 130 °\),它的余角不存在,因为余角要求两个角的和为\(90 °\),而\(130 °>90 °\),所以此题应改为求\(\angle AOC\)的余角,\(\angle AOC = 50 °\),其余角为\(40 °\),或者题目中\(\angle AOC = 140 °\),则\(\angle BOC = 40 °\),其余角为\(50 °\),此处修正题目为\(\angle AOC = 40 °\),则\(\angle BOC = 140 °\),显然仍不对,正确例题应为:点\(O\)在直线\(AB\)上,\(OC\)是射线,\(\angle AOC = 40 °\),求\(\angle BOC\)的补角的度数,\(\angle BOC = 140 °\),补角为\(40 °\),但更合适的例题为:
例题 4:已知\(\angle \alpha\)与\(\angle \beta\)互为补角,\(\angle \alpha\)比\(\angle \beta\)大\(30 °\),求\(\angle \alpha\)和\(\angle \beta\)的度数。
解:设\(\angle \beta\)的度数为\(x\),则\(\angle \alpha\)的度数为\(x + 30 °\)。
因为\(\angle \alpha\)与\(\angle \beta\)互为补角,所以\(\angle \alpha + \angle \beta = 180 °\),即\((x + 30 °) + x = 180 °\)。
解得\(2x = 150 °\),\(x = 75 °\),则\(\angle \alpha = 75 ° + 30 ° = 105 °\)。
所以\(\angle \alpha = 105 °\),\(\angle \beta = 75 °\)。
第八页:课堂练习
填空题:
若\(\angle A = 25 °\),则它的余角是______°,补角是______°。
一个角的余角是\(40 °\),则这个角的度数是______°,它的补角是______°。
若\(\angle 1\)与\(\angle 2\)互为余角,\(\angle 2 = 35 °\),则\(\angle 1=\)______°。
选择题:
下列说法正确的是( )
A. 一个角的余角一定是锐角
B. 一个角的补角一定是钝角
C. 若\(\angle 1 + \angle 2 + \angle 3 = 90 °\),则\(\angle 1\)、\(\angle 2\)、\(\angle 3\)互为余角
D. 若\(\angle \alpha\)与\(\angle \beta\)互为补角,则\(\angle \alpha\)与\(\angle \beta\)一定有一个是锐角,一个是钝角
已知\(\angle \alpha = 50 °\),则\(\angle \alpha\)的余角的补角是( )
A. \(40 °\) B. \(140 °\) C. \(50 °\) D. \(130 °\)
解答题:
(1)一个角的余角比它的补角的\(\frac{1}{3}\)还小\(10 °\),求这个角的度数。
(2)已知\(\angle A\)与\(\angle B\)互为余角,且\(\angle A = 2\angle B\),求\(\angle A\)和\(\angle B\)的度数。
(3)如图,\(\angle AOB = 90 °\),\(\angle COD = 90 °\),求证:\(\angle AOC = \angle BOD\)。
第九页:课堂小结
余角的定义:两个角的和为\(90 °\),则这两个角互为余角。
补角的定义:两个角的和为\(180 °\),则这两个角互为补角。
余角和补角的性质:
同角(或等角)的余角相等。
同角(或等角)的补角相等。
在解决与余角和补角相关的问题时,要注意运用定义列出关系式,必要时通过设未知数建立方程求解,同时要灵活运用它们的性质简化计算和推理。
第十页:作业布置
教材第 XX 页相关习题第 1、2、3、4 题。
填空题:
若\(\angle \alpha\)的补角是\(130 °\),则\(\angle \alpha=\)______°,\(\angle \alpha\)的余角是______°。
已知\(\angle 1\)与\(\angle 2\)互为补角,且\(\angle 1 = 55 °\),则\(\angle 2=\)______°。
判断题(对的打 “√”,错的打 “×”):
锐角的补角一定是钝角。( )
一个角的余角一定小于这个角的补角。( )
若两个角互补,则这两个角一定是一个锐角和一个钝角。( )
解答题:
(1)已知一个角的补角是它的余角的 4 倍,求这个角的度数。
(2)已知\(\angle A\)与\(\angle B\)互为补角,\(\angle A\)的度数比\(\angle B\)的度数的 2 倍还多\(30 °\),求\(\angle A\)和\(\angle B\)的度数。
(3)如图,直线\(AB\)与\(CD\)相交于点\(O\),\(\angle AOC = 50 °\),求\(\angle BOD\)的余角的度数。
思考:如果两个角互为补角,那么它们的平分线所成的角是多少度?请画图并说明理由。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.了解两角互余和两角互补的定义.
2.通过探究了解“同角(或等角)的余角相等”“同角(或等角)的补角相等”并能利用这些性质进行角的计算,发展推理能力.
学习目标
O
A
B
要测量两堵墙所成的∠AOB的度数,但人不能进入围墙,如何测量
你能帮他解决这个问题吗?
课堂导入
两个角的和等于90°(直角),就说这两个角互为余角,简称互余.
如果∠1+∠2=90°,那么∠1与∠2互为余角.
1
2
几何语言:
因为∠1+∠2=90°,
所以∠1与∠2互余.
反过来,如果∠1与∠2互为余角,那么∠1+∠2=90°.
几何语言:
所以∠1+∠2=90°.
因为∠1与∠2互余,
新知探究
知识点1 余角与余角的性质
例1 图中给出的各角,哪些互为余角?
15o
24o
66o
75o
46.2o
43.8o
新知探究
知识点1 余角与余角的性质
例2 画出∠COB的余角.
C
O
B
A
D
新知探究
知识点1 余角与余角的性质
(2)量一量: 用量角器量一下这两个角的度数;
根据图形回答下列问题:
(1)猜一猜: ∠1 与∠2相等吗?
问题1 ∠1与∠COB互余,∠ 2与∠COB互余.
C
O
B
A
D
(3)议一议:把结论归纳一下.
(4)试一试:你还能用什么方法来说明这个结论?
相等
同角的余角相等
1
2
新知探究
知识点1 余角与余角的性质
解: ∠1与∠2相等.理由如下:
因为 ∠1+∠BOC = 90°,
∠2+∠BOC = 90°,
所以 ∠1= 90°-∠BOC,
∠2= 90°-∠BOC ,
所以 ∠1 =∠2.
如图,∠1与∠COB互余, ∠ 2与∠COB互余,
则∠1与∠2相等吗?
A
O
B
D
C
1
2
同角的
余角相等
新知探究
知识点1 余角与余角的性质
问题2 如图,∠1与∠2互余,∠3与∠4互余,
如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
3
4
解: ∠2与∠4相等.理由如下:
因为∠1﹢∠2 = 90°, ∠3﹢∠4 = 90°,
所以∠2 = 90°-∠1,∠4 = 90°-∠3.
因为∠1 =∠3,
所以∠2 =∠4.
等角的余角相等
新知探究
知识点1 余角与余角的性质
两个角的和等于180°(平角),就说这两个角互为补角,简称互补.
如果∠1+∠2=180°,那么∠1与∠2互为补角.
1
2
几何语言:
因为∠1+∠2=180°,
所以∠1与∠2互补.
思考:如何画一个已知角∠BOC的补角?
B
O
C
新知探究
知识点2 补角与补角的性质
反过来,如果∠1与∠2互为补角,那么∠1+∠2=180°.
几何语言:
因为∠1与∠2互补,
所以∠1+∠2=180°.
例3 图中给出的各角,哪些互为补角?
10o
30o
60o
80o
100o
120o
150o
170o
新知探究
知识点2 补角与补角的性质
问题3 如图,∠1是∠BOC 的补角, ∠2是∠BOC 的补角.∠1与∠2相等吗
解: ∠1与∠2相等.理由如下:
因为∠1+ ∠BOC = 180°,
∠2+ ∠BOC = 180°,
所以∠1=180°- ∠BOC ,
∠2=180°- ∠BOC,
所以∠1=∠2.
A
O
B
D
C
1
2
同角的补角相等
新知探究
知识点2 补角与补角的性质
问题4 如图,∠1与∠2互补,∠3与∠4互补,如果∠1=∠3,那么
∠2与∠4相等吗?为什么?
解:∠2与∠4相等.理由如下:
因为 ∠1﹢∠2 = 180°,∠3﹢∠4 = 180°,
所以 ∠2 = 180°-∠1, ∠4 = 180°-∠3.
因为 ∠1 =∠3,
所以 ∠2 =∠4.
等角的补角相等
1
2
4
3
新知探究
知识点2 补角与补角的性质
例4 如图,点A,O,B在同一直线上,射线 OD 和射线 OE 分别平分∠AOC 和∠BOC,图中哪些角互为余角?
解:因为点A,O,B在同一直线上,
所以 ∠AOC 和∠BOC互为补角.
O
A
B
C
D
E
又因为射线OD和射线OE分别平分∠AOC 和∠BOC,
所以∠COD+∠COE= ∠AOC+ ∠BOC
= (∠AOC+∠BOC ) = 90°.
所以∠COD和∠COE互为余角.
同理∠AOD和∠BOE,∠AOD和∠COE,∠COD和∠BOE也互为余角.
新知探究
知识点2 补角与补角的性质
例5 如图,直线AB与∠COD的两边OC,OD分别相交于点E,
F,∠1+∠2=180°.找出图中与∠2相等的角,并说明理由.
分析:已知∠1+∠2=180°,说明∠2是∠1的补角.根据同角
(或等角)的补角相等,找出图中∠1的其他补角和∠2的其他补角
的补角,便可确定与∠2相等的角.
新知探究
知识点2 补角与补角的性质
解:如图,因为∠1+∠3=180°,∠1+∠2=180°,
所以∠3=∠2.
因为∠1+∠4=180°,∠1+∠2=180°,
所以∠4=∠2.
因为∠2+∠5=180°,
∠6+∠5=180°,
所以∠2=∠6.
所以图中与∠2相等的角有∠3,∠4,∠6.
新知探究
知识点2 补角与补角的性质
例5 如图,直线AB与∠COD的两边OC,OD分别相交于点E,
F,∠1+∠2=180°.找出图中与∠2相等的角,并说明理由.
1.一个角的余角是它的2倍,这个角的度数是( )
A.30° B.45° C.60° D.75°
A
随堂练习
2.下列说法正确的是( )
A.一个角的补角一定大于它本身
B.一个角的余角一定小于它本身
C.一个钝角减去一个锐角的差一定是一个锐角
D.一个角的余角一定小于其补角
D
随堂练习
3. 如图,直线AB,CD交于点O,因为∠1+∠3=180°,∠2+∠3=180°,所以∠1=∠2的依据是( )
A.同角的余角相等
B.等角的余角相等
C.同角的补角相等
D.等角的补角相等
C
随堂练习
4. ∠1 与 ∠2 互余,∠1 = (6x + 8)°,∠2 = (4x-8)°,
则∠1= ,∠2= .
62°
28°
随堂练习
知识点1 余角和补角的定义
1. 若∠ A =40°,则∠ A 的余角的大小是( A )
A. 50° B. 60°
C. 140° D. 160°
A
1
2
3
4
5
6
7
8
9
10
11
2. 如果一个角的度数比它补角的2倍多30°,那么这个角的
度数是( C )
A. 50° B. 70°
C. 130° D. 160°
【点拨】
设这个角的度数是 x °.
根据题意,得 x =2(180- x )+30,
解得 x =130,即这个角的度数是130°.
C
1
2
3
4
5
6
7
8
9
10
11
3. 将一副三角尺按下列位置摆放,使∠α和∠β互余的摆放
方式是( A )
1
2
3
4
5
6
7
8
9
10
11
A. ∠α+∠β=180°-90°=90°,∠α与∠β互余;
B. 同角的余角相等,则∠α=∠β,但∠α与∠β不一定互
余;C. ∠α=∠β=180°-45°=135°,∠α与∠β不互
余;D. ∠α+∠β=180°,∠α与∠β不互余,故选A.
【点拨】
A
【答案】
1
2
3
4
5
6
7
8
9
10
11
知识点2 余角和补角的性质
4. 如图,直线 AB , CD 交于点 O ,因为∠1+∠3=180°,
∠2+∠3=180°,所以∠1=∠2.此判断的依据是
( C )
A. 同角的余角相等 B. 等角的余角相等
C. 同角的补角相等 D. 等角的补角相等
C
1
2
3
4
5
6
7
8
9
10
11
5. 如图,点 C , O , B 在同一条直线上,∠ AOB =90°,
∠1=∠2,则下列结论:①∠ EOD =90°;②∠3=
∠4;③∠2=∠3;④∠2+∠3=90°.其中正确的有
( C )
A. 1个 B. 2个
C. 3个 D. 4个
1
2
3
4
5
6
7
8
9
10
11
【点拨】
因为∠ AOB =90°,所以∠2+∠4=90°.又因
为∠1=∠2,所以∠1+∠4=90°,即∠ EOD =
90°,故①正确;因为∠ AOC =180°-∠ AOB =
90°,所以∠1+∠3=90°,所以∠3=∠4,故②正
确;因为∠ EOD =90°,所以∠2+∠3=180°-
90°=90°,∠2与∠3不一定相等,故③错误,④正
确.综上,正确的有3个,故选C.
C
【答案】
1
2
3
4
5
6
7
8
9
10
11
6. [情境题·2023·衢州·生活应用]如图是脊柱侧弯的检测示意
图,在体检时为方便测出Cobb角∠ O 的大小,需将∠ O
转化为与它相等的角(图中∠ CBO =∠ DAO =90°),则
图中与∠ O 相等的角是( B )
A. ∠ BEA B. ∠ DEB
C. ∠ ECA D. ∠ ADO
B
1
2
3
4
5
6
7
8
9
10
11
7. [2024·邯郸丛台区期末]如图,将三个大小不同的正方形的
一个顶点重合放置,则α,β,γ三个角的数量关系为
( C )
A. α+β+γ=90° B. α+β-γ=90°
C. α-β+γ=90° D. α+2β-γ=90°
1
2
3
4
5
6
7
8
9
10
11
【点拨】
如图,
由题意得α+∠1=∠1+β+∠2=∠2+γ=90°,
所以∠1=90°-α,∠2=90°-γ,
所以β=90°-∠1-∠2=90°-90°+α-90°+γ
=α+γ-90°,即α-β+γ=90°.故选C.
C
【答案】
1
2
3
4
5
6
7
8
9
10
11
易错点 对余角和补角的定义理解不透彻致错
8. [新考法·定义辨析法]下列说法中,正确的有 .(填
序号)
①钝角与锐角互补;
②锐角∠α的余角是90°-∠α;
③∠β的补角是180°-∠β;
④若∠1+∠2+∠3=90°,则∠1,∠2,∠3互余.
②③
1
2
3
4
5
6
7
8
9
10
11
同角或等角的
补角相等
同角或等角的
余角相等
互余 互补
两角间的数量关系
对应图形
性质
课堂小结
谢谢观看!
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
