3.1用字母表示数 课件(共29张PPT)
文档属性
| 名称 | 3.1用字母表示数 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 00:00:00 | ||
图片预览








文档简介
(共29张PPT)
3.1用字母表示数
第三章 代数式
【2024新教材】2025-2026学年冀教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
第一页:标题页
3.1 用字母表示数
—— 开启代数世界的大门
(右下角添加授课教师姓名及日期)
第二页:引入
在我们的生活和学习中,经常会遇到一些不确定的数量。比如,一只青蛙一张嘴,两只眼睛四条腿;两只青蛙两张嘴,四只眼睛八条腿…… 如果有很多只青蛙,我们该如何简洁地表示它们的嘴、眼睛和腿的数量呢?这就需要用到用字母表示数的知识。用字母表示数不仅能简洁地表达数量关系,还能为我们解决复杂的数学问题带来便利。本节课我们就来学习如何用字母表示数。
第三页:用字母表示数的意义
简洁性:用字母表示数可以把数量关系简明地表达出来,避免重复表述。
例如,上面提到的青蛙问题,若用\(n\)表示青蛙的只数,那么嘴的数量就是\(n\)张,眼睛的数量是\(2n\)只,腿的数量是\(4n\)条。
一般性:字母可以表示任意的数或特定范围内的数,具有普遍意义。
比如,用\(a\)表示一个数,那么\(a + 5\)就表示比这个数大 5 的数,这里的\(a\)可以是任意整数、小数或分数。
抽象性:用字母表示数是从具体情境中抽象出数量关系的过程,是代数学习的基础。
像长方形的长用\(a\)表示,宽用\(b\)表示,那么长方形的面积就可以表示为\(ab\),这个式子适用于所有长方形面积的计算。
第四页:用字母表示数的书写规则
在用字母表示数时,需要遵循一定的书写规则,以保证表达的规范和清晰:
数字与字母相乘:数字要写在字母的前面,乘号可以省略不写,也可以记作 “ ”。
例如,\(5 x\)可以写作\(5x\)或\(5 ·x\),但不能写作\(x5\)。
字母与字母相乘:乘号可以省略不写,也可以记作 “ ”。
例如,\(a b\)可以写作\(ab\)或\(a ·b\)。
带分数与字母相乘:带分数要先化成假分数,再与字母相乘。
例如,\(1\frac{1}{2} x\)要写作\(\frac{3}{2}x\),而不能写作\(1\frac{1}{2}x\)。
字母与 1 或 - 1 相乘:1 可以省略不写。
例如,\(1 x\)写作\(x\),\(-1 x\)写作\(-x\)。
字母除以数:要写成分数的形式。
例如,\(x ·5\)写作\(\frac{x}{5}\)。
含有字母的式子表示数量时:若式子后面有单位,且式子是和或差的形式,要给式子加括号。
例如,\((a + 3)\)米,不能写作\(a + 3\)米。
第五页:用字母表示常见的数量关系
路程、速度、时间的关系:路程 = 速度 × 时间。若用\(s\)表示路程,\(v\)表示速度,\(t\)表示时间,则\(s = vt\)。
总价、单价、数量的关系:总价 = 单价 × 数量。若用\(c\)表示总价,\(p\)表示单价,\(n\)表示数量,则\(c = pn\)。
工作总量、工作效率、工作时间的关系:工作总量 = 工作效率 × 工作时间。若用\(w\)表示工作总量,\(e\)表示工作效率,\(t\)表示工作时间,则\(w = et\)。
实例:一辆汽车的速度是每小时\(v\)千米,行驶了\(t\)小时,那么它行驶的路程\(s = vt\)千米。如果\(v = 60\)千米 / 小时,\(t = 2\)小时,那么\(s = 60 2 = 120\)千米。
第六页:用字母表示运算定律和计算公式
运算定律:
加法交换律:两个数相加,交换加数的位置,和不变。用字母表示为\(a + b = b + a\)。
加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。用字母表示为\((a + b) + c = a + (b + c)\)。
乘法交换律:两个数相乘,交换因数的位置,积不变。用字母表示为\(ab = ba\)。
乘法结合律:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积不变。用字母表示为\((ab)c = a(bc)\)。
乘法分配律:两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。用字母表示为\((a + b)c = ac + bc\)。
计算公式:
正方形的周长:若用\(a\)表示正方形的边长,\(C\)表示周长,则\(C = 4a\)。
正方形的面积:若用\(a\)表示正方形的边长,\(S\)表示面积,则\(S = a^2\)(读作 “\(a\)的平方”,表示\(a a\))。
长方形的周长:若用\(a\)表示长,\(b\)表示宽,\(C\)表示周长,则\(C = 2(a + b)\)。
长方形的面积:若用\(a\)表示长,\(b\)表示宽,\(S\)表示面积,则\(S = ab\)。
第七页:例题解析(一)—— 用字母表示数的基本应用
例题 1:用含有字母的式子表示下列数量关系。
(1)比\(x\)大 8 的数;(2)\(a\)的 5 倍与\(b\)的和;(3)\(m\)的平方减去\(n\)的 3 倍。
解:(1)比\(x\)大 8 的数表示为\(x + 8\)。
(2)\(a\)的 5 倍与\(b\)的和表示为\(5a + b\)。
(3)\(m\)的平方减去\(n\)的 3 倍表示为\(m^2 - 3n\)。
例题 2:一个商店原有苹果\(a\)千克,卖出了 30 千克,又运来\(b\)千克,现在这个商店有苹果多少千克?
解:原有苹果\(a\)千克,卖出 30 千克后还剩\((a - 30)\)千克,又运来\(b\)千克,所以现在有苹果\((a - 30 + b)\)千克。
第八页:例题解析(二)—— 代入求值
例题 3:已知长方形的长\(a = 5\)厘米,宽\(b = 3\)厘米,求长方形的周长\(C\)和面积\(S\)。
解:根据长方形的周长公式\(C = 2(a + b)\),把\(a = 5\)厘米,\(b = 3\)厘米代入得:\(C = 2 (5 + 3) = 2 8 = 16\)(厘米)。
根据长方形的面积公式\(S = ab\),把\(a = 5\)厘米,\(b = 3\)厘米代入得:\(S = 5 3 = 15\)(平方厘米)。
所以长方形的周长是 16 厘米,面积是 15 平方厘米。
例题 4:当\(x = 10\)时,求\(3x + 20\)的值。
解:把\(x = 10\)代入\(3x + 20\)得:\(3 10 + 20 = 30 + 20 = 50\)。
第九页:课堂练习
填空题:
用字母表示乘法分配律是______。
小明今年\(a\)岁,爸爸比他大 28 岁,爸爸今年______岁。
一个三角形的底是\(a\)厘米,高是\(h\)厘米,它的面积是______平方厘米。
选择题:
下列式子中,符合书写规则的是( )
A. \(a5\) B. \(1\frac{1}{3}x\) C. \(x ·5\) D. \(2a + 3\)
当\(a = 4\),\(b = 5\)时,\(ab + 2\)的值是( )
A. 22 B. 18 C. 11 D. 9
解答题:
(1)用含有字母的式子表示下面的数量关系。
①\(x\)与\(y\)的和的 3 倍;②比\(a\)的 4 倍少 5 的数。
(2)一个正方形的边长是\(a\)米,它的周长是多少米?面积是多少平方米?当\(a = 6\)时,周长和面积各是多少?
(3)一辆自行车每小时行驶\(v\)千米,行驶了\(t\)小时,一共行驶了多少千米?如果\(v = 15\),\(t = 2\),一共行驶了多少千米?
第十页:课堂小结
用字母表示数的意义:具有简洁性、一般性和抽象性,能简洁表达数量关系。
用字母表示数的书写规则:注意数字与字母、字母与字母的乘除表示方法,以及带分数、1 或 - 1 与字母相乘的规则等。
用字母表示常见的数量关系、运算定律和计算公式,能帮助我们更方便地解决问题。
代入求值是用字母表示数的重要应用,将字母的具体数值代入式子中,可求出式子的值。
第十一页:作业布置
教材第 XX 页习题 3.1 第 1、2、3、4 题。
填空题:
每支铅笔\(a\)元,买了 5 支,应付______元。
一个数是\(x\),另一个数比它的 3 倍多 2,另一个数是______。
判断题(对的打 “√”,错的打 “×”):
\(a a\)可以写作\(2a\)。( )
因为\(2^2 = 2 2\),所以\(a^2 = a 2\)。( )
式子\(5x + 6\)可以表示 5 与\(x\)的和的 6 倍。( )
解答题:
(1)用含有字母的式子表示下列各题的数量关系。
①\(a\)除以\(b\)的商减去\(c\);②\(m\)与\(n\)的差的平方。
(2)一个长方形的长是\(2x\)米,宽是\(x\)米,它的周长和面积各是多少?当\(x = 3\)时,周长和面积分别是多少?
(3)某工厂每天生产\(a\)个零件,生产了 7 天,还剩下\(b\)个没生产,这批零件一共有多少个?如果\(a = 120\),\(b = 300\),这批零件一共有多少个?
思考:用字母表示数和用具体数字表示数有什么联系和区别?
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
学习目标
1.理解用字母表示数的意义,体会用字母表示数的必要性和优越性.
2.能用字母表示运算律、计算公式及各种数与数量关系.
3.逐步深化对字母表示数的意义的认识,体验用数学符号表达数量关系的过程,增强符号意识.
小明上小学时,在一堂数学课上,发现了下列等式:
1+2=2+1
3.5+5.6=5.6+3.5
(1)这几个式子反映了什么规律?
a + b = b + a
(2)能用更简明的方法表示出来吗?
加法交换律:两个数相加,交换加数的位置,和不变.
课堂导入
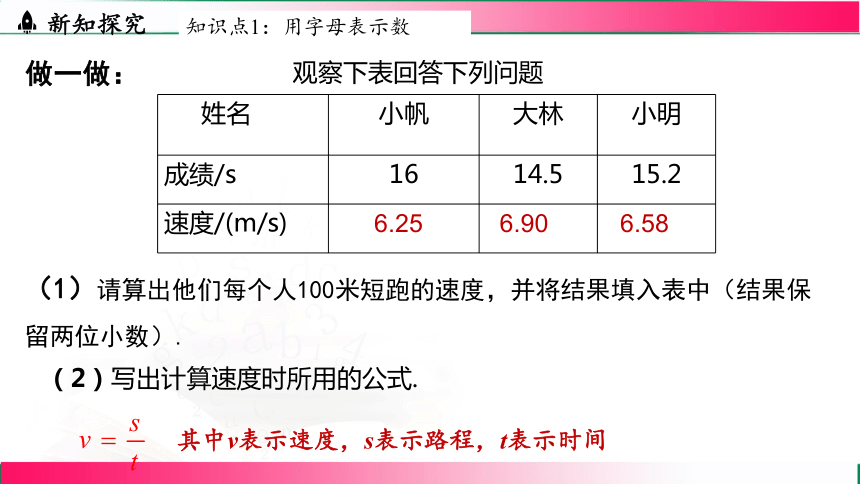
观察下表回答下列问题
(1)请算出他们每个人100米短跑的速度,并将结果填入表中(结果保留两位小数).
姓名 小帆 大林 小明
成绩/s 16 14.5 15.2
速度/(m/s)
做一做:
6.25
6.90
6.58
(2)写出计算速度时所用的公式.
其中v表示速度,s表示路程,t表示时间
新知探究
知识点1:用字母表示数
如何用字母表示它们
运算律 字 母 表 示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
a + b = b + a
(a + b) +c= a +(b + c)
ab = ba
(ab)c =a(bc)
a (b+ c )=ab+ac
新知探究
知识点2:用字母表示数的常见应用
1.长方形的面积公式S=ab
S 表示面积,a、b分别表示长与宽
2.圆的面积计算公式S=πr
S 表示面积,r表示圆的半径
3.长方体的体积计算公式V=abc
a,b,c分别表示长方体的长、宽、高
4.圆柱体积计算公式V=πr h.
V表示体积,r表示底面半径,h表示圆柱的高
新知探究
知识点2:用字母表示数的常见应用
在自然数范围内,回答下列问题.
(1)请用字母表示偶数和奇数.
偶数用字母表示为2m,奇数用字母表示为2m+1(m为自然数).
(2)两个偶数之和具有怎样的特征?两个奇数之和又具有怎样的特征?请你提出猜想,并证明猜想的正确性.
两个偶数的和是偶数,两个奇数的和也是偶数.
一起探究:
(3)如果P是正整数,那么与P相邻的两个自然数之和是偶数吗?请说明理由.
与P相邻的两个自然数之和是偶数.
知识点2:用字母表示数的常见应用
新知探究
用字母表示数,说明:
(1)任意两个奇数之和是偶数.
问题引导:(m,n为自然数)
(1)一个奇数怎么表示?
2m+ 1
(2)两个相邻的奇数怎么表示?
2m-1、2m+1
(3)任意两个奇数怎么表示?
2m+1和 2n+1
解:(2m+1)+(2n+1)
=2(m+ n+1).
新知探究
知识点2:用字母表示数的常见应用
(2)如果m为自然数,那么与m相邻的两个自然数之和是偶数.
问题引导:(m为自然数)
与m相邻的两个自然数怎么表示?
m-1和m+1
解:(m+1)+(m-1)
=2m.
新知探究
知识点2:用字母表示数的常见应用
(1)用字母表示数,同一问题中,同一字母只能表示同一数量,不同的数量要用不同的字母表示.
(2)用字母表示实际问题中的某一数量时,字母的取值需使这个问题有意义,并且符合实际.
(3)用字母表示数可简明表达问题中的数量关系、公式、法则、规律等.
1. 填空:
(1)-6℃下降2℃后是____℃;温度由t℃下降2℃度后是_____℃;
(2)今年李华m岁,去年李华_____ 岁,五年后李华 ____ 岁;
(3)三个连续偶数中间一个为2n,则其余两个为_____、 ;
(t -2)
(m-1)
(m+5)
2n-2
2n+2
随堂练习
-8
(4)某商店上月收入a元,本月收入比上月2 倍多10元,本月收入 元;
(5)城市市区人口a万人,市区绿化面积m万㎡,则平均每个人拥有绿地 ㎡;
(6)某城市5年前人均年收入为n元,预计今年人均年收入是5年前的2倍多500元,那么今年人均年收入将达________ 元.
(2a+10)
(2a+10)
(2n+500)
随堂练习
2.选择
(1)用字母表示乘法对加法的分配律是( )
A.a(b+c) B.ab+ac
C.a(b+c)=ab+ac D. ab=ba
C
(2)昨天的最高温度是27℃,今天气温比昨天下降t℃,今天的最高气温是( )
A.27+t B.27-t℃
C.(27+t)℃ D.(27-t)℃
D
随堂练习
(3)购买1个单价为a元的面包 和3瓶单价为b元的饮料,所需钱数为( )
A.(a+b)元. B.3(a+b)元.
C.(3a+b)元. D.(a+3b)元.
D
随堂练习
知识点1 用字母表示数字的数量关系
1. 如果某天石家庄的最低气温为 a ℃,中午12点的气温比最
低气温高了10℃,那么中午12点的气温为( C )
A. (10- a )℃ B. ( a -10)℃
C. ( a +10)℃ D. ( a +12)℃
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
2. [2024·重庆一中模拟]用式子表示: a 的2倍与3的和,下列
表示正确的是( B )
A. 2 a -3 B. 2 a +3
C. 2( a -3) D. 2( a +3)
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
3. (1)一个两位数,它的十位数字是 x ,个位数字是 y ,那么
这个两位数是( D )
A. x + y B. 10 xy
C. 10( x + y ) D. 10 x + y
【点拨】
十位上的数字乘10,再加上个位上的数字即可得到这
个两位数,故选D.
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
(2)设 x 表示两位数, y 表示三位数,如果把 x 放在 y 的左
边组成一个五位数,那么这个五位数可表示为( B )
A. xy B. 1 000 x + y
C. x + y D. 100 x + y
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
知识点2 用字母表示图形中的数量关系
4. [母题·2024·石家庄第四十二中学期末·教材P104习题B组
T3]如图,边长为 m 的正方形纸片上剪去四个直径都为 d
的半圆,则阴影部分的周长是( D )
A. m2-π d2 B. m2- π d2
C. 4 m -π d D. 4 m +2π d -4 d
1
2
3
4
5
6
7
8
9
10
11
12
13
14
【点拨】
原正方形的周长为4 m ,四个直径都为 d 的半圆的长
度和为2π d ,则阴影部分的周长是4 m +2π d -4 d .
D
【答案】
1
2
3
4
5
6
7
8
9
10
11
12
13
14
5. [2023·山西]如图是一组有规律的图案,它由若干个大小相
同的圆片组成,第1个图案中有4个白色圆片,第2个图案
中有6个白色圆片,第3个图案中有8个白色圆片,第4个图
案中有10个白色圆片,…,依此规律,第 n 个图案中
有 个白色圆片(用含 n 的式子表示).
(2+2 n )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
【点拨】
第1个图案中有2+2×1=4(个)白色圆片;
第2个图案中有2+2×2=6(个)白色圆片;
第3个图案中有2+2×3=8(个)白色圆片;
…
第 n 个图案中有(2+2 n )个白色圆片.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
知识点3 用字母表示实际中的数量关系
6. 某校利用课后服务开展了主题为“书香满校园”的读书活
动,现需购买甲、乙两种读本共100本供学生阅读,其中
甲种读本的单价为10元/本,乙种读本的单价为8元/本,设
购买甲种读本 x 本,则购买乙种读本的费用为( C )
A. 8 x 元 B. 10(100- x )元
C. 8(100- x )元 D. (100-8 x )元
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
7. [2023·河南]某校计划给每个年级配发 n 套劳动工具,则3
个年级共需配发 套劳动工具.
3 n
1
2
3
4
5
6
7
8
9
10
11
12
13
14
8. [情境题·2023·河南·生活应用]2023长春马拉松于5月21日
在南岭体育场鸣枪开跑,某同学参加了7.5公里健康跑项
目,他从起点开始以平均每分钟 x 公里的速度跑了10分
钟,此时他离健康跑终点的路程为 公
里.(用含 x 的式子表示)
(7.5-10 x )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
易错点 因混淆平方和(差)与和(差)的平方而致错
9. “ a 的2倍与 b 的和的平方”用式子表示为 .
(2 a + b )2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
课堂小结
用字母表示数
用字母表示数
用字母表示实际问题中的数量
谢谢观看!
3.1用字母表示数
第三章 代数式
【2024新教材】2025-2026学年冀教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
第一页:标题页
3.1 用字母表示数
—— 开启代数世界的大门
(右下角添加授课教师姓名及日期)
第二页:引入
在我们的生活和学习中,经常会遇到一些不确定的数量。比如,一只青蛙一张嘴,两只眼睛四条腿;两只青蛙两张嘴,四只眼睛八条腿…… 如果有很多只青蛙,我们该如何简洁地表示它们的嘴、眼睛和腿的数量呢?这就需要用到用字母表示数的知识。用字母表示数不仅能简洁地表达数量关系,还能为我们解决复杂的数学问题带来便利。本节课我们就来学习如何用字母表示数。
第三页:用字母表示数的意义
简洁性:用字母表示数可以把数量关系简明地表达出来,避免重复表述。
例如,上面提到的青蛙问题,若用\(n\)表示青蛙的只数,那么嘴的数量就是\(n\)张,眼睛的数量是\(2n\)只,腿的数量是\(4n\)条。
一般性:字母可以表示任意的数或特定范围内的数,具有普遍意义。
比如,用\(a\)表示一个数,那么\(a + 5\)就表示比这个数大 5 的数,这里的\(a\)可以是任意整数、小数或分数。
抽象性:用字母表示数是从具体情境中抽象出数量关系的过程,是代数学习的基础。
像长方形的长用\(a\)表示,宽用\(b\)表示,那么长方形的面积就可以表示为\(ab\),这个式子适用于所有长方形面积的计算。
第四页:用字母表示数的书写规则
在用字母表示数时,需要遵循一定的书写规则,以保证表达的规范和清晰:
数字与字母相乘:数字要写在字母的前面,乘号可以省略不写,也可以记作 “ ”。
例如,\(5 x\)可以写作\(5x\)或\(5 ·x\),但不能写作\(x5\)。
字母与字母相乘:乘号可以省略不写,也可以记作 “ ”。
例如,\(a b\)可以写作\(ab\)或\(a ·b\)。
带分数与字母相乘:带分数要先化成假分数,再与字母相乘。
例如,\(1\frac{1}{2} x\)要写作\(\frac{3}{2}x\),而不能写作\(1\frac{1}{2}x\)。
字母与 1 或 - 1 相乘:1 可以省略不写。
例如,\(1 x\)写作\(x\),\(-1 x\)写作\(-x\)。
字母除以数:要写成分数的形式。
例如,\(x ·5\)写作\(\frac{x}{5}\)。
含有字母的式子表示数量时:若式子后面有单位,且式子是和或差的形式,要给式子加括号。
例如,\((a + 3)\)米,不能写作\(a + 3\)米。
第五页:用字母表示常见的数量关系
路程、速度、时间的关系:路程 = 速度 × 时间。若用\(s\)表示路程,\(v\)表示速度,\(t\)表示时间,则\(s = vt\)。
总价、单价、数量的关系:总价 = 单价 × 数量。若用\(c\)表示总价,\(p\)表示单价,\(n\)表示数量,则\(c = pn\)。
工作总量、工作效率、工作时间的关系:工作总量 = 工作效率 × 工作时间。若用\(w\)表示工作总量,\(e\)表示工作效率,\(t\)表示工作时间,则\(w = et\)。
实例:一辆汽车的速度是每小时\(v\)千米,行驶了\(t\)小时,那么它行驶的路程\(s = vt\)千米。如果\(v = 60\)千米 / 小时,\(t = 2\)小时,那么\(s = 60 2 = 120\)千米。
第六页:用字母表示运算定律和计算公式
运算定律:
加法交换律:两个数相加,交换加数的位置,和不变。用字母表示为\(a + b = b + a\)。
加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。用字母表示为\((a + b) + c = a + (b + c)\)。
乘法交换律:两个数相乘,交换因数的位置,积不变。用字母表示为\(ab = ba\)。
乘法结合律:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积不变。用字母表示为\((ab)c = a(bc)\)。
乘法分配律:两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。用字母表示为\((a + b)c = ac + bc\)。
计算公式:
正方形的周长:若用\(a\)表示正方形的边长,\(C\)表示周长,则\(C = 4a\)。
正方形的面积:若用\(a\)表示正方形的边长,\(S\)表示面积,则\(S = a^2\)(读作 “\(a\)的平方”,表示\(a a\))。
长方形的周长:若用\(a\)表示长,\(b\)表示宽,\(C\)表示周长,则\(C = 2(a + b)\)。
长方形的面积:若用\(a\)表示长,\(b\)表示宽,\(S\)表示面积,则\(S = ab\)。
第七页:例题解析(一)—— 用字母表示数的基本应用
例题 1:用含有字母的式子表示下列数量关系。
(1)比\(x\)大 8 的数;(2)\(a\)的 5 倍与\(b\)的和;(3)\(m\)的平方减去\(n\)的 3 倍。
解:(1)比\(x\)大 8 的数表示为\(x + 8\)。
(2)\(a\)的 5 倍与\(b\)的和表示为\(5a + b\)。
(3)\(m\)的平方减去\(n\)的 3 倍表示为\(m^2 - 3n\)。
例题 2:一个商店原有苹果\(a\)千克,卖出了 30 千克,又运来\(b\)千克,现在这个商店有苹果多少千克?
解:原有苹果\(a\)千克,卖出 30 千克后还剩\((a - 30)\)千克,又运来\(b\)千克,所以现在有苹果\((a - 30 + b)\)千克。
第八页:例题解析(二)—— 代入求值
例题 3:已知长方形的长\(a = 5\)厘米,宽\(b = 3\)厘米,求长方形的周长\(C\)和面积\(S\)。
解:根据长方形的周长公式\(C = 2(a + b)\),把\(a = 5\)厘米,\(b = 3\)厘米代入得:\(C = 2 (5 + 3) = 2 8 = 16\)(厘米)。
根据长方形的面积公式\(S = ab\),把\(a = 5\)厘米,\(b = 3\)厘米代入得:\(S = 5 3 = 15\)(平方厘米)。
所以长方形的周长是 16 厘米,面积是 15 平方厘米。
例题 4:当\(x = 10\)时,求\(3x + 20\)的值。
解:把\(x = 10\)代入\(3x + 20\)得:\(3 10 + 20 = 30 + 20 = 50\)。
第九页:课堂练习
填空题:
用字母表示乘法分配律是______。
小明今年\(a\)岁,爸爸比他大 28 岁,爸爸今年______岁。
一个三角形的底是\(a\)厘米,高是\(h\)厘米,它的面积是______平方厘米。
选择题:
下列式子中,符合书写规则的是( )
A. \(a5\) B. \(1\frac{1}{3}x\) C. \(x ·5\) D. \(2a + 3\)
当\(a = 4\),\(b = 5\)时,\(ab + 2\)的值是( )
A. 22 B. 18 C. 11 D. 9
解答题:
(1)用含有字母的式子表示下面的数量关系。
①\(x\)与\(y\)的和的 3 倍;②比\(a\)的 4 倍少 5 的数。
(2)一个正方形的边长是\(a\)米,它的周长是多少米?面积是多少平方米?当\(a = 6\)时,周长和面积各是多少?
(3)一辆自行车每小时行驶\(v\)千米,行驶了\(t\)小时,一共行驶了多少千米?如果\(v = 15\),\(t = 2\),一共行驶了多少千米?
第十页:课堂小结
用字母表示数的意义:具有简洁性、一般性和抽象性,能简洁表达数量关系。
用字母表示数的书写规则:注意数字与字母、字母与字母的乘除表示方法,以及带分数、1 或 - 1 与字母相乘的规则等。
用字母表示常见的数量关系、运算定律和计算公式,能帮助我们更方便地解决问题。
代入求值是用字母表示数的重要应用,将字母的具体数值代入式子中,可求出式子的值。
第十一页:作业布置
教材第 XX 页习题 3.1 第 1、2、3、4 题。
填空题:
每支铅笔\(a\)元,买了 5 支,应付______元。
一个数是\(x\),另一个数比它的 3 倍多 2,另一个数是______。
判断题(对的打 “√”,错的打 “×”):
\(a a\)可以写作\(2a\)。( )
因为\(2^2 = 2 2\),所以\(a^2 = a 2\)。( )
式子\(5x + 6\)可以表示 5 与\(x\)的和的 6 倍。( )
解答题:
(1)用含有字母的式子表示下列各题的数量关系。
①\(a\)除以\(b\)的商减去\(c\);②\(m\)与\(n\)的差的平方。
(2)一个长方形的长是\(2x\)米,宽是\(x\)米,它的周长和面积各是多少?当\(x = 3\)时,周长和面积分别是多少?
(3)某工厂每天生产\(a\)个零件,生产了 7 天,还剩下\(b\)个没生产,这批零件一共有多少个?如果\(a = 120\),\(b = 300\),这批零件一共有多少个?
思考:用字母表示数和用具体数字表示数有什么联系和区别?
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
学习目标
1.理解用字母表示数的意义,体会用字母表示数的必要性和优越性.
2.能用字母表示运算律、计算公式及各种数与数量关系.
3.逐步深化对字母表示数的意义的认识,体验用数学符号表达数量关系的过程,增强符号意识.
小明上小学时,在一堂数学课上,发现了下列等式:
1+2=2+1
3.5+5.6=5.6+3.5
(1)这几个式子反映了什么规律?
a + b = b + a
(2)能用更简明的方法表示出来吗?
加法交换律:两个数相加,交换加数的位置,和不变.
课堂导入
观察下表回答下列问题
(1)请算出他们每个人100米短跑的速度,并将结果填入表中(结果保留两位小数).
姓名 小帆 大林 小明
成绩/s 16 14.5 15.2
速度/(m/s)
做一做:
6.25
6.90
6.58
(2)写出计算速度时所用的公式.
其中v表示速度,s表示路程,t表示时间
新知探究
知识点1:用字母表示数
如何用字母表示它们
运算律 字 母 表 示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
a + b = b + a
(a + b) +c= a +(b + c)
ab = ba
(ab)c =a(bc)
a (b+ c )=ab+ac
新知探究
知识点2:用字母表示数的常见应用
1.长方形的面积公式S=ab
S 表示面积,a、b分别表示长与宽
2.圆的面积计算公式S=πr
S 表示面积,r表示圆的半径
3.长方体的体积计算公式V=abc
a,b,c分别表示长方体的长、宽、高
4.圆柱体积计算公式V=πr h.
V表示体积,r表示底面半径,h表示圆柱的高
新知探究
知识点2:用字母表示数的常见应用
在自然数范围内,回答下列问题.
(1)请用字母表示偶数和奇数.
偶数用字母表示为2m,奇数用字母表示为2m+1(m为自然数).
(2)两个偶数之和具有怎样的特征?两个奇数之和又具有怎样的特征?请你提出猜想,并证明猜想的正确性.
两个偶数的和是偶数,两个奇数的和也是偶数.
一起探究:
(3)如果P是正整数,那么与P相邻的两个自然数之和是偶数吗?请说明理由.
与P相邻的两个自然数之和是偶数.
知识点2:用字母表示数的常见应用
新知探究
用字母表示数,说明:
(1)任意两个奇数之和是偶数.
问题引导:(m,n为自然数)
(1)一个奇数怎么表示?
2m+ 1
(2)两个相邻的奇数怎么表示?
2m-1、2m+1
(3)任意两个奇数怎么表示?
2m+1和 2n+1
解:(2m+1)+(2n+1)
=2(m+ n+1).
新知探究
知识点2:用字母表示数的常见应用
(2)如果m为自然数,那么与m相邻的两个自然数之和是偶数.
问题引导:(m为自然数)
与m相邻的两个自然数怎么表示?
m-1和m+1
解:(m+1)+(m-1)
=2m.
新知探究
知识点2:用字母表示数的常见应用
(1)用字母表示数,同一问题中,同一字母只能表示同一数量,不同的数量要用不同的字母表示.
(2)用字母表示实际问题中的某一数量时,字母的取值需使这个问题有意义,并且符合实际.
(3)用字母表示数可简明表达问题中的数量关系、公式、法则、规律等.
1. 填空:
(1)-6℃下降2℃后是____℃;温度由t℃下降2℃度后是_____℃;
(2)今年李华m岁,去年李华_____ 岁,五年后李华 ____ 岁;
(3)三个连续偶数中间一个为2n,则其余两个为_____、 ;
(t -2)
(m-1)
(m+5)
2n-2
2n+2
随堂练习
-8
(4)某商店上月收入a元,本月收入比上月2 倍多10元,本月收入 元;
(5)城市市区人口a万人,市区绿化面积m万㎡,则平均每个人拥有绿地 ㎡;
(6)某城市5年前人均年收入为n元,预计今年人均年收入是5年前的2倍多500元,那么今年人均年收入将达________ 元.
(2a+10)
(2a+10)
(2n+500)
随堂练习
2.选择
(1)用字母表示乘法对加法的分配律是( )
A.a(b+c) B.ab+ac
C.a(b+c)=ab+ac D. ab=ba
C
(2)昨天的最高温度是27℃,今天气温比昨天下降t℃,今天的最高气温是( )
A.27+t B.27-t℃
C.(27+t)℃ D.(27-t)℃
D
随堂练习
(3)购买1个单价为a元的面包 和3瓶单价为b元的饮料,所需钱数为( )
A.(a+b)元. B.3(a+b)元.
C.(3a+b)元. D.(a+3b)元.
D
随堂练习
知识点1 用字母表示数字的数量关系
1. 如果某天石家庄的最低气温为 a ℃,中午12点的气温比最
低气温高了10℃,那么中午12点的气温为( C )
A. (10- a )℃ B. ( a -10)℃
C. ( a +10)℃ D. ( a +12)℃
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
2. [2024·重庆一中模拟]用式子表示: a 的2倍与3的和,下列
表示正确的是( B )
A. 2 a -3 B. 2 a +3
C. 2( a -3) D. 2( a +3)
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
3. (1)一个两位数,它的十位数字是 x ,个位数字是 y ,那么
这个两位数是( D )
A. x + y B. 10 xy
C. 10( x + y ) D. 10 x + y
【点拨】
十位上的数字乘10,再加上个位上的数字即可得到这
个两位数,故选D.
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
(2)设 x 表示两位数, y 表示三位数,如果把 x 放在 y 的左
边组成一个五位数,那么这个五位数可表示为( B )
A. xy B. 1 000 x + y
C. x + y D. 100 x + y
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
知识点2 用字母表示图形中的数量关系
4. [母题·2024·石家庄第四十二中学期末·教材P104习题B组
T3]如图,边长为 m 的正方形纸片上剪去四个直径都为 d
的半圆,则阴影部分的周长是( D )
A. m2-π d2 B. m2- π d2
C. 4 m -π d D. 4 m +2π d -4 d
1
2
3
4
5
6
7
8
9
10
11
12
13
14
【点拨】
原正方形的周长为4 m ,四个直径都为 d 的半圆的长
度和为2π d ,则阴影部分的周长是4 m +2π d -4 d .
D
【答案】
1
2
3
4
5
6
7
8
9
10
11
12
13
14
5. [2023·山西]如图是一组有规律的图案,它由若干个大小相
同的圆片组成,第1个图案中有4个白色圆片,第2个图案
中有6个白色圆片,第3个图案中有8个白色圆片,第4个图
案中有10个白色圆片,…,依此规律,第 n 个图案中
有 个白色圆片(用含 n 的式子表示).
(2+2 n )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
【点拨】
第1个图案中有2+2×1=4(个)白色圆片;
第2个图案中有2+2×2=6(个)白色圆片;
第3个图案中有2+2×3=8(个)白色圆片;
…
第 n 个图案中有(2+2 n )个白色圆片.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
知识点3 用字母表示实际中的数量关系
6. 某校利用课后服务开展了主题为“书香满校园”的读书活
动,现需购买甲、乙两种读本共100本供学生阅读,其中
甲种读本的单价为10元/本,乙种读本的单价为8元/本,设
购买甲种读本 x 本,则购买乙种读本的费用为( C )
A. 8 x 元 B. 10(100- x )元
C. 8(100- x )元 D. (100-8 x )元
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
7. [2023·河南]某校计划给每个年级配发 n 套劳动工具,则3
个年级共需配发 套劳动工具.
3 n
1
2
3
4
5
6
7
8
9
10
11
12
13
14
8. [情境题·2023·河南·生活应用]2023长春马拉松于5月21日
在南岭体育场鸣枪开跑,某同学参加了7.5公里健康跑项
目,他从起点开始以平均每分钟 x 公里的速度跑了10分
钟,此时他离健康跑终点的路程为 公
里.(用含 x 的式子表示)
(7.5-10 x )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
易错点 因混淆平方和(差)与和(差)的平方而致错
9. “ a 的2倍与 b 的和的平方”用式子表示为 .
(2 a + b )2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
课堂小结
用字母表示数
用字母表示数
用字母表示实际问题中的数量
谢谢观看!
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
