3.2.1 代数式 课件(共27张PPT)
文档属性
| 名称 | 3.2.1 代数式 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
3.2.1代数式
第三章 代数式
【2024新教材】2025-2026学年冀教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
第一页:标题页
3.2.1 代数式
—— 从具体到抽象的数学表达
(右下角添加授课教师姓名及日期)
第二页:引入
在上一节课中,我们学习了用字母表示数,知道了字母可以简洁地表达数量关系。比如,“比\(x\)大 5 的数” 可以表示为\(x + 5\),“\(a\)的 3 倍与\(b\)的和” 可以表示为\(3a + b\)。这些用字母和运算符号连接而成的式子,就是我们今天要学习的代数式。代数式是代数学习中的重要概念,它能帮助我们更系统地表示和研究数量关系。
第三页:代数式的定义
定义:用运算符号(加、减、乘、除、乘方等)把数和表示数的字母连接而成的式子叫做代数式。
注意:
单独的一个数或者一个字母也是代数式。例如,\(5\)、\(a\)、\(-3\)、\(x\)等都是代数式。
代数式中不含有等号或不等号(如\(=\)、\(\neq\)、\(>\)、\(<\)等)。例如,\(x + 2 = 5\)不是代数式,而是等式;\(3x > 7\)也不是代数式,而是不等式。
实例:
属于代数式的有:\(2x\)、\(a + b\)、\(\frac{m}{n}\)(\(n\neq0\))、\(x^2 - 3\)、\(0\)、\(y\)等。
不属于代数式的有:\(x + 1 = 3\)、\(2y < 5\)、\(a \geq b\)等。
第四页:代数式的构成
代数式的构成包括以下几个部分:
数:如\(1\)、\(3.5\)、\(-2\)等。
字母:如\(a\)、\(b\)、\(x\)、\(y\)等,表示未知的数或特定的数量。
运算符号:包括加(\(+\))、减(\(-\))、乘(\(\times\)或省略不写)、除(\(\div\)或写成分数形式)、乘方(\(^2\)、\(^3\)等,如\(x^2\)表示\(x\times x\))。
实例解析:代数式\(3x^2 + 2y - 5\)由数\(3\)、\(2\)、\(-5\),字母\(x\)、\(y\),以及运算符号\(+\)、\(-\)、乘方和乘法(\(3\)与\(x^2\)的乘法,\(2\)与\(y\)的乘法)构成。
第五页:代数式的书写规范
代数式的书写要遵循一定的规范,以保证表达清晰、统一,这些规范与用字母表示数的书写规则基本一致:
数字与字母相乘:数字在前,字母在后,乘号可省略。例如,\(5\times a\)写作\(5a\),不写作\(a5\)。
字母与字母相乘:乘号可省略或写作 “ ”。例如,\(a\times b\)写作\(ab\)或\(a ·b\)。
带分数与字母相乘:带分数化为假分数。例如,\(1\frac{1}{2}\times x\)写作\(\frac{3}{2}x\),不写作\(1\frac{1}{2}x\)。
除法运算:写成分数形式。例如,\(x\div 4\)写作\(\frac{x}{4}\),\(m\div n\)写作\(\frac{m}{n}\)(\(n\neq0\))。
含有加减运算的代数式带单位:要给代数式加括号。例如,\((a + 2)\)米,不写作\(a + 2\)米。
乘方的表示:相同字母相乘用乘方表示。例如,\(x\times x\)写作\(x^2\),\(a\times a\times a\)写作\(a^3\)。
第六页:列代数式
列代数式就是把实际问题中的数量关系用代数式表示出来,步骤如下:
分析数量关系:明确题目中各数量之间的运算关系(如和、差、积、商、倍、分等)。
确定字母表示的量:选择合适的字母表示题目中的未知量。
写出代数式:根据数量关系,用运算符号把数和字母连接起来。
例题 1:用代数式表示下列数量关系。
(1)比\(a\)的 2 倍小 3 的数;
(2)\(x\)的平方与\(y\)的立方的和;
(3)\(m\)与\(n\)的差除以\(m\)与\(n\)的积的商。
解:(1)\(a\)的 2 倍是\(2a\),比它小 3 的数是\(2a - 3\)。
(2)\(x\)的平方是\(x^2\),\(y\)的立方是\(y^3\),它们的和是\(x^2 + y^3\)。
(3)\(m\)与\(n\)的差是\(m - n\),\(m\)与\(n\)的积是\(mn\),商是\(\frac{m - n}{mn}\)(\(m\neq0\),\(n\neq0\))。
第七页:代数式的意义
代数式的意义包括两方面:一是代数式所表示的数量关系,二是代数式在具体情境中的实际含义。
1. 解释代数式的数量关系:
例如,代数式\(3a + 2b\)可以表示 “\(a\)的 3 倍与\(b\)的 2 倍的和”。
代数式\(\frac{s}{t}\)(\(t\neq0\))可以表示 “\(s\)除以\(t\)的商”。
2. 结合情境解释代数式的实际含义:
若\(a\)表示一个苹果的质量(单位:克),则\(3a\)表示 “3 个苹果的总质量”。
若\(x\)表示一支铅笔的价格(单位:元),\(y\)表示一块橡皮的价格(单位:元),则\(2x + 3y\)表示 “买 2 支铅笔和 3 块橡皮的总价格”。
例题 2:说出下列代数式的意义。
(1)\(5x - y\);(2)\(\frac{a + b}{2}\)。
解:(1)\(5x - y\)可以表示 “\(x\)的 5 倍与\(y\)的差”。若\(x\)表示每千克苹果的价格,\(y\)表示买其他物品的花费,则\(5x - y\)表示 “买 5 千克苹果比买其他物品多花的钱(若结果为正)或少花的钱(若结果为负)”。
(2)\(\frac{a + b}{2}\)可以表示 “\(a\)与\(b\)的和的一半”。若\(a\)、\(b\)分别表示两个数,则\(\frac{a + b}{2}\)表示 “这两个数的平均数”。
第八页:例题解析(综合应用)
例题 3:一个长方形的长为\(a\)厘米,宽为\(b\)厘米,用代数式表示这个长方形的周长和面积,并说明当\(a = 8\),\(b = 5\)时,代数式的值的实际意义。
解:长方形的周长 = 2×(长 + 宽),用代数式表示为\(2(a + b)\)厘米;长方形的面积 = 长 × 宽,用代数式表示为\(ab\)平方厘米。
当\(a = 8\),\(b = 5\)时,周长\(2(a + b)=2 (8 + 5)=26\)厘米,表示这个长方形的实际周长是 26 厘米;面积\(ab = 8 5 = 40\)平方厘米,表示这个长方形的实际面积是 40 平方厘米。
例题 4:某班有学生\(m\)人,其中男生有\(n\)人,用代数式表示女生人数,并说明当\(m = 45\),\(n = 23\)时,代数式的值的意义。
解:女生人数 = 总人数 - 男生人数,用代数式表示为\((m - n)\)人。
当\(m = 45\),\(n = 23\)时,\(m - n = 45 - 23 = 22\)人,表示这个班的女生实际有 22 人。
第九页:课堂练习
填空题:
下列式子中,是代数式的有______(填序号)。
①\(3x + 5\) ②\(x = 2\) ③\(7\) ④\(a\) ⑤\(2y > 1\)
用代数式表示 “\(x\)的 3 倍与\(y\)的和的平方” 是______。
若\(a\)表示每本练习本的价格,那么\(5a\)表示______。
选择题:
下列代数式的书写正确的是( )
A. \(a\times 3\) B. \(x\div 2\) C. \(2\frac{1}{2}m\) D. \(\frac{1}{2}ab\)
代数式\(2a - b\)的意义是( )
A. \(a\)的 2 倍与\(b\)的差 B. \(a\)与\(b\)的差的 2 倍
C. \(a\)的 2 倍与\(b\)的和 D. \(a\)与\(b\)的 2 倍的差
解答题:
(1)用代数式表示下列数量关系。
①比\(m\)的倒数小 5 的数;②\(a\)与\(b\)的平方和。
(2)说出代数式\(3(m + n)\)的意义(至少两种)。
(3)一个三角形的底为\(x\)厘米,高为\(h\)厘米,用代数式表示这个三角形的面积。当\(x = 6\),\(h = 4\)时,这个三角形的面积是多少平方厘米?
第十页:课堂小结
代数式的定义:用运算符号把数和字母连接而成的式子,单独的一个数或字母也是代数式。
代数式的构成:包括数、字母和运算符号(加、减、乘、除、乘方等)。
代数式的书写规范:遵循与用字母表示数类似的规则,如数字在前、乘号省略、除法写成分数形式等。
列代数式:分析数量关系,用代数式表示实际问题中的数量。
代数式的意义:既可以表示数量关系,也可以结合具体情境表示实际含义。
第十一页:作业布置
教材第 XX 页习题 3.2 第 1、2、3 题。
填空题:
用代数式表示 “\(a\)的相反数与\(b\)的绝对值的和” 是______。
若\(x\)表示一个数,那么 “这个数的平方与这个数的 3 倍的差” 用代数式表示为______。
判断题(对的打 “√”,错的打 “×”):
代数式中一定含有字母。( )
\(x + 1 = 0\)是代数式。( )
\(ab\)表示\(a\)与\(b\)的积。( )
解答题:
(1)用代数式表示下列数量关系。
①\(x\)的一半与\(y\)的 3 倍的差;②\(m\)与\(n\)的和的倒数(\(m + n\neq0\))。
(2)解释代数式\(\frac{1}{2}ah\)的意义(结合几何图形或实际情境)。
(3)某工厂第一季度生产零件\(a\)个,第二季度比第一季度多生产\(b\)个,用代数式表示上半年共生产零件的个数。当\(a = 5000\),\(b = 500\)时,上半年共生产多少个零件?
思考:代数式与用字母表示数有什么联系?列代数式时,如何准确把握数量之间的关系?
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
学习目标
1.理解代数式的意义,体会代数式是表示数量和数量关系的数学模型,初步培养模型观念.
2.明确代数式的书写要求,并能按照要求正确书写代数式.
我们小时候都听过这样一段儿歌
“一只青蛙一张嘴,两只眼睛,四条腿,一声扑通跳下水……”请接下去.
n只青蛙, 张嘴, 只眼睛,
条腿, 声扑通跳下水.
n
2n
4n
n
课堂导入
代数式的概念
用运算符号连接数和字母的式子叫作代数式.(运算符号包括+、-、×、÷、乘方)
1.单独的一个数或一个表示数的字母也是代数式..
2.代数式中除了含有数,字母和运算符号外,还可以含有括号.
3.代数中不含有“=”、“>”、“<”.
【注意】
新知探究
知识点1 代数式的概念
代数式的概念
用含有字母的式子表示下列数量关系:
(1)买一个足球需要a元,买一个篮球需要b元,则买一个足球和一个篮球共需要___________ 元;
(2)某产品前年的产量是n件,去年的产量是前年产量的3倍少20件,去年的产量是___________ 件;
(3)某一正方形菜地的边长为am,它的面积是另一菜地面积的2倍,另一菜地的面积为___________ m2 .
新知探究
知识点1 代数式的概念
例1: 下列式子中,哪些是代数式?
(1)x+6;(2)x=2x-1;(3)a;(4)2n>3;(5)0.
解: 因为代数式不能含有“=”“>”或“<”,
所以是代数式的有:(1)(3)(5).
注意:代数式中的式是指由+、-、×、÷、乘方运算符号连接而成的式子.
新知探究
知识点1 代数式的概念
解:(1)2a+5表示的是a的2倍与5的和.
(2)2(a+5)表示的是a与5的和的2倍.
(3)a2+b2表示的是a的平方与b的平方的和.
(4)(a+b)2表示的是a与b的和的平方.
例2 指出下列各代数式的意义:
(1)2a+5; (2)2(a+5);(3)a2+b2; (4)(a+b)2.
新知探究
知识点2 代数式的意义
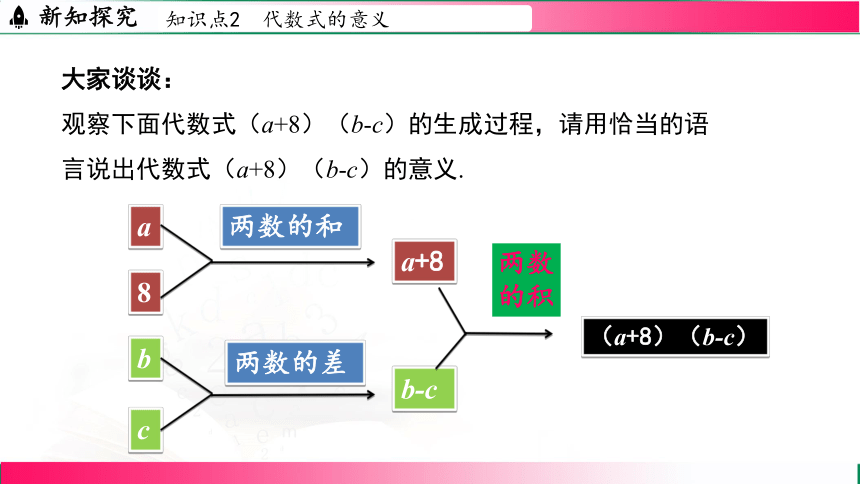
大家谈谈:
观察下面代数式(a+8)(b-c)的生成过程,请用恰当的语言说出代数式(a+8)(b-c)的意义.
a
8
两数的和
a+8
b
c
两数的差
b-c
两数
的积
(a+8)(b-c)
新知探究
知识点2 代数式的意义
例3 请用代数式表示:
(1)a,b的差与c的平方的和.
(2)百位数字是a,十位数字是b,个位数字是c的三位数.
(3)三个连续的的整数(用同一个字母表示),以及它们的和.
解:(1)(a-b)+ c2.
(2)100a+10b+ c.(其中a,b,c是0到9之间的整数,且a≠0.
(3)设m是正数,三个连续整数可表示为m-1,m,m+1,它们的和为(m-1)+m+(m+1).
新知探究
知识点3 列代数式
列代数式就是把实际问题中与数量有关的语句,用含有数、字母和运算符号的式子表示出来,也就是把文字语言转化为符号语言.
①要抓住关键词语,明确它们的意义以及它们之间的关系,如和、差、积、商及大、小、多、少、倍、分、倒数、相反数等;
②理清语句层次明确运算顺序,一般按“先读先写”的原则列出式子.
③牢记一些概念和公式.
新知探究
知识点3 列代数式
1.字母与字母,数与字母相乘时,“×” 号通常省略不写或写“·”;
代数式的书写要求:
2.数与字母相乘时,数字通常写在字母的左边;
100×t
100t 或100·t
b×2a
2ab或2·a·b
新知探究
知识点4 代数式的书写要求
3.除法运算一般以分数的形式表示;
s÷v
s
v
4.带分数与字母相乘时,通常把带分数化成假分数;
1
3
1 n
4n
3
5.在实际问题中含有单位时,一般要把代数式用括号括起来,再写单位.
例如:长方形周长为(2a+4b)米.
例4:判断下列式子书写是否规范,不规范的请改正.
新知探究
知识点4 代数式的书写要求
1.用代数式表示:
(1)一个数x与6的和;
(2)比-5小a的数;
(3)某校买书25本,每本a元,该校应付书费多少元?
(4)容量为60L的铁桶,贮满油,取出(x+1)L后,桶内还剩油多少升?
解:
(1) x+6;
(2) -5-a;
(3) 25a元;
(4)[60-(x+1)]L.
随堂练习
知识点1 代数式的定义
1. 下列式子中,不属于代数式的是( D )
A. a +3 B. 2 mn
C. 0 D. x > y
D
1
2
3
4
5
6
7
8
9
10
11
12
13
2. 下列各式中,是代数式的有( D )
① ;② a -1>0;③ ab = ba ;
④ a ;⑤0;⑥ ( a2- b2).
A. 1个 B. 2个
C. 3个 D. 4个
D
1
2
3
4
5
6
7
8
9
10
11
12
13
知识点2 代数式的书写规则
3. [2024·石家庄外国语学校月考]下列含有字母的式子中,符
合书写规范要求的是( C )
A. -1 a
D. ( x + y )÷ z
C
1
2
3
4
5
6
7
8
9
10
11
12
13
4. 下面不符合用字母表示数的书写要求的有( C )
①3 a ;②( x - y )÷( x + y );③( a + b )2;
④ x - y 米;⑤ ;⑥ .
A. 2个 B. 3个
C. 4个 D. 5个
C
1
2
3
4
5
6
7
8
9
10
11
12
13
知识点3 代数式表示的意义
5. [2023·河北]代数式-7 x 的意义可以是( C )
A. -7与 x 的和 B. -7与 x 的差
C. -7与 x 的积 D. -7与 x 的商
C
1
2
3
4
5
6
7
8
9
10
11
12
13
6. 一列火车长 m m,以每秒 n m的速度通过一个长为 p m的
桥洞,用代数式表示火车完全通过桥洞所需的时间,正确
的为( D )
D
1
2
3
4
5
6
7
8
9
10
11
12
13
7. 用文字语言叙述代数式 - ,不正确的是( A )
A. 1除以 a 与 b 的差的商
B. 比 a 的倒数小1除以 b 的商的数
C. 1除以 a 的商与1除以 b 的商的差
D. a 的倒数与 b 的倒数的差
A
1
2
3
4
5
6
7
8
9
10
11
12
13
8. 某商店举办促销活动,促销的方法是将原价 x 元的衣服以
元出售,则下列说法中,能正确表达该商店
促销方法的是( B )
A. 原价减去10元后再打八折
B. 原价打八折后再减去10元
C. 原价减去10元后再打两折
D. 原价打两折后再减去10元
B
1
2
3
4
5
6
7
8
9
10
11
12
13
易错点 理解不透数量关系而致错
9. [2024·连云港期末]甲数比乙数的4倍少1,则下列说法:①
设乙数为 x ,则甲数为4 x -1;②设甲数为 x ,则乙数为
x +1;③设甲数为 x ,则乙数为 ( x +1);④设甲数为
x ,则乙数为 ( x -1),其中正确的是( A )
A. ①③ B. ①②
C. ②④ D. ①④
A
1
2
3
4
5
6
7
8
9
10
11
12
13
利用代数式的特征说明其数学意义
10. 说出下列代数式的意义:
(1)8 a +7;(2)4- ;
(3) a2- b2;(4)( a - b )2.
【解】(1)8 a +7的意义是 a 的8倍与7的和.
(2)4- 的意义是4与 a 除以 b 的商的差.
(3) a2- b2的意义是 a 的平方与 b 的平方的差.
(4)( a - b )2的意义是 a 与 b 的差的平方.
1
2
3
4
5
6
7
8
9
10
11
12
13
利用图形的特征判断代数式表示阴影面积的方法
11. [母题 教材P104习题B组T3]下面四个代数式中,不能表
示图中阴影部分面积的是( D )
A. x2+3 x +6
B. ( x +3)( x +2)-2 x
C. 3( x +2)+ x2
D. x2+5 x
D
1
2
3
4
5
6
7
8
9
10
11
12
13
代数式
定义
应用
用运算符号连接数和字母的式子叫作代数式.单独一个数或一个表示数的字母也是代数式.
代数式所表示的意义
根据实际问题列代数式
课堂小结
谢谢观看!
3.2.1代数式
第三章 代数式
【2024新教材】2025-2026学年冀教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
第一页:标题页
3.2.1 代数式
—— 从具体到抽象的数学表达
(右下角添加授课教师姓名及日期)
第二页:引入
在上一节课中,我们学习了用字母表示数,知道了字母可以简洁地表达数量关系。比如,“比\(x\)大 5 的数” 可以表示为\(x + 5\),“\(a\)的 3 倍与\(b\)的和” 可以表示为\(3a + b\)。这些用字母和运算符号连接而成的式子,就是我们今天要学习的代数式。代数式是代数学习中的重要概念,它能帮助我们更系统地表示和研究数量关系。
第三页:代数式的定义
定义:用运算符号(加、减、乘、除、乘方等)把数和表示数的字母连接而成的式子叫做代数式。
注意:
单独的一个数或者一个字母也是代数式。例如,\(5\)、\(a\)、\(-3\)、\(x\)等都是代数式。
代数式中不含有等号或不等号(如\(=\)、\(\neq\)、\(>\)、\(<\)等)。例如,\(x + 2 = 5\)不是代数式,而是等式;\(3x > 7\)也不是代数式,而是不等式。
实例:
属于代数式的有:\(2x\)、\(a + b\)、\(\frac{m}{n}\)(\(n\neq0\))、\(x^2 - 3\)、\(0\)、\(y\)等。
不属于代数式的有:\(x + 1 = 3\)、\(2y < 5\)、\(a \geq b\)等。
第四页:代数式的构成
代数式的构成包括以下几个部分:
数:如\(1\)、\(3.5\)、\(-2\)等。
字母:如\(a\)、\(b\)、\(x\)、\(y\)等,表示未知的数或特定的数量。
运算符号:包括加(\(+\))、减(\(-\))、乘(\(\times\)或省略不写)、除(\(\div\)或写成分数形式)、乘方(\(^2\)、\(^3\)等,如\(x^2\)表示\(x\times x\))。
实例解析:代数式\(3x^2 + 2y - 5\)由数\(3\)、\(2\)、\(-5\),字母\(x\)、\(y\),以及运算符号\(+\)、\(-\)、乘方和乘法(\(3\)与\(x^2\)的乘法,\(2\)与\(y\)的乘法)构成。
第五页:代数式的书写规范
代数式的书写要遵循一定的规范,以保证表达清晰、统一,这些规范与用字母表示数的书写规则基本一致:
数字与字母相乘:数字在前,字母在后,乘号可省略。例如,\(5\times a\)写作\(5a\),不写作\(a5\)。
字母与字母相乘:乘号可省略或写作 “ ”。例如,\(a\times b\)写作\(ab\)或\(a ·b\)。
带分数与字母相乘:带分数化为假分数。例如,\(1\frac{1}{2}\times x\)写作\(\frac{3}{2}x\),不写作\(1\frac{1}{2}x\)。
除法运算:写成分数形式。例如,\(x\div 4\)写作\(\frac{x}{4}\),\(m\div n\)写作\(\frac{m}{n}\)(\(n\neq0\))。
含有加减运算的代数式带单位:要给代数式加括号。例如,\((a + 2)\)米,不写作\(a + 2\)米。
乘方的表示:相同字母相乘用乘方表示。例如,\(x\times x\)写作\(x^2\),\(a\times a\times a\)写作\(a^3\)。
第六页:列代数式
列代数式就是把实际问题中的数量关系用代数式表示出来,步骤如下:
分析数量关系:明确题目中各数量之间的运算关系(如和、差、积、商、倍、分等)。
确定字母表示的量:选择合适的字母表示题目中的未知量。
写出代数式:根据数量关系,用运算符号把数和字母连接起来。
例题 1:用代数式表示下列数量关系。
(1)比\(a\)的 2 倍小 3 的数;
(2)\(x\)的平方与\(y\)的立方的和;
(3)\(m\)与\(n\)的差除以\(m\)与\(n\)的积的商。
解:(1)\(a\)的 2 倍是\(2a\),比它小 3 的数是\(2a - 3\)。
(2)\(x\)的平方是\(x^2\),\(y\)的立方是\(y^3\),它们的和是\(x^2 + y^3\)。
(3)\(m\)与\(n\)的差是\(m - n\),\(m\)与\(n\)的积是\(mn\),商是\(\frac{m - n}{mn}\)(\(m\neq0\),\(n\neq0\))。
第七页:代数式的意义
代数式的意义包括两方面:一是代数式所表示的数量关系,二是代数式在具体情境中的实际含义。
1. 解释代数式的数量关系:
例如,代数式\(3a + 2b\)可以表示 “\(a\)的 3 倍与\(b\)的 2 倍的和”。
代数式\(\frac{s}{t}\)(\(t\neq0\))可以表示 “\(s\)除以\(t\)的商”。
2. 结合情境解释代数式的实际含义:
若\(a\)表示一个苹果的质量(单位:克),则\(3a\)表示 “3 个苹果的总质量”。
若\(x\)表示一支铅笔的价格(单位:元),\(y\)表示一块橡皮的价格(单位:元),则\(2x + 3y\)表示 “买 2 支铅笔和 3 块橡皮的总价格”。
例题 2:说出下列代数式的意义。
(1)\(5x - y\);(2)\(\frac{a + b}{2}\)。
解:(1)\(5x - y\)可以表示 “\(x\)的 5 倍与\(y\)的差”。若\(x\)表示每千克苹果的价格,\(y\)表示买其他物品的花费,则\(5x - y\)表示 “买 5 千克苹果比买其他物品多花的钱(若结果为正)或少花的钱(若结果为负)”。
(2)\(\frac{a + b}{2}\)可以表示 “\(a\)与\(b\)的和的一半”。若\(a\)、\(b\)分别表示两个数,则\(\frac{a + b}{2}\)表示 “这两个数的平均数”。
第八页:例题解析(综合应用)
例题 3:一个长方形的长为\(a\)厘米,宽为\(b\)厘米,用代数式表示这个长方形的周长和面积,并说明当\(a = 8\),\(b = 5\)时,代数式的值的实际意义。
解:长方形的周长 = 2×(长 + 宽),用代数式表示为\(2(a + b)\)厘米;长方形的面积 = 长 × 宽,用代数式表示为\(ab\)平方厘米。
当\(a = 8\),\(b = 5\)时,周长\(2(a + b)=2 (8 + 5)=26\)厘米,表示这个长方形的实际周长是 26 厘米;面积\(ab = 8 5 = 40\)平方厘米,表示这个长方形的实际面积是 40 平方厘米。
例题 4:某班有学生\(m\)人,其中男生有\(n\)人,用代数式表示女生人数,并说明当\(m = 45\),\(n = 23\)时,代数式的值的意义。
解:女生人数 = 总人数 - 男生人数,用代数式表示为\((m - n)\)人。
当\(m = 45\),\(n = 23\)时,\(m - n = 45 - 23 = 22\)人,表示这个班的女生实际有 22 人。
第九页:课堂练习
填空题:
下列式子中,是代数式的有______(填序号)。
①\(3x + 5\) ②\(x = 2\) ③\(7\) ④\(a\) ⑤\(2y > 1\)
用代数式表示 “\(x\)的 3 倍与\(y\)的和的平方” 是______。
若\(a\)表示每本练习本的价格,那么\(5a\)表示______。
选择题:
下列代数式的书写正确的是( )
A. \(a\times 3\) B. \(x\div 2\) C. \(2\frac{1}{2}m\) D. \(\frac{1}{2}ab\)
代数式\(2a - b\)的意义是( )
A. \(a\)的 2 倍与\(b\)的差 B. \(a\)与\(b\)的差的 2 倍
C. \(a\)的 2 倍与\(b\)的和 D. \(a\)与\(b\)的 2 倍的差
解答题:
(1)用代数式表示下列数量关系。
①比\(m\)的倒数小 5 的数;②\(a\)与\(b\)的平方和。
(2)说出代数式\(3(m + n)\)的意义(至少两种)。
(3)一个三角形的底为\(x\)厘米,高为\(h\)厘米,用代数式表示这个三角形的面积。当\(x = 6\),\(h = 4\)时,这个三角形的面积是多少平方厘米?
第十页:课堂小结
代数式的定义:用运算符号把数和字母连接而成的式子,单独的一个数或字母也是代数式。
代数式的构成:包括数、字母和运算符号(加、减、乘、除、乘方等)。
代数式的书写规范:遵循与用字母表示数类似的规则,如数字在前、乘号省略、除法写成分数形式等。
列代数式:分析数量关系,用代数式表示实际问题中的数量。
代数式的意义:既可以表示数量关系,也可以结合具体情境表示实际含义。
第十一页:作业布置
教材第 XX 页习题 3.2 第 1、2、3 题。
填空题:
用代数式表示 “\(a\)的相反数与\(b\)的绝对值的和” 是______。
若\(x\)表示一个数,那么 “这个数的平方与这个数的 3 倍的差” 用代数式表示为______。
判断题(对的打 “√”,错的打 “×”):
代数式中一定含有字母。( )
\(x + 1 = 0\)是代数式。( )
\(ab\)表示\(a\)与\(b\)的积。( )
解答题:
(1)用代数式表示下列数量关系。
①\(x\)的一半与\(y\)的 3 倍的差;②\(m\)与\(n\)的和的倒数(\(m + n\neq0\))。
(2)解释代数式\(\frac{1}{2}ah\)的意义(结合几何图形或实际情境)。
(3)某工厂第一季度生产零件\(a\)个,第二季度比第一季度多生产\(b\)个,用代数式表示上半年共生产零件的个数。当\(a = 5000\),\(b = 500\)时,上半年共生产多少个零件?
思考:代数式与用字母表示数有什么联系?列代数式时,如何准确把握数量之间的关系?
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
学习目标
1.理解代数式的意义,体会代数式是表示数量和数量关系的数学模型,初步培养模型观念.
2.明确代数式的书写要求,并能按照要求正确书写代数式.
我们小时候都听过这样一段儿歌
“一只青蛙一张嘴,两只眼睛,四条腿,一声扑通跳下水……”请接下去.
n只青蛙, 张嘴, 只眼睛,
条腿, 声扑通跳下水.
n
2n
4n
n
课堂导入
代数式的概念
用运算符号连接数和字母的式子叫作代数式.(运算符号包括+、-、×、÷、乘方)
1.单独的一个数或一个表示数的字母也是代数式..
2.代数式中除了含有数,字母和运算符号外,还可以含有括号.
3.代数中不含有“=”、“>”、“<”.
【注意】
新知探究
知识点1 代数式的概念
代数式的概念
用含有字母的式子表示下列数量关系:
(1)买一个足球需要a元,买一个篮球需要b元,则买一个足球和一个篮球共需要___________ 元;
(2)某产品前年的产量是n件,去年的产量是前年产量的3倍少20件,去年的产量是___________ 件;
(3)某一正方形菜地的边长为am,它的面积是另一菜地面积的2倍,另一菜地的面积为___________ m2 .
新知探究
知识点1 代数式的概念
例1: 下列式子中,哪些是代数式?
(1)x+6;(2)x=2x-1;(3)a;(4)2n>3;(5)0.
解: 因为代数式不能含有“=”“>”或“<”,
所以是代数式的有:(1)(3)(5).
注意:代数式中的式是指由+、-、×、÷、乘方运算符号连接而成的式子.
新知探究
知识点1 代数式的概念
解:(1)2a+5表示的是a的2倍与5的和.
(2)2(a+5)表示的是a与5的和的2倍.
(3)a2+b2表示的是a的平方与b的平方的和.
(4)(a+b)2表示的是a与b的和的平方.
例2 指出下列各代数式的意义:
(1)2a+5; (2)2(a+5);(3)a2+b2; (4)(a+b)2.
新知探究
知识点2 代数式的意义
大家谈谈:
观察下面代数式(a+8)(b-c)的生成过程,请用恰当的语言说出代数式(a+8)(b-c)的意义.
a
8
两数的和
a+8
b
c
两数的差
b-c
两数
的积
(a+8)(b-c)
新知探究
知识点2 代数式的意义
例3 请用代数式表示:
(1)a,b的差与c的平方的和.
(2)百位数字是a,十位数字是b,个位数字是c的三位数.
(3)三个连续的的整数(用同一个字母表示),以及它们的和.
解:(1)(a-b)+ c2.
(2)100a+10b+ c.(其中a,b,c是0到9之间的整数,且a≠0.
(3)设m是正数,三个连续整数可表示为m-1,m,m+1,它们的和为(m-1)+m+(m+1).
新知探究
知识点3 列代数式
列代数式就是把实际问题中与数量有关的语句,用含有数、字母和运算符号的式子表示出来,也就是把文字语言转化为符号语言.
①要抓住关键词语,明确它们的意义以及它们之间的关系,如和、差、积、商及大、小、多、少、倍、分、倒数、相反数等;
②理清语句层次明确运算顺序,一般按“先读先写”的原则列出式子.
③牢记一些概念和公式.
新知探究
知识点3 列代数式
1.字母与字母,数与字母相乘时,“×” 号通常省略不写或写“·”;
代数式的书写要求:
2.数与字母相乘时,数字通常写在字母的左边;
100×t
100t 或100·t
b×2a
2ab或2·a·b
新知探究
知识点4 代数式的书写要求
3.除法运算一般以分数的形式表示;
s÷v
s
v
4.带分数与字母相乘时,通常把带分数化成假分数;
1
3
1 n
4n
3
5.在实际问题中含有单位时,一般要把代数式用括号括起来,再写单位.
例如:长方形周长为(2a+4b)米.
例4:判断下列式子书写是否规范,不规范的请改正.
新知探究
知识点4 代数式的书写要求
1.用代数式表示:
(1)一个数x与6的和;
(2)比-5小a的数;
(3)某校买书25本,每本a元,该校应付书费多少元?
(4)容量为60L的铁桶,贮满油,取出(x+1)L后,桶内还剩油多少升?
解:
(1) x+6;
(2) -5-a;
(3) 25a元;
(4)[60-(x+1)]L.
随堂练习
知识点1 代数式的定义
1. 下列式子中,不属于代数式的是( D )
A. a +3 B. 2 mn
C. 0 D. x > y
D
1
2
3
4
5
6
7
8
9
10
11
12
13
2. 下列各式中,是代数式的有( D )
① ;② a -1>0;③ ab = ba ;
④ a ;⑤0;⑥ ( a2- b2).
A. 1个 B. 2个
C. 3个 D. 4个
D
1
2
3
4
5
6
7
8
9
10
11
12
13
知识点2 代数式的书写规则
3. [2024·石家庄外国语学校月考]下列含有字母的式子中,符
合书写规范要求的是( C )
A. -1 a
D. ( x + y )÷ z
C
1
2
3
4
5
6
7
8
9
10
11
12
13
4. 下面不符合用字母表示数的书写要求的有( C )
①3 a ;②( x - y )÷( x + y );③( a + b )2;
④ x - y 米;⑤ ;⑥ .
A. 2个 B. 3个
C. 4个 D. 5个
C
1
2
3
4
5
6
7
8
9
10
11
12
13
知识点3 代数式表示的意义
5. [2023·河北]代数式-7 x 的意义可以是( C )
A. -7与 x 的和 B. -7与 x 的差
C. -7与 x 的积 D. -7与 x 的商
C
1
2
3
4
5
6
7
8
9
10
11
12
13
6. 一列火车长 m m,以每秒 n m的速度通过一个长为 p m的
桥洞,用代数式表示火车完全通过桥洞所需的时间,正确
的为( D )
D
1
2
3
4
5
6
7
8
9
10
11
12
13
7. 用文字语言叙述代数式 - ,不正确的是( A )
A. 1除以 a 与 b 的差的商
B. 比 a 的倒数小1除以 b 的商的数
C. 1除以 a 的商与1除以 b 的商的差
D. a 的倒数与 b 的倒数的差
A
1
2
3
4
5
6
7
8
9
10
11
12
13
8. 某商店举办促销活动,促销的方法是将原价 x 元的衣服以
元出售,则下列说法中,能正确表达该商店
促销方法的是( B )
A. 原价减去10元后再打八折
B. 原价打八折后再减去10元
C. 原价减去10元后再打两折
D. 原价打两折后再减去10元
B
1
2
3
4
5
6
7
8
9
10
11
12
13
易错点 理解不透数量关系而致错
9. [2024·连云港期末]甲数比乙数的4倍少1,则下列说法:①
设乙数为 x ,则甲数为4 x -1;②设甲数为 x ,则乙数为
x +1;③设甲数为 x ,则乙数为 ( x +1);④设甲数为
x ,则乙数为 ( x -1),其中正确的是( A )
A. ①③ B. ①②
C. ②④ D. ①④
A
1
2
3
4
5
6
7
8
9
10
11
12
13
利用代数式的特征说明其数学意义
10. 说出下列代数式的意义:
(1)8 a +7;(2)4- ;
(3) a2- b2;(4)( a - b )2.
【解】(1)8 a +7的意义是 a 的8倍与7的和.
(2)4- 的意义是4与 a 除以 b 的商的差.
(3) a2- b2的意义是 a 的平方与 b 的平方的差.
(4)( a - b )2的意义是 a 与 b 的差的平方.
1
2
3
4
5
6
7
8
9
10
11
12
13
利用图形的特征判断代数式表示阴影面积的方法
11. [母题 教材P104习题B组T3]下面四个代数式中,不能表
示图中阴影部分面积的是( D )
A. x2+3 x +6
B. ( x +3)( x +2)-2 x
C. 3( x +2)+ x2
D. x2+5 x
D
1
2
3
4
5
6
7
8
9
10
11
12
13
代数式
定义
应用
用运算符号连接数和字母的式子叫作代数式.单独一个数或一个表示数的字母也是代数式.
代数式所表示的意义
根据实际问题列代数式
课堂小结
谢谢观看!
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
