4.1.2多项式 课件(共29张PPT)
文档属性
| 名称 | 4.1.2多项式 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 00:00:00 | ||
图片预览








文档简介
(共29张PPT)
4.1.2多项式
第四章 整式的加减
【2024新教材】2025-2026学年冀教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
第一页:标题页
4.1.2 多项式
—— 由单项式组成的代数式
(右下角添加授课教师姓名及日期)
第二页:引入
在前面我们学习了单项式,知道像\(3x\)、\(-5a^2\)、\(2xy\)这样的式子是单项式。但在实际问题中,我们还会遇到更复杂的代数式,比如 “一个数\(x\)的 3 倍与 5 的和” 可以表示为\(3x + 5\),“边长为\(a\)的正方形的面积与边长为\(b\)的正方形的面积的差” 可以表示为\(a^2 - b^2\)。这些式子是由几个单项式相加或相减组成的,它们就是我们今天要学习的多项式。本节课我们将学习多项式的定义、项、次数等知识,理解多项式的构成和特征。
第三页:多项式的定义
定义:几个单项式的和组成的代数式叫做多项式。
实例:整式中只含有乘法(包括乘方)和加减法运算,不含有除法运算(除非除数是一个数)。
像\(\frac{1}{x}\)、\(\frac{x + 1}{x}\)这样含有除法运算且除数是字母的式子不是整式。
第七页:例题解析(一)—— 判断多项式及确定项、次数
例题 1:判断下列各式是不是多项式,若是,请指出它的项、常数项和次数,并说明它是几次几项式。
(1)\(3x^2 - 2x + 1\);(2)\(5a + b^2\);(3)\(\frac{1}{x} + 2x\);(4)\(4\)。
解:(1)是多项式。项是\(3x^2\)、\(-2x\)、\(1\);常数项是\(1\);次数最高的项是\(3x^2\),次数是 2;所以它是二次三项式。
(2)是多项式。项是\(5a\)、\(b^2\);没有常数项(或常数项为 0);次数最高的项是\(b^2\),次数是 2;所以它是二次二项式。
(3)不是多项式,因为含有除法运算且除数是字母,不是整式。
(4)不是多项式,它是一个单项式(单独的一个数是单项式)。
例题 2:指出多项式\(-x^3y + 3x^2 - 7\)的项、次数,并说明它是几次几项式。
解:该多项式的项是\(-x^3y\)、\(3x^2\)、\(-7\)。
项\(-x^3y\)的次数是\(3 + 1 = 4\),项\(3x^2\)的次数是 2,项\(-7\)的次数是 0,次数最高的项的次数是 4。
所以它是四次三项式。
第八页:例题解析(二)—— 根据条件写多项式
例题 3:写出一个二次三项式,使它的项分别为\(x^2\)、\(-2x\)、\(3\)。
解:二次三项式是指次数为 2,含有三项的多项式。根据要求,这个多项式可以是\(x^2 - 2x + 3\)(注意项的符号)。
例题 4:若多项式\(ax^2 + bx + c\)是关于\(x\)的二次三项式,求\(a\)、\(b\)、\(c\)满足的条件。
解:因为该多项式是关于\(x\)的二次三项式,所以:
次数最高的项的次数是 2,即\(ax^2\)的次数是 2,所以\(a \neq 0\)(若\(a = 0\),则最高次项的次数不是 2)。
含有三项,即\(ax^2\)、\(bx\)、\(c\)都不能为 0(若其中一项为 0,则项数会减少),所以\(b \neq 0\),\(c \neq 0\)。
第九页:易错点分析
在学习多项式时,容易出现以下错误:
忽略项的符号:例如,认为多项式\(2x^2 - 3x + 1\)的项是\(2x^2\)、\(3x\)、\(1\),而正确的项是\(2x^2\)、\(-3x\)、\(1\)。
混淆多项式的次数和项的次数:例如,认为多项式\(x^3 + 2x^2y\)的次数是\(3 + 2 + 1 = 6\),而正确的次数是项\(2x^2y\)的次数\(2 + 1 = 3\)(或项\(x^3\)的次数 3)。
错误判断多项式的项数:例如,认为多项式\(3x^2 + 5\)是三项式,而实际上它含有两项,是二项式(常数项是一项)。
将单项式误认为多项式:例如,认为\(5x\)是多项式,而实际上它是单项式。
例题 5:判断下列说法是否正确,若不正确请改正。
(1)多项式\(x^2 + 2x - 1\)的项是\(x^2\)、\(2x\)、\(1\),次数是 2,是二次三项式。
(2)多项式\(3x^3y + 2xy\)的次数是\(3 + 3 + 1 + 1 = 8\)。
(3)单项式和多项式都是整式,整式都是多项式。
解:(1)不正确。多项式\(x^2 + 2x - 1\)的项是\(x^2\)、\(2x\)、\(-1\),次数是 2,是二次三项式。
(2)不正确。多项式\(3x^3y + 2xy\)的次数是项\(3x^3y\)的次数\(3 + 1 = 4\)。
(3)不正确。单项式和多项式都是整式,但整式不一定都是多项式,单项式也是整式。
第十页:课堂练习
填空题:
多项式\(2x - 3\)的项是______,常数项是______,次数是______,是______次______项式。
多项式\(x^2y + 3xy - 5\)的项是______,常数项是______,次数是______,是______次______项式。
若多项式\(ax^3 + bx + c\)是关于\(x\)的三次三项式,则\(a\),\(b\),\(c\)______(填 “≠0” 或 “=0”)。
选择题:
下列各式中,是多项式的是( )
A. \(3x\) B. \(\frac{1}{x} + 1\) C. \(x^2 + 2x - 3\) D. \(5\)
多项式\(2x^3 - x^2y^2 + y^3\)的次数是( )
A. 3 B. 4 C. 5 D. 2
解答题:
(1)指出下列多项式的项、常数项、次数,并说明它们是几次几项式:
①\(4x^2 - 3x + 7\);②\(-x^3 + 2x^2y - xy^2 + 1\)。
(2)写出一个三次四项式,使它含有项\(x^3\)、\(-2xy\)、\(5\)。
(3)若多项式\(x^{|m|} + (m - 2)x + 8\)是关于\(x\)的二次三项式,求\(m\)的值。
第十一页:课堂小结
多项式的定义:几个单项式的和组成的代数式。
多项式的项:多项式中的每个单项式,包括它前面的符号;不含字母的项是常数项。
多项式的次数:多项式中次数最高的项的次数;含有几项就是几项式。
整式的概念:单项式和多项式统称为整式。
注意区分多项式的项与项的符号、多项式的次数与项的次数,避免将单项式误认为多项式。
第十二页:作业布置
教材第 XX 页习题 4.1 第 3、4、5 题。
填空题:
多项式\(-3x^2 + 5x - 1\)的项是______,次数是______,是______次______项式。
若一个多项式是五次三项式,则它的最高次项的次数是______,含有______项。
判断题(对的打 “√”,错的打 “×”):
多项式都是整式,整式都是多项式。( )
多项式\(x^2 - 1\)的次数是 2,是二次二项式。( )
多项式\(3x + 2y\)的项是\(3x\)和\(2y\),次数是 1,是一次二项式。( )
解答题:
(1)指出多项式\(5a^4b - 3a^3b^2 + 2a^2b^3 - ab^4 + 6\)的项、次数,并说明它是几次几项式。
(2)写出一个含有字母\(x\)、\(y\)的四次三项式。
(3)已知多项式\((m - 1)x^3 + 2x^2 + (n + 1)x + 1\)是关于\(x\)的二次二项式,求\(m\)、\(n\)的值。
思考:多项式与单项式有什么区别和联系?请举例说明。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.理解整式的概念,能说出单项式、多项式、整式之间的联系.
2.能正确识别多项式、整式,并能准确说出多项式的次数和项.
3.会分析具体问题中的数量关系并能用整式表示, 建立数学符号意识,提升抽象能力.
学习目标
复习
问题1:什么叫单项式?
由数与字母或字母与字母相乘组成的代数式叫作单项式,单独的一个数或一个字母也是单项式.
问题2:怎么确定一个单项式的系数和次数?
单项式中的数字因数叫作这个单项式的系数.
一个单项式中,所有字母的指数的和叫作这个单项式的次数.
的系数为______,次数是_______,可以叫做____次单项式.
课堂导入
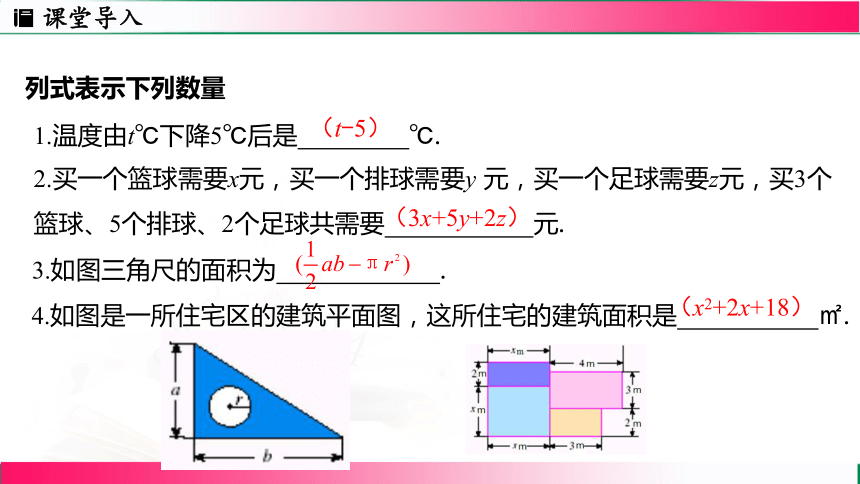
1.温度由t℃下降5℃后是 ℃.
2.买一个篮球需要x元,买一个排球需要y 元,买一个足球需要z元,买3个篮球、5个排球、2个足球共需要 元.
(3x+5y+2z)
(t-5)
列式表示下列数量
3.如图三角尺的面积为 .
4.如图是一所住宅区的建筑平面图,这所住宅的建筑面积是 ㎡.
(x2+2x+18)
课堂导入
3x+5y+2z
x2+2x+18
t-5
它们是单项式吗?这些式子有什么共同特点?与单项式有什么关系?
上述几个式子都是两个或者多个单项式相加的形式.
t
-5
+
3x
5y
2z
+
+
+
x2
2x
18
+
+
像这些由单项式相加组成的代数式叫作多项式..
新知探究
知识点1 多项式的相关概念
4.多项式含有几项,这个多项式就叫作几项式.
多项式: 3x3 +5x +8
常数项
次数
5.多项式的次数是几,这个多项式就叫作几次式.
三次三项式
1.多项式中的每一个单项式都叫作这个多项式的项.
2.不含字母的项叫作常数项..
3.多项式里,最高次项的次数,叫作这个多项式的次数..
项
新知探究
知识点1 多项式的相关概念
(1)多项式的各项应包括它前面的符号;
(3)要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的;
(4)一个多项式的最高次项可以不唯一.
(2)多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号;
新知探究
知识点1 多项式的相关概念
解:(1)( 150-m ),它的项是150和-m,次数是1.
(3)100c+10b+a,它的项是100c,10b和a,次数是1.
例1 写出多项式,并指出它们的项和次数.
(1)目前,在地球上生存的动物约有150万种.其中,无脊椎动物约有m万种,脊椎动物约有 万种.
(2)如图,城楼门口的形状,下部是长方形,上部是半圆形.它的面积是 .
(3)一个三位数的个位数字为a,十位数字为b,百位数字为c,这个三位数可表示为_________.
(2) 它的项是2ra和 ,次数是2.
新知探究
知识点1 多项式的相关概念
思考: 观察下面的式子,试着将它们分类:
3x+5y+2z,0.8p,v+2.5,a2h,-n,mn,
多项式:
单项式:
0.8p
a2h
-n
mn
3x+5y+2z
v+2.5
单项式和多项式统称为整式..
新知探究
知识点2 整式
解:(1)这个组合体的体积是a3+a2b.
(2)这个代数式是多项式,它是三次二项式.
例2 如图所示是一个正方体和一个长方体组成的组合体.
(1)请用代数式表示这个组合体的体积.
(2)这个代数式是多项式还是单项式?如果是多项式,请你说出它是几次几项式.
新知探究
知识点2 整式
1.多项式-5x2-2x的二次项系数、一次项系数和常数项分别是( )
A.-5,-2,0 B.5,-2,0
C.-5,-2,1 D.-5,2,1
A
随堂练习
2.下列说法正确的是( )
A.多项式5x-23是三次二项式
B.多项式2x+y是二次二项式
C.多项式ax-by-3是二次三项式
D.多项式x2y+x2-1是二次三项式
C
随堂练习
3.有a名男生和b名女生在社区做义工.为建花坛,男生每人搬了40块砖,女生每人搬了30块砖,他们一共搬了 块砖.
(40a+30b)
随堂练习
多项式
项
次数
4.下列整式中哪些是多项式?是多项式的指出其项和次数:
解:
1
4
2
随堂练习
5.已知-5xm+104xm+1-4xmy2是关于x,y的六次多项式,求m的值,并写出该多项式.
解:由题意得m+2=6,所以m=4.
【分析】该多项式最高次项为-4xmy2,其次数为m+2,故m+2=6.
所以该多项式为-5x4+104x5-4x4y2.
随堂练习
1. [新考法·定义识别法]在 x2-2,-1,-2 x -1,π, ,
x2+ +1,4 x 中,多项式有( C )
A. 1个 B. 2个
C. 3个 D. 4个
【点拨】
多项式有 x2-2,-2 x -1, .对于 x2+ +1,由
于 不是单项式,所以 x2+ +1不是多项式.
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
知识点1 多项式的定义
2. [新考法·规律探究法]一组按规律排列的代数式: a +2
b , a2-2 b3, a3+2 b5, a4-2 b7,…,则第 n 个式子
是 .
【点拨】
根据已知的式子可以得到每个式子的第一项中 a 的次
数是式子的序数;第二项的符号是+,-,+,-,…;
第二项中 b 的次数是序数的2倍减1.
an +(-1) n+1·2 b2 n-1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
知识点2 多项式的项与次数
3. 若多项式 xy| m- n|+( n -2) x2 y2+1是关于 x , y 的三次
多项式,则 mn = .
【点拨】
因为多项式 xy| m- n|+( n -2) x2 y2+1是关于 x , y
的三次多项式,
所以 n -2=0,1+| m - n |=3.
所以 n =2,| m - n |=2.
所以 m - n =2或 n - m =2.
所以 m =4或 m =0.所以 mn =0或8.
0或8
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4. 多项式- x2- x -1的各项分别是( B )
【点拨】
多项式的每一项都包括它前面的符号,故本题多项式
的各项分别是- x2,- x ,-1.
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5. [2024·成都青羊区模拟]多项式1+2 xy -3 xy2的次数及最
高次项的系数分别是( A )
A. 3,-3 B. 2,-3
C. 5,-3 D. 2,3
A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
知识点3 整式及整式的值
6. 把下列各式分别填在相应的大括号里.
4, , + b ,π R2-π r2, x2,2 x -3,- x2+ yz ,
a2+ +2.
单项式: ;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
多项式: ;
整式: .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7. 下列说法错误的是( C )
A. m 是单项式也是整式
C. 整式一定是单项式
D. 整式不一定是多项式
【点拨】
单项式是整式,多项式也是整式.整式中含加减运算
的是多项式,不含加减运算的是单项式.
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8. [新考法·2023·南通·整体求值法]若 a2-4 a -12=0,则2 a2
-8 a -8的值为( D )
A. 24 B. 20
C. 18 D. 16
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9. [2023·重庆]用长度相同的木棍按如图所示的规律拼图案,
其中第①个图案用了9根木棍,第②个图案用了14根木
棍,第③个图案用了19根木棍,第④个图案用了24根木
棍,…,按此规律排列下去,则第⑧个图案用的木棍根数
是( B )
A. 39 B. 44
C. 49 D. 54
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10. [2024·周口期末]已知关于 x 的多项式( a + b ) x5+( a -3)
x3-2( b +2) x2+2 ax +1不含 x3和 x2项,则当 x =-1
时,这个多项式的值为 .
【点拨】
因为多项式不含 x3和 x2项,所以 a -3=0, b +2=
0.所以 a =3, b =-2.所以原多项式为 x5+6 x +1.当 x
=-1时,原式=(-1)5+6×(-1)+1=-6.
-6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
多项式
及整式
多项式
由单项式相加组成的代数式叫作多项式
多项式中的每一个单项式都叫作这个多项式的项
单项式+多项式
整式
课堂小结
多项式里,最高次项的次数,叫作这个多项式的次数
谢谢观看!
4.1.2多项式
第四章 整式的加减
【2024新教材】2025-2026学年冀教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
第一页:标题页
4.1.2 多项式
—— 由单项式组成的代数式
(右下角添加授课教师姓名及日期)
第二页:引入
在前面我们学习了单项式,知道像\(3x\)、\(-5a^2\)、\(2xy\)这样的式子是单项式。但在实际问题中,我们还会遇到更复杂的代数式,比如 “一个数\(x\)的 3 倍与 5 的和” 可以表示为\(3x + 5\),“边长为\(a\)的正方形的面积与边长为\(b\)的正方形的面积的差” 可以表示为\(a^2 - b^2\)。这些式子是由几个单项式相加或相减组成的,它们就是我们今天要学习的多项式。本节课我们将学习多项式的定义、项、次数等知识,理解多项式的构成和特征。
第三页:多项式的定义
定义:几个单项式的和组成的代数式叫做多项式。
实例:整式中只含有乘法(包括乘方)和加减法运算,不含有除法运算(除非除数是一个数)。
像\(\frac{1}{x}\)、\(\frac{x + 1}{x}\)这样含有除法运算且除数是字母的式子不是整式。
第七页:例题解析(一)—— 判断多项式及确定项、次数
例题 1:判断下列各式是不是多项式,若是,请指出它的项、常数项和次数,并说明它是几次几项式。
(1)\(3x^2 - 2x + 1\);(2)\(5a + b^2\);(3)\(\frac{1}{x} + 2x\);(4)\(4\)。
解:(1)是多项式。项是\(3x^2\)、\(-2x\)、\(1\);常数项是\(1\);次数最高的项是\(3x^2\),次数是 2;所以它是二次三项式。
(2)是多项式。项是\(5a\)、\(b^2\);没有常数项(或常数项为 0);次数最高的项是\(b^2\),次数是 2;所以它是二次二项式。
(3)不是多项式,因为含有除法运算且除数是字母,不是整式。
(4)不是多项式,它是一个单项式(单独的一个数是单项式)。
例题 2:指出多项式\(-x^3y + 3x^2 - 7\)的项、次数,并说明它是几次几项式。
解:该多项式的项是\(-x^3y\)、\(3x^2\)、\(-7\)。
项\(-x^3y\)的次数是\(3 + 1 = 4\),项\(3x^2\)的次数是 2,项\(-7\)的次数是 0,次数最高的项的次数是 4。
所以它是四次三项式。
第八页:例题解析(二)—— 根据条件写多项式
例题 3:写出一个二次三项式,使它的项分别为\(x^2\)、\(-2x\)、\(3\)。
解:二次三项式是指次数为 2,含有三项的多项式。根据要求,这个多项式可以是\(x^2 - 2x + 3\)(注意项的符号)。
例题 4:若多项式\(ax^2 + bx + c\)是关于\(x\)的二次三项式,求\(a\)、\(b\)、\(c\)满足的条件。
解:因为该多项式是关于\(x\)的二次三项式,所以:
次数最高的项的次数是 2,即\(ax^2\)的次数是 2,所以\(a \neq 0\)(若\(a = 0\),则最高次项的次数不是 2)。
含有三项,即\(ax^2\)、\(bx\)、\(c\)都不能为 0(若其中一项为 0,则项数会减少),所以\(b \neq 0\),\(c \neq 0\)。
第九页:易错点分析
在学习多项式时,容易出现以下错误:
忽略项的符号:例如,认为多项式\(2x^2 - 3x + 1\)的项是\(2x^2\)、\(3x\)、\(1\),而正确的项是\(2x^2\)、\(-3x\)、\(1\)。
混淆多项式的次数和项的次数:例如,认为多项式\(x^3 + 2x^2y\)的次数是\(3 + 2 + 1 = 6\),而正确的次数是项\(2x^2y\)的次数\(2 + 1 = 3\)(或项\(x^3\)的次数 3)。
错误判断多项式的项数:例如,认为多项式\(3x^2 + 5\)是三项式,而实际上它含有两项,是二项式(常数项是一项)。
将单项式误认为多项式:例如,认为\(5x\)是多项式,而实际上它是单项式。
例题 5:判断下列说法是否正确,若不正确请改正。
(1)多项式\(x^2 + 2x - 1\)的项是\(x^2\)、\(2x\)、\(1\),次数是 2,是二次三项式。
(2)多项式\(3x^3y + 2xy\)的次数是\(3 + 3 + 1 + 1 = 8\)。
(3)单项式和多项式都是整式,整式都是多项式。
解:(1)不正确。多项式\(x^2 + 2x - 1\)的项是\(x^2\)、\(2x\)、\(-1\),次数是 2,是二次三项式。
(2)不正确。多项式\(3x^3y + 2xy\)的次数是项\(3x^3y\)的次数\(3 + 1 = 4\)。
(3)不正确。单项式和多项式都是整式,但整式不一定都是多项式,单项式也是整式。
第十页:课堂练习
填空题:
多项式\(2x - 3\)的项是______,常数项是______,次数是______,是______次______项式。
多项式\(x^2y + 3xy - 5\)的项是______,常数项是______,次数是______,是______次______项式。
若多项式\(ax^3 + bx + c\)是关于\(x\)的三次三项式,则\(a\),\(b\),\(c\)______(填 “≠0” 或 “=0”)。
选择题:
下列各式中,是多项式的是( )
A. \(3x\) B. \(\frac{1}{x} + 1\) C. \(x^2 + 2x - 3\) D. \(5\)
多项式\(2x^3 - x^2y^2 + y^3\)的次数是( )
A. 3 B. 4 C. 5 D. 2
解答题:
(1)指出下列多项式的项、常数项、次数,并说明它们是几次几项式:
①\(4x^2 - 3x + 7\);②\(-x^3 + 2x^2y - xy^2 + 1\)。
(2)写出一个三次四项式,使它含有项\(x^3\)、\(-2xy\)、\(5\)。
(3)若多项式\(x^{|m|} + (m - 2)x + 8\)是关于\(x\)的二次三项式,求\(m\)的值。
第十一页:课堂小结
多项式的定义:几个单项式的和组成的代数式。
多项式的项:多项式中的每个单项式,包括它前面的符号;不含字母的项是常数项。
多项式的次数:多项式中次数最高的项的次数;含有几项就是几项式。
整式的概念:单项式和多项式统称为整式。
注意区分多项式的项与项的符号、多项式的次数与项的次数,避免将单项式误认为多项式。
第十二页:作业布置
教材第 XX 页习题 4.1 第 3、4、5 题。
填空题:
多项式\(-3x^2 + 5x - 1\)的项是______,次数是______,是______次______项式。
若一个多项式是五次三项式,则它的最高次项的次数是______,含有______项。
判断题(对的打 “√”,错的打 “×”):
多项式都是整式,整式都是多项式。( )
多项式\(x^2 - 1\)的次数是 2,是二次二项式。( )
多项式\(3x + 2y\)的项是\(3x\)和\(2y\),次数是 1,是一次二项式。( )
解答题:
(1)指出多项式\(5a^4b - 3a^3b^2 + 2a^2b^3 - ab^4 + 6\)的项、次数,并说明它是几次几项式。
(2)写出一个含有字母\(x\)、\(y\)的四次三项式。
(3)已知多项式\((m - 1)x^3 + 2x^2 + (n + 1)x + 1\)是关于\(x\)的二次二项式,求\(m\)、\(n\)的值。
思考:多项式与单项式有什么区别和联系?请举例说明。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.理解整式的概念,能说出单项式、多项式、整式之间的联系.
2.能正确识别多项式、整式,并能准确说出多项式的次数和项.
3.会分析具体问题中的数量关系并能用整式表示, 建立数学符号意识,提升抽象能力.
学习目标
复习
问题1:什么叫单项式?
由数与字母或字母与字母相乘组成的代数式叫作单项式,单独的一个数或一个字母也是单项式.
问题2:怎么确定一个单项式的系数和次数?
单项式中的数字因数叫作这个单项式的系数.
一个单项式中,所有字母的指数的和叫作这个单项式的次数.
的系数为______,次数是_______,可以叫做____次单项式.
课堂导入
1.温度由t℃下降5℃后是 ℃.
2.买一个篮球需要x元,买一个排球需要y 元,买一个足球需要z元,买3个篮球、5个排球、2个足球共需要 元.
(3x+5y+2z)
(t-5)
列式表示下列数量
3.如图三角尺的面积为 .
4.如图是一所住宅区的建筑平面图,这所住宅的建筑面积是 ㎡.
(x2+2x+18)
课堂导入
3x+5y+2z
x2+2x+18
t-5
它们是单项式吗?这些式子有什么共同特点?与单项式有什么关系?
上述几个式子都是两个或者多个单项式相加的形式.
t
-5
+
3x
5y
2z
+
+
+
x2
2x
18
+
+
像这些由单项式相加组成的代数式叫作多项式..
新知探究
知识点1 多项式的相关概念
4.多项式含有几项,这个多项式就叫作几项式.
多项式: 3x3 +5x +8
常数项
次数
5.多项式的次数是几,这个多项式就叫作几次式.
三次三项式
1.多项式中的每一个单项式都叫作这个多项式的项.
2.不含字母的项叫作常数项..
3.多项式里,最高次项的次数,叫作这个多项式的次数..
项
新知探究
知识点1 多项式的相关概念
(1)多项式的各项应包括它前面的符号;
(3)要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的;
(4)一个多项式的最高次项可以不唯一.
(2)多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号;
新知探究
知识点1 多项式的相关概念
解:(1)( 150-m ),它的项是150和-m,次数是1.
(3)100c+10b+a,它的项是100c,10b和a,次数是1.
例1 写出多项式,并指出它们的项和次数.
(1)目前,在地球上生存的动物约有150万种.其中,无脊椎动物约有m万种,脊椎动物约有 万种.
(2)如图,城楼门口的形状,下部是长方形,上部是半圆形.它的面积是 .
(3)一个三位数的个位数字为a,十位数字为b,百位数字为c,这个三位数可表示为_________.
(2) 它的项是2ra和 ,次数是2.
新知探究
知识点1 多项式的相关概念
思考: 观察下面的式子,试着将它们分类:
3x+5y+2z,0.8p,v+2.5,a2h,-n,mn,
多项式:
单项式:
0.8p
a2h
-n
mn
3x+5y+2z
v+2.5
单项式和多项式统称为整式..
新知探究
知识点2 整式
解:(1)这个组合体的体积是a3+a2b.
(2)这个代数式是多项式,它是三次二项式.
例2 如图所示是一个正方体和一个长方体组成的组合体.
(1)请用代数式表示这个组合体的体积.
(2)这个代数式是多项式还是单项式?如果是多项式,请你说出它是几次几项式.
新知探究
知识点2 整式
1.多项式-5x2-2x的二次项系数、一次项系数和常数项分别是( )
A.-5,-2,0 B.5,-2,0
C.-5,-2,1 D.-5,2,1
A
随堂练习
2.下列说法正确的是( )
A.多项式5x-23是三次二项式
B.多项式2x+y是二次二项式
C.多项式ax-by-3是二次三项式
D.多项式x2y+x2-1是二次三项式
C
随堂练习
3.有a名男生和b名女生在社区做义工.为建花坛,男生每人搬了40块砖,女生每人搬了30块砖,他们一共搬了 块砖.
(40a+30b)
随堂练习
多项式
项
次数
4.下列整式中哪些是多项式?是多项式的指出其项和次数:
解:
1
4
2
随堂练习
5.已知-5xm+104xm+1-4xmy2是关于x,y的六次多项式,求m的值,并写出该多项式.
解:由题意得m+2=6,所以m=4.
【分析】该多项式最高次项为-4xmy2,其次数为m+2,故m+2=6.
所以该多项式为-5x4+104x5-4x4y2.
随堂练习
1. [新考法·定义识别法]在 x2-2,-1,-2 x -1,π, ,
x2+ +1,4 x 中,多项式有( C )
A. 1个 B. 2个
C. 3个 D. 4个
【点拨】
多项式有 x2-2,-2 x -1, .对于 x2+ +1,由
于 不是单项式,所以 x2+ +1不是多项式.
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
知识点1 多项式的定义
2. [新考法·规律探究法]一组按规律排列的代数式: a +2
b , a2-2 b3, a3+2 b5, a4-2 b7,…,则第 n 个式子
是 .
【点拨】
根据已知的式子可以得到每个式子的第一项中 a 的次
数是式子的序数;第二项的符号是+,-,+,-,…;
第二项中 b 的次数是序数的2倍减1.
an +(-1) n+1·2 b2 n-1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
知识点2 多项式的项与次数
3. 若多项式 xy| m- n|+( n -2) x2 y2+1是关于 x , y 的三次
多项式,则 mn = .
【点拨】
因为多项式 xy| m- n|+( n -2) x2 y2+1是关于 x , y
的三次多项式,
所以 n -2=0,1+| m - n |=3.
所以 n =2,| m - n |=2.
所以 m - n =2或 n - m =2.
所以 m =4或 m =0.所以 mn =0或8.
0或8
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4. 多项式- x2- x -1的各项分别是( B )
【点拨】
多项式的每一项都包括它前面的符号,故本题多项式
的各项分别是- x2,- x ,-1.
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5. [2024·成都青羊区模拟]多项式1+2 xy -3 xy2的次数及最
高次项的系数分别是( A )
A. 3,-3 B. 2,-3
C. 5,-3 D. 2,3
A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
知识点3 整式及整式的值
6. 把下列各式分别填在相应的大括号里.
4, , + b ,π R2-π r2, x2,2 x -3,- x2+ yz ,
a2+ +2.
单项式: ;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
多项式: ;
整式: .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7. 下列说法错误的是( C )
A. m 是单项式也是整式
C. 整式一定是单项式
D. 整式不一定是多项式
【点拨】
单项式是整式,多项式也是整式.整式中含加减运算
的是多项式,不含加减运算的是单项式.
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8. [新考法·2023·南通·整体求值法]若 a2-4 a -12=0,则2 a2
-8 a -8的值为( D )
A. 24 B. 20
C. 18 D. 16
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9. [2023·重庆]用长度相同的木棍按如图所示的规律拼图案,
其中第①个图案用了9根木棍,第②个图案用了14根木
棍,第③个图案用了19根木棍,第④个图案用了24根木
棍,…,按此规律排列下去,则第⑧个图案用的木棍根数
是( B )
A. 39 B. 44
C. 49 D. 54
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10. [2024·周口期末]已知关于 x 的多项式( a + b ) x5+( a -3)
x3-2( b +2) x2+2 ax +1不含 x3和 x2项,则当 x =-1
时,这个多项式的值为 .
【点拨】
因为多项式不含 x3和 x2项,所以 a -3=0, b +2=
0.所以 a =3, b =-2.所以原多项式为 x5+6 x +1.当 x
=-1时,原式=(-1)5+6×(-1)+1=-6.
-6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
多项式
及整式
多项式
由单项式相加组成的代数式叫作多项式
多项式中的每一个单项式都叫作这个多项式的项
单项式+多项式
整式
课堂小结
多项式里,最高次项的次数,叫作这个多项式的次数
谢谢观看!
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
