5.3.2用去括号法、去分母法解一元一次方程一元一次方程 课件(共34张PPT)
文档属性
| 名称 | 5.3.2用去括号法、去分母法解一元一次方程一元一次方程 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 06:49:21 | ||
图片预览










文档简介
(共34张PPT)
5.3.2用去括号法、去分母法解一元一次方程
第五章 一元一次方程
【2024新教材】2025-2026学年冀教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
第一部分:用去括号法解一元一次方程
一、适用场景
当一元一次方程中含有括号时,需要先通过去括号将方程化简,再进行移项、合并同类项等操作。例如方程\(2(x - 3) + 5 = 3x - 1\),括号的存在会阻碍直接移项,因此需先去括号。
二、去括号的依据
去括号的依据是乘法分配律:\(a(b + c) = ab + ac\)。在去括号时,要将括号外的系数与括号内的每一项分别相乘,确保不遗漏任何一项。
三、去括号的步骤及注意事项
运用乘法分配律去括号:将括号外的数或字母与括号内的每一项相乘。
实例:对于\(3(2x - 5)\),去括号后为\(3 2x + 3 (-5) = 6x - 15\)。
处理括号前的符号:
若括号前是 “+” 号,去括号后括号内各项符号不变。例如\(+(x + 2y) = x + 2y\)。
若括号前是 “-” 号,去括号后括号内各项符号都要改变。例如\(-(3a - b) = -3a + b\)。
合并同类项(若有):去括号后,若方程同侧有同类项,可先合并,使方程更简洁。
四、例题解析
例题 1:解方程\(4(x - 1) + 2 = 3(x + 2)\)。
解:步骤 1:去括号,根据乘法分配律得\(4x - 4 + 2 = 3x + 6\)。
步骤 2:合并左侧常数项,得\(4x - 2 = 3x + 6\)。
步骤 3:移项,将\(3x\)移到左侧(变号为\(-3x\)),将\(-2\)移到右侧(变号为\(+2\)),得\(4x - 3x = 6 + 2\)。
步骤 4:合并同类项,得\(x = 8\)。
例题 2:解方程\(5 - 2(3x - 1) = 4(1 - x)\)。
解:步骤 1:去括号,注意括号前是 “-2” 和 “4”,得\(5 - 6x + 2 = 4 - 4x\)。
步骤 2:合并左侧常数项,得\(7 - 6x = 4 - 4x\)。
步骤 3:移项,将\(-4x\)移到左侧(变号为\(+4x\)),将 7 移到右侧(变号为\(-7\)),得\(-6x + 4x = 4 - 7\)。
步骤 4:合并同类项,得\(-2x = -3\)。
步骤 5:系数化为 1,两边同时除以\(-2\),得\(x = \frac{3}{2}\)。
第二部分:用去分母法解一元一次方程
一、适用场景
当一元一次方程中含有分母时(如\(\frac{x - 1}{2} = \frac{2x + 3}{3}\)),为了简化计算,需要先去掉分母,将方程转化为不含分母的形式。
二、去分母的依据
去分母的依据是等式的性质 2:等式两边同时乘同一个不为 0 的数,所得结果仍是等式。这里的 “同一个数” 通常是方程中所有分母的最小公倍数。
三、去分母的步骤及注意事项
确定最小公倍数:找出方程中所有分母的最小公倍数,作为去分母时的乘数。
实例:方程\(\frac{x}{2} + \frac{x - 1}{3} = 1\)中,分母是 2 和 3,最小公倍数是 6。
方程两边同乘最小公倍数:确保方程中的每一项(包括不含分母的项)都乘这个最小公倍数,避免漏乘。
实例:上述方程两边同乘 6,得\(6 \frac{x}{2} + 6 \frac{x - 1}{3} = 6 1\),即\(3x + 2(x - 1) = 6\)。
去括号(若有):去分母后若出现括号,按去括号法则去掉括号。
后续步骤:移项、合并同类项、系数化为 1,与常规解方程步骤相同。
四、注意事项
去分母时,不含分母的项也要乘最小公倍数,否则会破坏等式平衡。
若分子是多项式,去分母后需给分子加上括号,避免符号错误。例如\(\frac{x - 1}{2}\)乘 2 后应变为\((x - 1)\),而不是\(x - 1\)(当分母前有负号时尤为重要)。
五、例题解析
例题 3:解方程\(\frac{2x - 1}{3} - \frac{x + 1}{2} = 1\)。
解:步骤 1:确定分母 3 和 2 的最小公倍数是 6,方程两边同乘 6,得\(6 \frac{2x - 1}{3} - 6 \frac{x + 1}{2} = 6 1\)。
步骤 2:化简得\(2(2x - 1) - 3(x + 1) = 6\)。
步骤 3:去括号,得\(4x - 2 - 3x - 3 = 6\)。
步骤 4:合并同类项,得\(x - 5 = 6\)。
步骤 5:移项,得\(x = 6 + 5 = 11\)。
例题 4:解方程\(\frac{3x + 1}{4} - 1 = \frac{x - 1}{2}\)。
解:步骤 1:分母 4 和 2 的最小公倍数是 4,两边同乘 4,得\(3x + 1 - 4 = 2(x - 1)\)(注意 “-1” 乘 4 得 - 4)。
步骤 2:去括号,得\(3x + 1 - 4 = 2x - 2\)。
步骤 3:合并左侧常数项,得\(3x - 3 = 2x - 2\)。
步骤 4:移项,得\(3x - 2x = -2 + 3\)。
步骤 5:合并同类项,得\(x = 1\)。
第三部分:综合练习
用去括号法解下列方程:
(1)\(3(2x + 5) = 2(4x + 3) - 3\)
(2)\(7 - (x - 2) = 3(2x + 1)\)
用去分母法解下列方程:
(1)\(\frac{x + 1}{5} = \frac{3x - 1}{3} - 2\)
(2)\(\frac{2x - 1}{6} - \frac{3x + 1}{4} = \frac{x}{2}\)
第四部分:易错点总结
去括号时的错误:
漏乘括号内的项,如\(2(x + 3)\)去括号后误写为\(2x + 3\)(正确应为\(2x + 6\))。
括号前是负号时,部分项未变号,如\(-(2x - 1)\)去括号后误写为\(-2x - 1\)(正确应为\(-2x + 1\))。
去分母时的错误:
漏乘不含分母的项,如\(\frac{x}{2} + 1 = 3\)去分母时误写为\(x + 1 = 6\)(正确应为\(x + 2 = 6\))。
分子是多项式时未加括号,如\(\frac{x - 1}{2} 2\)误写为\(x - 1\)(当分母前有负号时,如\(-\frac{x - 1}{2} 2\),易误写为\(-x - 1\),正确应为\(-(x - 1) = -x + 1\))。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
学习目标
1.能利用去括号、去分母解一元一次方程,并理解每一步变形的依据,提高运算能力,体会化归思想.
2.归纳解一元一次方程的一般步骤,并能灵活运用到解方程中.
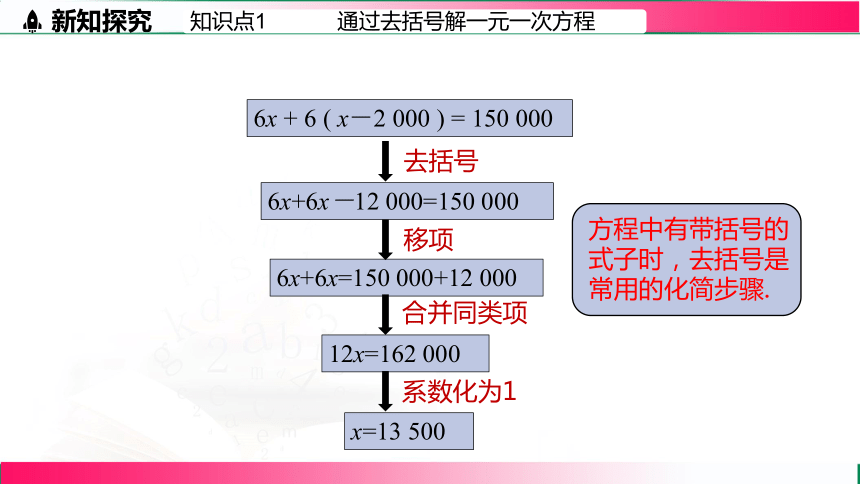
问题1 某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2 000度,全年用电15万度,这个工厂去年上半年每月平均用电多少度?
【分析】若设上半年每月平均用电x度,则下半年每月平均用电 度,上半年共用电 度,下半年共用电 度
因为全年共用了15万度电,所以,可列方程 .
(x-2 000)
6(x-2 000)
6x
6x+ 6(x-2 000)=150 000
你会解这个方程吗?
方程的左边有带括号的式子,可以尝试去括号!赶快动手试一试吧!
课堂导入
去括号
6x + 6 ( x-2 000 ) = 150 000
6x+6x-12 000=150 000
6x+6x=150 000+12 000
12x=162 000
x=13 500
移项
合并同类项
系数化为1
方程中有带括号的式子时,去括号是常用的化简步骤.
新知探究
知识点1 通过去括号解一元一次方程
例1 解方程: 6(2x -5) +20= 4(1-2x).
解:
去括号,得 12x-30+20=4-8x.
移项,得
12x+8x=4+30-20.
合并同类项,得
20x=14.
两边同时除以20,得
x= .
新知探究
知识点1 通过去括号解一元一次方程
去括号必须注意的事项:
1.如果括号外的因数是负数时,去括号后,原括号内各项的符号要改变;
2.乘数与括号内多项式相乘时,乘数应乘括号内的每一项,不要漏乘.
新知探究
知识点1 通过去括号解一元一次方程
如何求毕达哥拉斯的学生有多少名?
毕达哥拉斯是古希腊著名的数学家,有一次有位数学家问他:“尊敬的毕达哥拉斯先生,请告诉我,有多少名学生在你的学习里听你讲课?”毕达哥拉斯回答说:“我的学生,现在有 在学习数学, 在学习音乐, 沉默无言,此外,还有三名妇女.
课堂导入
你有不同的解法吗?
解:设毕达哥拉斯的学生有x名.根据题意,可列方程
这个方程怎么解?
移项,得
合并同类项,得
两边同时除以 ,得
新知探究
知识点2 通过去分母解一元一次方程
提 示:像上面这样的方程中有些系数是分数,如果能化去分母,把系数化为整数,则可以使解方程中的计算更方便些.
这个方程中各分母的最小公倍数是28,方程两边乘28.
新知探究
知识点2 通过去分母解一元一次方程
解:去分母得
移项,得
合并同类项,得
两边同时除以-3,得
把分数化成整数计算更简单!
两种解法有什么不同?你认为哪种解法比较好?
新知探究
知识点2 通过去分母解一元一次方程
利用去分母解一元一次方程:
1.解系数是分数的方程时,将方程的左、右两边同时乘各分母的最小公倍数可化去分母,将系数化为整数.
2.去分母的依据是等式的基本性质2.
新知探究
知识点2 通过去分母解一元一次方程
例2 解方程:
解:去分母,得
去括号,得
移项,合并同类项,得
两边同时除以4,得
小心漏乘,记得添括号!
新知探究
知识点2 通过去分母解一元一次方程
解一元一次方程的一般步骤是:
未知数的系数化为1
去分母、去括号、
移项、合并同类项
一元一次方程
ax=b
(a,b是常数,a≠0)
两边都除以a,得
新知探究
知识点2 通过去分母解一元一次方程
1.解方程2-3(2x-3)=0时,下列去括号正确的是( )
A.2-6x+9=0 B.2-6x-3=0
C.2-6x-9=0 D.2-6x+3=0
A
随堂练习
2.解方程 时,为了去分母,应将方程两边同乘以( )
A.30 B.15
C.10 D.6
A
随堂练习
3.若x=2是方程(2k-7)x=k+7的解,则k的值是( )
A.1 B.-1 C.7 D.-7
C
4.若关于x的一元一次方程 的解是x=-1,则k的值是( )
A. B.1 C. D.0
B
随堂练习
5.若式子 与 的值相等,x= .
6.如果规定符号“*”的运算规则为a*b= (其中a,b为有理数),那么方程3*x= 的解是x=________.
5
随堂练习
7.下面方程的求解是否正确?如不正确,请改正.
解方程 2(2x+3)=2+x.
解 去括号,得 4x+3=2+x.
移项,得 4x +x = 2-3.
化简,得 5x = -1.
方程两边都除以5 ,得
x = -
应改为4 x +6 =2+x
应改为4 x– x = 2-6
应改为3x =-4
应改为 x =
方程两边都除以3,得
随堂练习
8.下列方程的解法对不对?如果不对,你能找出错在哪里吗?
解方程:
解:去分母,得 4x-1-3x + 6 = 1.
移项,合并同类项,得 x=4.
方程右边的“1”去分母时漏乘最小公倍数6
去括号符号错误
约去分母3后,(2x-1)×2在去括号时出错
随堂练习
知识点1 去括号法
1. 下列四种变形中,属于去括号的是( C )
A. 5 x +4=0,则5 x =-4
C. 3 x -(2-4 x )=5,则3 x -2+4 x =5
D. 5 x =2+1,则5 x =3
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
2. [2024·贵阳十七中月考]解方程-2(2 x +1)= x 时,去括号
正确的是( D )
A. -4 x +1=- x B. -4 x +2=- x
C. -4 x -1= x D. -4 x -2= x
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
知识点2 用去括号法解一元一次方程
3. 方程2( x -3)=6的解是 .
【点拨】
2( x -3)=6,去括号,得2 x -6=6,解得 x =6.
x =6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
4. [2024·西工大附中月考]若2( a +3)的值与4互为相反数,则
a 的值为 .
【点拨】
由题意得2( a +3)+4=0,2 a +6+4=0,2 a =-
10, a =-5.
-5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
5. 解方程:
10 x -4(3- x )-5(2+7 x )=15 x -9( x -2).
【解】去括号,得10 x -12+4 x -10-35 x =15 x -9 x +
18.合并同类项,得-21 x -22=6 x +18.
移项,得-21 x -6 x =22+18.
合并同类项,得-27 x =40.
系数化为1,得 x =- .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
知识点3 去分母法
6. 解方程 -1= ,为了去分母应给方程两边同时乘
的最合适的数是( C )
A. 6 B. 9 C. 12 D. 24
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
7. [2024·重庆一中月考]解一元一次方程 ( x +1)=1- x
时,去分母正确的是( D )
A. 3( x +1)=1-2 x B. 2( x +1)=1-3 x
C. 2( x +1)=6-3 x D. 3( x +1)=6-2 x
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
知识点4 用去分母法解一元一次方程
8. [2024·合肥四十五中月考]根据下列解方程 =
的过程,请在前面的括号内填写变形步骤,在后面的括号
内填写变形依据.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
解:原方程可变形为 = .( 分数的基本性质 )
去分母,得3(3 x +5)=2(2 x -1).( 等式的性质2 )
去括号,得9 x +15=4 x -2.( 去括号法则(或分配律) )
( 移项 ),得9 x -4 x =-15-2.( 等式的性质1 )
( 合并同类项 ),得5 x =-17.
( 系数化为1 ),得 x =- .( 等式的性质2 )
分数的基本性质
等式的性质2
去括号法则(或分配律)
移项
等式的性质1
合并同类项
系数化为1
等式的性质2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
9. [新考法·2024·衢州·过程辨析法]小红在解方程 = +
1时,第一步出现了错误:
解:2×7 x =(4 x -1)+1,
…
1
2
3
4
5
6
7
8
9
10
11
12
13
14
(1)请在方框内用横线标出小红的错误处;
【解】如图.
解:2×7 x =(4 x -1)+ 1 ,
…
1
2
3
4
5
6
7
8
9
10
11
12
13
14
(2)写出正确的解答过程.
【解】去分母,得2×7 x =(4 x -1)+6,去括号,
得14 x =4 x -1+6,移项,得14 x -4 x =-1+6,合
并同类项,得10 x =5,系数化为1,得 x = .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
课堂小结
解一元一次方程
利用去括号与去分母解一元一次方程
解一元一次方程的步骤
利用去括号解方程
利用去分母解方程
去分母
去括号
移项
合并同类项
未知数系数化为1
谢谢观看!
5.3.2用去括号法、去分母法解一元一次方程
第五章 一元一次方程
【2024新教材】2025-2026学年冀教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
第一部分:用去括号法解一元一次方程
一、适用场景
当一元一次方程中含有括号时,需要先通过去括号将方程化简,再进行移项、合并同类项等操作。例如方程\(2(x - 3) + 5 = 3x - 1\),括号的存在会阻碍直接移项,因此需先去括号。
二、去括号的依据
去括号的依据是乘法分配律:\(a(b + c) = ab + ac\)。在去括号时,要将括号外的系数与括号内的每一项分别相乘,确保不遗漏任何一项。
三、去括号的步骤及注意事项
运用乘法分配律去括号:将括号外的数或字母与括号内的每一项相乘。
实例:对于\(3(2x - 5)\),去括号后为\(3 2x + 3 (-5) = 6x - 15\)。
处理括号前的符号:
若括号前是 “+” 号,去括号后括号内各项符号不变。例如\(+(x + 2y) = x + 2y\)。
若括号前是 “-” 号,去括号后括号内各项符号都要改变。例如\(-(3a - b) = -3a + b\)。
合并同类项(若有):去括号后,若方程同侧有同类项,可先合并,使方程更简洁。
四、例题解析
例题 1:解方程\(4(x - 1) + 2 = 3(x + 2)\)。
解:步骤 1:去括号,根据乘法分配律得\(4x - 4 + 2 = 3x + 6\)。
步骤 2:合并左侧常数项,得\(4x - 2 = 3x + 6\)。
步骤 3:移项,将\(3x\)移到左侧(变号为\(-3x\)),将\(-2\)移到右侧(变号为\(+2\)),得\(4x - 3x = 6 + 2\)。
步骤 4:合并同类项,得\(x = 8\)。
例题 2:解方程\(5 - 2(3x - 1) = 4(1 - x)\)。
解:步骤 1:去括号,注意括号前是 “-2” 和 “4”,得\(5 - 6x + 2 = 4 - 4x\)。
步骤 2:合并左侧常数项,得\(7 - 6x = 4 - 4x\)。
步骤 3:移项,将\(-4x\)移到左侧(变号为\(+4x\)),将 7 移到右侧(变号为\(-7\)),得\(-6x + 4x = 4 - 7\)。
步骤 4:合并同类项,得\(-2x = -3\)。
步骤 5:系数化为 1,两边同时除以\(-2\),得\(x = \frac{3}{2}\)。
第二部分:用去分母法解一元一次方程
一、适用场景
当一元一次方程中含有分母时(如\(\frac{x - 1}{2} = \frac{2x + 3}{3}\)),为了简化计算,需要先去掉分母,将方程转化为不含分母的形式。
二、去分母的依据
去分母的依据是等式的性质 2:等式两边同时乘同一个不为 0 的数,所得结果仍是等式。这里的 “同一个数” 通常是方程中所有分母的最小公倍数。
三、去分母的步骤及注意事项
确定最小公倍数:找出方程中所有分母的最小公倍数,作为去分母时的乘数。
实例:方程\(\frac{x}{2} + \frac{x - 1}{3} = 1\)中,分母是 2 和 3,最小公倍数是 6。
方程两边同乘最小公倍数:确保方程中的每一项(包括不含分母的项)都乘这个最小公倍数,避免漏乘。
实例:上述方程两边同乘 6,得\(6 \frac{x}{2} + 6 \frac{x - 1}{3} = 6 1\),即\(3x + 2(x - 1) = 6\)。
去括号(若有):去分母后若出现括号,按去括号法则去掉括号。
后续步骤:移项、合并同类项、系数化为 1,与常规解方程步骤相同。
四、注意事项
去分母时,不含分母的项也要乘最小公倍数,否则会破坏等式平衡。
若分子是多项式,去分母后需给分子加上括号,避免符号错误。例如\(\frac{x - 1}{2}\)乘 2 后应变为\((x - 1)\),而不是\(x - 1\)(当分母前有负号时尤为重要)。
五、例题解析
例题 3:解方程\(\frac{2x - 1}{3} - \frac{x + 1}{2} = 1\)。
解:步骤 1:确定分母 3 和 2 的最小公倍数是 6,方程两边同乘 6,得\(6 \frac{2x - 1}{3} - 6 \frac{x + 1}{2} = 6 1\)。
步骤 2:化简得\(2(2x - 1) - 3(x + 1) = 6\)。
步骤 3:去括号,得\(4x - 2 - 3x - 3 = 6\)。
步骤 4:合并同类项,得\(x - 5 = 6\)。
步骤 5:移项,得\(x = 6 + 5 = 11\)。
例题 4:解方程\(\frac{3x + 1}{4} - 1 = \frac{x - 1}{2}\)。
解:步骤 1:分母 4 和 2 的最小公倍数是 4,两边同乘 4,得\(3x + 1 - 4 = 2(x - 1)\)(注意 “-1” 乘 4 得 - 4)。
步骤 2:去括号,得\(3x + 1 - 4 = 2x - 2\)。
步骤 3:合并左侧常数项,得\(3x - 3 = 2x - 2\)。
步骤 4:移项,得\(3x - 2x = -2 + 3\)。
步骤 5:合并同类项,得\(x = 1\)。
第三部分:综合练习
用去括号法解下列方程:
(1)\(3(2x + 5) = 2(4x + 3) - 3\)
(2)\(7 - (x - 2) = 3(2x + 1)\)
用去分母法解下列方程:
(1)\(\frac{x + 1}{5} = \frac{3x - 1}{3} - 2\)
(2)\(\frac{2x - 1}{6} - \frac{3x + 1}{4} = \frac{x}{2}\)
第四部分:易错点总结
去括号时的错误:
漏乘括号内的项,如\(2(x + 3)\)去括号后误写为\(2x + 3\)(正确应为\(2x + 6\))。
括号前是负号时,部分项未变号,如\(-(2x - 1)\)去括号后误写为\(-2x - 1\)(正确应为\(-2x + 1\))。
去分母时的错误:
漏乘不含分母的项,如\(\frac{x}{2} + 1 = 3\)去分母时误写为\(x + 1 = 6\)(正确应为\(x + 2 = 6\))。
分子是多项式时未加括号,如\(\frac{x - 1}{2} 2\)误写为\(x - 1\)(当分母前有负号时,如\(-\frac{x - 1}{2} 2\),易误写为\(-x - 1\),正确应为\(-(x - 1) = -x + 1\))。
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
学习目标
1.能利用去括号、去分母解一元一次方程,并理解每一步变形的依据,提高运算能力,体会化归思想.
2.归纳解一元一次方程的一般步骤,并能灵活运用到解方程中.
问题1 某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2 000度,全年用电15万度,这个工厂去年上半年每月平均用电多少度?
【分析】若设上半年每月平均用电x度,则下半年每月平均用电 度,上半年共用电 度,下半年共用电 度
因为全年共用了15万度电,所以,可列方程 .
(x-2 000)
6(x-2 000)
6x
6x+ 6(x-2 000)=150 000
你会解这个方程吗?
方程的左边有带括号的式子,可以尝试去括号!赶快动手试一试吧!
课堂导入
去括号
6x + 6 ( x-2 000 ) = 150 000
6x+6x-12 000=150 000
6x+6x=150 000+12 000
12x=162 000
x=13 500
移项
合并同类项
系数化为1
方程中有带括号的式子时,去括号是常用的化简步骤.
新知探究
知识点1 通过去括号解一元一次方程
例1 解方程: 6(2x -5) +20= 4(1-2x).
解:
去括号,得 12x-30+20=4-8x.
移项,得
12x+8x=4+30-20.
合并同类项,得
20x=14.
两边同时除以20,得
x= .
新知探究
知识点1 通过去括号解一元一次方程
去括号必须注意的事项:
1.如果括号外的因数是负数时,去括号后,原括号内各项的符号要改变;
2.乘数与括号内多项式相乘时,乘数应乘括号内的每一项,不要漏乘.
新知探究
知识点1 通过去括号解一元一次方程
如何求毕达哥拉斯的学生有多少名?
毕达哥拉斯是古希腊著名的数学家,有一次有位数学家问他:“尊敬的毕达哥拉斯先生,请告诉我,有多少名学生在你的学习里听你讲课?”毕达哥拉斯回答说:“我的学生,现在有 在学习数学, 在学习音乐, 沉默无言,此外,还有三名妇女.
课堂导入
你有不同的解法吗?
解:设毕达哥拉斯的学生有x名.根据题意,可列方程
这个方程怎么解?
移项,得
合并同类项,得
两边同时除以 ,得
新知探究
知识点2 通过去分母解一元一次方程
提 示:像上面这样的方程中有些系数是分数,如果能化去分母,把系数化为整数,则可以使解方程中的计算更方便些.
这个方程中各分母的最小公倍数是28,方程两边乘28.
新知探究
知识点2 通过去分母解一元一次方程
解:去分母得
移项,得
合并同类项,得
两边同时除以-3,得
把分数化成整数计算更简单!
两种解法有什么不同?你认为哪种解法比较好?
新知探究
知识点2 通过去分母解一元一次方程
利用去分母解一元一次方程:
1.解系数是分数的方程时,将方程的左、右两边同时乘各分母的最小公倍数可化去分母,将系数化为整数.
2.去分母的依据是等式的基本性质2.
新知探究
知识点2 通过去分母解一元一次方程
例2 解方程:
解:去分母,得
去括号,得
移项,合并同类项,得
两边同时除以4,得
小心漏乘,记得添括号!
新知探究
知识点2 通过去分母解一元一次方程
解一元一次方程的一般步骤是:
未知数的系数化为1
去分母、去括号、
移项、合并同类项
一元一次方程
ax=b
(a,b是常数,a≠0)
两边都除以a,得
新知探究
知识点2 通过去分母解一元一次方程
1.解方程2-3(2x-3)=0时,下列去括号正确的是( )
A.2-6x+9=0 B.2-6x-3=0
C.2-6x-9=0 D.2-6x+3=0
A
随堂练习
2.解方程 时,为了去分母,应将方程两边同乘以( )
A.30 B.15
C.10 D.6
A
随堂练习
3.若x=2是方程(2k-7)x=k+7的解,则k的值是( )
A.1 B.-1 C.7 D.-7
C
4.若关于x的一元一次方程 的解是x=-1,则k的值是( )
A. B.1 C. D.0
B
随堂练习
5.若式子 与 的值相等,x= .
6.如果规定符号“*”的运算规则为a*b= (其中a,b为有理数),那么方程3*x= 的解是x=________.
5
随堂练习
7.下面方程的求解是否正确?如不正确,请改正.
解方程 2(2x+3)=2+x.
解 去括号,得 4x+3=2+x.
移项,得 4x +x = 2-3.
化简,得 5x = -1.
方程两边都除以5 ,得
x = -
应改为4 x +6 =2+x
应改为4 x– x = 2-6
应改为3x =-4
应改为 x =
方程两边都除以3,得
随堂练习
8.下列方程的解法对不对?如果不对,你能找出错在哪里吗?
解方程:
解:去分母,得 4x-1-3x + 6 = 1.
移项,合并同类项,得 x=4.
方程右边的“1”去分母时漏乘最小公倍数6
去括号符号错误
约去分母3后,(2x-1)×2在去括号时出错
随堂练习
知识点1 去括号法
1. 下列四种变形中,属于去括号的是( C )
A. 5 x +4=0,则5 x =-4
C. 3 x -(2-4 x )=5,则3 x -2+4 x =5
D. 5 x =2+1,则5 x =3
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
2. [2024·贵阳十七中月考]解方程-2(2 x +1)= x 时,去括号
正确的是( D )
A. -4 x +1=- x B. -4 x +2=- x
C. -4 x -1= x D. -4 x -2= x
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
知识点2 用去括号法解一元一次方程
3. 方程2( x -3)=6的解是 .
【点拨】
2( x -3)=6,去括号,得2 x -6=6,解得 x =6.
x =6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
4. [2024·西工大附中月考]若2( a +3)的值与4互为相反数,则
a 的值为 .
【点拨】
由题意得2( a +3)+4=0,2 a +6+4=0,2 a =-
10, a =-5.
-5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
5. 解方程:
10 x -4(3- x )-5(2+7 x )=15 x -9( x -2).
【解】去括号,得10 x -12+4 x -10-35 x =15 x -9 x +
18.合并同类项,得-21 x -22=6 x +18.
移项,得-21 x -6 x =22+18.
合并同类项,得-27 x =40.
系数化为1,得 x =- .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
知识点3 去分母法
6. 解方程 -1= ,为了去分母应给方程两边同时乘
的最合适的数是( C )
A. 6 B. 9 C. 12 D. 24
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
7. [2024·重庆一中月考]解一元一次方程 ( x +1)=1- x
时,去分母正确的是( D )
A. 3( x +1)=1-2 x B. 2( x +1)=1-3 x
C. 2( x +1)=6-3 x D. 3( x +1)=6-2 x
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
知识点4 用去分母法解一元一次方程
8. [2024·合肥四十五中月考]根据下列解方程 =
的过程,请在前面的括号内填写变形步骤,在后面的括号
内填写变形依据.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
解:原方程可变形为 = .( 分数的基本性质 )
去分母,得3(3 x +5)=2(2 x -1).( 等式的性质2 )
去括号,得9 x +15=4 x -2.( 去括号法则(或分配律) )
( 移项 ),得9 x -4 x =-15-2.( 等式的性质1 )
( 合并同类项 ),得5 x =-17.
( 系数化为1 ),得 x =- .( 等式的性质2 )
分数的基本性质
等式的性质2
去括号法则(或分配律)
移项
等式的性质1
合并同类项
系数化为1
等式的性质2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
9. [新考法·2024·衢州·过程辨析法]小红在解方程 = +
1时,第一步出现了错误:
解:2×7 x =(4 x -1)+1,
…
1
2
3
4
5
6
7
8
9
10
11
12
13
14
(1)请在方框内用横线标出小红的错误处;
【解】如图.
解:2×7 x =(4 x -1)+ 1 ,
…
1
2
3
4
5
6
7
8
9
10
11
12
13
14
(2)写出正确的解答过程.
【解】去分母,得2×7 x =(4 x -1)+6,去括号,
得14 x =4 x -1+6,移项,得14 x -4 x =-1+6,合
并同类项,得10 x =5,系数化为1,得 x = .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
课堂小结
解一元一次方程
利用去括号与去分母解一元一次方程
解一元一次方程的步骤
利用去括号解方程
利用去分母解方程
去分母
去括号
移项
合并同类项
未知数系数化为1
谢谢观看!
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
