5.4.2用一元一次方程解行程问题、工程问题 课件(共29张PPT)
文档属性
| 名称 | 5.4.2用一元一次方程解行程问题、工程问题 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 00:00:00 | ||
图片预览






文档简介
(共29张PPT)
5.4.2用一元一次方程解行程问题、工程问题
第五章 一元一次方程
【2024新教材】2025-2026学年冀教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
第一页:标题页
5.4.2 用一元一次方程解行程问题、工程问题
—— 实际问题中的等量关系探索
(右下角添加授课教师姓名及日期)
第二页:引入
在生活中,行程问题和工程问题十分常见。比如 “甲、乙两人从两地同时出发相向而行,多久后相遇”“一项工程,甲单独做需要多少天完成,乙单独做需要多少天完成,两人合作需要几天完成” 等。这些问题看似复杂,但都可以通过分析其中的数量关系,用一元一次方程来解决。本节课我们就来学习如何运用一元一次方程解决行程问题和工程问题,掌握其中的解题思路和方法。
第三页:行程问题
一、基本数量关系
行程问题的基本数量关系为:路程 = 速度 × 时间,由此可变形得到:速度 = 路程 ÷ 时间,时间 = 路程 ÷ 速度。
二、常见类型及等量关系
相遇问题:
特点:两人或两物体从两地同时出发,相向而行,最终相遇。
等量关系:甲走的路程 + 乙走的路程 = 两地之间的总路程。
追及问题:
特点:两人或两物体同向运动,快者从后面追上慢者。
等量关系:快者走的路程 - 慢者走的路程 = 出发时两者之间的距离(或慢者先走的路程)。
同向而行(不同时出发):
等量关系:慢者先走的路程 + 慢者后走的路程 = 快者走的路程。
环形跑道问题:
相遇(反向而行):两人走的路程之和 = 环形跑道的周长。
追及(同向而行):快者走的路程 - 慢者走的路程 = 环形跑道的周长。
三、例题解析(行程问题)
例题 1(相遇问题):A、B 两地相距 450 千米,甲、乙两车分别从 A、B 两地同时出发,相向而行。甲车的速度为 60 千米 / 小时,乙车的速度为 90 千米 / 小时,经过几小时两车相遇?
解:步骤 1:审题,已知两地距离、两车速度,相向而行,求相遇时间。
步骤 2:设未知数,设经过\(x\)小时两车相遇。
步骤 3:找等量关系,甲车行驶的路程 + 乙车行驶的路程 = A、B 两地的距离。
步骤 4:列方程,甲车行驶的路程为\(60x\)千米,乙车行驶的路程为\(90x\)千米,可列方程\(60x + 90x = 450\)。
步骤 5:解方程,合并同类项得\(150x = 450\),系数化为 1 得\(x = 3\)。
步骤 6:检验并作答,检验:\(60 3 + 90 3 = 180 + 270 = 450\)(千米),符合题意。
答:经过 3 小时两车相遇。甲先做 3 天的工作量为\(\frac{1}{12} 3 = \frac{1}{4}\)。
甲、乙合作\(x\)天的工作量为\((\frac{1}{12} + \frac{1}{18})x\)。
等量关系:甲先做的工作量 + 甲、乙合作的工作量 = 总工作量(单位 “1”)。
列方程:\(\frac{1}{4} + (\frac{1}{12} + \frac{1}{18})x = 1\)。
解方程:先计算括号内的工作效率和,\(\frac{1}{12} + \frac{1}{18} = \frac{3 + 2}{36} = \frac{5}{36}\)。
方程变为\(\frac{1}{4} + \frac{5}{36}x = 1\),移项得\(\frac{5}{36}x = 1 - \frac{1}{4} = \frac{3}{4}\)。
系数化为 1 得\(x = \frac{3}{4} \frac{36}{5} = \frac{27}{5} = 5.4\)。
检验:\(\frac{1}{4} + \frac{5}{36} \frac{27}{5} = \frac{1}{4} + \frac{3}{4} = 1\),符合题意。
答:还需要\(\frac{27}{5}\)天才能完成这项工作。
第五页:易错点分析
行程问题:
忽略单位统一:如速度单位是千米 / 小时,时间单位是分钟,未进行单位换算就直接计算。
混淆相遇和追及的等量关系:相遇问题中误将 “路程差” 作为等量关系,追及问题中误将 “路程和” 作为等量关系。
环形跑道问题中,未明确是同向还是反向而行,导致等量关系错误。
工程问题:
总工作量未看作单位 “1”:在多人合作问题中,不知道将总工作量设为 1,导致无法表示工作效率。
工作效率计算错误:某人单独完成工作需要\(n\)天,其工作效率误算为\(n\),而实际应为\(\frac{1}{n}\)。
忽略合作过程中的工作量叠加:如甲先做一部分,乙再加入合作,未将甲先做的工作量计入总工作量。
例题 7:指出下列解题过程中的错误,并改正。
问题:甲、乙两人分别从相距 100 千米的 A、B 两地同时出发,同向而行,甲的速度是 8 千米 / 小时,乙的速度是 6 千米 / 小时,甲在乙后面,经过多少小时甲能追上乙?
错误解法:
设经过\(x\)小时甲能追上乙。
列方程:\(8x + 6x = 100\)。
解方程:\(14x = 100\),\(x = \frac{50}{7}\)。
答:经过\(\frac{50}{7}\)小时甲能追上乙。
错误分析:这是追及问题,等量关系应为甲走的路程 - 乙走的路程 = 两地距离,而错误地用了路程和。
正确解法:
设经过\(x\)小时甲能追上乙。
列方程:\(8x - 6x = 100\)。
解方程:\(2x = 100\),\(x = 50\)。
答:经过 50 小时甲能追上乙。
第六页:课堂练习
填空题:
甲、乙两人相距 30 千米,相向而行,甲的速度是 4 千米 / 小时,乙的速度是 6 千米 / 小时,______小时后两人相遇。
一项工程,甲单独做需要 8 天完成,乙单独做需要 10 天完成,甲、乙合作每天完成这项工程的______,合作______天可以完成这项工程。
一辆汽车以 60 千米 / 小时的速度行驶,行驶\(x\)小时的路程是______千米;若行驶\(y\)千米,需要______小时。
选择题:
甲、乙两人在环形跑道上跑步,跑道一圈长 400 米,甲每秒跑 6 米,乙每秒跑 4 米,若两人同时同地同向出发,经过( )秒甲第一次追上乙。
A. 100 B. 200 C. 300 D. 400
一项工作,甲单独做需要 10 天,乙单独做需要 15 天,甲先做 2 天,然后两人合作,还需要( )天完成。
A. 4.8 B. 5 C. 5.2 D. 6
解答题:
(1)A、B 两地相距 240 千米,一辆快车和一辆慢车同时从 A 地出发开往 B 地,快车的速度是 80 千米 / 小时,慢车的速度是 60 千米 / 小时,快车比慢车早到几小时?
(2)一项工程,甲队单独做需要 10 天完成,乙队单独做需要 15 天完成,丙队单独做需要 20 天完成。三队合作,几天能完成这项工程的\(\frac{3}{4}\)?
(3)甲、乙两人分别从 A、B 两地同时出发,相向而行,甲的速度是 5 千米 / 小时,乙的速度是 4 千米 / 小时,两人相遇时,甲比乙多走了 3 千米,求 A、B 两地的距离。
第七页:课堂小结
行程问题:
基本数量关系:路程 = 速度 × 时间。
关键是根据不同类型(相遇、追及、环形跑道等)找到对应的等量关系。
工程问题:
基本数量关系:工作量 = 工作效率 × 工作时间,总工作量通常看作单位 “1”。
合作问题的等量关系:各部分工作量之和 = 总工作量。
解决这两类问题的一般步骤:审题→设未知数→找等量关系→列方程→解方程→检验作答。
注意单位统一和实际意义的检验,避免常见错误。
第八页:作业布置
教材第 XX 页习题 5.4 第 5、6、7、8 题。
填空题:
甲每小时走 5 千米,乙每小时走 3 千米,两人同时同地出发,同向而行,\(t\)小时后两人相距______千米。
一项工作,甲的工作效率是\(\frac{1}{a}\),乙的工作效率是\(\frac{1}{b}\),两人合作的工作效率是______。
解答题:
(1)甲、乙两站相距 300 千米,一列慢车从甲站开出,速度是 60 千米 / 小时,一列快车从乙站开出,速度是 80 千米 / 小时。两车同时开出,相向而行,经过多少小时相遇?
(2)一项工程,甲单独做需要 20 天完成,乙单独做需要 30 天完成,甲、乙合作了几天后,乙因事请假,甲继续做,从开工到完成任务共用了 16 天,乙请假了几天?
(3)一条环形跑道长 200 米,甲、乙两人同时从同一地点出发,同向而行,甲每分钟跑 110 米,乙每分钟跑 90 米,经过多少分钟甲第三次追上乙?
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
学习目标
1.经历用一元一次方程解决实际问题的过程,提高发现和提出问题、分析和解决问题的能力.
2.通过对行程和工程问题的解决过程,进一步体会“各分量之和=总量”这个基本的等量关系.
3.在解决行程和工程问题的过程中,能够借助图示或列表,用代数式表达问题中的各量.
试一试:
B地
A地
如图所示,甲、乙两车分别在A,B两地.若两车同时出发,相向而行,两小时后相遇.相遇时甲车比乙车多行进24km;相遇后半小时,甲车到达B地,求甲、乙两车的行进速度分别是多少.
小组讨论解决此问题的方法.
可以用列方程的方法解答
甲
乙
课堂导入
相遇问题
甲、乙两地间的路程为375km.一辆轿车和一辆公共汽车分别从甲、乙两地同时出发沿公路相向而行.轿车的平均速度为90km/h,公共汽车的平均速度为60km/h.它们出发后多少小时在途中相遇?
问题1:找出本题中的等量关系.
轿车行驶的路程+公共汽车行驶的路程=甲乙两地间的路程.
新知探究
知识点1 行程问题
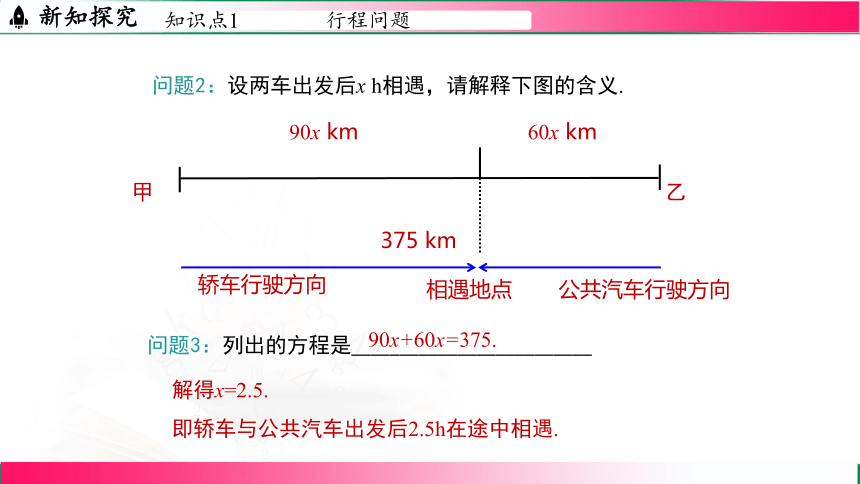
问题2:设两车出发后x h相遇,请解释下图的含义.
375 km
甲
乙
90x km
60x km
轿车行驶方向
公共汽车行驶方向
相遇地点
问题3:列出的方程是_________________________
90x+60x=375.
解得x=2.5.
即轿车与公共汽车出发后2.5h在途中相遇.
新知探究
知识点1 行程问题
相遇问题中常见的等量关系:
总路程=速度和×时间
甲走的路程+乙走的路程=甲、乙之间的距离
【注意】相向而行的始发时间和地点
相遇问题
新知探究
知识点1 行程问题
例1 小明与小红的家相距20km,小明从家里出发骑自行车去小红家,两人商定小红到时候从家里出发骑自行车去接小明. 已知小明骑车的速度为13 km/h,小红骑车的速度是12 km/h.
(1)如果两人同时出发,那么他们经过多少小时相遇?
(2)如果小明先走30min,那么小红骑车要走多少小时才能与小明相遇?
【分析】由于小明与小红都从家里出发,相向而行,所以相遇时,
他们走的路程的和等于两家之间的距离,即
小明走的路程+小红走的路程=两家之间的距离(20 km).
新知探究
知识点1 行程问题
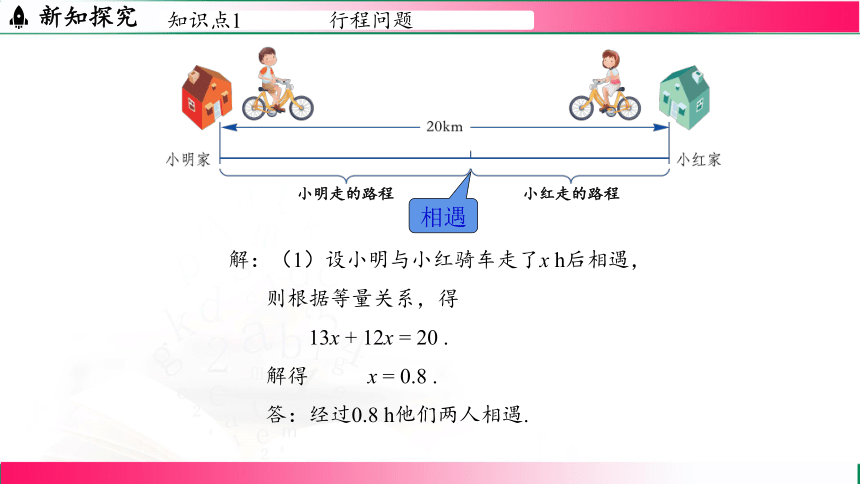
解:(1)设小明与小红骑车走了x h后相遇,
则根据等量关系,得
13x + 12x = 20 .
解得 x = 0.8 .
答:经过0.8 h他们两人相遇.
小明走的路程
小红走的路程
相遇
新知探究
知识点1 行程问题
(2)如果小明先走30min,那么小红骑车要走多少小时才能与小明相遇?
小明先走的路程
小红出发后小明走的路程
小红走的路程
解:(2)设小红骑车走了t h后与小明相遇,
则根据等量关系,得
13(0.5 + t )+12t = 20 .
解得 t = 0.54 .
答:小红骑车走0.54h后与小明相遇.
相遇
新知探究
知识点1 行程问题
例2 一项工作,小李单独做需要6h完成,小王单独做需要9h完成.如果小李先做2h后,再由两人合做,那么还需几小时才能完成 ?
【分析】如果设还需两人合做x h才能完成,那么有下面分析图.
工程问题
小李单独做2h完成的工作量
小王、小李合做xh完成的工作量
总工作量
新知探究
知识点2 工程问题
解:设两人合做x小时才能完成.依题意,得
解得
答:两人合做 小时才能完成这项工作.
新知探究
知识点2 工程问题
2.相等关系:
(1)按工作时间:各时间段的工作量之和=完成的工作量.
(2)按工作者:若一项工作有甲、乙两人参与,则甲的工作
量+乙的工作量=完成的工作量.
工程问题
1.三个基本量:
工程问题中的三个基本量:工作总量、工作效率、工作时间.
它们之间的关系是:工作总量=工作效率×工作时间.
若把工作量看作1,则工作效率=
新知探究
知识点2 工程问题
1.某公路的干线上有相距108 km 的 A,B两个车站,某日14时整,甲、乙两车分别从A,B两站同时出发,相向而行.已知甲车的速度为45 km/h,乙车的速度为36 km/h,则两车相遇的时间是( )
A.14时20分 B.15时20分
C.15时40分 D.14时40分
B
随堂练习
2.甲、乙两人骑摩托车同时从相距170千米的A,B两地相向而行,2小时后相遇.如果甲比乙每小时多行5千米,则乙每小时行( )
A.30千米 B.40千米 C.50千米 D.45千米
B
随堂练习
3.甲、乙两人在400米的环形跑道上练习长跑,他们同时同地反向而跑,甲的速度是6米/秒,乙的速度是4米/秒,则他们首次相遇时,两人都跑了( )
A.40秒 B.50秒 C.60秒 D.70秒
A
随堂练习
4.一项工作,甲独做需18天,乙独做需24天,如果两人合做8天后,余下的工作再由甲独做x天完成,那么所列方程为____________.
5.整理一批图书,由1个人做需20 h完成.现在先由若干人做2 h,然后增加2个人再做4 h,完成了这项工作,则开始时,参与整理图书的有 人.
2
随堂练习
知识点1 流(风)速问题
1. 一艘轮船从甲地到乙地顺流行驶,用了4 h,从乙地返回
到甲地逆流行驶,用了6 h,已知轮船在静水中的平均速
度是20 km/h,那么水流速度是 .
4 km/h
1
2
3
4
5
知识点2 行速问题
2. [新考向·传承数学文化]《九章算术》是中国古代的一部数
学专著,其中记载了一道有趣的题:“今有凫起南海,七
日至北海;雁起北海,九日至南海,今凫雁俱起,问何日
相逢?”大意是:今有野鸭从南海起飞,7天到北海;大
雁从北海起飞,9天到南海,现野鸭从南海、大雁从北海
同时起飞,问经过多少天相遇?设经过 x 天相遇,根据题
意可列方程为( A )
1
2
3
4
5
C. (9-7) x =1 D. (9+7) x =1
【点拨】
根据题意得 x + x =1,
所以 x =1.故选A.
A
【答案】
1
2
3
4
5
3. [2023·连云港]元朝朱世杰所著的《算学启蒙》中,记载了
这样一道题:良马日行二百四十里,驽马日行一百五十
里,驽马先行一十二日,问良马几何日追及之?其大意
是:快马每天行240里,慢马每天行150里,慢马先行12
天,快马几天可追上慢马?若设快马 x 天可追上慢马,由
题意得( D )
1
2
3
4
5
C. 240( x -12)=150 x D. 240 x =150( x +12)
【点拨】
因为慢马先行12天,快马 x 天可追上慢马,
所以快马追上慢马时,慢马行了( x +12)天.
根据题意得240 x =150( x +12).
故选D.
【答案】
D
1
2
3
4
5
利用方程解追及问题
4. 如图,跑道由两条半圆跑道 AB , CD 和两条直跑道 AD ,
BC 组成,两条半圆跑道的长都是122 m,两条直跑道的长
都是85 m.小斌站在 C 处,小强站在 B 处,两人同时出
发,按逆时针方向跑步,小斌每秒跑7 m,小强每秒跑12
m.当小强第一次追上小斌时,他们的位置在( C )
A. 半圆跑道 AB 上 B. 直跑道 BC 上
C. 半圆跑道 CD 上 D. 直跑道 AD 上
1
2
3
4
5
【点拨】
设 x s后,小强第一次追上小斌,
根据题意得12 x -7 x =85,解得 x =17,
所以7 x =7×17=119.又因为119<122,
所以当小强第一次追上小斌时,他们的位置在半圆跑
道 CD 上.
C
【答案】
1
2
3
4
5
利用方程解航行问题
5. 有甲、乙两艘船,现同时由A地顺流而下,乙船到B地时
接到通知,于是立即逆流而上到达C地执行任务,甲船继
续顺流航行.已知甲、乙两船在静水中的速度都是7.5
km/h,水流速度为2.5 km/h,A,C两地间的距离为10
km.如果乙船由A地经B地再到达C地共用了4 h,问:乙
船从B地到达C地时,甲船距离B地有多远?
1
2
3
4
5
【解】设乙船由B地到C地用了 x h,则乙船从B地到达C
地时,甲船距离B地(7.5+2.5) x km.
当C地在A,B两地之间时,由题意得
(7.5+2.5)×(4- x )-(7.5-2.5) x =10,
解得 x =2,所以(7.5+2.5) x =10×2=20;
当C地在B,A两地的延长线上时,
由题意得(7.5-2.5) x -(4- x )(7.5+2.5)=10,
1
2
3
4
5
解得 x = ,所以(7.5+2.5) x =10× = .
答:乙船由B地到达C地时,甲船距离B地20 km或
km.
1
2
3
4
5
甲的工作量+乙的工作量=完成的工作量
列一元一次方程解决相遇、工程问题
相遇问题
工程问题
总路程=速度和×时间
甲走的路程+乙走的路程=甲、乙之间的距离
工作总量=工作效率×工作时间
各时间段的工作量之和=完成的工作量
课堂小结
谢谢观看!
5.4.2用一元一次方程解行程问题、工程问题
第五章 一元一次方程
【2024新教材】2025-2026学年冀教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
第一页:标题页
5.4.2 用一元一次方程解行程问题、工程问题
—— 实际问题中的等量关系探索
(右下角添加授课教师姓名及日期)
第二页:引入
在生活中,行程问题和工程问题十分常见。比如 “甲、乙两人从两地同时出发相向而行,多久后相遇”“一项工程,甲单独做需要多少天完成,乙单独做需要多少天完成,两人合作需要几天完成” 等。这些问题看似复杂,但都可以通过分析其中的数量关系,用一元一次方程来解决。本节课我们就来学习如何运用一元一次方程解决行程问题和工程问题,掌握其中的解题思路和方法。
第三页:行程问题
一、基本数量关系
行程问题的基本数量关系为:路程 = 速度 × 时间,由此可变形得到:速度 = 路程 ÷ 时间,时间 = 路程 ÷ 速度。
二、常见类型及等量关系
相遇问题:
特点:两人或两物体从两地同时出发,相向而行,最终相遇。
等量关系:甲走的路程 + 乙走的路程 = 两地之间的总路程。
追及问题:
特点:两人或两物体同向运动,快者从后面追上慢者。
等量关系:快者走的路程 - 慢者走的路程 = 出发时两者之间的距离(或慢者先走的路程)。
同向而行(不同时出发):
等量关系:慢者先走的路程 + 慢者后走的路程 = 快者走的路程。
环形跑道问题:
相遇(反向而行):两人走的路程之和 = 环形跑道的周长。
追及(同向而行):快者走的路程 - 慢者走的路程 = 环形跑道的周长。
三、例题解析(行程问题)
例题 1(相遇问题):A、B 两地相距 450 千米,甲、乙两车分别从 A、B 两地同时出发,相向而行。甲车的速度为 60 千米 / 小时,乙车的速度为 90 千米 / 小时,经过几小时两车相遇?
解:步骤 1:审题,已知两地距离、两车速度,相向而行,求相遇时间。
步骤 2:设未知数,设经过\(x\)小时两车相遇。
步骤 3:找等量关系,甲车行驶的路程 + 乙车行驶的路程 = A、B 两地的距离。
步骤 4:列方程,甲车行驶的路程为\(60x\)千米,乙车行驶的路程为\(90x\)千米,可列方程\(60x + 90x = 450\)。
步骤 5:解方程,合并同类项得\(150x = 450\),系数化为 1 得\(x = 3\)。
步骤 6:检验并作答,检验:\(60 3 + 90 3 = 180 + 270 = 450\)(千米),符合题意。
答:经过 3 小时两车相遇。甲先做 3 天的工作量为\(\frac{1}{12} 3 = \frac{1}{4}\)。
甲、乙合作\(x\)天的工作量为\((\frac{1}{12} + \frac{1}{18})x\)。
等量关系:甲先做的工作量 + 甲、乙合作的工作量 = 总工作量(单位 “1”)。
列方程:\(\frac{1}{4} + (\frac{1}{12} + \frac{1}{18})x = 1\)。
解方程:先计算括号内的工作效率和,\(\frac{1}{12} + \frac{1}{18} = \frac{3 + 2}{36} = \frac{5}{36}\)。
方程变为\(\frac{1}{4} + \frac{5}{36}x = 1\),移项得\(\frac{5}{36}x = 1 - \frac{1}{4} = \frac{3}{4}\)。
系数化为 1 得\(x = \frac{3}{4} \frac{36}{5} = \frac{27}{5} = 5.4\)。
检验:\(\frac{1}{4} + \frac{5}{36} \frac{27}{5} = \frac{1}{4} + \frac{3}{4} = 1\),符合题意。
答:还需要\(\frac{27}{5}\)天才能完成这项工作。
第五页:易错点分析
行程问题:
忽略单位统一:如速度单位是千米 / 小时,时间单位是分钟,未进行单位换算就直接计算。
混淆相遇和追及的等量关系:相遇问题中误将 “路程差” 作为等量关系,追及问题中误将 “路程和” 作为等量关系。
环形跑道问题中,未明确是同向还是反向而行,导致等量关系错误。
工程问题:
总工作量未看作单位 “1”:在多人合作问题中,不知道将总工作量设为 1,导致无法表示工作效率。
工作效率计算错误:某人单独完成工作需要\(n\)天,其工作效率误算为\(n\),而实际应为\(\frac{1}{n}\)。
忽略合作过程中的工作量叠加:如甲先做一部分,乙再加入合作,未将甲先做的工作量计入总工作量。
例题 7:指出下列解题过程中的错误,并改正。
问题:甲、乙两人分别从相距 100 千米的 A、B 两地同时出发,同向而行,甲的速度是 8 千米 / 小时,乙的速度是 6 千米 / 小时,甲在乙后面,经过多少小时甲能追上乙?
错误解法:
设经过\(x\)小时甲能追上乙。
列方程:\(8x + 6x = 100\)。
解方程:\(14x = 100\),\(x = \frac{50}{7}\)。
答:经过\(\frac{50}{7}\)小时甲能追上乙。
错误分析:这是追及问题,等量关系应为甲走的路程 - 乙走的路程 = 两地距离,而错误地用了路程和。
正确解法:
设经过\(x\)小时甲能追上乙。
列方程:\(8x - 6x = 100\)。
解方程:\(2x = 100\),\(x = 50\)。
答:经过 50 小时甲能追上乙。
第六页:课堂练习
填空题:
甲、乙两人相距 30 千米,相向而行,甲的速度是 4 千米 / 小时,乙的速度是 6 千米 / 小时,______小时后两人相遇。
一项工程,甲单独做需要 8 天完成,乙单独做需要 10 天完成,甲、乙合作每天完成这项工程的______,合作______天可以完成这项工程。
一辆汽车以 60 千米 / 小时的速度行驶,行驶\(x\)小时的路程是______千米;若行驶\(y\)千米,需要______小时。
选择题:
甲、乙两人在环形跑道上跑步,跑道一圈长 400 米,甲每秒跑 6 米,乙每秒跑 4 米,若两人同时同地同向出发,经过( )秒甲第一次追上乙。
A. 100 B. 200 C. 300 D. 400
一项工作,甲单独做需要 10 天,乙单独做需要 15 天,甲先做 2 天,然后两人合作,还需要( )天完成。
A. 4.8 B. 5 C. 5.2 D. 6
解答题:
(1)A、B 两地相距 240 千米,一辆快车和一辆慢车同时从 A 地出发开往 B 地,快车的速度是 80 千米 / 小时,慢车的速度是 60 千米 / 小时,快车比慢车早到几小时?
(2)一项工程,甲队单独做需要 10 天完成,乙队单独做需要 15 天完成,丙队单独做需要 20 天完成。三队合作,几天能完成这项工程的\(\frac{3}{4}\)?
(3)甲、乙两人分别从 A、B 两地同时出发,相向而行,甲的速度是 5 千米 / 小时,乙的速度是 4 千米 / 小时,两人相遇时,甲比乙多走了 3 千米,求 A、B 两地的距离。
第七页:课堂小结
行程问题:
基本数量关系:路程 = 速度 × 时间。
关键是根据不同类型(相遇、追及、环形跑道等)找到对应的等量关系。
工程问题:
基本数量关系:工作量 = 工作效率 × 工作时间,总工作量通常看作单位 “1”。
合作问题的等量关系:各部分工作量之和 = 总工作量。
解决这两类问题的一般步骤:审题→设未知数→找等量关系→列方程→解方程→检验作答。
注意单位统一和实际意义的检验,避免常见错误。
第八页:作业布置
教材第 XX 页习题 5.4 第 5、6、7、8 题。
填空题:
甲每小时走 5 千米,乙每小时走 3 千米,两人同时同地出发,同向而行,\(t\)小时后两人相距______千米。
一项工作,甲的工作效率是\(\frac{1}{a}\),乙的工作效率是\(\frac{1}{b}\),两人合作的工作效率是______。
解答题:
(1)甲、乙两站相距 300 千米,一列慢车从甲站开出,速度是 60 千米 / 小时,一列快车从乙站开出,速度是 80 千米 / 小时。两车同时开出,相向而行,经过多少小时相遇?
(2)一项工程,甲单独做需要 20 天完成,乙单独做需要 30 天完成,甲、乙合作了几天后,乙因事请假,甲继续做,从开工到完成任务共用了 16 天,乙请假了几天?
(3)一条环形跑道长 200 米,甲、乙两人同时从同一地点出发,同向而行,甲每分钟跑 110 米,乙每分钟跑 90 米,经过多少分钟甲第三次追上乙?
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
学习目标
1.经历用一元一次方程解决实际问题的过程,提高发现和提出问题、分析和解决问题的能力.
2.通过对行程和工程问题的解决过程,进一步体会“各分量之和=总量”这个基本的等量关系.
3.在解决行程和工程问题的过程中,能够借助图示或列表,用代数式表达问题中的各量.
试一试:
B地
A地
如图所示,甲、乙两车分别在A,B两地.若两车同时出发,相向而行,两小时后相遇.相遇时甲车比乙车多行进24km;相遇后半小时,甲车到达B地,求甲、乙两车的行进速度分别是多少.
小组讨论解决此问题的方法.
可以用列方程的方法解答
甲
乙
课堂导入
相遇问题
甲、乙两地间的路程为375km.一辆轿车和一辆公共汽车分别从甲、乙两地同时出发沿公路相向而行.轿车的平均速度为90km/h,公共汽车的平均速度为60km/h.它们出发后多少小时在途中相遇?
问题1:找出本题中的等量关系.
轿车行驶的路程+公共汽车行驶的路程=甲乙两地间的路程.
新知探究
知识点1 行程问题
问题2:设两车出发后x h相遇,请解释下图的含义.
375 km
甲
乙
90x km
60x km
轿车行驶方向
公共汽车行驶方向
相遇地点
问题3:列出的方程是_________________________
90x+60x=375.
解得x=2.5.
即轿车与公共汽车出发后2.5h在途中相遇.
新知探究
知识点1 行程问题
相遇问题中常见的等量关系:
总路程=速度和×时间
甲走的路程+乙走的路程=甲、乙之间的距离
【注意】相向而行的始发时间和地点
相遇问题
新知探究
知识点1 行程问题
例1 小明与小红的家相距20km,小明从家里出发骑自行车去小红家,两人商定小红到时候从家里出发骑自行车去接小明. 已知小明骑车的速度为13 km/h,小红骑车的速度是12 km/h.
(1)如果两人同时出发,那么他们经过多少小时相遇?
(2)如果小明先走30min,那么小红骑车要走多少小时才能与小明相遇?
【分析】由于小明与小红都从家里出发,相向而行,所以相遇时,
他们走的路程的和等于两家之间的距离,即
小明走的路程+小红走的路程=两家之间的距离(20 km).
新知探究
知识点1 行程问题
解:(1)设小明与小红骑车走了x h后相遇,
则根据等量关系,得
13x + 12x = 20 .
解得 x = 0.8 .
答:经过0.8 h他们两人相遇.
小明走的路程
小红走的路程
相遇
新知探究
知识点1 行程问题
(2)如果小明先走30min,那么小红骑车要走多少小时才能与小明相遇?
小明先走的路程
小红出发后小明走的路程
小红走的路程
解:(2)设小红骑车走了t h后与小明相遇,
则根据等量关系,得
13(0.5 + t )+12t = 20 .
解得 t = 0.54 .
答:小红骑车走0.54h后与小明相遇.
相遇
新知探究
知识点1 行程问题
例2 一项工作,小李单独做需要6h完成,小王单独做需要9h完成.如果小李先做2h后,再由两人合做,那么还需几小时才能完成 ?
【分析】如果设还需两人合做x h才能完成,那么有下面分析图.
工程问题
小李单独做2h完成的工作量
小王、小李合做xh完成的工作量
总工作量
新知探究
知识点2 工程问题
解:设两人合做x小时才能完成.依题意,得
解得
答:两人合做 小时才能完成这项工作.
新知探究
知识点2 工程问题
2.相等关系:
(1)按工作时间:各时间段的工作量之和=完成的工作量.
(2)按工作者:若一项工作有甲、乙两人参与,则甲的工作
量+乙的工作量=完成的工作量.
工程问题
1.三个基本量:
工程问题中的三个基本量:工作总量、工作效率、工作时间.
它们之间的关系是:工作总量=工作效率×工作时间.
若把工作量看作1,则工作效率=
新知探究
知识点2 工程问题
1.某公路的干线上有相距108 km 的 A,B两个车站,某日14时整,甲、乙两车分别从A,B两站同时出发,相向而行.已知甲车的速度为45 km/h,乙车的速度为36 km/h,则两车相遇的时间是( )
A.14时20分 B.15时20分
C.15时40分 D.14时40分
B
随堂练习
2.甲、乙两人骑摩托车同时从相距170千米的A,B两地相向而行,2小时后相遇.如果甲比乙每小时多行5千米,则乙每小时行( )
A.30千米 B.40千米 C.50千米 D.45千米
B
随堂练习
3.甲、乙两人在400米的环形跑道上练习长跑,他们同时同地反向而跑,甲的速度是6米/秒,乙的速度是4米/秒,则他们首次相遇时,两人都跑了( )
A.40秒 B.50秒 C.60秒 D.70秒
A
随堂练习
4.一项工作,甲独做需18天,乙独做需24天,如果两人合做8天后,余下的工作再由甲独做x天完成,那么所列方程为____________.
5.整理一批图书,由1个人做需20 h完成.现在先由若干人做2 h,然后增加2个人再做4 h,完成了这项工作,则开始时,参与整理图书的有 人.
2
随堂练习
知识点1 流(风)速问题
1. 一艘轮船从甲地到乙地顺流行驶,用了4 h,从乙地返回
到甲地逆流行驶,用了6 h,已知轮船在静水中的平均速
度是20 km/h,那么水流速度是 .
4 km/h
1
2
3
4
5
知识点2 行速问题
2. [新考向·传承数学文化]《九章算术》是中国古代的一部数
学专著,其中记载了一道有趣的题:“今有凫起南海,七
日至北海;雁起北海,九日至南海,今凫雁俱起,问何日
相逢?”大意是:今有野鸭从南海起飞,7天到北海;大
雁从北海起飞,9天到南海,现野鸭从南海、大雁从北海
同时起飞,问经过多少天相遇?设经过 x 天相遇,根据题
意可列方程为( A )
1
2
3
4
5
C. (9-7) x =1 D. (9+7) x =1
【点拨】
根据题意得 x + x =1,
所以 x =1.故选A.
A
【答案】
1
2
3
4
5
3. [2023·连云港]元朝朱世杰所著的《算学启蒙》中,记载了
这样一道题:良马日行二百四十里,驽马日行一百五十
里,驽马先行一十二日,问良马几何日追及之?其大意
是:快马每天行240里,慢马每天行150里,慢马先行12
天,快马几天可追上慢马?若设快马 x 天可追上慢马,由
题意得( D )
1
2
3
4
5
C. 240( x -12)=150 x D. 240 x =150( x +12)
【点拨】
因为慢马先行12天,快马 x 天可追上慢马,
所以快马追上慢马时,慢马行了( x +12)天.
根据题意得240 x =150( x +12).
故选D.
【答案】
D
1
2
3
4
5
利用方程解追及问题
4. 如图,跑道由两条半圆跑道 AB , CD 和两条直跑道 AD ,
BC 组成,两条半圆跑道的长都是122 m,两条直跑道的长
都是85 m.小斌站在 C 处,小强站在 B 处,两人同时出
发,按逆时针方向跑步,小斌每秒跑7 m,小强每秒跑12
m.当小强第一次追上小斌时,他们的位置在( C )
A. 半圆跑道 AB 上 B. 直跑道 BC 上
C. 半圆跑道 CD 上 D. 直跑道 AD 上
1
2
3
4
5
【点拨】
设 x s后,小强第一次追上小斌,
根据题意得12 x -7 x =85,解得 x =17,
所以7 x =7×17=119.又因为119<122,
所以当小强第一次追上小斌时,他们的位置在半圆跑
道 CD 上.
C
【答案】
1
2
3
4
5
利用方程解航行问题
5. 有甲、乙两艘船,现同时由A地顺流而下,乙船到B地时
接到通知,于是立即逆流而上到达C地执行任务,甲船继
续顺流航行.已知甲、乙两船在静水中的速度都是7.5
km/h,水流速度为2.5 km/h,A,C两地间的距离为10
km.如果乙船由A地经B地再到达C地共用了4 h,问:乙
船从B地到达C地时,甲船距离B地有多远?
1
2
3
4
5
【解】设乙船由B地到C地用了 x h,则乙船从B地到达C
地时,甲船距离B地(7.5+2.5) x km.
当C地在A,B两地之间时,由题意得
(7.5+2.5)×(4- x )-(7.5-2.5) x =10,
解得 x =2,所以(7.5+2.5) x =10×2=20;
当C地在B,A两地的延长线上时,
由题意得(7.5-2.5) x -(4- x )(7.5+2.5)=10,
1
2
3
4
5
解得 x = ,所以(7.5+2.5) x =10× = .
答:乙船由B地到达C地时,甲船距离B地20 km或
km.
1
2
3
4
5
甲的工作量+乙的工作量=完成的工作量
列一元一次方程解决相遇、工程问题
相遇问题
工程问题
总路程=速度和×时间
甲走的路程+乙走的路程=甲、乙之间的距离
工作总量=工作效率×工作时间
各时间段的工作量之和=完成的工作量
课堂小结
谢谢观看!
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
