5.2 解一元一次方程-第4课时 利用去分母解一元一次方程 课件(共32张PPT)
文档属性
| 名称 | 5.2 解一元一次方程-第4课时 利用去分母解一元一次方程 课件(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 07:43:57 | ||
图片预览










文档简介
(共32张PPT)
5.2 解一元一次方程-第4课时
利用去分母解一元一次方程
第五章 一元一次方程
【2024新教材】人教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
幻灯片 1:封面
标题:第 4 课时 利用去分母解一元一次方程
副标题:跨越分数方程的障碍
背景图:设计带有分数、方程与桥梁元素的图案,寓意学生通过学习跨越分数方程的难题,激发学习动力
幻灯片 2:目录
复习回顾
情境引入
去分母的原理与方法
利用去分母解方程的步骤
典型例题讲解
课堂练习与互动
课堂小结
课后作业布置
幻灯片 3:复习回顾
回顾去括号解方程:展示方程\(3(2x - 1)=2(x + 3) - 1\),邀请学生快速说出解题步骤,回顾去括号(将\(3\)与\(2\)分别乘入括号内各项)、移项、合并同类项、系数化为\(1\)的过程,强化去括号解方程的方法 。
复习等式性质 2:再次强调等式性质 2“等式两边乘同一个数,或除以同一个不为\(0\)的数,结果仍相等”,提问学生 “若\(3x = 15\),如何利用等式性质 2 求解”,为去分母的原理讲解做铺垫 。
提问引入新课:“我们已经会解含括号的方程,那如果方程中出现分数,像\(\frac{x}{2} + 3 = 5\),怎样求解更简便呢?今天我们就来学习利用去分母解一元一次方程。”
幻灯片 4:情境引入
问题展示:“小明看一本故事书,第一天看了全书的\(\frac{1}{3}\),第二天看了全书的\(\frac{1}{4}\),还剩下\(50\)页没看,这本故事书一共有多少页?”
引导思考:设这本故事书一共有\(x\)页,根据页数关系列出方程\(\frac{1}{3}x + \frac{1}{4}x + 50 = x\)。引导学生观察方程,发现方程中含有分数,计算不便,从而引出需要通过去分母将方程简化求解的需求 。
幻灯片 5:去分母的原理与方法
原理讲解:以方程\(\frac{x}{2} = 3\)为例,根据等式性质 2,在等式两边同时乘以分母\(2\),即\(\frac{x}{2} 2 = 3 2\),得到\(x = 6\),解释去分母的原理是利用等式性质,消除方程中的分母,使方程转化为整数形式,便于计算 。
方法总结:总结去分母的方法,先找出方程中各分母的最小公倍数,然后根据等式性质 2,将方程两边同时乘以这个最小公倍数,把方程中的分母去掉。强调方程两边的每一项都要乘以最小公倍数,不能漏乘 。
要点强调:重点强调去分母时要准确找出最小公倍数,并且确保每一项都乘到,这是去分母正确与否的关键,避免出现漏乘导致错误。
幻灯片 6:利用去分母解方程的步骤
步骤总结:
第一步:找出方程中所有分母的最小公倍数。
第二步:根据等式性质 2,将方程两边同时乘以最小公倍数,去掉分母。
第三步:运用去括号法则(若有括号),去掉括号。
第四步:移项,将含有未知数的项移到等号左边,常数项移到等号右边,注意移项变号。
第五步:合并同类项,将等号两边的同类项进行合并。
第六步:利用等式性质 2,在等式两边同时除以未知数的系数,求出方程的解 。
示例说明:以方程\(\frac{x - 1}{2} = \frac{2x + 1}{3}\)为例,详细展示步骤。首先找出分母\(2\)和\(3\)的最小公倍数是\(6\);然后方程两边同时乘以\(6\),得到\(6 \frac{x - 1}{2} = 6 \frac{2x + 1}{3}\),即\(3(x - 1) = 2(2x + 1)\);接着去括号\(3x - 3 = 4x + 2\);再移项\(3x - 4x = 2 + 3\);合并同类项\(-x = 5\);最后系数化为\(1\),\(x = -5\) 。
幻灯片 7:典型例题讲解 - 例 1
题目:解方程\(\frac{x}{3} + 2 = 5\)
分析解答:
第一步,分母只有\(3\),最小公倍数就是\(3\)。
第二步,方程两边同时乘以\(3\),\(3 \frac{x}{3} + 3 2 = 3 5\),得到\(x + 6 = 15\)。
第三步,移项\(x = 15 - 6\)。
第四步,合并同类项\(x = 9\)。
展示完整解题过程:\(
\begin{align*}
\frac{x}{3} + 2 &= 5\\
3 \frac{x}{3} + 3 2 &= 3 5\\
x + 6 &= 15\\
x &= 15 - 6\\
x &= 9
\end{align*}
\)
幻灯片 8:典型例题讲解 - 例 2
题目:解方程\(\frac{2x - 1}{4} = \frac{x + 2}{3} - 1\)
分析解答:
第一步,分母\(4\)和\(3\)的最小公倍数是\(12\)。
第二步,方程两边同时乘以\(12\),\(12 \frac{2x - 1}{4} = 12 \frac{x + 2}{3} - 12 1\),得到\(3(2x - 1) = 4(x + 2) - 12\)。
第三步,去括号\(6x - 3 = 4x + 8 - 12\)。
第四步,移项\(6x - 4x = 8 - 12 + 3\)。
第五步,合并同类项\(2x = -1\)。
第六步,系数化为\(1\),\(x = -\frac{1}{2}\)。
呈现详细步骤:\(
\begin{align*}
\frac{2x - 1}{4} &= \frac{x + 2}{3} - 1\\
12 \frac{2x - 1}{4} &= 12 \frac{x + 2}{3} - 12 1\\
3(2x - 1) &= 4(x + 2) - 12\\
6x - 3 &= 4x + 8 - 12\\
6x - 4x &= 8 - 12 + 3\\
2x &= -1\\
x &= -\frac{1}{2}
\end{align*}
\)
幻灯片 9:典型例题讲解 - 例 3
题目:解方程\(\frac{0.1x - 0.2}{0.02} - \frac{x + 1}{0.5} = 3\)
分析解答:
第一步,先将方程中的小数分母化为整数,根据分数基本性质,\(\frac{0.1x - 0.2}{0.02}=\frac{(0.1x - 0.2) 100}{0.02 100}=\frac{10x - 20}{2}\),\(\frac{x + 1}{0.5}=\frac{(x + 1) 10}{0.5 10}=\frac{10x + 10}{5}\),原方程变为\(\frac{10x - 20}{2} - \frac{10x + 10}{5} = 3\),此时分母\(2\)和\(5\)的最小公倍数是\(10\)。
第二步,方程两边同时乘以\(10\),\(10 \frac{10x - 20}{2} - 10 \frac{10x + 10}{5} = 10 3\),得到\(5(10x - 20) - 2(10x + 10) = 30\)。
第三步,去括号\(50x - 100 - 20x - 20 = 30\)。
第四步,移项\(50x - 20x = 30 + 100 + 20\)。
第五步,合并同类项\(30x = 150\)。
第六步,系数化为\(1\),\(x = 5\)。
展示完整过程:\(
\begin{align*}
\frac{0.1x - 0.2}{0.02} - \frac{x + 1}{0.5} &= 3\\
\frac{10x - 20}{2} - \frac{10x + 10}{5} &= 3\\
10 \frac{10x - 20}{2} - 10 \frac{10x + 10}{5} &= 10 3\\
5(10x - 20) - 2(10x + 10) &= 30\\
50x - 100 - 20x - 20 &= 30\\
50x - 20x &= 30 + 100 + 20\\
30x &= 150\\
x &= 5
\end{align*}
\)
幻灯片 10:课堂练习与互动
题目展示:
解方程:
\(\frac{x}{4} - 1 = 3\)
\(\frac{3x + 1}{2} = \frac{2x - 1}{3} + 2\)
\(\frac{0.2x - 0.1}{0.3} - \frac{0.1x + 0.2}{0.2} = 1\)
已知方程\(\frac{x - a}{2} = \frac{2x - 1}{3}\)的解是\(x = -1\),求\(a\)的值。
课堂互动:让学生在练习本上独立完成练习,教师巡视课堂,观察学生去分母是否正确(有无漏乘)、去括号、移项、合并同类项和系数化为\(1\)过程中是否出现错误。选取学生上台板演,组织其他学生进行点评,共同纠正问题,强化利用去分母解方程的方法 。
幻灯片 11:课堂小结
知识回顾:总结利用去分母解一元一次方程的方法,强调去分母的原理是等式性质 2,回顾找最小公倍数、去分母、去括号、移项、合并同类项、系数化为\(1\)的完整步骤 。
方法总结:强调去分母时要仔细找对最小公倍数,每一项都要乘到;后续的去括号、移项等步骤要按照之前学过的方法准确计算 。
重点强调:点明去分母是解决分数方程的重要方法,在后续学习和实际应用中经常用到,鼓励学生多练习,熟练掌握 。
幻灯片 12:课后作业布置
基础作业:
解方程:
\(\frac{x}{5} + 4 = 7\)
\(\frac{2x - 3}{3} = \frac{x + 1}{2} - 1\)
\(\frac{0.3x + 0.5}{0.2} - \frac{2x - 1}{3} = 1\)
已知方程\(\frac{x + 1}{3} = \frac{ax - 1}{6}\)的解是\(x = 5\),求\(a\)的值。
拓展作业:结合实际生活,如折扣计算、比例分配等场景,编写一道需要利用去分母解一元一次方程的应用题,并完整解答,提高知识应用能力 。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.会通过去分母解一元一次方程.
2.归纳解一元一次方程的一般步骤,体会解方程中的化归思想.
学习目标
课堂导入
你能解下面的方程吗?
(3y+1)=(7+y)
还有其他解法吗?
去括号, 得 y+ = + y.
移项,得 y- y = - .
合并同类项,得 y =
系数化为1,得 y =1.
知识点 解一元一次方程——去分母
新知探究
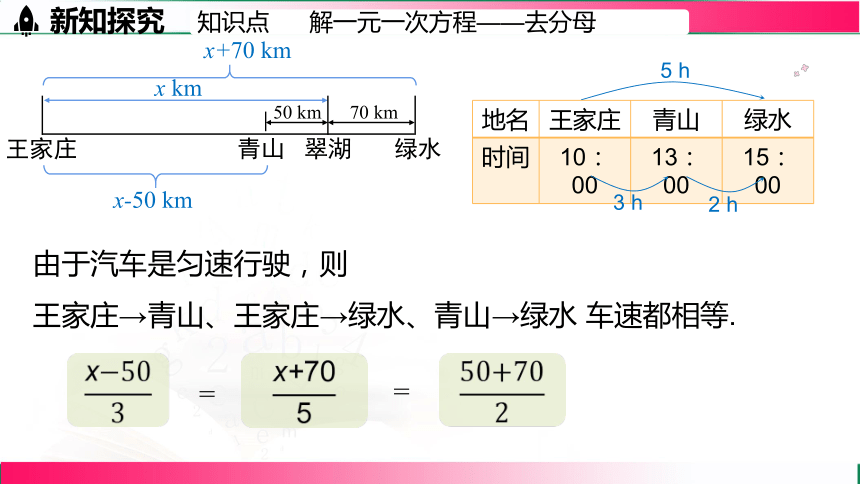
问题 如图,翠湖在青山、绿水两地之间,距青山50 km,距绿水70 km. 某天,一辆汽车匀速行驶,途经王家庄、青山、绿水三地的时间如表所示.王家庄距翠湖的路程有多远?
x km
王家庄
翠湖
绿水
青山
50 km
70 km
地名 王家庄 青山 绿水
时间 10:00 13:00 15:00
设王家庄距翠湖的路程为x km.
x-50 km
x+70 km
3 h
2 h
5 h
透过表格,你能得到什么信息?
知识点 解一元一次方程——去分母
新知探究
由于汽车是匀速行驶,则
王家庄→青山、王家庄→绿水、青山→绿水 车速都相等.
地名 王家庄 青山 绿水
时间 10:00 13:00 15:00
x km
王家庄
翠湖
绿水
青山
50 km
70 km
x-50 km
x+70 km
3 h
2 h
5 h
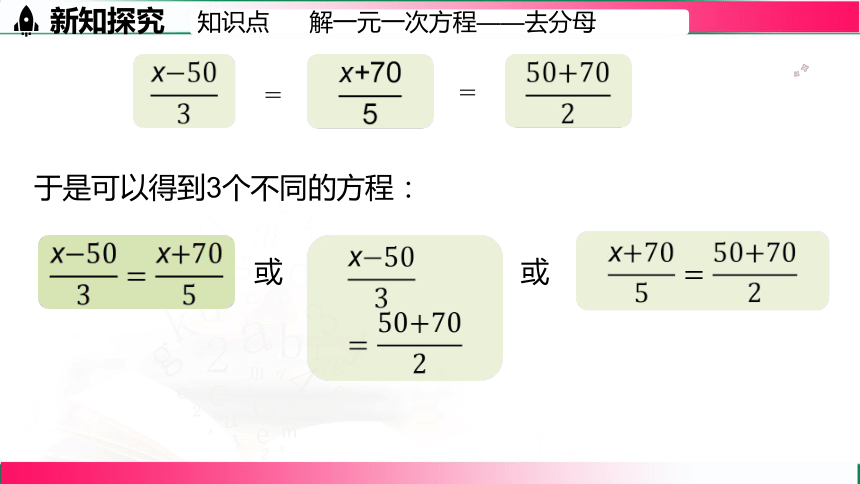
=
=
或
或
=
=
于是可以得到3个不同的方程:
知识点 解一元一次方程——去分母
新知探究
知识点 解一元一次方程——去分母
新知探究
如果能化去分母,把未知数的系数化成整数,就可以使解方程中的计算更简便些.
5(x-50)3(x+70).
×15.
15×
思考
这个方程中未知数的系数是多少?
x的系数是
x的系数是
根据等式的性质2:等式两边乘同一个数,结果仍相等.
这个方程中各分母的最小公倍数是15,方程两边都乘15,得
知识点 解一元一次方程——去分母
新知探究
去括号,得
5x-250=3x+210.
移项,得
5x-3x=210+250.
合并同类项,得
2x=460.
系数化为1,得
x=230.
因此,王家庄距翠湖的路程为230 km.
5(x-50)3(x+70).
知识点 解一元一次方程——去分母
新知探究
为了更全面地研究问题,我们再以方程-2
为例,以框图的形式展示解这类一元一次方程的步骤.
5(3x+1)– 10×2 =(3x – 2)– 2(2x+3)
15x + 5 – 20 = 3x – 2 – 4x – 6
去分母
去括号
方程两边的每一项都要乘分母的最小公倍数10.
依据:等式的性质2.
你能说出每个步骤的依据吗?
依据:分配律.
知识点 解一元一次方程——去分母
新知探究
15x + 5 – 20 = 3x – 2 – 4x – 6
15x – 3x + 4x = – 2 – 6 – 5+20
16x = 7
移项
合并同类项
系数化为1
依据:等式的性质1.
依据:等式的性质2.
依据:分配律.
你能说出每个步骤的依据吗?
知识点 解一元一次方程——去分母
新知探究
归纳
解一元一次方程的一般步骤包括:去分母、去括号、移项、合并同类项、系数化为1等. 通过这些步骤,可以使以x为未知数的方程逐步转化为x=m的形式,这个过程主要依据等式的性质和运算律等.
知识点 解一元一次方程——去分母
新知探究
例 解下列方程:
解:(1)去分母(方程两边乘4),得
2(x + 1) – 4 = 8 +(2 – x).
去括号,得 2x + 2 – 4 = 8 + 2 – x.
移项,得 2x + x = 8 + 2 – 2 + 4 .
合并同类项,得 3x = 12.
系数化为1,得 x = 4.
知识点 解一元一次方程——去分母
新知探究
例 解下列方程:
.
(2)去分母(方程两边乘6),得
18x+3(x-1)=18-2(2x-1).
去括号,得18x+3x-3=18-4x+2.
移项,得18x+3x+4x=18+2+3.
合并同类项,得25x=23.
系数化为1,得x= .
知识点1 利用去分母解一元一次方程
1.将方程的两边同乘____可得到 ,这步
变形叫________,其依据是_____________.
10
去分母
等式的性质2
2.解方程 ,去分母时,方程两边乘各分母的最小公倍数
( )
B
A.10 B.12 C.24 D.6
3.解一元一次方程 时,去分母正确的是( )
D
A. B.
C. D.
4.(16分)解方程:
(1) ;
解:,, ,
, .
(2) ;
解:,,, .
(3) ;
解: ,
,, ,
.
(4) .
解:, ,
,, .
5.(8分)小红在解方程 时,第一步出现了错误:
(1)请在如图的方框内用横线划出小红的错误处;
解:划线如图所示.
(2)写出你的解答过程.
解: ,
去分母,得 .
移项,得 .
合并同类项,得 .
系数化为1,得 .
知识点2 去分母解一元一次方程的应用
6.[2024无锡中考]《九章算术》中有一道“凫雁相逢”问题
(凫:野鸭),大意如下:野鸭从南海飞到北海需要7天,大雁从北海
飞到南海需要9天.如果野鸭、大雁分别从南海、北海同时起飞,经过多
少天相遇?设经过 天相遇,则下列方程正确的是( )
A
A. B. C. D.
7. 一针绘梦乡,一线织华装,中国传统手工艺在新的时
代里正绽放出更加绚丽的光彩.某传统手工坊计划制作一批折扇,如果
每人做7把,那么会比计划多做9把;如果每人做5把,将比计划少做5把.
设计划做 把折扇,则可列方程为__________.
8.(8分) 巴黎奥运会上,我国获得金、银、铜牌总共91
枚.已知获得的银牌数是铜牌数的,获得的金牌数是铜牌数的 ,求在这
届奥运会上我国获得的金牌数.
解:设在这届奥运会上我国获得的铜牌数是 枚,
由题意得 ,
解得,所以 .
答:在这届奥运会上我国获得的金牌数是40枚.
9.若和互为相反数,则 的值为( )
B
A. B.3 C.1 D.
10.[2025保定莲池区期末]我国古代数学著作《九章算术》中有一道
“以绳测井”的题:以绳测井,若将绳三折测之,绳多四尺;若将绳四折
测之,绳多一尺,井深几何?这道题大致意思是:用绳子测量水井深度,
如果将绳子折成三等份,那么每等份井外余绳四尺;如果将绳子折成四
等份,那么每等份井外余绳一尺.问井深多少尺?下列说法不正确的是
( )
A
A.设井深为尺,所列方程为
B.设绳子的长为尺,所列方程为
C.绳子的长是36尺
D.井深8尺
11.(8分)解方程:
(1) ;
解:去分母,得 ,去括号,
得,移项、合并同类项,得 ,
两边都除以18,得 .
(2) .
解:原方程变形为 ,
去分母,得 ,
去括号,得 ,
移项、合并同类项,得 ,
系数化为1,得 .
12.(12分) [2025广州期末]如图是两张不同类型
的火车车票:(“ 次”表示动车,“ 次”表示高铁).
(1)根据车票中的信息填空:两车行驶方向______(填“相同”或“不
同”),出发时刻相差___ ;
相同
1
(2)已知该动车和高铁的平均速度分别为, ,如果
两车均按车票信息准时出发,且同时到达终点,求, 两地之间的距离;
解:设,两地之间的距离为 ,
由题意可得 ,
解得 .
答:,两地之间的距离为 .
(3)在(2)的条件下,请直接写出在_____________时刻,两车相距
.
10:30或12:00
课堂小结
解一元一次方程的一般步骤:
去括号
移项
合并同类项
系数化为1
去分母
谢谢观看!
5.2 解一元一次方程-第4课时
利用去分母解一元一次方程
第五章 一元一次方程
【2024新教材】人教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
幻灯片 1:封面
标题:第 4 课时 利用去分母解一元一次方程
副标题:跨越分数方程的障碍
背景图:设计带有分数、方程与桥梁元素的图案,寓意学生通过学习跨越分数方程的难题,激发学习动力
幻灯片 2:目录
复习回顾
情境引入
去分母的原理与方法
利用去分母解方程的步骤
典型例题讲解
课堂练习与互动
课堂小结
课后作业布置
幻灯片 3:复习回顾
回顾去括号解方程:展示方程\(3(2x - 1)=2(x + 3) - 1\),邀请学生快速说出解题步骤,回顾去括号(将\(3\)与\(2\)分别乘入括号内各项)、移项、合并同类项、系数化为\(1\)的过程,强化去括号解方程的方法 。
复习等式性质 2:再次强调等式性质 2“等式两边乘同一个数,或除以同一个不为\(0\)的数,结果仍相等”,提问学生 “若\(3x = 15\),如何利用等式性质 2 求解”,为去分母的原理讲解做铺垫 。
提问引入新课:“我们已经会解含括号的方程,那如果方程中出现分数,像\(\frac{x}{2} + 3 = 5\),怎样求解更简便呢?今天我们就来学习利用去分母解一元一次方程。”
幻灯片 4:情境引入
问题展示:“小明看一本故事书,第一天看了全书的\(\frac{1}{3}\),第二天看了全书的\(\frac{1}{4}\),还剩下\(50\)页没看,这本故事书一共有多少页?”
引导思考:设这本故事书一共有\(x\)页,根据页数关系列出方程\(\frac{1}{3}x + \frac{1}{4}x + 50 = x\)。引导学生观察方程,发现方程中含有分数,计算不便,从而引出需要通过去分母将方程简化求解的需求 。
幻灯片 5:去分母的原理与方法
原理讲解:以方程\(\frac{x}{2} = 3\)为例,根据等式性质 2,在等式两边同时乘以分母\(2\),即\(\frac{x}{2} 2 = 3 2\),得到\(x = 6\),解释去分母的原理是利用等式性质,消除方程中的分母,使方程转化为整数形式,便于计算 。
方法总结:总结去分母的方法,先找出方程中各分母的最小公倍数,然后根据等式性质 2,将方程两边同时乘以这个最小公倍数,把方程中的分母去掉。强调方程两边的每一项都要乘以最小公倍数,不能漏乘 。
要点强调:重点强调去分母时要准确找出最小公倍数,并且确保每一项都乘到,这是去分母正确与否的关键,避免出现漏乘导致错误。
幻灯片 6:利用去分母解方程的步骤
步骤总结:
第一步:找出方程中所有分母的最小公倍数。
第二步:根据等式性质 2,将方程两边同时乘以最小公倍数,去掉分母。
第三步:运用去括号法则(若有括号),去掉括号。
第四步:移项,将含有未知数的项移到等号左边,常数项移到等号右边,注意移项变号。
第五步:合并同类项,将等号两边的同类项进行合并。
第六步:利用等式性质 2,在等式两边同时除以未知数的系数,求出方程的解 。
示例说明:以方程\(\frac{x - 1}{2} = \frac{2x + 1}{3}\)为例,详细展示步骤。首先找出分母\(2\)和\(3\)的最小公倍数是\(6\);然后方程两边同时乘以\(6\),得到\(6 \frac{x - 1}{2} = 6 \frac{2x + 1}{3}\),即\(3(x - 1) = 2(2x + 1)\);接着去括号\(3x - 3 = 4x + 2\);再移项\(3x - 4x = 2 + 3\);合并同类项\(-x = 5\);最后系数化为\(1\),\(x = -5\) 。
幻灯片 7:典型例题讲解 - 例 1
题目:解方程\(\frac{x}{3} + 2 = 5\)
分析解答:
第一步,分母只有\(3\),最小公倍数就是\(3\)。
第二步,方程两边同时乘以\(3\),\(3 \frac{x}{3} + 3 2 = 3 5\),得到\(x + 6 = 15\)。
第三步,移项\(x = 15 - 6\)。
第四步,合并同类项\(x = 9\)。
展示完整解题过程:\(
\begin{align*}
\frac{x}{3} + 2 &= 5\\
3 \frac{x}{3} + 3 2 &= 3 5\\
x + 6 &= 15\\
x &= 15 - 6\\
x &= 9
\end{align*}
\)
幻灯片 8:典型例题讲解 - 例 2
题目:解方程\(\frac{2x - 1}{4} = \frac{x + 2}{3} - 1\)
分析解答:
第一步,分母\(4\)和\(3\)的最小公倍数是\(12\)。
第二步,方程两边同时乘以\(12\),\(12 \frac{2x - 1}{4} = 12 \frac{x + 2}{3} - 12 1\),得到\(3(2x - 1) = 4(x + 2) - 12\)。
第三步,去括号\(6x - 3 = 4x + 8 - 12\)。
第四步,移项\(6x - 4x = 8 - 12 + 3\)。
第五步,合并同类项\(2x = -1\)。
第六步,系数化为\(1\),\(x = -\frac{1}{2}\)。
呈现详细步骤:\(
\begin{align*}
\frac{2x - 1}{4} &= \frac{x + 2}{3} - 1\\
12 \frac{2x - 1}{4} &= 12 \frac{x + 2}{3} - 12 1\\
3(2x - 1) &= 4(x + 2) - 12\\
6x - 3 &= 4x + 8 - 12\\
6x - 4x &= 8 - 12 + 3\\
2x &= -1\\
x &= -\frac{1}{2}
\end{align*}
\)
幻灯片 9:典型例题讲解 - 例 3
题目:解方程\(\frac{0.1x - 0.2}{0.02} - \frac{x + 1}{0.5} = 3\)
分析解答:
第一步,先将方程中的小数分母化为整数,根据分数基本性质,\(\frac{0.1x - 0.2}{0.02}=\frac{(0.1x - 0.2) 100}{0.02 100}=\frac{10x - 20}{2}\),\(\frac{x + 1}{0.5}=\frac{(x + 1) 10}{0.5 10}=\frac{10x + 10}{5}\),原方程变为\(\frac{10x - 20}{2} - \frac{10x + 10}{5} = 3\),此时分母\(2\)和\(5\)的最小公倍数是\(10\)。
第二步,方程两边同时乘以\(10\),\(10 \frac{10x - 20}{2} - 10 \frac{10x + 10}{5} = 10 3\),得到\(5(10x - 20) - 2(10x + 10) = 30\)。
第三步,去括号\(50x - 100 - 20x - 20 = 30\)。
第四步,移项\(50x - 20x = 30 + 100 + 20\)。
第五步,合并同类项\(30x = 150\)。
第六步,系数化为\(1\),\(x = 5\)。
展示完整过程:\(
\begin{align*}
\frac{0.1x - 0.2}{0.02} - \frac{x + 1}{0.5} &= 3\\
\frac{10x - 20}{2} - \frac{10x + 10}{5} &= 3\\
10 \frac{10x - 20}{2} - 10 \frac{10x + 10}{5} &= 10 3\\
5(10x - 20) - 2(10x + 10) &= 30\\
50x - 100 - 20x - 20 &= 30\\
50x - 20x &= 30 + 100 + 20\\
30x &= 150\\
x &= 5
\end{align*}
\)
幻灯片 10:课堂练习与互动
题目展示:
解方程:
\(\frac{x}{4} - 1 = 3\)
\(\frac{3x + 1}{2} = \frac{2x - 1}{3} + 2\)
\(\frac{0.2x - 0.1}{0.3} - \frac{0.1x + 0.2}{0.2} = 1\)
已知方程\(\frac{x - a}{2} = \frac{2x - 1}{3}\)的解是\(x = -1\),求\(a\)的值。
课堂互动:让学生在练习本上独立完成练习,教师巡视课堂,观察学生去分母是否正确(有无漏乘)、去括号、移项、合并同类项和系数化为\(1\)过程中是否出现错误。选取学生上台板演,组织其他学生进行点评,共同纠正问题,强化利用去分母解方程的方法 。
幻灯片 11:课堂小结
知识回顾:总结利用去分母解一元一次方程的方法,强调去分母的原理是等式性质 2,回顾找最小公倍数、去分母、去括号、移项、合并同类项、系数化为\(1\)的完整步骤 。
方法总结:强调去分母时要仔细找对最小公倍数,每一项都要乘到;后续的去括号、移项等步骤要按照之前学过的方法准确计算 。
重点强调:点明去分母是解决分数方程的重要方法,在后续学习和实际应用中经常用到,鼓励学生多练习,熟练掌握 。
幻灯片 12:课后作业布置
基础作业:
解方程:
\(\frac{x}{5} + 4 = 7\)
\(\frac{2x - 3}{3} = \frac{x + 1}{2} - 1\)
\(\frac{0.3x + 0.5}{0.2} - \frac{2x - 1}{3} = 1\)
已知方程\(\frac{x + 1}{3} = \frac{ax - 1}{6}\)的解是\(x = 5\),求\(a\)的值。
拓展作业:结合实际生活,如折扣计算、比例分配等场景,编写一道需要利用去分母解一元一次方程的应用题,并完整解答,提高知识应用能力 。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.会通过去分母解一元一次方程.
2.归纳解一元一次方程的一般步骤,体会解方程中的化归思想.
学习目标
课堂导入
你能解下面的方程吗?
(3y+1)=(7+y)
还有其他解法吗?
去括号, 得 y+ = + y.
移项,得 y- y = - .
合并同类项,得 y =
系数化为1,得 y =1.
知识点 解一元一次方程——去分母
新知探究
问题 如图,翠湖在青山、绿水两地之间,距青山50 km,距绿水70 km. 某天,一辆汽车匀速行驶,途经王家庄、青山、绿水三地的时间如表所示.王家庄距翠湖的路程有多远?
x km
王家庄
翠湖
绿水
青山
50 km
70 km
地名 王家庄 青山 绿水
时间 10:00 13:00 15:00
设王家庄距翠湖的路程为x km.
x-50 km
x+70 km
3 h
2 h
5 h
透过表格,你能得到什么信息?
知识点 解一元一次方程——去分母
新知探究
由于汽车是匀速行驶,则
王家庄→青山、王家庄→绿水、青山→绿水 车速都相等.
地名 王家庄 青山 绿水
时间 10:00 13:00 15:00
x km
王家庄
翠湖
绿水
青山
50 km
70 km
x-50 km
x+70 km
3 h
2 h
5 h
=
=
或
或
=
=
于是可以得到3个不同的方程:
知识点 解一元一次方程——去分母
新知探究
知识点 解一元一次方程——去分母
新知探究
如果能化去分母,把未知数的系数化成整数,就可以使解方程中的计算更简便些.
5(x-50)3(x+70).
×15.
15×
思考
这个方程中未知数的系数是多少?
x的系数是
x的系数是
根据等式的性质2:等式两边乘同一个数,结果仍相等.
这个方程中各分母的最小公倍数是15,方程两边都乘15,得
知识点 解一元一次方程——去分母
新知探究
去括号,得
5x-250=3x+210.
移项,得
5x-3x=210+250.
合并同类项,得
2x=460.
系数化为1,得
x=230.
因此,王家庄距翠湖的路程为230 km.
5(x-50)3(x+70).
知识点 解一元一次方程——去分母
新知探究
为了更全面地研究问题,我们再以方程-2
为例,以框图的形式展示解这类一元一次方程的步骤.
5(3x+1)– 10×2 =(3x – 2)– 2(2x+3)
15x + 5 – 20 = 3x – 2 – 4x – 6
去分母
去括号
方程两边的每一项都要乘分母的最小公倍数10.
依据:等式的性质2.
你能说出每个步骤的依据吗?
依据:分配律.
知识点 解一元一次方程——去分母
新知探究
15x + 5 – 20 = 3x – 2 – 4x – 6
15x – 3x + 4x = – 2 – 6 – 5+20
16x = 7
移项
合并同类项
系数化为1
依据:等式的性质1.
依据:等式的性质2.
依据:分配律.
你能说出每个步骤的依据吗?
知识点 解一元一次方程——去分母
新知探究
归纳
解一元一次方程的一般步骤包括:去分母、去括号、移项、合并同类项、系数化为1等. 通过这些步骤,可以使以x为未知数的方程逐步转化为x=m的形式,这个过程主要依据等式的性质和运算律等.
知识点 解一元一次方程——去分母
新知探究
例 解下列方程:
解:(1)去分母(方程两边乘4),得
2(x + 1) – 4 = 8 +(2 – x).
去括号,得 2x + 2 – 4 = 8 + 2 – x.
移项,得 2x + x = 8 + 2 – 2 + 4 .
合并同类项,得 3x = 12.
系数化为1,得 x = 4.
知识点 解一元一次方程——去分母
新知探究
例 解下列方程:
.
(2)去分母(方程两边乘6),得
18x+3(x-1)=18-2(2x-1).
去括号,得18x+3x-3=18-4x+2.
移项,得18x+3x+4x=18+2+3.
合并同类项,得25x=23.
系数化为1,得x= .
知识点1 利用去分母解一元一次方程
1.将方程的两边同乘____可得到 ,这步
变形叫________,其依据是_____________.
10
去分母
等式的性质2
2.解方程 ,去分母时,方程两边乘各分母的最小公倍数
( )
B
A.10 B.12 C.24 D.6
3.解一元一次方程 时,去分母正确的是( )
D
A. B.
C. D.
4.(16分)解方程:
(1) ;
解:,, ,
, .
(2) ;
解:,,, .
(3) ;
解: ,
,, ,
.
(4) .
解:, ,
,, .
5.(8分)小红在解方程 时,第一步出现了错误:
(1)请在如图的方框内用横线划出小红的错误处;
解:划线如图所示.
(2)写出你的解答过程.
解: ,
去分母,得 .
移项,得 .
合并同类项,得 .
系数化为1,得 .
知识点2 去分母解一元一次方程的应用
6.[2024无锡中考]《九章算术》中有一道“凫雁相逢”问题
(凫:野鸭),大意如下:野鸭从南海飞到北海需要7天,大雁从北海
飞到南海需要9天.如果野鸭、大雁分别从南海、北海同时起飞,经过多
少天相遇?设经过 天相遇,则下列方程正确的是( )
A
A. B. C. D.
7. 一针绘梦乡,一线织华装,中国传统手工艺在新的时
代里正绽放出更加绚丽的光彩.某传统手工坊计划制作一批折扇,如果
每人做7把,那么会比计划多做9把;如果每人做5把,将比计划少做5把.
设计划做 把折扇,则可列方程为__________.
8.(8分) 巴黎奥运会上,我国获得金、银、铜牌总共91
枚.已知获得的银牌数是铜牌数的,获得的金牌数是铜牌数的 ,求在这
届奥运会上我国获得的金牌数.
解:设在这届奥运会上我国获得的铜牌数是 枚,
由题意得 ,
解得,所以 .
答:在这届奥运会上我国获得的金牌数是40枚.
9.若和互为相反数,则 的值为( )
B
A. B.3 C.1 D.
10.[2025保定莲池区期末]我国古代数学著作《九章算术》中有一道
“以绳测井”的题:以绳测井,若将绳三折测之,绳多四尺;若将绳四折
测之,绳多一尺,井深几何?这道题大致意思是:用绳子测量水井深度,
如果将绳子折成三等份,那么每等份井外余绳四尺;如果将绳子折成四
等份,那么每等份井外余绳一尺.问井深多少尺?下列说法不正确的是
( )
A
A.设井深为尺,所列方程为
B.设绳子的长为尺,所列方程为
C.绳子的长是36尺
D.井深8尺
11.(8分)解方程:
(1) ;
解:去分母,得 ,去括号,
得,移项、合并同类项,得 ,
两边都除以18,得 .
(2) .
解:原方程变形为 ,
去分母,得 ,
去括号,得 ,
移项、合并同类项,得 ,
系数化为1,得 .
12.(12分) [2025广州期末]如图是两张不同类型
的火车车票:(“ 次”表示动车,“ 次”表示高铁).
(1)根据车票中的信息填空:两车行驶方向______(填“相同”或“不
同”),出发时刻相差___ ;
相同
1
(2)已知该动车和高铁的平均速度分别为, ,如果
两车均按车票信息准时出发,且同时到达终点,求, 两地之间的距离;
解:设,两地之间的距离为 ,
由题意可得 ,
解得 .
答:,两地之间的距离为 .
(3)在(2)的条件下,请直接写出在_____________时刻,两车相距
.
10:30或12:00
课堂小结
解一元一次方程的一般步骤:
去括号
移项
合并同类项
系数化为1
去分母
谢谢观看!
同课章节目录
