5.3 实际问题与一元一次方程-第4课时 分段计费问题与方案决策问题 课件(共28张PPT)
文档属性
| 名称 | 5.3 实际问题与一元一次方程-第4课时 分段计费问题与方案决策问题 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 07:42:50 | ||
图片预览




文档简介
(共28张PPT)
5.3 实际问题与一元一次方程-第4课时
分段计费问题与方案决策问题
第五章 一元一次方程
【2024新教材】人教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
幻灯片 1:封面
标题:第 4 课时 分段计费问题与方案决策问题
副标题:用方程权衡生活中的选择与成本
背景图:选用水电费账单、出租车计价器、不同购物优惠方案对比图等元素,营造生活场景氛围,激发学生学习兴趣
幻灯片 2:目录
复习回顾
分段计费问题讲解
方案决策问题讲解
课堂练习与互动
课堂小结
课后作业布置
幻灯片 3:复习回顾
回顾积分问题:简要回顾上节课积分问题的常见类型(体育赛事积分、竞赛活动积分等)、积分规则以及根据等量关系列方程求解的方法,提问学生解决积分问题的关键步骤,强化根据实际情况建立方程模型的思维 。
回顾方程知识:快速复习一元一次方程的解法,展示方程\(3(x - 2) + 4x = 15\),邀请学生简述求解过程(去括号、移项、合并同类项、系数化为 1),为解决新问题做好知识铺垫 。
提问引入新课:“在生活中,我们会遇到很多不同的收费方式,比如水电费按用量分段收费,购物时有多种优惠方案可供选择。这些问题该如何用数学知识解决呢?这节课我们就来学习分段计费问题与方案决策问题。”
幻灯片 4:分段计费问题讲解 - 情境引入
问题展示:“某地居民生活用电基本价格为每度\(0.50\)元,若每月用电量超过\(a\)度,超出部分按基本电价的\(80\%\)收费。某户九月份用电\(100\)度,共交电费\(46\)元,求\(a\)的值。”
引导分析:设每月用电量超过\(a\)度时开始加价收费。不超过\(a\)度的部分电费为\(0.5a\)元,超过\(a\)度部分的用电量为\((100 - a)\)度,这部分电费为\(0.5 80\% (100 - a)\)元。根据 “总电费 = 不超过部分电费 + 超过部分电费” 这一等量关系,列出方程\(0.5a + 0.5 80\% (100 - a) = 46\) 。
幻灯片 5:分段计费问题讲解 - 解题过程
解方程:\(
\begin{align*}
0.5a + 0.5 0.8 (100 - a) &= 46\\
0.5a + 0.4 (100 - a) &= 46\\
0.5a + 40 - 0.4a &= 46\\
0.5a - 0.4a &= 46 - 40\\
0.1a &= 6\\
a &= 60
\end{align*}
\)
方法总结:分段计费问题的关键是明确各段的计费标准,找出总费用与各段费用之间的关系,以此作为等量关系列出方程 。
幻灯片 6:分段计费问题 - 巩固练习
题目展示:“某城市按以下规定收取每月煤气费:用煤气如果不超过\(60\)立方米,按每立方米\(0.8\)元收费;如果超过\(60\)立方米,超过部分按每立方米\(1.2\)元收费。已知某用户\(10\)月份的煤气费平均每立方米\(0.88\)元,求该用户\(10\)月份应交的煤气费是多少元?”
互动环节:让学生独立思考,尝试找出等量关系并列出方程,教师巡视指导,选取学生分享解题思路 。
幻灯片 7:方案决策问题讲解 - 情境引入
问题展示:“某商场在促销期间规定:商场内所有商品按标价的\(80\%\)出售;同时,当顾客在该商场内消费满一定金额后,还可按如下方案获得相应金额的奖券:
| 消费金额\(a\)(元)|\(200\leq a < 400\)|\(400\leq a < 500\)|\(500\leq a < 700\)|\(700\leq a < 900\)|...|
|----|----|----|----|----|----|
| 获奖券金额(元)|30|60|100|130|...|
根据上述促销方法,顾客在该商场购物可以获得双重优惠。例如,购买标价为\(400\)元的商品,则消费金额为\(400 80\% = 320\)元,获得的优惠额为\(400 (1 - 80\%) + 30 = 110\)元。购买一件标价为\(1000\)元的商品,顾客得到的优惠额是多少?对于标价在\(500\)元与\(800\)元之间(含\(500\)元和\(800\)元)的商品,顾客购买标价为多少元的商品,可以得到\(\frac{1}{3}\)的优惠率?”
引导分析:先计算购买标价\(1000\)元商品的消费金额、优惠额。对于求优惠率为\(\frac{1}{3}\)时商品标价,设商品标价为\(x\)元,分\(500\leq x < 700\)和\(700\leq x < 800\)两种情况,根据 “优惠率 = 优惠额 ÷ 标价” 列出方程 。
幻灯片 8:方案决策问题讲解 - 解题过程
计算标价\(1000\)元商品优惠额:消费金额为\(1000 80\% = 800\)元,奖券金额\(130\)元,优惠额为\(1000 (1 - 80\%) + 130 = 330\)元 。
求解优惠率为\(\frac{1}{3}\)时商品标价:
当\(500\leq x < 700\)时,列出方程\([x(1 - 80\%) + 100] ·x = \frac{1}{3}\),\(
\begin{align*}
(0.2x + 100) ·x &= \frac{1}{3}\\
0.2x + 100 &= \frac{1}{3}x\\
\frac{1}{3}x - 0.2x &= 100\\
\frac{1}{3}x - \frac{1}{5}x &= 100\\
\frac{5 - 3}{15}x &= 100\\
\frac{2}{15}x &= 100\\
x &= 750
\end{align*}
\)
当\(700\leq x < 800\)时,列出方程\([x(1 - 80\%) + 130] ·x = \frac{1}{3}\),\(
\begin{align*}
(0.2x + 130) ·x &= \frac{1}{3}\\
0.2x + 130 &= \frac{1}{3}x\\
\frac{1}{3}x - 0.2x &= 130\\
\frac{1}{3}x - \frac{1}{5}x &= 130\\
\frac{2}{15}x &= 130\\
x &= 975 è
\end{align*}
\)
方法总结:方案决策问题要分析不同方案的计算方式,根据题目要求(如优惠率、成本比较等)找出等量关系,必要时需分类讨论 。
幻灯片 9:方案决策问题 - 巩固练习
题目展示:“某通讯公司推出了甲、乙两种收费标准供手机用户选择:
甲种收费标准:每月收取月租费\(10\)元,另外每通话\(1\)分钟加收\(0.2\)元;
乙种收费标准:不收取月租费,每通话\(1\)分钟收费\(0.3\)元。
(1)若某用户每月通话时间为\(x\)分钟,请分别表示出两种收费标准下该用户每月应缴的费用;
(2)若某用户估计每月通话时间为\(100\)分钟,应选择哪种收费标准比较合算?”
互动环节:引导学生分析题目,设未知数,列出不同方案的费用表达式,再进行比较,邀请学生上台板演 。
幻灯片 10:课堂练习与互动
题目展示:
为鼓励居民节约用水,某城市对居民生活用水实行 “阶梯水价”,计费方法如下表:
| 每户每月用水量\(m\)(立方米)| 水价(元 / 立方米)|
|----|----|
|\(18\)立方米及以下 | 2.5|
|\(18\)立方米以上但不超过\(25\)立方米的部分 | 3.3|
|\(25\)立方米以上的部分 | 6|
若某户居民本月交水费\(84.2\)元,求该户居民本月的用水量。
某旅行社组织一批游客外出旅游,原计划租用\(45\)座客车若干辆,但有\(15\)人没有座位;若租用同样数量的\(60\)座客车,则多出一辆车,且其余客车恰好坐满。已知\(45\)座客车租金为每辆\(220\)元,\(60\)座客车租金为每辆\(300\)元,问:
(1)这批游客的人数是多少?原计划租用\(45\)座客车多少辆?
(2)若租用同一种车,要使每位游客都有座位,应该怎样租用才合算?
互动环节:学生独立完成练习,教师巡视指导,选取学生上台展示解题过程,组织其他学生进行讨论和评价,教师针对学生出现的问题进行集中讲解 。
幻灯片 11:课堂小结
知识回顾:总结分段计费问题和方案决策问题的特点及解题方法,回顾如何根据不同情况找出等量关系并列出方程 。
方法总结:强调解决分段计费问题要明确各段计费标准,方案决策问题要分析不同方案的差异,必要时分类讨论,建立合适的方程模型求解 。
重点强调:提醒学生在解决实际问题时,要仔细审题,准确理解题意,注意单位统一和取值范围 。
幻灯片 12:课后作业布置
基础作业:
某市为更有效地利用水资源,制定了居民用水收费标准:如果一户每月用水量不超过\(15\)立方米,每立方米按\(1.8\)元收费;如果超过\(15\)立方米,超过部分按每立方米\(2.3\)元收费,其余仍按每立方米\(1.8\)元计算。另外,每立方米加收污水处理费\(1\)元。若某户一月份共支付水费\(58.5\)元,求该户一月份用水量。
某牛奶加工厂现有鲜奶\(9\)吨,若在市场上直接销售鲜奶,每吨可获取利润\(500\)元;制成酸奶销售,每吨可获取利润\(1200\)元;制成奶片销售,每吨可获取利润\(2000\)元。该工厂的生产能力是:如制成酸奶,每天可加工\(3\)吨;制成奶片,每天可加工\(1\)吨。受人员限制,两种加工方式不可同时进行;受气温条件限制,这批牛奶必须在\(4\)天内全部销售或加工完毕。为此,该厂设计了两种可行方案:
方案一:尽可能多的制成奶片,其余直接销售鲜奶;
方案二:将一部分制成奶片,其余制成酸奶销售,并恰好\(4\)天完成。
你认为选择哪种方案获利最多?为什么?
拓展作业:观察生活中更多的分段计费和方案决策场景,如快递收费、旅游出行方案等,选取一个实际问题进行详细分析,建立数学模型并求解,形成一篇小报告 。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1. 会从空调的综合费用比较计费方式中寻找数量关系,列出方程.
2. 体会分类思想和方程思想在解决问题中的作用,能够根据已知条件选择分类关键点分析问题,选择最优方案.
学习目标
课堂导入
同学们,你们去过电器商场吗?
在冰箱、洗衣机、空调等家用电器上,我们常会看到右图这样的小标识,你知道这是什么意思吗?
课堂导入
中国能效标识又称能源效率标识,是附在耗能产品或其最小包装物上,表示产品能源效率等级等性能指标的一种信息标签.
等级越低,表示能耗越低,越节电.
我发现能耗低的电器比能耗高的电器价格贵,但能耗低的电器比较省电,电费低,我该怎么选择呢?
知识点 方案选择问题
新知探究
耗能高
中国能效标识
耗能低
12345
探究
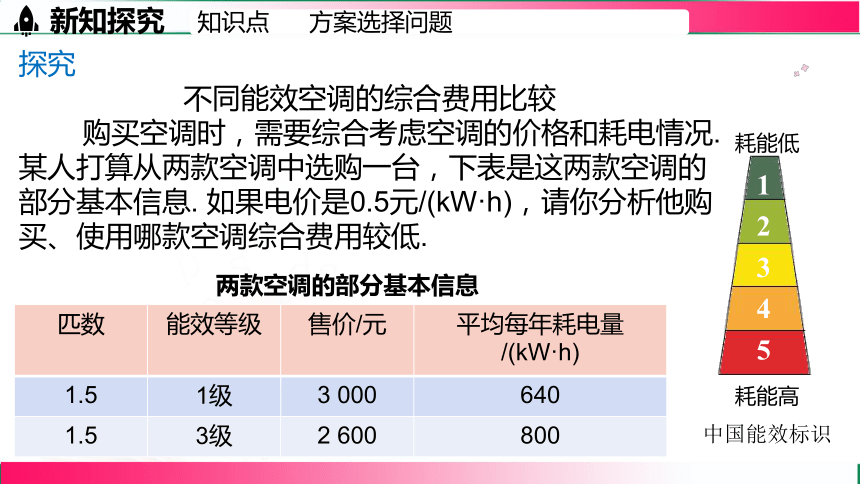
不同能效空调的综合费用比较
购买空调时,需要综合考虑空调的价格和耗电情况.
某人打算从两款空调中选购一台,下表是这两款空调的部分基本信息. 如果电价是0.5元/(kW·h),请你分析他购买、使用哪款空调综合费用较低.
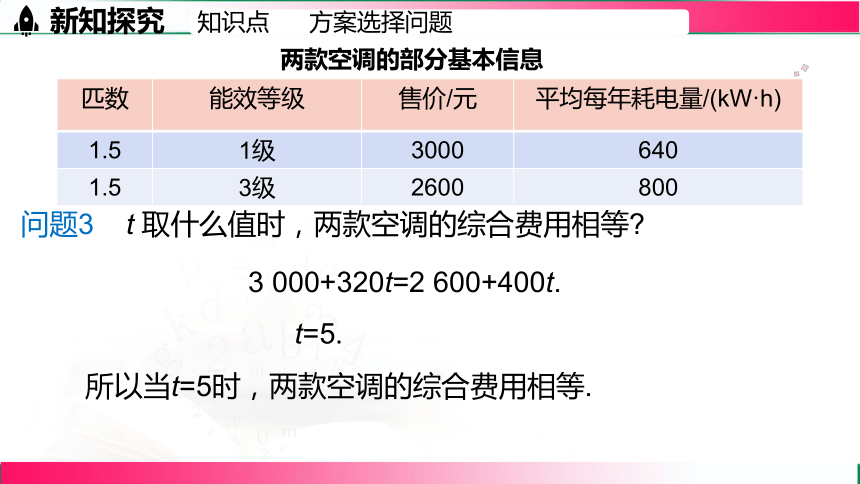
两款空调的部分基本信息
匹数 能效等级 售价/元 平均每年耗电量/(kW·h)
1.5 1级 3 000 640
1.5 3级 2 600 800
知识点 方案选择问题
新知探究
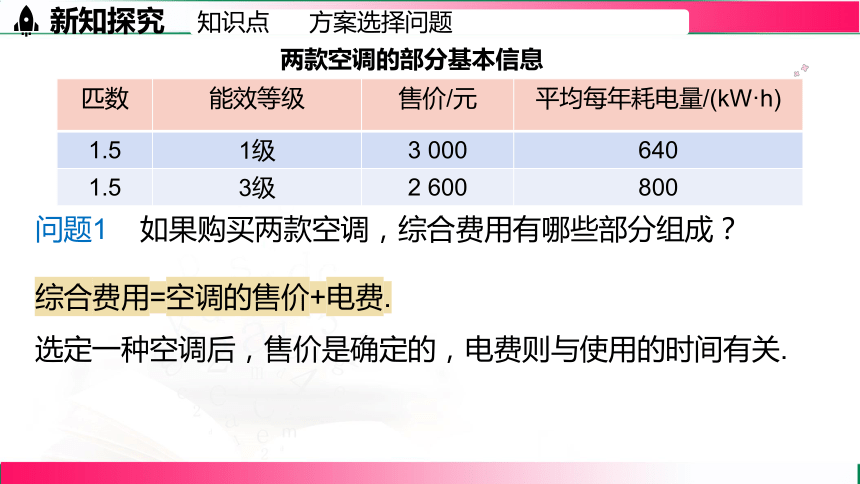
综合费用=空调的售价+电费.
选定一种空调后,售价是确定的,电费则与使用的时间有关.
问题1 如果购买两款空调,综合费用有哪些部分组成?
两款空调的部分基本信息
匹数 能效等级 售价/元 平均每年耗电量/(kW·h)
1.5 1级 3 000 640
1.5 3级 2 600 800
知识点 方案选择问题
新知探究
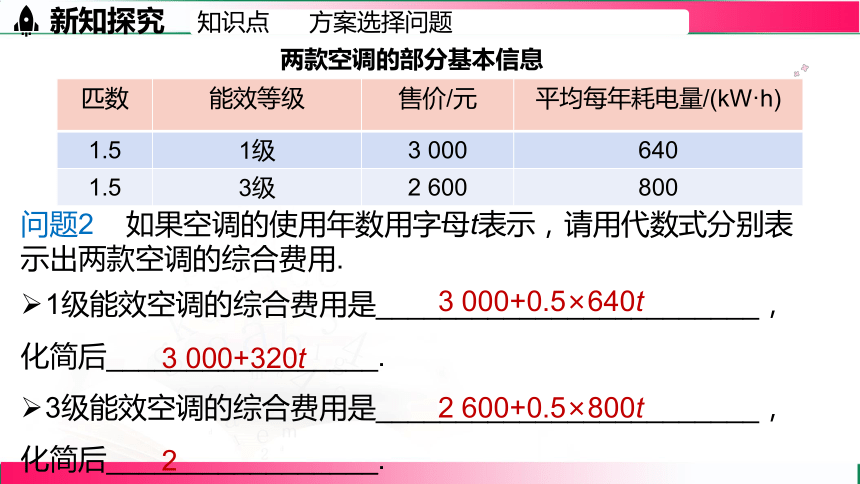
问题2 如果空调的使用年数用字母t表示,请用代数式分别表示出两款空调的综合费用.
两款空调的部分基本信息
匹数 能效等级 售价/元 平均每年耗电量/(kW·h)
1.5 1级 3 000 640
1.5 3级 2 600 800
1级能效空调的综合费用是________________________,
化简后_________________.
3级能效空调的综合费用是________________________,
化简后_________________.
3 000+0.5×640t
3 000+320t
2 600+400t
2 600+0.5×800t
知识点 方案选择问题
新知探究
两款空调的部分基本信息
匹数 能效等级 售价/元 平均每年耗电量/(kW·h)
1.5 1级 3000 640
1.5 3级 2600 800
问题3 t 取什么值时,两款空调的综合费用相等
3 000+320t=2 600+400t.
t=5.
所以当t=5时,两款空调的综合费用相等.
知识点 方案选择问题
新知探究
问题4 t 取什么值时,1级能效空调的综合费用较低 t 取什么值时,3级能效空调的综合费用较低
表示1级能效空调的综合费用:
3 000+320t.
表示3级能效空调的综合费用:
2 600+400t.
(3 000+320t)+(80t-400)
变形
3 000+320t+80(t-5).
讨论80(t-5)的
正负即可.
当t<5时,80(t-5)是负数,这表明3级能效空调的综合费用较低;
当t>5时,80(t-5)是正数,这表明1级能效空调的综合费用较低.
知识点 方案选择问题
新知探究
为了比较两款空调的综合费用,我们把表示3级能效空调的综合费用的式子2 600+400t变形为1级能效空调的综合费用3 000+320t与另外一个式子的和,即
(3 000+320t)+(80t-400),
也就是
3 000+320t +80(t-5).
知识点 方案选择问题
新知探究
由此可见,同样是1.5匹的空调,1级能效空调虽然售价高,但由于比较省电,使用年份长(超过5年)时综合费用反而低.根据相关行业标准,空调的安全使用年限是10年(从生产日期计起),因此购买、使用1级能效空调更划算.
通常,1级能效空调既节能又省钱!
审题
更优惠
费用相同
列方程
用未知数表示费用
设未知数
选择最优方案问题的一般步骤:
知识点 方案选择问题
新知探究
知识点1 分段计费问题
1. 石家庄出租车收费标准如下:起步价8元(即行驶路程不超过
,付车费8元),每增加 ,加收1.6元.小轩从家到河北博物院
的路程为 ,乘出租车需付车费27.2元,则可列方程为( )
C
A. B.
C. D.
2.[2025重庆綦江区期末]某航空公司规定:乘坐飞机普通舱的旅客每
人最多只能免费托运的行李,超过部分每千克按机票价格的
购买行李票,一位旅客托运了 的行李,这样,机票和行李票共付
了1 339元,则该旅客的机票价格是( )
B
A.1 020元 B.1 030元 C.1 040元 D.1 050元
3.(8分)[2025烟台期末]“水是生命之源”,某自来水公司为鼓励用
户节约用水,按以下规定收取水费:
月用水量/吨 单价/(元/吨)
不超过20吨的部分 2
超过20吨的部分 2.5
另:每吨水加收0.3元的城市污水处理费 (1)若某用户11月份共用水25吨,则他应缴水费____元.
60
(2)若某用户12月份应缴水费为74元,则该用户12月份用水多少吨?
解:因为(元) 元,
所以该用户12月份用水量超过20吨,
设该用户12月份用水 吨,
由题意,得,解得 .
答:该用户12月份用水30吨.
知识点2 方案决策问题
4.某服装商店出售一种优惠购物卡,花200元买这种卡后,凭卡可在这
家商店按八折购物,下列情况买卡购物合算的是( )
C
A.购物900元 B.购物500元 C.购物1 200元 D.购物1 000元
5.元旦期间,某超市推出如下优惠方案:(1)一次性购物超过100元但
不超过300元,在原价基础上一律打九折;(2)一次性购物超过300元,
在原价基础上一律打八折,王老师购物后付款252元,则他所购物品的
原价是______________.
280元或315元
6.(8分)[2025洛阳期末]“天下无双圣境,世界第一仙山”的老君山,
是河南洛阳 级著名旅游景区.原门票价格为130元/张,某旅行社推出
一种团队票(人数 ),团队票可选择两种购票优惠方案:
方案一:全体人员打八折.
方案二:有5人可以免票,剩下的人员打九折.
设某团队有 人.
(1)该团队选择方案一的费用为______元,选择方案二的费用为
____________元.(用含 的代数式表示)
(2)若该团队无论选择哪种方案购票,费用恰好一样,则该团队共多
少人?
解:由题意得 ,
解得 .
答:该团队共45人.
7.[2025唐山丰南区期末]甲、乙两店以同样价格出售一种商品,并推
出不同的优惠方案,在甲店累计购物超过100元后,超出100元的部分打
九折;在乙店累计购物超过50元后,超出50元的部分打九五折,则顾客
到两店购物花费一样时( )
D
A.累计购物不超过50元
B.累计购物超过50元不超过100元
C.累计购物超过100元
D.累计购物不超过50元或刚好为150元
8.(12分)[2025郑州期末]某市对居民生活用电实行阶梯电价,具体
收费标准如下表:
档次 月用电量 电价/(元/千瓦时)
第1档 不超过240千瓦时的部分
第2档 超过240千瓦时但不超过400千瓦时的部分 0.65
第3档 超过400千瓦时的部分
已知10月份该市居民老李家用电200千瓦时,交电费120元;9月份老李
家交电费157元.
(1)表中 的值为____;
0.6
(2)老李家9月份的用电量为___________;
260千瓦时
(3)若8月份老李家用电的平均电价为0.7元/千瓦时,求老李家8月份的
用电量.
解:因为 ,
所以老李家8月份的用电量超过400千瓦时.
设老李家8月份的用电量为 千瓦时.
由题意,得,解得 .
答:老李家8月份的用电量为560千瓦时.
9.(12分)[2025杭州上城区期末]红领巾球馆计划购买某品牌的乒乓
球拍和乒乓球,已知该品牌的乒乓球拍每副定价150元,乒乓球每盒定
价15元.元旦期间该品牌决定开展促销活动,活动期间向客户提供两种
优惠方案,即
方案一:买一副乒乓球拍送两盒乒乓球;
方案二:乒乓球拍和乒乓球都按定价的 付款.
该球馆计划购买乒乓球拍10副,乒乓球盒(, 为整数).
(1)当 时,若该球馆按方案一购买,需付款_______元;若该球
馆按方案二购买,需付款_______元.
1 800
1 890
(2)当 为何值时,分别按两种方案购买所需费用一样?
解:由题意得 ,
解得,所以当 时,分别按两种方案购买所需费用一样.
(3)若 ,能否找到一种更为省钱的购买方案?如果能,请你写
出购买方案,并计算出此方案所需费用;如果不能,请说明理由.
解:先按方案一购买10副乒乓球拍可得20盒乒乓球,再按方案二购买20
盒乒乓球,需付款 (元).
课堂小结
选择最优方案问题的一般步骤:
审题
更优惠
费用相同
列方程
用未知数表示费用
设未知数
谢谢观看!
5.3 实际问题与一元一次方程-第4课时
分段计费问题与方案决策问题
第五章 一元一次方程
【2024新教材】人教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
幻灯片 1:封面
标题:第 4 课时 分段计费问题与方案决策问题
副标题:用方程权衡生活中的选择与成本
背景图:选用水电费账单、出租车计价器、不同购物优惠方案对比图等元素,营造生活场景氛围,激发学生学习兴趣
幻灯片 2:目录
复习回顾
分段计费问题讲解
方案决策问题讲解
课堂练习与互动
课堂小结
课后作业布置
幻灯片 3:复习回顾
回顾积分问题:简要回顾上节课积分问题的常见类型(体育赛事积分、竞赛活动积分等)、积分规则以及根据等量关系列方程求解的方法,提问学生解决积分问题的关键步骤,强化根据实际情况建立方程模型的思维 。
回顾方程知识:快速复习一元一次方程的解法,展示方程\(3(x - 2) + 4x = 15\),邀请学生简述求解过程(去括号、移项、合并同类项、系数化为 1),为解决新问题做好知识铺垫 。
提问引入新课:“在生活中,我们会遇到很多不同的收费方式,比如水电费按用量分段收费,购物时有多种优惠方案可供选择。这些问题该如何用数学知识解决呢?这节课我们就来学习分段计费问题与方案决策问题。”
幻灯片 4:分段计费问题讲解 - 情境引入
问题展示:“某地居民生活用电基本价格为每度\(0.50\)元,若每月用电量超过\(a\)度,超出部分按基本电价的\(80\%\)收费。某户九月份用电\(100\)度,共交电费\(46\)元,求\(a\)的值。”
引导分析:设每月用电量超过\(a\)度时开始加价收费。不超过\(a\)度的部分电费为\(0.5a\)元,超过\(a\)度部分的用电量为\((100 - a)\)度,这部分电费为\(0.5 80\% (100 - a)\)元。根据 “总电费 = 不超过部分电费 + 超过部分电费” 这一等量关系,列出方程\(0.5a + 0.5 80\% (100 - a) = 46\) 。
幻灯片 5:分段计费问题讲解 - 解题过程
解方程:\(
\begin{align*}
0.5a + 0.5 0.8 (100 - a) &= 46\\
0.5a + 0.4 (100 - a) &= 46\\
0.5a + 40 - 0.4a &= 46\\
0.5a - 0.4a &= 46 - 40\\
0.1a &= 6\\
a &= 60
\end{align*}
\)
方法总结:分段计费问题的关键是明确各段的计费标准,找出总费用与各段费用之间的关系,以此作为等量关系列出方程 。
幻灯片 6:分段计费问题 - 巩固练习
题目展示:“某城市按以下规定收取每月煤气费:用煤气如果不超过\(60\)立方米,按每立方米\(0.8\)元收费;如果超过\(60\)立方米,超过部分按每立方米\(1.2\)元收费。已知某用户\(10\)月份的煤气费平均每立方米\(0.88\)元,求该用户\(10\)月份应交的煤气费是多少元?”
互动环节:让学生独立思考,尝试找出等量关系并列出方程,教师巡视指导,选取学生分享解题思路 。
幻灯片 7:方案决策问题讲解 - 情境引入
问题展示:“某商场在促销期间规定:商场内所有商品按标价的\(80\%\)出售;同时,当顾客在该商场内消费满一定金额后,还可按如下方案获得相应金额的奖券:
| 消费金额\(a\)(元)|\(200\leq a < 400\)|\(400\leq a < 500\)|\(500\leq a < 700\)|\(700\leq a < 900\)|...|
|----|----|----|----|----|----|
| 获奖券金额(元)|30|60|100|130|...|
根据上述促销方法,顾客在该商场购物可以获得双重优惠。例如,购买标价为\(400\)元的商品,则消费金额为\(400 80\% = 320\)元,获得的优惠额为\(400 (1 - 80\%) + 30 = 110\)元。购买一件标价为\(1000\)元的商品,顾客得到的优惠额是多少?对于标价在\(500\)元与\(800\)元之间(含\(500\)元和\(800\)元)的商品,顾客购买标价为多少元的商品,可以得到\(\frac{1}{3}\)的优惠率?”
引导分析:先计算购买标价\(1000\)元商品的消费金额、优惠额。对于求优惠率为\(\frac{1}{3}\)时商品标价,设商品标价为\(x\)元,分\(500\leq x < 700\)和\(700\leq x < 800\)两种情况,根据 “优惠率 = 优惠额 ÷ 标价” 列出方程 。
幻灯片 8:方案决策问题讲解 - 解题过程
计算标价\(1000\)元商品优惠额:消费金额为\(1000 80\% = 800\)元,奖券金额\(130\)元,优惠额为\(1000 (1 - 80\%) + 130 = 330\)元 。
求解优惠率为\(\frac{1}{3}\)时商品标价:
当\(500\leq x < 700\)时,列出方程\([x(1 - 80\%) + 100] ·x = \frac{1}{3}\),\(
\begin{align*}
(0.2x + 100) ·x &= \frac{1}{3}\\
0.2x + 100 &= \frac{1}{3}x\\
\frac{1}{3}x - 0.2x &= 100\\
\frac{1}{3}x - \frac{1}{5}x &= 100\\
\frac{5 - 3}{15}x &= 100\\
\frac{2}{15}x &= 100\\
x &= 750
\end{align*}
\)
当\(700\leq x < 800\)时,列出方程\([x(1 - 80\%) + 130] ·x = \frac{1}{3}\),\(
\begin{align*}
(0.2x + 130) ·x &= \frac{1}{3}\\
0.2x + 130 &= \frac{1}{3}x\\
\frac{1}{3}x - 0.2x &= 130\\
\frac{1}{3}x - \frac{1}{5}x &= 130\\
\frac{2}{15}x &= 130\\
x &= 975 è
\end{align*}
\)
方法总结:方案决策问题要分析不同方案的计算方式,根据题目要求(如优惠率、成本比较等)找出等量关系,必要时需分类讨论 。
幻灯片 9:方案决策问题 - 巩固练习
题目展示:“某通讯公司推出了甲、乙两种收费标准供手机用户选择:
甲种收费标准:每月收取月租费\(10\)元,另外每通话\(1\)分钟加收\(0.2\)元;
乙种收费标准:不收取月租费,每通话\(1\)分钟收费\(0.3\)元。
(1)若某用户每月通话时间为\(x\)分钟,请分别表示出两种收费标准下该用户每月应缴的费用;
(2)若某用户估计每月通话时间为\(100\)分钟,应选择哪种收费标准比较合算?”
互动环节:引导学生分析题目,设未知数,列出不同方案的费用表达式,再进行比较,邀请学生上台板演 。
幻灯片 10:课堂练习与互动
题目展示:
为鼓励居民节约用水,某城市对居民生活用水实行 “阶梯水价”,计费方法如下表:
| 每户每月用水量\(m\)(立方米)| 水价(元 / 立方米)|
|----|----|
|\(18\)立方米及以下 | 2.5|
|\(18\)立方米以上但不超过\(25\)立方米的部分 | 3.3|
|\(25\)立方米以上的部分 | 6|
若某户居民本月交水费\(84.2\)元,求该户居民本月的用水量。
某旅行社组织一批游客外出旅游,原计划租用\(45\)座客车若干辆,但有\(15\)人没有座位;若租用同样数量的\(60\)座客车,则多出一辆车,且其余客车恰好坐满。已知\(45\)座客车租金为每辆\(220\)元,\(60\)座客车租金为每辆\(300\)元,问:
(1)这批游客的人数是多少?原计划租用\(45\)座客车多少辆?
(2)若租用同一种车,要使每位游客都有座位,应该怎样租用才合算?
互动环节:学生独立完成练习,教师巡视指导,选取学生上台展示解题过程,组织其他学生进行讨论和评价,教师针对学生出现的问题进行集中讲解 。
幻灯片 11:课堂小结
知识回顾:总结分段计费问题和方案决策问题的特点及解题方法,回顾如何根据不同情况找出等量关系并列出方程 。
方法总结:强调解决分段计费问题要明确各段计费标准,方案决策问题要分析不同方案的差异,必要时分类讨论,建立合适的方程模型求解 。
重点强调:提醒学生在解决实际问题时,要仔细审题,准确理解题意,注意单位统一和取值范围 。
幻灯片 12:课后作业布置
基础作业:
某市为更有效地利用水资源,制定了居民用水收费标准:如果一户每月用水量不超过\(15\)立方米,每立方米按\(1.8\)元收费;如果超过\(15\)立方米,超过部分按每立方米\(2.3\)元收费,其余仍按每立方米\(1.8\)元计算。另外,每立方米加收污水处理费\(1\)元。若某户一月份共支付水费\(58.5\)元,求该户一月份用水量。
某牛奶加工厂现有鲜奶\(9\)吨,若在市场上直接销售鲜奶,每吨可获取利润\(500\)元;制成酸奶销售,每吨可获取利润\(1200\)元;制成奶片销售,每吨可获取利润\(2000\)元。该工厂的生产能力是:如制成酸奶,每天可加工\(3\)吨;制成奶片,每天可加工\(1\)吨。受人员限制,两种加工方式不可同时进行;受气温条件限制,这批牛奶必须在\(4\)天内全部销售或加工完毕。为此,该厂设计了两种可行方案:
方案一:尽可能多的制成奶片,其余直接销售鲜奶;
方案二:将一部分制成奶片,其余制成酸奶销售,并恰好\(4\)天完成。
你认为选择哪种方案获利最多?为什么?
拓展作业:观察生活中更多的分段计费和方案决策场景,如快递收费、旅游出行方案等,选取一个实际问题进行详细分析,建立数学模型并求解,形成一篇小报告 。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1. 会从空调的综合费用比较计费方式中寻找数量关系,列出方程.
2. 体会分类思想和方程思想在解决问题中的作用,能够根据已知条件选择分类关键点分析问题,选择最优方案.
学习目标
课堂导入
同学们,你们去过电器商场吗?
在冰箱、洗衣机、空调等家用电器上,我们常会看到右图这样的小标识,你知道这是什么意思吗?
课堂导入
中国能效标识又称能源效率标识,是附在耗能产品或其最小包装物上,表示产品能源效率等级等性能指标的一种信息标签.
等级越低,表示能耗越低,越节电.
我发现能耗低的电器比能耗高的电器价格贵,但能耗低的电器比较省电,电费低,我该怎么选择呢?
知识点 方案选择问题
新知探究
耗能高
中国能效标识
耗能低
12345
探究
不同能效空调的综合费用比较
购买空调时,需要综合考虑空调的价格和耗电情况.
某人打算从两款空调中选购一台,下表是这两款空调的部分基本信息. 如果电价是0.5元/(kW·h),请你分析他购买、使用哪款空调综合费用较低.
两款空调的部分基本信息
匹数 能效等级 售价/元 平均每年耗电量/(kW·h)
1.5 1级 3 000 640
1.5 3级 2 600 800
知识点 方案选择问题
新知探究
综合费用=空调的售价+电费.
选定一种空调后,售价是确定的,电费则与使用的时间有关.
问题1 如果购买两款空调,综合费用有哪些部分组成?
两款空调的部分基本信息
匹数 能效等级 售价/元 平均每年耗电量/(kW·h)
1.5 1级 3 000 640
1.5 3级 2 600 800
知识点 方案选择问题
新知探究
问题2 如果空调的使用年数用字母t表示,请用代数式分别表示出两款空调的综合费用.
两款空调的部分基本信息
匹数 能效等级 售价/元 平均每年耗电量/(kW·h)
1.5 1级 3 000 640
1.5 3级 2 600 800
1级能效空调的综合费用是________________________,
化简后_________________.
3级能效空调的综合费用是________________________,
化简后_________________.
3 000+0.5×640t
3 000+320t
2 600+400t
2 600+0.5×800t
知识点 方案选择问题
新知探究
两款空调的部分基本信息
匹数 能效等级 售价/元 平均每年耗电量/(kW·h)
1.5 1级 3000 640
1.5 3级 2600 800
问题3 t 取什么值时,两款空调的综合费用相等
3 000+320t=2 600+400t.
t=5.
所以当t=5时,两款空调的综合费用相等.
知识点 方案选择问题
新知探究
问题4 t 取什么值时,1级能效空调的综合费用较低 t 取什么值时,3级能效空调的综合费用较低
表示1级能效空调的综合费用:
3 000+320t.
表示3级能效空调的综合费用:
2 600+400t.
(3 000+320t)+(80t-400)
变形
3 000+320t+80(t-5).
讨论80(t-5)的
正负即可.
当t<5时,80(t-5)是负数,这表明3级能效空调的综合费用较低;
当t>5时,80(t-5)是正数,这表明1级能效空调的综合费用较低.
知识点 方案选择问题
新知探究
为了比较两款空调的综合费用,我们把表示3级能效空调的综合费用的式子2 600+400t变形为1级能效空调的综合费用3 000+320t与另外一个式子的和,即
(3 000+320t)+(80t-400),
也就是
3 000+320t +80(t-5).
知识点 方案选择问题
新知探究
由此可见,同样是1.5匹的空调,1级能效空调虽然售价高,但由于比较省电,使用年份长(超过5年)时综合费用反而低.根据相关行业标准,空调的安全使用年限是10年(从生产日期计起),因此购买、使用1级能效空调更划算.
通常,1级能效空调既节能又省钱!
审题
更优惠
费用相同
列方程
用未知数表示费用
设未知数
选择最优方案问题的一般步骤:
知识点 方案选择问题
新知探究
知识点1 分段计费问题
1. 石家庄出租车收费标准如下:起步价8元(即行驶路程不超过
,付车费8元),每增加 ,加收1.6元.小轩从家到河北博物院
的路程为 ,乘出租车需付车费27.2元,则可列方程为( )
C
A. B.
C. D.
2.[2025重庆綦江区期末]某航空公司规定:乘坐飞机普通舱的旅客每
人最多只能免费托运的行李,超过部分每千克按机票价格的
购买行李票,一位旅客托运了 的行李,这样,机票和行李票共付
了1 339元,则该旅客的机票价格是( )
B
A.1 020元 B.1 030元 C.1 040元 D.1 050元
3.(8分)[2025烟台期末]“水是生命之源”,某自来水公司为鼓励用
户节约用水,按以下规定收取水费:
月用水量/吨 单价/(元/吨)
不超过20吨的部分 2
超过20吨的部分 2.5
另:每吨水加收0.3元的城市污水处理费 (1)若某用户11月份共用水25吨,则他应缴水费____元.
60
(2)若某用户12月份应缴水费为74元,则该用户12月份用水多少吨?
解:因为(元) 元,
所以该用户12月份用水量超过20吨,
设该用户12月份用水 吨,
由题意,得,解得 .
答:该用户12月份用水30吨.
知识点2 方案决策问题
4.某服装商店出售一种优惠购物卡,花200元买这种卡后,凭卡可在这
家商店按八折购物,下列情况买卡购物合算的是( )
C
A.购物900元 B.购物500元 C.购物1 200元 D.购物1 000元
5.元旦期间,某超市推出如下优惠方案:(1)一次性购物超过100元但
不超过300元,在原价基础上一律打九折;(2)一次性购物超过300元,
在原价基础上一律打八折,王老师购物后付款252元,则他所购物品的
原价是______________.
280元或315元
6.(8分)[2025洛阳期末]“天下无双圣境,世界第一仙山”的老君山,
是河南洛阳 级著名旅游景区.原门票价格为130元/张,某旅行社推出
一种团队票(人数 ),团队票可选择两种购票优惠方案:
方案一:全体人员打八折.
方案二:有5人可以免票,剩下的人员打九折.
设某团队有 人.
(1)该团队选择方案一的费用为______元,选择方案二的费用为
____________元.(用含 的代数式表示)
(2)若该团队无论选择哪种方案购票,费用恰好一样,则该团队共多
少人?
解:由题意得 ,
解得 .
答:该团队共45人.
7.[2025唐山丰南区期末]甲、乙两店以同样价格出售一种商品,并推
出不同的优惠方案,在甲店累计购物超过100元后,超出100元的部分打
九折;在乙店累计购物超过50元后,超出50元的部分打九五折,则顾客
到两店购物花费一样时( )
D
A.累计购物不超过50元
B.累计购物超过50元不超过100元
C.累计购物超过100元
D.累计购物不超过50元或刚好为150元
8.(12分)[2025郑州期末]某市对居民生活用电实行阶梯电价,具体
收费标准如下表:
档次 月用电量 电价/(元/千瓦时)
第1档 不超过240千瓦时的部分
第2档 超过240千瓦时但不超过400千瓦时的部分 0.65
第3档 超过400千瓦时的部分
已知10月份该市居民老李家用电200千瓦时,交电费120元;9月份老李
家交电费157元.
(1)表中 的值为____;
0.6
(2)老李家9月份的用电量为___________;
260千瓦时
(3)若8月份老李家用电的平均电价为0.7元/千瓦时,求老李家8月份的
用电量.
解:因为 ,
所以老李家8月份的用电量超过400千瓦时.
设老李家8月份的用电量为 千瓦时.
由题意,得,解得 .
答:老李家8月份的用电量为560千瓦时.
9.(12分)[2025杭州上城区期末]红领巾球馆计划购买某品牌的乒乓
球拍和乒乓球,已知该品牌的乒乓球拍每副定价150元,乒乓球每盒定
价15元.元旦期间该品牌决定开展促销活动,活动期间向客户提供两种
优惠方案,即
方案一:买一副乒乓球拍送两盒乒乓球;
方案二:乒乓球拍和乒乓球都按定价的 付款.
该球馆计划购买乒乓球拍10副,乒乓球盒(, 为整数).
(1)当 时,若该球馆按方案一购买,需付款_______元;若该球
馆按方案二购买,需付款_______元.
1 800
1 890
(2)当 为何值时,分别按两种方案购买所需费用一样?
解:由题意得 ,
解得,所以当 时,分别按两种方案购买所需费用一样.
(3)若 ,能否找到一种更为省钱的购买方案?如果能,请你写
出购买方案,并计算出此方案所需费用;如果不能,请说明理由.
解:先按方案一购买10副乒乓球拍可得20盒乒乓球,再按方案二购买20
盒乒乓球,需付款 (元).
课堂小结
选择最优方案问题的一般步骤:
审题
更优惠
费用相同
列方程
用未知数表示费用
设未知数
谢谢观看!
同课章节目录
