第二章 有理数的运算【章末复习】 课件(共52张PPT)
文档属性
| 名称 | 第二章 有理数的运算【章末复习】 课件(共52张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 08:53:47 | ||
图片预览











文档简介
(共52张PPT)
章末复习
第二章 有理数的运算
【2024新教材】人教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
第二章 有理数的运算 章末复习
一、知识梳理
(一)有理数的加法
运算法则:
同号两数相加,取相同的符号,并把绝对值相加。例如,\(3 + 5 = 8\),\(( - 3)+( - 5)= - 8\) 。
绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。互为相反数的两个数相加得 0。比如,\(3+( - 5)= - 2\) ,\(5+( - 5)=0\) 。
一个数同 0 相加,仍得这个数,如\(0 + 7 = 7\) 。
运算律:
加法交换律:\(a + b = b + a\) 。例如,\(2 + 3 = 3 + 2\) 。
加法结合律:\((a + b)+c = a+(b + c)\) 。像\((1 + 2)+3 = 1+(2 + 3)\) ,通过加法结合律可以使计算更简便,在多个有理数相加时,可以把互为相反数的数结合在一起,或把同号的数结合在一起先进行计算 。
(二)有理数的减法
运算法则:减去一个数,等于加上这个数的相反数。用字母表示为\(a - b = a+( - b)\) 。例如,\(5 - 3 = 5+( - 3)=2\) ,\(5-( - 3)=5 + 3 = 8\) 。
有理数加减法混合运算:统一成加法运算后,运用加法交换律和结合律进行简便计算。如计算\(3 - 5 + 7 - 2\) ,可转化为\(3+( - 5)+7+( - 2)=(3 + 7)+[( - 5)+( - 2)] = 10+( - 7)=3\) 。
(三)有理数的乘法
运算法则:
两数相乘,同号得正,异号得负,并把绝对值相乘。例如,\(3 5 = 15\) ,\(( - 3) ( - 5)=15\) ,\(3 ( - 5)= - 15\) 。
任何数与 0 相乘,都得 0,如\(0 6 = 0\) 。
运算律:
乘法交换律:\(ab = ba\) 。例如,\(2 3 = 3 2\) 。
乘法结合律:\((ab)c = a(bc)\) 。如\((2 3) 4 = 2 (3 4)\) ,在多个有理数相乘时,运用乘法结合律可将便于计算的数结合在一起先算 。
乘法分配律:\(a(b + c)=ab + ac\) 。比如\(2 (3 + 4)=2 3 + 2 4\) ,利用乘法分配律可以简化一些乘法与加法混合的运算 。
(四)有理数的除法
运算法则:
除以一个不等于 0 的数,等于乘这个数的倒数。用字母表示为\(a ·b = a \frac{1}{b}(b 0)\) 。例如,\(6 ·3 = 6 \frac{1}{3}=2\) ,\(6 ·( - 3)=6 ( - \frac{1}{3})=-2\) 。
两数相除,同号得正,异号得负,并把绝对值相除。0 除以任何一个不等于 0 的数,都得 0。如\(0 ·5 = 0\) ,\(( - 6) ·( - 2)=3\) ,\(6 ·( - 2)= - 3\) 。
有理数乘除法混合运算:先将除法转化为乘法,再按照乘法法则进行计算 。
(五)有理数的乘方
乘方的意义:求\(n\)个相同因数\(a\)的积的运算,叫做乘方,记作\(a^n\) ,其中\(a\)是底数,\(n\)是指数,\(a^n\)的结果叫做幂。例如,\(2^3\)表示 3 个 2 相乘,\(2^3 = 2 2 2 = 8\) ;\(( - 2)^3=( - 2) ( - 2) ( - 2)= - 8\) 。
乘方运算的符号规律:正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数;0 的任何正整数次幂都是 0 。
(六)有理数的混合运算
运算顺序:
先乘方,再乘除,最后加减。例如计算\(2 + 3 2^2\) ,先算\(2^2 = 4\) ,再算\(3 4 = 12\) ,最后算\(2 + 12 = 14\) 。
同级运算,从左到右进行。如计算\(12 ·3 2\) ,先算\(12 ·3 = 4\) ,再算\(4 2 = 8\) 。
如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行 。比如计算\([(2 + 3) 2 - 1] ·3\) ,先算小括号里的\(2 + 3 = 5\) ,再算中括号里的\(5 2 - 1 = 10 - 1 = 9\) ,最后算\(9 ·3 = 3\) 。
运算技巧:在进行有理数混合运算时,要观察式子的特点,合理运用运算律进行简便运算 。
(七)近似数与有效数字
准确数与近似数:
准确数是指可以精确表示的数,它与实际完全符合。例如,教室里有 30 张桌子,30 就是准确数 。
近似数是指与准确数相近的一个数,通常是由于测量、计算等原因无法得到精确值,或者不需要精确值时使用。比如,测量一个人的身高约为 1.75 米,1.75 就是近似数 。
近似数的精确度:
四舍五入法:这是最常用的表示近似数精确度的方法。例如,将 3.14159 精确到百分位(即保留两位小数),看千分位上的数字 1,因为 1 小于 5,所以舍去千分位及后面的数字,得到 3.14 。
有效数字法:从一个数的左边第一个非 0 数字起,到末位数字止,所有的数字,包括 0,都是这个数的有效数字。例如,0.025 有两个有效数字 2 和 5;1.030 有四个有效数字 1、0、3、0 。
二、重点题型讲解
(一)有理数的加减运算
例 1:计算\(( - 3)+5+( - 8)+7\) 。
分析:运用加法交换律和结合律,将同号的数分别结合在一起进行计算。
解答:\(
\begin{align*}
&( - 3)+5+( - 8)+7\\
=&[( - 3)+( - 8)]+(5 + 7)\\
=& - 11 + 12\\
=&1
\end{align*}
\)
例 2:计算\(1 - 2 + 3 - 4 + 5 - 6 + \cdots + 99 - 100\) 。
分析:可以将相邻的两个数看作一组,每组的计算结果都是\(-1\) ,一共有 50 组。
解答:\(
\begin{align*}
&1 - 2 + 3 - 4 + 5 - 6 + \cdots + 99 - 100\\
=&(1 - 2)+(3 - 4)+(5 - 6)+\cdots+(99 - 100)\\
=&( - 1)+( - 1)+( - 1)+\cdots+( - 1)\\
=& - 1 50\\
=& - 50
\end{align*}
\)
(二)有理数的乘除运算
例 3:计算\(( - \frac{3}{4}) ( - \frac{4}{3}) ·( - 2)\) 。
分析:先计算乘法,再计算除法,注意运算符号的确定。
解答:\(
\begin{align*}
&( - \frac{3}{4}) ( - \frac{4}{3}) ·( - 2)\\
=&1 ·( - 2)\\
=& - \frac{1}{2}
\end{align*}
\)
例 4:计算\(( - 24) ·( - \frac{1}{2}+\frac{3}{4}-\frac{1}{3})\) 。
分析:先计算括号内的式子,再进行除法运算,括号内通分计算。
解答:\(
\begin{align*}
&( - 24) ·( - \frac{1}{2}+\frac{3}{4}-\frac{1}{3})\\
=&( - 24) ·( - \frac{6}{12}+\frac{9}{12}-\frac{4}{12})\\
=&( - 24) ·( - \frac{1}{12})\\
=&( - 24) ( - 12)\\
=&288
\end{align*}
\)
(三)有理数的乘方运算
例 5:计算\(( - 2)^4\) 。
分析:根据乘方的意义,\(( - 2)^4\)表示 4 个\(-2\)相乘。
解答:\(( - 2)^4=( - 2) ( - 2) ( - 2) ( - 2)=16\) 。
例 6:计算\(-2^4\) 。
分析:这里的负号在乘方运算之前,先算\(2^4\) ,再加上负号。
解答:\(-2^4 = - (2 2 2 2)= - 16\) 。
(四)有理数的混合运算
例 7:计算\( - 3^2 ( - \frac{1}{3})^2 - ( - 2)^3 ·( - \frac{1}{2})^2\) 。
分析:按照先乘方,再乘除,最后加减的顺序进行计算。
解答:\(
\begin{align*}
& - 3^2 ( - \frac{1}{3})^2 - ( - 2)^3 ·( - \frac{1}{2})^2\\
=& - 9 \frac{1}{9}-( - 8) ·\frac{1}{4}\\
=& - 1 - ( - 8) 4\\
=& - 1 + 32\\
=&31
\end{align*}
\)
(五)近似数与有效数字
例 8:用四舍五入法,按括号中的要求对下列各数取近似数
0.34482(精确到百分位)
分析:精确到百分位,即保留两位小数,看千分位上的数字 4,4 小于 5,舍去千分位及后面的数字。
解答:0.34482≈0.34
1.5972(精确到 0.01)
分析:精确到 0.01 也就是精确到百分位,看千分位上的数字 7,7 大于 5,向百分位进 1,9 加上 1 满十再向十分位进 1。
解答:1.5972≈1.60
47155(精确到千位)
分析:先将原数写成科学记数法的形式\(4.7155 10^4\) ,精确到千位,就看百位上的数字 1,1 小于 5,舍去百位及后面的数字,所以\(4.7155 10^4 4.7 10^4\) 。
解答:47155≈4.7×10^4
例 9:说出下列近似数的有效数字
0.03080
分析:从左边第一个非 0 数字 3 起,到末位数字 0 止,所有数字 3、0、8、0 都是有效数字。
解答:有效数字为 3、0、8、0 。
2.4 万
分析:先将 2.4 万还原为 24000,从左边第一个非 0 数字 2 起,到末位数字 4 止,有效数字是 2、4 。
解答:有效数字为 2、4 。
三、易错点剖析
(一)符号问题
在有理数的加减法运算中,容易忽略符号的变化。例如,计算\(3 - 5\) ,错误地写成\(3 - 5 = 2\) ,忽略了减去一个数等于加上它的相反数,正确结果应该是\(3+( - 5)= - 2\) 。
在有理数的乘除法运算中,也容易出现符号错误。比如,计算\(( - 3) ( - 4) ·( - 2)\) ,有些同学会先算\(3 4 = 12\) ,再算\(12 ·( - 2)= - 6\) ,忽略了负负得正,正确的计算应该是\(( - 3) ( - 4)=12\) ,\(12 ·( - 2)= - 6\) 。
在乘方运算中,底数为负数时,要注意指数的奇偶性对结果符号的影响。如\(( - 2)^3\)和\(-2^3\) ,\(( - 2)^3=( - 2) ( - 2) ( - 2)= - 8\) ,而\(-2^3 = - (2 2 2)= - 8\) ,虽然结果相同,但意义不同 。
(二)运算顺序问题
在有理数的混合运算中,一定要严格按照先乘方,再乘除,最后加减的顺序进行计算。如果有括号,先算括号内的。例如,计算\(2 + 3 2^2\) ,有些同学会先算\(2 + 3 = 5\) ,再算\(5 2^2 = 5 4 = 20\) ,这是错误的,应该先算\(2^2 = 4\) ,再算\(3 4 = 12\) ,最后算\(2 + 12 = 14\) 。
对于同级运算,要从左到右依次进行。如计算\(12 ·3 2\) ,不能先算\(3 2 = 6\) ,再算\(12 ·6 = 2\) ,而应该先算\(12 ·3 = 4\) ,再算\(4 2 = 8\) 。
(三)近似数与有效数字问题
在确定近似数的有效数字时,容易忽略从左边第一个非 0 数字起这一条件。例如,对于近似数 0.0250,有些同学会认为有效数字是 2、5,而忽略了后面的 0,正确的有效数字是 2、5、0 。
在将一个数用四舍五入法取近似数时,要注意看清精确到的数位。如将 3.14159 精确到千分位,应该是 3.142,而不是 3.141 。
四、课堂总结
回顾运算规则:全面回顾有理数的加、减、乘、除、乘方运算的法则和运算律,强调运算顺序以及在运算过程中符号的确定方法。
** 总结解题
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
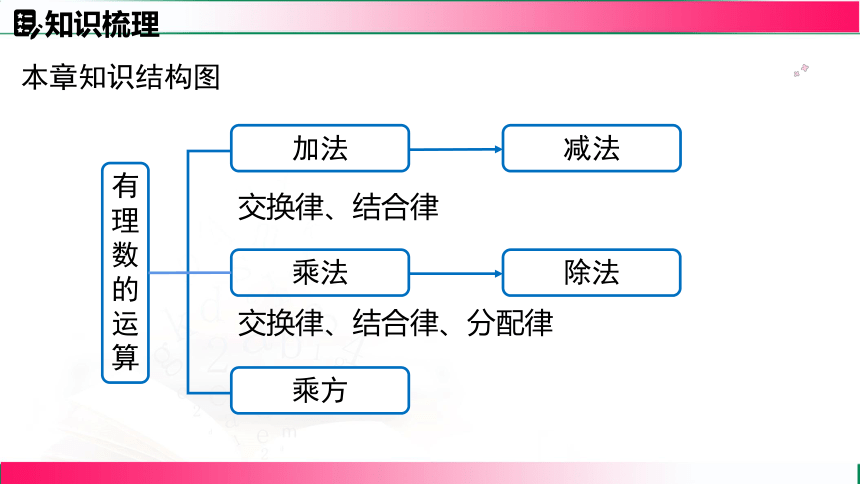
本章知识结构图
知识梳理
有理数的运算
加法
乘法
减法
乘方
除法
交换律、结合律
交换律、结合律、分配律
知识梳理
有理数加法法则:
同号两数相加,和取相同的符号,且和的绝对值等于加数的绝对值的和.
绝对值不相等的异号两数相加,和取绝对值较大的加数的符号,且和的绝对值等于加数的绝对值中较大者与较小者的差.
互为相反数的两个数相加得0.
一个数与0相加,仍得这个数.
有理数减法法则:
减去一个数,等于加这个数的相反数.
有理数乘法法则:
两数相乘,同号得正,异号得负,且积的绝对值等于乘数的绝对值的积.
任何数与0相乘,都得0.
知识梳理
有理数除法法则:
除以一个不等于0的数,等于乘这个数的倒数.
两数相除,同号得正,异号得负,且商的绝对值等于被除数的绝对值除以除数的绝对值的商.
0除以任何一个不等于0的数,都得0.
知识梳理
1.计算.
(1)150+250 =_____; (2)-15+(-23) =_____; (3)-5-65=_____;
(4)-26-(-15) =______; (5)(-6)×(-16) =______;
(6)(- )×27=_______;(7)8÷(-16) =_______;
(8)(-25)÷(-) =_______; (9)(-)÷(-) =_______.
400
-38
-70
-11
96
-9
-
随堂练习
2.五袋白糖以每袋50干克为标准,超过的记为正,不足的记为负,称量记录如下:
+4.5,-4,+2.3,-3.5,+2.5
(1)这五袋白糖共超过标准多少干克?
(2)这五袋白糖的总质量是多少千克?
解:(1)+4.5-4+2.3-3.5+2.5=1.8(千克).
(2)50×5+1.8=251.8(千克).
随堂练习
数轴上表示两点间的距离
数轴上两点A,B的距离| AB | 与这两点所对应的数a,b的关系为:| AB | = | a-b |.
知识梳理
随堂练习
3. 分别求出数轴上两点间的距离:
(1)表示 2的点与表示-7的点;
(2)表示-3的点与表示-1的点.
解:(1)2-(-7)=2+7=9;
(2)-1-(-3)=-1+3=2.
有理数加减乘除混合运算顺序:
1.先算乘除,再算加减;
2.同级运算从左往右依次计算;
3.如有括号,先算括号内的;
4.能用运算律的,应利用运算律.
知识梳理
4.计算:
(1)(-0.02)×(-20)×(-5)×4.5;
解:(1)(-0.02)×(-20)×(-5)×4.5
=-0.02×20×5×4.5
=-9;
随堂练习
4.计算:
(2) (-6.5) ×(-2)÷(-) ÷(-5);
解:(2)(-6.5)×(-2)÷(-)÷(-5)
=6.5×2×3×
=7.8;
随堂练习
4.计算:
(3) 0+(- )-2-(-1.5); (4)(-66)×4-(-2.5)÷(-0.1).
解:(3) 0+(- )-2-(-1.5)
=0- -2+1.5
=(0+1.5)+(-0.2-2)
=1.5-2.2
=-0.7;
(4)(-66)×4-(-2.5)÷(-0.1)
=-264-25
=-289.
随堂练习
乘方
一般地,n个相同的乘数a相乘,记作 an,读作“a的n次方”.求n个相同乘数的积的运算,叫作乘方,乘方的结果叫作幂.
根据有理数的乘法法则可以得出:
1.负数的奇次幂是负数,负数的偶次幂是正数;
2.正数的任何次幂都是正数;
3.0的任何正整数次幂都是0.
知识梳理
5.计算:
(1) (-3)3=_____; (2) (-2)4 =_____;
(3) (-1.7)2=_____; (4) (-)3 =_____;
(5) -(-2)2 =_____; (6) (-2)2(-3)2=_____.
-27
16
2.89
-
-4
36
随堂练习
知识梳理
有理数的混合运算顺序:
1.先乘方,再乘除,最后加减;
2.同级运算,从左到右进行;
3.如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.
6.计算:
(1)(-2)2×5-(-2)3÷4; (2)-(3-5)+32×(1-3).
解:(1)原式=4×5-(-8)÷4
=20+2
=22;
解:(2)原式=-(-2)+9×(-2)
=2-18
=-16.
随堂练习
7.计算:
(1) -22×(- )+8(-2)2; (2) (-3)2 2×(-) 2+4-22×(-);
随堂练习
解:(1)原式=2+8÷4
=4.
解:(2)原式=9×+4+
= +4+
= .
随堂练习
7.计算:
(3) {1+[()3] ×(-2)4 } ( );
解:(3)原式=[1+() ×16] ( )
= (1+1) ()
=
=
= .
知识梳理
科学记数法.
把一个大于10的数表示成 a×10n 的形式(其中a 大于或等于1且小于10,n是正整数),这种记法是科学记数法.
用科学记数法表示一个n位整数(n ≥2),其中10的指数是
n-1.
随堂练习
8.一只苍蝇的腹内细菌多达2 800万个,用科学记数法表示为____________个.
9. 新时代十年来,我国建成世界上规模最大的社会保障体系.其中基本医疗保险的参保人数由5.4亿增加到13.6亿,参保率稳定在95%.将数据13.6亿用科学记数法表示为1.36×10n”的形式,则n的值是_____(备注:1亿=100 000 000).
9
2.8×107
随堂练习
10. 用科学记数法表示下列各数:
(1) 100 000 000;
(2) 4 500 000;
(3) 692 400 000 000.
1×108 .
4.5×106.
6.924×1011 .
近似数:是指与准确数相近的一个数.
精确度:近似数与准确数的接近程度可以用精确度表示.
知识梳理
11.用四舍五入法对下列各数取近似数:
(1)0.004 57(精确到0.000 1);
(2)566.123 5(精确到个位);
(3)3.896 3(精确到0.01):
(4)0.057 1(精确到千分位)
随堂练习
(1)0.004 57≈0.004 6.
(2)566.123 5≈566.
(4)0.057 1≈0.057.
(3)3.896 3≈3.90.
随堂练习
12. 近似数1.20是由数a四舍五入得到的,那么数a的取值范围是( )
A.1.15C.1.195分析:近似数1.20精确到百分位,它是将数a的千分位上的数字四舍五入得到的.
对于数a ,若千分位上的数字大于或等于5,则百分位上的数字应是“9”,十分位上的数字应是“1”;
若千分位上的数字小于5,则百分位上的数字应是“0”,十分位上的数字应是“2”.
故1.195≤a<1.205.
D
一、核心考点巩固
考点1 有理数的运算
1.如图,比数轴上点 表示的数大1的数是( )
B
A. B.0 C.1 D.2
2.[2025宁波期中]要使算式的运算结果最小,则“ ”内应填入
的运算符号是( )
C
A. B.- C.× D.
3.[2025上海期中]一个数的相反数的倒数是 ,那么这个数是( )
B
A. B. C. D.
4.[2025泰安期末]下列计算正确的是( )
C
A. B.
C. D.
5. 可化为( )
D
A. B.
C. D.
6.甲、乙、丙、丁4位同学,学了有理数的乘方之后,发表了以下见解,
观点正确的有( )
甲: 是2个5相加;
乙:与 是不同的结果;
丙:中底数是 ,指数是4;
丁:是 个4相乘.
B
A.0个 B.1个 C.2个 D.3个
7.[2025成都期末]有理数, 在数轴上对应点的位置如图所示,则下
列结论正确的是( )
A
A. B. C. D.
8.(16分)计算:
(1) ;
解:原式
.
(2) ;
解:原式 .
(3) ;
解:原式
.
(4) .
解:原式 .
9.(8分) 对于有理数, ,定义一种新运算“@”,规定
.
(1)计算@ 的值;
解:因为 ,
所以@ .
(2)计算 的值.
解:因为 ,
所以 .
考点2 有理数的运算的应用
10.[2025长沙调研]火星赤道夏季白天最高温度可达 ,晚上最低
温度可达 ,则火星赤道夏季昼夜温差最大为( )
C
A. B. C. D.
11.手机移动收付款给生活带来便捷.如图是小华某天手机移动收付款账
单的明细(正数表示收入,负数表示支出,单位:元),小华这天使用
手机移动收付款的最终结果是( )
C
A.收入19元 B.支出8元 C.收入6元 D.支出5元
12.将0,, ,1,2这五个数分别填在如图所示的五个
小正方形内,使横向三个数之和与纵向三个数之和相等,
则填入中间位置的小正方形内的数不可以是( )
A
A.1 B. C.2 D.0
13.(8分)某摩托车厂家计划本周每天生产250辆摩托车,由于工厂实
行轮休,每天上班人数不一定相等,故实际每天生产的摩托车数量也不
一样.实际每天生产的摩托车数量与计划相比情况如下表(超产为正,
减产为负,单位:辆):
星期 一 二 三 四 五 六 日
增减
(1)星期六生产了多少辆摩托车?
解: (辆).
答:星期六生产了241辆摩托车.
(2)本周实际总产量与计划相比是增加了还是减少了?增加或减少了
多少?产量最多的一天比产量最少的一天多生产了多少辆?
解: (辆),所以本周实际总产
量与计划相比减少了,减少了21辆.
产量最多的一天为星期五,产量最少的一天为星期日,
产量最多的一天比产量最少的一天多生产了 (辆).
14.(12分)某粮食仓库一周7天内进出粮食的吨数如下(“ ”表示进库,
“-”表示出库):,,,,,, .
(1)经过这7天,仓库里的粮食是增多了还是减少了?增多或减少了多
少吨?
解:因为 .
所以经过这7天,仓库里的粮食减少了,减少了9吨.
(2)经过这7天,仓库管理员结算发现仓库里还存有100吨粮食,那么7
天前,仓库里存有粮食多少吨?
解:因为 .
所以7天前,仓库里存有粮食109吨.
(3)如果进仓库的粮食装卸费是每吨2元,出仓库的粮食装卸费是每吨
3元,求这7天要付多少元装卸费.
解:由题意得,进仓库的装卸费为
(元),
出仓库的装卸费为
(元),
(元),
所以这7天要付407元装卸费.
考点3 科学记数法
15. 是一款先进的人工智能助手,可提供高效、
精准的信息检索和智能对话服务.其活跃用户数在上线21天后达到了
3 370万.将3 370万用科学记数法表示为( )
C
A. B. C. D.
16. 下面是琳琳作业中的一道题目:
“ ”处都是0但发生破损,琳琳查阅后发现本题答案为1,则破损处“0”
的个数为( )
B
A.5 B.4 C.3 D.2
考点4 近似数
17.下列说法中正确的有( )
①近似数2.75精确到0.01;
②由四舍五入得到的近似数 精确到百分位;
③近似数6.9和6.90表示的意义是一样的;
④将30 491按四舍五入精确到千位得到的近似数是3.1万.
D
A.4个 B.3个 C.2个 D.1个
二、思想方法演练
思想1 分类讨论思想
18.若,则 的值不可能是 ( )
D
A.2 B.0 C. D.1
19.已知,,若,则 _________.
10或
思想2 数形结合思想
20.(12分)【问题探索】将一根木棒放在数轴(单位长度为 )上,
如图,木棒左端与数轴上的点重合,右端与数轴上的点 重合.
(1)若将木棒沿数轴向右水平移动,则当它的左端移动到点 时,它的
右端在数轴上所对应的数为30;若将木棒沿数轴向左水平移动,则当它
的右端移动到点 时,它的左端在数轴上所对应的数为6,由此可得这根
木棒的长为___ .
8
(2)图中点所表示的数是____,点 所表示的数是____.
14
22
【实际应用】由 的启发,请借助“数轴”这个工具解决下面问题:
(3)一天,妙妙去问奶奶的年龄,奶奶说:“我若是你现在这么大,你
还要35年才出生;你若是我现在这么大,我就115岁啦!”请问妙妙现在
多少岁了?
解:当奶奶像妙妙这么大时,妙妙为“ 岁”,
所以奶奶与妙妙的年龄差为 (岁),
所以妙妙现在的年龄为 (岁).
谢谢观看!
章末复习
第二章 有理数的运算
【2024新教材】人教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
第二章 有理数的运算 章末复习
一、知识梳理
(一)有理数的加法
运算法则:
同号两数相加,取相同的符号,并把绝对值相加。例如,\(3 + 5 = 8\),\(( - 3)+( - 5)= - 8\) 。
绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。互为相反数的两个数相加得 0。比如,\(3+( - 5)= - 2\) ,\(5+( - 5)=0\) 。
一个数同 0 相加,仍得这个数,如\(0 + 7 = 7\) 。
运算律:
加法交换律:\(a + b = b + a\) 。例如,\(2 + 3 = 3 + 2\) 。
加法结合律:\((a + b)+c = a+(b + c)\) 。像\((1 + 2)+3 = 1+(2 + 3)\) ,通过加法结合律可以使计算更简便,在多个有理数相加时,可以把互为相反数的数结合在一起,或把同号的数结合在一起先进行计算 。
(二)有理数的减法
运算法则:减去一个数,等于加上这个数的相反数。用字母表示为\(a - b = a+( - b)\) 。例如,\(5 - 3 = 5+( - 3)=2\) ,\(5-( - 3)=5 + 3 = 8\) 。
有理数加减法混合运算:统一成加法运算后,运用加法交换律和结合律进行简便计算。如计算\(3 - 5 + 7 - 2\) ,可转化为\(3+( - 5)+7+( - 2)=(3 + 7)+[( - 5)+( - 2)] = 10+( - 7)=3\) 。
(三)有理数的乘法
运算法则:
两数相乘,同号得正,异号得负,并把绝对值相乘。例如,\(3 5 = 15\) ,\(( - 3) ( - 5)=15\) ,\(3 ( - 5)= - 15\) 。
任何数与 0 相乘,都得 0,如\(0 6 = 0\) 。
运算律:
乘法交换律:\(ab = ba\) 。例如,\(2 3 = 3 2\) 。
乘法结合律:\((ab)c = a(bc)\) 。如\((2 3) 4 = 2 (3 4)\) ,在多个有理数相乘时,运用乘法结合律可将便于计算的数结合在一起先算 。
乘法分配律:\(a(b + c)=ab + ac\) 。比如\(2 (3 + 4)=2 3 + 2 4\) ,利用乘法分配律可以简化一些乘法与加法混合的运算 。
(四)有理数的除法
运算法则:
除以一个不等于 0 的数,等于乘这个数的倒数。用字母表示为\(a ·b = a \frac{1}{b}(b 0)\) 。例如,\(6 ·3 = 6 \frac{1}{3}=2\) ,\(6 ·( - 3)=6 ( - \frac{1}{3})=-2\) 。
两数相除,同号得正,异号得负,并把绝对值相除。0 除以任何一个不等于 0 的数,都得 0。如\(0 ·5 = 0\) ,\(( - 6) ·( - 2)=3\) ,\(6 ·( - 2)= - 3\) 。
有理数乘除法混合运算:先将除法转化为乘法,再按照乘法法则进行计算 。
(五)有理数的乘方
乘方的意义:求\(n\)个相同因数\(a\)的积的运算,叫做乘方,记作\(a^n\) ,其中\(a\)是底数,\(n\)是指数,\(a^n\)的结果叫做幂。例如,\(2^3\)表示 3 个 2 相乘,\(2^3 = 2 2 2 = 8\) ;\(( - 2)^3=( - 2) ( - 2) ( - 2)= - 8\) 。
乘方运算的符号规律:正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数;0 的任何正整数次幂都是 0 。
(六)有理数的混合运算
运算顺序:
先乘方,再乘除,最后加减。例如计算\(2 + 3 2^2\) ,先算\(2^2 = 4\) ,再算\(3 4 = 12\) ,最后算\(2 + 12 = 14\) 。
同级运算,从左到右进行。如计算\(12 ·3 2\) ,先算\(12 ·3 = 4\) ,再算\(4 2 = 8\) 。
如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行 。比如计算\([(2 + 3) 2 - 1] ·3\) ,先算小括号里的\(2 + 3 = 5\) ,再算中括号里的\(5 2 - 1 = 10 - 1 = 9\) ,最后算\(9 ·3 = 3\) 。
运算技巧:在进行有理数混合运算时,要观察式子的特点,合理运用运算律进行简便运算 。
(七)近似数与有效数字
准确数与近似数:
准确数是指可以精确表示的数,它与实际完全符合。例如,教室里有 30 张桌子,30 就是准确数 。
近似数是指与准确数相近的一个数,通常是由于测量、计算等原因无法得到精确值,或者不需要精确值时使用。比如,测量一个人的身高约为 1.75 米,1.75 就是近似数 。
近似数的精确度:
四舍五入法:这是最常用的表示近似数精确度的方法。例如,将 3.14159 精确到百分位(即保留两位小数),看千分位上的数字 1,因为 1 小于 5,所以舍去千分位及后面的数字,得到 3.14 。
有效数字法:从一个数的左边第一个非 0 数字起,到末位数字止,所有的数字,包括 0,都是这个数的有效数字。例如,0.025 有两个有效数字 2 和 5;1.030 有四个有效数字 1、0、3、0 。
二、重点题型讲解
(一)有理数的加减运算
例 1:计算\(( - 3)+5+( - 8)+7\) 。
分析:运用加法交换律和结合律,将同号的数分别结合在一起进行计算。
解答:\(
\begin{align*}
&( - 3)+5+( - 8)+7\\
=&[( - 3)+( - 8)]+(5 + 7)\\
=& - 11 + 12\\
=&1
\end{align*}
\)
例 2:计算\(1 - 2 + 3 - 4 + 5 - 6 + \cdots + 99 - 100\) 。
分析:可以将相邻的两个数看作一组,每组的计算结果都是\(-1\) ,一共有 50 组。
解答:\(
\begin{align*}
&1 - 2 + 3 - 4 + 5 - 6 + \cdots + 99 - 100\\
=&(1 - 2)+(3 - 4)+(5 - 6)+\cdots+(99 - 100)\\
=&( - 1)+( - 1)+( - 1)+\cdots+( - 1)\\
=& - 1 50\\
=& - 50
\end{align*}
\)
(二)有理数的乘除运算
例 3:计算\(( - \frac{3}{4}) ( - \frac{4}{3}) ·( - 2)\) 。
分析:先计算乘法,再计算除法,注意运算符号的确定。
解答:\(
\begin{align*}
&( - \frac{3}{4}) ( - \frac{4}{3}) ·( - 2)\\
=&1 ·( - 2)\\
=& - \frac{1}{2}
\end{align*}
\)
例 4:计算\(( - 24) ·( - \frac{1}{2}+\frac{3}{4}-\frac{1}{3})\) 。
分析:先计算括号内的式子,再进行除法运算,括号内通分计算。
解答:\(
\begin{align*}
&( - 24) ·( - \frac{1}{2}+\frac{3}{4}-\frac{1}{3})\\
=&( - 24) ·( - \frac{6}{12}+\frac{9}{12}-\frac{4}{12})\\
=&( - 24) ·( - \frac{1}{12})\\
=&( - 24) ( - 12)\\
=&288
\end{align*}
\)
(三)有理数的乘方运算
例 5:计算\(( - 2)^4\) 。
分析:根据乘方的意义,\(( - 2)^4\)表示 4 个\(-2\)相乘。
解答:\(( - 2)^4=( - 2) ( - 2) ( - 2) ( - 2)=16\) 。
例 6:计算\(-2^4\) 。
分析:这里的负号在乘方运算之前,先算\(2^4\) ,再加上负号。
解答:\(-2^4 = - (2 2 2 2)= - 16\) 。
(四)有理数的混合运算
例 7:计算\( - 3^2 ( - \frac{1}{3})^2 - ( - 2)^3 ·( - \frac{1}{2})^2\) 。
分析:按照先乘方,再乘除,最后加减的顺序进行计算。
解答:\(
\begin{align*}
& - 3^2 ( - \frac{1}{3})^2 - ( - 2)^3 ·( - \frac{1}{2})^2\\
=& - 9 \frac{1}{9}-( - 8) ·\frac{1}{4}\\
=& - 1 - ( - 8) 4\\
=& - 1 + 32\\
=&31
\end{align*}
\)
(五)近似数与有效数字
例 8:用四舍五入法,按括号中的要求对下列各数取近似数
0.34482(精确到百分位)
分析:精确到百分位,即保留两位小数,看千分位上的数字 4,4 小于 5,舍去千分位及后面的数字。
解答:0.34482≈0.34
1.5972(精确到 0.01)
分析:精确到 0.01 也就是精确到百分位,看千分位上的数字 7,7 大于 5,向百分位进 1,9 加上 1 满十再向十分位进 1。
解答:1.5972≈1.60
47155(精确到千位)
分析:先将原数写成科学记数法的形式\(4.7155 10^4\) ,精确到千位,就看百位上的数字 1,1 小于 5,舍去百位及后面的数字,所以\(4.7155 10^4 4.7 10^4\) 。
解答:47155≈4.7×10^4
例 9:说出下列近似数的有效数字
0.03080
分析:从左边第一个非 0 数字 3 起,到末位数字 0 止,所有数字 3、0、8、0 都是有效数字。
解答:有效数字为 3、0、8、0 。
2.4 万
分析:先将 2.4 万还原为 24000,从左边第一个非 0 数字 2 起,到末位数字 4 止,有效数字是 2、4 。
解答:有效数字为 2、4 。
三、易错点剖析
(一)符号问题
在有理数的加减法运算中,容易忽略符号的变化。例如,计算\(3 - 5\) ,错误地写成\(3 - 5 = 2\) ,忽略了减去一个数等于加上它的相反数,正确结果应该是\(3+( - 5)= - 2\) 。
在有理数的乘除法运算中,也容易出现符号错误。比如,计算\(( - 3) ( - 4) ·( - 2)\) ,有些同学会先算\(3 4 = 12\) ,再算\(12 ·( - 2)= - 6\) ,忽略了负负得正,正确的计算应该是\(( - 3) ( - 4)=12\) ,\(12 ·( - 2)= - 6\) 。
在乘方运算中,底数为负数时,要注意指数的奇偶性对结果符号的影响。如\(( - 2)^3\)和\(-2^3\) ,\(( - 2)^3=( - 2) ( - 2) ( - 2)= - 8\) ,而\(-2^3 = - (2 2 2)= - 8\) ,虽然结果相同,但意义不同 。
(二)运算顺序问题
在有理数的混合运算中,一定要严格按照先乘方,再乘除,最后加减的顺序进行计算。如果有括号,先算括号内的。例如,计算\(2 + 3 2^2\) ,有些同学会先算\(2 + 3 = 5\) ,再算\(5 2^2 = 5 4 = 20\) ,这是错误的,应该先算\(2^2 = 4\) ,再算\(3 4 = 12\) ,最后算\(2 + 12 = 14\) 。
对于同级运算,要从左到右依次进行。如计算\(12 ·3 2\) ,不能先算\(3 2 = 6\) ,再算\(12 ·6 = 2\) ,而应该先算\(12 ·3 = 4\) ,再算\(4 2 = 8\) 。
(三)近似数与有效数字问题
在确定近似数的有效数字时,容易忽略从左边第一个非 0 数字起这一条件。例如,对于近似数 0.0250,有些同学会认为有效数字是 2、5,而忽略了后面的 0,正确的有效数字是 2、5、0 。
在将一个数用四舍五入法取近似数时,要注意看清精确到的数位。如将 3.14159 精确到千分位,应该是 3.142,而不是 3.141 。
四、课堂总结
回顾运算规则:全面回顾有理数的加、减、乘、除、乘方运算的法则和运算律,强调运算顺序以及在运算过程中符号的确定方法。
** 总结解题
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
本章知识结构图
知识梳理
有理数的运算
加法
乘法
减法
乘方
除法
交换律、结合律
交换律、结合律、分配律
知识梳理
有理数加法法则:
同号两数相加,和取相同的符号,且和的绝对值等于加数的绝对值的和.
绝对值不相等的异号两数相加,和取绝对值较大的加数的符号,且和的绝对值等于加数的绝对值中较大者与较小者的差.
互为相反数的两个数相加得0.
一个数与0相加,仍得这个数.
有理数减法法则:
减去一个数,等于加这个数的相反数.
有理数乘法法则:
两数相乘,同号得正,异号得负,且积的绝对值等于乘数的绝对值的积.
任何数与0相乘,都得0.
知识梳理
有理数除法法则:
除以一个不等于0的数,等于乘这个数的倒数.
两数相除,同号得正,异号得负,且商的绝对值等于被除数的绝对值除以除数的绝对值的商.
0除以任何一个不等于0的数,都得0.
知识梳理
1.计算.
(1)150+250 =_____; (2)-15+(-23) =_____; (3)-5-65=_____;
(4)-26-(-15) =______; (5)(-6)×(-16) =______;
(6)(- )×27=_______;(7)8÷(-16) =_______;
(8)(-25)÷(-) =_______; (9)(-)÷(-) =_______.
400
-38
-70
-11
96
-9
-
随堂练习
2.五袋白糖以每袋50干克为标准,超过的记为正,不足的记为负,称量记录如下:
+4.5,-4,+2.3,-3.5,+2.5
(1)这五袋白糖共超过标准多少干克?
(2)这五袋白糖的总质量是多少千克?
解:(1)+4.5-4+2.3-3.5+2.5=1.8(千克).
(2)50×5+1.8=251.8(千克).
随堂练习
数轴上表示两点间的距离
数轴上两点A,B的距离| AB | 与这两点所对应的数a,b的关系为:| AB | = | a-b |.
知识梳理
随堂练习
3. 分别求出数轴上两点间的距离:
(1)表示 2的点与表示-7的点;
(2)表示-3的点与表示-1的点.
解:(1)2-(-7)=2+7=9;
(2)-1-(-3)=-1+3=2.
有理数加减乘除混合运算顺序:
1.先算乘除,再算加减;
2.同级运算从左往右依次计算;
3.如有括号,先算括号内的;
4.能用运算律的,应利用运算律.
知识梳理
4.计算:
(1)(-0.02)×(-20)×(-5)×4.5;
解:(1)(-0.02)×(-20)×(-5)×4.5
=-0.02×20×5×4.5
=-9;
随堂练习
4.计算:
(2) (-6.5) ×(-2)÷(-) ÷(-5);
解:(2)(-6.5)×(-2)÷(-)÷(-5)
=6.5×2×3×
=7.8;
随堂练习
4.计算:
(3) 0+(- )-2-(-1.5); (4)(-66)×4-(-2.5)÷(-0.1).
解:(3) 0+(- )-2-(-1.5)
=0- -2+1.5
=(0+1.5)+(-0.2-2)
=1.5-2.2
=-0.7;
(4)(-66)×4-(-2.5)÷(-0.1)
=-264-25
=-289.
随堂练习
乘方
一般地,n个相同的乘数a相乘,记作 an,读作“a的n次方”.求n个相同乘数的积的运算,叫作乘方,乘方的结果叫作幂.
根据有理数的乘法法则可以得出:
1.负数的奇次幂是负数,负数的偶次幂是正数;
2.正数的任何次幂都是正数;
3.0的任何正整数次幂都是0.
知识梳理
5.计算:
(1) (-3)3=_____; (2) (-2)4 =_____;
(3) (-1.7)2=_____; (4) (-)3 =_____;
(5) -(-2)2 =_____; (6) (-2)2(-3)2=_____.
-27
16
2.89
-
-4
36
随堂练习
知识梳理
有理数的混合运算顺序:
1.先乘方,再乘除,最后加减;
2.同级运算,从左到右进行;
3.如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.
6.计算:
(1)(-2)2×5-(-2)3÷4; (2)-(3-5)+32×(1-3).
解:(1)原式=4×5-(-8)÷4
=20+2
=22;
解:(2)原式=-(-2)+9×(-2)
=2-18
=-16.
随堂练习
7.计算:
(1) -22×(- )+8(-2)2; (2) (-3)2 2×(-) 2+4-22×(-);
随堂练习
解:(1)原式=2+8÷4
=4.
解:(2)原式=9×+4+
= +4+
= .
随堂练习
7.计算:
(3) {1+[()3] ×(-2)4 } ( );
解:(3)原式=[1+() ×16] ( )
= (1+1) ()
=
=
= .
知识梳理
科学记数法.
把一个大于10的数表示成 a×10n 的形式(其中a 大于或等于1且小于10,n是正整数),这种记法是科学记数法.
用科学记数法表示一个n位整数(n ≥2),其中10的指数是
n-1.
随堂练习
8.一只苍蝇的腹内细菌多达2 800万个,用科学记数法表示为____________个.
9. 新时代十年来,我国建成世界上规模最大的社会保障体系.其中基本医疗保险的参保人数由5.4亿增加到13.6亿,参保率稳定在95%.将数据13.6亿用科学记数法表示为1.36×10n”的形式,则n的值是_____(备注:1亿=100 000 000).
9
2.8×107
随堂练习
10. 用科学记数法表示下列各数:
(1) 100 000 000;
(2) 4 500 000;
(3) 692 400 000 000.
1×108 .
4.5×106.
6.924×1011 .
近似数:是指与准确数相近的一个数.
精确度:近似数与准确数的接近程度可以用精确度表示.
知识梳理
11.用四舍五入法对下列各数取近似数:
(1)0.004 57(精确到0.000 1);
(2)566.123 5(精确到个位);
(3)3.896 3(精确到0.01):
(4)0.057 1(精确到千分位)
随堂练习
(1)0.004 57≈0.004 6.
(2)566.123 5≈566.
(4)0.057 1≈0.057.
(3)3.896 3≈3.90.
随堂练习
12. 近似数1.20是由数a四舍五入得到的,那么数a的取值范围是( )
A.1.15
对于数a ,若千分位上的数字大于或等于5,则百分位上的数字应是“9”,十分位上的数字应是“1”;
若千分位上的数字小于5,则百分位上的数字应是“0”,十分位上的数字应是“2”.
故1.195≤a<1.205.
D
一、核心考点巩固
考点1 有理数的运算
1.如图,比数轴上点 表示的数大1的数是( )
B
A. B.0 C.1 D.2
2.[2025宁波期中]要使算式的运算结果最小,则“ ”内应填入
的运算符号是( )
C
A. B.- C.× D.
3.[2025上海期中]一个数的相反数的倒数是 ,那么这个数是( )
B
A. B. C. D.
4.[2025泰安期末]下列计算正确的是( )
C
A. B.
C. D.
5. 可化为( )
D
A. B.
C. D.
6.甲、乙、丙、丁4位同学,学了有理数的乘方之后,发表了以下见解,
观点正确的有( )
甲: 是2个5相加;
乙:与 是不同的结果;
丙:中底数是 ,指数是4;
丁:是 个4相乘.
B
A.0个 B.1个 C.2个 D.3个
7.[2025成都期末]有理数, 在数轴上对应点的位置如图所示,则下
列结论正确的是( )
A
A. B. C. D.
8.(16分)计算:
(1) ;
解:原式
.
(2) ;
解:原式 .
(3) ;
解:原式
.
(4) .
解:原式 .
9.(8分) 对于有理数, ,定义一种新运算“@”,规定
.
(1)计算@ 的值;
解:因为 ,
所以@ .
(2)计算 的值.
解:因为 ,
所以 .
考点2 有理数的运算的应用
10.[2025长沙调研]火星赤道夏季白天最高温度可达 ,晚上最低
温度可达 ,则火星赤道夏季昼夜温差最大为( )
C
A. B. C. D.
11.手机移动收付款给生活带来便捷.如图是小华某天手机移动收付款账
单的明细(正数表示收入,负数表示支出,单位:元),小华这天使用
手机移动收付款的最终结果是( )
C
A.收入19元 B.支出8元 C.收入6元 D.支出5元
12.将0,, ,1,2这五个数分别填在如图所示的五个
小正方形内,使横向三个数之和与纵向三个数之和相等,
则填入中间位置的小正方形内的数不可以是( )
A
A.1 B. C.2 D.0
13.(8分)某摩托车厂家计划本周每天生产250辆摩托车,由于工厂实
行轮休,每天上班人数不一定相等,故实际每天生产的摩托车数量也不
一样.实际每天生产的摩托车数量与计划相比情况如下表(超产为正,
减产为负,单位:辆):
星期 一 二 三 四 五 六 日
增减
(1)星期六生产了多少辆摩托车?
解: (辆).
答:星期六生产了241辆摩托车.
(2)本周实际总产量与计划相比是增加了还是减少了?增加或减少了
多少?产量最多的一天比产量最少的一天多生产了多少辆?
解: (辆),所以本周实际总产
量与计划相比减少了,减少了21辆.
产量最多的一天为星期五,产量最少的一天为星期日,
产量最多的一天比产量最少的一天多生产了 (辆).
14.(12分)某粮食仓库一周7天内进出粮食的吨数如下(“ ”表示进库,
“-”表示出库):,,,,,, .
(1)经过这7天,仓库里的粮食是增多了还是减少了?增多或减少了多
少吨?
解:因为 .
所以经过这7天,仓库里的粮食减少了,减少了9吨.
(2)经过这7天,仓库管理员结算发现仓库里还存有100吨粮食,那么7
天前,仓库里存有粮食多少吨?
解:因为 .
所以7天前,仓库里存有粮食109吨.
(3)如果进仓库的粮食装卸费是每吨2元,出仓库的粮食装卸费是每吨
3元,求这7天要付多少元装卸费.
解:由题意得,进仓库的装卸费为
(元),
出仓库的装卸费为
(元),
(元),
所以这7天要付407元装卸费.
考点3 科学记数法
15. 是一款先进的人工智能助手,可提供高效、
精准的信息检索和智能对话服务.其活跃用户数在上线21天后达到了
3 370万.将3 370万用科学记数法表示为( )
C
A. B. C. D.
16. 下面是琳琳作业中的一道题目:
“ ”处都是0但发生破损,琳琳查阅后发现本题答案为1,则破损处“0”
的个数为( )
B
A.5 B.4 C.3 D.2
考点4 近似数
17.下列说法中正确的有( )
①近似数2.75精确到0.01;
②由四舍五入得到的近似数 精确到百分位;
③近似数6.9和6.90表示的意义是一样的;
④将30 491按四舍五入精确到千位得到的近似数是3.1万.
D
A.4个 B.3个 C.2个 D.1个
二、思想方法演练
思想1 分类讨论思想
18.若,则 的值不可能是 ( )
D
A.2 B.0 C. D.1
19.已知,,若,则 _________.
10或
思想2 数形结合思想
20.(12分)【问题探索】将一根木棒放在数轴(单位长度为 )上,
如图,木棒左端与数轴上的点重合,右端与数轴上的点 重合.
(1)若将木棒沿数轴向右水平移动,则当它的左端移动到点 时,它的
右端在数轴上所对应的数为30;若将木棒沿数轴向左水平移动,则当它
的右端移动到点 时,它的左端在数轴上所对应的数为6,由此可得这根
木棒的长为___ .
8
(2)图中点所表示的数是____,点 所表示的数是____.
14
22
【实际应用】由 的启发,请借助“数轴”这个工具解决下面问题:
(3)一天,妙妙去问奶奶的年龄,奶奶说:“我若是你现在这么大,你
还要35年才出生;你若是我现在这么大,我就115岁啦!”请问妙妙现在
多少岁了?
解:当奶奶像妙妙这么大时,妙妙为“ 岁”,
所以奶奶与妙妙的年龄差为 (岁),
所以妙妙现在的年龄为 (岁).
谢谢观看!
同课章节目录
