第三章 代数式【章末复习】 课件(共37张PPT)
文档属性
| 名称 | 第三章 代数式【章末复习】 课件(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 00:00:00 | ||
图片预览










文档简介
章末复习
第三章 代数式
【2024新教材】人教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
第三章 代数式 章末复习
一、知识梳理
(一)代数式的概念
定义:用运算符号(加、减、乘、除、乘方等)把数和表示数的字母连接而成的式子叫做代数式。单独的一个数或者一个字母也叫做代数式,如\(5\),\(x\),\(a + b\),\(3x^2\),\(\frac{m}{n}\)等 。强调代数式中不含有等号、不等号等关系符号,像\(a - 5 = 3\)(等式)、\(x > 2\)(不等式)都不属于代数式。
书写规范:
数字与字母相乘时,数字写在字母前面,乘号可省略或写成 “\(\cdot\)”,带分数要化为假分数,如\(4a\),\(\frac{5}{2}x\) 。
字母与字母相乘,乘号通常省略,按字母表顺序书写,如\(ab\) 。
除法运算写成分数形式,如\(m\div n\)写成\(\frac{m}{n}\) 。
代数式是和或差的形式且后面带单位时,需用括号括起来,如\((a + b)\)米 。
(二)列代数式
一般步骤:
分析数量关系,明确题目中各数量间的运算、大小等关系 。
设未知数,选取合适字母表示关键数量,其他数量用含此字母的代数式表示 。
根据数量关系和设出的未知数,运用运算符号列出代数式 。
常见数量关系表示:
和差关系:如 “\(a\)与\(b\)的和的\(3\)倍” 表示为\(3(a + b)\),“\(m\)比\(n\)的平方小\(5\)” 表示为\(n^2 - m = 5\)(可变形为\(m = n^2 - 5\)) 。
倍数关系:“\(x\)的\(\frac{1}{2}\)与\(y\)的\(3\)倍的差” 表示为\(\frac{1}{2}x - 3y\),“\(a\)是\(b\)的\(k\)倍多\(c\)” 表示为\(a = kb + c\) 。
实际问题关系:结合生活场景,如购买商品、行程问题等,根据相关公式和数量关系列代数式 。
复杂数量关系分析方法:
分段分析,将复杂关系分成简单部分分别分析再综合 。
列表分析,通过列表呈现多个数量及其变化,便于理清关系 。
(三)代数式的值
概念:用数值代替代数式里的字母,按代数式中的运算关系计算得出的结果,叫做代数式的值。代数式的值由字母取值决定,字母取值要使代数式有意义 。
求值方法:
直接代入求值:明确字母取值,代入代数式,按运算顺序计算。代入时注意数字与字母对应,字母值为负数、分数时合理添加括号 。
利用公式列代数式求值:确定问题涉及的公式,将已知量用字母表示并代入公式列代数式,给定字母具体数值时进行计算。要准确理解公式中字母含义,注意运算顺序和符号 。
(四)反比例关系(选学内容)
概念:两种相关联的量,一种量变化,另一种量也变化,若对应两个数的乘积一定,这两种量成反比例关系,用字母表示为\(xy = k\)(\(k\)为常数,\(k???0\)) 。
判断方法:分析两种量是否相关联,再看对应乘积是否一定 。
性质:一个量增大,另一个量减小;反之亦然。反比例函数\(y=\frac{k}{x}\)(\(k\)为常数,\(k???0\))图像是双曲线 。
二、典型例题讲解
(一)代数式的书写与判断
例 1:下列式子中,哪些是代数式?
①\(3x - 1\) ②\(2 + 3 = 5\) ③\(a\) ④\(x \geq 0\) ⑤\(\frac{1}{x + y}\)
分析:根据代数式定义,式子中不能有等号、不等号等关系符号。①③⑤是用运算符号把数和字母连接而成,或单独的数、字母,属于代数式;②是等式,④是不等式,不属于代数式 。
解答:①③⑤是代数式,②④不是代数式 。
例 2:将下列数量关系用代数式正确表示:
\(a\)与\(b\)的\(2\)倍的差的平方
分析:先表示出\(b\)的\(2\)倍为\(2b\),再求\(a\)与\(2b\)的差为\(a - 2b\),最后对差求平方 。
解答:\((a - 2b)^2\) 。
比\(m\)的立方少\(\frac{1}{3}\)的数
分析:\(m\)的立方是\(m^3\),比它少\(\frac{1}{3}\),用\(m^3\)减去\(\frac{1}{3}\) 。
解答:\(m^3 - \frac{1}{3}\) 。
(二)列代数式
例 3:用代数式表示:
某商店购进一批商品,每件进价为\(a\)元,售价提高\(40\%\)后标价,再打\(8\)折销售,此时售价是多少元?
分析:售价提高\(40\%\)后的标价为\(a(1 + 40\%)\)元,在此基础上打\(8\)折,即标价乘以\(0.8\) 。
解答:此时售价为\(a(1 + 40\%)??0.8 = 1.12a\)元 。
一个梯形的上底为\(a\),下底为\(b\),高为\(h\),若上底增加\(2\),下底减少\(2\),高不变,梯形面积会发生变化吗?用代数式表示变化前后的梯形面积。
分析:根据梯形面积公式\(S = \frac{(?????? + ??????)??é??}{2}\),变化前面积为\(\frac{(a + b)h}{2}\);变化后上底为\(a + 2\),下底为\(b - 2\),面积为\(\frac{(a + 2 + b - 2)h}{2}=\frac{(a + b)h}{2}\) 。
解答:变化前梯形面积\(S_1 = \frac{(a + b)h}{2}\),变化后梯形面积\(S_2 = \frac{(a + b)h}{2}\),面积不变 。
(三)代数式的值
例 4:当\(x = -2\),\(y = \frac{1}{3}\)时,求代数式\(\frac{3x - 2y}{xy}\)的值。
分析:将\(x = -2\),\(y = \frac{1}{3}\)代入代数式,先分别计算分子\(3x - 2y = 3??(-2) - 2??\frac{1}{3}=-6 - \frac{2}{3}=-\frac{20}{3}\),分母\(xy = (-2)??\frac{1}{3}=-\frac{2}{3}\),再进行除法运算 。
解答:当\(x = -2\),\(y = \frac{1}{3}\)时,\(
\begin{align*}
\frac{3x - 2y}{xy}&=\frac{-\frac{20}{3}}{-\frac{2}{3}}\\
&=-\frac{20}{3}??(-\frac{3}{2})\\
&= 10
\end{align*}
\)
例 5:已知圆的半径\(r = 5\)厘米,根据圆的面积公式\(S = \pi r^2\),求圆的面积(\(\pi\)取\(3.14\))。
分析:将\(r = 5\),\(\pi = 3.14\)代入圆的面积公式\(S = \pi r^2\)进行计算 。
解答:当\(r = 5\),\(\pi = 3.14\)时,\(S = 3.14??5^2 = 3.14??25 = 78.5\)平方厘米 。
三、易错点剖析
(一)代数式书写易错点
数字与字母相乘时,数字未写在字母前面,或带分数未化为假分数 。如误将\(3??a\)写成\(a3\),\(2\frac{1}{2}x\)未写成\(\frac{5}{2}x\) 。
除法运算未写成分数形式,如把\(m\div n\)写成\(m?·n\) 。
和差形式带单位时,未加括号,如\(a + b\)米应写成\((a + b)\)米 。
(二)列代数式易错点
分析数量关系错误,导致代数式列写错误。例如,“\(a\)与\(b\)的和的平方” 误写成\(a + b^2\),正确的是\((a + b)^2\) 。
设未知数不明确,或未根据设出的未知数正确表示其他数量 。
(三)求代数式的值易错点
代入数值时,数字与字母对应错误 。
字母值为负数、分数时,未合理添加括号,导致运算顺序错误 。如计算\(x^2 - 2y\),当\(x = -2\),\(y = \frac{1}{2}\)时,误算为\(-2^2 - 2??\frac{1}{2}\),正确的是\((-2)^2 - 2??\frac{1}{2}\) 。
利用公式求值时,对公式中字母含义理解错误,或运算顺序错误 。
四、课堂总结
知识回顾:全面回顾代数式的概念、列代数式的方法、代数式求值的方式以及反比例关系的相关知识,梳理各知识点之间的联系 。
方法归纳:总结代数式书写规范、列代数式的步骤和技巧、求代数式的值的注意事项,以及判断反比例关系的方法,帮助学生形成系统的知识体系 。
学习建议:鼓励学生在日常学习中多观察生活中的数量关系,加强列代数式和求代数式的值的练习,注意避免易错点,提高运用代数式解决实际问题的能力 。
五、作业布置
基础作业
判断下列式子是否为代数式:
\(5 - 3x\)
\(a = 2\)
\(\frac{1}{x}\)
\(x > 1\)
用代数式表示:
\(a\)的\(3\)倍与\(b\)的和的一半
比\(m\)的平方小\(3\)的数
某商品原价为\(p\)元,先降价\(10\%\),再提价\(10\%\),此时的价格
当\(m = -1\),\(n = 2\)时,求代数式\(m^2 + 2mn - n^2\)的值。
拓展作业
某工厂生产某种产品,每件产品的成本为\(50\)元,出厂价为\(80\)元。若该厂每月生产\(x\)件产品,用代数式表示每月的利润(利润 = 出厂价 × 数量 - 成本 × 数量);当\(x = 1000\)时,求每月的利润 。
观察下列等式:\(1 = 1^2\),\(1 + 3 = 2^2\),\(1 + 3 + 5 = 3^2\),\(1 + 3 + 5 + 7 = 4^2\),…… ,用含\(n\)(\(n\)为正整数)的代数式表示这一规律,并求\(1 + 3 + 5 + \cdots + 2023\)的值 。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识梳理
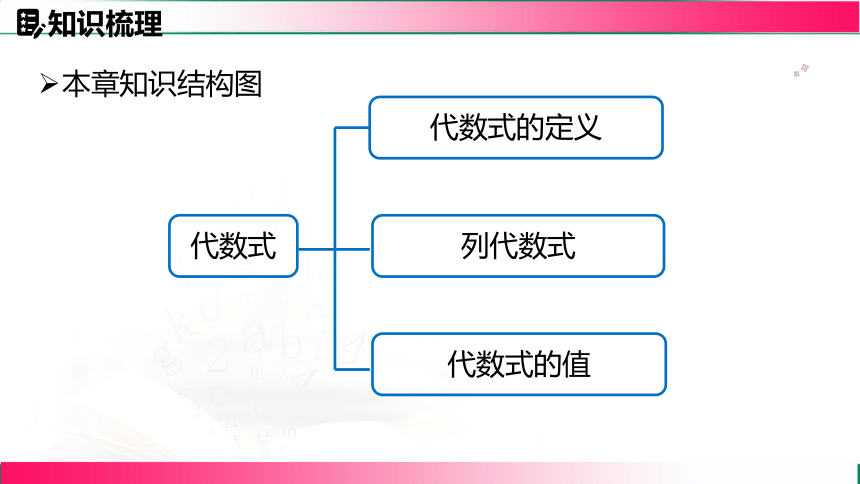
代数式
代数式的定义
列代数式
代数式的值
本章知识结构图
知识梳理
代数式:用运算符号把数或表示数的字母连接起来的式子叫作代数式.
单独的一个数或字母也是代数式,例如,2,t都是代数式.
知识梳理
{00A15C55-8517-42AA-B614-E9B94910E393}类型
书写规定
示例
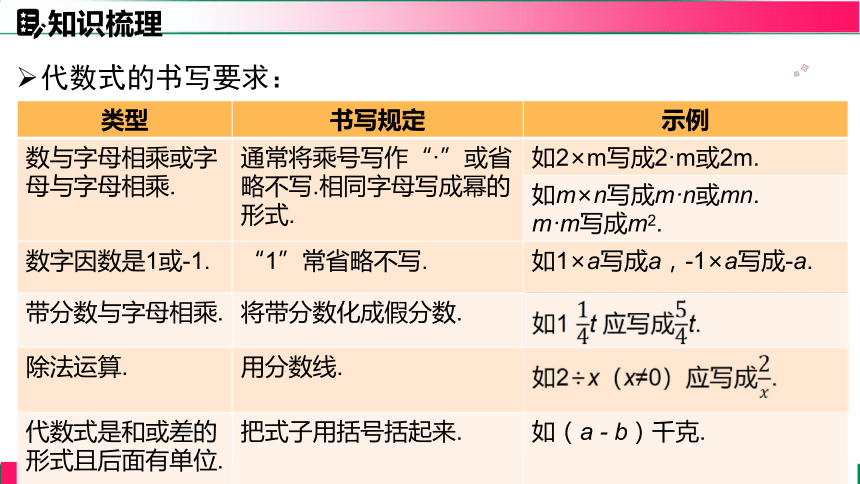
数与字母相乘或字母与字母相乘.
通常将乘号写作“·”或省略不写.相同字母写成幂的形式.
如2×m写成2·m或2m.
如m×n写成m·n或mn.
m·m写成m2.
数字因数是1或-1.
“1”常省略不写.
如1×a写成a,-1×a写成-a.
带分数与字母相乘.
将带分数化成假分数.
如1 14t 应写成54t.
除法运算.
用分数线.
如2÷x(x≠0)应写成2????.
代数式是和或差的形式且后面有单位.
把式子用括号括起来.
如(a - b)千克.
{00A15C55-8517-42AA-B614-E9B94910E393}类型
书写规定
示例
数与字母相乘或字母与字母相乘.
通常将乘号写作“·”或省略不写.相同字母写成幂的形式.
如2×m写成2·m或2m.
如m×n写成m·n或mn.
m·m写成m2.
数字因数是1或-1.
“1”常省略不写.
如1×a写成a,-1×a写成-a.
带分数与字母相乘.
将带分数化成假分数.
除法运算.
用分数线.
代数式是和或差的形式且后面有单位.
把式子用括号括起来.
如(a - b)千克.
代数式的书写要求:
知识梳理
列代数式
在解决一些数学问题与实际问题时,需要先把问题中的数量关系用含有数、字母和运算符号的式子表示出来,也就是列代数式.
列代数式的步骤:
(1)分析条件,找出数量关系.
(2)用含有数、字母和运算符号的式子表示出来.
知识梳理
反比例关系:两个相关联的量,一个量变化,另一个量也随着变化,且这两个量的乘积一定,这两个量就叫作成反比例的量,它们之间的关系叫作反比例关系.
反比例关系的表示方法:如果用字母x和y表示两个相关联的量,用k表示它们的积(k是一个确定的值,且k≠0),反比例关系可以用xy=k或y=????????来表示,其中k叫作比例系数.
两个量的变化规律:一个量随着另一个量的增大而减小.
?
知识梳理
代数式的值:一般地,用数值代替代数式中的字母,按照代数式中的运算关系计算得出的结果,叫作代数式的值.当字母取不同的数值时,代数式的值一般也不同.
求代数式的值的步骤:
1.代 .
2.算.
3.验.
随堂练习
1.用代数式表示:
(1)比a的3倍小4的数.
(2)a的一半与b的和的平方.
(3)我国自主研发的一种近防炮,每分钟可发射10 000发炮弹.近防炮 t min能发射多少发炮弹?
(4)购买n件单价为c元的商品要花多少元?若支付1000元还有剩余,应找回多少元?
cn元.
3a-4.
(12a+b)2.
?
10 000t 发.
(1000-cn)元.
随堂练习
解:(1)最高气温是(t+15)℃.
(2)第一次降价后的售价是0.8b元.
第二次降价后的售价是(0.8b-10)元.
2.用代数式表示:
(1)某地冬季一天的温差是15℃,这天的最低气温是t℃,最高气温是多少?
(2)某种商品原价为每件b元,第一次降价打8折,第二次降价每件又降10元,第一次降价后的售价是多少元?第二次降价后的售价是多少元
随堂练习
3.说出下列各组代数式的意义有什么不同?
(1)3x-4与3(x-4);
(2)a2-b2与(a-b)2 .
解:(1)3x-4的意义是x的3倍与4的差,3(x-4)的意义是x与4的差的3倍.
(2) a2-b2的意义是a的平方与b的平方的差,或者a与b的平方的差, (a-b)2的意义是a与b的差的平方.
随堂练习
4.(1)若一个长方形的长为p,宽为q,则2(p+q)表示什么?
(2)举两个例子说明代数式3a+2b表示的实际问题中的数量关系.
解:(1) 2(p+q)表示长方形的周长,
(2)例:①笔的单价是a元,笔记本的单价是b元,买3支笔,2个笔记本的花费是(3a+2b)元.
②苹果的单价是3 元/kg,香蕉的单价是2 元/kg,买a kg苹果,b kg香蕉共花费(3a+2b)元.
③甲、乙两个工程队共修一条路,甲工程队每天修a km,乙工程队每天修b km,甲工程队工作3天,乙工程队工作 2天共修了(3a+2b) km.
随堂练习
5.用一根绳子围成一个长方形,相邻两边的长分别为x m和y m.
(1)当绳子的长为12 m时,用式子表示y与x的关系;
(2)当长方形的面积为12 m2时,用式子表示y与x的关系;
解:(1)2(x+y)=12.
(2) xy=12.
随堂练习
5.用一根绳子围成一个长方形,相邻两边的长分别为x m和y m.
(3)当长方形的周长一定时,相邻两边的长成反比例关系吗?当长方形的面积一定时呢?为什么?
解:(3)当周长一定时,x与y的和一定,x与y不成反比例关系.
当面积一定时,x与y的积一定,x与y成反比例关系.
随堂练习
6.若2b-a=5,求代数式5(a﹣2b)2﹣3(a﹣2b)﹣60的值.
解:因为2b﹣a=5,所以a﹣2b=﹣5,
所以原式=5×(﹣5)2﹣3×(﹣5)﹣60
=125+15﹣60
=80.
随堂练习
7.根据下列a,b的值,分别求代数式a2-b2与(a-b)2的值:
(1)a=-1,b=-3;(2)a=2,b=-12.
?
解:(1)当a=-1,b=-3时,
a2-b2=(-1) 2 -(-3) 2 =1-9=-8.
(a-b)2 =[-1- (-3)] 2 =4.
(2)当a=2,b=-12时,a2-b2=22 -(-12) 2 = 154;
(a-b)2 =[2- (-12)] 2 = 254.
?
随堂练习
8.用含字母的式子填空:
(1)长方形的宽为4,长比宽多a,则长方形的长为______,面积为_________;
(2)一件衬衣的进价为a 元,售价为2a 元,则每件衬衣的利润为_______元;
(3)一个数的倒数为a,则这个数是_____.
4+a
4(4+a)
(2a-a)
1a
?
随堂练习
9.如图,正方形ABCD的边长为a.
(1)根据图中数据,用含a,b的代数式表示阴影部分的面积S;
(2)当a=6,b=2时,求阴影部分的面积.
解:(1)S= 12?a2- 12×4b= 12?a2-2b.
(2)当a=6,b=2时, S= 12×62- 2×2
=18-4
=14.
?
4
b
a
A
B
C
D
随堂练习
10.如图,用棋子摆出一组形如正方形的图形,按照这种方法摆下去,摆第n个图形需要多少枚棋子?
第1个
第2个
第3个
解:第1个图形共有4枚棋子;
第2个图形共有8枚棋子;
第3个图形共有12枚棋子;
......
第n个图形共有4n枚棋子.
一、核心考点巩固
考点1 代数式的书写规范及意义
1.下列各代数式符合书写规范的是( )
B
A.????×???????? B.???????????????????? C.????÷???? D.????????????????????
?
2.下列不能表示“???????? ”的意义的是( )
?
D
A.3的????倍 B.????的3倍 C.3个????相加 D.3个???? 相乘
?
3.下列代数式的意义表述错误的是( )
B
A.????????+????????表示????????与????????的和 B.????????+????????表示????与???? 和的平方
C.?????????????????表示9减去????的????????所得的差 D.????????????????表示????????除以???????? 所得的商
?
考点2 列代数式
4. 为落实“双减”政策,某校利用课后服务开展了主题为
“书香满校园”的读书活动.现需购买甲、乙两种读本共100本供学生阅读,
其中甲种读本的单价为10元,乙种读本的单价为8元,设购买甲种读本????
本,则购买乙种读本的费用为( )
?
C
A.????????元 B.?????????????????????????元 C.?????????????????????元 D.????????????????????? 元
?
5.驴肉火烧为河北省著名小吃,驴肉醇香,火烧酥脆.某店销售两种口味
的火烧,驴肉火烧12元一个,焖子火烧5元一个.为增加销量,该店推出
优惠活动,买一个驴肉火烧赠送一个焖子火烧.若嘉琪需购买???? 个驴肉火
烧和????个焖子火烧?????
C
A.????????+????????????元 B.????????+????????????元 C.????????+????????????+????元 D.????????+????????????+???? 元
?
6.[2025杭州期末]一件衣服的进价为????元,商家按进价提高????????% 标价,
则这件衣服的标价是______元.
?
????.????????
?
考点3 反比例关系
7.[2025福州期中]下列说法错误的是( )
A
A.正方形的面积与边长成反比例
B.如果????????=????,那么????和???? 成反比例
C.路程一定,时间与速度成反比例
D.分数值一定,分子和分母成正比例
?
8.当三角形的面积为?????????????????时,它的底边长????????????与底边上的高???????????? 之
间的关系式为_______,底边长????????????与底边上的高???????????? 之间为____比
例关系(填“正”或“反”).
?
????=????????????
?
反
9.(8分)[2025渭南期中]某运输队要为灾区运送一批救灾物资.如果
要一次把所有的物资全部送到,每辆车的载质量与所需车的数量见下表:
载质量/吨
2.5
4
5
10
数量/辆
40
25
20
10
(1)这批救灾物资共有_____吨;
100
(2)每辆车的载质量与所需车的数量成反比例关系吗?为什么?
解:成反比例关系.因为每辆车的载质量与所需车的数量的乘积等于100,
为定值.
考点4 求代数式的值
10.若????=????,????=????????,则代数式?????????????????+???? 的值为( )
?
D
A.????? B.1 C.7 D.13
?
11.[2025安庆期中]已知有理数????,????满足(?????????)????+????+????=???? ,则
????????= ___.
?
9
12.(8分)已知????与????????的积为1,????和????的和为?????,???? 的绝对值为4.
?
(1)求????,????,???? 的值;
?
解:依题意,得????????????=????,????+????=?????,????=???? ,
所以????=????,????=?????,????=????或?????
?
(2)求?????????+????????????? 的值.
?
解:当????=????,????=?????,????=???? 时,
?????????+?????????????=?????????+????×??????????=??????????????????=????????? ;
当????=????,????=?????,????=????? 时,
?????????+?????????????=?????????+????×?????+????=?????????????+????=????? .
?
13.(8分)[2025广州期末]如图,某长方形广场的四角
都有一块半径相同的????????圆形的草地,已知圆形的半径为???? 米,
长方形的长为????米,宽为???? 米.
?
(1)请列式表示广场空地的面积;
解:由图可得,广场空地的面积为????????????????????? 平方米.
?
(2)若长方形的长为300米,宽为200米,圆形的半径为10米,计算广
场空地的面积(计算结果保留???? ).
?
解:当长方形的长为300米,宽为200米,圆形的半径为10米时,
广场空地的面积为????????????×?????????????????×????????????=?????????????????????????????????????? 平方米.
?
14.(8分)某公司用????,????两种型号的车运输某种砂石料,其中???? 型车一
车能运输15吨这种砂石料,????型车一车能运输12吨这种砂石料.其中???? 型
车运输了????车,????型车运输了???? 车.
?
(1)若共运输了????吨这种砂石料,用含????,????的代数式表示???? ;
?
解:????=????????????+???????????? .
?
(2)若这种砂石料每吨80元,当????=????????,????=???????? 时,此公司购买砂石
料应该付款多少元?
?
解:当????=????????,????=????????时,????????????+????????????=????????×????????+????????×????????=????????????
(吨),
????????????×????????=????????????????????? (元).
答:此公司购买砂石料应该付款26 400元.
?
二、思想方法演练
思想1 数形结合思想
15.为开展劳动教育,某校想把一块周长为????????????? 的长方
形荒地按如图所示等距外扩????????? ,改造成一个长方形劳
动基地,并且用栅栏围起来,则需要栅栏( )
?
B
A.????????+???????????? B.????????+???????????? C.????????????? D.?????????????
?
思想2 从特殊到一般的思想
16.下列图形都是由同样大小的小圆圈按一定规律组成的,其中图①中
一共有6个小圆圈,图②中一共有9个小圆圈,图③中一共有12个小圆
圈,? ,按此规律排列下去,则图 中小圆圈的个数为( )
?
C
A.????????????? B.????????+???? C.????????+???? D.?????????????
?
谢谢观看!
第三章 代数式
【2024新教材】人教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
第三章 代数式 章末复习
一、知识梳理
(一)代数式的概念
定义:用运算符号(加、减、乘、除、乘方等)把数和表示数的字母连接而成的式子叫做代数式。单独的一个数或者一个字母也叫做代数式,如\(5\),\(x\),\(a + b\),\(3x^2\),\(\frac{m}{n}\)等 。强调代数式中不含有等号、不等号等关系符号,像\(a - 5 = 3\)(等式)、\(x > 2\)(不等式)都不属于代数式。
书写规范:
数字与字母相乘时,数字写在字母前面,乘号可省略或写成 “\(\cdot\)”,带分数要化为假分数,如\(4a\),\(\frac{5}{2}x\) 。
字母与字母相乘,乘号通常省略,按字母表顺序书写,如\(ab\) 。
除法运算写成分数形式,如\(m\div n\)写成\(\frac{m}{n}\) 。
代数式是和或差的形式且后面带单位时,需用括号括起来,如\((a + b)\)米 。
(二)列代数式
一般步骤:
分析数量关系,明确题目中各数量间的运算、大小等关系 。
设未知数,选取合适字母表示关键数量,其他数量用含此字母的代数式表示 。
根据数量关系和设出的未知数,运用运算符号列出代数式 。
常见数量关系表示:
和差关系:如 “\(a\)与\(b\)的和的\(3\)倍” 表示为\(3(a + b)\),“\(m\)比\(n\)的平方小\(5\)” 表示为\(n^2 - m = 5\)(可变形为\(m = n^2 - 5\)) 。
倍数关系:“\(x\)的\(\frac{1}{2}\)与\(y\)的\(3\)倍的差” 表示为\(\frac{1}{2}x - 3y\),“\(a\)是\(b\)的\(k\)倍多\(c\)” 表示为\(a = kb + c\) 。
实际问题关系:结合生活场景,如购买商品、行程问题等,根据相关公式和数量关系列代数式 。
复杂数量关系分析方法:
分段分析,将复杂关系分成简单部分分别分析再综合 。
列表分析,通过列表呈现多个数量及其变化,便于理清关系 。
(三)代数式的值
概念:用数值代替代数式里的字母,按代数式中的运算关系计算得出的结果,叫做代数式的值。代数式的值由字母取值决定,字母取值要使代数式有意义 。
求值方法:
直接代入求值:明确字母取值,代入代数式,按运算顺序计算。代入时注意数字与字母对应,字母值为负数、分数时合理添加括号 。
利用公式列代数式求值:确定问题涉及的公式,将已知量用字母表示并代入公式列代数式,给定字母具体数值时进行计算。要准确理解公式中字母含义,注意运算顺序和符号 。
(四)反比例关系(选学内容)
概念:两种相关联的量,一种量变化,另一种量也变化,若对应两个数的乘积一定,这两种量成反比例关系,用字母表示为\(xy = k\)(\(k\)为常数,\(k???0\)) 。
判断方法:分析两种量是否相关联,再看对应乘积是否一定 。
性质:一个量增大,另一个量减小;反之亦然。反比例函数\(y=\frac{k}{x}\)(\(k\)为常数,\(k???0\))图像是双曲线 。
二、典型例题讲解
(一)代数式的书写与判断
例 1:下列式子中,哪些是代数式?
①\(3x - 1\) ②\(2 + 3 = 5\) ③\(a\) ④\(x \geq 0\) ⑤\(\frac{1}{x + y}\)
分析:根据代数式定义,式子中不能有等号、不等号等关系符号。①③⑤是用运算符号把数和字母连接而成,或单独的数、字母,属于代数式;②是等式,④是不等式,不属于代数式 。
解答:①③⑤是代数式,②④不是代数式 。
例 2:将下列数量关系用代数式正确表示:
\(a\)与\(b\)的\(2\)倍的差的平方
分析:先表示出\(b\)的\(2\)倍为\(2b\),再求\(a\)与\(2b\)的差为\(a - 2b\),最后对差求平方 。
解答:\((a - 2b)^2\) 。
比\(m\)的立方少\(\frac{1}{3}\)的数
分析:\(m\)的立方是\(m^3\),比它少\(\frac{1}{3}\),用\(m^3\)减去\(\frac{1}{3}\) 。
解答:\(m^3 - \frac{1}{3}\) 。
(二)列代数式
例 3:用代数式表示:
某商店购进一批商品,每件进价为\(a\)元,售价提高\(40\%\)后标价,再打\(8\)折销售,此时售价是多少元?
分析:售价提高\(40\%\)后的标价为\(a(1 + 40\%)\)元,在此基础上打\(8\)折,即标价乘以\(0.8\) 。
解答:此时售价为\(a(1 + 40\%)??0.8 = 1.12a\)元 。
一个梯形的上底为\(a\),下底为\(b\),高为\(h\),若上底增加\(2\),下底减少\(2\),高不变,梯形面积会发生变化吗?用代数式表示变化前后的梯形面积。
分析:根据梯形面积公式\(S = \frac{(?????? + ??????)??é??}{2}\),变化前面积为\(\frac{(a + b)h}{2}\);变化后上底为\(a + 2\),下底为\(b - 2\),面积为\(\frac{(a + 2 + b - 2)h}{2}=\frac{(a + b)h}{2}\) 。
解答:变化前梯形面积\(S_1 = \frac{(a + b)h}{2}\),变化后梯形面积\(S_2 = \frac{(a + b)h}{2}\),面积不变 。
(三)代数式的值
例 4:当\(x = -2\),\(y = \frac{1}{3}\)时,求代数式\(\frac{3x - 2y}{xy}\)的值。
分析:将\(x = -2\),\(y = \frac{1}{3}\)代入代数式,先分别计算分子\(3x - 2y = 3??(-2) - 2??\frac{1}{3}=-6 - \frac{2}{3}=-\frac{20}{3}\),分母\(xy = (-2)??\frac{1}{3}=-\frac{2}{3}\),再进行除法运算 。
解答:当\(x = -2\),\(y = \frac{1}{3}\)时,\(
\begin{align*}
\frac{3x - 2y}{xy}&=\frac{-\frac{20}{3}}{-\frac{2}{3}}\\
&=-\frac{20}{3}??(-\frac{3}{2})\\
&= 10
\end{align*}
\)
例 5:已知圆的半径\(r = 5\)厘米,根据圆的面积公式\(S = \pi r^2\),求圆的面积(\(\pi\)取\(3.14\))。
分析:将\(r = 5\),\(\pi = 3.14\)代入圆的面积公式\(S = \pi r^2\)进行计算 。
解答:当\(r = 5\),\(\pi = 3.14\)时,\(S = 3.14??5^2 = 3.14??25 = 78.5\)平方厘米 。
三、易错点剖析
(一)代数式书写易错点
数字与字母相乘时,数字未写在字母前面,或带分数未化为假分数 。如误将\(3??a\)写成\(a3\),\(2\frac{1}{2}x\)未写成\(\frac{5}{2}x\) 。
除法运算未写成分数形式,如把\(m\div n\)写成\(m?·n\) 。
和差形式带单位时,未加括号,如\(a + b\)米应写成\((a + b)\)米 。
(二)列代数式易错点
分析数量关系错误,导致代数式列写错误。例如,“\(a\)与\(b\)的和的平方” 误写成\(a + b^2\),正确的是\((a + b)^2\) 。
设未知数不明确,或未根据设出的未知数正确表示其他数量 。
(三)求代数式的值易错点
代入数值时,数字与字母对应错误 。
字母值为负数、分数时,未合理添加括号,导致运算顺序错误 。如计算\(x^2 - 2y\),当\(x = -2\),\(y = \frac{1}{2}\)时,误算为\(-2^2 - 2??\frac{1}{2}\),正确的是\((-2)^2 - 2??\frac{1}{2}\) 。
利用公式求值时,对公式中字母含义理解错误,或运算顺序错误 。
四、课堂总结
知识回顾:全面回顾代数式的概念、列代数式的方法、代数式求值的方式以及反比例关系的相关知识,梳理各知识点之间的联系 。
方法归纳:总结代数式书写规范、列代数式的步骤和技巧、求代数式的值的注意事项,以及判断反比例关系的方法,帮助学生形成系统的知识体系 。
学习建议:鼓励学生在日常学习中多观察生活中的数量关系,加强列代数式和求代数式的值的练习,注意避免易错点,提高运用代数式解决实际问题的能力 。
五、作业布置
基础作业
判断下列式子是否为代数式:
\(5 - 3x\)
\(a = 2\)
\(\frac{1}{x}\)
\(x > 1\)
用代数式表示:
\(a\)的\(3\)倍与\(b\)的和的一半
比\(m\)的平方小\(3\)的数
某商品原价为\(p\)元,先降价\(10\%\),再提价\(10\%\),此时的价格
当\(m = -1\),\(n = 2\)时,求代数式\(m^2 + 2mn - n^2\)的值。
拓展作业
某工厂生产某种产品,每件产品的成本为\(50\)元,出厂价为\(80\)元。若该厂每月生产\(x\)件产品,用代数式表示每月的利润(利润 = 出厂价 × 数量 - 成本 × 数量);当\(x = 1000\)时,求每月的利润 。
观察下列等式:\(1 = 1^2\),\(1 + 3 = 2^2\),\(1 + 3 + 5 = 3^2\),\(1 + 3 + 5 + 7 = 4^2\),…… ,用含\(n\)(\(n\)为正整数)的代数式表示这一规律,并求\(1 + 3 + 5 + \cdots + 2023\)的值 。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识梳理
代数式
代数式的定义
列代数式
代数式的值
本章知识结构图
知识梳理
代数式:用运算符号把数或表示数的字母连接起来的式子叫作代数式.
单独的一个数或字母也是代数式,例如,2,t都是代数式.
知识梳理
{00A15C55-8517-42AA-B614-E9B94910E393}类型
书写规定
示例
数与字母相乘或字母与字母相乘.
通常将乘号写作“·”或省略不写.相同字母写成幂的形式.
如2×m写成2·m或2m.
如m×n写成m·n或mn.
m·m写成m2.
数字因数是1或-1.
“1”常省略不写.
如1×a写成a,-1×a写成-a.
带分数与字母相乘.
将带分数化成假分数.
如1 14t 应写成54t.
除法运算.
用分数线.
如2÷x(x≠0)应写成2????.
代数式是和或差的形式且后面有单位.
把式子用括号括起来.
如(a - b)千克.
{00A15C55-8517-42AA-B614-E9B94910E393}类型
书写规定
示例
数与字母相乘或字母与字母相乘.
通常将乘号写作“·”或省略不写.相同字母写成幂的形式.
如2×m写成2·m或2m.
如m×n写成m·n或mn.
m·m写成m2.
数字因数是1或-1.
“1”常省略不写.
如1×a写成a,-1×a写成-a.
带分数与字母相乘.
将带分数化成假分数.
除法运算.
用分数线.
代数式是和或差的形式且后面有单位.
把式子用括号括起来.
如(a - b)千克.
代数式的书写要求:
知识梳理
列代数式
在解决一些数学问题与实际问题时,需要先把问题中的数量关系用含有数、字母和运算符号的式子表示出来,也就是列代数式.
列代数式的步骤:
(1)分析条件,找出数量关系.
(2)用含有数、字母和运算符号的式子表示出来.
知识梳理
反比例关系:两个相关联的量,一个量变化,另一个量也随着变化,且这两个量的乘积一定,这两个量就叫作成反比例的量,它们之间的关系叫作反比例关系.
反比例关系的表示方法:如果用字母x和y表示两个相关联的量,用k表示它们的积(k是一个确定的值,且k≠0),反比例关系可以用xy=k或y=????????来表示,其中k叫作比例系数.
两个量的变化规律:一个量随着另一个量的增大而减小.
?
知识梳理
代数式的值:一般地,用数值代替代数式中的字母,按照代数式中的运算关系计算得出的结果,叫作代数式的值.当字母取不同的数值时,代数式的值一般也不同.
求代数式的值的步骤:
1.代 .
2.算.
3.验.
随堂练习
1.用代数式表示:
(1)比a的3倍小4的数.
(2)a的一半与b的和的平方.
(3)我国自主研发的一种近防炮,每分钟可发射10 000发炮弹.近防炮 t min能发射多少发炮弹?
(4)购买n件单价为c元的商品要花多少元?若支付1000元还有剩余,应找回多少元?
cn元.
3a-4.
(12a+b)2.
?
10 000t 发.
(1000-cn)元.
随堂练习
解:(1)最高气温是(t+15)℃.
(2)第一次降价后的售价是0.8b元.
第二次降价后的售价是(0.8b-10)元.
2.用代数式表示:
(1)某地冬季一天的温差是15℃,这天的最低气温是t℃,最高气温是多少?
(2)某种商品原价为每件b元,第一次降价打8折,第二次降价每件又降10元,第一次降价后的售价是多少元?第二次降价后的售价是多少元
随堂练习
3.说出下列各组代数式的意义有什么不同?
(1)3x-4与3(x-4);
(2)a2-b2与(a-b)2 .
解:(1)3x-4的意义是x的3倍与4的差,3(x-4)的意义是x与4的差的3倍.
(2) a2-b2的意义是a的平方与b的平方的差,或者a与b的平方的差, (a-b)2的意义是a与b的差的平方.
随堂练习
4.(1)若一个长方形的长为p,宽为q,则2(p+q)表示什么?
(2)举两个例子说明代数式3a+2b表示的实际问题中的数量关系.
解:(1) 2(p+q)表示长方形的周长,
(2)例:①笔的单价是a元,笔记本的单价是b元,买3支笔,2个笔记本的花费是(3a+2b)元.
②苹果的单价是3 元/kg,香蕉的单价是2 元/kg,买a kg苹果,b kg香蕉共花费(3a+2b)元.
③甲、乙两个工程队共修一条路,甲工程队每天修a km,乙工程队每天修b km,甲工程队工作3天,乙工程队工作 2天共修了(3a+2b) km.
随堂练习
5.用一根绳子围成一个长方形,相邻两边的长分别为x m和y m.
(1)当绳子的长为12 m时,用式子表示y与x的关系;
(2)当长方形的面积为12 m2时,用式子表示y与x的关系;
解:(1)2(x+y)=12.
(2) xy=12.
随堂练习
5.用一根绳子围成一个长方形,相邻两边的长分别为x m和y m.
(3)当长方形的周长一定时,相邻两边的长成反比例关系吗?当长方形的面积一定时呢?为什么?
解:(3)当周长一定时,x与y的和一定,x与y不成反比例关系.
当面积一定时,x与y的积一定,x与y成反比例关系.
随堂练习
6.若2b-a=5,求代数式5(a﹣2b)2﹣3(a﹣2b)﹣60的值.
解:因为2b﹣a=5,所以a﹣2b=﹣5,
所以原式=5×(﹣5)2﹣3×(﹣5)﹣60
=125+15﹣60
=80.
随堂练习
7.根据下列a,b的值,分别求代数式a2-b2与(a-b)2的值:
(1)a=-1,b=-3;(2)a=2,b=-12.
?
解:(1)当a=-1,b=-3时,
a2-b2=(-1) 2 -(-3) 2 =1-9=-8.
(a-b)2 =[-1- (-3)] 2 =4.
(2)当a=2,b=-12时,a2-b2=22 -(-12) 2 = 154;
(a-b)2 =[2- (-12)] 2 = 254.
?
随堂练习
8.用含字母的式子填空:
(1)长方形的宽为4,长比宽多a,则长方形的长为______,面积为_________;
(2)一件衬衣的进价为a 元,售价为2a 元,则每件衬衣的利润为_______元;
(3)一个数的倒数为a,则这个数是_____.
4+a
4(4+a)
(2a-a)
1a
?
随堂练习
9.如图,正方形ABCD的边长为a.
(1)根据图中数据,用含a,b的代数式表示阴影部分的面积S;
(2)当a=6,b=2时,求阴影部分的面积.
解:(1)S= 12?a2- 12×4b= 12?a2-2b.
(2)当a=6,b=2时, S= 12×62- 2×2
=18-4
=14.
?
4
b
a
A
B
C
D
随堂练习
10.如图,用棋子摆出一组形如正方形的图形,按照这种方法摆下去,摆第n个图形需要多少枚棋子?
第1个
第2个
第3个
解:第1个图形共有4枚棋子;
第2个图形共有8枚棋子;
第3个图形共有12枚棋子;
......
第n个图形共有4n枚棋子.
一、核心考点巩固
考点1 代数式的书写规范及意义
1.下列各代数式符合书写规范的是( )
B
A.????×???????? B.???????????????????? C.????÷???? D.????????????????????
?
2.下列不能表示“???????? ”的意义的是( )
?
D
A.3的????倍 B.????的3倍 C.3个????相加 D.3个???? 相乘
?
3.下列代数式的意义表述错误的是( )
B
A.????????+????????表示????????与????????的和 B.????????+????????表示????与???? 和的平方
C.?????????????????表示9减去????的????????所得的差 D.????????????????表示????????除以???????? 所得的商
?
考点2 列代数式
4. 为落实“双减”政策,某校利用课后服务开展了主题为
“书香满校园”的读书活动.现需购买甲、乙两种读本共100本供学生阅读,
其中甲种读本的单价为10元,乙种读本的单价为8元,设购买甲种读本????
本,则购买乙种读本的费用为( )
?
C
A.????????元 B.?????????????????????????元 C.?????????????????????元 D.????????????????????? 元
?
5.驴肉火烧为河北省著名小吃,驴肉醇香,火烧酥脆.某店销售两种口味
的火烧,驴肉火烧12元一个,焖子火烧5元一个.为增加销量,该店推出
优惠活动,买一个驴肉火烧赠送一个焖子火烧.若嘉琪需购买???? 个驴肉火
烧和????个焖子火烧?????
C
A.????????+????????????元 B.????????+????????????元 C.????????+????????????+????元 D.????????+????????????+???? 元
?
6.[2025杭州期末]一件衣服的进价为????元,商家按进价提高????????% 标价,
则这件衣服的标价是______元.
?
????.????????
?
考点3 反比例关系
7.[2025福州期中]下列说法错误的是( )
A
A.正方形的面积与边长成反比例
B.如果????????=????,那么????和???? 成反比例
C.路程一定,时间与速度成反比例
D.分数值一定,分子和分母成正比例
?
8.当三角形的面积为?????????????????时,它的底边长????????????与底边上的高???????????? 之
间的关系式为_______,底边长????????????与底边上的高???????????? 之间为____比
例关系(填“正”或“反”).
?
????=????????????
?
反
9.(8分)[2025渭南期中]某运输队要为灾区运送一批救灾物资.如果
要一次把所有的物资全部送到,每辆车的载质量与所需车的数量见下表:
载质量/吨
2.5
4
5
10
数量/辆
40
25
20
10
(1)这批救灾物资共有_____吨;
100
(2)每辆车的载质量与所需车的数量成反比例关系吗?为什么?
解:成反比例关系.因为每辆车的载质量与所需车的数量的乘积等于100,
为定值.
考点4 求代数式的值
10.若????=????,????=????????,则代数式?????????????????+???? 的值为( )
?
D
A.????? B.1 C.7 D.13
?
11.[2025安庆期中]已知有理数????,????满足(?????????)????+????+????=???? ,则
????????= ___.
?
9
12.(8分)已知????与????????的积为1,????和????的和为?????,???? 的绝对值为4.
?
(1)求????,????,???? 的值;
?
解:依题意,得????????????=????,????+????=?????,????=???? ,
所以????=????,????=?????,????=????或?????
?
(2)求?????????+????????????? 的值.
?
解:当????=????,????=?????,????=???? 时,
?????????+?????????????=?????????+????×??????????=??????????????????=????????? ;
当????=????,????=?????,????=????? 时,
?????????+?????????????=?????????+????×?????+????=?????????????+????=????? .
?
13.(8分)[2025广州期末]如图,某长方形广场的四角
都有一块半径相同的????????圆形的草地,已知圆形的半径为???? 米,
长方形的长为????米,宽为???? 米.
?
(1)请列式表示广场空地的面积;
解:由图可得,广场空地的面积为????????????????????? 平方米.
?
(2)若长方形的长为300米,宽为200米,圆形的半径为10米,计算广
场空地的面积(计算结果保留???? ).
?
解:当长方形的长为300米,宽为200米,圆形的半径为10米时,
广场空地的面积为????????????×?????????????????×????????????=?????????????????????????????????????? 平方米.
?
14.(8分)某公司用????,????两种型号的车运输某种砂石料,其中???? 型车一
车能运输15吨这种砂石料,????型车一车能运输12吨这种砂石料.其中???? 型
车运输了????车,????型车运输了???? 车.
?
(1)若共运输了????吨这种砂石料,用含????,????的代数式表示???? ;
?
解:????=????????????+???????????? .
?
(2)若这种砂石料每吨80元,当????=????????,????=???????? 时,此公司购买砂石
料应该付款多少元?
?
解:当????=????????,????=????????时,????????????+????????????=????????×????????+????????×????????=????????????
(吨),
????????????×????????=????????????????????? (元).
答:此公司购买砂石料应该付款26 400元.
?
二、思想方法演练
思想1 数形结合思想
15.为开展劳动教育,某校想把一块周长为????????????? 的长方
形荒地按如图所示等距外扩????????? ,改造成一个长方形劳
动基地,并且用栅栏围起来,则需要栅栏( )
?
B
A.????????+???????????? B.????????+???????????? C.????????????? D.?????????????
?
思想2 从特殊到一般的思想
16.下列图形都是由同样大小的小圆圈按一定规律组成的,其中图①中
一共有6个小圆圈,图②中一共有9个小圆圈,图③中一共有12个小圆
圈,? ,按此规律排列下去,则图 中小圆圈的个数为( )
?
C
A.????????????? B.????????+???? C.????????+???? D.?????????????
?
谢谢观看!
同课章节目录
