第六章 几何图形初步【章末复习】 课件(共66张PPT)
文档属性
| 名称 | 第六章 几何图形初步【章末复习】 课件(共66张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 13.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 08:55:52 | ||
图片预览






文档简介
章末复习
第六章 几何图形初步
【2024新教材】人教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
幻灯片 1:封面
标题:第六章 几何图形初步 章末复习
副标题:梳理图形脉络,深化几何认知
背景图:由立体图形、平面图形、点线面体元素构成的抽象几何画卷,搭配柔和光影,展现几何图形的魅力与知识的系统性
幻灯片 2:目录
知识框架总览
立体图形与平面图形回顾
点、线、面、体知识整合
直线、射线、线段要点强化
角的相关知识梳理
典型例题精讲
综合练习与巩固
课堂小结
课后作业布置
幻灯片 3:知识框架总览
讲解说明:结合思维导图,介绍各板块知识在几何图形初步体系中的地位,强调知识间从基础元素到复杂图形、从概念认知到运算应用的逻辑关联,帮助学生建立整体知识架构。
幻灯片 4:立体图形与平面图形回顾
概念与区别:回顾立体图形(如正方体、长方体等)是各部分不都在同一平面内,具有长、宽、高;平面图形(如三角形、圆形等)各部分都在同一平面内,只有长和宽。通过对比表格加深印象:
| 图形类型 | 维度 | 构成 | 示例 |
|----|----|----|----|
| 立体图形 | 三维 | 由面围成 | 正方体、圆柱 |
| 平面图形 | 二维 | 由点、线组成 | 正方形、圆 |
联系与应用:说明立体图形的每个面都是平面图形,如长方体的面是长方形或正方形;生活中建筑设计、产品造型等都涉及立体与平面图形的转化应用。
幻灯片 5:点、线、面、体知识整合
元素概念:复习点是表示位置的基本元素;线由点运动形成,分直线、射线、线段;面由线运动形成,有平面和曲面;体由面围成。
动态关系:通过动画演示 “点动成线、线动成面、面动成体” 的过程,如笔尖移动成线、挥舞荧光棒成面、旋转长方形成圆柱,强化动态联系认知。
幻灯片 6:直线、射线、线段要点强化
定义与特征:对比回顾直线无端点、向两方无限延伸;射线有一个端点、向一方无限延伸;线段有两个端点、可度量长度。展示对应图形加深记忆。
表示方法:梳理直线(如直线\(AB\)、直线\(l\))、射线(如射线\(OA\))、线段(如线段\(CD\)、线段\(a\))的表示规则,强调射线表示时端点字母在前的要点。
性质应用:重温 “两点确定一条直线” 的性质及在生活中的应用,如砌墙拉线;讲解线段的和差运算与中点性质,通过实例巩固。
幻灯片 7:角的相关知识梳理
角的概念:回顾角的静态(由公共端点的两条射线组成)与动态(射线绕端点旋转形成)定义,以及角的三种表示方法(三个大写字母、一个大写字母、数字或希腊字母)。
角的度量与运算:复习度、分、秒的度量单位及换算(\(1^{\circ}=60'\),\(1' = 60''\));角的比较方法(度量法、叠合法);角的和差运算及角平分线的性质(若\(OC\)平分\(\angle AOB\),则\(\angle AOC = \angle BOC = \frac{1}{2}\angle AOB\))。
余角和补角:总结余角(两角和为\(90^{\circ}\))、补角(两角和为\(180^{\circ}\))的概念;同角(等角)的余角相等、补角相等的性质及应用,通过方程解决角度计算问题的思路。
幻灯片 8:典型例题精讲 - 立体图形与平面图形
题目:将一个正方体的表面沿某些棱剪开,展开成一个平面图形,下列图形中可能是展开图的是( )
A.
B.
C.
D.
解答:根据正方体展开图的特征,分析各选项。A、B、D 选项不符合展开图规律,C 选项是 “1 - 4 - 1” 型展开图,所以选 C。
思路:讲解正方体展开图的常见类型,培养学生空间想象能力和图形辨析能力。
幻灯片 9:典型例题精讲 - 直线、射线、线段
题目:已知线段\(AB = 8cm\),在直线\(AB\)上取一点\(C\),使\(BC = 3cm\),求线段\(AC\)的长度。
解答:分两种情况,当点\(C\)在线段\(AB\)上时,\(AC = AB - BC = 8 - 3 = 5cm\);当点\(C\)在线段\(AB\)的延长线上时,\(AC = AB + BC = 8 + 3 = 11cm\)。
思路:强调分类讨论思想,根据点\(C\)的位置不同进行分析,避免漏解。
幻灯片 10:典型例题精讲 - 角
题目:一个角的补角比它的余角的\(3\)倍还多\(10^{\circ}\),求这个角的度数。
解答:设这个角的度数为\(x^{\circ}\),则它的补角为\((180 - x)^{\circ}\),余角为\((90 - x)^{\circ}\)。根据题意列方程\(180 - x = 3(90 - x) + 10\),解方程:\(
\begin{align*}
180 - x &= 270 - 3x + 10\\
- x + 3x &= 270 + 10 - 180\\
2x &= 100\\
x &= 50
\end{align*}
\)
所以这个角的度数是\(50^{\circ}\)。
思路:引导学生利用余角和补角的关系设未知数、列方程,体现方程思想在角度问题中的应用。
幻灯片 11:综合练习与巩固
题目展示:
下列图形中,属于立体图形的是( )
A. 三角形 B. 圆 C. 圆柱 D. 梯形
已知\(\angle A = 35^{\circ}15'\),则\(\angle A\)的余角为______。
如图,点\(C\)是线段\(AB\)上一点,\(AC < CB\),\(M\)、\(N\)分别是\(AB\)、\(CB\)的中点,\(AC = 8cm\),\(NB = 5cm\),求线段\(MN\)的长度。
互动环节:学生独立完成练习,教师巡视指导,选取学生上台展示解题过程,针对共性问题和易错点集中讲解,引导学生互评,加深理解。
幻灯片 12:课堂小结
知识总结:再次梳理几何图形初步的核心知识,从图形分类到基本元素,从线的性质到角的运算,强化知识体系。
方法归纳:总结分类讨论、方程思想、空间想象等解题方法,鼓励学生在解决几何问题时灵活运用。
学习建议:建议学生多观察生活中的几何图形,通过画图、制作模型等方式提升空间思维能力,加强练习巩固知识。
幻灯片 13:课后作业布置
基础作业:
画出一个三棱柱的立体图形和它的展开图。
已知\(\angle\alpha = 62^{\circ}\),求\(\angle\alpha\)的补角与余角的差。
已知线段\(AD = 6cm\),线段\(AC = BD = 4cm\),\(E\)、\(F\)分别是线段\(AB\)、\(CD\)的中点,求线段\(EF\)的长度。
拓展作业:以 “几何图形在生活中的应用” 为主题,收集图片、资料,制作一份手抄报,展示几何图形在建筑、艺术、科技等领域的应用实例,并简要分析其中的几何原理。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
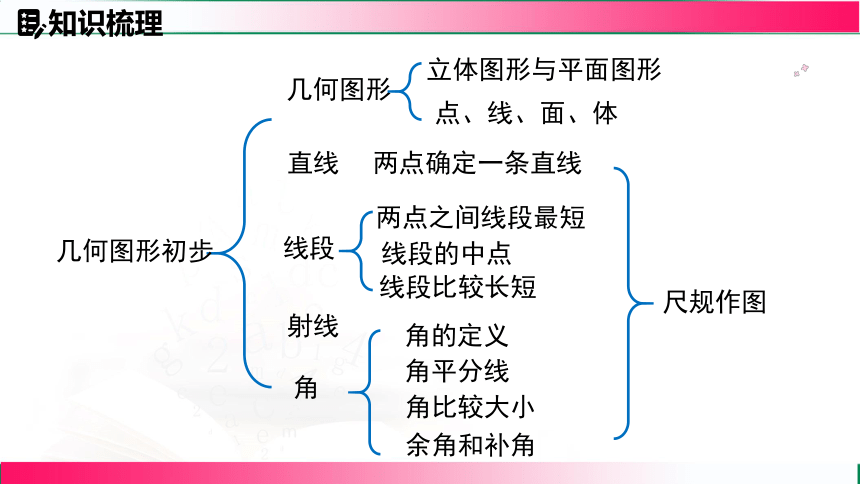
知识梳理
几何图形初步
直线
线段
线段的中点
角的定义
两点之间线段最短
射线
角
角平分线
两点确定一条直线
线段比较长短
角比较大小
尺规作图
余角和补角
几何图形
点、线、面、体
立体图形与平面图形
知识回顾
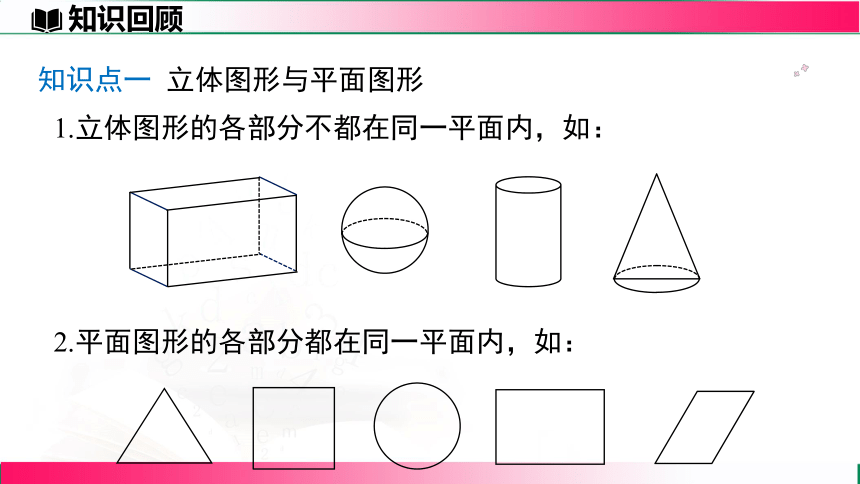
知识点一 立体图形与平面图形
1.立体图形的各部分不都在同一平面内,如:
2.平面图形的各部分都在同一平面内,如:
知识回顾
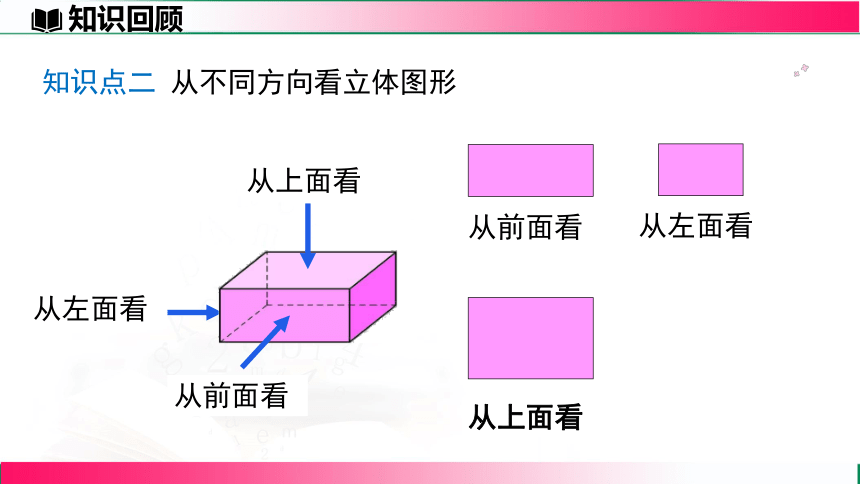
知识点二 从不同方向看立体图形
从上面看
从前面看
从左面看
从上面看
从左面看
从前面看
知识回顾
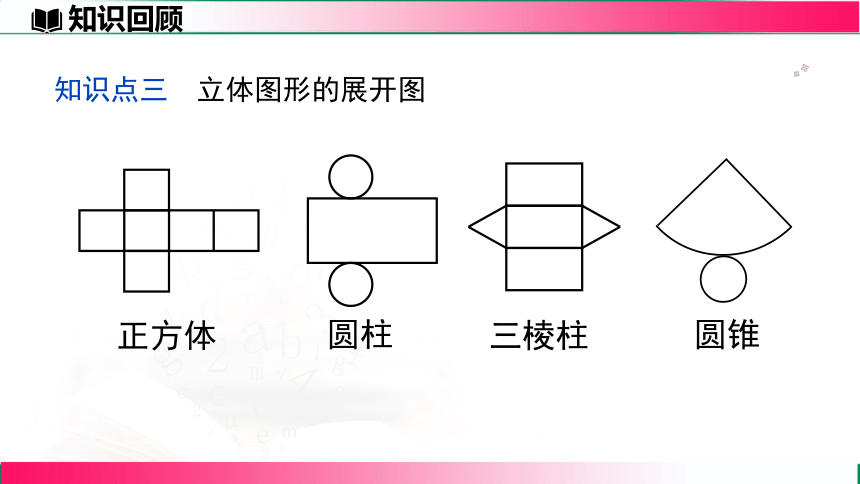
知识点三 立体图形的展开图
正方体
圆柱
三棱柱
圆锥
知识回顾
知识点四 点、线、面、体之间的联系
1.体是由面围成,面与面相交成线,线与线相交成点;
2.点动成线、线动成面、面动成体.
知识回顾
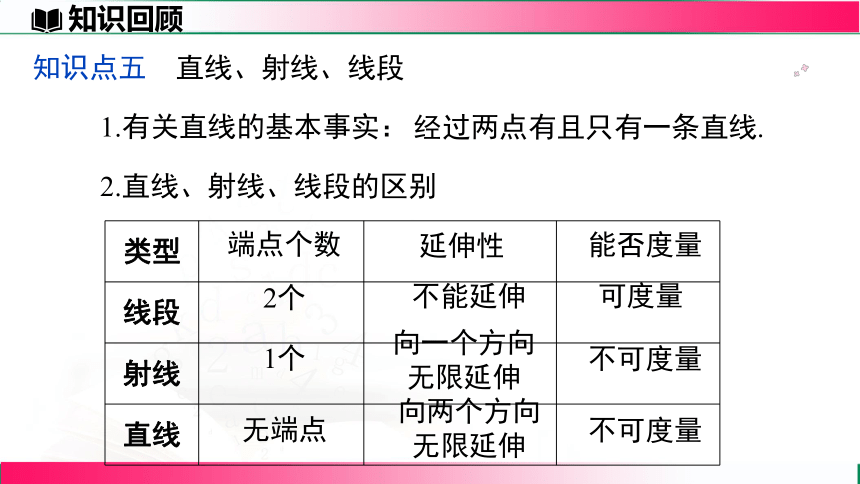
知识点五 直线、射线、线段
1.有关直线的基本事实:
经过两点有且只有一条直线.
2.直线、射线、线段的区别
类型
线段
射线
直线
端点个数
2个
不能延伸
延伸性
能否度量
可度量
1个
向一个方向
无限延伸
不可度量
无端点
向两个方向
无限延伸
不可度量
知识回顾
4.有关线段的基本事实:
两点之间,线段最短.
3.线段的中点
因为C是线段AB的中点,
所以AC=BC= AB,AB=2AC=2BC.
A
C
B
5.连接两点的线段的长度,叫作这两点间的距离.
几何语言:
知识点五 直线、射线、线段
知识回顾
知识点六 角
1.角的定义
(1)有公共端点的两条射线组成的图形,叫作角;
(2)角也可以看作由一条射线绕着它的端点旋转而形成的图形.
2.角的度量
度、分、秒的互化:
1°=60′,1′=60″
知识回顾
知识点六 角
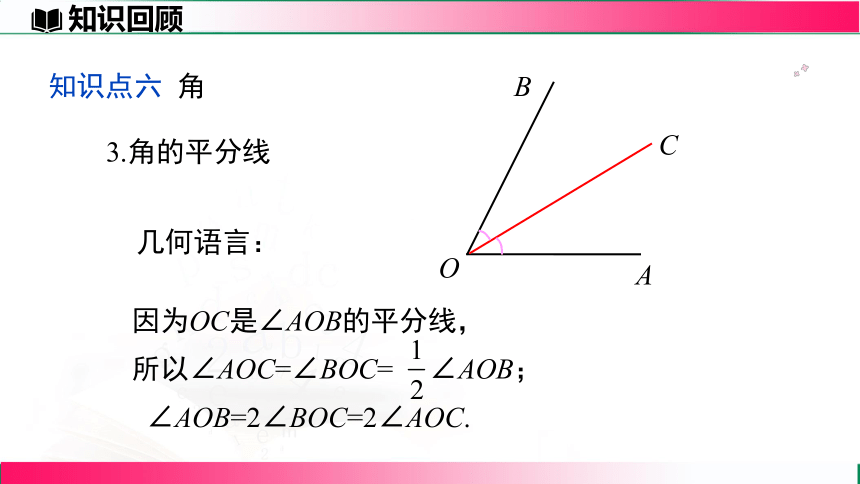
3.角的平分线
O
B
A
C
几何语言:
因为OC是∠AOB的平分线,
所以∠AOC=∠BOC= ∠AOB;
∠AOB=2∠BOC=2∠AOC.
知识回顾
知识点七 余角和补角
(1)定义
①如果两个角的和等于90°(直角),就说这两个角互为余角(简称这两个角互余).
②如果两个角的和等于180°(平角),就说这两个角互为补角(简称这两个角互补 ).
(2)性质
①同角 (等角)的余角相等.
②同角 (等角)的补角相等.
重难剖析
1.根据下列多面体的平面展开图,填写多面体的名称.
(1)_______,(2)_______,(3)________.
长方体
三棱柱
三棱锥
(1) (2) (3)
重难剖析
2 .将下面的平面图形绕轴旋转一周,得到的立体图形是( )
C
旋转轴
A B C D
重难剖析
3.如图,在平整的地面上,用若干个棱长完全相同的小正方体堆成一个几何体.
请画出这个几何体从前面、左面、上面看到的形状图.
从前面看
从左面看
从上面看
解:如图所示.
重难剖析
4.下列叙述正确的是( A )
A.线段AB可表示为线段BA
B.射线CD可表示为射线DC
C.直线最长,线段最短
D.射线是直线长度的一半
A
重难剖析
5.如图,一共有? 1条直线,是? 直线A C;能用字母表示的射线有? 7 条,它们分别是射线 DA,DC,BA,B C,DB, AC ,其中在同一条直线上的射线是射线? D ADDC , .
1
7
DA,DC,BA,BC,DB,AC(或AD),CA(或CD)
DA,DC,AC(或AD),CA(或CD)
直线AC(或直线AD,或直线CD)
重难剖析
6.如图,线段AB=32 cm,点C在AB上,且AC∶CB=5∶3,点D是AC的中点,点O是AB的中点,求DB与OC的长.
分析:从图上可以看出DB=AB-AD,
而D是AC的中点,所以AD= 12AC,
结合AC∶CB=5∶3,AB=32 cm,
故AC和BC可求,OC=OB-BC=12AB-BC.
?
重难剖析
解:因为AC∶CB=5∶3,AC+CB=AB,
所以AC=55+3AB=58×32= 20 (cm),
BC=35+3AB=38×32=12 (cm).
因为D是AC的中点,所以AD=12AC=10 cm,
所以DB=AB-AD=32-10=22(cm).
?
重难剖析
因为O是AB的中点,
所以OB=12AB=16 cm,
所以OC=OB-BC=16-12=4(cm),
所以DB=22 cm,OC=4 cm.
?
重难剖析
7.下午2时15分到5时30分,时钟的时针转过的度数为______.
分析:时钟被分成12个大格,相当于把圆分成12等份,
每一等份等于30°.
分针转360°时,时针转一格,即30°.
从2时15分到5时30分,时针走了(5.5-2.25)格,
即30°×(5.5-2.25)=97.5°.
97.5°
重难剖析
8.如图,∠AOB=∠COD=90° ,∠BOC=42° ,则∠AOD=( )
A.48° B.148°
C.138° D.128°
分析:由图可知∠AOB,∠BOC,∠COD,∠AOD组成一个周角,
所以∠AOD=360°-∠AOB-∠COD-∠BOC=138°.
故选C.
C
重难剖析
9.如图,将一副三角尺按下列位置摆放,使∠α和∠β互余的摆放方式是( )
A. B.
C. D.
A
∠α与∠β互余
∠α =∠β
∠α =∠β
∠α与∠β互补
重难剖析
10. 如图,直线AB,CD相交于点O,OA平分∠EOC.
(1) 若∠EOC=70°,求∠BOD的度数;
所以∠AOC =12∠EOC =12×70°=35°.
?
解:(1)因为直线AB,CD相交于点O,
所以∠AOC=∠BOD.
因为OA平分∠EOC,
所以∠BOD =∠AOC =35°.
O
A
C
B
D
E
重难剖析
(2) 若∠EOC∶ ∠EOD=2∶3,求∠BOD的度数.
解:(2)设∠EOC=2x°,∠EOD=3x°,
由∠EOC+∠EOD=180°,
得2x+3x =180,解得x =36.
所以∠EOC = 2x°=72°,
所以∠AOC=12∠EOC=12×72°=36°,
所以∠BOD=∠AOC=36°.
?
O
A
C
B
D
E
重难剖析
11.一只蚂蚁从 O 点出发,沿东北方向爬行 2.5 cm,碰到障碍物 B 后,折向北偏西60°方向爬行3 cm到 C点. 画出蚂蚁的爬行路线.
北
O
B
2.5 cm
C
3 cm
60°
45°
解:如图所示.
能力提升
1.将下图所示表面带有图案的正方体沿某些棱展开后,得到的图形是( )
A.
B.
C.
D.
C
能力提升
2.用小立方块搭一个几何体,使得它从前面看和从上面看得到的图,如图所示.
这样的几何体只有一种吗?它最少需要多少个小立方块?最多需要多少个小立方块?
从前面看
从上面看
能力提升
2.用小立方块搭一个几何体,使得它从前面看和从上面看得到的图,如图所示.
这样的几何体只有一种吗?它最少需要多少个小立方块?最多需要多少个小立方块?
从前面看
从上面看
1
1
1
1
1
3
2
最少摆法示意图(不唯一)
能力提升
2.用小立方块搭一个几何体,使得它从前面看和从上面看得到的图,如图所示.
这样的几何体只有一种吗?它最少需要多少个小立方块?最多需要多少个小立方块?
从前面看
从上面看
3
3
3
2
2
2
1
最多摆法示意图
能力提升
最少摆法(不唯一)所需小立方块个数:3+2+1+1+1+1+1=
10(个).
1
1
1
1
1
3
2
3
3
3
2
2
2
1
最多摆法所需小立方块个数:3+3+3+2+2+2+1=16 (个).
解:如图所示.
能力提升
解:(1)因为C,D分别是线段OA,OB的中点,
所以OC=12AO,OD=12BO.
所以CD=OC+OD=12?(OA+OB)=12AB=12a.
?
3.如图,已知线段AB=a,点O是线段AB上的动点,且不与点A,B重合,点C,D分别是线段OA,OB的中点.
(1)求线段CD的长.
(2)当点O在线段AB的延长线上时,其他条件不变,请画出图形,并求出 CD的长;比较(1)(2)的结果,你发现了什么规律?
A C O D B
能力提升
解:(2)当点O在线段AB的延长线上时,如图所示.
因为C,D分别是线段OA,OB的中点,
所以OC=12OA,OD=12OB,
所以CD=OC-OD=12(OA-OB)=12AB=12a.
比较(1)(2)的结果发现,线段DC的长都等于线段AB的一半.
?
A C B D O
能力提升
双中点线段长度计算规律
(1)线段上的一点把线段分成两条线段,这两条线段的中点间的距离等于原线段长度的一半;
(2)线段延长线上的一点和原线段的两个端点构成两条线段,这两条线段的中点间的距离等于原线段长度的一半.
一、核心考点巩固
考点1 立体图形与平面图形
1.下列几何体中,是棱锥的为( )
C
A. B. C. D.
2.下雨时汽车的雨刷器会把玻璃上的雨水刷干净,运用数学知识解释这
一现象为__________.
线动成面
考点2 展开与折叠、从不同方向看立体图形
3.[2024河南中考]信阳毛尖是中国十大名茶之一.如图是信阳毛尖茶叶
的包装盒,从前面看到的平面图形为( )
A
A. B. C. D.
4.下列图形中,为四棱柱的侧面展开图的是( )
A
A. B. C. D.
5.[2024宜宾中考]如图是正方体的表面展开图,将
其折叠成正方体后,距顶点???? 最远的点是( )
?
B
A.????点 B.????点 C.????点 D.???? 点
?
考点3 直线、射线、线段
6.[2025上海期末]如图,下列说法正确的是( )
D
A.直线????????和直线???????? 不是同一条直线
B.点????是直线???????? 的一个端点
C.射线????????和射线???????? 不是同一条射线
D.点????在线段???????? 上
?
7. 生活中,有下列两个现象(如图),对于这两个现象
的解释,正确的是( )
D
A.均用两点之间线段最短来解释
B.均用两点确定一条直线来解释
C.现象1用两点之间线段最短来解释,现象2用两点确定一条直线来解释
D.现象1用两点确定一条直线来解释,现象2用两点之间线段最短来解释
8.(12分)如图,在同一个平面内有四个点,请用直尺
和圆规按下列要求作图(不写作图步骤,保留作图痕
迹):
(1)作射线???????? ;
?
解:射线???????? 如图所示.
?
(2)作直线????????与直线????????相交于点???? ;
?
解:直线????????,直线????????,点???? 如图所示.
?
(3)在射线????????上作线段????????′,使线段????????′与线段???????? 相等.
?
解:线段????????′ 如图所示.
?
考点4 线段的计算
9.[2025金华期末]如图,在操作课上,同学们按老师的要求操作:①
作射线????????;②在射线????????上顺次截取????????=????????=??????????????;③在射线????????
上截取????????=?????????????;④在线段????????上截取????????=????.?????????????,发现点???? 在线段
????????上.由操作可知,线段????????= ( )
?
C
A.????.????????????? B.????????????? C.????.????????????? D.?????????????
?
10.如图,已知线段????????=????????,延长线段????????至点????,使得????????=???????????? ,若
点????在线段????????上,且????????=????,则线段???????? 的长是( )
?
B
A.5 B.7 C.8 D.12
11.(8分)已知点????在线段????????上,点????在线段???????? 上.
?
(1)如图①,若????????=?????????????,????????=?????????????,????为线段???????? 的中点,求线
段???????? 的长度;
?
解:因为????????=?????????????,????????=????????????? ,
所以????????=????????+????????=????+????=???????????????? .
因为????为线段???????? 的中点,
所以????????=????????????????=????????×????????=???????????? ,
所以????????=?????????????????=?????????=???????????? .
?
(2)如图②,若????????=????????????????=????????????????,????为线段????????的中点,????????=????????????? ,
求线段???????? 的长度.
?
解:设????????=????????????? ,
因为????????=????????????????=???????????????? ,
所以????????=????????????=?????????????????,????????=????????????=????????????????? ,
所以????????=?????????????????=?????????????=????????(????????) ,
?
所以????????=????????+????????=????????+????????=????????(????????) .
因为????为线段???????? 的中点,
所以????????=????????????????=????????×????????=????????(????????) ,
所以????????=????????+????????=????????+????????=????????(????????) .
又因为????????=????????????? ,
所以????????=???? ,
解得????=???? ,
所以????????=????????=????×????=???????????????? .
?
考点5 角及角度的有关计算
12.[教材P?????????????练习T?????(????)变式]若∠????=?????????????????′,∠????=?????????????????′????????″ ,
∠????=????????.????????? ,则( )
?
A
A.∠????>∠????>∠???? B.∠????>∠????>∠????
C.∠????>∠????>∠???? D.∠????>∠????>∠????
?
(第13题)
13.[2025台州路桥区期末]如图,在灯塔???? 处测得轮船
????位于北偏西????????? 方向上,轮船????位于南偏东????????? 方向
上,轮船????在∠????????????的平分线上,则在灯塔???? 处观测轮船
???? 的方向为( )
?
C
A.南偏东????????? B.南偏东????????? C.北偏东????????? D.北偏东?????????
?
(第14题)
14.[2025保定期末]如图,将一副三角尺????????? 角和?????????
角的顶点????叠放在一起,将三角尺????????????绕点???? 转动,在转
动过程中三角尺????????????的边????????始终在∠???????????? 的内部.对于下
列结论,判断正确的是( )
?
A
结论Ⅰ:∠?????????????∠???????????? 的值保持不变;
结论Ⅱ:∠????????????+∠???????????? 的值保持不变
?
A.Ⅰ和Ⅱ都对 B.Ⅰ和Ⅱ都不对 C.Ⅰ不对Ⅱ对 D.Ⅰ对Ⅱ不对
15.(8分)如图,????????是∠????????????的平分线,????????是∠???????????? 的平分线.
?
(1)如果∠????????????=????????? ,∠????????????=????????? ,则∠???????????? 的度
数为_____;
?
?????????
?
(2)如果∠????????????=????????? ,求∠???????????? 的度数.
?
解:因为????????是∠????????????的平分线,????????是∠???????????? 的平分线,
所以∠????????????=????∠????????????,∠????????????=????∠???????????? .
所以∠????????????=∠????????????+∠????????????=????(∠????????????+∠????????????)=????∠????????????=????????????? .
?
考点6 余角和补角
16.[2025长沙望城区期末]一个角的补角比这个角的余角的3倍少????????? ,
这个角的度数是( )
?
B
A.????????? B.????????? C.????????? D.?????????
?
17.如图,用量角器度量几个角的度数,下列结论正确
的有( )
B
①∠????????????=????????? ;
②∠????????????与∠???????????? 互补;
③∠????????????=∠???????????? ;
④∠????????????是∠???????????? 的余角;
⑤????????平分∠???????????? .
?
A.1个 B.2个 C.3个 D.4个
18.(8分)[2025武汉青山区期末]如图,∠????????????=∠????????????=????????? ,射
线????????平分∠???????????? .
?
(1)①图中与∠???????????? 互余的角有_______________;
②若∠????????????=???? ,则∠????????????=__________(用含???? 的代数式表示);
?
∠????????????,∠????????????
?
??????????????????
?
(2)若∠????????????:∠????????????=????:????,求∠???????????? 的度数.
?
解:设∠????????????=???????? ,
因为∠????????????:∠????????????=????:???? ,
所以∠????????????=???????? .
因为????????平分∠???????????? ,
所以∠????????????=???????? .
?
因为∠????????????=????????? ,
所以∠????????????+∠????????????=????????? ,
所以????????+????????=????????=????????? ,所以????=????????? ,
所以∠????????????=????????=????????? ,
所以∠????????????=∠????????????+∠????????????=?????????+?????????=????????????? .
?
二、思想方法演练
思想1 分类讨论思想
19.已知点????在直线????????上,????????=?????????????,????????=?????????????????,点????,???? 分别为
????????,????????的中点,则线段???????? 的长为_____________.
?
??????????????或?????????????
?
20. 如图①,已知????????是∠???????????? 内部的一条射线,图中有三
个角:∠????????????,∠????????????和∠???????????? ,当其中一个角是另一个角的两倍时,称
射线????????为∠????????????的“巧分线”.如图②,如果∠????????????=????????? ,????????是∠????????????
的“巧分线”,则∠????????????= _________________.
?
????????? 或????????? 或?????????
?
思想2 方程思想
21.(8分)如图,线段????????=????????????????=????????????????,点????,????分别是线段????????,????????
的中点,????????=?????????????????,求线段???????? 的长.
?
解:因为????????=????????????????=???????????????? ,
所以设????????=????????????? ,
则????????=?????????????????,????????=????????????????? .
所以易知????????=????????????????? .
又因为点????,????分别是线段????????,????????的中点,所以????????=????????????????=????????????????? ,
????????=????????????????=????????????????????? .
又因为????????=?????????????????,??????????????????????????=????????,所以??????????????????????????????=???????? ,
解得????=????.所以????????=????????????????? .
?
思想3 整体思想
22.(8分)将两块三角尺按如图方式摆放,其中∠????????????=????????? ,
∠????????????=????????? ,作????????平分∠????????????,????????平分∠???????????? .
?
(1)当∠????????????=????????? 时,∠????????????= _______;
?
????????.?????
?
(2)当∠????????????在∠????????????内转动时,∠???????????? 的度数是否保持不变?请说明
理由.
?
解:当∠????????????在∠????????????内转动时,∠???????????? 的度数保持不变.理由如下:
因为∠????????????=????????? ,∠????????????=????????? ,
所以∠????????????+∠????????????=???????????????????=????????? .
因为????????平分∠????????????,????????平分∠???????????? ,
所以∠????????????=????????∠????????????,∠????????????=????????∠???????????? ,
?
所以∠????????????+∠????????????=????????∠????????????+????????∠????????????=????????∠????????????+∠????????????=????????×?????????=????????.????? ,
?
所以∠????????????=∠????????????+∠????????????+∠????????????=?????????+????????.?????=????????.????? .
所以∠???????????? 的度数保持不变.
?
谢谢观看!
第六章 几何图形初步
【2024新教材】人教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
幻灯片 1:封面
标题:第六章 几何图形初步 章末复习
副标题:梳理图形脉络,深化几何认知
背景图:由立体图形、平面图形、点线面体元素构成的抽象几何画卷,搭配柔和光影,展现几何图形的魅力与知识的系统性
幻灯片 2:目录
知识框架总览
立体图形与平面图形回顾
点、线、面、体知识整合
直线、射线、线段要点强化
角的相关知识梳理
典型例题精讲
综合练习与巩固
课堂小结
课后作业布置
幻灯片 3:知识框架总览
讲解说明:结合思维导图,介绍各板块知识在几何图形初步体系中的地位,强调知识间从基础元素到复杂图形、从概念认知到运算应用的逻辑关联,帮助学生建立整体知识架构。
幻灯片 4:立体图形与平面图形回顾
概念与区别:回顾立体图形(如正方体、长方体等)是各部分不都在同一平面内,具有长、宽、高;平面图形(如三角形、圆形等)各部分都在同一平面内,只有长和宽。通过对比表格加深印象:
| 图形类型 | 维度 | 构成 | 示例 |
|----|----|----|----|
| 立体图形 | 三维 | 由面围成 | 正方体、圆柱 |
| 平面图形 | 二维 | 由点、线组成 | 正方形、圆 |
联系与应用:说明立体图形的每个面都是平面图形,如长方体的面是长方形或正方形;生活中建筑设计、产品造型等都涉及立体与平面图形的转化应用。
幻灯片 5:点、线、面、体知识整合
元素概念:复习点是表示位置的基本元素;线由点运动形成,分直线、射线、线段;面由线运动形成,有平面和曲面;体由面围成。
动态关系:通过动画演示 “点动成线、线动成面、面动成体” 的过程,如笔尖移动成线、挥舞荧光棒成面、旋转长方形成圆柱,强化动态联系认知。
幻灯片 6:直线、射线、线段要点强化
定义与特征:对比回顾直线无端点、向两方无限延伸;射线有一个端点、向一方无限延伸;线段有两个端点、可度量长度。展示对应图形加深记忆。
表示方法:梳理直线(如直线\(AB\)、直线\(l\))、射线(如射线\(OA\))、线段(如线段\(CD\)、线段\(a\))的表示规则,强调射线表示时端点字母在前的要点。
性质应用:重温 “两点确定一条直线” 的性质及在生活中的应用,如砌墙拉线;讲解线段的和差运算与中点性质,通过实例巩固。
幻灯片 7:角的相关知识梳理
角的概念:回顾角的静态(由公共端点的两条射线组成)与动态(射线绕端点旋转形成)定义,以及角的三种表示方法(三个大写字母、一个大写字母、数字或希腊字母)。
角的度量与运算:复习度、分、秒的度量单位及换算(\(1^{\circ}=60'\),\(1' = 60''\));角的比较方法(度量法、叠合法);角的和差运算及角平分线的性质(若\(OC\)平分\(\angle AOB\),则\(\angle AOC = \angle BOC = \frac{1}{2}\angle AOB\))。
余角和补角:总结余角(两角和为\(90^{\circ}\))、补角(两角和为\(180^{\circ}\))的概念;同角(等角)的余角相等、补角相等的性质及应用,通过方程解决角度计算问题的思路。
幻灯片 8:典型例题精讲 - 立体图形与平面图形
题目:将一个正方体的表面沿某些棱剪开,展开成一个平面图形,下列图形中可能是展开图的是( )
A.
B.
C.
D.
解答:根据正方体展开图的特征,分析各选项。A、B、D 选项不符合展开图规律,C 选项是 “1 - 4 - 1” 型展开图,所以选 C。
思路:讲解正方体展开图的常见类型,培养学生空间想象能力和图形辨析能力。
幻灯片 9:典型例题精讲 - 直线、射线、线段
题目:已知线段\(AB = 8cm\),在直线\(AB\)上取一点\(C\),使\(BC = 3cm\),求线段\(AC\)的长度。
解答:分两种情况,当点\(C\)在线段\(AB\)上时,\(AC = AB - BC = 8 - 3 = 5cm\);当点\(C\)在线段\(AB\)的延长线上时,\(AC = AB + BC = 8 + 3 = 11cm\)。
思路:强调分类讨论思想,根据点\(C\)的位置不同进行分析,避免漏解。
幻灯片 10:典型例题精讲 - 角
题目:一个角的补角比它的余角的\(3\)倍还多\(10^{\circ}\),求这个角的度数。
解答:设这个角的度数为\(x^{\circ}\),则它的补角为\((180 - x)^{\circ}\),余角为\((90 - x)^{\circ}\)。根据题意列方程\(180 - x = 3(90 - x) + 10\),解方程:\(
\begin{align*}
180 - x &= 270 - 3x + 10\\
- x + 3x &= 270 + 10 - 180\\
2x &= 100\\
x &= 50
\end{align*}
\)
所以这个角的度数是\(50^{\circ}\)。
思路:引导学生利用余角和补角的关系设未知数、列方程,体现方程思想在角度问题中的应用。
幻灯片 11:综合练习与巩固
题目展示:
下列图形中,属于立体图形的是( )
A. 三角形 B. 圆 C. 圆柱 D. 梯形
已知\(\angle A = 35^{\circ}15'\),则\(\angle A\)的余角为______。
如图,点\(C\)是线段\(AB\)上一点,\(AC < CB\),\(M\)、\(N\)分别是\(AB\)、\(CB\)的中点,\(AC = 8cm\),\(NB = 5cm\),求线段\(MN\)的长度。
互动环节:学生独立完成练习,教师巡视指导,选取学生上台展示解题过程,针对共性问题和易错点集中讲解,引导学生互评,加深理解。
幻灯片 12:课堂小结
知识总结:再次梳理几何图形初步的核心知识,从图形分类到基本元素,从线的性质到角的运算,强化知识体系。
方法归纳:总结分类讨论、方程思想、空间想象等解题方法,鼓励学生在解决几何问题时灵活运用。
学习建议:建议学生多观察生活中的几何图形,通过画图、制作模型等方式提升空间思维能力,加强练习巩固知识。
幻灯片 13:课后作业布置
基础作业:
画出一个三棱柱的立体图形和它的展开图。
已知\(\angle\alpha = 62^{\circ}\),求\(\angle\alpha\)的补角与余角的差。
已知线段\(AD = 6cm\),线段\(AC = BD = 4cm\),\(E\)、\(F\)分别是线段\(AB\)、\(CD\)的中点,求线段\(EF\)的长度。
拓展作业:以 “几何图形在生活中的应用” 为主题,收集图片、资料,制作一份手抄报,展示几何图形在建筑、艺术、科技等领域的应用实例,并简要分析其中的几何原理。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识梳理
几何图形初步
直线
线段
线段的中点
角的定义
两点之间线段最短
射线
角
角平分线
两点确定一条直线
线段比较长短
角比较大小
尺规作图
余角和补角
几何图形
点、线、面、体
立体图形与平面图形
知识回顾
知识点一 立体图形与平面图形
1.立体图形的各部分不都在同一平面内,如:
2.平面图形的各部分都在同一平面内,如:
知识回顾
知识点二 从不同方向看立体图形
从上面看
从前面看
从左面看
从上面看
从左面看
从前面看
知识回顾
知识点三 立体图形的展开图
正方体
圆柱
三棱柱
圆锥
知识回顾
知识点四 点、线、面、体之间的联系
1.体是由面围成,面与面相交成线,线与线相交成点;
2.点动成线、线动成面、面动成体.
知识回顾
知识点五 直线、射线、线段
1.有关直线的基本事实:
经过两点有且只有一条直线.
2.直线、射线、线段的区别
类型
线段
射线
直线
端点个数
2个
不能延伸
延伸性
能否度量
可度量
1个
向一个方向
无限延伸
不可度量
无端点
向两个方向
无限延伸
不可度量
知识回顾
4.有关线段的基本事实:
两点之间,线段最短.
3.线段的中点
因为C是线段AB的中点,
所以AC=BC= AB,AB=2AC=2BC.
A
C
B
5.连接两点的线段的长度,叫作这两点间的距离.
几何语言:
知识点五 直线、射线、线段
知识回顾
知识点六 角
1.角的定义
(1)有公共端点的两条射线组成的图形,叫作角;
(2)角也可以看作由一条射线绕着它的端点旋转而形成的图形.
2.角的度量
度、分、秒的互化:
1°=60′,1′=60″
知识回顾
知识点六 角
3.角的平分线
O
B
A
C
几何语言:
因为OC是∠AOB的平分线,
所以∠AOC=∠BOC= ∠AOB;
∠AOB=2∠BOC=2∠AOC.
知识回顾
知识点七 余角和补角
(1)定义
①如果两个角的和等于90°(直角),就说这两个角互为余角(简称这两个角互余).
②如果两个角的和等于180°(平角),就说这两个角互为补角(简称这两个角互补 ).
(2)性质
①同角 (等角)的余角相等.
②同角 (等角)的补角相等.
重难剖析
1.根据下列多面体的平面展开图,填写多面体的名称.
(1)_______,(2)_______,(3)________.
长方体
三棱柱
三棱锥
(1) (2) (3)
重难剖析
2 .将下面的平面图形绕轴旋转一周,得到的立体图形是( )
C
旋转轴
A B C D
重难剖析
3.如图,在平整的地面上,用若干个棱长完全相同的小正方体堆成一个几何体.
请画出这个几何体从前面、左面、上面看到的形状图.
从前面看
从左面看
从上面看
解:如图所示.
重难剖析
4.下列叙述正确的是( A )
A.线段AB可表示为线段BA
B.射线CD可表示为射线DC
C.直线最长,线段最短
D.射线是直线长度的一半
A
重难剖析
5.如图,一共有? 1条直线,是? 直线A C;能用字母表示的射线有? 7 条,它们分别是射线 DA,DC,BA,B C,DB, AC ,其中在同一条直线上的射线是射线? D ADDC , .
1
7
DA,DC,BA,BC,DB,AC(或AD),CA(或CD)
DA,DC,AC(或AD),CA(或CD)
直线AC(或直线AD,或直线CD)
重难剖析
6.如图,线段AB=32 cm,点C在AB上,且AC∶CB=5∶3,点D是AC的中点,点O是AB的中点,求DB与OC的长.
分析:从图上可以看出DB=AB-AD,
而D是AC的中点,所以AD= 12AC,
结合AC∶CB=5∶3,AB=32 cm,
故AC和BC可求,OC=OB-BC=12AB-BC.
?
重难剖析
解:因为AC∶CB=5∶3,AC+CB=AB,
所以AC=55+3AB=58×32= 20 (cm),
BC=35+3AB=38×32=12 (cm).
因为D是AC的中点,所以AD=12AC=10 cm,
所以DB=AB-AD=32-10=22(cm).
?
重难剖析
因为O是AB的中点,
所以OB=12AB=16 cm,
所以OC=OB-BC=16-12=4(cm),
所以DB=22 cm,OC=4 cm.
?
重难剖析
7.下午2时15分到5时30分,时钟的时针转过的度数为______.
分析:时钟被分成12个大格,相当于把圆分成12等份,
每一等份等于30°.
分针转360°时,时针转一格,即30°.
从2时15分到5时30分,时针走了(5.5-2.25)格,
即30°×(5.5-2.25)=97.5°.
97.5°
重难剖析
8.如图,∠AOB=∠COD=90° ,∠BOC=42° ,则∠AOD=( )
A.48° B.148°
C.138° D.128°
分析:由图可知∠AOB,∠BOC,∠COD,∠AOD组成一个周角,
所以∠AOD=360°-∠AOB-∠COD-∠BOC=138°.
故选C.
C
重难剖析
9.如图,将一副三角尺按下列位置摆放,使∠α和∠β互余的摆放方式是( )
A. B.
C. D.
A
∠α与∠β互余
∠α =∠β
∠α =∠β
∠α与∠β互补
重难剖析
10. 如图,直线AB,CD相交于点O,OA平分∠EOC.
(1) 若∠EOC=70°,求∠BOD的度数;
所以∠AOC =12∠EOC =12×70°=35°.
?
解:(1)因为直线AB,CD相交于点O,
所以∠AOC=∠BOD.
因为OA平分∠EOC,
所以∠BOD =∠AOC =35°.
O
A
C
B
D
E
重难剖析
(2) 若∠EOC∶ ∠EOD=2∶3,求∠BOD的度数.
解:(2)设∠EOC=2x°,∠EOD=3x°,
由∠EOC+∠EOD=180°,
得2x+3x =180,解得x =36.
所以∠EOC = 2x°=72°,
所以∠AOC=12∠EOC=12×72°=36°,
所以∠BOD=∠AOC=36°.
?
O
A
C
B
D
E
重难剖析
11.一只蚂蚁从 O 点出发,沿东北方向爬行 2.5 cm,碰到障碍物 B 后,折向北偏西60°方向爬行3 cm到 C点. 画出蚂蚁的爬行路线.
北
O
B
2.5 cm
C
3 cm
60°
45°
解:如图所示.
能力提升
1.将下图所示表面带有图案的正方体沿某些棱展开后,得到的图形是( )
A.
B.
C.
D.
C
能力提升
2.用小立方块搭一个几何体,使得它从前面看和从上面看得到的图,如图所示.
这样的几何体只有一种吗?它最少需要多少个小立方块?最多需要多少个小立方块?
从前面看
从上面看
能力提升
2.用小立方块搭一个几何体,使得它从前面看和从上面看得到的图,如图所示.
这样的几何体只有一种吗?它最少需要多少个小立方块?最多需要多少个小立方块?
从前面看
从上面看
1
1
1
1
1
3
2
最少摆法示意图(不唯一)
能力提升
2.用小立方块搭一个几何体,使得它从前面看和从上面看得到的图,如图所示.
这样的几何体只有一种吗?它最少需要多少个小立方块?最多需要多少个小立方块?
从前面看
从上面看
3
3
3
2
2
2
1
最多摆法示意图
能力提升
最少摆法(不唯一)所需小立方块个数:3+2+1+1+1+1+1=
10(个).
1
1
1
1
1
3
2
3
3
3
2
2
2
1
最多摆法所需小立方块个数:3+3+3+2+2+2+1=16 (个).
解:如图所示.
能力提升
解:(1)因为C,D分别是线段OA,OB的中点,
所以OC=12AO,OD=12BO.
所以CD=OC+OD=12?(OA+OB)=12AB=12a.
?
3.如图,已知线段AB=a,点O是线段AB上的动点,且不与点A,B重合,点C,D分别是线段OA,OB的中点.
(1)求线段CD的长.
(2)当点O在线段AB的延长线上时,其他条件不变,请画出图形,并求出 CD的长;比较(1)(2)的结果,你发现了什么规律?
A C O D B
能力提升
解:(2)当点O在线段AB的延长线上时,如图所示.
因为C,D分别是线段OA,OB的中点,
所以OC=12OA,OD=12OB,
所以CD=OC-OD=12(OA-OB)=12AB=12a.
比较(1)(2)的结果发现,线段DC的长都等于线段AB的一半.
?
A C B D O
能力提升
双中点线段长度计算规律
(1)线段上的一点把线段分成两条线段,这两条线段的中点间的距离等于原线段长度的一半;
(2)线段延长线上的一点和原线段的两个端点构成两条线段,这两条线段的中点间的距离等于原线段长度的一半.
一、核心考点巩固
考点1 立体图形与平面图形
1.下列几何体中,是棱锥的为( )
C
A. B. C. D.
2.下雨时汽车的雨刷器会把玻璃上的雨水刷干净,运用数学知识解释这
一现象为__________.
线动成面
考点2 展开与折叠、从不同方向看立体图形
3.[2024河南中考]信阳毛尖是中国十大名茶之一.如图是信阳毛尖茶叶
的包装盒,从前面看到的平面图形为( )
A
A. B. C. D.
4.下列图形中,为四棱柱的侧面展开图的是( )
A
A. B. C. D.
5.[2024宜宾中考]如图是正方体的表面展开图,将
其折叠成正方体后,距顶点???? 最远的点是( )
?
B
A.????点 B.????点 C.????点 D.???? 点
?
考点3 直线、射线、线段
6.[2025上海期末]如图,下列说法正确的是( )
D
A.直线????????和直线???????? 不是同一条直线
B.点????是直线???????? 的一个端点
C.射线????????和射线???????? 不是同一条射线
D.点????在线段???????? 上
?
7. 生活中,有下列两个现象(如图),对于这两个现象
的解释,正确的是( )
D
A.均用两点之间线段最短来解释
B.均用两点确定一条直线来解释
C.现象1用两点之间线段最短来解释,现象2用两点确定一条直线来解释
D.现象1用两点确定一条直线来解释,现象2用两点之间线段最短来解释
8.(12分)如图,在同一个平面内有四个点,请用直尺
和圆规按下列要求作图(不写作图步骤,保留作图痕
迹):
(1)作射线???????? ;
?
解:射线???????? 如图所示.
?
(2)作直线????????与直线????????相交于点???? ;
?
解:直线????????,直线????????,点???? 如图所示.
?
(3)在射线????????上作线段????????′,使线段????????′与线段???????? 相等.
?
解:线段????????′ 如图所示.
?
考点4 线段的计算
9.[2025金华期末]如图,在操作课上,同学们按老师的要求操作:①
作射线????????;②在射线????????上顺次截取????????=????????=??????????????;③在射线????????
上截取????????=?????????????;④在线段????????上截取????????=????.?????????????,发现点???? 在线段
????????上.由操作可知,线段????????= ( )
?
C
A.????.????????????? B.????????????? C.????.????????????? D.?????????????
?
10.如图,已知线段????????=????????,延长线段????????至点????,使得????????=???????????? ,若
点????在线段????????上,且????????=????,则线段???????? 的长是( )
?
B
A.5 B.7 C.8 D.12
11.(8分)已知点????在线段????????上,点????在线段???????? 上.
?
(1)如图①,若????????=?????????????,????????=?????????????,????为线段???????? 的中点,求线
段???????? 的长度;
?
解:因为????????=?????????????,????????=????????????? ,
所以????????=????????+????????=????+????=???????????????? .
因为????为线段???????? 的中点,
所以????????=????????????????=????????×????????=???????????? ,
所以????????=?????????????????=?????????=???????????? .
?
(2)如图②,若????????=????????????????=????????????????,????为线段????????的中点,????????=????????????? ,
求线段???????? 的长度.
?
解:设????????=????????????? ,
因为????????=????????????????=???????????????? ,
所以????????=????????????=?????????????????,????????=????????????=????????????????? ,
所以????????=?????????????????=?????????????=????????(????????) ,
?
所以????????=????????+????????=????????+????????=????????(????????) .
因为????为线段???????? 的中点,
所以????????=????????????????=????????×????????=????????(????????) ,
所以????????=????????+????????=????????+????????=????????(????????) .
又因为????????=????????????? ,
所以????????=???? ,
解得????=???? ,
所以????????=????????=????×????=???????????????? .
?
考点5 角及角度的有关计算
12.[教材P?????????????练习T?????(????)变式]若∠????=?????????????????′,∠????=?????????????????′????????″ ,
∠????=????????.????????? ,则( )
?
A
A.∠????>∠????>∠???? B.∠????>∠????>∠????
C.∠????>∠????>∠???? D.∠????>∠????>∠????
?
(第13题)
13.[2025台州路桥区期末]如图,在灯塔???? 处测得轮船
????位于北偏西????????? 方向上,轮船????位于南偏东????????? 方向
上,轮船????在∠????????????的平分线上,则在灯塔???? 处观测轮船
???? 的方向为( )
?
C
A.南偏东????????? B.南偏东????????? C.北偏东????????? D.北偏东?????????
?
(第14题)
14.[2025保定期末]如图,将一副三角尺????????? 角和?????????
角的顶点????叠放在一起,将三角尺????????????绕点???? 转动,在转
动过程中三角尺????????????的边????????始终在∠???????????? 的内部.对于下
列结论,判断正确的是( )
?
A
结论Ⅰ:∠?????????????∠???????????? 的值保持不变;
结论Ⅱ:∠????????????+∠???????????? 的值保持不变
?
A.Ⅰ和Ⅱ都对 B.Ⅰ和Ⅱ都不对 C.Ⅰ不对Ⅱ对 D.Ⅰ对Ⅱ不对
15.(8分)如图,????????是∠????????????的平分线,????????是∠???????????? 的平分线.
?
(1)如果∠????????????=????????? ,∠????????????=????????? ,则∠???????????? 的度
数为_____;
?
?????????
?
(2)如果∠????????????=????????? ,求∠???????????? 的度数.
?
解:因为????????是∠????????????的平分线,????????是∠???????????? 的平分线,
所以∠????????????=????∠????????????,∠????????????=????∠???????????? .
所以∠????????????=∠????????????+∠????????????=????(∠????????????+∠????????????)=????∠????????????=????????????? .
?
考点6 余角和补角
16.[2025长沙望城区期末]一个角的补角比这个角的余角的3倍少????????? ,
这个角的度数是( )
?
B
A.????????? B.????????? C.????????? D.?????????
?
17.如图,用量角器度量几个角的度数,下列结论正确
的有( )
B
①∠????????????=????????? ;
②∠????????????与∠???????????? 互补;
③∠????????????=∠???????????? ;
④∠????????????是∠???????????? 的余角;
⑤????????平分∠???????????? .
?
A.1个 B.2个 C.3个 D.4个
18.(8分)[2025武汉青山区期末]如图,∠????????????=∠????????????=????????? ,射
线????????平分∠???????????? .
?
(1)①图中与∠???????????? 互余的角有_______________;
②若∠????????????=???? ,则∠????????????=__________(用含???? 的代数式表示);
?
∠????????????,∠????????????
?
??????????????????
?
(2)若∠????????????:∠????????????=????:????,求∠???????????? 的度数.
?
解:设∠????????????=???????? ,
因为∠????????????:∠????????????=????:???? ,
所以∠????????????=???????? .
因为????????平分∠???????????? ,
所以∠????????????=???????? .
?
因为∠????????????=????????? ,
所以∠????????????+∠????????????=????????? ,
所以????????+????????=????????=????????? ,所以????=????????? ,
所以∠????????????=????????=????????? ,
所以∠????????????=∠????????????+∠????????????=?????????+?????????=????????????? .
?
二、思想方法演练
思想1 分类讨论思想
19.已知点????在直线????????上,????????=?????????????,????????=?????????????????,点????,???? 分别为
????????,????????的中点,则线段???????? 的长为_____________.
?
??????????????或?????????????
?
20. 如图①,已知????????是∠???????????? 内部的一条射线,图中有三
个角:∠????????????,∠????????????和∠???????????? ,当其中一个角是另一个角的两倍时,称
射线????????为∠????????????的“巧分线”.如图②,如果∠????????????=????????? ,????????是∠????????????
的“巧分线”,则∠????????????= _________________.
?
????????? 或????????? 或?????????
?
思想2 方程思想
21.(8分)如图,线段????????=????????????????=????????????????,点????,????分别是线段????????,????????
的中点,????????=?????????????????,求线段???????? 的长.
?
解:因为????????=????????????????=???????????????? ,
所以设????????=????????????? ,
则????????=?????????????????,????????=????????????????? .
所以易知????????=????????????????? .
又因为点????,????分别是线段????????,????????的中点,所以????????=????????????????=????????????????? ,
????????=????????????????=????????????????????? .
又因为????????=?????????????????,??????????????????????????=????????,所以??????????????????????????????=???????? ,
解得????=????.所以????????=????????????????? .
?
思想3 整体思想
22.(8分)将两块三角尺按如图方式摆放,其中∠????????????=????????? ,
∠????????????=????????? ,作????????平分∠????????????,????????平分∠???????????? .
?
(1)当∠????????????=????????? 时,∠????????????= _______;
?
????????.?????
?
(2)当∠????????????在∠????????????内转动时,∠???????????? 的度数是否保持不变?请说明
理由.
?
解:当∠????????????在∠????????????内转动时,∠???????????? 的度数保持不变.理由如下:
因为∠????????????=????????? ,∠????????????=????????? ,
所以∠????????????+∠????????????=???????????????????=????????? .
因为????????平分∠????????????,????????平分∠???????????? ,
所以∠????????????=????????∠????????????,∠????????????=????????∠???????????? ,
?
所以∠????????????+∠????????????=????????∠????????????+????????∠????????????=????????∠????????????+∠????????????=????????×?????????=????????.????? ,
?
所以∠????????????=∠????????????+∠????????????+∠????????????=?????????+????????.?????=????????.????? .
所以∠???????????? 的度数保持不变.
?
谢谢观看!
同课章节目录
