第四章 整式的加减【章末复习】 课件(共37张PPT)
文档属性
| 名称 | 第四章 整式的加减【章末复习】 课件(共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 08:55:22 | ||
图片预览











文档简介
(共37张PPT)
章末复习
第四章 整式的加减
【2024新教材】人教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
第四章 整式的加减 章末复习
一、知识梳理
(一)整式的相关概念
单项式
定义:由数与字母的积组成的代数式叫做单项式,单独的一个数或者一个字母也叫做单项式。例如\(5\),\(a\),\(3xy\),\(-\frac{2}{3}x^2y\)等 。
系数:单项式中的数字因数叫做这个单项式的系数。如\(3xy\)的系数是\(3\),\(-\frac{2}{3}x^2y\)的系数是\(-\frac{2}{3}\),注意系数包括前面的符号 。
次数:一个单项式中,所有字母的指数的和叫做这个单项式的次数。对于\(3xy\),\(x\)的次数是\(1\),\(y\)的次数是\(1\),所以次数为\(1 + 1 = 2\);单独的一个非零数的次数是\(0\) 。
多项式
定义:几个单项式的和叫做多项式。在多项式中,每个单项式叫做多项式的项,其中不含字母的项叫做常数项。例如多项式\(2x^2 - 3x + 1\),它的项是\(2x^2\),\(-3x\),\(1\),\(1\)是常数项 。
次数:多项式里,次数最高项的次数,叫做这个多项式的次数。在\(2x^2 - 3x + 1\)中,\(2x^2\)的次数最高为\(2\),所以该多项式是二次三项式 。
整式:单项式与多项式统称为整式,整式的分母中不含有字母 。
(二)整式的加减运算
同类项
定义:所含字母相同,并且相同字母的指数也相同的项叫做同类项,几个常数项也是同类项。如\(5x^2y\)与\(-2x^2y\),\(3\)与\(7\) 。
判断要点:判断同类项需同时满足 “字母相同” 和 “相同字母指数相同”,与系数和字母顺序无关 。
合并同类项
定义:把多项式中的同类项合并成一项叫做合并同类项。
法则:同类项的系数相加,所得结果作为系数,字母和字母的指数不变。例如\(3x^2 + 5x^2 = (3 + 5)x^2 = 8x^2\) 。
去括号法则
当括号前是 “\(+\)” 号时,把括号和它前面的 “\(+\)” 号去掉后,原括号里各项的符号都不改变,如\(+(a - b + c)=a - b + c\) 。
当括号前是 “\(-\)” 号时,把括号和它前面的 “\(-\)” 号去掉后,原括号里各项的符号都要改变,如\(-(a + b - c)= -a - b + c\) 。
整式加减的法则与步骤
法则:整式的加减运算,先去括号,再合并同类项。
步骤:①若有括号,先按去括号法则去括号;②找出式子中的同类项;③根据合并同类项法则合并同类项;④检查结果是否为最简形式 。
二、典型例题讲解
(一)整式概念的理解与应用
例 1:下列式子中,哪些是单项式?哪些是多项式?哪些是整式?\(3x - 1\),\(\frac{2}{x}\),\(-5\),\(a^2 - 2ab + b^2\),\(0\),\(\frac{1}{3}xy^2\)
分析:根据单项式、多项式、整式的定义进行判断。\(\frac{2}{x}\)分母含有字母,不属于整式;\(3x - 1\),\(a^2 - 2ab + b^2\)是几个单项式的和,是多项式;\(-5\),\(0\),\(\frac{1}{3}xy^2\)是数与字母的积或单独的数、字母,是单项式;单项式和多项式都属于整式 。
解答:单项式:\(-5\),\(0\),\(\frac{1}{3}xy^2\);多项式:\(3x - 1\),\(a^2 - 2ab + b^2\);整式:\(3x - 1\),\(-5\),\(a^2 - 2ab + b^2\),\(0\),\(\frac{1}{3}xy^2\) 。
例 2:指出单项式\(-\frac{4}{3}x^2y^3\)的系数和次数。
分析:根据单项式系数和次数的定义,数字因数\(-\frac{4}{3}\)是系数,\(x\)的次数\(2\)加上\(y\)的次数\(3\),和为\(5\),即次数为\(5\) 。
解答:系数是\(-\frac{4}{3}\),次数是\(5\) 。
(二)同类项与合并同类项
例 3:判断下列各组中的两项是否为同类项
\(3x^2y\)与\(-2yx^2\)
分析:都含有字母\(x\)和\(y\),且\(x\)的次数都是\(2\),\(y\)的次数都是\(1\),字母顺序不影响同类项判断,所以是同类项 。
解答:是同类项。
\(4ab\)与\(4abc\)
分析:所含字母不同,\(4abc\)多了字母\(c\),不满足同类项定义 。
解答:不是同类项。
例 4:合并同类项\(3a^2b - 2ab^2 + 4a^2b + 3ab^2\)
分析:先找出同类项,\(3a^2b\)与\(4a^2b\)是同类项,\(-2ab^2\)与\(3ab^2\)是同类项,再根据合并同类项法则进行合并 。
解答:\(
\begin{align*}
&3a^2b - 2ab^2 + 4a^2b + 3ab^2\\
=&(3a^2b + 4a^2b)+(-2ab^2 + 3ab^2)\\
=&7a^2b + ab^2
\end{align*}
\)
(三)去括号与整式加减
例 5:先去括号,再合并同类项\((2x^2 - 3x + 1) - (x^2 + 2x - 5)\)
分析:先根据去括号法则去掉括号,括号前是 “\(-\)” 号,括号内各项符号改变;再找出同类项进行合并 。
解答:\(
\begin{align*}
&(2x^2 - 3x + 1) - (x^2 + 2x - 5)\\
=&2x^2 - 3x + 1 - x^2 - 2x + 5\\
=&(2x^2 - x^2)+(-3x - 2x)+(1 + 5)\\
=&x^2 - 5x + 6
\end{align*}
\)
例 6:已知\(A = 3x^2 - 2x + 1\),\(B = x^2 + 3x - 2\),求\(2A - 3B\)。
分析:先将\(A\)、\(B\)代入\(2A - 3B\),再去括号,最后合并同类项 。
解答:\(
\begin{align*}
2A - 3B&=2(3x^2 - 2x + 1) - 3(x^2 + 3x - 2)\\
&=6x^2 - 4x + 2 - 3x^2 - 9x + 6\\
&=(6x^2 - 3x^2)+(-4x - 9x)+(2 + 6)\\
&=3x^2 - 13x + 8
\end{align*}
\)
三、易错点剖析
(一)整式概念易错点
误认为分母含有字母的式子是整式,如\(\frac{1}{x}\)不是整式 。
混淆单项式次数与多项式次数,例如认为多项式\(2x^3 - 3x^2 + 1\)的次数是\(3 + 2 = 5\),错误,应为最高次项\(2x^3\)的次数\(3\) 。
(二)同类项与合并同类项易错点
判断同类项时,忽略 “相同字母指数相同” 条件,如把\(3x^2y\)与\(3xy^2\)误判为同类项 。
合并同类项时,系数计算错误或遗漏同类项,如\(4x^2 + 3x^2 = 7x^4\)(错误,指数应不变) 。
(三)去括号与整式加减易错点
去括号时,不注意括号前符号,导致括号内项的符号改变错误,如\(-(2x - 3y)= -2x - 3y\)(错误,\(-3y\)符号未变) 。
整式加减运算时,没有按照先去括号,再合并同类项的顺序进行,或在合并同类项时出现计算失误 。
四、课堂总结
知识回顾:全面回顾整式的相关概念、同类项与合并同类项、去括号法则以及整式加减运算的知识,梳理知识脉络,明确各知识点之间的联系 。
方法归纳:总结判断整式、同类项的方法,合并同类项、去括号以及整式加减运算的步骤和技巧,帮助学生形成系统的解题思路 。
强调注意事项:再次强调易错点,提醒学生在解题过程中仔细审题,认真计算,避免因粗心导致错误 。
五、作业布置
基础作业
下列式子中,单项式有______;多项式有______;整式有______。\(-2\),\(a\),\(\frac{1}{x}\),\(3x - 1\),\(a^2 + 2ab + b^2\),\(\frac{2}{3}xy\)
指出单项式\(-\frac{3}{2}xy^2\)的系数和次数,多项式\(3x^2 - 2x + 1\)的项和次数。
合并同类项:\(5x^2 - 3x + 2x^2 + 4x\),\(3a^2b - 2ab^2 + ab^2 - 2a^2b\) 。
先去括号,再合并同类项:\((3x^2 - 2x + 1) + (2x^2 + 3x - 5)\),\((4a^2 - 3a + 2) - (2a^2 + 5a - 1)\) 。
拓展作业
已知\(A = 2x^2 - 3xy + y^2\),\(B = -x^2 + xy - 5y^2\),求\(3A - 2B\) 。
若多项式\(2x^2 + ax - y + 6\)与\(2bx^2 - 3x + 5y - 1\)的差与字母\(x\)的取值无关,求\(a\)、\(b\)的值 。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识梳理
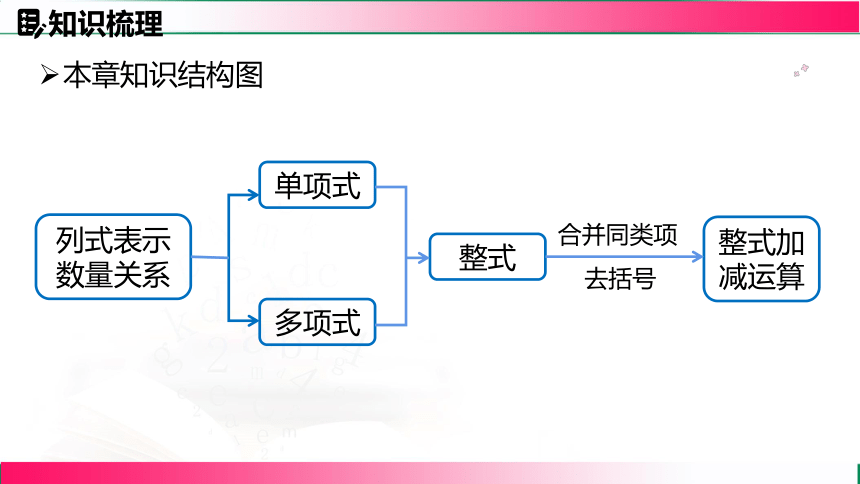
列式表示数量关系
本章知识结构图
单项式
多项式
整式
整式加减运算
合并同类项
去括号
知识梳理
整式
多项式:几个单项式的和叫作多项式.
单项式:由数或字母的积组成的代数式叫作单项式. 单独的一个数或一个字母也是单项式.
单项式的系数:单项式中的数字因数.
单项式的次数:一个单项式中,所有字母的指数的和.
多项式的项:每个单项式叫作多项式的项.
多项式的次数:次数最高项的次数.
常数项:不含字母的项.
知识梳理
合并同类项:把多项式中的同类项合并成一项,叫作合并同类项.
合并同类项法则:
合并同类项后,所得项的系数是合并前各同类项的系数的和,字母连同它的指数不变.
知识梳理
去括号法则:
1.如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
2.如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
知识梳理
整式加减计算的一般步骤:
如果有括号的先去括号,再合并同类项.
求整式的值的一般步骤:
先将式子化简,再代入数值进行计算.
随堂练习
1. 对于式子-7πx2yz,下列说法正确的是( )
A.它的系数为-7 B.它的次数为3
C.它的次数为5 D.它的系数为-7π
D
随堂练习
2. 多项式-3x2-6xy+1的各项分别为( )
A.-3x2,6xy,1 B.-3x2,-6xy,1
C.-3x2,-6xy,-1 D.3x2,6xy,1
B
随堂练习
解: a2b是单项式,系数为 ,次数为3;
是单项式,系数为, 次数为6;
x2+y2-1是多项式,共有x2,y2,-1三项,次数为2;
x是单项式,系数为1,次数为1;
3.下列整式中哪些是单项式?哪些是多项式?是单项式的指出系数和次数,是多项式的指出项和次数:
a2b,,x2+y2-1, x ,3x2-y+3xy3+x4-1,32t3,2x-y.
随堂练习
解:3x2-y+3xy3 +x4-1是多项式,有3x2,-y,3xy3,x4,-1五项,次数为4;
32t3是单项式,系数为32,次数为3;
2x-y是多项式,有2x,-y两项,次数为1.
3.下列整式中哪些是单项式?哪些是多项式?是单项式的指出系数和次数,是多项式的指出项和次数:
a2b,,x2+y2-1, x ,3x2-y+3xy3+x4-1,32t3,2x-y.
随堂练习
4. 先化简,再求值.
5x2+4-3x2-5x-2x2-5+6x,其中x =-3.
解:5x2+4-3x2-5x-2x2-5+6x
= (5-3-2)x2+(-5+6)x-1
= x-1.
当x = -3时,原式 =-3-1 =-4.
随堂练习
5. 先化简,再求值.
(-x2+5+4x)+(5x-4+2x2),其中x=-2.
解:(-x2+5+4x)+(5x-4+2x2)
=-x2+5+4x+5x-4+2x2
=x2+9x+1.
当x=-2时,原式=(-2)2+9×(-2)+1=-13.
随堂练习
6. 一种商品每件成本为a元,原来按成本增加22%定出价格,每件售价为多少元?现在由于库存积压减价,按原价的85%出售,现售价为多少元?每件还能盈利多少元?
解:售价为a×(1+22%)= 1.22a(元).
现售价为1.22a×85% = 1.037a(元).
每件还能盈利:1.037a-a = 0.037a(元).
随堂练习
7. 有理数a,b,c在数轴上的位置如图所示,化简
|b-a|+|a+b|-|c|-|b-c|+|a+c|.
解:由题意,得b所以b-a<0,a+b<0,b-c<0,a+c>0,
所以|b-a|+|a+b|-|c|-|b-c|+|a+c|
=-(b-a)-(a+b)+c+(b-c)+(a+c)
=-b+a-a-b+c+b-c+a+c
= a-b+c.
b c 0 a
随堂练习
8. 甲地的海拔是h m,乙地比甲地高20 m,丙地比甲地低30 m,列式表示乙、丙两地的海拔,并计算这两地的高度差.
解:乙地的海拔是(h+20) m,丙地的海拔是(h-30) m;
乙、丙两地的高度差是
(h+20)-(h-30)= h+20-h+30=50(m).
随堂练习
9. 某轮船顺水航行3 h,逆水航行1.5 h,已知轮船在静水中的速度是a km/h,水流速度是y km/h,轮船共航行多少千米?
解:3(a+y)+1.5(a-y)
= 3a+3y+l.5a-1.5y
= (4.5a+1.5y)(千米).
答:轮船共航行(4.5a+1.5y)千米.
随堂练习
10. 观察下图并填表(单位:cm):
梯形个数 1 2 3 4 5 6 n
图形周长 5a 8a 11a 14a
17a
20a
(3n+2)a
a
2a
a
随堂练习
11. 如下图所示,由一些点组成形如三角形的图形,每条“边”(包括两个顶点)有 n(n>1)个点,每个图形总的点数S是多少?当n=5,7,11时,S是多少?
n=2 n=3 n=4 n=5
解:每个图形总的点数S=3n-3;
当n=5时,S=12;当n=7时,S=18;当n=11时,S=30.
一、核心考点巩固
考点1 整式的有关概念
1.下列式子:,,, ,0,其中整式的个数是( )
C
A.2 B.5 C.4 D.3
2.下列说法正确的是( )
B
A.单项式 的次数是1
B. 是三次三项式
C.单项式 的系数是2
D.,,5是多项式 的项
3.已知与是同类项,则 的值为( )
C
A.2 B. C.1 D.
考点2 整式的加减
4.若,,则 是( )
D
A. B. C. D.
5.已知为常数,, ,
若多项式不含一次项,则多项式 的常数项是( )
A
A.35 B.40 C.45 D.50
6.(4分)化简: .
解:原式
.
考点3 整式的化简求值
7.[2025杭州月考]当, 时,
的值是( )
B
A.0 B.6 C. D.9
8.若,互为相反数,则 的值为____.
9.(4分)先化简,再求值:
,其中
.
解:因为 ,
所以, ,
所以, .
原式
,
当,时,原式 .
10.(4分)有这样一道计算题:计算
的值,其中 ,
.小明同学把“”错看成“ ”,但计算结果仍正确;小颖
同学把“”错看成“ ”,计算结果也是正确的,你知道其中的
道理吗?请加以说明.
解: .
因为化简结果中不含项,所以小明同学把“”错看成“ ”,但
计算结果仍正确.因为化简结果中是“”,“1”,“ ”的平方是一样的,
所以小颖同学把“”错看成“ ”,计算结果也是正确的.
考点4 整式加减的应用
11.[2025成都期末]若一个三位数的个位数字是1,十位数字是 ,
百位数字是,把 的百位数字和十位数字互换得到一个新的三位
数,则 ____________.
12.(8分)我国出租车收费标准因地而异.甲市为:起步价(3千米及3千
米以内)6元,超过3千米后每千米为1.5元;乙市为:起步价
(3千米及3千米以内)10元,超过3千米后每千米为1.2元.
(1)在甲、乙两市乘坐出租车 千米的价差是多少元?
解:在甲市乘坐出租车千米的价钱为 元,在乙
市乘坐出租车千米的价钱为 元,故在甲、乙
两市乘坐出租车 千米的价差是
元.
(2)如果在甲、乙两市乘坐出租车的路程都为10千米,那么哪个市的
收费高些?高多少?
解:当 时,在甲市乘坐出租车的价钱为
(元),在乙市乘坐出租车的价钱为
(元).
因为 (元),
所以乙市的收费高些,高1.9元.
二、思想方法演练
思想1 数形结合思想
13.(8分)[2025保定期末]劳动技术课程是基础
教育的重要课程之一,其根本使命是全面提高未来
国民的基本劳动技术素养,培养具有技术知识、创
新思维、实践能力的一代新人.我校将利用天台劳
动基地展开一系列的劳动实践操作活动.如图所示,天台上有块长为
,宽为的长方形空地,现在将其中三面留出宽都是 的小
路,中间余下的长方形部分作为菜地.
(1)用含 的式子表示菜地的周长;
解:菜地的周长为
.
(2)当 时,求菜地的周长.
解:当时, .
答:当时,菜地的周长是 .
思想2 整体思想
14.(12分)数学中,会运用整体思想在求代数式的值时非常重要,例
如:已知 ,则代数式
,
请根据以上材料解答以下问题:
(1)若整式,求整式 的值;
解:因为 ,
所以 .
所以 .
(2)若,求 的值;
解: .
(3)当时,多项式的值是5,求当 时,多项
式 的值.
解:当时, ,
所以 .
当 时,
.
谢谢观看!
章末复习
第四章 整式的加减
【2024新教材】人教版数学 七年级上册
授课教师:********
班 级:********
时 间:********
第四章 整式的加减 章末复习
一、知识梳理
(一)整式的相关概念
单项式
定义:由数与字母的积组成的代数式叫做单项式,单独的一个数或者一个字母也叫做单项式。例如\(5\),\(a\),\(3xy\),\(-\frac{2}{3}x^2y\)等 。
系数:单项式中的数字因数叫做这个单项式的系数。如\(3xy\)的系数是\(3\),\(-\frac{2}{3}x^2y\)的系数是\(-\frac{2}{3}\),注意系数包括前面的符号 。
次数:一个单项式中,所有字母的指数的和叫做这个单项式的次数。对于\(3xy\),\(x\)的次数是\(1\),\(y\)的次数是\(1\),所以次数为\(1 + 1 = 2\);单独的一个非零数的次数是\(0\) 。
多项式
定义:几个单项式的和叫做多项式。在多项式中,每个单项式叫做多项式的项,其中不含字母的项叫做常数项。例如多项式\(2x^2 - 3x + 1\),它的项是\(2x^2\),\(-3x\),\(1\),\(1\)是常数项 。
次数:多项式里,次数最高项的次数,叫做这个多项式的次数。在\(2x^2 - 3x + 1\)中,\(2x^2\)的次数最高为\(2\),所以该多项式是二次三项式 。
整式:单项式与多项式统称为整式,整式的分母中不含有字母 。
(二)整式的加减运算
同类项
定义:所含字母相同,并且相同字母的指数也相同的项叫做同类项,几个常数项也是同类项。如\(5x^2y\)与\(-2x^2y\),\(3\)与\(7\) 。
判断要点:判断同类项需同时满足 “字母相同” 和 “相同字母指数相同”,与系数和字母顺序无关 。
合并同类项
定义:把多项式中的同类项合并成一项叫做合并同类项。
法则:同类项的系数相加,所得结果作为系数,字母和字母的指数不变。例如\(3x^2 + 5x^2 = (3 + 5)x^2 = 8x^2\) 。
去括号法则
当括号前是 “\(+\)” 号时,把括号和它前面的 “\(+\)” 号去掉后,原括号里各项的符号都不改变,如\(+(a - b + c)=a - b + c\) 。
当括号前是 “\(-\)” 号时,把括号和它前面的 “\(-\)” 号去掉后,原括号里各项的符号都要改变,如\(-(a + b - c)= -a - b + c\) 。
整式加减的法则与步骤
法则:整式的加减运算,先去括号,再合并同类项。
步骤:①若有括号,先按去括号法则去括号;②找出式子中的同类项;③根据合并同类项法则合并同类项;④检查结果是否为最简形式 。
二、典型例题讲解
(一)整式概念的理解与应用
例 1:下列式子中,哪些是单项式?哪些是多项式?哪些是整式?\(3x - 1\),\(\frac{2}{x}\),\(-5\),\(a^2 - 2ab + b^2\),\(0\),\(\frac{1}{3}xy^2\)
分析:根据单项式、多项式、整式的定义进行判断。\(\frac{2}{x}\)分母含有字母,不属于整式;\(3x - 1\),\(a^2 - 2ab + b^2\)是几个单项式的和,是多项式;\(-5\),\(0\),\(\frac{1}{3}xy^2\)是数与字母的积或单独的数、字母,是单项式;单项式和多项式都属于整式 。
解答:单项式:\(-5\),\(0\),\(\frac{1}{3}xy^2\);多项式:\(3x - 1\),\(a^2 - 2ab + b^2\);整式:\(3x - 1\),\(-5\),\(a^2 - 2ab + b^2\),\(0\),\(\frac{1}{3}xy^2\) 。
例 2:指出单项式\(-\frac{4}{3}x^2y^3\)的系数和次数。
分析:根据单项式系数和次数的定义,数字因数\(-\frac{4}{3}\)是系数,\(x\)的次数\(2\)加上\(y\)的次数\(3\),和为\(5\),即次数为\(5\) 。
解答:系数是\(-\frac{4}{3}\),次数是\(5\) 。
(二)同类项与合并同类项
例 3:判断下列各组中的两项是否为同类项
\(3x^2y\)与\(-2yx^2\)
分析:都含有字母\(x\)和\(y\),且\(x\)的次数都是\(2\),\(y\)的次数都是\(1\),字母顺序不影响同类项判断,所以是同类项 。
解答:是同类项。
\(4ab\)与\(4abc\)
分析:所含字母不同,\(4abc\)多了字母\(c\),不满足同类项定义 。
解答:不是同类项。
例 4:合并同类项\(3a^2b - 2ab^2 + 4a^2b + 3ab^2\)
分析:先找出同类项,\(3a^2b\)与\(4a^2b\)是同类项,\(-2ab^2\)与\(3ab^2\)是同类项,再根据合并同类项法则进行合并 。
解答:\(
\begin{align*}
&3a^2b - 2ab^2 + 4a^2b + 3ab^2\\
=&(3a^2b + 4a^2b)+(-2ab^2 + 3ab^2)\\
=&7a^2b + ab^2
\end{align*}
\)
(三)去括号与整式加减
例 5:先去括号,再合并同类项\((2x^2 - 3x + 1) - (x^2 + 2x - 5)\)
分析:先根据去括号法则去掉括号,括号前是 “\(-\)” 号,括号内各项符号改变;再找出同类项进行合并 。
解答:\(
\begin{align*}
&(2x^2 - 3x + 1) - (x^2 + 2x - 5)\\
=&2x^2 - 3x + 1 - x^2 - 2x + 5\\
=&(2x^2 - x^2)+(-3x - 2x)+(1 + 5)\\
=&x^2 - 5x + 6
\end{align*}
\)
例 6:已知\(A = 3x^2 - 2x + 1\),\(B = x^2 + 3x - 2\),求\(2A - 3B\)。
分析:先将\(A\)、\(B\)代入\(2A - 3B\),再去括号,最后合并同类项 。
解答:\(
\begin{align*}
2A - 3B&=2(3x^2 - 2x + 1) - 3(x^2 + 3x - 2)\\
&=6x^2 - 4x + 2 - 3x^2 - 9x + 6\\
&=(6x^2 - 3x^2)+(-4x - 9x)+(2 + 6)\\
&=3x^2 - 13x + 8
\end{align*}
\)
三、易错点剖析
(一)整式概念易错点
误认为分母含有字母的式子是整式,如\(\frac{1}{x}\)不是整式 。
混淆单项式次数与多项式次数,例如认为多项式\(2x^3 - 3x^2 + 1\)的次数是\(3 + 2 = 5\),错误,应为最高次项\(2x^3\)的次数\(3\) 。
(二)同类项与合并同类项易错点
判断同类项时,忽略 “相同字母指数相同” 条件,如把\(3x^2y\)与\(3xy^2\)误判为同类项 。
合并同类项时,系数计算错误或遗漏同类项,如\(4x^2 + 3x^2 = 7x^4\)(错误,指数应不变) 。
(三)去括号与整式加减易错点
去括号时,不注意括号前符号,导致括号内项的符号改变错误,如\(-(2x - 3y)= -2x - 3y\)(错误,\(-3y\)符号未变) 。
整式加减运算时,没有按照先去括号,再合并同类项的顺序进行,或在合并同类项时出现计算失误 。
四、课堂总结
知识回顾:全面回顾整式的相关概念、同类项与合并同类项、去括号法则以及整式加减运算的知识,梳理知识脉络,明确各知识点之间的联系 。
方法归纳:总结判断整式、同类项的方法,合并同类项、去括号以及整式加减运算的步骤和技巧,帮助学生形成系统的解题思路 。
强调注意事项:再次强调易错点,提醒学生在解题过程中仔细审题,认真计算,避免因粗心导致错误 。
五、作业布置
基础作业
下列式子中,单项式有______;多项式有______;整式有______。\(-2\),\(a\),\(\frac{1}{x}\),\(3x - 1\),\(a^2 + 2ab + b^2\),\(\frac{2}{3}xy\)
指出单项式\(-\frac{3}{2}xy^2\)的系数和次数,多项式\(3x^2 - 2x + 1\)的项和次数。
合并同类项:\(5x^2 - 3x + 2x^2 + 4x\),\(3a^2b - 2ab^2 + ab^2 - 2a^2b\) 。
先去括号,再合并同类项:\((3x^2 - 2x + 1) + (2x^2 + 3x - 5)\),\((4a^2 - 3a + 2) - (2a^2 + 5a - 1)\) 。
拓展作业
已知\(A = 2x^2 - 3xy + y^2\),\(B = -x^2 + xy - 5y^2\),求\(3A - 2B\) 。
若多项式\(2x^2 + ax - y + 6\)与\(2bx^2 - 3x + 5y - 1\)的差与字母\(x\)的取值无关,求\(a\)、\(b\)的值 。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识梳理
列式表示数量关系
本章知识结构图
单项式
多项式
整式
整式加减运算
合并同类项
去括号
知识梳理
整式
多项式:几个单项式的和叫作多项式.
单项式:由数或字母的积组成的代数式叫作单项式. 单独的一个数或一个字母也是单项式.
单项式的系数:单项式中的数字因数.
单项式的次数:一个单项式中,所有字母的指数的和.
多项式的项:每个单项式叫作多项式的项.
多项式的次数:次数最高项的次数.
常数项:不含字母的项.
知识梳理
合并同类项:把多项式中的同类项合并成一项,叫作合并同类项.
合并同类项法则:
合并同类项后,所得项的系数是合并前各同类项的系数的和,字母连同它的指数不变.
知识梳理
去括号法则:
1.如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
2.如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
知识梳理
整式加减计算的一般步骤:
如果有括号的先去括号,再合并同类项.
求整式的值的一般步骤:
先将式子化简,再代入数值进行计算.
随堂练习
1. 对于式子-7πx2yz,下列说法正确的是( )
A.它的系数为-7 B.它的次数为3
C.它的次数为5 D.它的系数为-7π
D
随堂练习
2. 多项式-3x2-6xy+1的各项分别为( )
A.-3x2,6xy,1 B.-3x2,-6xy,1
C.-3x2,-6xy,-1 D.3x2,6xy,1
B
随堂练习
解: a2b是单项式,系数为 ,次数为3;
是单项式,系数为, 次数为6;
x2+y2-1是多项式,共有x2,y2,-1三项,次数为2;
x是单项式,系数为1,次数为1;
3.下列整式中哪些是单项式?哪些是多项式?是单项式的指出系数和次数,是多项式的指出项和次数:
a2b,,x2+y2-1, x ,3x2-y+3xy3+x4-1,32t3,2x-y.
随堂练习
解:3x2-y+3xy3 +x4-1是多项式,有3x2,-y,3xy3,x4,-1五项,次数为4;
32t3是单项式,系数为32,次数为3;
2x-y是多项式,有2x,-y两项,次数为1.
3.下列整式中哪些是单项式?哪些是多项式?是单项式的指出系数和次数,是多项式的指出项和次数:
a2b,,x2+y2-1, x ,3x2-y+3xy3+x4-1,32t3,2x-y.
随堂练习
4. 先化简,再求值.
5x2+4-3x2-5x-2x2-5+6x,其中x =-3.
解:5x2+4-3x2-5x-2x2-5+6x
= (5-3-2)x2+(-5+6)x-1
= x-1.
当x = -3时,原式 =-3-1 =-4.
随堂练习
5. 先化简,再求值.
(-x2+5+4x)+(5x-4+2x2),其中x=-2.
解:(-x2+5+4x)+(5x-4+2x2)
=-x2+5+4x+5x-4+2x2
=x2+9x+1.
当x=-2时,原式=(-2)2+9×(-2)+1=-13.
随堂练习
6. 一种商品每件成本为a元,原来按成本增加22%定出价格,每件售价为多少元?现在由于库存积压减价,按原价的85%出售,现售价为多少元?每件还能盈利多少元?
解:售价为a×(1+22%)= 1.22a(元).
现售价为1.22a×85% = 1.037a(元).
每件还能盈利:1.037a-a = 0.037a(元).
随堂练习
7. 有理数a,b,c在数轴上的位置如图所示,化简
|b-a|+|a+b|-|c|-|b-c|+|a+c|.
解:由题意,得b
所以|b-a|+|a+b|-|c|-|b-c|+|a+c|
=-(b-a)-(a+b)+c+(b-c)+(a+c)
=-b+a-a-b+c+b-c+a+c
= a-b+c.
b c 0 a
随堂练习
8. 甲地的海拔是h m,乙地比甲地高20 m,丙地比甲地低30 m,列式表示乙、丙两地的海拔,并计算这两地的高度差.
解:乙地的海拔是(h+20) m,丙地的海拔是(h-30) m;
乙、丙两地的高度差是
(h+20)-(h-30)= h+20-h+30=50(m).
随堂练习
9. 某轮船顺水航行3 h,逆水航行1.5 h,已知轮船在静水中的速度是a km/h,水流速度是y km/h,轮船共航行多少千米?
解:3(a+y)+1.5(a-y)
= 3a+3y+l.5a-1.5y
= (4.5a+1.5y)(千米).
答:轮船共航行(4.5a+1.5y)千米.
随堂练习
10. 观察下图并填表(单位:cm):
梯形个数 1 2 3 4 5 6 n
图形周长 5a 8a 11a 14a
17a
20a
(3n+2)a
a
2a
a
随堂练习
11. 如下图所示,由一些点组成形如三角形的图形,每条“边”(包括两个顶点)有 n(n>1)个点,每个图形总的点数S是多少?当n=5,7,11时,S是多少?
n=2 n=3 n=4 n=5
解:每个图形总的点数S=3n-3;
当n=5时,S=12;当n=7时,S=18;当n=11时,S=30.
一、核心考点巩固
考点1 整式的有关概念
1.下列式子:,,, ,0,其中整式的个数是( )
C
A.2 B.5 C.4 D.3
2.下列说法正确的是( )
B
A.单项式 的次数是1
B. 是三次三项式
C.单项式 的系数是2
D.,,5是多项式 的项
3.已知与是同类项,则 的值为( )
C
A.2 B. C.1 D.
考点2 整式的加减
4.若,,则 是( )
D
A. B. C. D.
5.已知为常数,, ,
若多项式不含一次项,则多项式 的常数项是( )
A
A.35 B.40 C.45 D.50
6.(4分)化简: .
解:原式
.
考点3 整式的化简求值
7.[2025杭州月考]当, 时,
的值是( )
B
A.0 B.6 C. D.9
8.若,互为相反数,则 的值为____.
9.(4分)先化简,再求值:
,其中
.
解:因为 ,
所以, ,
所以, .
原式
,
当,时,原式 .
10.(4分)有这样一道计算题:计算
的值,其中 ,
.小明同学把“”错看成“ ”,但计算结果仍正确;小颖
同学把“”错看成“ ”,计算结果也是正确的,你知道其中的
道理吗?请加以说明.
解: .
因为化简结果中不含项,所以小明同学把“”错看成“ ”,但
计算结果仍正确.因为化简结果中是“”,“1”,“ ”的平方是一样的,
所以小颖同学把“”错看成“ ”,计算结果也是正确的.
考点4 整式加减的应用
11.[2025成都期末]若一个三位数的个位数字是1,十位数字是 ,
百位数字是,把 的百位数字和十位数字互换得到一个新的三位
数,则 ____________.
12.(8分)我国出租车收费标准因地而异.甲市为:起步价(3千米及3千
米以内)6元,超过3千米后每千米为1.5元;乙市为:起步价
(3千米及3千米以内)10元,超过3千米后每千米为1.2元.
(1)在甲、乙两市乘坐出租车 千米的价差是多少元?
解:在甲市乘坐出租车千米的价钱为 元,在乙
市乘坐出租车千米的价钱为 元,故在甲、乙
两市乘坐出租车 千米的价差是
元.
(2)如果在甲、乙两市乘坐出租车的路程都为10千米,那么哪个市的
收费高些?高多少?
解:当 时,在甲市乘坐出租车的价钱为
(元),在乙市乘坐出租车的价钱为
(元).
因为 (元),
所以乙市的收费高些,高1.9元.
二、思想方法演练
思想1 数形结合思想
13.(8分)[2025保定期末]劳动技术课程是基础
教育的重要课程之一,其根本使命是全面提高未来
国民的基本劳动技术素养,培养具有技术知识、创
新思维、实践能力的一代新人.我校将利用天台劳
动基地展开一系列的劳动实践操作活动.如图所示,天台上有块长为
,宽为的长方形空地,现在将其中三面留出宽都是 的小
路,中间余下的长方形部分作为菜地.
(1)用含 的式子表示菜地的周长;
解:菜地的周长为
.
(2)当 时,求菜地的周长.
解:当时, .
答:当时,菜地的周长是 .
思想2 整体思想
14.(12分)数学中,会运用整体思想在求代数式的值时非常重要,例
如:已知 ,则代数式
,
请根据以上材料解答以下问题:
(1)若整式,求整式 的值;
解:因为 ,
所以 .
所以 .
(2)若,求 的值;
解: .
(3)当时,多项式的值是5,求当 时,多项
式 的值.
解:当时, ,
所以 .
当 时,
.
谢谢观看!
同课章节目录
