10.1.4 概率的基本性质 教学课件(共24张PPT)-人教A版高中数学(2019)必修二
文档属性
| 名称 | 10.1.4 概率的基本性质 教学课件(共24张PPT)-人教A版高中数学(2019)必修二 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 16:32:13 | ||
图片预览







文档简介
(共24张PPT)
10.1.4概率的基本性质
导入
2024巴黎奥运会射击项目,中国队表现惊艳,共斩获 5 金 2 银 3 铜,位居奖牌榜榜首。其中7 月 27 日,黄雨婷、盛李豪获得 10 米气步枪混合团体金牌,为中国代表团摘得巴黎奥运会第一金,这也是巴黎奥运会产生的首枚金牌。这一成绩刷新了队伍奥运会历史最佳战绩,展现出强大实力与青春风采
导入
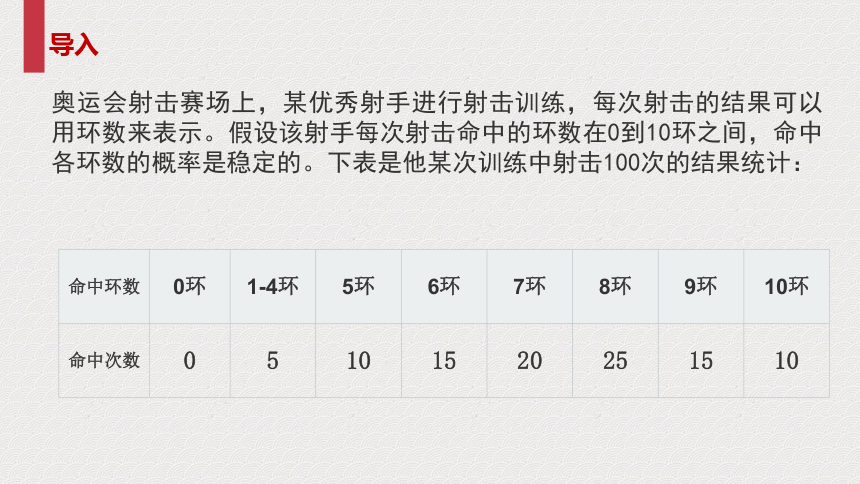
奥运会射击赛场上,某优秀射手进行射击训练,每次射击的结果可以用环数来表示。假设该射手每次射击命中的环数在0到10环之间,命中各环数的概率是稳定的。下表是他某次训练中射击100次的结果统计:
命中环数 0环 1-4环 5环 6环 7环 8环 9环 10环
命中次数 0 5 10 15 20 25 15 10
导入
环节1
环节4
环节3
环节2
思考问题:
问题1:观察命中各环数的频率,你能得到什么共同特点嘛?
问题2:命中靶子的概率是多少?命中0环的概率呢?
问题3:"命中10环"和"命中9环"这两个事件有什么关系?它们的概率和与"命中9环或10环"的概率有何联系?
问题4:"5-7环”的概率等于命中5环、6环、7环这三个事件三个概率之和
问题5:命中小于五环和命中不小于五环的概率之间有什么关系?
问题6:"命中10环"与"命中9环或10环"概率有什么关系?
问题7:写出"命中环数为6、8、10环"和"命中环数大于7“的概率,并分析两个事件的和事件、交事件概率之间的关系。
基本概念回顾
环节1
环节4
环节3
环节2
1.若A,B表示随机事件,则A∩B与A∪B也表示事件.( )
2.若两个事件是互斥事件,则这两个事件是对立事件.( )
3.若两个事件是对立事件,则这两个事件也是互斥事件.( )
4.若事件A与B是互斥事件,则在一次试验中事件A和B至少有一个发生.( )
×
×
√
√
性质1:概率的非负性
环节1
环节4
环节3
环节2
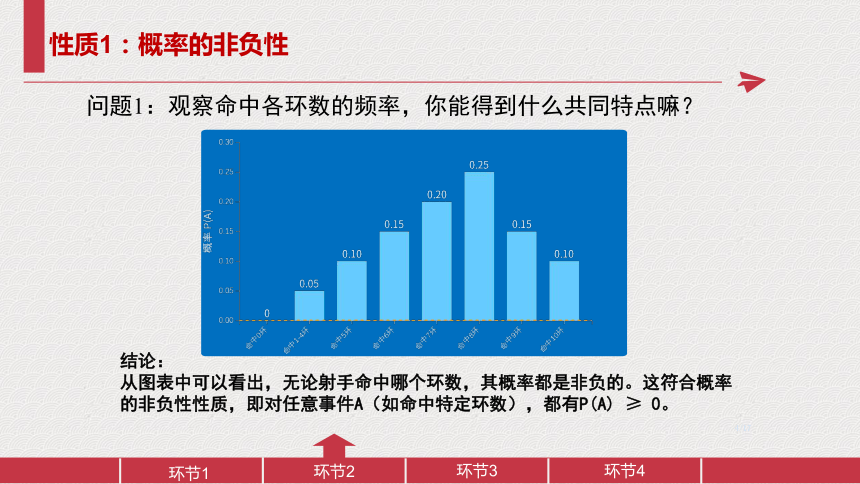
结论:
从图表中可以看出,无论射手命中哪个环数,其概率都是非负的。这符合概率的非负性性质,即对任意事件A(如命中特定环数),都有P(A) ≥ 0。
4/17
问题1:观察命中各环数的频率,你能得到什么共同特点嘛?
性质1:概率的非负性
环节1
环节4
环节3
环节2
非负性定义:
对任意事件A,都有P(A) ≥ 0
概率的非负性表示任何事件发生的可能性都不会是负数。这一性质是概率的公理基础,也是我们理解概率概念的起点。
为什么概率不能为负?
1.负概率没有实际意义,无法在现实世界中观测到
2.概率表示事件发生的可能性,可能性不可能为负
3.概率是对频率的数学抽象,频率总是非负的
性质2:概率的规范性
环节1
环节4
环节3
环节2
规范性定义:
必然事件的概率为1,不可能事件的概率为0,即 P(Ω)=1,P( )=0.
理解要点:
必然事件(全集Ω)包含所有可能结果,其概率为1
不可能事件(空集 )不包含任何结果,其概率为0
任何随机事件的概率P(A)都满足:0 ≤ P(A) ≤ 1
问题2:命中靶子的概率是多少?命中0环的概率呢?
性质3:互斥事件的概率加法公式
环节1
环节4
环节3
环节2
问题3:"命中10环"和"命中9环"这两个事件有什么关系?它们的概率和与"命中9环或10环"的概率有何联系?
一般地,因为事件A与事件B互斥,即A与B不含有相同的样本点,
所以 n(A∪B)=n(A)+n(B),这就等价于P(A∪B)=P(A)+P(B),
即两个互斥事件的和事件的概率等于这两个事件的概率之和.
所以我们有互斥事件概率加法公式:
如果事件A和事件B互斥,那么P(A∪B)=P(A)+P(B).
互斥事件加法公式的推广
环节1
环节4
环节3
环节2
问题4:"命中5-7环”的概率是否等于命中5环、6环、7环这三个事件三个概率之和
推广公式:
如果事件A1,A2, ,Am两两互斥,那么事件A1∪A2∪ ∪Am发生的概率等于这m个事件分别发生的概率之和,即
P(A1∪A2∪ ∪Am)=P(A1)+P(A2)+ +P(Am).
性质4:对立事件的概率公式
环节1
环节4
环节3
环节2
问题5:命中小于五环和命中不小于五环的概率之间有什么关系?
因为事件A与事件B互为对立事件,
事件A与事件B互斥(A∩B= ),事件A∪B为必然事件(A∪B=Ω),
所以 P(A∪B)=P(A)+P(B),P(A∪B)=1,
所以有 P(A∪B)=P(A)+P(B)=1.
事件A与事件B互为对立事件,那么P(A)=1-P(B),P(B)=1-P(A).
性质5:概率的单调性
环节1
环节4
环节3
环节2
问题6:"命中10环"与"命中9环或10环"概率有什么关系?
一般地,对于事件A与事件B,如果A B,即只要事件A发生,则事件
B一定发生,那么事件A的概率不超过事件B的概率.于是我们有概率的单调性.如果A B,那么P(A) ≤ P(B).
由性质5可知对于任意事件A,因为 A Ω,所以P( ) ≤ P(A)≤ P(Ω),
即0≤ P(A)≤1.
性质6:一般加法公式
环节1
环节4
环节3
环节2
问题7:写出"命中环数为6、8、10环"和"命中环数大于7“的概率,并分析两个事件的和事件、并事件概率之间的关系。
设A,B是一个试验中的两个事件,我们有
P(A∪B)=P(A)+P(B)-P(A∩B)
显然,性质3 是性质6 的特殊情况.当A,B互斥时,P(A∩B)=P( )=0,所以
P(A∪B)=P(A)+P(B)-P(A∩B)=P(A)+P(B)-0=P(A)+P(B).
辨析
环节1
环节4
环节3
环节2
思考辨析(正确的画“√”,错误的画“×”)
(1)A、B为两个事件,则P(A+B)=P(A)+P(B). ( )
(2)若A与B为互斥事件,则P(A)+P(B)=1. ( )
(3)若事件A、B、C两两互斥,则P(A)+P(B)+P(C)=1. ( )
(4)统计某班同学们的数学测试成绩,事件“所有同学的成绩都大于60分”的对立事件为“所有同学的成绩都小于60分”. ( )
(5)若P(A)+P(B)=1,则事件A与B为对立事件. ( )
×
×
×
×
×
性质6 设A,B是一个试验中的两个事件,我们有
P(A∪B)=P(A)+P(B)-P(A∩B).
总结
环节1
环节4
环节3
环节2
性质3 如果事件A和事件B互斥,那么P(A∪B)=P(A)+P(B).
性质4 事件A与事件B互为对立事件,那么P(A)=1-P(B),P(B)=1-P(A).
性质1 对任意的事件A,都有P(A)≥0;
性质2 必然事件的概率为1,不可能事件的概率为0,即 P(Ω)=1,P( )=0;
性质5 如果A B,那么P(A) ≤ P(B); 对于任意事件A,0≤ P(A)≤1;
例题1
环节1
环节4
环节3
环节2
5/17
2024年某国航天事业捷报频传,取得了多项重大成功。假设航天任务的成功与否是随机事件,且各次任务相互独立。已知某阶段某国计划执行三次航天发射任务,每次成功的概率分别为0.98、0.95和0.90。
(1) 求这三次任务全部成功的概率。
(2) 求至少有一次任务成功的概率。
例题1
环节1
环节4
环节3
环节2
5/17
解:
(1)由于任务相互独立,全部成功的概率等于各次任务成功概率的乘积:P(全部成功) = 0.98 × 0.95 × 0.90 = 0.8379
(2)可以利用对立事件概率公式。"至少有一次成功"的对立事件是"三次都失败":
P(至少一次成功)
= 1 - P(三次都失败)
= 1 - (1-0.98)×(1-0.95)×(1-0.90)
= 1 - 0.02×0.05×0.10 = 0.9995
例题2
环节1
环节4
环节3
环节2
在2024年巴黎奥运会上,中国体育代表团取得了优异成绩。假设奥运会乒乓球男子单打比赛中,中国选手A和外国选手B进入决赛。根据以往战绩估计,A战胜B的概率为0.7,B战胜A的概率为0.3(不存在平局)。
(1)A和B在决赛中相遇,求A夺冠的概率。
(2)若A半决赛失利未能进入决赛,则决赛中A不可能夺冠。已知A进入决赛的概率为0.8,求A最终夺冠的概率。
例题2
环节1
环节4
环节3
环节2
解:
(1)根据对立事件概率之和为1,A夺冠的概率即为A战胜B的概率,直接得出P(A夺冠) = 0.7
(2)A最终夺冠是A进入决赛和A战胜B两个事件的交事件,且A进入决赛和A战胜B两个事件相互独立,
例题3
环节1
环节4
环节3
环节2
为了推广一种新饮料,某饮料生产企业开展了有奖促销活动:将6罐这种饮料装一箱,每箱中都放置2罐能够中奖的饮料.若从一箱中随机抽出2罐,能中奖的概率为多少
例题4
环节1
环节4
环节3
环节2
一个盒子中装有标号为1,2,3,4,5的5张标签,随机地选取两张标签,根据下列条件求两张标签上的数字为相等整数的概率:
(1)标签的选取是不放回的;
(2)标签的选取是有放回的.
课后作业与拓展
环节1
环节4
环节3
环节2
书面作业
课本习题
课本第236页习题10.1的第8、9、10题
提示:巩固概率基本性质的应用
实践作业
调查分析
调查2024年发生的某一随机事件(例如,某地区的天气统计、某体育
比赛的胜负情况等)
收集相关数据,计算事件发生的概率
运用概率的基本性质分析其中的规律
撰写一份简短的调查报告(字数不限)
提示:培养应用数学的能力和关注社会的意识
生活中的概率应用
天气预报
分析天气数据,计算降水概率
体育赛事
计算球队取胜或平局的概率
彩票抽奖
分析中奖概率和奖项设置
交通出行
计算交通拥堵概率和出行时间
学习建议
运用概率思维理性分析问题
从日常事件中发现概率规律
将所学知识与社会热点相结合
培养数学应用意识和责任感
概率不仅是数学工具,也是认识世界的一种视角
感谢聆听
Thanks for watching
10.1.4概率的基本性质
导入
2024巴黎奥运会射击项目,中国队表现惊艳,共斩获 5 金 2 银 3 铜,位居奖牌榜榜首。其中7 月 27 日,黄雨婷、盛李豪获得 10 米气步枪混合团体金牌,为中国代表团摘得巴黎奥运会第一金,这也是巴黎奥运会产生的首枚金牌。这一成绩刷新了队伍奥运会历史最佳战绩,展现出强大实力与青春风采
导入
奥运会射击赛场上,某优秀射手进行射击训练,每次射击的结果可以用环数来表示。假设该射手每次射击命中的环数在0到10环之间,命中各环数的概率是稳定的。下表是他某次训练中射击100次的结果统计:
命中环数 0环 1-4环 5环 6环 7环 8环 9环 10环
命中次数 0 5 10 15 20 25 15 10
导入
环节1
环节4
环节3
环节2
思考问题:
问题1:观察命中各环数的频率,你能得到什么共同特点嘛?
问题2:命中靶子的概率是多少?命中0环的概率呢?
问题3:"命中10环"和"命中9环"这两个事件有什么关系?它们的概率和与"命中9环或10环"的概率有何联系?
问题4:"5-7环”的概率等于命中5环、6环、7环这三个事件三个概率之和
问题5:命中小于五环和命中不小于五环的概率之间有什么关系?
问题6:"命中10环"与"命中9环或10环"概率有什么关系?
问题7:写出"命中环数为6、8、10环"和"命中环数大于7“的概率,并分析两个事件的和事件、交事件概率之间的关系。
基本概念回顾
环节1
环节4
环节3
环节2
1.若A,B表示随机事件,则A∩B与A∪B也表示事件.( )
2.若两个事件是互斥事件,则这两个事件是对立事件.( )
3.若两个事件是对立事件,则这两个事件也是互斥事件.( )
4.若事件A与B是互斥事件,则在一次试验中事件A和B至少有一个发生.( )
×
×
√
√
性质1:概率的非负性
环节1
环节4
环节3
环节2
结论:
从图表中可以看出,无论射手命中哪个环数,其概率都是非负的。这符合概率的非负性性质,即对任意事件A(如命中特定环数),都有P(A) ≥ 0。
4/17
问题1:观察命中各环数的频率,你能得到什么共同特点嘛?
性质1:概率的非负性
环节1
环节4
环节3
环节2
非负性定义:
对任意事件A,都有P(A) ≥ 0
概率的非负性表示任何事件发生的可能性都不会是负数。这一性质是概率的公理基础,也是我们理解概率概念的起点。
为什么概率不能为负?
1.负概率没有实际意义,无法在现实世界中观测到
2.概率表示事件发生的可能性,可能性不可能为负
3.概率是对频率的数学抽象,频率总是非负的
性质2:概率的规范性
环节1
环节4
环节3
环节2
规范性定义:
必然事件的概率为1,不可能事件的概率为0,即 P(Ω)=1,P( )=0.
理解要点:
必然事件(全集Ω)包含所有可能结果,其概率为1
不可能事件(空集 )不包含任何结果,其概率为0
任何随机事件的概率P(A)都满足:0 ≤ P(A) ≤ 1
问题2:命中靶子的概率是多少?命中0环的概率呢?
性质3:互斥事件的概率加法公式
环节1
环节4
环节3
环节2
问题3:"命中10环"和"命中9环"这两个事件有什么关系?它们的概率和与"命中9环或10环"的概率有何联系?
一般地,因为事件A与事件B互斥,即A与B不含有相同的样本点,
所以 n(A∪B)=n(A)+n(B),这就等价于P(A∪B)=P(A)+P(B),
即两个互斥事件的和事件的概率等于这两个事件的概率之和.
所以我们有互斥事件概率加法公式:
如果事件A和事件B互斥,那么P(A∪B)=P(A)+P(B).
互斥事件加法公式的推广
环节1
环节4
环节3
环节2
问题4:"命中5-7环”的概率是否等于命中5环、6环、7环这三个事件三个概率之和
推广公式:
如果事件A1,A2, ,Am两两互斥,那么事件A1∪A2∪ ∪Am发生的概率等于这m个事件分别发生的概率之和,即
P(A1∪A2∪ ∪Am)=P(A1)+P(A2)+ +P(Am).
性质4:对立事件的概率公式
环节1
环节4
环节3
环节2
问题5:命中小于五环和命中不小于五环的概率之间有什么关系?
因为事件A与事件B互为对立事件,
事件A与事件B互斥(A∩B= ),事件A∪B为必然事件(A∪B=Ω),
所以 P(A∪B)=P(A)+P(B),P(A∪B)=1,
所以有 P(A∪B)=P(A)+P(B)=1.
事件A与事件B互为对立事件,那么P(A)=1-P(B),P(B)=1-P(A).
性质5:概率的单调性
环节1
环节4
环节3
环节2
问题6:"命中10环"与"命中9环或10环"概率有什么关系?
一般地,对于事件A与事件B,如果A B,即只要事件A发生,则事件
B一定发生,那么事件A的概率不超过事件B的概率.于是我们有概率的单调性.如果A B,那么P(A) ≤ P(B).
由性质5可知对于任意事件A,因为 A Ω,所以P( ) ≤ P(A)≤ P(Ω),
即0≤ P(A)≤1.
性质6:一般加法公式
环节1
环节4
环节3
环节2
问题7:写出"命中环数为6、8、10环"和"命中环数大于7“的概率,并分析两个事件的和事件、并事件概率之间的关系。
设A,B是一个试验中的两个事件,我们有
P(A∪B)=P(A)+P(B)-P(A∩B)
显然,性质3 是性质6 的特殊情况.当A,B互斥时,P(A∩B)=P( )=0,所以
P(A∪B)=P(A)+P(B)-P(A∩B)=P(A)+P(B)-0=P(A)+P(B).
辨析
环节1
环节4
环节3
环节2
思考辨析(正确的画“√”,错误的画“×”)
(1)A、B为两个事件,则P(A+B)=P(A)+P(B). ( )
(2)若A与B为互斥事件,则P(A)+P(B)=1. ( )
(3)若事件A、B、C两两互斥,则P(A)+P(B)+P(C)=1. ( )
(4)统计某班同学们的数学测试成绩,事件“所有同学的成绩都大于60分”的对立事件为“所有同学的成绩都小于60分”. ( )
(5)若P(A)+P(B)=1,则事件A与B为对立事件. ( )
×
×
×
×
×
性质6 设A,B是一个试验中的两个事件,我们有
P(A∪B)=P(A)+P(B)-P(A∩B).
总结
环节1
环节4
环节3
环节2
性质3 如果事件A和事件B互斥,那么P(A∪B)=P(A)+P(B).
性质4 事件A与事件B互为对立事件,那么P(A)=1-P(B),P(B)=1-P(A).
性质1 对任意的事件A,都有P(A)≥0;
性质2 必然事件的概率为1,不可能事件的概率为0,即 P(Ω)=1,P( )=0;
性质5 如果A B,那么P(A) ≤ P(B); 对于任意事件A,0≤ P(A)≤1;
例题1
环节1
环节4
环节3
环节2
5/17
2024年某国航天事业捷报频传,取得了多项重大成功。假设航天任务的成功与否是随机事件,且各次任务相互独立。已知某阶段某国计划执行三次航天发射任务,每次成功的概率分别为0.98、0.95和0.90。
(1) 求这三次任务全部成功的概率。
(2) 求至少有一次任务成功的概率。
例题1
环节1
环节4
环节3
环节2
5/17
解:
(1)由于任务相互独立,全部成功的概率等于各次任务成功概率的乘积:P(全部成功) = 0.98 × 0.95 × 0.90 = 0.8379
(2)可以利用对立事件概率公式。"至少有一次成功"的对立事件是"三次都失败":
P(至少一次成功)
= 1 - P(三次都失败)
= 1 - (1-0.98)×(1-0.95)×(1-0.90)
= 1 - 0.02×0.05×0.10 = 0.9995
例题2
环节1
环节4
环节3
环节2
在2024年巴黎奥运会上,中国体育代表团取得了优异成绩。假设奥运会乒乓球男子单打比赛中,中国选手A和外国选手B进入决赛。根据以往战绩估计,A战胜B的概率为0.7,B战胜A的概率为0.3(不存在平局)。
(1)A和B在决赛中相遇,求A夺冠的概率。
(2)若A半决赛失利未能进入决赛,则决赛中A不可能夺冠。已知A进入决赛的概率为0.8,求A最终夺冠的概率。
例题2
环节1
环节4
环节3
环节2
解:
(1)根据对立事件概率之和为1,A夺冠的概率即为A战胜B的概率,直接得出P(A夺冠) = 0.7
(2)A最终夺冠是A进入决赛和A战胜B两个事件的交事件,且A进入决赛和A战胜B两个事件相互独立,
例题3
环节1
环节4
环节3
环节2
为了推广一种新饮料,某饮料生产企业开展了有奖促销活动:将6罐这种饮料装一箱,每箱中都放置2罐能够中奖的饮料.若从一箱中随机抽出2罐,能中奖的概率为多少
例题4
环节1
环节4
环节3
环节2
一个盒子中装有标号为1,2,3,4,5的5张标签,随机地选取两张标签,根据下列条件求两张标签上的数字为相等整数的概率:
(1)标签的选取是不放回的;
(2)标签的选取是有放回的.
课后作业与拓展
环节1
环节4
环节3
环节2
书面作业
课本习题
课本第236页习题10.1的第8、9、10题
提示:巩固概率基本性质的应用
实践作业
调查分析
调查2024年发生的某一随机事件(例如,某地区的天气统计、某体育
比赛的胜负情况等)
收集相关数据,计算事件发生的概率
运用概率的基本性质分析其中的规律
撰写一份简短的调查报告(字数不限)
提示:培养应用数学的能力和关注社会的意识
生活中的概率应用
天气预报
分析天气数据,计算降水概率
体育赛事
计算球队取胜或平局的概率
彩票抽奖
分析中奖概率和奖项设置
交通出行
计算交通拥堵概率和出行时间
学习建议
运用概率思维理性分析问题
从日常事件中发现概率规律
将所学知识与社会热点相结合
培养数学应用意识和责任感
概率不仅是数学工具,也是认识世界的一种视角
感谢聆听
Thanks for watching
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
