1.4解直角三角形(共11张PPT)北师大版数学九年级下册
文档属性
| 名称 | 1.4解直角三角形(共11张PPT)北师大版数学九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 174.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 23:22:23 | ||
图片预览



文档简介
(共11张PPT)
1.4 解直角三角形
一、交流预习
在日常生活中,我们常常遇到与直角三角形有关的问题,知道直角三角形的边可以求出角,知道角也可以求出相应的边.如图所示,在Rt△ABC中共有几个元素 我们如何利用已知元素求出其他的元素呢
A
C
B
一、互助探究
分析:
1.直角三角形中已知两边可以利用 定理求出第三条边.
2.直角三角形中,已知两边可以利用 求∠A(或∠B)的度数.
3.再利用 求∠B(或∠A)的度数.
解:在Rt△ABC中,a2+b2=c2,a= ,b= ,
∴c=
在Rt△ABC中,sin B= ,
∴∠B=30°,∴∠A=60°.
例1 在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且a= ,b= ,求这个三角形的其他元素.
二、互助探究
已知一条边和一个角解直角三角形
例2 在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且b=30,∠B=25°.求这个三角形的其他元素(边长精确到1).
解:在Rt△ABC中,∠C=90°,∠B=25°,
∴∠A=65°.
∵sin B=
∵tan B=
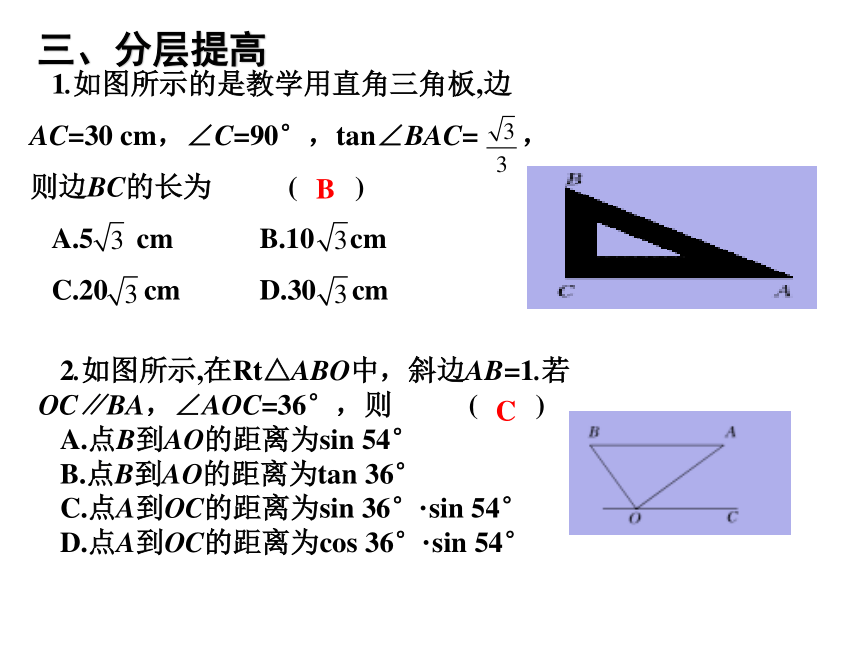
1.如图所示的是教学用直角三角板,边AC=30 cm,∠C=90°,tan∠BAC= ,则边BC的长为 ( )
A.5 cm B.10 cm
C.20 cm D.30 cm
三、分层提高
2.如图所示,在Rt△ABO中,斜边AB=1.若OC∥BA,∠AOC=36°,则 ( )
A.点B到AO的距离为sin 54°
B.点B到AO的距离为tan 36°
C.点A到OC的距离为sin 36°·sin 54°
D.点A到OC的距离为cos 36°·sin 54°
C
B
3.如图所示,已知在Rt△ABC中,斜边BC上的高AD=4,cos B= ,则AC= .
三、分层提高
4.如图所示,在△ABC中,AB=AC=5,sin∠ABC=0.8,则BC= .
5.如图所示,在Rt△ABC中,∠C=90°,AB=10,
cos A= ,求BC的长和tan B的值.
6
5
这节课我们都复习了
哪些知识?
你有哪些收获?
自己觉得哪些
地方容易出错?
我想对我的师傅
(学友)说……
四、归纳总结
五、巩固反馈
1.在△ABC中,∠C=90°,解这个直角三角形.
⑴∠A=60°,斜边上的高CD = ;
⑵∠A=60°,a+b=3+ .
60°
A
B
C
D
┓
┓
2.在Rt△ABC中,∠C=90°,AD=2AC=2BD,
且DE⊥AB.
(1)求tanB;
(2)若DE=1,求CE的长.
A
C
B
E
D
1.在△ABC中,∠C=90°,解这个直角三角形.
⑴∠A=60°,斜边上的高CD = ;
⑵∠A=60°,a+b=3+ .
解:(1)∠B = 90°-∠A = 30°
AC=
60°
A
B
C
D
┓
┓
五、巩固反馈
2.在Rt△ABC中∠C=90°,AD=2AC=2BD,
且DE⊥AB.
(1)求tanB;
(2)若DE=1,求CE的长.
A
C
B
E
D
CE=5
五、巩固反馈
谢谢
1.4 解直角三角形
一、交流预习
在日常生活中,我们常常遇到与直角三角形有关的问题,知道直角三角形的边可以求出角,知道角也可以求出相应的边.如图所示,在Rt△ABC中共有几个元素 我们如何利用已知元素求出其他的元素呢
A
C
B
一、互助探究
分析:
1.直角三角形中已知两边可以利用 定理求出第三条边.
2.直角三角形中,已知两边可以利用 求∠A(或∠B)的度数.
3.再利用 求∠B(或∠A)的度数.
解:在Rt△ABC中,a2+b2=c2,a= ,b= ,
∴c=
在Rt△ABC中,sin B= ,
∴∠B=30°,∴∠A=60°.
例1 在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且a= ,b= ,求这个三角形的其他元素.
二、互助探究
已知一条边和一个角解直角三角形
例2 在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且b=30,∠B=25°.求这个三角形的其他元素(边长精确到1).
解:在Rt△ABC中,∠C=90°,∠B=25°,
∴∠A=65°.
∵sin B=
∵tan B=
1.如图所示的是教学用直角三角板,边AC=30 cm,∠C=90°,tan∠BAC= ,则边BC的长为 ( )
A.5 cm B.10 cm
C.20 cm D.30 cm
三、分层提高
2.如图所示,在Rt△ABO中,斜边AB=1.若OC∥BA,∠AOC=36°,则 ( )
A.点B到AO的距离为sin 54°
B.点B到AO的距离为tan 36°
C.点A到OC的距离为sin 36°·sin 54°
D.点A到OC的距离为cos 36°·sin 54°
C
B
3.如图所示,已知在Rt△ABC中,斜边BC上的高AD=4,cos B= ,则AC= .
三、分层提高
4.如图所示,在△ABC中,AB=AC=5,sin∠ABC=0.8,则BC= .
5.如图所示,在Rt△ABC中,∠C=90°,AB=10,
cos A= ,求BC的长和tan B的值.
6
5
这节课我们都复习了
哪些知识?
你有哪些收获?
自己觉得哪些
地方容易出错?
我想对我的师傅
(学友)说……
四、归纳总结
五、巩固反馈
1.在△ABC中,∠C=90°,解这个直角三角形.
⑴∠A=60°,斜边上的高CD = ;
⑵∠A=60°,a+b=3+ .
60°
A
B
C
D
┓
┓
2.在Rt△ABC中,∠C=90°,AD=2AC=2BD,
且DE⊥AB.
(1)求tanB;
(2)若DE=1,求CE的长.
A
C
B
E
D
1.在△ABC中,∠C=90°,解这个直角三角形.
⑴∠A=60°,斜边上的高CD = ;
⑵∠A=60°,a+b=3+ .
解:(1)∠B = 90°-∠A = 30°
AC=
60°
A
B
C
D
┓
┓
五、巩固反馈
2.在Rt△ABC中∠C=90°,AD=2AC=2BD,
且DE⊥AB.
(1)求tanB;
(2)若DE=1,求CE的长.
A
C
B
E
D
CE=5
五、巩固反馈
谢谢
