2026年中考数学一轮复习 反比例函数(含解析)
文档属性
| 名称 | 2026年中考数学一轮复习 反比例函数(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 17:54:32 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
中考数学一轮复习 反比例函数
一.选择题(共10小题)
1.(2024 香洲区校级一模)若反比例函数在每个象限内的函数值随的增大而减小,则
A. B. C. D.
2.(2024 晋江市模拟)如图,反比例函数图象经过正方形的顶点,边与轴交于点,若正方形的面积为12,,则的值为
A.3 B. C. D.
3.(2024 天元区校级一模)如图,点是反比例函数图象上的一点,轴于点,且面积为4.若点也是该图象上的一点,则的值为
A. B. C.2 D.4
4.(2024 江北区校级模拟)反比例函数一定经过的点是
A. B. C. D.
5.(2024 甘肃模拟)电路上在电压保持不变的条件下,电流(A)与电阻成反比例关系,与的函数图象如图,关于函数解析式是
A. B. C. D.
6.(2024 浙江)反比例函数的图象上有,两点.下列正确的选项是
A.当时, B.当时,
C.当时, D.当时,
7.(2024 十堰模拟)某个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.如图所示的是该台灯的电流(A)与电阻的关系图象,该图象经过点.根据图象可知,下列说法正确的是
A.当时,
B.与的函数关系式是
C.当时,
D.当时,的取值范围是
8.(2024 赣州模拟)如图所示为某新款茶吧机,开机加热时每分钟上升,加热到,停止加热,水温开始下降,此时水温与通电时间成反比例关系.当水温降至时,饮水机再自动加热,若水温在时接通电源,水温与通电时间之间的关系如图所示,则下列说法中错误的是
A.水温从加热到,需要
B.水温下降过程中,与的函数关系式是
C.上午10点接通电源,可以保证当天能喝到不低于的水
D.在一个加热周期内水温不低于的时间为
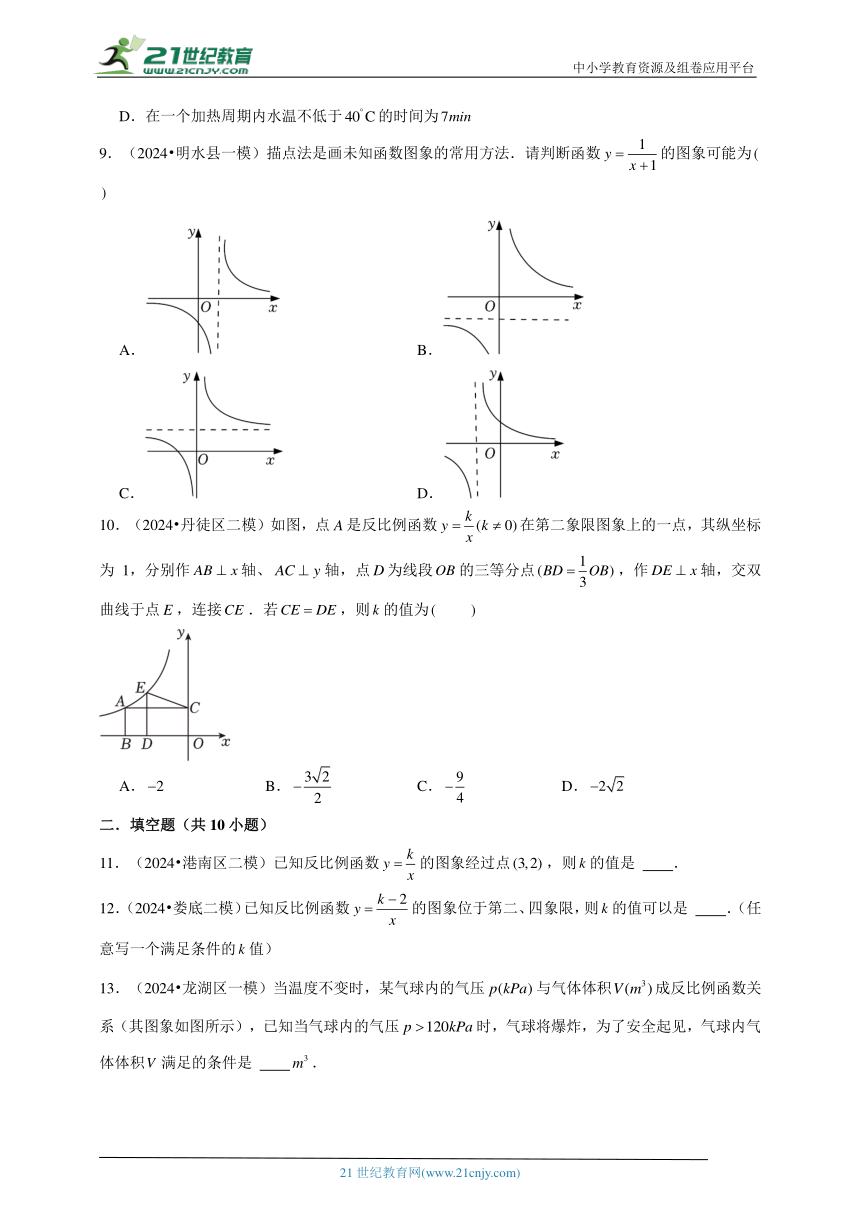
9.(2024 明水县一模)描点法是画未知函数图象的常用方法.请判断函数的图象可能为
A. B.
C. D.
10.(2024 丹徒区二模)如图,点是反比例函数在第二象限图象上的一点,其纵坐标为1,分别作轴、轴,点为线段的三等分点,作轴,交双曲线于点,连接.若,则的值为
A. B. C. D.
二.填空题(共10小题)
11.(2024 港南区二模)已知反比例函数的图象经过点,则的值是 .
12.(2024 娄底二模)已知反比例函数的图象位于第二、四象限,则的值可以是 .(任意写一个满足条件的值)
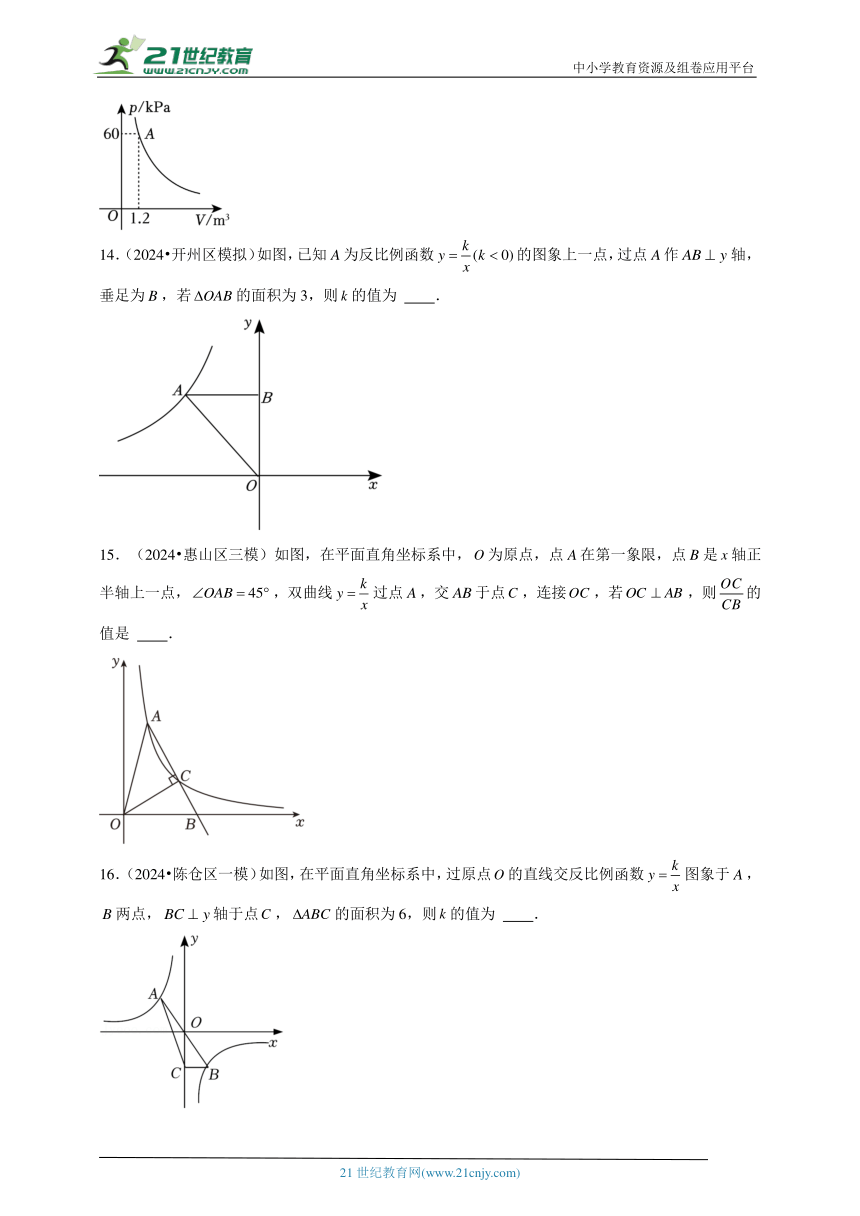
13.(2024 龙湖区一模)当温度不变时,某气球内的气压与气体体积成反比例函数关系(其图象如图所示),已知当气球内的气压时,气球将爆炸,为了安全起见,气球内气体体积满足的条件是 .
14.(2024 开州区模拟)如图,已知为反比例函数的图象上一点,过点作轴,垂足为,若的面积为3,则的值为 .
15.(2024 惠山区三模)如图,在平面直角坐标系中,为原点,点在第一象限,点是轴正半轴上一点,,双曲线过点,交于点,连接,若,则的值是 .
16.(2024 陈仓区一模)如图,在平面直角坐标系中,过原点的直线交反比例函数图象于,两点,轴于点,的面积为6,则的值为 .
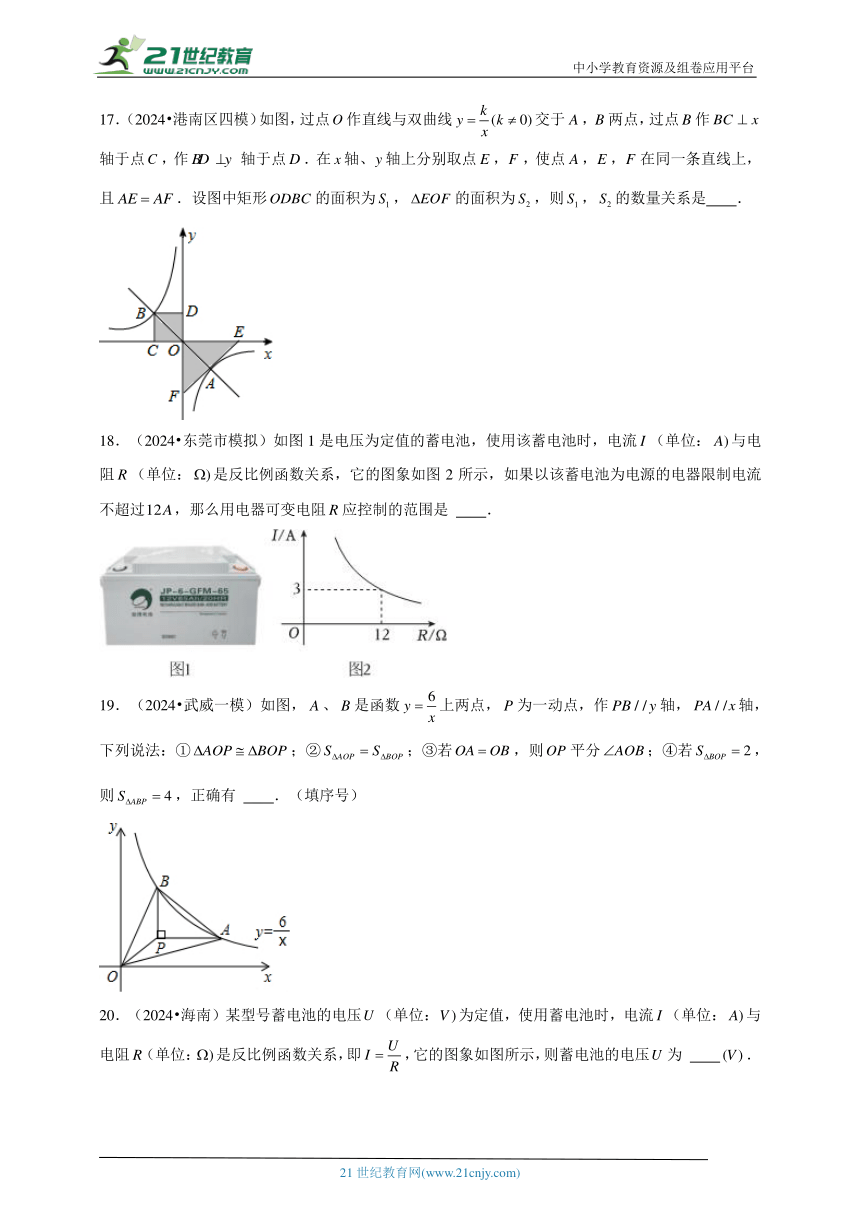
17.(2024 港南区四模)如图,过点作直线与双曲线交于,两点,过点作轴于点,作轴于点.在轴、轴上分别取点,,使点,,在同一条直线上,且.设图中矩形的面积为,的面积为,则,的数量关系是 .
18.(2024 东莞市模拟)如图1是电压为定值的蓄电池,使用该蓄电池时,电流(单位:与电阻(单位:是反比例函数关系,它的图象如图2所示,如果以该蓄电池为电源的电器限制电流不超过,那么用电器可变电阻应控制的范围是 .
19.(2024 武威一模)如图,、是函数上两点,为一动点,作轴,轴,下列说法:①;②;③若,则平分;④若,则,正确有 .(填序号)
20.(2024 海南)某型号蓄电池的电压(单位:为定值,使用蓄电池时,电流(单位:与电阻(单位:是反比例函数关系,即,它的图象如图所示,则蓄电池的电压为 .
三.解答题(共5小题)
21.(2024 绵阳)如图,在边长为4的菱形中,对角线与相交于点,边在轴上,,,点在反比例函数的图象上.
(1)求点,,的坐标及反比例函数的解析式;
(2)将菱形向右平移,当点恰好在反比例函数的图象上时,边与函数图象交于点,求点到轴的距离.
22.(2024 凉州区一模)已知,与成正比例,与成反比例,且当时,;当时,.求时,的值.
23.(2024 宁江区校级模拟)世界的面食之根就在山西.山西面食是中华民族饮食文化中的重要组成部分.如图,厨师将一定质量的面团做成拉面时,面条的总长度是面条横截面面积的反比例函数,其图象经过,两点.
(1)求与之间的函数关系式;
(2)求的值,并解释它的实际意义.
24.(2024 富顺县二模)如图,在平面直角坐标系中,一次函数与反比例函数的图象交于,两点,一次函数的图象与轴交于点.
(1)求一次函数的解析式;
(2)根据函数的图象,直接写出不等式的解集;
(3)点是轴上一点,且的面积等于面积的2倍,求点的坐标.
25.(2024 阳信县一模)如图,一次函数的图象与函数的图象交于点和点.
(1)求的值;
(2)若,根据图象直接写出当时的取值范围;
(3)点在线段上,过点作轴的垂线,交函数的图象于点,若的面积为1,求点的坐标.
中考数学一轮复习 反比例函数
参考答案与试题解析
一.选择题(共10小题)
1.(2024 香洲区校级一模)若反比例函数在每个象限内的函数值随的增大而减小,则
A. B. C. D.
【答案】
【考点】反比例函数的性质
【专题】反比例函数及其应用;运算能力
【分析】根据反比例函数的性质即可得到结论.
【解答】解:反比例函数在每个象限内的函数值随的增大而减小,
,
,
故选:.
【点评】本题考查了反比例函数的性质,熟练掌握反比例函数的性质是解题的关键.
2.(2024 晋江市模拟)如图,反比例函数图象经过正方形的顶点,边与轴交于点,若正方形的面积为12,,则的值为
A.3 B. C. D.
【答案】
【考点】反比例函数系数的几何意义;反比例函数图象上点的坐标特征;正方形的性质
【专题】代数几何综合题;矩形 菱形 正方形;推理能力;应用意识
【分析】过作轴于,过作轴于,于,交值于,通过证得,,得出,,由,根据平行线分线段成比例定理求得,利用勾股定理以及正方形的面积即可求得的坐标,进而求得的值.
【解答】解:过作轴于,过作轴于,于,交值于,
四边形是正方形,
,,
,
,
在与中,
,
,
,,
同理,,
,,
轴,
,
,
,
,
,正方形的面积为12,
,
,
,
,,
反比例函数图象经过正方形的顶点,
,
解法二:,
设,,
,
由题意,
,
.
故选:.
【点评】本题考查了反比例函数的系数的几何意义,正方形的性质,全等三角形的判定与性质,相似三角形的判定和性质,正确的作出辅助线是解题的关键.
3.(2024 天元区校级一模)如图,点是反比例函数图象上的一点,轴于点,且面积为4.若点也是该图象上的一点,则的值为
A. B. C.2 D.4
【答案】
【考点】反比例函数图象上点的坐标特征;反比例函数系数的几何意义
【专题】反比例函数及其应用;运算能力
【分析】根据反比例函数系数的几何意义求出的值,再代入计算即可.
【解答】解:由反比例函数系数的几何意义可知,,而,
,
反比例函数的关系式为,
把点代入得,
,
故选:.
【点评】本题考查反比例函数系数的几何意义,掌握反比例函数系数的几何意义以及反比例函数图象上点的坐标的特征是正确解答的前提.
4.(2024 江北区校级模拟)反比例函数一定经过的点是
A. B. C. D.
【答案】
【考点】反比例函数图象上点的坐标特征
【专题】反比例函数及其应用;运算能力
【分析】根据对各选项进行逐一判断即可.
【解答】解:反比例函数,
,
、,此点不在函数图象上,故本选项不合题意;
、,此点在函数图象上,故本选项符合题意;
、,此点不在函数图象上,故本选项不合题意;
、,此点不在函数图象上,故本选项不合题意.
故选:.
【点评】本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数中为定值是解答此题的关键.
5.(2024 甘肃模拟)电路上在电压保持不变的条件下,电流(A)与电阻成反比例关系,与的函数图象如图,关于函数解析式是
A. B. C. D.
【考点】:根据实际问题列反比例函数关系式
【专题】29:跨学科
【分析】根据电压电流电阻得到稳定电压的值,让即可.
【解答】解:当,时,
电压,
.
故选:.
【点评】考查列反比例函数关系式,关键是根据题中所给的值确定常量电压的值.
6.(2024 浙江)反比例函数的图象上有,两点.下列正确的选项是
A.当时, B.当时,
C.当时, D.当时,
【答案】
【考点】反比例函数图象上点的坐标特征
【专题】反比例函数及其应用;推理能力
【分析】先根据反比例函数的解析式判断出函数图象所在的象限,再对各选项进行逐一判断即可.
【解答】解:反比例函数中,,
此函数图象的两个分支分别位于第一、三象限,在每一象限内随的增大而减小,
、当时,,
,
,正确,符合题意;
、当时,点在第三象限,点在第一象限,
,,
,原结论错误,不符合题意;
、由知,当时,,原结论错误,不符合题意;
、当时,,
,在第一象限,
,
,原结论错误,不符合题意.
故选:.
【点评】本题考查的是反比例函数图象上点的坐标特征,熟知反比例函数的图象与系数的关系是解题的关键.
7.(2024 十堰模拟)某个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.如图所示的是该台灯的电流(A)与电阻的关系图象,该图象经过点.根据图象可知,下列说法正确的是
A.当时,
B.与的函数关系式是
C.当时,
D.当时,的取值范围是
【答案】
【考点】反比例函数的应用;一次函数与一元一次不等式
【专题】反比例函数及其应用;运算能力
【分析】设与的函数关系式是,利用待定系数法求出,然后求出当时,,再由,得到随增大而减小,由此对各选项逐一判断即可.
【解答】解:设与的函数关系式是,
该图象经过点,
,
,
与的函数关系式是,故不符合题意;
当时,,
,
随增大而减小,
当时,,当时,,当时,的取值范围是,故、不符合题意,符合题意.
故选:.
【点评】本题主要考查了反比例函数的实际应用,正确求出反比例函数解析式是解题的关键.
8.(2024 赣州模拟)如图所示为某新款茶吧机,开机加热时每分钟上升,加热到,停止加热,水温开始下降,此时水温与通电时间成反比例关系.当水温降至时,饮水机再自动加热,若水温在时接通电源,水温与通电时间之间的关系如图所示,则下列说法中错误的是
A.水温从加热到,需要
B.水温下降过程中,与的函数关系式是
C.上午10点接通电源,可以保证当天能喝到不低于的水
D.在一个加热周期内水温不低于的时间为
【答案】
【考点】反比例函数的应用
【专题】一次函数及其应用;反比例函数及其应用;运算能力;应用意识
【分析】根据水温升高的速度,即可求出水温从加热到所需的时间;设水温下降过程中,与的函数关系式为,根据待定系数法即可求解;先求出当水温下降到20摄氏度所需时间为,即一个循环为,,将代入反比例函数解析式中求出此时水温即可判断;分别求出在加热过程和降温过程中水温为40摄氏度时的时间,再相减即可判断.
【解答】解:开机加热时每分钟上升,
水温从加热到,所需时间为,故选项正确,不符合题意;
设水温下降过程中,与的函数关系式为,
由题意得,点在反比例函数的图象上,
,
解得:,
水温下降过程中,与的函数关系式是,故选项正确,不符合题意;
令,则,
,
从开机加热到水温降至需要,即一个循环为,
水温与通电时间的函数关系式为,
上午10点到共30分钟,,
当时,,
即此时的水温为,故选项正确,不符合题意;
在加热过程中,水温为时,,
解得:,
在降温过程中,水温为时,,
解得:,
,
一个加热周期内水温不低于的时间为,故选项错误,符合题意.
故选:.
【点评】本题主要考查反比例函数和一次函数的应用、用待定系数法求反比例函数解析数,解题关键在于读懂图象,灵活运用所学知识解决问题.
9.(2024 明水县一模)描点法是画未知函数图象的常用方法.请判断函数的图象可能为
A. B.
C. D.
【答案】
【考点】反比例函数的图象
【专题】推理能力;反比例函数及其应用;几何直观
【分析】根据反比例函数的性质可知函数在第一、三象限,对称中心为原点,根据函数平移的规律,把向左平移1个单位得到,对称中心为,据此即可判断.
【解答】解:,
函数在第一、三象限,对称中心为原点,
把向左平移1个单位得到,对称中心为,
故选:.
【点评】本题考查了反比例函数的图象和性质,函数与函数的关系是解题的关键.
10.(2024 丹徒区二模)如图,点是反比例函数在第二象限图象上的一点,其纵坐标为1,分别作轴、轴,点为线段的三等分点,作轴,交双曲线于点,连接.若,则的值为
A. B. C. D.
【答案】
【考点】反比例函数图象上点的坐标特征
【专题】反比例函数及其应用;运算能力
【分析】根据反比例函数图象上点的坐标特征解答即可.
【解答】解:设,则,,,,,
,
,
解得.
故选:.
【点评】本题考查了反比例函数图象上点的坐标特征,熟练掌握反比例函数图象上点的坐标特征是关键.
二.填空题(共10小题)
11.(2024 港南区二模)已知反比例函数的图象经过点,则的值是 6 .
【考点】待定系数法求反比例函数解析式
【分析】把点代入反比例函数中,可直接求的值.
【解答】解:依题意,得时,,
所以,,
故答案为:6.
【点评】本题考查了待定系数法求反比例函数解析式,反比例函数图象上点的坐标特点.关键是设函数关系式,根据已知条件求函数关系式.
12.(2024 娄底二模)已知反比例函数的图象位于第二、四象限,则的值可以是 0 .(任意写一个满足条件的值)
【答案】0(答案不唯一).
【考点】反比例函数的性质
【专题】反比例函数及其应用;应用意识
【分析】先根据反比例函数的图象位于第二、四象限得出的取值范围,进而可而得出答案.
【解答】解:反比例函数的图象位于第二、四象限,
,
,
的值可以是0,
故答案为:0(答案不唯一).
【点评】本题考查的是反比例函数的图象与系数的关系,掌握反比例函数的性质是关键.
13.(2024 龙湖区一模)当温度不变时,某气球内的气压与气体体积成反比例函数关系(其图象如图所示),已知当气球内的气压时,气球将爆炸,为了安全起见,气球内气体体积满足的条件是 .
【答案】.
【考点】反比例函数的应用
【专题】反比例函数及其应用;应用意识
【分析】根据题意可知温度不变时,气球内气体的气压是气体体积的反比例函数,且过点故;故当,可判断应满足的条件.
【解答】解:设球内气体的气压和气体体积的关系式为,
图象过点,
,
,
由已知得图象在第一象限内,
随的增大而减小,
当时,,
,即不小于,
故答案为:.
【点评】本题考查反比例函数的应用,解题的关键是根据图象上的已知点的坐标,利用待定系数法求出函数解析式.
14.(2024 开州区模拟)如图,已知为反比例函数的图象上一点,过点作轴,垂足为,若的面积为3,则的值为 .
【答案】.
【考点】反比例函数图象上点的坐标特征;反比例函数系数的几何意义
【专题】反比例函数及其应用;应用意识
【分析】利用反比例函数比例系数的几何意义得到,然后根据反比例函数的性质确定的值.
【解答】解:轴,
,
而,
.
故答案为:.
【点评】本题考查了反比例函数比例系数的几何意义:在反比例函数图象中任取一点,过这一个点向轴和轴分别作垂线,与坐标轴围成的矩形的面积是定值.在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是,且保持不变.
15.(2024 惠山区三模)如图,在平面直角坐标系中,为原点,点在第一象限,点是轴正半轴上一点,,双曲线过点,交于点,连接,若,则的值是 .
【答案】.
【考点】反比例函数图象上点的坐标特征
【专题】反比例函数及其应用;推理能力
【分析】过点作,得,设线段,可得点坐标,由点,点在反比例函数上即可的,的比值,最后通过求解即可.
【解答】解:过点作,如图:
则,
,
,
,
,,
设,可得:
点、,
双曲线过点,点,
,,
,
,
解得:或(舍去),
,,
,
,
,
故答案为:.
【点评】本题考查了反比例函数图象上点的坐标特征,解题关键是掌握“铅锤法”作直角三角形,
16.(2024 陈仓区一模)如图,在平面直角坐标系中,过原点的直线交反比例函数图象于,两点,轴于点,的面积为6,则的值为 .
【答案】.
【考点】反比例函数系数的几何意义
【专题】推理能力;反比例函数及其应用;运算能力
【分析】根据反比例函数的对称性和反比例函数系数的几何意义,可求出,再根据图象所在的象限确定的值即可.
【解答】解:由对称性可知,,
,
轴,的面积为6,
,
又,
,
故答案为:.
【点评】本题考查反比例函数系数的几何意义,掌握反比例函数系数的几何意义以及反比例函数的性质是正确解答的关键.
17.(2024 港南区四模)如图,过点作直线与双曲线交于,两点,过点作轴于点,作轴于点.在轴、轴上分别取点,,使点,,在同一条直线上,且.设图中矩形的面积为,的面积为,则,的数量关系是 .
【考点】反比例函数系数的几何意义;三角形中位线定理
【分析】过点作轴于点,根据反比例函数图象系数的几何意义即可得出、,再根据中位线的性质即可得出,由此即可得出、的数学量关系.
【解答】解:过点作轴于点,如图所示.
轴,轴,轴,
,.
.轴,轴,
,,
,
,
即.
故答案为:.
【点评】本题考查了反比例函数图象系数的几何意义以及三角形的中位线,根据反比例函数图象系数的几何意义找出、是解题的关键.
18.(2024 东莞市模拟)如图1是电压为定值的蓄电池,使用该蓄电池时,电流(单位:与电阻(单位:是反比例函数关系,它的图象如图2所示,如果以该蓄电池为电源的电器限制电流不超过,那么用电器可变电阻应控制的范围是 .
【答案】.
【考点】反比例函数的应用
【专题】反比例函数及其应用;运算能力
【分析】设电流(单位:与电阻(单位:是反比例函数关系为,利用待定系数求出,再求出当,,最后根据反比例函数的增减性进行求解即可.
【解答】解:设电流(单位:与电阻(单位:是反比例函数关系为,
把点代入中得,,
,
,
当时,,
解得,
,
电流随电阻的增大而减小,
限制电流不能超过,那么用电器可变电阻应控制的范围是,
故答案为:.
【点评】本题主要考查了反比例函数的实际应用,正确求出是解题的关键.
19.(2024 武威一模)如图,、是函数上两点,为一动点,作轴,轴,下列说法:①;②;③若,则平分;④若,则,正确有 ②③④ .(填序号)
【答案】②③④.
【考点】反比例函数系数的几何意义;反比例函数图象上点的坐标特征;全等三角形的判定与性质
【专题】反比例函数及其应用;图形的全等;应用意识
【分析】根据点是动点,得到与不一定相等,判断出①错误;设出点的坐标,得出,,利用三角形面积公式计算即可判断出②正确;利用角平分线定理的逆定理判断出③正确;求出矩形,进而得出,根据三角形的面积公式计算,即可得出结论.
【解答】解:点是动点,
与不一定相等,
与不一定全等,故①错误;
设,
轴,
,
,
,
轴,
,
,
,
,②正确;
如图1,作于,于,
,,
,
,,,
平分,③正确;
如图2,延长交轴于,延长交轴于,
轴,轴,又,
四边形是矩形,
点,在双曲线上,
,
,
,
,
,
,
,
,
,④正确;
故答案为②③④.
【点评】本题考查的是反比例函数的性质、三角形面积公式、角平分线定理逆定理、矩形的判定和性质,掌握反比例函数图象上点的坐标特征、正确作出辅助线是解本题的关键.
20.(2024 海南)某型号蓄电池的电压(单位:为定值,使用蓄电池时,电流(单位:与电阻(单位:是反比例函数关系,即,它的图象如图所示,则蓄电池的电压为 64 .
【答案】64.
【考点】反比例函数的应用
【专题】跨学科;反比例函数及其应用;推理能力
【分析】根据题意,先列出反比例函数解析式,根据函数图象过代入计算出值即可.
【解答】解:电流(单位:与电阻(单位:是反比例函数关系,
,
由图象可知,当时,,
.
故答案为:64.
【点评】本题考查了反比例函数的应用,熟练掌握反比例函数的性质是关键.
三.解答题(共5小题)
21.(2024 绵阳)如图,在边长为4的菱形中,对角线与相交于点,边在轴上,,,点在反比例函数的图象上.
(1)求点,,的坐标及反比例函数的解析式;
(2)将菱形向右平移,当点恰好在反比例函数的图象上时,边与函数图象交于点,求点到轴的距离.
【答案】(1),,,,,反比例函数的解析式为;
(2).
【考点】反比例函数综合题
【专题】代数几何综合题;应用意识
【分析】(1)判断出△是等边三角形,求出点坐标,可得结论;
(2)求出平移后,,的对应点,,的坐标,求出直线的解析式,构建方程组求出点的坐标即可.
【解答】解:(1)过点作于点.
四边形是菱形,
,,
,
△是等边三角形,
,
,,
,
,
,
,,,,
,
,
点在反比例函数的图象上,
,
反比例函数的解析式为;
(2)对于反比例函数,
当时,,
当点恰好在反比例函数的图象上时,点的对应点,
菱形向右平移了4个单位,
,的对应点,,,
直线的解析式为,
由,
解得或,
,
点的坐标为,,
点到轴的距离为.
【点评】本题属于反比例函数综合题,考查了反比例函数的性质,一次函数的性质,菱形的性质,等边三角形的判定和性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
22.(2024 凉州区一模)已知,与成正比例,与成反比例,且当时,;当时,.求时,的值.
【考点】待定系数法求反比例函数解析式
【分析】首先根据正比例和反比例的定义可得,再把,;,代入得到关于、的方程组,再解可得、的值,进而可得与的解析式,再把代入计算出的值即可.
【解答】解:与成正比例,
,
与成反比例,
,
,
,
当时,;当时,,
,
解得:,
,
当时,.
【点评】此题主要考查了待定系数法求反比例函数解析式,关键是正确表示出与的关系式.
23.(2024 宁江区校级模拟)世界的面食之根就在山西.山西面食是中华民族饮食文化中的重要组成部分.如图,厨师将一定质量的面团做成拉面时,面条的总长度是面条横截面面积的反比例函数,其图象经过,两点.
(1)求与之间的函数关系式;
(2)求的值,并解释它的实际意义.
【答案】(1)与之间的函数表达式为:;
(2)当面条的横截面积为时,面条长度为.
【考点】反比例函数的应用
【专题】反比例函数及其应用;应用意识
【分析】(1)直接利用待定系数法得出反比例函数解析式即可;
(2)利用(1)中所求进而得出的值,得出其实际意义.
【解答】解:(1)设与之间的函数表达式为:,
将代入可得:,
与之间的函数表达式为:;
(2)将代入可得,
实际意义:当面条的横截面积为时,面条长度为.
【点评】此题主要考查了反比例函数的应用,正确得出理解与代表的意义是解题关键.
24.(2024 富顺县二模)如图,在平面直角坐标系中,一次函数与反比例函数的图象交于,两点,一次函数的图象与轴交于点.
(1)求一次函数的解析式;
(2)根据函数的图象,直接写出不等式的解集;
(3)点是轴上一点,且的面积等于面积的2倍,求点的坐标.
【考点】反比例函数与一次函数的交点问题
【专题】一次函数及其应用;反比例函数及其应用;几何直观;运算能力
【分析】(1)利用待定系数法求出,的坐标即可解决问题.
(2)观察图象写出一次函数的图象不在反比例函数的图象上方的自变量的取值范围即可解决问题.
(3)根据,求出的面积,设,构建方程即可解决问题.
【解答】解:(1)反比例函数的图象经过点,,
,,
解得,,
,,
把、的坐标代入得,
解得,
一次函数的解析式为.
(2)观察图象,不等式的解集为:或.
(3)连接,,由题意,
,
设,
由题意,
解得,
或.
【点评】本题考查了待定系数法求函数的解析式,根据函数的解析式求点的坐标,根据三角形的面积求点的坐标,注意数形结合思想的应用.
25.(2024 阳信县一模)如图,一次函数的图象与函数的图象交于点和点.
(1)求的值;
(2)若,根据图象直接写出当时的取值范围;
(3)点在线段上,过点作轴的垂线,交函数的图象于点,若的面积为1,求点的坐标.
【考点】反比例函数与一次函数的交点问题
【专题】一次函数及其应用;反比例函数及其应用;几何直观;运算能力
【分析】(1)根据一次函数解析式求得点的坐标,然后利用待定系数法即可求得的值;
(2)解析式联立成方程组,解方程组求得点的坐标,然后根据图象求得即可;
(3)设,则,得到,由的面积为1即可求得的值,从而求得点的坐标.
【解答】解:(1)一次函数的图象与过点,
,
点,
点在反比例函数的图象上,
;
(2)由,解得或,
,
若,当时的取值范围是;
(3)设,则,
,
的面积为1,
,即,
整理得,
解得或3,
点的坐标为或.
【点评】本题是一次函数与反比例函数的交点问题,考查了一次函数图象上点的坐标特征,函数与不等式的关系以及三角形的面积,求得交点坐标是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
中考数学一轮复习 反比例函数
一.选择题(共10小题)
1.(2024 香洲区校级一模)若反比例函数在每个象限内的函数值随的增大而减小,则
A. B. C. D.
2.(2024 晋江市模拟)如图,反比例函数图象经过正方形的顶点,边与轴交于点,若正方形的面积为12,,则的值为
A.3 B. C. D.
3.(2024 天元区校级一模)如图,点是反比例函数图象上的一点,轴于点,且面积为4.若点也是该图象上的一点,则的值为
A. B. C.2 D.4
4.(2024 江北区校级模拟)反比例函数一定经过的点是
A. B. C. D.
5.(2024 甘肃模拟)电路上在电压保持不变的条件下,电流(A)与电阻成反比例关系,与的函数图象如图,关于函数解析式是
A. B. C. D.
6.(2024 浙江)反比例函数的图象上有,两点.下列正确的选项是
A.当时, B.当时,
C.当时, D.当时,
7.(2024 十堰模拟)某个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.如图所示的是该台灯的电流(A)与电阻的关系图象,该图象经过点.根据图象可知,下列说法正确的是
A.当时,
B.与的函数关系式是
C.当时,
D.当时,的取值范围是
8.(2024 赣州模拟)如图所示为某新款茶吧机,开机加热时每分钟上升,加热到,停止加热,水温开始下降,此时水温与通电时间成反比例关系.当水温降至时,饮水机再自动加热,若水温在时接通电源,水温与通电时间之间的关系如图所示,则下列说法中错误的是
A.水温从加热到,需要
B.水温下降过程中,与的函数关系式是
C.上午10点接通电源,可以保证当天能喝到不低于的水
D.在一个加热周期内水温不低于的时间为
9.(2024 明水县一模)描点法是画未知函数图象的常用方法.请判断函数的图象可能为
A. B.
C. D.
10.(2024 丹徒区二模)如图,点是反比例函数在第二象限图象上的一点,其纵坐标为1,分别作轴、轴,点为线段的三等分点,作轴,交双曲线于点,连接.若,则的值为
A. B. C. D.
二.填空题(共10小题)
11.(2024 港南区二模)已知反比例函数的图象经过点,则的值是 .
12.(2024 娄底二模)已知反比例函数的图象位于第二、四象限,则的值可以是 .(任意写一个满足条件的值)
13.(2024 龙湖区一模)当温度不变时,某气球内的气压与气体体积成反比例函数关系(其图象如图所示),已知当气球内的气压时,气球将爆炸,为了安全起见,气球内气体体积满足的条件是 .
14.(2024 开州区模拟)如图,已知为反比例函数的图象上一点,过点作轴,垂足为,若的面积为3,则的值为 .
15.(2024 惠山区三模)如图,在平面直角坐标系中,为原点,点在第一象限,点是轴正半轴上一点,,双曲线过点,交于点,连接,若,则的值是 .
16.(2024 陈仓区一模)如图,在平面直角坐标系中,过原点的直线交反比例函数图象于,两点,轴于点,的面积为6,则的值为 .
17.(2024 港南区四模)如图,过点作直线与双曲线交于,两点,过点作轴于点,作轴于点.在轴、轴上分别取点,,使点,,在同一条直线上,且.设图中矩形的面积为,的面积为,则,的数量关系是 .
18.(2024 东莞市模拟)如图1是电压为定值的蓄电池,使用该蓄电池时,电流(单位:与电阻(单位:是反比例函数关系,它的图象如图2所示,如果以该蓄电池为电源的电器限制电流不超过,那么用电器可变电阻应控制的范围是 .
19.(2024 武威一模)如图,、是函数上两点,为一动点,作轴,轴,下列说法:①;②;③若,则平分;④若,则,正确有 .(填序号)
20.(2024 海南)某型号蓄电池的电压(单位:为定值,使用蓄电池时,电流(单位:与电阻(单位:是反比例函数关系,即,它的图象如图所示,则蓄电池的电压为 .
三.解答题(共5小题)
21.(2024 绵阳)如图,在边长为4的菱形中,对角线与相交于点,边在轴上,,,点在反比例函数的图象上.
(1)求点,,的坐标及反比例函数的解析式;
(2)将菱形向右平移,当点恰好在反比例函数的图象上时,边与函数图象交于点,求点到轴的距离.
22.(2024 凉州区一模)已知,与成正比例,与成反比例,且当时,;当时,.求时,的值.
23.(2024 宁江区校级模拟)世界的面食之根就在山西.山西面食是中华民族饮食文化中的重要组成部分.如图,厨师将一定质量的面团做成拉面时,面条的总长度是面条横截面面积的反比例函数,其图象经过,两点.
(1)求与之间的函数关系式;
(2)求的值,并解释它的实际意义.
24.(2024 富顺县二模)如图,在平面直角坐标系中,一次函数与反比例函数的图象交于,两点,一次函数的图象与轴交于点.
(1)求一次函数的解析式;
(2)根据函数的图象,直接写出不等式的解集;
(3)点是轴上一点,且的面积等于面积的2倍,求点的坐标.
25.(2024 阳信县一模)如图,一次函数的图象与函数的图象交于点和点.
(1)求的值;
(2)若,根据图象直接写出当时的取值范围;
(3)点在线段上,过点作轴的垂线,交函数的图象于点,若的面积为1,求点的坐标.
中考数学一轮复习 反比例函数
参考答案与试题解析
一.选择题(共10小题)
1.(2024 香洲区校级一模)若反比例函数在每个象限内的函数值随的增大而减小,则
A. B. C. D.
【答案】
【考点】反比例函数的性质
【专题】反比例函数及其应用;运算能力
【分析】根据反比例函数的性质即可得到结论.
【解答】解:反比例函数在每个象限内的函数值随的增大而减小,
,
,
故选:.
【点评】本题考查了反比例函数的性质,熟练掌握反比例函数的性质是解题的关键.
2.(2024 晋江市模拟)如图,反比例函数图象经过正方形的顶点,边与轴交于点,若正方形的面积为12,,则的值为
A.3 B. C. D.
【答案】
【考点】反比例函数系数的几何意义;反比例函数图象上点的坐标特征;正方形的性质
【专题】代数几何综合题;矩形 菱形 正方形;推理能力;应用意识
【分析】过作轴于,过作轴于,于,交值于,通过证得,,得出,,由,根据平行线分线段成比例定理求得,利用勾股定理以及正方形的面积即可求得的坐标,进而求得的值.
【解答】解:过作轴于,过作轴于,于,交值于,
四边形是正方形,
,,
,
,
在与中,
,
,
,,
同理,,
,,
轴,
,
,
,
,
,正方形的面积为12,
,
,
,
,,
反比例函数图象经过正方形的顶点,
,
解法二:,
设,,
,
由题意,
,
.
故选:.
【点评】本题考查了反比例函数的系数的几何意义,正方形的性质,全等三角形的判定与性质,相似三角形的判定和性质,正确的作出辅助线是解题的关键.
3.(2024 天元区校级一模)如图,点是反比例函数图象上的一点,轴于点,且面积为4.若点也是该图象上的一点,则的值为
A. B. C.2 D.4
【答案】
【考点】反比例函数图象上点的坐标特征;反比例函数系数的几何意义
【专题】反比例函数及其应用;运算能力
【分析】根据反比例函数系数的几何意义求出的值,再代入计算即可.
【解答】解:由反比例函数系数的几何意义可知,,而,
,
反比例函数的关系式为,
把点代入得,
,
故选:.
【点评】本题考查反比例函数系数的几何意义,掌握反比例函数系数的几何意义以及反比例函数图象上点的坐标的特征是正确解答的前提.
4.(2024 江北区校级模拟)反比例函数一定经过的点是
A. B. C. D.
【答案】
【考点】反比例函数图象上点的坐标特征
【专题】反比例函数及其应用;运算能力
【分析】根据对各选项进行逐一判断即可.
【解答】解:反比例函数,
,
、,此点不在函数图象上,故本选项不合题意;
、,此点在函数图象上,故本选项符合题意;
、,此点不在函数图象上,故本选项不合题意;
、,此点不在函数图象上,故本选项不合题意.
故选:.
【点评】本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数中为定值是解答此题的关键.
5.(2024 甘肃模拟)电路上在电压保持不变的条件下,电流(A)与电阻成反比例关系,与的函数图象如图,关于函数解析式是
A. B. C. D.
【考点】:根据实际问题列反比例函数关系式
【专题】29:跨学科
【分析】根据电压电流电阻得到稳定电压的值,让即可.
【解答】解:当,时,
电压,
.
故选:.
【点评】考查列反比例函数关系式,关键是根据题中所给的值确定常量电压的值.
6.(2024 浙江)反比例函数的图象上有,两点.下列正确的选项是
A.当时, B.当时,
C.当时, D.当时,
【答案】
【考点】反比例函数图象上点的坐标特征
【专题】反比例函数及其应用;推理能力
【分析】先根据反比例函数的解析式判断出函数图象所在的象限,再对各选项进行逐一判断即可.
【解答】解:反比例函数中,,
此函数图象的两个分支分别位于第一、三象限,在每一象限内随的增大而减小,
、当时,,
,
,正确,符合题意;
、当时,点在第三象限,点在第一象限,
,,
,原结论错误,不符合题意;
、由知,当时,,原结论错误,不符合题意;
、当时,,
,在第一象限,
,
,原结论错误,不符合题意.
故选:.
【点评】本题考查的是反比例函数图象上点的坐标特征,熟知反比例函数的图象与系数的关系是解题的关键.
7.(2024 十堰模拟)某个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.如图所示的是该台灯的电流(A)与电阻的关系图象,该图象经过点.根据图象可知,下列说法正确的是
A.当时,
B.与的函数关系式是
C.当时,
D.当时,的取值范围是
【答案】
【考点】反比例函数的应用;一次函数与一元一次不等式
【专题】反比例函数及其应用;运算能力
【分析】设与的函数关系式是,利用待定系数法求出,然后求出当时,,再由,得到随增大而减小,由此对各选项逐一判断即可.
【解答】解:设与的函数关系式是,
该图象经过点,
,
,
与的函数关系式是,故不符合题意;
当时,,
,
随增大而减小,
当时,,当时,,当时,的取值范围是,故、不符合题意,符合题意.
故选:.
【点评】本题主要考查了反比例函数的实际应用,正确求出反比例函数解析式是解题的关键.
8.(2024 赣州模拟)如图所示为某新款茶吧机,开机加热时每分钟上升,加热到,停止加热,水温开始下降,此时水温与通电时间成反比例关系.当水温降至时,饮水机再自动加热,若水温在时接通电源,水温与通电时间之间的关系如图所示,则下列说法中错误的是
A.水温从加热到,需要
B.水温下降过程中,与的函数关系式是
C.上午10点接通电源,可以保证当天能喝到不低于的水
D.在一个加热周期内水温不低于的时间为
【答案】
【考点】反比例函数的应用
【专题】一次函数及其应用;反比例函数及其应用;运算能力;应用意识
【分析】根据水温升高的速度,即可求出水温从加热到所需的时间;设水温下降过程中,与的函数关系式为,根据待定系数法即可求解;先求出当水温下降到20摄氏度所需时间为,即一个循环为,,将代入反比例函数解析式中求出此时水温即可判断;分别求出在加热过程和降温过程中水温为40摄氏度时的时间,再相减即可判断.
【解答】解:开机加热时每分钟上升,
水温从加热到,所需时间为,故选项正确,不符合题意;
设水温下降过程中,与的函数关系式为,
由题意得,点在反比例函数的图象上,
,
解得:,
水温下降过程中,与的函数关系式是,故选项正确,不符合题意;
令,则,
,
从开机加热到水温降至需要,即一个循环为,
水温与通电时间的函数关系式为,
上午10点到共30分钟,,
当时,,
即此时的水温为,故选项正确,不符合题意;
在加热过程中,水温为时,,
解得:,
在降温过程中,水温为时,,
解得:,
,
一个加热周期内水温不低于的时间为,故选项错误,符合题意.
故选:.
【点评】本题主要考查反比例函数和一次函数的应用、用待定系数法求反比例函数解析数,解题关键在于读懂图象,灵活运用所学知识解决问题.
9.(2024 明水县一模)描点法是画未知函数图象的常用方法.请判断函数的图象可能为
A. B.
C. D.
【答案】
【考点】反比例函数的图象
【专题】推理能力;反比例函数及其应用;几何直观
【分析】根据反比例函数的性质可知函数在第一、三象限,对称中心为原点,根据函数平移的规律,把向左平移1个单位得到,对称中心为,据此即可判断.
【解答】解:,
函数在第一、三象限,对称中心为原点,
把向左平移1个单位得到,对称中心为,
故选:.
【点评】本题考查了反比例函数的图象和性质,函数与函数的关系是解题的关键.
10.(2024 丹徒区二模)如图,点是反比例函数在第二象限图象上的一点,其纵坐标为1,分别作轴、轴,点为线段的三等分点,作轴,交双曲线于点,连接.若,则的值为
A. B. C. D.
【答案】
【考点】反比例函数图象上点的坐标特征
【专题】反比例函数及其应用;运算能力
【分析】根据反比例函数图象上点的坐标特征解答即可.
【解答】解:设,则,,,,,
,
,
解得.
故选:.
【点评】本题考查了反比例函数图象上点的坐标特征,熟练掌握反比例函数图象上点的坐标特征是关键.
二.填空题(共10小题)
11.(2024 港南区二模)已知反比例函数的图象经过点,则的值是 6 .
【考点】待定系数法求反比例函数解析式
【分析】把点代入反比例函数中,可直接求的值.
【解答】解:依题意,得时,,
所以,,
故答案为:6.
【点评】本题考查了待定系数法求反比例函数解析式,反比例函数图象上点的坐标特点.关键是设函数关系式,根据已知条件求函数关系式.
12.(2024 娄底二模)已知反比例函数的图象位于第二、四象限,则的值可以是 0 .(任意写一个满足条件的值)
【答案】0(答案不唯一).
【考点】反比例函数的性质
【专题】反比例函数及其应用;应用意识
【分析】先根据反比例函数的图象位于第二、四象限得出的取值范围,进而可而得出答案.
【解答】解:反比例函数的图象位于第二、四象限,
,
,
的值可以是0,
故答案为:0(答案不唯一).
【点评】本题考查的是反比例函数的图象与系数的关系,掌握反比例函数的性质是关键.
13.(2024 龙湖区一模)当温度不变时,某气球内的气压与气体体积成反比例函数关系(其图象如图所示),已知当气球内的气压时,气球将爆炸,为了安全起见,气球内气体体积满足的条件是 .
【答案】.
【考点】反比例函数的应用
【专题】反比例函数及其应用;应用意识
【分析】根据题意可知温度不变时,气球内气体的气压是气体体积的反比例函数,且过点故;故当,可判断应满足的条件.
【解答】解:设球内气体的气压和气体体积的关系式为,
图象过点,
,
,
由已知得图象在第一象限内,
随的增大而减小,
当时,,
,即不小于,
故答案为:.
【点评】本题考查反比例函数的应用,解题的关键是根据图象上的已知点的坐标,利用待定系数法求出函数解析式.
14.(2024 开州区模拟)如图,已知为反比例函数的图象上一点,过点作轴,垂足为,若的面积为3,则的值为 .
【答案】.
【考点】反比例函数图象上点的坐标特征;反比例函数系数的几何意义
【专题】反比例函数及其应用;应用意识
【分析】利用反比例函数比例系数的几何意义得到,然后根据反比例函数的性质确定的值.
【解答】解:轴,
,
而,
.
故答案为:.
【点评】本题考查了反比例函数比例系数的几何意义:在反比例函数图象中任取一点,过这一个点向轴和轴分别作垂线,与坐标轴围成的矩形的面积是定值.在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是,且保持不变.
15.(2024 惠山区三模)如图,在平面直角坐标系中,为原点,点在第一象限,点是轴正半轴上一点,,双曲线过点,交于点,连接,若,则的值是 .
【答案】.
【考点】反比例函数图象上点的坐标特征
【专题】反比例函数及其应用;推理能力
【分析】过点作,得,设线段,可得点坐标,由点,点在反比例函数上即可的,的比值,最后通过求解即可.
【解答】解:过点作,如图:
则,
,
,
,
,,
设,可得:
点、,
双曲线过点,点,
,,
,
,
解得:或(舍去),
,,
,
,
,
故答案为:.
【点评】本题考查了反比例函数图象上点的坐标特征,解题关键是掌握“铅锤法”作直角三角形,
16.(2024 陈仓区一模)如图,在平面直角坐标系中,过原点的直线交反比例函数图象于,两点,轴于点,的面积为6,则的值为 .
【答案】.
【考点】反比例函数系数的几何意义
【专题】推理能力;反比例函数及其应用;运算能力
【分析】根据反比例函数的对称性和反比例函数系数的几何意义,可求出,再根据图象所在的象限确定的值即可.
【解答】解:由对称性可知,,
,
轴,的面积为6,
,
又,
,
故答案为:.
【点评】本题考查反比例函数系数的几何意义,掌握反比例函数系数的几何意义以及反比例函数的性质是正确解答的关键.
17.(2024 港南区四模)如图,过点作直线与双曲线交于,两点,过点作轴于点,作轴于点.在轴、轴上分别取点,,使点,,在同一条直线上,且.设图中矩形的面积为,的面积为,则,的数量关系是 .
【考点】反比例函数系数的几何意义;三角形中位线定理
【分析】过点作轴于点,根据反比例函数图象系数的几何意义即可得出、,再根据中位线的性质即可得出,由此即可得出、的数学量关系.
【解答】解:过点作轴于点,如图所示.
轴,轴,轴,
,.
.轴,轴,
,,
,
,
即.
故答案为:.
【点评】本题考查了反比例函数图象系数的几何意义以及三角形的中位线,根据反比例函数图象系数的几何意义找出、是解题的关键.
18.(2024 东莞市模拟)如图1是电压为定值的蓄电池,使用该蓄电池时,电流(单位:与电阻(单位:是反比例函数关系,它的图象如图2所示,如果以该蓄电池为电源的电器限制电流不超过,那么用电器可变电阻应控制的范围是 .
【答案】.
【考点】反比例函数的应用
【专题】反比例函数及其应用;运算能力
【分析】设电流(单位:与电阻(单位:是反比例函数关系为,利用待定系数求出,再求出当,,最后根据反比例函数的增减性进行求解即可.
【解答】解:设电流(单位:与电阻(单位:是反比例函数关系为,
把点代入中得,,
,
,
当时,,
解得,
,
电流随电阻的增大而减小,
限制电流不能超过,那么用电器可变电阻应控制的范围是,
故答案为:.
【点评】本题主要考查了反比例函数的实际应用,正确求出是解题的关键.
19.(2024 武威一模)如图,、是函数上两点,为一动点,作轴,轴,下列说法:①;②;③若,则平分;④若,则,正确有 ②③④ .(填序号)
【答案】②③④.
【考点】反比例函数系数的几何意义;反比例函数图象上点的坐标特征;全等三角形的判定与性质
【专题】反比例函数及其应用;图形的全等;应用意识
【分析】根据点是动点,得到与不一定相等,判断出①错误;设出点的坐标,得出,,利用三角形面积公式计算即可判断出②正确;利用角平分线定理的逆定理判断出③正确;求出矩形,进而得出,根据三角形的面积公式计算,即可得出结论.
【解答】解:点是动点,
与不一定相等,
与不一定全等,故①错误;
设,
轴,
,
,
,
轴,
,
,
,
,②正确;
如图1,作于,于,
,,
,
,,,
平分,③正确;
如图2,延长交轴于,延长交轴于,
轴,轴,又,
四边形是矩形,
点,在双曲线上,
,
,
,
,
,
,
,
,
,④正确;
故答案为②③④.
【点评】本题考查的是反比例函数的性质、三角形面积公式、角平分线定理逆定理、矩形的判定和性质,掌握反比例函数图象上点的坐标特征、正确作出辅助线是解本题的关键.
20.(2024 海南)某型号蓄电池的电压(单位:为定值,使用蓄电池时,电流(单位:与电阻(单位:是反比例函数关系,即,它的图象如图所示,则蓄电池的电压为 64 .
【答案】64.
【考点】反比例函数的应用
【专题】跨学科;反比例函数及其应用;推理能力
【分析】根据题意,先列出反比例函数解析式,根据函数图象过代入计算出值即可.
【解答】解:电流(单位:与电阻(单位:是反比例函数关系,
,
由图象可知,当时,,
.
故答案为:64.
【点评】本题考查了反比例函数的应用,熟练掌握反比例函数的性质是关键.
三.解答题(共5小题)
21.(2024 绵阳)如图,在边长为4的菱形中,对角线与相交于点,边在轴上,,,点在反比例函数的图象上.
(1)求点,,的坐标及反比例函数的解析式;
(2)将菱形向右平移,当点恰好在反比例函数的图象上时,边与函数图象交于点,求点到轴的距离.
【答案】(1),,,,,反比例函数的解析式为;
(2).
【考点】反比例函数综合题
【专题】代数几何综合题;应用意识
【分析】(1)判断出△是等边三角形,求出点坐标,可得结论;
(2)求出平移后,,的对应点,,的坐标,求出直线的解析式,构建方程组求出点的坐标即可.
【解答】解:(1)过点作于点.
四边形是菱形,
,,
,
△是等边三角形,
,
,,
,
,
,
,,,,
,
,
点在反比例函数的图象上,
,
反比例函数的解析式为;
(2)对于反比例函数,
当时,,
当点恰好在反比例函数的图象上时,点的对应点,
菱形向右平移了4个单位,
,的对应点,,,
直线的解析式为,
由,
解得或,
,
点的坐标为,,
点到轴的距离为.
【点评】本题属于反比例函数综合题,考查了反比例函数的性质,一次函数的性质,菱形的性质,等边三角形的判定和性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
22.(2024 凉州区一模)已知,与成正比例,与成反比例,且当时,;当时,.求时,的值.
【考点】待定系数法求反比例函数解析式
【分析】首先根据正比例和反比例的定义可得,再把,;,代入得到关于、的方程组,再解可得、的值,进而可得与的解析式,再把代入计算出的值即可.
【解答】解:与成正比例,
,
与成反比例,
,
,
,
当时,;当时,,
,
解得:,
,
当时,.
【点评】此题主要考查了待定系数法求反比例函数解析式,关键是正确表示出与的关系式.
23.(2024 宁江区校级模拟)世界的面食之根就在山西.山西面食是中华民族饮食文化中的重要组成部分.如图,厨师将一定质量的面团做成拉面时,面条的总长度是面条横截面面积的反比例函数,其图象经过,两点.
(1)求与之间的函数关系式;
(2)求的值,并解释它的实际意义.
【答案】(1)与之间的函数表达式为:;
(2)当面条的横截面积为时,面条长度为.
【考点】反比例函数的应用
【专题】反比例函数及其应用;应用意识
【分析】(1)直接利用待定系数法得出反比例函数解析式即可;
(2)利用(1)中所求进而得出的值,得出其实际意义.
【解答】解:(1)设与之间的函数表达式为:,
将代入可得:,
与之间的函数表达式为:;
(2)将代入可得,
实际意义:当面条的横截面积为时,面条长度为.
【点评】此题主要考查了反比例函数的应用,正确得出理解与代表的意义是解题关键.
24.(2024 富顺县二模)如图,在平面直角坐标系中,一次函数与反比例函数的图象交于,两点,一次函数的图象与轴交于点.
(1)求一次函数的解析式;
(2)根据函数的图象,直接写出不等式的解集;
(3)点是轴上一点,且的面积等于面积的2倍,求点的坐标.
【考点】反比例函数与一次函数的交点问题
【专题】一次函数及其应用;反比例函数及其应用;几何直观;运算能力
【分析】(1)利用待定系数法求出,的坐标即可解决问题.
(2)观察图象写出一次函数的图象不在反比例函数的图象上方的自变量的取值范围即可解决问题.
(3)根据,求出的面积,设,构建方程即可解决问题.
【解答】解:(1)反比例函数的图象经过点,,
,,
解得,,
,,
把、的坐标代入得,
解得,
一次函数的解析式为.
(2)观察图象,不等式的解集为:或.
(3)连接,,由题意,
,
设,
由题意,
解得,
或.
【点评】本题考查了待定系数法求函数的解析式,根据函数的解析式求点的坐标,根据三角形的面积求点的坐标,注意数形结合思想的应用.
25.(2024 阳信县一模)如图,一次函数的图象与函数的图象交于点和点.
(1)求的值;
(2)若,根据图象直接写出当时的取值范围;
(3)点在线段上,过点作轴的垂线,交函数的图象于点,若的面积为1,求点的坐标.
【考点】反比例函数与一次函数的交点问题
【专题】一次函数及其应用;反比例函数及其应用;几何直观;运算能力
【分析】(1)根据一次函数解析式求得点的坐标,然后利用待定系数法即可求得的值;
(2)解析式联立成方程组,解方程组求得点的坐标,然后根据图象求得即可;
(3)设,则,得到,由的面积为1即可求得的值,从而求得点的坐标.
【解答】解:(1)一次函数的图象与过点,
,
点,
点在反比例函数的图象上,
;
(2)由,解得或,
,
若,当时的取值范围是;
(3)设,则,
,
的面积为1,
,即,
整理得,
解得或3,
点的坐标为或.
【点评】本题是一次函数与反比例函数的交点问题,考查了一次函数图象上点的坐标特征,函数与不等式的关系以及三角形的面积,求得交点坐标是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
