2026年中考数学一轮复习 平面直角坐标系(含解析)
文档属性
| 名称 | 2026年中考数学一轮复习 平面直角坐标系(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 17:59:49 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中考数学一轮复面直角坐标系
一.选择题(共10小题)
1.(2024 新城区模拟)在平面直角坐标系中,点所在的象限是
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.(2024 沿河县一模)如图,小明用手盖住的点的坐标可能为
A. B. C. D.
3.(2024 钱塘区三模)在平面直角坐标系中,坐标为的点在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.(2024 仁和区一模)已知点的坐标为,直线轴,且,则点的坐标为
A.或 B.或
C.或 D.或
5.(2024 杭州三模)如图,弹性小球从点出发,沿所示方向运动,每当小球碰到正方形的边时反弹,反弹时反射角等于入射角,当小球第1次碰到正方形的边时的点为,第2次碰到正方形的边时的点为,,第次碰到正方形的边时的点为,则点的坐标是
A. B. C. D.
6.(2024 喀什地区二模)若点在第二象限,且到轴的距离是3,到轴的距离是1,则点的坐标是
A. B. C. D.
7.(2024 恩施市模拟)在平面直角坐标系中,第四象限内的点到轴的距离是3,到轴的距离是2,已知平行于轴且,则点的坐标是
A.或 B.
C. D.或
8.(2024 泗阳县一模)如果点在第二象限,那么点在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.(2024 沈丘县二模)如图,在一单位为1的方格纸上,△,△,△,都是斜边在轴上,斜边长分别为2,4,6,的等腰直角三角形,若的顶点坐标分别为,,,则依图中所示规律,的坐标为
A. B. C. D.
10.(2024 杭州三模)点在第二象限,距离轴5个单位长度,距离轴3个单位长度,则点的坐标为
A. B. C. D.
二.填空题(共10小题)
11.(2024 朔州模拟)我国水墨画发展有着悠远历史,相传始于唐代,成于五代,盛于宋元,明清及近代以来续有发展,重于意境优美,图为水墨画“早有蜻蜓立上头”,若将其放在平面直角坐标系中,点,,则点坐标为 .
12.(2024 岳阳县一模)若点在轴上,则的坐标是 .
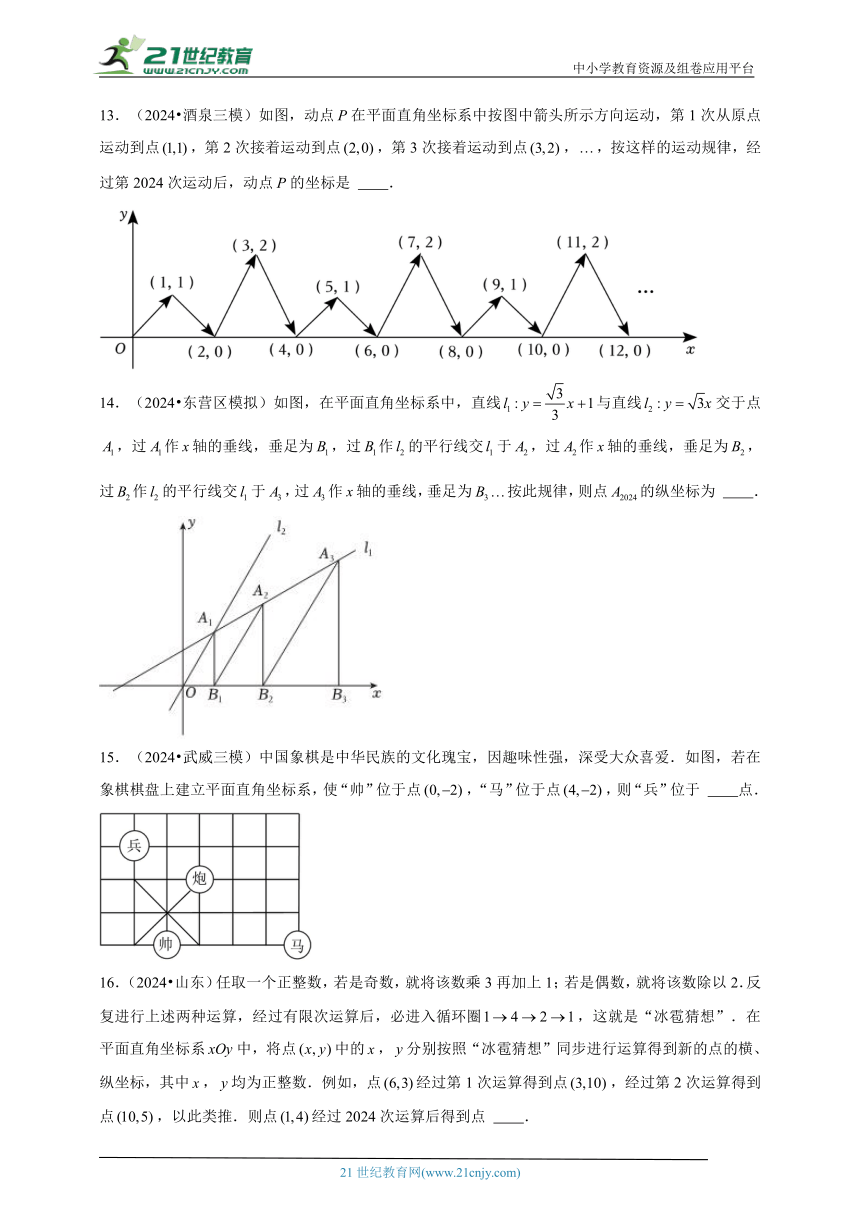
13.(2024 酒泉三模)如图,动点在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点,第2次接着运动到点,第3次接着运动到点,,按这样的运动规律,经过第2024次运动后,动点的坐标是 .
14.(2024 东营区模拟)如图,在平面直角坐标系中,直线与直线交于点,过作轴的垂线,垂足为,过作的平行线交于,过作轴的垂线,垂足为,过作的平行线交于,过作轴的垂线,垂足为按此规律,则点的纵坐标为 .
15.(2024 武威三模)中国象棋是中华民族的文化瑰宝,因趣味性强,深受大众喜爱.如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点,“马”位于点,则“兵”位于 点.
16.(2024 山东)任取一个正整数,若是奇数,就将该数乘3再加上1;若是偶数,就将该数除以2.反复进行上述两种运算,经过有限次运算后,必进入循环圈,这就是“冰雹猜想”.在平面直角坐标系中,将点中的,分别按照“冰雹猜想”同步进行运算得到新的点的横、纵坐标,其中,均为正整数.例如,点经过第1次运算得到点,经过第2次运算得到点,以此类推.则点经过2024次运算后得到点 .
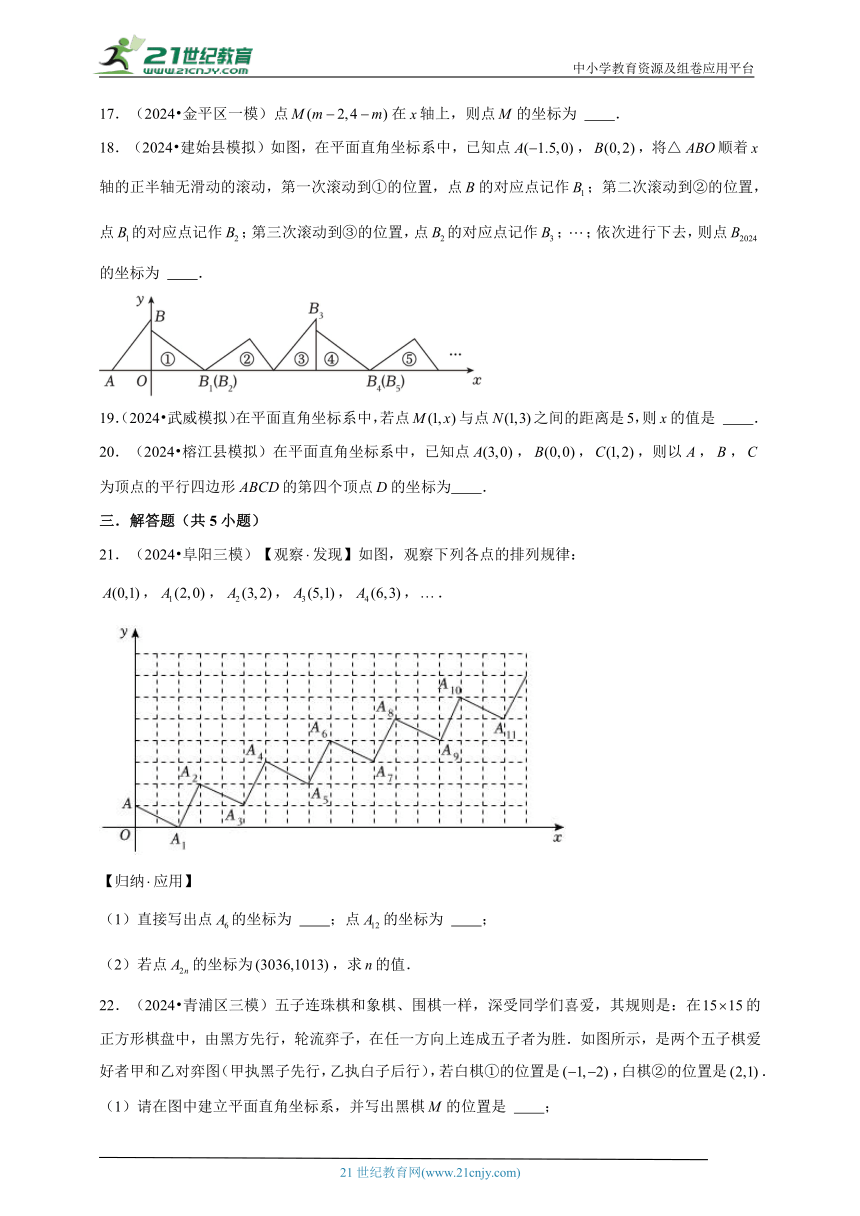
17.(2024 金平区一模)点在轴上,则点的坐标为 .
18.(2024 建始县模拟)如图,在平面直角坐标系中,已知点,,将△顺着轴的正半轴无滑动的滚动,第一次滚动到①的位置,点的对应点记作;第二次滚动到②的位置,点的对应点记作;第三次滚动到③的位置,点的对应点记作;;依次进行下去,则点的坐标为 .
19.(2024 武威模拟)在平面直角坐标系中,若点与点之间的距离是5,则的值是 .
20.(2024 榕江县模拟)在平面直角坐标系中,已知点,,,则以,,为顶点的平行四边形的第四个顶点的坐标为 .
三.解答题(共5小题)
21.(2024 阜阳三模)【观察发现】如图,观察下列各点的排列规律:
,,,,,.
【归纳应用】
(1)直接写出点的坐标为 ;点的坐标为 ;
(2)若点的坐标为,求的值.
22.(2024 青浦区三模)五子连珠棋和象棋、围棋一样,深受同学们喜爱,其规则是:在的正方形棋盘中,由黑方先行,轮流弈子,在任一方向上连成五子者为胜.如图所示,是两个五子棋爱好者甲和乙对弈图(甲执黑子先行,乙执白子后行),若白棋①的位置是,白棋②的位置是.
(1)请在图中建立平面直角坐标系,并写出黑棋的位置是 ;
(2)甲必须在何处落子,才不会让乙在短时间内获胜,直接写出对应的点的位置.
23.(2024 奉贤区三模)国际象棋玩过么?国王走一步能够移动到相邻的8个方格中的随意一个,那么国王从格子, 走到格子, 的最少步数就是数学的一种距离,叫“切比雪夫距离”.在平面直角坐标系中,对于任意两点, 与, 的“切比雪夫距离”,给出如下定义:若,则点, 与, 的“切比雪夫距离”为;若,则点, 与, 的“切比雪夫距离”为;
(1)已知,
①若的坐标为,则点与的“切比雪夫距离”为 ;
②若为轴上的动点,那么点与 “切比雪夫距离”的最小值为 ;
(2)已知,,设点与的“切比雪夫距离”为,若,求(用含的式子表示).
24.(2024 吴江区二模)已知点回答下列问题:
(1)点在轴上,求出点的坐标;
(2)点在第二象限,且它到轴、轴的距离相等,求的值
25.(2024 中山市三模)如图所示是地球截面图,其中,分别表示南回归线和北回归线,表示赤道,点表示太原市的位置.现已知地球南回归线的纬度是南纬,太原市的纬度是北纬,而冬至正午时,太阳光直射南回归线(光线的延长线经过地心,则太原市冬至正午时,太阳光线与地面水平线的夹角的度数是 .
中考数学一轮复面直角坐标系
参考答案与试题解析
一.选择题(共10小题)
1.(2024 新城区模拟)在平面直角坐标系中,点所在的象限是
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】
【考点】点的坐标
【专题】平面直角坐标系;数据分析观念
【分析】根据点横纵坐标符号判定即可.
【解答】解:,,,
点在第二象限,
故选:.
【点评】本题考查点所在象限,熟练掌握平面直角坐标系各象限内事业的坐标符号:第一象限,第二象限,第三象限,第四象限是解题的关键.
2.(2024 沿河县一模)如图,小明用手盖住的点的坐标可能为
A. B. C. D.
【答案】
【考点】点的坐标
【专题】平面直角坐标系;数据分析观念
【分析】先判断出小手盖住的点在第二象限,再根据各象限内点的坐标特征解答.
【解答】解:由图可知,小手盖住的点在第二象限,
,,,中只有在第二象限.
故选:.
【点评】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限;第二象限;第三象限;第四象限.
3.(2024 钱塘区三模)在平面直角坐标系中,坐标为的点在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】
【考点】点的坐标
【专题】平面直角坐标系;应用意识
【分析】根据象限内点的坐标特征即可得出答案.
【解答】解:横坐标为负,纵坐标为正的点在第二象限内.
故选:.
【点评】本题主要考查点的坐标,牢记各象限内点的坐标性质是解题的关键.
4.(2024 仁和区一模)已知点的坐标为,直线轴,且,则点的坐标为
A.或 B.或
C.或 D.或
【答案】
【考点】坐标与图形性质
【专题】应用意识;平面直角坐标系
【分析】根据平行于轴的直线上的点的纵坐标相等求出点的纵坐标,再分点在点的左边与右边两种情况求出点的横坐标,即可得解.
【解答】解:轴,点的坐标为,
点的纵坐标为2,
,
点在点的左边时,横坐标为,
点在点的右边时,横坐标为,
点的坐标为或.
故选:.
【点评】本题考查了坐标与图形性质,主要利用了平行于轴的直线是上的点的纵坐标相等的性质,难点在于要分情况讨论.
5.(2024 杭州三模)如图,弹性小球从点出发,沿所示方向运动,每当小球碰到正方形的边时反弹,反弹时反射角等于入射角,当小球第1次碰到正方形的边时的点为,第2次碰到正方形的边时的点为,,第次碰到正方形的边时的点为,则点的坐标是
A. B. C. D.
【答案】
【考点】规律型:点的坐标
【专题】规律型;平面直角坐标系;运算能力;推理能力
【分析】按照反弹角度依次画图,探索反弹规律,即可求出答案.
【解答】解:根据反射角等于入射角画图如下,
由图中可知,,,,,最后再反射到,由此可知,每6次循环一次,
,
点的坐标与相同,
.
故选:.
【点评】本题考查了点的坐标规律探究性问题,解题的关键在于寻找循环坐标,得出规律.
6.(2024 喀什地区二模)若点在第二象限,且到轴的距离是3,到轴的距离是1,则点的坐标是
A. B. C. D.
【答案】
【考点】点的坐标
【专题】平面直角坐标系;几何直观
【分析】根据到轴的距离是纵坐标的绝对值,到轴的距离是横坐标的绝对值进行求解即可.
【解答】解:点到轴的距离是3,到轴的距离是1,
点的横坐标的绝对值为1,纵坐标的绝对值为3,
又点在第二象限,
点的坐标为.
故选:.
【点评】本题考查了平面直角坐标系各象限坐标符号的特征和点到坐标轴的距离,掌握各象限坐标符号的特征和点到坐标轴的距离是关键.
7.(2024 恩施市模拟)在平面直角坐标系中,第四象限内的点到轴的距离是3,到轴的距离是2,已知平行于轴且,则点的坐标是
A.或 B.
C. D.或
【答案】
【考点】坐标与图形性质
【专题】平面直角坐标系;推理能力
【分析】先根据题意得出点坐标,根据平行于轴设出点的坐标,进而可得出结论.
【解答】解:第四象限内的点到轴的距离是3,到轴的距离是2,
,
平行于轴,
设,
,
,
或,
或.
故选:.
【点评】本题考查的是坐标与图形性质,熟知平行于轴的直线上各点的纵坐标相等是解题的关键.
8.(2024 泗阳县一模)如果点在第二象限,那么点在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】
【考点】点的坐标
【专题】平面直角坐标系;符号意识
【分析】根据各象限内点的坐标的符号特征解答即可.
【解答】解:点在第二象限,
,,
,
点在第一象限.
故选:.
【点评】本题考查了各象限内点的坐标的符号特征以及解不等式,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限;第二象限;第三象限;第四象限.
9.(2024 沈丘县二模)如图,在一单位为1的方格纸上,△,△,△,都是斜边在轴上,斜边长分别为2,4,6,的等腰直角三角形,若的顶点坐标分别为,,,则依图中所示规律,的坐标为
A. B. C. D.
【答案】
【考点】规律型:点的坐标
【专题】规律型;平面直角坐标系;等腰三角形与直角三角形;推理能力
【分析】根据脚码确定出脚码为偶数时的点的坐标,得到规律当脚码是2、6、时,横坐标为1,纵坐标为脚码的一半的相反数,当脚码是4、8、时,横坐标是1,纵坐标为脚码的一半,然后确定出第2022个点的坐标即可.
【解答】解:各三角形都是等腰直角三角形,
直角顶点的纵坐标的长度为斜边的一半,
,,,,,,,
,
点在第四象限,横坐标是1,纵坐标的绝对值是,
的坐标为.
故选:.
【点评】本题是对点的坐标变化规律的考查,根据2020是偶数,求出点的脚码是偶数时的变化规律是解题的关键.
10.(2024 杭州三模)点在第二象限,距离轴5个单位长度,距离轴3个单位长度,则点的坐标为
A. B. C. D.
【答案】
【考点】点的坐标
【专题】平面直角坐标系;符号意识
【分析】首先确定点的横纵坐标的正负号,再根据距坐标轴的距离确定点的坐标.
【解答】解:点位于第二象限,
点的横坐标为负数,纵坐标为正数,
点距离轴5个单位长度,距离轴3个单位长度,
点的坐标为.
故选:.
【点评】此题主要考查了点的坐标,解决本题的关键是掌握好四个象限的点的坐标的特征:第一象限正正,第二象限负正,第三象限负负,第四象限正负.
二.填空题(共10小题)
11.(2024 朔州模拟)我国水墨画发展有着悠远历史,相传始于唐代,成于五代,盛于宋元,明清及近代以来续有发展,重于意境优美,图为水墨画“早有蜻蜓立上头”,若将其放在平面直角坐标系中,点,,则点坐标为 .
【答案】.
【考点】点的坐标
【专题】平面直角坐标系;运算能力
【分析】根据已知点的坐标,找出原点,建立平面直角坐标系,然后根据点的位置,写出点的坐标.
【解答】解:如图所示,根据点,,建立坐标系,如图所示:
点坐标为:,
故答案为:.
【点评】本题主要考查了点的坐标,解题关键是熟练掌握根据已知点的坐标,找出坐标原点.
12.(2024 岳阳县一模)若点在轴上,则的坐标是 .
【答案】.
【考点】点的坐标
【专题】符号意识;平面直角坐标系
【分析】根据轴上点的横坐标为0解答即可.
【解答】解:由题意得:,
,
,
的坐标是,
故答案为:.
【点评】本题考查了点的坐标特征,熟知轴上点的横坐标为0是解题的关键.
13.(2024 酒泉三模)如图,动点在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点,第2次接着运动到点,第3次接着运动到点,,按这样的运动规律,经过第2024次运动后,动点的坐标是 .
【考点】规律型:点的坐标
【专题】规律型;几何直观;推理能力
【分析】观察点的坐标变化发现每个点的横坐标与运动的次数相等,纵坐标是1,0,2,0,每4个数一个循环,按照此规律解答即可.
【解答】解:观察点的坐标变化可知:
第1次从原点运动到点,
第2次接着运动到点,
第3次接着运动到点,
第4次接着运动到点,
第5次接着运动到点,
,
按这样的运动规律,发现每个点的横坐标与运动的次数相等,纵坐标是1,0,2,0,每4个数一个循环,
由于,
所以经过第2024次运动后,动点的坐标是.
故答案为:.
【点评】本题考查了点的坐标规律探求,属于常考题型,由已知点的坐标变化找出规律是解题的关键.
14.(2024 东营区模拟)如图,在平面直角坐标系中,直线与直线交于点,过作轴的垂线,垂足为,过作的平行线交于,过作轴的垂线,垂足为,过作的平行线交于,过作轴的垂线,垂足为按此规律,则点的纵坐标为 . .
【答案】.
【考点】规律型:点的坐标
【专题】规律型;推理能力
【分析】联立直线与直线的表达式并解得:,,故,,依次求出:点的纵坐标为、的纵坐标为,即可求解.
【解答】解:联立直线与直线的表达式并解得:,,故,;
则点,,则直线的表达式为:,
将点坐标代入上式并解得:直线的表达式为:,
将表达式与直线的表达式联立并解得:,,即点的纵坐标为;
同理可得的纵坐标为,
按此规律,则点的纵坐标为,
故答案为:.
【点评】本题考查了两直线的交点,要求利用图象求解各问题,要认真体会点的坐标,一次函数与二元一次方程组之间的内在联系.
15.(2024 武威三模)中国象棋是中华民族的文化瑰宝,因趣味性强,深受大众喜爱.如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点,“马”位于点,则“兵”位于 点.
【答案】.
【考点】坐标确定位置
【专题】平面直角坐标系;几何直观
【分析】直接利用已知点坐标建立平面直角坐标系,进而得出点的坐标.
【解答】解:如图所示:“兵”位于点.
故答案为:.
【点评】此题主要考查了坐标确定位置,正确得出原点位置是解题关键.
16.(2024 山东)任取一个正整数,若是奇数,就将该数乘3再加上1;若是偶数,就将该数除以2.反复进行上述两种运算,经过有限次运算后,必进入循环圈,这就是“冰雹猜想”.在平面直角坐标系中,将点中的,分别按照“冰雹猜想”同步进行运算得到新的点的横、纵坐标,其中,均为正整数.例如,点经过第1次运算得到点,经过第2次运算得到点,以此类推.则点经过2024次运算后得到点 .
【考点】规律型:点的坐标
【专题】规律型;推理能力
【分析】根据新定义依次计算出各点的坐标,然后找出规律,最后应用规律求解即可.
【解答】解:点经过1次运算后得到点为,即为,
经过2次运算后得到点为,即为,
经过3次运算后得到点为,即为,
,
发现规律:点经过3次运算后还是,
,
点经过2024次运算后得到点,
故答案为:.
【点评】本题考查了规律型:点的坐标,解答本题的关键是找到规律点经过3次运算后还是.
17.(2024 金平区一模)点在轴上,则点的坐标为 .
【考点】点的坐标
【专题】平面直角坐标系;符号意识
【分析】直接利用在轴上点的坐标性质得出纵坐标为零,进而得出答案.
【解答】解:是轴上的点,
,
解得:.
.
点的坐标为.
故答案为.
【点评】此题主要考查了点的坐标,正确把握轴上点的坐标性质是解题关键.
18.(2024 建始县模拟)如图,在平面直角坐标系中,已知点,,将△顺着轴的正半轴无滑动的滚动,第一次滚动到①的位置,点的对应点记作;第二次滚动到②的位置,点的对应点记作;第三次滚动到③的位置,点的对应点记作;;依次进行下去,则点的坐标为 .
【答案】.
【考点】规律型:点的坐标
【专题】推理能力;规律型
【分析】先求出,再利用先利用翻转的性质、点坐标的变化规律分别求出点,,,,,的坐标,再归纳总结出一般规律,由此即可得出答案.
【解答】解;,,
,
由翻转的性质得:,则,
由翻转过程可知,点,重合,则,
点的横坐标为,纵坐标为2,即,
同理可得:点,重合,点,的横坐标为,纵坐标为0,
即,,
点的横坐标为,纵坐标为2,即,
归纳类推得出以下规律:(其中,为正整数),
(1)点,,,,的横坐标变化规律为2,8,14,,,纵坐标均为0,
(2)点,,,,的横坐标变化规律为2,8,14,,,纵坐标均为0,
(3)点,,,的横坐标变化规律为6,12,,,纵坐标均为2,
,
点的坐标变化规律符合(1),
则点的横坐标为,纵坐标为0,即,
故答案为:.
【点评】本题考查了规律型的点的坐标,数形结合并发现循环规律是解题的关键.
19.(2024 武威模拟)在平面直角坐标系中,若点与点之间的距离是5,则的值是 或8 .
【考点】坐标与图形性质
【专题】线段、角、相交线与平行线
【分析】点、的横坐标相等,则直线在平行于轴的直线上,根据两点间的距离,可列出等式,从而解得的值.
【解答】解:点与点之间的距离是5,
,
解得或8.
故答案为:或8.
【点评】本题是基础题,考查了坐标与图形的性质,当两点的横坐标相等时,则这两点在平行于轴的直线上.
20.(2024 榕江县模拟)在平面直角坐标系中,已知点,,,则以,,为顶点的平行四边形的第四个顶点的坐标为 .
【答案】.
【考点】坐标与图形性质
【专题】应用意识;平面直角坐标系
【分析】根据题意画出图形,根据平行四边形的性质将点向右平移3个单位得到,即可求解.
【解答】解:点,,,是平行四边形,
,,
将点向右平移3个单位得到,
如图所示,
故答案为:.
【点评】本题考查了坐标与图形性质、平行四边形的性质,数形结合是解答本题的关键.
三.解答题(共5小题)
21.(2024 阜阳三模)【观察发现】如图,观察下列各点的排列规律:
,,,,,.
【归纳应用】
(1)直接写出点的坐标为 ;点的坐标为 ;
(2)若点的坐标为,求的值.
【答案】(1);;(2)1012.
【考点】规律型:点的坐标
【专题】规律型;运算能力
【分析】(1)根据图形写出坐标即可;
(2)根据题意得到,,,,以此类推得到,再根据点的坐标为建立等式求解,即可解题.
【解答】解:(1)由图知,点的坐标为,
点的坐标为;
故答案为:;.
(2),,,,,
且,,,,以此类推,
,即,
点的坐标为,
,解得.
【点评】本题考查平面直角坐标系中点的坐标,以及坐标找规律,一元一次方程的应用,解题的关键在于通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.
22.(2024 青浦区三模)五子连珠棋和象棋、围棋一样,深受同学们喜爱,其规则是:在的正方形棋盘中,由黑方先行,轮流弈子,在任一方向上连成五子者为胜.如图所示,是两个五子棋爱好者甲和乙对弈图(甲执黑子先行,乙执白子后行),若白棋①的位置是,白棋②的位置是.
(1)请在图中建立平面直角坐标系,并写出黑棋的位置是 ;
(2)甲必须在何处落子,才不会让乙在短时间内获胜,直接写出对应的点的位置.
【答案】(1);
(2)或.
【考点】坐标确定位置
【专题】几何直观;平面直角坐标系
【分析】(1)利用直角坐标系写出黑棋的位置的坐标即可;
根据五子连棋的规则,乙已把,,,三点凑成在一条直线,甲只有在此三点两端任加一点即可保证不会让乙在短时间内获胜,据此即可确定点的坐标.
【解答】解:(1)黑棋的位置如图所示:
黑棋的坐标为,
故答案为:;
(2)根据题意得,乙执的白棋已有三点,,,在一条直线上,
甲只有在此直线上距离,,最近的地方占取一点才能保证不会让乙在短时间内获胜,
即为点或.
【点评】本题考查了点的坐标的确定及生活中的棋类常识,正确理解题意和识图是解题的关键.
23.(2024 奉贤区三模)国际象棋玩过么?国王走一步能够移动到相邻的8个方格中的随意一个,那么国王从格子, 走到格子, 的最少步数就是数学的一种距离,叫“切比雪夫距离”.在平面直角坐标系中,对于任意两点, 与, 的“切比雪夫距离”,给出如下定义:若,则点, 与, 的“切比雪夫距离”为;若,则点, 与, 的“切比雪夫距离”为;
(1)已知,
①若的坐标为,则点与的“切比雪夫距离”为 3 ;
②若为轴上的动点,那么点与 “切比雪夫距离”的最小值为 ;
(2)已知,,设点与的“切比雪夫距离”为,若,求(用含的式子表示).
【答案】(1)①3;②2;(2)
【考点】坐标与图形性质;两点间的距离公式
【专题】一次方程(组及应用;运算能力
【分析】(1)①结合题意,根据“切比雪夫距离”的定义求解即可;②设点,分和两种情况讨论,即可获得答案;
(2)结合已知条件,分两种情况讨论:当时,由,,可确定此时点与的“切比雪夫距离”;当时,易得,,令,解得,即当时,点与的“切比雪夫距离” ;当时,可有,此时点与的“切比雪夫距离” .即可获得答案.
【解答】解:(1)①,,
又,,
,
根据“切比雪夫距离”的定义,点与的“切比雪夫距离”为3.
②若为轴上的动点,则可设点,
当时,,
又,
,
此时点与 “切比雪夫距离”的值为;
当时,,
又,
,
此时点与 “切比雪夫距离”的值为2.
综上所述,若为轴上的动点,那么点与 “切比雪夫距离”的最小值为2.
(2)根据已知条件,,,
则当时,
,
,
此时点与的“切比雪夫距离” ;
当时,
可有,,
令,解得,
即当时,可有,此时点与的“切比雪夫距离” ,
当时,可有,此时点与的“切比雪夫距离” .
综上所述,点与的“切比雪夫距离” .
【点评】本题主要考查了新定义“切比雪夫距离”、平面直角坐标系中点的坐标特征、化简绝对值以及一元一次不等式的应用等知识,理解题意,灵活运用相关知识是解题关键.
24.(2024 吴江区二模)已知点回答下列问题:
(1)点在轴上,求出点的坐标;
(2)点在第二象限,且它到轴、轴的距离相等,求的值
【答案】(1);
(2)2025.
【考点】点的坐标
【专题】平面直角坐标系;符号意识
【分析】(1)根据轴上点的特点作答即可;
(2)根据点到轴和轴相等列出,再结合第二象限点的特点求出,代入即可.
【解答】解:(1)在轴上,
,
解得:,
,
;
(2)点到轴和轴距离相等,
,
在第二象限,
,,
,,
,
解得:,
.
【点评】本题主要考查的是点的坐标,熟知平面直角坐标系内点的坐标特点是解题的关键.
25.(2024 中山市三模)如图所示是地球截面图,其中,分别表示南回归线和北回归线,表示赤道,点表示太原市的位置.现已知地球南回归线的纬度是南纬,太原市的纬度是北纬,而冬至正午时,太阳光直射南回归线(光线的延长线经过地心,则太原市冬至正午时,太阳光线与地面水平线的夹角的度数是 .
【答案】.
【考点】坐标确定位置;平行线的性质
【专题】推理能力;平面直角坐标系;运算能力
【分析】设与交于点,先由三角形内角和定理求出.,再根据平行线的性质求解即可.
【解答】解:如图,设与交于点,
,,
,
在中,,,
,
,
,
故答案为:.
【点评】本题考查了三角形内角和定理,平行线的性质,读懂题意并熟练掌握知识点是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
中考数学一轮复面直角坐标系
一.选择题(共10小题)
1.(2024 新城区模拟)在平面直角坐标系中,点所在的象限是
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.(2024 沿河县一模)如图,小明用手盖住的点的坐标可能为
A. B. C. D.
3.(2024 钱塘区三模)在平面直角坐标系中,坐标为的点在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.(2024 仁和区一模)已知点的坐标为,直线轴,且,则点的坐标为
A.或 B.或
C.或 D.或
5.(2024 杭州三模)如图,弹性小球从点出发,沿所示方向运动,每当小球碰到正方形的边时反弹,反弹时反射角等于入射角,当小球第1次碰到正方形的边时的点为,第2次碰到正方形的边时的点为,,第次碰到正方形的边时的点为,则点的坐标是
A. B. C. D.
6.(2024 喀什地区二模)若点在第二象限,且到轴的距离是3,到轴的距离是1,则点的坐标是
A. B. C. D.
7.(2024 恩施市模拟)在平面直角坐标系中,第四象限内的点到轴的距离是3,到轴的距离是2,已知平行于轴且,则点的坐标是
A.或 B.
C. D.或
8.(2024 泗阳县一模)如果点在第二象限,那么点在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.(2024 沈丘县二模)如图,在一单位为1的方格纸上,△,△,△,都是斜边在轴上,斜边长分别为2,4,6,的等腰直角三角形,若的顶点坐标分别为,,,则依图中所示规律,的坐标为
A. B. C. D.
10.(2024 杭州三模)点在第二象限,距离轴5个单位长度,距离轴3个单位长度,则点的坐标为
A. B. C. D.
二.填空题(共10小题)
11.(2024 朔州模拟)我国水墨画发展有着悠远历史,相传始于唐代,成于五代,盛于宋元,明清及近代以来续有发展,重于意境优美,图为水墨画“早有蜻蜓立上头”,若将其放在平面直角坐标系中,点,,则点坐标为 .
12.(2024 岳阳县一模)若点在轴上,则的坐标是 .
13.(2024 酒泉三模)如图,动点在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点,第2次接着运动到点,第3次接着运动到点,,按这样的运动规律,经过第2024次运动后,动点的坐标是 .
14.(2024 东营区模拟)如图,在平面直角坐标系中,直线与直线交于点,过作轴的垂线,垂足为,过作的平行线交于,过作轴的垂线,垂足为,过作的平行线交于,过作轴的垂线,垂足为按此规律,则点的纵坐标为 .
15.(2024 武威三模)中国象棋是中华民族的文化瑰宝,因趣味性强,深受大众喜爱.如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点,“马”位于点,则“兵”位于 点.
16.(2024 山东)任取一个正整数,若是奇数,就将该数乘3再加上1;若是偶数,就将该数除以2.反复进行上述两种运算,经过有限次运算后,必进入循环圈,这就是“冰雹猜想”.在平面直角坐标系中,将点中的,分别按照“冰雹猜想”同步进行运算得到新的点的横、纵坐标,其中,均为正整数.例如,点经过第1次运算得到点,经过第2次运算得到点,以此类推.则点经过2024次运算后得到点 .
17.(2024 金平区一模)点在轴上,则点的坐标为 .
18.(2024 建始县模拟)如图,在平面直角坐标系中,已知点,,将△顺着轴的正半轴无滑动的滚动,第一次滚动到①的位置,点的对应点记作;第二次滚动到②的位置,点的对应点记作;第三次滚动到③的位置,点的对应点记作;;依次进行下去,则点的坐标为 .
19.(2024 武威模拟)在平面直角坐标系中,若点与点之间的距离是5,则的值是 .
20.(2024 榕江县模拟)在平面直角坐标系中,已知点,,,则以,,为顶点的平行四边形的第四个顶点的坐标为 .
三.解答题(共5小题)
21.(2024 阜阳三模)【观察发现】如图,观察下列各点的排列规律:
,,,,,.
【归纳应用】
(1)直接写出点的坐标为 ;点的坐标为 ;
(2)若点的坐标为,求的值.
22.(2024 青浦区三模)五子连珠棋和象棋、围棋一样,深受同学们喜爱,其规则是:在的正方形棋盘中,由黑方先行,轮流弈子,在任一方向上连成五子者为胜.如图所示,是两个五子棋爱好者甲和乙对弈图(甲执黑子先行,乙执白子后行),若白棋①的位置是,白棋②的位置是.
(1)请在图中建立平面直角坐标系,并写出黑棋的位置是 ;
(2)甲必须在何处落子,才不会让乙在短时间内获胜,直接写出对应的点的位置.
23.(2024 奉贤区三模)国际象棋玩过么?国王走一步能够移动到相邻的8个方格中的随意一个,那么国王从格子, 走到格子, 的最少步数就是数学的一种距离,叫“切比雪夫距离”.在平面直角坐标系中,对于任意两点, 与, 的“切比雪夫距离”,给出如下定义:若,则点, 与, 的“切比雪夫距离”为;若,则点, 与, 的“切比雪夫距离”为;
(1)已知,
①若的坐标为,则点与的“切比雪夫距离”为 ;
②若为轴上的动点,那么点与 “切比雪夫距离”的最小值为 ;
(2)已知,,设点与的“切比雪夫距离”为,若,求(用含的式子表示).
24.(2024 吴江区二模)已知点回答下列问题:
(1)点在轴上,求出点的坐标;
(2)点在第二象限,且它到轴、轴的距离相等,求的值
25.(2024 中山市三模)如图所示是地球截面图,其中,分别表示南回归线和北回归线,表示赤道,点表示太原市的位置.现已知地球南回归线的纬度是南纬,太原市的纬度是北纬,而冬至正午时,太阳光直射南回归线(光线的延长线经过地心,则太原市冬至正午时,太阳光线与地面水平线的夹角的度数是 .
中考数学一轮复面直角坐标系
参考答案与试题解析
一.选择题(共10小题)
1.(2024 新城区模拟)在平面直角坐标系中,点所在的象限是
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】
【考点】点的坐标
【专题】平面直角坐标系;数据分析观念
【分析】根据点横纵坐标符号判定即可.
【解答】解:,,,
点在第二象限,
故选:.
【点评】本题考查点所在象限,熟练掌握平面直角坐标系各象限内事业的坐标符号:第一象限,第二象限,第三象限,第四象限是解题的关键.
2.(2024 沿河县一模)如图,小明用手盖住的点的坐标可能为
A. B. C. D.
【答案】
【考点】点的坐标
【专题】平面直角坐标系;数据分析观念
【分析】先判断出小手盖住的点在第二象限,再根据各象限内点的坐标特征解答.
【解答】解:由图可知,小手盖住的点在第二象限,
,,,中只有在第二象限.
故选:.
【点评】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限;第二象限;第三象限;第四象限.
3.(2024 钱塘区三模)在平面直角坐标系中,坐标为的点在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】
【考点】点的坐标
【专题】平面直角坐标系;应用意识
【分析】根据象限内点的坐标特征即可得出答案.
【解答】解:横坐标为负,纵坐标为正的点在第二象限内.
故选:.
【点评】本题主要考查点的坐标,牢记各象限内点的坐标性质是解题的关键.
4.(2024 仁和区一模)已知点的坐标为,直线轴,且,则点的坐标为
A.或 B.或
C.或 D.或
【答案】
【考点】坐标与图形性质
【专题】应用意识;平面直角坐标系
【分析】根据平行于轴的直线上的点的纵坐标相等求出点的纵坐标,再分点在点的左边与右边两种情况求出点的横坐标,即可得解.
【解答】解:轴,点的坐标为,
点的纵坐标为2,
,
点在点的左边时,横坐标为,
点在点的右边时,横坐标为,
点的坐标为或.
故选:.
【点评】本题考查了坐标与图形性质,主要利用了平行于轴的直线是上的点的纵坐标相等的性质,难点在于要分情况讨论.
5.(2024 杭州三模)如图,弹性小球从点出发,沿所示方向运动,每当小球碰到正方形的边时反弹,反弹时反射角等于入射角,当小球第1次碰到正方形的边时的点为,第2次碰到正方形的边时的点为,,第次碰到正方形的边时的点为,则点的坐标是
A. B. C. D.
【答案】
【考点】规律型:点的坐标
【专题】规律型;平面直角坐标系;运算能力;推理能力
【分析】按照反弹角度依次画图,探索反弹规律,即可求出答案.
【解答】解:根据反射角等于入射角画图如下,
由图中可知,,,,,最后再反射到,由此可知,每6次循环一次,
,
点的坐标与相同,
.
故选:.
【点评】本题考查了点的坐标规律探究性问题,解题的关键在于寻找循环坐标,得出规律.
6.(2024 喀什地区二模)若点在第二象限,且到轴的距离是3,到轴的距离是1,则点的坐标是
A. B. C. D.
【答案】
【考点】点的坐标
【专题】平面直角坐标系;几何直观
【分析】根据到轴的距离是纵坐标的绝对值,到轴的距离是横坐标的绝对值进行求解即可.
【解答】解:点到轴的距离是3,到轴的距离是1,
点的横坐标的绝对值为1,纵坐标的绝对值为3,
又点在第二象限,
点的坐标为.
故选:.
【点评】本题考查了平面直角坐标系各象限坐标符号的特征和点到坐标轴的距离,掌握各象限坐标符号的特征和点到坐标轴的距离是关键.
7.(2024 恩施市模拟)在平面直角坐标系中,第四象限内的点到轴的距离是3,到轴的距离是2,已知平行于轴且,则点的坐标是
A.或 B.
C. D.或
【答案】
【考点】坐标与图形性质
【专题】平面直角坐标系;推理能力
【分析】先根据题意得出点坐标,根据平行于轴设出点的坐标,进而可得出结论.
【解答】解:第四象限内的点到轴的距离是3,到轴的距离是2,
,
平行于轴,
设,
,
,
或,
或.
故选:.
【点评】本题考查的是坐标与图形性质,熟知平行于轴的直线上各点的纵坐标相等是解题的关键.
8.(2024 泗阳县一模)如果点在第二象限,那么点在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】
【考点】点的坐标
【专题】平面直角坐标系;符号意识
【分析】根据各象限内点的坐标的符号特征解答即可.
【解答】解:点在第二象限,
,,
,
点在第一象限.
故选:.
【点评】本题考查了各象限内点的坐标的符号特征以及解不等式,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限;第二象限;第三象限;第四象限.
9.(2024 沈丘县二模)如图,在一单位为1的方格纸上,△,△,△,都是斜边在轴上,斜边长分别为2,4,6,的等腰直角三角形,若的顶点坐标分别为,,,则依图中所示规律,的坐标为
A. B. C. D.
【答案】
【考点】规律型:点的坐标
【专题】规律型;平面直角坐标系;等腰三角形与直角三角形;推理能力
【分析】根据脚码确定出脚码为偶数时的点的坐标,得到规律当脚码是2、6、时,横坐标为1,纵坐标为脚码的一半的相反数,当脚码是4、8、时,横坐标是1,纵坐标为脚码的一半,然后确定出第2022个点的坐标即可.
【解答】解:各三角形都是等腰直角三角形,
直角顶点的纵坐标的长度为斜边的一半,
,,,,,,,
,
点在第四象限,横坐标是1,纵坐标的绝对值是,
的坐标为.
故选:.
【点评】本题是对点的坐标变化规律的考查,根据2020是偶数,求出点的脚码是偶数时的变化规律是解题的关键.
10.(2024 杭州三模)点在第二象限,距离轴5个单位长度,距离轴3个单位长度,则点的坐标为
A. B. C. D.
【答案】
【考点】点的坐标
【专题】平面直角坐标系;符号意识
【分析】首先确定点的横纵坐标的正负号,再根据距坐标轴的距离确定点的坐标.
【解答】解:点位于第二象限,
点的横坐标为负数,纵坐标为正数,
点距离轴5个单位长度,距离轴3个单位长度,
点的坐标为.
故选:.
【点评】此题主要考查了点的坐标,解决本题的关键是掌握好四个象限的点的坐标的特征:第一象限正正,第二象限负正,第三象限负负,第四象限正负.
二.填空题(共10小题)
11.(2024 朔州模拟)我国水墨画发展有着悠远历史,相传始于唐代,成于五代,盛于宋元,明清及近代以来续有发展,重于意境优美,图为水墨画“早有蜻蜓立上头”,若将其放在平面直角坐标系中,点,,则点坐标为 .
【答案】.
【考点】点的坐标
【专题】平面直角坐标系;运算能力
【分析】根据已知点的坐标,找出原点,建立平面直角坐标系,然后根据点的位置,写出点的坐标.
【解答】解:如图所示,根据点,,建立坐标系,如图所示:
点坐标为:,
故答案为:.
【点评】本题主要考查了点的坐标,解题关键是熟练掌握根据已知点的坐标,找出坐标原点.
12.(2024 岳阳县一模)若点在轴上,则的坐标是 .
【答案】.
【考点】点的坐标
【专题】符号意识;平面直角坐标系
【分析】根据轴上点的横坐标为0解答即可.
【解答】解:由题意得:,
,
,
的坐标是,
故答案为:.
【点评】本题考查了点的坐标特征,熟知轴上点的横坐标为0是解题的关键.
13.(2024 酒泉三模)如图,动点在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点,第2次接着运动到点,第3次接着运动到点,,按这样的运动规律,经过第2024次运动后,动点的坐标是 .
【考点】规律型:点的坐标
【专题】规律型;几何直观;推理能力
【分析】观察点的坐标变化发现每个点的横坐标与运动的次数相等,纵坐标是1,0,2,0,每4个数一个循环,按照此规律解答即可.
【解答】解:观察点的坐标变化可知:
第1次从原点运动到点,
第2次接着运动到点,
第3次接着运动到点,
第4次接着运动到点,
第5次接着运动到点,
,
按这样的运动规律,发现每个点的横坐标与运动的次数相等,纵坐标是1,0,2,0,每4个数一个循环,
由于,
所以经过第2024次运动后,动点的坐标是.
故答案为:.
【点评】本题考查了点的坐标规律探求,属于常考题型,由已知点的坐标变化找出规律是解题的关键.
14.(2024 东营区模拟)如图,在平面直角坐标系中,直线与直线交于点,过作轴的垂线,垂足为,过作的平行线交于,过作轴的垂线,垂足为,过作的平行线交于,过作轴的垂线,垂足为按此规律,则点的纵坐标为 . .
【答案】.
【考点】规律型:点的坐标
【专题】规律型;推理能力
【分析】联立直线与直线的表达式并解得:,,故,,依次求出:点的纵坐标为、的纵坐标为,即可求解.
【解答】解:联立直线与直线的表达式并解得:,,故,;
则点,,则直线的表达式为:,
将点坐标代入上式并解得:直线的表达式为:,
将表达式与直线的表达式联立并解得:,,即点的纵坐标为;
同理可得的纵坐标为,
按此规律,则点的纵坐标为,
故答案为:.
【点评】本题考查了两直线的交点,要求利用图象求解各问题,要认真体会点的坐标,一次函数与二元一次方程组之间的内在联系.
15.(2024 武威三模)中国象棋是中华民族的文化瑰宝,因趣味性强,深受大众喜爱.如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点,“马”位于点,则“兵”位于 点.
【答案】.
【考点】坐标确定位置
【专题】平面直角坐标系;几何直观
【分析】直接利用已知点坐标建立平面直角坐标系,进而得出点的坐标.
【解答】解:如图所示:“兵”位于点.
故答案为:.
【点评】此题主要考查了坐标确定位置,正确得出原点位置是解题关键.
16.(2024 山东)任取一个正整数,若是奇数,就将该数乘3再加上1;若是偶数,就将该数除以2.反复进行上述两种运算,经过有限次运算后,必进入循环圈,这就是“冰雹猜想”.在平面直角坐标系中,将点中的,分别按照“冰雹猜想”同步进行运算得到新的点的横、纵坐标,其中,均为正整数.例如,点经过第1次运算得到点,经过第2次运算得到点,以此类推.则点经过2024次运算后得到点 .
【考点】规律型:点的坐标
【专题】规律型;推理能力
【分析】根据新定义依次计算出各点的坐标,然后找出规律,最后应用规律求解即可.
【解答】解:点经过1次运算后得到点为,即为,
经过2次运算后得到点为,即为,
经过3次运算后得到点为,即为,
,
发现规律:点经过3次运算后还是,
,
点经过2024次运算后得到点,
故答案为:.
【点评】本题考查了规律型:点的坐标,解答本题的关键是找到规律点经过3次运算后还是.
17.(2024 金平区一模)点在轴上,则点的坐标为 .
【考点】点的坐标
【专题】平面直角坐标系;符号意识
【分析】直接利用在轴上点的坐标性质得出纵坐标为零,进而得出答案.
【解答】解:是轴上的点,
,
解得:.
.
点的坐标为.
故答案为.
【点评】此题主要考查了点的坐标,正确把握轴上点的坐标性质是解题关键.
18.(2024 建始县模拟)如图,在平面直角坐标系中,已知点,,将△顺着轴的正半轴无滑动的滚动,第一次滚动到①的位置,点的对应点记作;第二次滚动到②的位置,点的对应点记作;第三次滚动到③的位置,点的对应点记作;;依次进行下去,则点的坐标为 .
【答案】.
【考点】规律型:点的坐标
【专题】推理能力;规律型
【分析】先求出,再利用先利用翻转的性质、点坐标的变化规律分别求出点,,,,,的坐标,再归纳总结出一般规律,由此即可得出答案.
【解答】解;,,
,
由翻转的性质得:,则,
由翻转过程可知,点,重合,则,
点的横坐标为,纵坐标为2,即,
同理可得:点,重合,点,的横坐标为,纵坐标为0,
即,,
点的横坐标为,纵坐标为2,即,
归纳类推得出以下规律:(其中,为正整数),
(1)点,,,,的横坐标变化规律为2,8,14,,,纵坐标均为0,
(2)点,,,,的横坐标变化规律为2,8,14,,,纵坐标均为0,
(3)点,,,的横坐标变化规律为6,12,,,纵坐标均为2,
,
点的坐标变化规律符合(1),
则点的横坐标为,纵坐标为0,即,
故答案为:.
【点评】本题考查了规律型的点的坐标,数形结合并发现循环规律是解题的关键.
19.(2024 武威模拟)在平面直角坐标系中,若点与点之间的距离是5,则的值是 或8 .
【考点】坐标与图形性质
【专题】线段、角、相交线与平行线
【分析】点、的横坐标相等,则直线在平行于轴的直线上,根据两点间的距离,可列出等式,从而解得的值.
【解答】解:点与点之间的距离是5,
,
解得或8.
故答案为:或8.
【点评】本题是基础题,考查了坐标与图形的性质,当两点的横坐标相等时,则这两点在平行于轴的直线上.
20.(2024 榕江县模拟)在平面直角坐标系中,已知点,,,则以,,为顶点的平行四边形的第四个顶点的坐标为 .
【答案】.
【考点】坐标与图形性质
【专题】应用意识;平面直角坐标系
【分析】根据题意画出图形,根据平行四边形的性质将点向右平移3个单位得到,即可求解.
【解答】解:点,,,是平行四边形,
,,
将点向右平移3个单位得到,
如图所示,
故答案为:.
【点评】本题考查了坐标与图形性质、平行四边形的性质,数形结合是解答本题的关键.
三.解答题(共5小题)
21.(2024 阜阳三模)【观察发现】如图,观察下列各点的排列规律:
,,,,,.
【归纳应用】
(1)直接写出点的坐标为 ;点的坐标为 ;
(2)若点的坐标为,求的值.
【答案】(1);;(2)1012.
【考点】规律型:点的坐标
【专题】规律型;运算能力
【分析】(1)根据图形写出坐标即可;
(2)根据题意得到,,,,以此类推得到,再根据点的坐标为建立等式求解,即可解题.
【解答】解:(1)由图知,点的坐标为,
点的坐标为;
故答案为:;.
(2),,,,,
且,,,,以此类推,
,即,
点的坐标为,
,解得.
【点评】本题考查平面直角坐标系中点的坐标,以及坐标找规律,一元一次方程的应用,解题的关键在于通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.
22.(2024 青浦区三模)五子连珠棋和象棋、围棋一样,深受同学们喜爱,其规则是:在的正方形棋盘中,由黑方先行,轮流弈子,在任一方向上连成五子者为胜.如图所示,是两个五子棋爱好者甲和乙对弈图(甲执黑子先行,乙执白子后行),若白棋①的位置是,白棋②的位置是.
(1)请在图中建立平面直角坐标系,并写出黑棋的位置是 ;
(2)甲必须在何处落子,才不会让乙在短时间内获胜,直接写出对应的点的位置.
【答案】(1);
(2)或.
【考点】坐标确定位置
【专题】几何直观;平面直角坐标系
【分析】(1)利用直角坐标系写出黑棋的位置的坐标即可;
根据五子连棋的规则,乙已把,,,三点凑成在一条直线,甲只有在此三点两端任加一点即可保证不会让乙在短时间内获胜,据此即可确定点的坐标.
【解答】解:(1)黑棋的位置如图所示:
黑棋的坐标为,
故答案为:;
(2)根据题意得,乙执的白棋已有三点,,,在一条直线上,
甲只有在此直线上距离,,最近的地方占取一点才能保证不会让乙在短时间内获胜,
即为点或.
【点评】本题考查了点的坐标的确定及生活中的棋类常识,正确理解题意和识图是解题的关键.
23.(2024 奉贤区三模)国际象棋玩过么?国王走一步能够移动到相邻的8个方格中的随意一个,那么国王从格子, 走到格子, 的最少步数就是数学的一种距离,叫“切比雪夫距离”.在平面直角坐标系中,对于任意两点, 与, 的“切比雪夫距离”,给出如下定义:若,则点, 与, 的“切比雪夫距离”为;若,则点, 与, 的“切比雪夫距离”为;
(1)已知,
①若的坐标为,则点与的“切比雪夫距离”为 3 ;
②若为轴上的动点,那么点与 “切比雪夫距离”的最小值为 ;
(2)已知,,设点与的“切比雪夫距离”为,若,求(用含的式子表示).
【答案】(1)①3;②2;(2)
【考点】坐标与图形性质;两点间的距离公式
【专题】一次方程(组及应用;运算能力
【分析】(1)①结合题意,根据“切比雪夫距离”的定义求解即可;②设点,分和两种情况讨论,即可获得答案;
(2)结合已知条件,分两种情况讨论:当时,由,,可确定此时点与的“切比雪夫距离”;当时,易得,,令,解得,即当时,点与的“切比雪夫距离” ;当时,可有,此时点与的“切比雪夫距离” .即可获得答案.
【解答】解:(1)①,,
又,,
,
根据“切比雪夫距离”的定义,点与的“切比雪夫距离”为3.
②若为轴上的动点,则可设点,
当时,,
又,
,
此时点与 “切比雪夫距离”的值为;
当时,,
又,
,
此时点与 “切比雪夫距离”的值为2.
综上所述,若为轴上的动点,那么点与 “切比雪夫距离”的最小值为2.
(2)根据已知条件,,,
则当时,
,
,
此时点与的“切比雪夫距离” ;
当时,
可有,,
令,解得,
即当时,可有,此时点与的“切比雪夫距离” ,
当时,可有,此时点与的“切比雪夫距离” .
综上所述,点与的“切比雪夫距离” .
【点评】本题主要考查了新定义“切比雪夫距离”、平面直角坐标系中点的坐标特征、化简绝对值以及一元一次不等式的应用等知识,理解题意,灵活运用相关知识是解题关键.
24.(2024 吴江区二模)已知点回答下列问题:
(1)点在轴上,求出点的坐标;
(2)点在第二象限,且它到轴、轴的距离相等,求的值
【答案】(1);
(2)2025.
【考点】点的坐标
【专题】平面直角坐标系;符号意识
【分析】(1)根据轴上点的特点作答即可;
(2)根据点到轴和轴相等列出,再结合第二象限点的特点求出,代入即可.
【解答】解:(1)在轴上,
,
解得:,
,
;
(2)点到轴和轴距离相等,
,
在第二象限,
,,
,,
,
解得:,
.
【点评】本题主要考查的是点的坐标,熟知平面直角坐标系内点的坐标特点是解题的关键.
25.(2024 中山市三模)如图所示是地球截面图,其中,分别表示南回归线和北回归线,表示赤道,点表示太原市的位置.现已知地球南回归线的纬度是南纬,太原市的纬度是北纬,而冬至正午时,太阳光直射南回归线(光线的延长线经过地心,则太原市冬至正午时,太阳光线与地面水平线的夹角的度数是 .
【答案】.
【考点】坐标确定位置;平行线的性质
【专题】推理能力;平面直角坐标系;运算能力
【分析】设与交于点,先由三角形内角和定理求出.,再根据平行线的性质求解即可.
【解答】解:如图,设与交于点,
,,
,
在中,,,
,
,
,
故答案为:.
【点评】本题考查了三角形内角和定理,平行线的性质,读懂题意并熟练掌握知识点是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
