4.1 第1课时 三角形的有关概念 课件(共23张PPT) 2025-2026学年度湘教版数学八年级上册
文档属性
| 名称 | 4.1 第1课时 三角形的有关概念 课件(共23张PPT) 2025-2026学年度湘教版数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 22:09:53 | ||
图片预览





文档简介
(共23张PPT)
第4章
三角形
八年级数学湘教版·上册
4.1 第1课时 三角形的有关概念
授课人:XXXX
学习目标
1.三角形的概念,三角形任意两边之和大于第三边的应用;(重点)
2.已知三角形的两边求第三边的范围.(难点)
新课导入
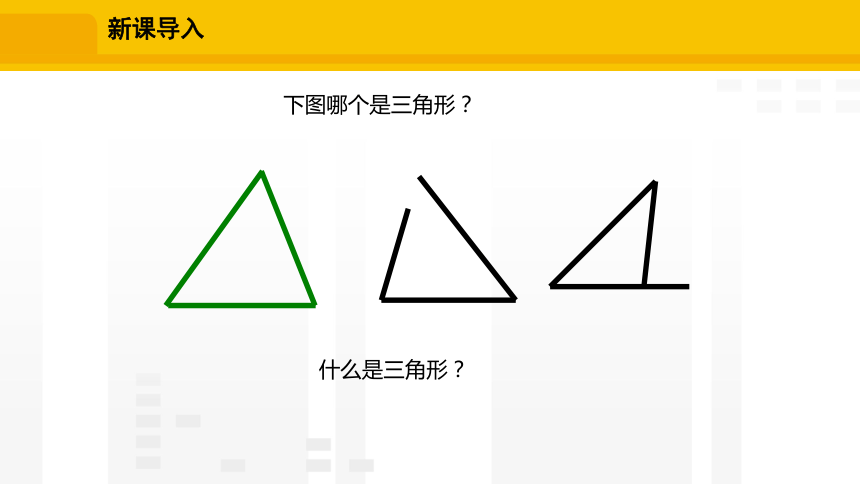
下图哪个是三角形?
什么是三角形?
新课导入
观察下图,找一找图中的三角形,并把它们勾画出来.
1.什么样的图形叫作三角形?
如何表示一个三角形?
什么是三角形的顶点、边、内角?
3.什么样的三角形是等腰三角形或等边三角形?
等腰三角形的腰、顶角、底角分别指什么?
4.在三角形中,三条边要满足什么关系?
2.在三角形中,角的对边是指什么?
边的对角是指什么?
问题
新知探究
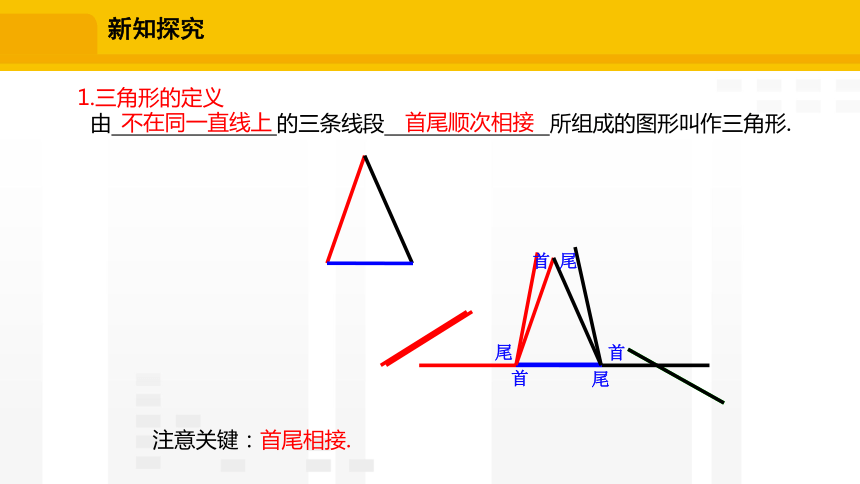
1.三角形的定义
由 的三条线段 所组成的图形叫作三角形.
新知探究
不在同一直线上
首尾顺次相接
首
首
首
尾
尾
尾
注意关键:首尾相接.
←顶点
←内角(简称三角形的角)
边→
A
B
C
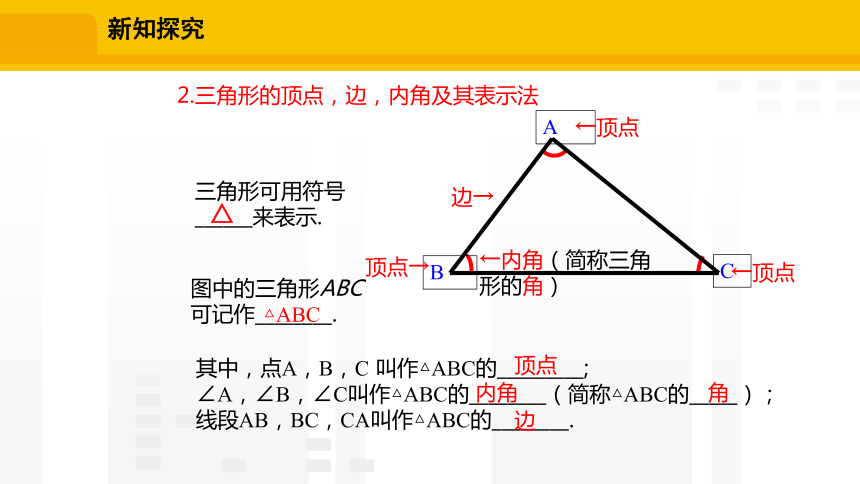
2.三角形的顶点,边,内角及其表示法
三角形可用符号
______来表示.
图中的三角形ABC
可记作________.
顶点→
←顶点
其中,点A,B,C 叫作△ABC的_________;
∠A,∠B,∠C叫作△ABC的________(简称△ABC的_____);
线段AB,BC,CA叫作△ABC的________.
△
△ABC
顶点
内角
角
边
新知探究
新知探究
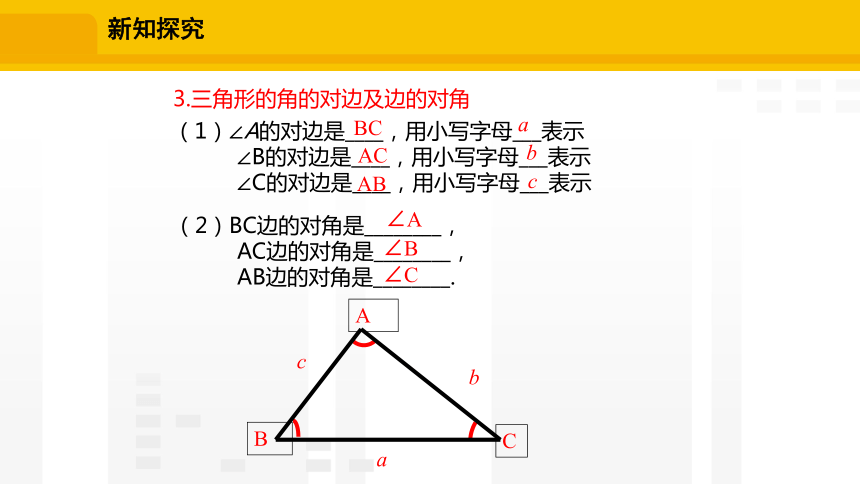
(1)∠A的对边是____,用小写字母___表示
∠B的对边是____,用小写字母___表示
∠C的对边是____,用小写字母___表示
A
B
C
a
3.三角形的角的对边及边的对角
(2)BC边的对角是________,
AC边的对角是________,
AB边的对角是________.
BC
a
AC
b
b
AB
c
c
∠A
∠B
∠C
新知探究
在三角形的概念中你认为需要注意:
1.不在同一条直线上.
2.三条线段.
3.首尾顺次相接.
图中有几个三角形?用符号表示出来.
△ABD,△ABE,△ABC, △ADE,△ADC, △AEC
A
D
B
E
C
按边的顺序找
BD,BE,BC,DE,DC,EC
新知探究
在等腰三角形中,相等的两边都叫作_____,另一边叫作_____,两腰的夹角叫作______,腰和底边的夹角叫作 .
新知探究
有两条边相等的三角形叫作等腰三角形.
三条边都相等的三角形叫作等边三角形.
等边三角形
不等边三角形
等边三角形也是等腰三角形吗?
腰
腰
底
顶角
底角
底角
等腰三角形
腰
底
顶角
底角
如图,等腰三角形ABC中,AB=AC,那么腰是___________,
底是____,顶角是______,底角是__________.
等边三角形是特殊的______三角形,即底边和腰相等的等腰三角形.
B
A
C
AB, AC
BC
∠A
∠B和∠C
等腰
新知探究
新知探究
在一个三角形中,任意两边之和与第三边的长度之间有怎样的大小关系?为什么
在△ABC中,BC是连接B,C两点的一条线段,
由基本事实“两点之间线段最短”可得 AB + AC > BC.
同理可得
AB + BC > AC,
AC + BC > AB .
AB > BC-AC
AC > BC-AB
BC > AC-AB
新知探究
新知探究
三角形的任意两边之和大于第三边.
三角形的任意两边之差小于第三边.
判断三条线段能否组成三角形,是否一定要检验三条线段中任何两条的和都大于第三条?根据你刚才的解题经验,有没有更简便的判断方法?
思 考:
只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.
1.下列长度的各组线段能否组成一个三角形?
(1) 15cm,10cm,7cm (2) 4cm,5cm,10cm
(3) 3cm,8cm,5cm (4) 4cm,5cm,6cm
(1)能 (2)不能 (3)不能 (4)能
新知探究
2.一个三角形的两边长分别是2cm,5cm,则第三边长x的取值范围是多少
分析: x应满足大于5-2﹦3cm,小于5 + 2 ﹦7cm,
解:3<x<7.
新知探究
新知探究
例1 如图,D是△ABC的边AC上一点,AD=BD,
试判断AC与BC的大小.
解: 在△BDC 中,有 BD+DC>BC
又 AD = BD,
则 BD+DC = AD+DC = AC,
所以 AC >BC.
(三角形的任意两边之和大于第三边).
课堂小结
三角形的有关概念:
三角形三边的关系;三角形按边分类
三角形第三边大于两边之差,小于两边之和
三角形边角表示方法
课堂小测
1.下列三条线段,能构成三角形的是 ( )
A,1cm,2cm,3 cm B,2cm,3cm ,4cm
C,6cm,8cm ,15cm D,12cm,3cm,8cm
2.一个等腰三角形的一边是5cm,另一边是9cm,则这个三角形的周长是( )
A,19cm B,23cm C,19cm或23cm D,无法确定
B
C
课堂小测
3.有长为3,5,7,10四根木条,要摆出一个三角形,有___ 种摆法.
4.一个等腰三角形的一边是2cm,另一边是9cm,则这个三角形的周长是______.
2
20cm
5.在三角形ABC中,AB=7,BC=3,并且AC为奇数,那么三角形ABC的周长是
.
15或17或19
课堂小测
6.已知a,b,c是三角形的三条边.化简|a+b-c|+|c-b-a|.
解:因为a,b,c是三角形的三边
所以 a+b-c>0(两边之和大于第三边)
c-b-a <0(两边之差小于第三边)
所以|a+b-c|+|c-b-a|=a+b-c-c+b+a
=2a+2b-2c
课堂小测
7.如图,O为△ABC 内一点. 求证:
证明:由三角形三边的关系可知:
在△AOB中,OA+OB>AB ①
在△BOC中,OC+OA>AC ②
在△AOC中,OB+OC>BC ③
将上面的三式相加,即
①+②+③,得 2(OA+OB+OC)>AB+BC+AC
所以
第4章
三角形
八年级数学湘教版·上册
4.1 第1课时 三角形的有关概念
授课人:XXXX
学习目标
1.三角形的概念,三角形任意两边之和大于第三边的应用;(重点)
2.已知三角形的两边求第三边的范围.(难点)
新课导入
下图哪个是三角形?
什么是三角形?
新课导入
观察下图,找一找图中的三角形,并把它们勾画出来.
1.什么样的图形叫作三角形?
如何表示一个三角形?
什么是三角形的顶点、边、内角?
3.什么样的三角形是等腰三角形或等边三角形?
等腰三角形的腰、顶角、底角分别指什么?
4.在三角形中,三条边要满足什么关系?
2.在三角形中,角的对边是指什么?
边的对角是指什么?
问题
新知探究
1.三角形的定义
由 的三条线段 所组成的图形叫作三角形.
新知探究
不在同一直线上
首尾顺次相接
首
首
首
尾
尾
尾
注意关键:首尾相接.
←顶点
←内角(简称三角形的角)
边→
A
B
C
2.三角形的顶点,边,内角及其表示法
三角形可用符号
______来表示.
图中的三角形ABC
可记作________.
顶点→
←顶点
其中,点A,B,C 叫作△ABC的_________;
∠A,∠B,∠C叫作△ABC的________(简称△ABC的_____);
线段AB,BC,CA叫作△ABC的________.
△
△ABC
顶点
内角
角
边
新知探究
新知探究
(1)∠A的对边是____,用小写字母___表示
∠B的对边是____,用小写字母___表示
∠C的对边是____,用小写字母___表示
A
B
C
a
3.三角形的角的对边及边的对角
(2)BC边的对角是________,
AC边的对角是________,
AB边的对角是________.
BC
a
AC
b
b
AB
c
c
∠A
∠B
∠C
新知探究
在三角形的概念中你认为需要注意:
1.不在同一条直线上.
2.三条线段.
3.首尾顺次相接.
图中有几个三角形?用符号表示出来.
△ABD,△ABE,△ABC, △ADE,△ADC, △AEC
A
D
B
E
C
按边的顺序找
BD,BE,BC,DE,DC,EC
新知探究
在等腰三角形中,相等的两边都叫作_____,另一边叫作_____,两腰的夹角叫作______,腰和底边的夹角叫作 .
新知探究
有两条边相等的三角形叫作等腰三角形.
三条边都相等的三角形叫作等边三角形.
等边三角形
不等边三角形
等边三角形也是等腰三角形吗?
腰
腰
底
顶角
底角
底角
等腰三角形
腰
底
顶角
底角
如图,等腰三角形ABC中,AB=AC,那么腰是___________,
底是____,顶角是______,底角是__________.
等边三角形是特殊的______三角形,即底边和腰相等的等腰三角形.
B
A
C
AB, AC
BC
∠A
∠B和∠C
等腰
新知探究
新知探究
在一个三角形中,任意两边之和与第三边的长度之间有怎样的大小关系?为什么
在△ABC中,BC是连接B,C两点的一条线段,
由基本事实“两点之间线段最短”可得 AB + AC > BC.
同理可得
AB + BC > AC,
AC + BC > AB .
AB > BC-AC
AC > BC-AB
BC > AC-AB
新知探究
新知探究
三角形的任意两边之和大于第三边.
三角形的任意两边之差小于第三边.
判断三条线段能否组成三角形,是否一定要检验三条线段中任何两条的和都大于第三条?根据你刚才的解题经验,有没有更简便的判断方法?
思 考:
只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.
1.下列长度的各组线段能否组成一个三角形?
(1) 15cm,10cm,7cm (2) 4cm,5cm,10cm
(3) 3cm,8cm,5cm (4) 4cm,5cm,6cm
(1)能 (2)不能 (3)不能 (4)能
新知探究
2.一个三角形的两边长分别是2cm,5cm,则第三边长x的取值范围是多少
分析: x应满足大于5-2﹦3cm,小于5 + 2 ﹦7cm,
解:3<x<7.
新知探究
新知探究
例1 如图,D是△ABC的边AC上一点,AD=BD,
试判断AC与BC的大小.
解: 在△BDC 中,有 BD+DC>BC
又 AD = BD,
则 BD+DC = AD+DC = AC,
所以 AC >BC.
(三角形的任意两边之和大于第三边).
课堂小结
三角形的有关概念:
三角形三边的关系;三角形按边分类
三角形第三边大于两边之差,小于两边之和
三角形边角表示方法
课堂小测
1.下列三条线段,能构成三角形的是 ( )
A,1cm,2cm,3 cm B,2cm,3cm ,4cm
C,6cm,8cm ,15cm D,12cm,3cm,8cm
2.一个等腰三角形的一边是5cm,另一边是9cm,则这个三角形的周长是( )
A,19cm B,23cm C,19cm或23cm D,无法确定
B
C
课堂小测
3.有长为3,5,7,10四根木条,要摆出一个三角形,有___ 种摆法.
4.一个等腰三角形的一边是2cm,另一边是9cm,则这个三角形的周长是______.
2
20cm
5.在三角形ABC中,AB=7,BC=3,并且AC为奇数,那么三角形ABC的周长是
.
15或17或19
课堂小测
6.已知a,b,c是三角形的三条边.化简|a+b-c|+|c-b-a|.
解:因为a,b,c是三角形的三边
所以 a+b-c>0(两边之和大于第三边)
c-b-a <0(两边之差小于第三边)
所以|a+b-c|+|c-b-a|=a+b-c-c+b+a
=2a+2b-2c
课堂小测
7.如图,O为△ABC 内一点. 求证:
证明:由三角形三边的关系可知:
在△AOB中,OA+OB>AB ①
在△BOC中,OC+OA>AC ②
在△AOC中,OB+OC>BC ③
将上面的三式相加,即
①+②+③,得 2(OA+OB+OC)>AB+BC+AC
所以
同课章节目录
