4.2.2 证明、举反例 课件(共19张PPT) 2025-2026学年度湘教版数学八年级上册
文档属性
| 名称 | 4.2.2 证明、举反例 课件(共19张PPT) 2025-2026学年度湘教版数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 544.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 22:12:03 | ||
图片预览






文档简介
(共19张PPT)
第4章
三角形
八年级数学湘教版·上册
4.2.2 证明、举反例
授课人:XXXX
学习目标
1.了解证明的基本步骤和书写格式;(重点)
2.理解反证法的推理依据及方法.(难点)
新课导入
采用剪拼或度量的方法,猜测“三角形的外角和”等于多少度.
观察、操作、实验是人们认识事物的重要手段,而且人们可以从中猜测发现出一些结论.
从剪拼或度量可以猜测三角形的三个外角之和等于360°,但是剪拼时难以真正拼成一个周角,只是接近周角;分别度量这三个角后再相加,结果可能接近360°,但不能很准确地都得到360°.
另外,由于不同形状的三角形有无数个,我们也不可能用剪拼或度量的方法来一一验证,因此,我们只能猜测任何一个三角形的外角和都为360°.
像此例的第(2)题那样,从一个命题的条件出发,运用定义、基本事实以及已经判断其成立的真命题,进行逻辑推理、计算,得出这个命题的结论成立,这一过程就是通常所说的证明.
像此例的第(1)题那样,找出一个例子,使之符合命题的条件,但不满足命题的结论,从而判断这个命题为假命题,这种做法称为举反例.
(2)如果a是整数,那么a是有理数;
解 如果a是整数,
根据有理数的定义:“整数和分数统称为有理数”
得出a是有理.因此命题(2)真.
(1)如果a是有理数,那么a是整数.
解 0.5是有理数,
因此命题(1)为假.
但是0.5不是整数.
新知探究
新知探究
我们把正确的命题称为真命题,把错误的命题称为假命题.
新知探究
在分析出这一命题的条件和结论后,我们就可以按如下步骤进行:
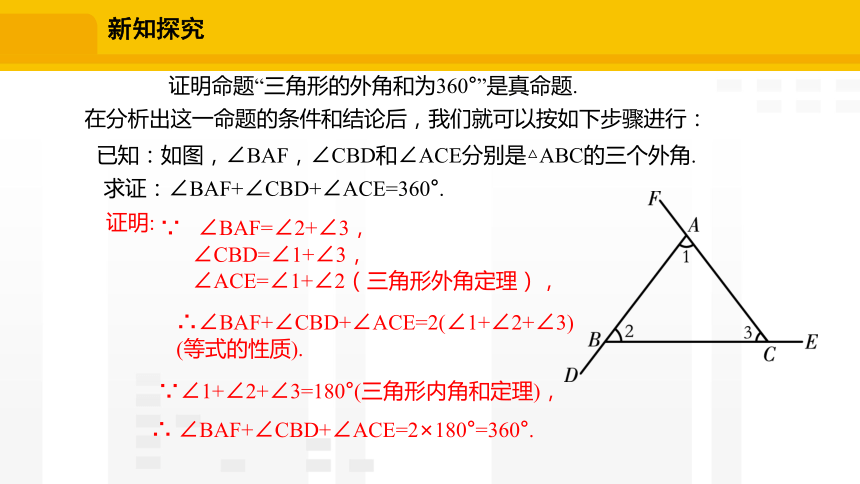
已知:如图,∠BAF,∠CBD和∠ACE分别是△ABC的三个外角.
求证:∠BAF+∠CBD+∠ACE=360°.
证明命题“三角形的外角和为360°”是真命题.
证明:
∵ ∠BAF=∠2+∠3,
∠CBD=∠1+∠3,
∠ACE=∠1+∠2(三角形外角定理),
∴∠BAF+∠CBD+∠ACE=2(∠1+∠2+∠3)
(等式的性质).
∵∠1+∠2+∠3=180°(三角形内角和定理),
∴ ∠BAF+∠CBD+∠ACE=2×180°=360°.
新知探究
证明与图形有关的命题时,一般有以下步骤:
第一步:根据题意,画出图形.
第二步:根据命题的条件和结论,结合图形,写
出已知、求证.
第三步:通过分析,找出证明的途径,写出证明
的过程.
例1 已知:如图,在△ABC中,∠B=∠C,点D在线段BA
的延长线上,射线AE平分∠DAC.
求证:AE∥BC.
证明:∵∠DAC =∠B +∠C(三角形外角定理),
∠B=∠C(已知),
∴ ∠DAC=2∠B(等式的性质).
又∵AE平分∠DAC(已知),
∴∠DAC=2∠DAE(角平分线的定义),
∴∠DAE=∠B(等量代换),
∴AE∥BC(同位角相等,两直线平行).
新知探究
解析:这个命题的结论是“至少有一个”,也就是说可能出现“有一个” “有两个” “有三个”这三种情况. 如果直接来证明,将很繁琐,因此,我们将从另外一个角度来证明.
新知探究
例2 已知:∠A,∠B,∠C是△ABC的内角.
求证:∠A,∠B,∠C中至少有一个角大于或等于60°.
证明:假设∠A,∠B,∠C 中没有一个角大于或等于60°,
即∠A<60°,∠B<60°,∠C<60°,
则∠A+∠B+∠C<180°.
这与“三角形的内角和等于180°”矛盾,
所以假设不正确.
因此,∠A, ∠B, ∠C中至少有一个角大于或等于60°.
新知探究
像这样,先假设命题不成立,从这样的假设出发,经过推理得出与已知条件、定义、基本事实、真命题等产生矛盾,得出假设不成立,从而判断所求证命题正确.这种证明方法叫作反证法.
反证法是一种间接证明的方法,其基本的思路可归结为“否定结论,导出矛盾,肯定结论”.
新知探究
应用反证法的情形:
(1) 直接证明困难;
(2) 需分成很多类进行讨论;
(3) 结论为“至少”、“至多”、“有无穷多个”
的一类命题;
(4) 结论为 “唯一”类命题.
新知探究
用反正法证明时,导出矛盾的几种可能:
(1)与原命题的条件矛盾;
(3)与定义、公理、定理、性质矛盾;
(2)与假设矛盾;
(4)与客观事实矛盾.
课堂小结
命题的证明
反证法:反设结论,推理,导出矛盾,证得结论.
直接证明:(画图)写出已知、求证,写出证明过程.
课堂小测
(1)证明命题:一个角的两边分别平行于另一个角的两边,且方向相同,则这两个角相等.
已知:如图,AB∥A′B′,BC∥B′C′.
求证:∠B= ∠B′
证明:∵ AB∥A′B′ ( )
∴ ∠ B′= ∠α( )
∵ BC∥B′C′ ( )
∴ ∠ B = ∠α( )
∴ ∠ B = ∠B′ ( )
已 知
两直线平行,同位角相等
已 知
两直线平行,同位角相等
等量代换
1. 填空
.
课堂小测
(2) 已知:如图,∠A+∠B= 180°.
求证:∠C+∠D= 180°.
证明:∵∠A+∠B= 180°(已知),
∴ AD∥BC( ),
∴ ∠C+∠D= 180( ).
同旁内角互补,两直线平行
两直线平行,同旁内角互补
课堂小测
2. 已知:如图,AB与CD 相交于点E.
求证:∠A+∠C=∠B+∠D.
证明: ∵ AB与CD 相交于点E ,
∴ ∠AEC=∠BED (对顶角相等).
又 ∵∠A+∠C +∠AEC =∠B+∠D +∠BED =180°
(三角形内角和等于180°),
∴
∠A+∠C=∠B+∠D.
课堂小测
3.求证:△ABC中不能有两个钝角.
证明:假设△ABC中能有两个钝角,
即∠A<90°,∠B>90°,∠C>90°,
所以∠A+∠B+∠C>180°,
与三角形的内角和为180°矛盾,
所以假设不成立,因此原命题正确,
即△ABC中不能有两个钝角.
课堂小测
4.已知:如图有a,b,c三条直线,且a//c,b//c.
求证:a//b.
A
a
b
c
证明:假设a与b不平行,则可设它们相交于点A.
那么过点A 就有两条直线a,b分别与直线c平行,
这与“过直线外一点有且只有一条直线与已知直
线平行”矛盾,故假设不成立. ∴a//b.
课堂小测
(3)两条直线被第三条直线所截,同位角相等;
两条相交的直线a,b被第三条直线l所截(如图),它们的同位角不相等.
-1和-3的积是-1×(-3)>0,-1和-3不是正数.
5.举反例说明下列命题是假命题:
(1)两个锐角的和是钝角;
(2)如果数a,b的积ab>0,那么a,b都是正数;
直角三角形的两个锐角和不是钝角.
a
b
l
第4章
三角形
八年级数学湘教版·上册
4.2.2 证明、举反例
授课人:XXXX
学习目标
1.了解证明的基本步骤和书写格式;(重点)
2.理解反证法的推理依据及方法.(难点)
新课导入
采用剪拼或度量的方法,猜测“三角形的外角和”等于多少度.
观察、操作、实验是人们认识事物的重要手段,而且人们可以从中猜测发现出一些结论.
从剪拼或度量可以猜测三角形的三个外角之和等于360°,但是剪拼时难以真正拼成一个周角,只是接近周角;分别度量这三个角后再相加,结果可能接近360°,但不能很准确地都得到360°.
另外,由于不同形状的三角形有无数个,我们也不可能用剪拼或度量的方法来一一验证,因此,我们只能猜测任何一个三角形的外角和都为360°.
像此例的第(2)题那样,从一个命题的条件出发,运用定义、基本事实以及已经判断其成立的真命题,进行逻辑推理、计算,得出这个命题的结论成立,这一过程就是通常所说的证明.
像此例的第(1)题那样,找出一个例子,使之符合命题的条件,但不满足命题的结论,从而判断这个命题为假命题,这种做法称为举反例.
(2)如果a是整数,那么a是有理数;
解 如果a是整数,
根据有理数的定义:“整数和分数统称为有理数”
得出a是有理.因此命题(2)真.
(1)如果a是有理数,那么a是整数.
解 0.5是有理数,
因此命题(1)为假.
但是0.5不是整数.
新知探究
新知探究
我们把正确的命题称为真命题,把错误的命题称为假命题.
新知探究
在分析出这一命题的条件和结论后,我们就可以按如下步骤进行:
已知:如图,∠BAF,∠CBD和∠ACE分别是△ABC的三个外角.
求证:∠BAF+∠CBD+∠ACE=360°.
证明命题“三角形的外角和为360°”是真命题.
证明:
∵ ∠BAF=∠2+∠3,
∠CBD=∠1+∠3,
∠ACE=∠1+∠2(三角形外角定理),
∴∠BAF+∠CBD+∠ACE=2(∠1+∠2+∠3)
(等式的性质).
∵∠1+∠2+∠3=180°(三角形内角和定理),
∴ ∠BAF+∠CBD+∠ACE=2×180°=360°.
新知探究
证明与图形有关的命题时,一般有以下步骤:
第一步:根据题意,画出图形.
第二步:根据命题的条件和结论,结合图形,写
出已知、求证.
第三步:通过分析,找出证明的途径,写出证明
的过程.
例1 已知:如图,在△ABC中,∠B=∠C,点D在线段BA
的延长线上,射线AE平分∠DAC.
求证:AE∥BC.
证明:∵∠DAC =∠B +∠C(三角形外角定理),
∠B=∠C(已知),
∴ ∠DAC=2∠B(等式的性质).
又∵AE平分∠DAC(已知),
∴∠DAC=2∠DAE(角平分线的定义),
∴∠DAE=∠B(等量代换),
∴AE∥BC(同位角相等,两直线平行).
新知探究
解析:这个命题的结论是“至少有一个”,也就是说可能出现“有一个” “有两个” “有三个”这三种情况. 如果直接来证明,将很繁琐,因此,我们将从另外一个角度来证明.
新知探究
例2 已知:∠A,∠B,∠C是△ABC的内角.
求证:∠A,∠B,∠C中至少有一个角大于或等于60°.
证明:假设∠A,∠B,∠C 中没有一个角大于或等于60°,
即∠A<60°,∠B<60°,∠C<60°,
则∠A+∠B+∠C<180°.
这与“三角形的内角和等于180°”矛盾,
所以假设不正确.
因此,∠A, ∠B, ∠C中至少有一个角大于或等于60°.
新知探究
像这样,先假设命题不成立,从这样的假设出发,经过推理得出与已知条件、定义、基本事实、真命题等产生矛盾,得出假设不成立,从而判断所求证命题正确.这种证明方法叫作反证法.
反证法是一种间接证明的方法,其基本的思路可归结为“否定结论,导出矛盾,肯定结论”.
新知探究
应用反证法的情形:
(1) 直接证明困难;
(2) 需分成很多类进行讨论;
(3) 结论为“至少”、“至多”、“有无穷多个”
的一类命题;
(4) 结论为 “唯一”类命题.
新知探究
用反正法证明时,导出矛盾的几种可能:
(1)与原命题的条件矛盾;
(3)与定义、公理、定理、性质矛盾;
(2)与假设矛盾;
(4)与客观事实矛盾.
课堂小结
命题的证明
反证法:反设结论,推理,导出矛盾,证得结论.
直接证明:(画图)写出已知、求证,写出证明过程.
课堂小测
(1)证明命题:一个角的两边分别平行于另一个角的两边,且方向相同,则这两个角相等.
已知:如图,AB∥A′B′,BC∥B′C′.
求证:∠B= ∠B′
证明:∵ AB∥A′B′ ( )
∴ ∠ B′= ∠α( )
∵ BC∥B′C′ ( )
∴ ∠ B = ∠α( )
∴ ∠ B = ∠B′ ( )
已 知
两直线平行,同位角相等
已 知
两直线平行,同位角相等
等量代换
1. 填空
.
课堂小测
(2) 已知:如图,∠A+∠B= 180°.
求证:∠C+∠D= 180°.
证明:∵∠A+∠B= 180°(已知),
∴ AD∥BC( ),
∴ ∠C+∠D= 180( ).
同旁内角互补,两直线平行
两直线平行,同旁内角互补
课堂小测
2. 已知:如图,AB与CD 相交于点E.
求证:∠A+∠C=∠B+∠D.
证明: ∵ AB与CD 相交于点E ,
∴ ∠AEC=∠BED (对顶角相等).
又 ∵∠A+∠C +∠AEC =∠B+∠D +∠BED =180°
(三角形内角和等于180°),
∴
∠A+∠C=∠B+∠D.
课堂小测
3.求证:△ABC中不能有两个钝角.
证明:假设△ABC中能有两个钝角,
即∠A<90°,∠B>90°,∠C>90°,
所以∠A+∠B+∠C>180°,
与三角形的内角和为180°矛盾,
所以假设不成立,因此原命题正确,
即△ABC中不能有两个钝角.
课堂小测
4.已知:如图有a,b,c三条直线,且a//c,b//c.
求证:a//b.
A
a
b
c
证明:假设a与b不平行,则可设它们相交于点A.
那么过点A 就有两条直线a,b分别与直线c平行,
这与“过直线外一点有且只有一条直线与已知直
线平行”矛盾,故假设不成立. ∴a//b.
课堂小测
(3)两条直线被第三条直线所截,同位角相等;
两条相交的直线a,b被第三条直线l所截(如图),它们的同位角不相等.
-1和-3的积是-1×(-3)>0,-1和-3不是正数.
5.举反例说明下列命题是假命题:
(1)两个锐角的和是钝角;
(2)如果数a,b的积ab>0,那么a,b都是正数;
直角三角形的两个锐角和不是钝角.
a
b
l
同课章节目录
