4.3.3 第2课时 全等三角形的判定定理(角角边) 课件(共19张PPT) 2025-2026学年度湘教版数学八年级上册
文档属性
| 名称 | 4.3.3 第2课时 全等三角形的判定定理(角角边) 课件(共19张PPT) 2025-2026学年度湘教版数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 568.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 00:00:00 | ||
图片预览


文档简介
(共19张PPT)
第4章
三角形
八年级数学湘教版·上册
4.3.3 第2课时 全等三角形的判定定理(角角边)
授课人:XXXX
学习目标
1.三角形全等的识别:AAS;(重点)
2.会寻找已知条件,并准确运用相关定理证明.(难点)
新课导入
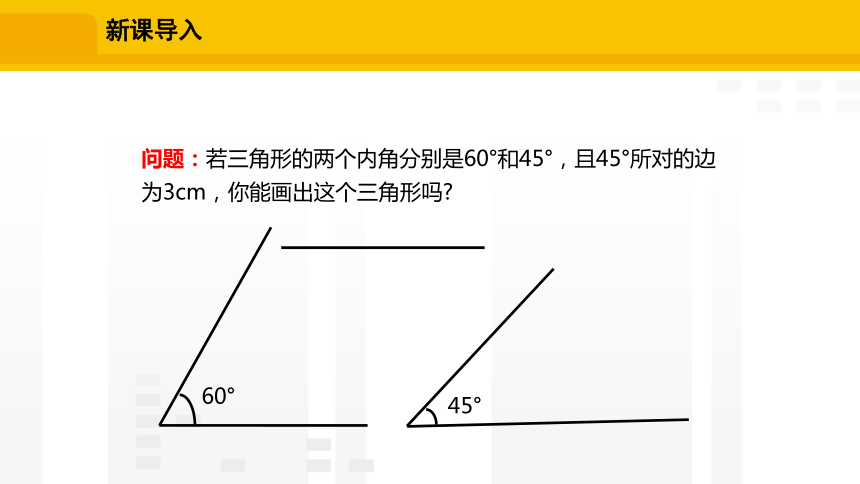
问题:若三角形的两个内角分别是60°和45°,且45°所对的边为3cm,你能画出这个三角形吗
60°
45°
新课导入
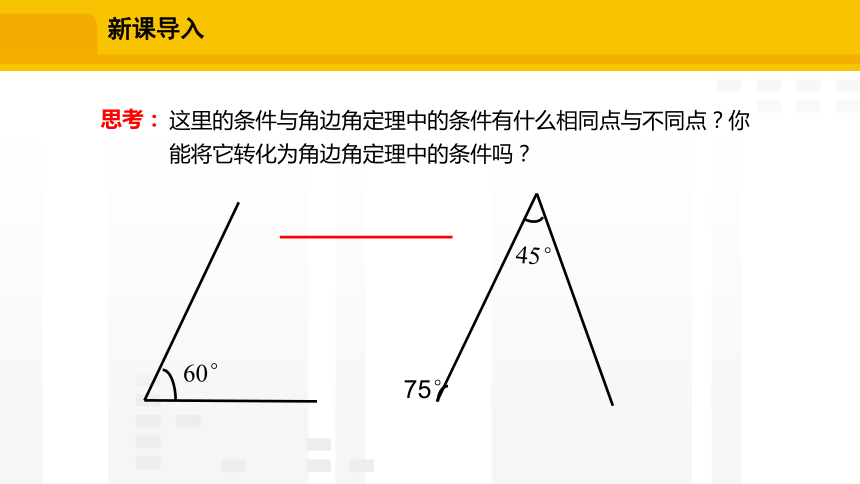
思考:
这里的条件与角边角定理中的条件有什么相同点与不同点?你能将它转化为角边角定理中的条件吗?
60°
45°
75°
新课导入
回顾旧知
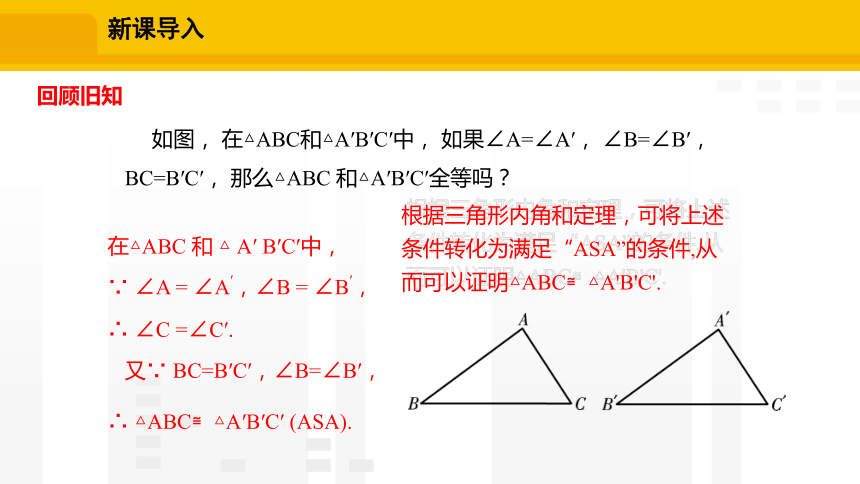
在△ABC 和 △ A′ B′C′中,
∵ ∠A = ∠A′,∠B = ∠B′,
∴ ∠C =∠C′.
又∵ BC=B′C′,∠B=∠B′,
∴ △ABC≌△A′B′C′ (ASA).
如图, 在△ABC和△A′B′C′中, 如果∠A=∠A′, ∠B=∠B′,
BC=B′C′, 那么△ABC 和△A′B′C′全等吗?
根据三角形内角和定理,可将上述条件转化为满足“ASA”的条件,从而可以证明△ABC≌△A'B'C'.
新知探究
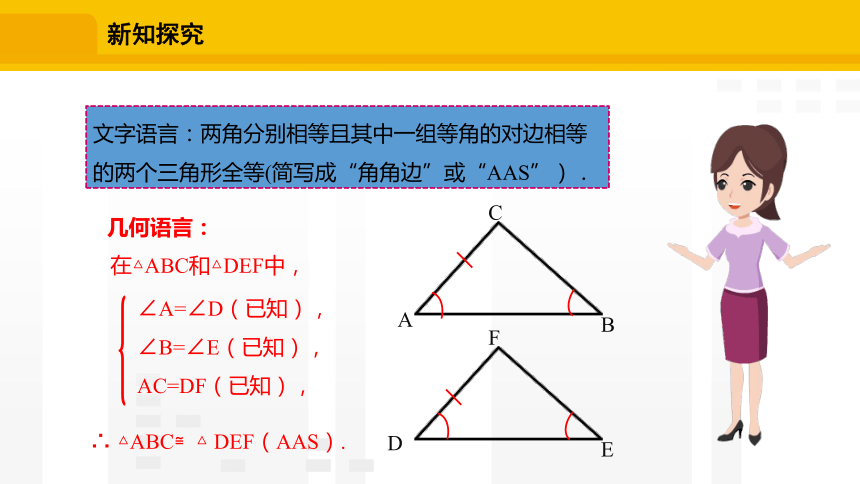
文字语言:两角分别相等且其中一组等角的对边相等的两个三角形全等(简写成“角角边”或“AAS”).
几何语言:
A
B
C
D
E
F
∠A=∠D(已知),
∠B=∠E(已知),
AC=DF(已知),
在△ABC和△DEF中,
∴ △ABC≌△ DEF(AAS).
新知探究
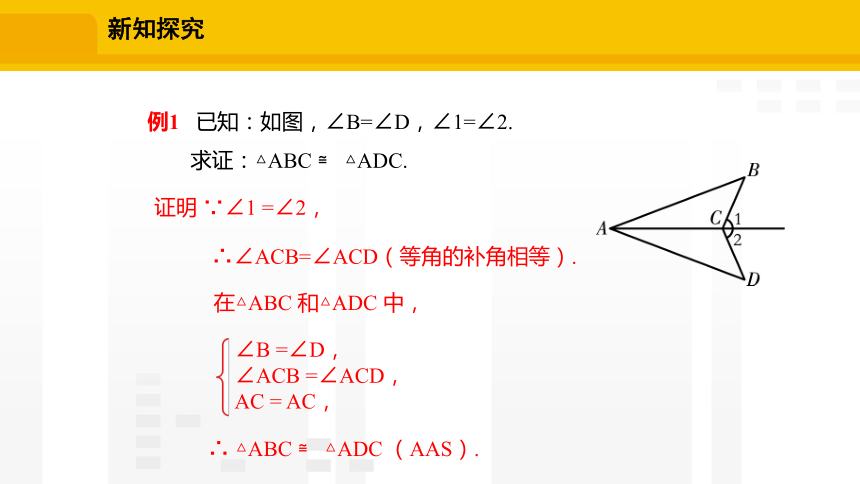
例1 已知:如图,∠B=∠D,∠1=∠2.
求证:△ABC ≌ △ADC.
证明 ∵∠1 =∠2,
∴∠ACB=∠ACD(等角的补角相等).
在△ABC 和△ADC 中,
∴ △ABC ≌ △ADC (AAS).
∠B =∠D,
∠ACB =∠ACD,
AC = AC,
新知探究
例2 已知:如图,点B,F,C,E在同一条直线上,AC∥FD,∠A=∠D,BF=EC.
求证:△ABC≌△DEF.
证明: ∵ AC∥FD,
∴∠ACB =∠DFE.
∵ BF= EC,
∴ BF+FC=EC+FC,
即 BC=EF .
在△ABC 和△DEF中,
∴ △ABC≌△DEF(AAS).
∠A =∠D,
∠ACB =∠DFE,
BC = EF,
新知探究
例3 如图,点B,F,C,D在同一条直线上,AB=ED,AB∥ED,AC∥EF.
求证:△ABC≌△EDF;BF=CD.
B
F
C
D
E
A
证明:∵ AB∥ED,AC∥EF(已知),
∴∠B=∠D,∠ACB=∠EFD.
(两直线平行,内错角相等)
在△ABC和△EDF中,
∠B=∠D(已证),
∠ACB=∠EFD(已证),
AB=ED(已知),
∴ △ABC≌△EDF(AAS),
∴BC=DF,∴BF=CD.
新知探究
例4 如图,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,
BD⊥直线m,CE⊥直线m,垂足分别为点D,E.
求证:(1)△BDA≌△AEC;
证明:(1)∵BD⊥m,CE⊥m,∴∠ADB=∠CEA=90°,
∴∠ABD+∠BAD=90°.
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∠ABD=∠CAE.
在△BDA和△AEC中,
∠ADB=∠CEA=90°,
∠ABD=∠CAE,
AB=AC,
∴△BDA≌△AEC(AAS).
新知探究
(2)DE=BD+CE.
∴BD=AE,AD=CE,
∴DE=DA+AE=BD+CE.
证明:∵△BDA≌△AEC,
注意:利用全等三角形可以解决线段之间的关系,比如线段的相等关系、和差关系等,解决问题的关键是运用全等三角形的判定与性质进行线段之间的转化.
新知探究
如图,已知△ABC ≌△A′B′C′ ,AD,A′D′ 分别是△ABC 和△A′B′C′的高.试说明AD= A′D′.
A
B
C
D
A′
B′
C′
D′
新知探究
解:∵△ABC ≌△A′B′C′ ,
∴AB=A'B',∠ABD=∠A'B'D'.
∵AD⊥BC,A'D'⊥B'C',∴∠ADB=∠A'D'B'=90°.
在△ABD和△A'B'D'中,
∠ADB=∠A'D'B'(已证),
∠ABD=∠A'B'D'(已证),
AB=A'B'(已证),
∴△ABD≌△A'B'D' (AAS),∴AD=A'D'.
A
B
C
D
A′
B′
C′
D′
新知探究
全等三角形对应边上的高也相等.
课堂小结
全等三角形判定
“角角边”(AAS)
应用:证明角相等,边相等.
内容:两角和其中一角的对边对应相等的两个三角形全等(简写成 “AAS”).
课堂小测
1. 已知:如图,∠1=∠2,AD=AE.
求证:△ADC ≌△AEB.
∴ △ADC≌△AEB(AAS).
∠2 =∠1,
∠A =∠ A,
AD = AE,
证明:
∵ 在△ADC 和△AEB 中,
课堂小测
2. 已知:在△ABC中,∠ABC =∠ACB, BD⊥AC于点D,CE⊥AB 于点E.
求证:BD=CE.
证明: 由题意可知△BEC 和△BDC 均为直角三角形,
∵ 在Rt△BEC 和Rt△CDB 中,
∴ Rt△BEC≌ Rt△CDB(AAS),
∠ABC =∠ACB ,
BC = BC ,
∠BEC =∠CDB=90° ,
∴BD=CE.
课堂小测
3.已知:如图, AB⊥BC,AD⊥DC,∠1=∠2. 求证:AB=AD.
A
C
D
B
1
2
证明: ∵ AB⊥BC,AD⊥DC,
∴ ∠ B=∠D=90 °.
在△ABC和△ADC中,
∠1=∠2 (已知),
∠ B=∠D(已证),
AC=AC (公共边),
∴ △ABC≌△ADC(AAS),
∴AB=AD.
解: △ABC 和△ADE 全等.
∵∠1=∠2(已知),
∴∠1+∠DAC=∠2+∠DAC,即∠BAC=∠DAE.
在△ABC 和△ADE 中,
课堂小测
A
B
C
D
E
1
2
4. 如图,已知∠C=∠E,∠1=∠2,AB=AD,△ABC 和△ADE全等吗?为什么?
∴ △ABC≌△ADE(AAS).
∠BAC =∠DAE,
AB = AD ,
∠C =∠E,
第4章
三角形
八年级数学湘教版·上册
4.3.3 第2课时 全等三角形的判定定理(角角边)
授课人:XXXX
学习目标
1.三角形全等的识别:AAS;(重点)
2.会寻找已知条件,并准确运用相关定理证明.(难点)
新课导入
问题:若三角形的两个内角分别是60°和45°,且45°所对的边为3cm,你能画出这个三角形吗
60°
45°
新课导入
思考:
这里的条件与角边角定理中的条件有什么相同点与不同点?你能将它转化为角边角定理中的条件吗?
60°
45°
75°
新课导入
回顾旧知
在△ABC 和 △ A′ B′C′中,
∵ ∠A = ∠A′,∠B = ∠B′,
∴ ∠C =∠C′.
又∵ BC=B′C′,∠B=∠B′,
∴ △ABC≌△A′B′C′ (ASA).
如图, 在△ABC和△A′B′C′中, 如果∠A=∠A′, ∠B=∠B′,
BC=B′C′, 那么△ABC 和△A′B′C′全等吗?
根据三角形内角和定理,可将上述条件转化为满足“ASA”的条件,从而可以证明△ABC≌△A'B'C'.
新知探究
文字语言:两角分别相等且其中一组等角的对边相等的两个三角形全等(简写成“角角边”或“AAS”).
几何语言:
A
B
C
D
E
F
∠A=∠D(已知),
∠B=∠E(已知),
AC=DF(已知),
在△ABC和△DEF中,
∴ △ABC≌△ DEF(AAS).
新知探究
例1 已知:如图,∠B=∠D,∠1=∠2.
求证:△ABC ≌ △ADC.
证明 ∵∠1 =∠2,
∴∠ACB=∠ACD(等角的补角相等).
在△ABC 和△ADC 中,
∴ △ABC ≌ △ADC (AAS).
∠B =∠D,
∠ACB =∠ACD,
AC = AC,
新知探究
例2 已知:如图,点B,F,C,E在同一条直线上,AC∥FD,∠A=∠D,BF=EC.
求证:△ABC≌△DEF.
证明: ∵ AC∥FD,
∴∠ACB =∠DFE.
∵ BF= EC,
∴ BF+FC=EC+FC,
即 BC=EF .
在△ABC 和△DEF中,
∴ △ABC≌△DEF(AAS).
∠A =∠D,
∠ACB =∠DFE,
BC = EF,
新知探究
例3 如图,点B,F,C,D在同一条直线上,AB=ED,AB∥ED,AC∥EF.
求证:△ABC≌△EDF;BF=CD.
B
F
C
D
E
A
证明:∵ AB∥ED,AC∥EF(已知),
∴∠B=∠D,∠ACB=∠EFD.
(两直线平行,内错角相等)
在△ABC和△EDF中,
∠B=∠D(已证),
∠ACB=∠EFD(已证),
AB=ED(已知),
∴ △ABC≌△EDF(AAS),
∴BC=DF,∴BF=CD.
新知探究
例4 如图,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,
BD⊥直线m,CE⊥直线m,垂足分别为点D,E.
求证:(1)△BDA≌△AEC;
证明:(1)∵BD⊥m,CE⊥m,∴∠ADB=∠CEA=90°,
∴∠ABD+∠BAD=90°.
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∠ABD=∠CAE.
在△BDA和△AEC中,
∠ADB=∠CEA=90°,
∠ABD=∠CAE,
AB=AC,
∴△BDA≌△AEC(AAS).
新知探究
(2)DE=BD+CE.
∴BD=AE,AD=CE,
∴DE=DA+AE=BD+CE.
证明:∵△BDA≌△AEC,
注意:利用全等三角形可以解决线段之间的关系,比如线段的相等关系、和差关系等,解决问题的关键是运用全等三角形的判定与性质进行线段之间的转化.
新知探究
如图,已知△ABC ≌△A′B′C′ ,AD,A′D′ 分别是△ABC 和△A′B′C′的高.试说明AD= A′D′.
A
B
C
D
A′
B′
C′
D′
新知探究
解:∵△ABC ≌△A′B′C′ ,
∴AB=A'B',∠ABD=∠A'B'D'.
∵AD⊥BC,A'D'⊥B'C',∴∠ADB=∠A'D'B'=90°.
在△ABD和△A'B'D'中,
∠ADB=∠A'D'B'(已证),
∠ABD=∠A'B'D'(已证),
AB=A'B'(已证),
∴△ABD≌△A'B'D' (AAS),∴AD=A'D'.
A
B
C
D
A′
B′
C′
D′
新知探究
全等三角形对应边上的高也相等.
课堂小结
全等三角形判定
“角角边”(AAS)
应用:证明角相等,边相等.
内容:两角和其中一角的对边对应相等的两个三角形全等(简写成 “AAS”).
课堂小测
1. 已知:如图,∠1=∠2,AD=AE.
求证:△ADC ≌△AEB.
∴ △ADC≌△AEB(AAS).
∠2 =∠1,
∠A =∠ A,
AD = AE,
证明:
∵ 在△ADC 和△AEB 中,
课堂小测
2. 已知:在△ABC中,∠ABC =∠ACB, BD⊥AC于点D,CE⊥AB 于点E.
求证:BD=CE.
证明: 由题意可知△BEC 和△BDC 均为直角三角形,
∵ 在Rt△BEC 和Rt△CDB 中,
∴ Rt△BEC≌ Rt△CDB(AAS),
∠ABC =∠ACB ,
BC = BC ,
∠BEC =∠CDB=90° ,
∴BD=CE.
课堂小测
3.已知:如图, AB⊥BC,AD⊥DC,∠1=∠2. 求证:AB=AD.
A
C
D
B
1
2
证明: ∵ AB⊥BC,AD⊥DC,
∴ ∠ B=∠D=90 °.
在△ABC和△ADC中,
∠1=∠2 (已知),
∠ B=∠D(已证),
AC=AC (公共边),
∴ △ABC≌△ADC(AAS),
∴AB=AD.
解: △ABC 和△ADE 全等.
∵∠1=∠2(已知),
∴∠1+∠DAC=∠2+∠DAC,即∠BAC=∠DAE.
在△ABC 和△ADE 中,
课堂小测
A
B
C
D
E
1
2
4. 如图,已知∠C=∠E,∠1=∠2,AB=AD,△ABC 和△ADE全等吗?为什么?
∴ △ABC≌△ADE(AAS).
∠BAC =∠DAE,
AB = AD ,
∠C =∠E,
同课章节目录
