4.3.4 全等三角形的判定定理(边边边) 课件(共18张PPT) 2025-2026学年度湘教版数学八年级上册
文档属性
| 名称 | 4.3.4 全等三角形的判定定理(边边边) 课件(共18张PPT) 2025-2026学年度湘教版数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 22:16:20 | ||
图片预览



文档简介
(共18张PPT)
第4章
三角形
八年级数学湘教版·上册
4.3.4 全等三角形的判定定理(边边边)
授课人:XXXX
学习目标
1.三角形全等的识别:SSS;(重点)
2.全面掌握三角形的稳定性,并会运用三角形的稳定性去解决实际问题.(难点)
新课导入
回顾旧知
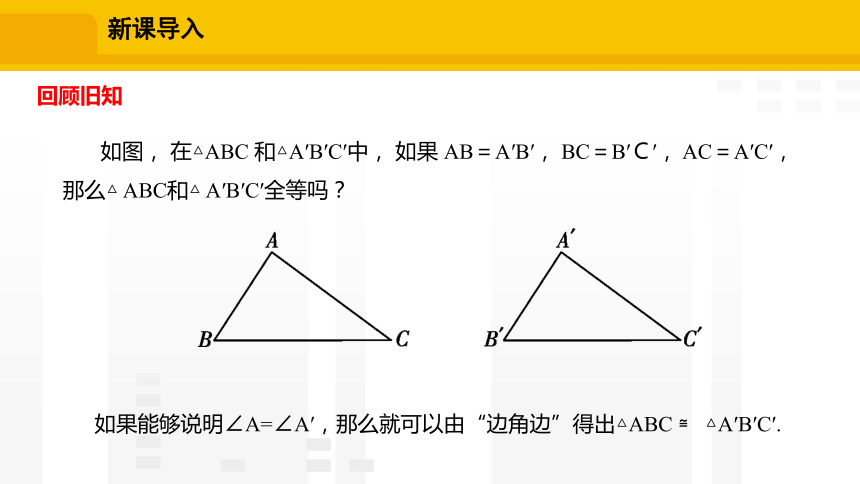
如果能够说明∠A=∠A′,那么就可以由“边角边”得出△ABC ≌ △A′B′C′.
如图, 在△ABC 和△A′B′C′中, 如果 AB=A′B′, BC=B′C′, AC=A′C′,那么△ ABC和△ A′B′C′全等吗?
新课导入
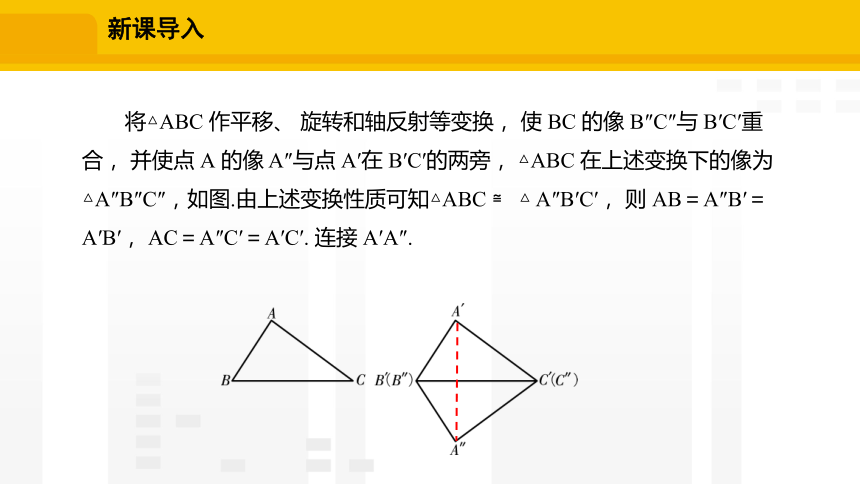
将△ABC 作平移、 旋转和轴反射等变换, 使 BC 的像 B″C″与 B′C′重合, 并使点 A 的像 A″与点 A′在 B′C′的两旁, △ABC 在上述变换下的像为△A″B″C″,如图.由上述变换性质可知△ABC ≌ △ A″B′C′, 则 AB=A″B′=A′B′, AC=A″C′=A′C′. 连接 A′A″.
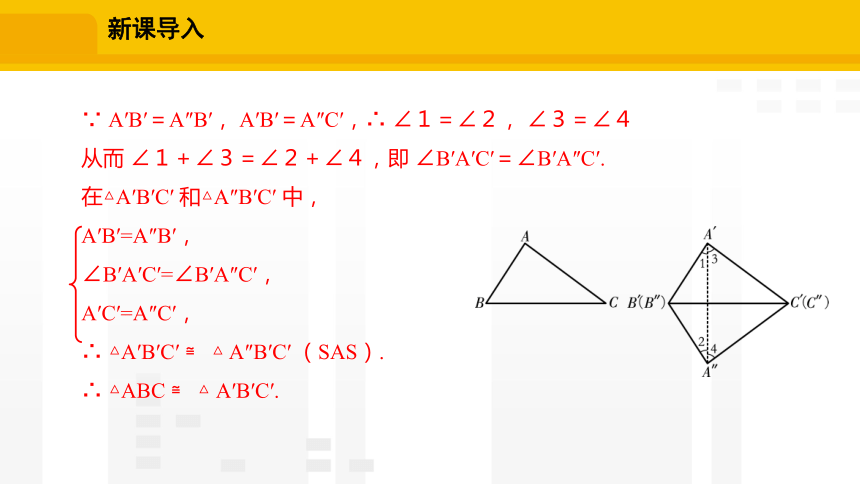
∵ A′B′=A″B′, A′B′=A″C′,∴ ∠1=∠2, ∠3=∠4
从而 ∠1+∠3=∠2+∠4,即 ∠B′A′C′=∠B′A″C′.
在△A′B′C′ 和△A″B′C′ 中,
A′B′=A″B′,
∠B′A′C′=∠B′A″C′,
A′C′=A″C′,
∴ △A′B′C′ ≌ △ A″B′C′ (SAS).
∴ △ABC ≌ △ A′B′C′.
新课导入
新知探究
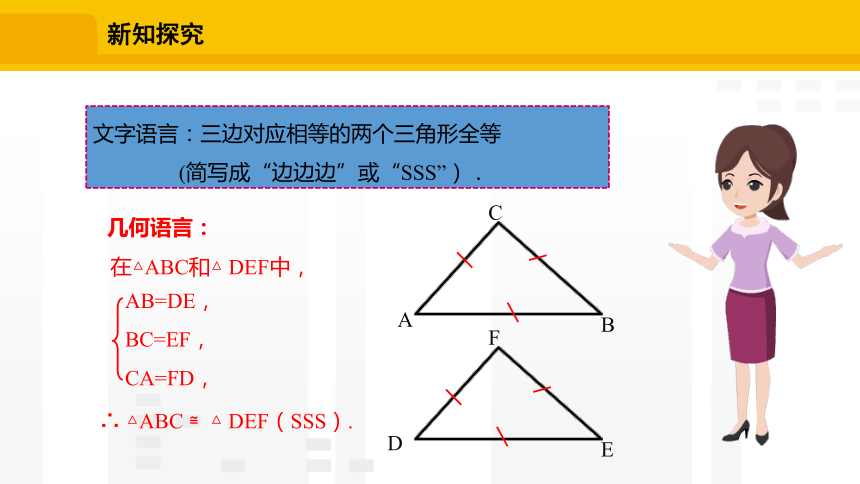
文字语言:三边对应相等的两个三角形全等
(简写成“边边边”或“SSS”).
几何语言:
A
B
C
D
E
F
在△ABC和△ DEF中,
∴ △ABC ≌△ DEF(SSS).
AB=DE,
BC=EF,
CA=FD,
新知探究
例1 已知:如图,AB=CD ,BC=DA.
求证: ∠B=∠D.
证明:
在△ABC和△CDA中,
∴ △ABC≌△CDA(SSS),
AB=CD,
BC=DA,
AC=CA(公共边),
∴ ∠B =∠D.
新知探究
例2 已知:如图,在△ABC中,AB=AC,点D,E 在BC上,且AD=AE,
BE=CD.求证:△ABD ≌△ACE.
证明: ∵ BE = CD,
∴ BE-DE = CD-DE,
即BD = CE.
在△ABD 和△ACE 中,
∴ △ABD ≌△ACE (SSS).
AB = AC,
BD = CE,
AD = AE,
新知探究
例3 已知:如图,AC与BD 相交于点O,且AB= DC,AC = DB.
求证:∠A =∠D.
证明 : 连接BC.
在△ABC 和△DCB 中,
∴ △ABC ≌△DCB (SSS),
∴ ∠A =∠D.
AB = DC,
BC = CB (公共边),
AC = DB ,
新知探究
由“边边边”可知,只要三角形三边的长度确定,那么这个三角形的形状和大小也就固定了,三角形的这个性质叫作三角形的稳定性.
新知探究
三角形的稳定性在生产和生活中有广泛的应用.
如日常生活中的定位锁、房屋的人字梁屋顶等都采用三角形结构,其道理就是运用三角形的稳定性.
新知探究
课堂小结
全等三角形判定
“边边边”(SSS)
三角形的稳定性:三角形三边的长度确定了,这个三角形的形状和大小就完全确定了.
内容:三边分别相等的两个三角形全等
(简写成 “SSS”).
课堂小测
证明: △ABC≌△DCB
理由如下:
AB = CD
AC = DB
=
SSS
2. 如图,D,F是线段BC上的两点,
AB=EC,AF=ED,要使△ABF≌△ECD ,
还需要条件 .
A
E
B D F C
A
B
C
D
△ABC ≌ ( )
1. 如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由.
△DCB
BC
CB
BF=CD(答案不唯一)
课堂小测
3.如图,AB=CD,AD=BC,则下列结论:
①△ABC≌△CDB;②△ABC≌△CDA;③△ABD ≌△CDB;④BA∥DC.
其中结论正确的个数是 ( )
A . 1 B. 2 C. 3 D. 4
C
4.如图,桥梁的斜拉钢索是三角形的结构,主要是为了 ( )
A.节省材料,节约成本
B.保持对称
C.利用三角形的稳定性
D美观漂亮
C
O
A
B
C
D
课堂小测
5.如图, 已知 AD=BC, AC=BD. 那么∠1 与∠2 相等吗?
解:
在△ABC 和△BAD 中,
∴ △ABC ≌△BAD(SSS),
BC=AD ,
BA = AB (公共边),
AC = BD,
∴ ∠1 =∠2.
课堂小测
6. 如图, 点 A, C, B, D 在同一条直线上, AC=BD, AE=CF,BE=DF.
求证: AE∥CF, BE∥DF.
在△ABE 和△CDF 中,
∴ △ABE ≌△CDF(SSS),
AE = CF,
AB = CD,
BE= DF,
∴ ∠A =∠DCF,∠ABE =∠D,
证明:∵AC=BD,
∴AC+BC=BD+BC, 即 AB=CD.
∴AE∥CF, BE∥DF.
课堂小测
7. 已知:如图,AB=AD,BC=DC. 求证:∠B =∠D.
证明: 如图,连接AC.
∴ △ACB ≌△ ACD (SSS),
∴ ∠B =∠D.
在△ACB 和△ACD 中,
AB = AD,
BC = CD ,
AC = AC (公共边) ,
第4章
三角形
八年级数学湘教版·上册
4.3.4 全等三角形的判定定理(边边边)
授课人:XXXX
学习目标
1.三角形全等的识别:SSS;(重点)
2.全面掌握三角形的稳定性,并会运用三角形的稳定性去解决实际问题.(难点)
新课导入
回顾旧知
如果能够说明∠A=∠A′,那么就可以由“边角边”得出△ABC ≌ △A′B′C′.
如图, 在△ABC 和△A′B′C′中, 如果 AB=A′B′, BC=B′C′, AC=A′C′,那么△ ABC和△ A′B′C′全等吗?
新课导入
将△ABC 作平移、 旋转和轴反射等变换, 使 BC 的像 B″C″与 B′C′重合, 并使点 A 的像 A″与点 A′在 B′C′的两旁, △ABC 在上述变换下的像为△A″B″C″,如图.由上述变换性质可知△ABC ≌ △ A″B′C′, 则 AB=A″B′=A′B′, AC=A″C′=A′C′. 连接 A′A″.
∵ A′B′=A″B′, A′B′=A″C′,∴ ∠1=∠2, ∠3=∠4
从而 ∠1+∠3=∠2+∠4,即 ∠B′A′C′=∠B′A″C′.
在△A′B′C′ 和△A″B′C′ 中,
A′B′=A″B′,
∠B′A′C′=∠B′A″C′,
A′C′=A″C′,
∴ △A′B′C′ ≌ △ A″B′C′ (SAS).
∴ △ABC ≌ △ A′B′C′.
新课导入
新知探究
文字语言:三边对应相等的两个三角形全等
(简写成“边边边”或“SSS”).
几何语言:
A
B
C
D
E
F
在△ABC和△ DEF中,
∴ △ABC ≌△ DEF(SSS).
AB=DE,
BC=EF,
CA=FD,
新知探究
例1 已知:如图,AB=CD ,BC=DA.
求证: ∠B=∠D.
证明:
在△ABC和△CDA中,
∴ △ABC≌△CDA(SSS),
AB=CD,
BC=DA,
AC=CA(公共边),
∴ ∠B =∠D.
新知探究
例2 已知:如图,在△ABC中,AB=AC,点D,E 在BC上,且AD=AE,
BE=CD.求证:△ABD ≌△ACE.
证明: ∵ BE = CD,
∴ BE-DE = CD-DE,
即BD = CE.
在△ABD 和△ACE 中,
∴ △ABD ≌△ACE (SSS).
AB = AC,
BD = CE,
AD = AE,
新知探究
例3 已知:如图,AC与BD 相交于点O,且AB= DC,AC = DB.
求证:∠A =∠D.
证明 : 连接BC.
在△ABC 和△DCB 中,
∴ △ABC ≌△DCB (SSS),
∴ ∠A =∠D.
AB = DC,
BC = CB (公共边),
AC = DB ,
新知探究
由“边边边”可知,只要三角形三边的长度确定,那么这个三角形的形状和大小也就固定了,三角形的这个性质叫作三角形的稳定性.
新知探究
三角形的稳定性在生产和生活中有广泛的应用.
如日常生活中的定位锁、房屋的人字梁屋顶等都采用三角形结构,其道理就是运用三角形的稳定性.
新知探究
课堂小结
全等三角形判定
“边边边”(SSS)
三角形的稳定性:三角形三边的长度确定了,这个三角形的形状和大小就完全确定了.
内容:三边分别相等的两个三角形全等
(简写成 “SSS”).
课堂小测
证明: △ABC≌△DCB
理由如下:
AB = CD
AC = DB
=
SSS
2. 如图,D,F是线段BC上的两点,
AB=EC,AF=ED,要使△ABF≌△ECD ,
还需要条件 .
A
E
B D F C
A
B
C
D
△ABC ≌ ( )
1. 如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由.
△DCB
BC
CB
BF=CD(答案不唯一)
课堂小测
3.如图,AB=CD,AD=BC,则下列结论:
①△ABC≌△CDB;②△ABC≌△CDA;③△ABD ≌△CDB;④BA∥DC.
其中结论正确的个数是 ( )
A . 1 B. 2 C. 3 D. 4
C
4.如图,桥梁的斜拉钢索是三角形的结构,主要是为了 ( )
A.节省材料,节约成本
B.保持对称
C.利用三角形的稳定性
D美观漂亮
C
O
A
B
C
D
课堂小测
5.如图, 已知 AD=BC, AC=BD. 那么∠1 与∠2 相等吗?
解:
在△ABC 和△BAD 中,
∴ △ABC ≌△BAD(SSS),
BC=AD ,
BA = AB (公共边),
AC = BD,
∴ ∠1 =∠2.
课堂小测
6. 如图, 点 A, C, B, D 在同一条直线上, AC=BD, AE=CF,BE=DF.
求证: AE∥CF, BE∥DF.
在△ABE 和△CDF 中,
∴ △ABE ≌△CDF(SSS),
AE = CF,
AB = CD,
BE= DF,
∴ ∠A =∠DCF,∠ABE =∠D,
证明:∵AC=BD,
∴AC+BC=BD+BC, 即 AB=CD.
∴AE∥CF, BE∥DF.
课堂小测
7. 已知:如图,AB=AD,BC=DC. 求证:∠B =∠D.
证明: 如图,连接AC.
∴ △ACB ≌△ ACD (SSS),
∴ ∠B =∠D.
在△ACB 和△ACD 中,
AB = AD,
BC = CD ,
AC = AC (公共边) ,
同课章节目录
