4.3.5 全等三角形的应用 课件(共22张PPT) 2025-2026学年度湘教版数学八年级上册
文档属性
| 名称 | 4.3.5 全等三角形的应用 课件(共22张PPT) 2025-2026学年度湘教版数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 624.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 22:17:18 | ||
图片预览


文档简介
(共22张PPT)
第4章
三角形
八年级数学湘教版·上册
4.3.5 全等三角形的应用
授课人:XXXX
学习目标
1.全面认清条件,能正确地利用判定条件判定三角形全等;(重点)
2.运用全等三角形的判定定理解决线段相等与角相等的相关实际性问题.(难点)
新课导入
回顾旧知
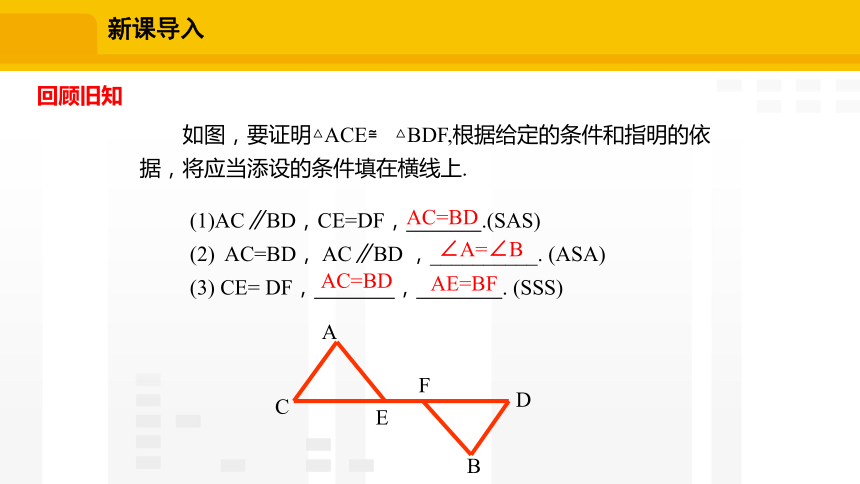
如图,要证明△ACE≌ △BDF,根据给定的条件和指明的依据,将应当添设的条件填在横线上.
(1)AC∥BD,CE=DF, .(SAS)
(2) AC=BD, AC∥BD ,__________. (ASA)
(3) CE= DF, , . (SSS)
C
B
A
E
F
D
AC=BD
∠A=∠B
AC=BD
AE=BF
新课导入
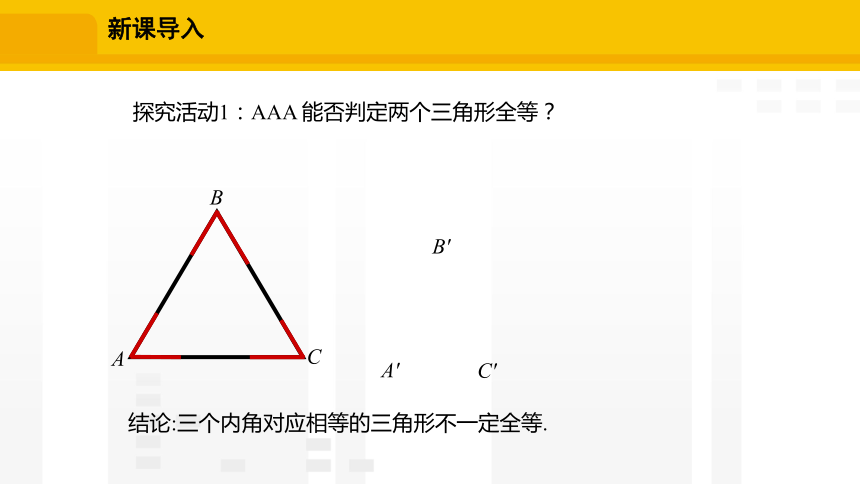
探究活动1:AAA 能否判定两个三角形全等?
结论:三个内角对应相等的三角形不一定全等.
A
B
C
A′
B′
C′
新课导入
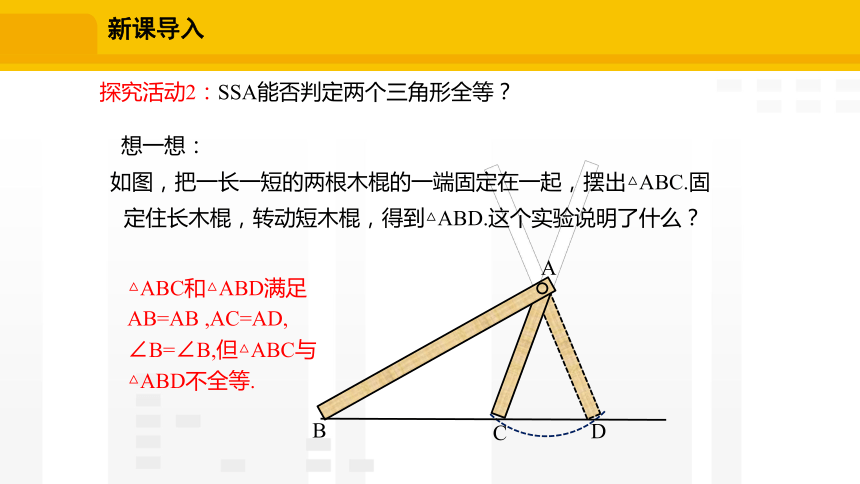
想一想:
如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC.固定住长木棍,转动短木棍,得到△ABD.这个实验说明了什么?
B
A
C
D
△ABC和△ABD满足AB=AB ,AC=AD,
∠B=∠B,但△ABC与△ABD不全等.
探究活动2:SSA能否判定两个三角形全等?
新课导入
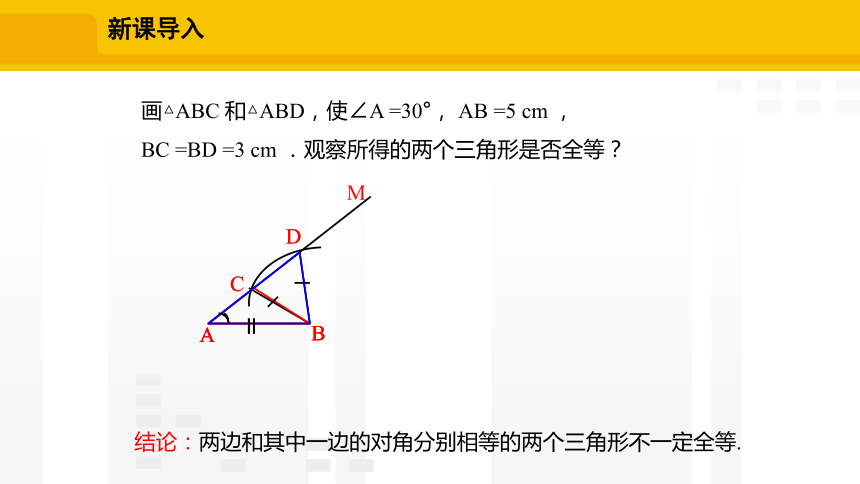
画△ABC 和△ABD,使∠A =30°, AB =5 cm ,
BC =BD =3 cm .观察所得的两个三角形是否全等?
A
B
M
C
D
A
B
C
A
B
D
结论:两边和其中一边的对角分别相等的两个三角形不一定全等.
新知探究
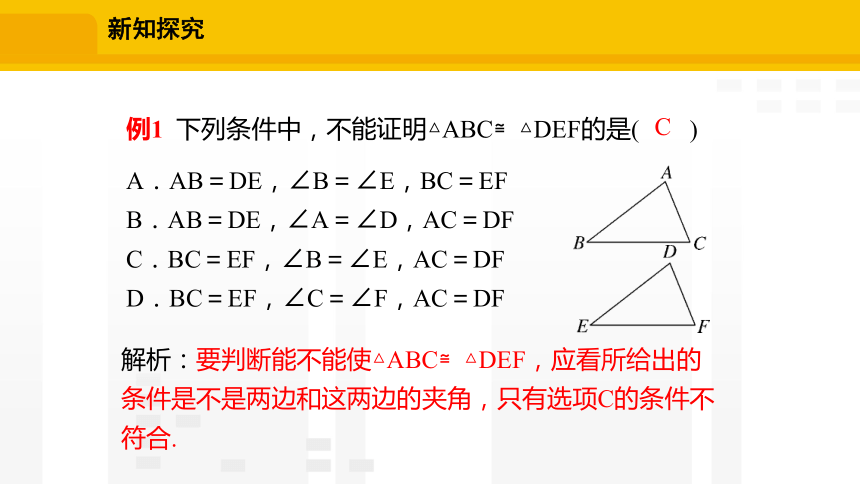
例1 下列条件中,不能证明△ABC≌△DEF的是( )
A.AB=DE,∠B=∠E,BC=EF
B.AB=DE,∠A=∠D,AC=DF
C.BC=EF,∠B=∠E,AC=DF
D.BC=EF,∠C=∠F,AC=DF
解析:要判断能不能使△ABC≌△DEF,应看所给出的条件是不是两边和这两边的夹角,只有选项C的条件不符合.
C
新知探究
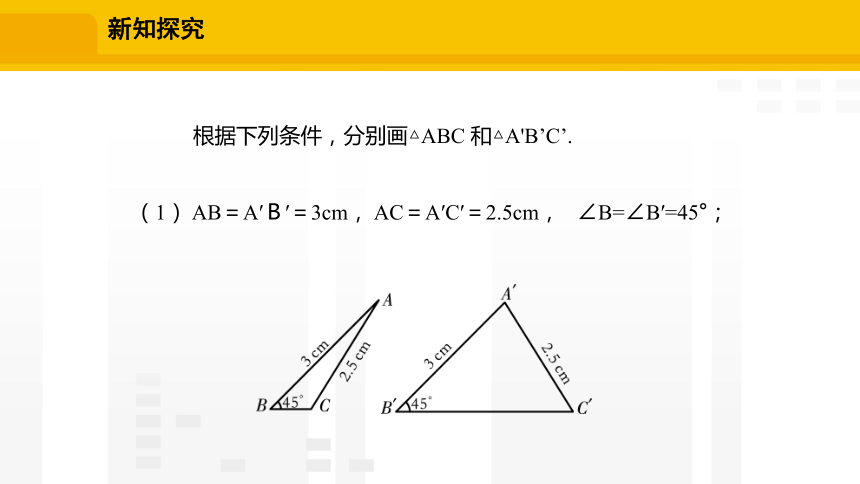
根据下列条件,分别画△ABC 和△A'B’C’.
(1) AB=A′B′=3cm, AC=A′C′=2.5cm, ∠B=∠B′=45°;
新知探究
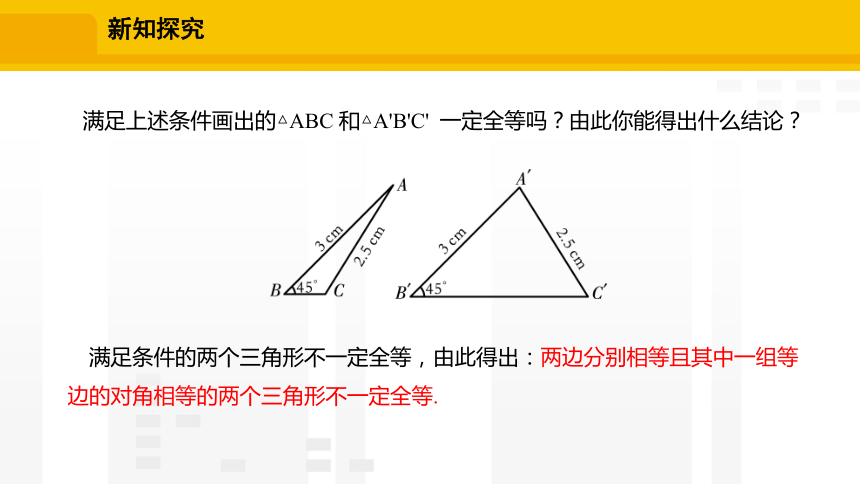
满足上述条件画出的△ABC 和△A'B'C' 一定全等吗?由此你能得出什么结论?
满足条件的两个三角形不一定全等,由此得出:两边分别相等且其中一组等边的对角相等的两个三角形不一定全等.
新知探究
(2) ∠A=∠A′= 80°,∠B=∠B ′= 30°,
∠C=∠C ′=70°.
满足上述条件画出的△ABC 和 △A'B'C' 一定全等吗?由此你能得出什么结论?
满足条件的两个三角形不一定全等,由此得出:三角分别相等的两个三角形不一定全等.
新知探究
判断三角形全等时,注意两边与其中一边的对角相等的两个三角形不一定全等.解题时要根据已知条件的位置来考虑,只具备SSA时是不能判定三角形全等的.
新知探究
例2 如图,在四边形ABCD中,AB=AD,BC=DC,E为AC上的一动点(不与A重合),在点E移动的过程中BE和DE是否相等?若相等,请写出证明过程;若不相等,请说明理由.
解:相等.理由如下:
在△ABC和△ADC中,
AB=AD,AC=AC,BC=DC,
∴△ABC≌△ADC(SSS),∴∠DAE=∠BAE.
在△ADE和△ABE中,
AB=AD,∠DAE=∠BAE,AE=AE,
∴△ADE≌△ABE(SAS),∴BE=DE.
新知探究
判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.本题要特别注意“SSA”不能作为全等三角形一种证明方法使用.
新知探究
例3 如图,已知CA=CB,AD=BD,M,N分别是CA,CB的中点,
求证:DM=DN.
在△ACD与△BCD中
证明:
CA=CB (已知)
AD=BD (已知)
CD=CD (公共边)
∴△ACD≌△BCD(SSS)
连接CD,如图所示.
∴∠A=∠B
又∵M,N分别是CA,CB的中点
∴AM=BN
新知探究
在△AMD与△BND中
AM=BN (已证)
∠A=∠B (已证)
AD=BD (已知)
∴△AMD≌△BND(SAS)
∴DM=DN
新知探究
例4 某地在山区修建高速公路时需挖通一条隧道. 为估测这条隧
道的长度(如图),需测出这座山A,B间的距离,结合所学
知识,你能给出什么好方法吗?
解: 选择某一合适的地点O,使得从O点能测出AO与BO的长度. 连接AO并延长至A′,使 OA′=OA;连接BO并延长至 B′,使 OB′=OB,连接 A′B′,这样就构造出两个三角形.
新知探究
O
A′
B′
在△AOB 和△A′OB′中,
OA=OA′,
∠AOB=∠A′OB′,
OB=OB′,
∴ △AOB≌△A′OB′ (SAS),
∴ AB=A′B′.
因此只要测出A′B′的长度就能得到这座山A,B间的距离.
课堂小结
判断三角形全等思路
已知一边一角:边为角的对边,找任一角(AAS);边为角的一边,找夹角的另一边(SAS);找边的对角(AAS),找夹角的另一角(ASA).
已知两边:找夹角(SAS);找另一边(SSS).
已知两角:找夹边(ASA);找除夹边外的任意一边(AAS).
课堂小测
1.如图,已知AC=DB,∠ACB=∠DBC,则有△ABC≌△ ,理由是 ,
且有∠ABC=∠ ,AB= .
A
B
C
D
DCB
SAS
DCB
DC
课堂小测
2. 如图,CD⊥AB于D点,BE⊥AC于E点,BE,CD交于O点,且AO平分∠BAC.求证:OB=OC.
证明:∵BE⊥AC,CD⊥AB,
∴∠ADC=∠BDC=∠AEB=∠CEB=90°.
∵AO平分∠BAC,
∴∠1=∠2.
在△AOD和△AOE中,
∴△AOD≌△AOE(AAS),
∴ OD=OE.
∠ADC=∠AEB,
∠1=∠2,
OA=OA,
课堂小测
∠BDC=∠CEB,
∠BOD=∠COE,
OD=OE,
在△BOD和△COE中,
∴△BOD≌△COE(ASA),
∴ OB=OC.
课堂小测
3.如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
(1)求证:△ABE≌DCE;
(2)当∠AEB=50°,求∠EBC的度数.
(1)证明:∵在△ABE和△DCE中,
∴△ABE≌△DCE(AAS).
(2)解:∵△ABE≌△DCE,
∴BE=EC,
∴∠EBC=∠ECB,
∵∠EBC+∠ECB=∠AEB=50°,
∴∠EBC=25°.
∠A=∠D,
∠AEB=∠DEC,
AB=DC,
第4章
三角形
八年级数学湘教版·上册
4.3.5 全等三角形的应用
授课人:XXXX
学习目标
1.全面认清条件,能正确地利用判定条件判定三角形全等;(重点)
2.运用全等三角形的判定定理解决线段相等与角相等的相关实际性问题.(难点)
新课导入
回顾旧知
如图,要证明△ACE≌ △BDF,根据给定的条件和指明的依据,将应当添设的条件填在横线上.
(1)AC∥BD,CE=DF, .(SAS)
(2) AC=BD, AC∥BD ,__________. (ASA)
(3) CE= DF, , . (SSS)
C
B
A
E
F
D
AC=BD
∠A=∠B
AC=BD
AE=BF
新课导入
探究活动1:AAA 能否判定两个三角形全等?
结论:三个内角对应相等的三角形不一定全等.
A
B
C
A′
B′
C′
新课导入
想一想:
如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC.固定住长木棍,转动短木棍,得到△ABD.这个实验说明了什么?
B
A
C
D
△ABC和△ABD满足AB=AB ,AC=AD,
∠B=∠B,但△ABC与△ABD不全等.
探究活动2:SSA能否判定两个三角形全等?
新课导入
画△ABC 和△ABD,使∠A =30°, AB =5 cm ,
BC =BD =3 cm .观察所得的两个三角形是否全等?
A
B
M
C
D
A
B
C
A
B
D
结论:两边和其中一边的对角分别相等的两个三角形不一定全等.
新知探究
例1 下列条件中,不能证明△ABC≌△DEF的是( )
A.AB=DE,∠B=∠E,BC=EF
B.AB=DE,∠A=∠D,AC=DF
C.BC=EF,∠B=∠E,AC=DF
D.BC=EF,∠C=∠F,AC=DF
解析:要判断能不能使△ABC≌△DEF,应看所给出的条件是不是两边和这两边的夹角,只有选项C的条件不符合.
C
新知探究
根据下列条件,分别画△ABC 和△A'B’C’.
(1) AB=A′B′=3cm, AC=A′C′=2.5cm, ∠B=∠B′=45°;
新知探究
满足上述条件画出的△ABC 和△A'B'C' 一定全等吗?由此你能得出什么结论?
满足条件的两个三角形不一定全等,由此得出:两边分别相等且其中一组等边的对角相等的两个三角形不一定全等.
新知探究
(2) ∠A=∠A′= 80°,∠B=∠B ′= 30°,
∠C=∠C ′=70°.
满足上述条件画出的△ABC 和 △A'B'C' 一定全等吗?由此你能得出什么结论?
满足条件的两个三角形不一定全等,由此得出:三角分别相等的两个三角形不一定全等.
新知探究
判断三角形全等时,注意两边与其中一边的对角相等的两个三角形不一定全等.解题时要根据已知条件的位置来考虑,只具备SSA时是不能判定三角形全等的.
新知探究
例2 如图,在四边形ABCD中,AB=AD,BC=DC,E为AC上的一动点(不与A重合),在点E移动的过程中BE和DE是否相等?若相等,请写出证明过程;若不相等,请说明理由.
解:相等.理由如下:
在△ABC和△ADC中,
AB=AD,AC=AC,BC=DC,
∴△ABC≌△ADC(SSS),∴∠DAE=∠BAE.
在△ADE和△ABE中,
AB=AD,∠DAE=∠BAE,AE=AE,
∴△ADE≌△ABE(SAS),∴BE=DE.
新知探究
判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.本题要特别注意“SSA”不能作为全等三角形一种证明方法使用.
新知探究
例3 如图,已知CA=CB,AD=BD,M,N分别是CA,CB的中点,
求证:DM=DN.
在△ACD与△BCD中
证明:
CA=CB (已知)
AD=BD (已知)
CD=CD (公共边)
∴△ACD≌△BCD(SSS)
连接CD,如图所示.
∴∠A=∠B
又∵M,N分别是CA,CB的中点
∴AM=BN
新知探究
在△AMD与△BND中
AM=BN (已证)
∠A=∠B (已证)
AD=BD (已知)
∴△AMD≌△BND(SAS)
∴DM=DN
新知探究
例4 某地在山区修建高速公路时需挖通一条隧道. 为估测这条隧
道的长度(如图),需测出这座山A,B间的距离,结合所学
知识,你能给出什么好方法吗?
解: 选择某一合适的地点O,使得从O点能测出AO与BO的长度. 连接AO并延长至A′,使 OA′=OA;连接BO并延长至 B′,使 OB′=OB,连接 A′B′,这样就构造出两个三角形.
新知探究
O
A′
B′
在△AOB 和△A′OB′中,
OA=OA′,
∠AOB=∠A′OB′,
OB=OB′,
∴ △AOB≌△A′OB′ (SAS),
∴ AB=A′B′.
因此只要测出A′B′的长度就能得到这座山A,B间的距离.
课堂小结
判断三角形全等思路
已知一边一角:边为角的对边,找任一角(AAS);边为角的一边,找夹角的另一边(SAS);找边的对角(AAS),找夹角的另一角(ASA).
已知两边:找夹角(SAS);找另一边(SSS).
已知两角:找夹边(ASA);找除夹边外的任意一边(AAS).
课堂小测
1.如图,已知AC=DB,∠ACB=∠DBC,则有△ABC≌△ ,理由是 ,
且有∠ABC=∠ ,AB= .
A
B
C
D
DCB
SAS
DCB
DC
课堂小测
2. 如图,CD⊥AB于D点,BE⊥AC于E点,BE,CD交于O点,且AO平分∠BAC.求证:OB=OC.
证明:∵BE⊥AC,CD⊥AB,
∴∠ADC=∠BDC=∠AEB=∠CEB=90°.
∵AO平分∠BAC,
∴∠1=∠2.
在△AOD和△AOE中,
∴△AOD≌△AOE(AAS),
∴ OD=OE.
∠ADC=∠AEB,
∠1=∠2,
OA=OA,
课堂小测
∠BDC=∠CEB,
∠BOD=∠COE,
OD=OE,
在△BOD和△COE中,
∴△BOD≌△COE(ASA),
∴ OB=OC.
课堂小测
3.如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
(1)求证:△ABE≌DCE;
(2)当∠AEB=50°,求∠EBC的度数.
(1)证明:∵在△ABE和△DCE中,
∴△ABE≌△DCE(AAS).
(2)解:∵△ABE≌△DCE,
∴BE=EC,
∴∠EBC=∠ECB,
∵∠EBC+∠ECB=∠AEB=50°,
∴∠EBC=25°.
∠A=∠D,
∠AEB=∠DEC,
AB=DC,
同课章节目录
