第三章数据的集中趋势与离散程度单元测试卷苏科版2025—2026学年九年级上册
文档属性
| 名称 | 第三章数据的集中趋势与离散程度单元测试卷苏科版2025—2026学年九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 762.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第三章数据的集中趋势与离散程度单元测试卷苏科版2025—2026学年九年级上册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题4分,满分40分)
题号 1 3 4 5 6 7 8 9 10
答案
1.在某次试验中,甲、乙两种水稻品种进行产量稳定试验,各选取了8块条件相同的试验田,同时播种并核定亩产,结果甲、乙两种水稻的平均产量均为1 200千克/亩, 为保证产量稳定,适合推广的品种为( )
A.甲 B.乙 C.甲、乙均可 D.无法确定
2.内厝中学初三某学习小组7位同学,为学校家庭困难学生捐款,捐款金额分别为5元,10元,6元,6元,7元,8元,9元,则这组数据的众数为( )
A.6 B.7 C.8 D.9
3.某商场进了一批橘子,每箱橘子的质量约为千克,进入仓库前,从中随机抽出箱称重,得到箱橘子的质量如下:(单位:千克),,,,,,,,,,这箱橘子质量的众数是( )
A. B. C. D.
4.某次八年级数学能力竞赛中,获得一等奖的5位同学得分由高到低依次为96,92,88,88,84,那么这组得分的中位数是( )
A.84 B.88 C.92 D.96
5.一组数据,,,,,,有唯一的众数,则为( )
A. B. C. D.
6.一组数据:0,1,2,2,5,若添加一个数据2,则下列刻画数据的指标发生变化的是( )
A.平均数 B.中位数 C.众数 D.方差
7.某中学校史展览馆要招募一名讲解员,小明经历了笔试和试讲两轮测试.他的笔试和试讲成绩分别为90分,98分.综合成绩中笔试占,试讲占,那么小明的综合成绩为( )
A.93.2分 B.94分 C.94.8分 D.95分
8.一组数据3,5,7,9,x的平均数为6,则x的值为( )
A.3 B.4 C.5 D.6
9.某公司要招聘一名职员,根据实际需要,从学历、专业技能、沟通能力和创新思维四个方面对应聘者进行打分,并按的比例确定每人最终得分.其中一名应聘者学历、专业技能、沟通能力和创新思维的得分依次是5分、8分、7分、9分,则他的最终得分是( )
A.分 B.分 C.分 D.分
10.A,B,C,D,E五位同学依次围成一个圆圈做益智游戏,规则是:每个人心里先想好一个实数,并把这个数悄悄地告诉相邻的两个人,然后每个人把与自己相邻的两个人告诉自己的数的平均数报出来.若A,B,C,D,E五位同学报出来的数恰好分别是1,2,3,4,5,则D同学心里想的那个数是( )
A.-3 B.4 C.5 D.9
二.填空题(每小题5分,满分20分)
11.已知一组数据的方差为,则关于数据的平均数为 ;
12.如图是某班体育成绩统计表,已知这组数据的众数为26分,中位数为27分,全班共有38人,则的值为 .
成绩(分) 23 24 25 26 27 28 29 30
人数(人) 2 3 5 6 4 3
13.某班体育老师为了解同学们一周参加课外体育锻炼的时长,随机调查了位同学,得到如表数据:这位同学一周参加课外体育锻炼时长的平均数是 小时.
时长(小时)
人数
14.求一组数据方差的算式为:,由算式提供的信息,则该组数据的方差 .
三.解答题(共6小题,总分60分,每题须有必要的文字说明和解答过程)
15.本学期开学初,九年级一名体育老师对自己所教班级的50名女生进行了仰卧起坐的测试(满分为7分),根据测试成绩制作了下面两个统计图.
根据统计图解答下列问题:
(1)本次测试的学生中,得6分的学生有多少人?
(2)本次测试的平均分是多少分?中位数是多少?众数是多少?
(3)通过一段时间的训练,体育老师对50名女生的仰卧起坐进行第二次测试,测得成绩的最低分为5分,且得6分和7分的人数共有45人,平均分比第一次提高了0.8分,问第二次测试中得6分、7分的学生各有多少人?
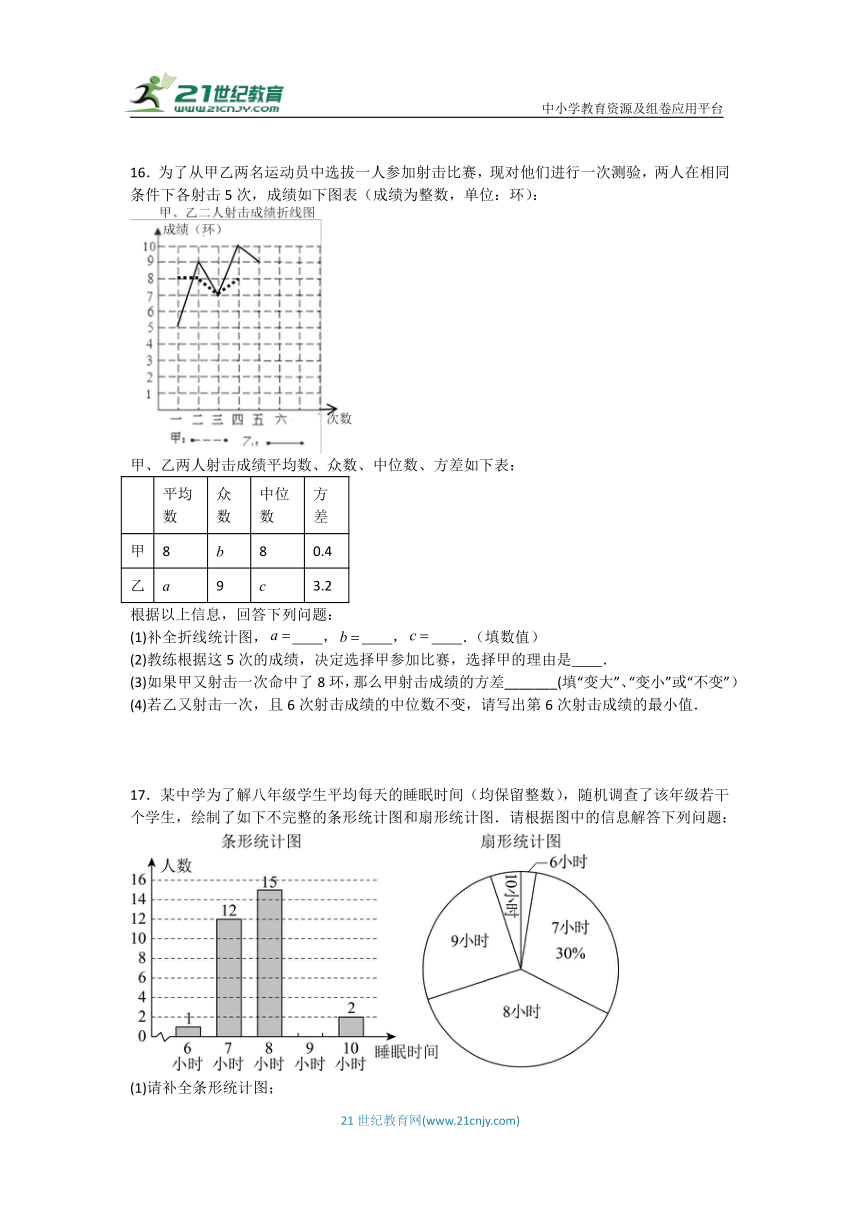
16.为了从甲乙两名运动员中选拔一人参加射击比赛,现对他们进行一次测验,两人在相同条件下各射击5次,成绩如下图表(成绩为整数,单位:环):
甲、乙两人射击成绩平均数、众数、中位数、方差如下表:
平均数 众数 中位数 方差
甲 8 b 8 0.4
乙 a 9 c 3.2
根据以上信息,回答下列问题:
(1)补全折线统计图, , , .(填数值)
(2)教练根据这5次的成绩,决定选择甲参加比赛,选择甲的理由是 .
(3)如果甲又射击一次命中了8环,那么甲射击成绩的方差_______(填“变大”、“变小”或“不变”)
(4)若乙又射击一次,且6次射击成绩的中位数不变,请写出第6次射击成绩的最小值.
17.某中学为了解八年级学生平均每天的睡眠时间(均保留整数),随机调查了该年级若干个学生,绘制了如下不完整的条形统计图和扇形统计图.请根据图中的信息解答下列问题:
(1)请补全条形统计图;
(2)这组数据的众数是 ;中位数是 ;
(3)根据调查统计结果,估计该校八年级学生平均每天的睡眠时间.
18.九年级甲、乙两名同学期末考试的成绩(单位:分)如表:
语文 数学 英语 历史 理化 体育
甲 75 93 85 84 95 90
乙 85 85 91 85 89 85
根据表格中的数据,回答下列问题:
(1)甲的总分为522分,则甲的平均成绩是_______分,乙的总分为520分,_______的成绩好一些.
(2)经计算知,,你认为_______不偏科;(填“甲”或者“乙”)
(3)乙的六科考试成绩的中位数是________分,众数是_________分.
(4)中考录取计算总分时,历史和体育科目的权重都是0.3,其它科的权重都是1,请问谁的成绩更好一些?
19.劳动课已正式成为中小学的一门独立课程,合肥市某中学提前尝试建立劳动教育实践基地,将劳动教育纳入日常教育教学中.某日,学校从七、八年级班级管理的花圃中,分别随机抽取了20个花圃对管理情况进行了评分(满分100分,数据分组为A组,,B组:,C组:,D组:,x表示评分的分数),现将评分情况绘制成了不完整的统计图:
(1)补全图1中的条形统计图,图2中C组所对应的圆心角为______;
(2)若八年级B组得分情况为89,88,87,87,86,85.
①八年级B组得分的方差为______;
②八年级20个花圃得分的中位数为______分.
20.为了丰富班级的“阅读角”,八年级某班发起图书征集活动,将同学们上交的书籍情况制成了如图所示尚不完整的统计图.请根据以下信息,解答下列问题:
(1)这个班级有______人,请你补全条形统计图;
(2)学生捐书数量的众数是______本,中位数是______本;
(3)为了丰富“阅读角”的书目类别,在统计完学生的捐书情况后,老师也参与了捐书.若学习委员将老师捐书的本数和原统计的捐书数量合并成一组新数据后,发现平均数增大了,则老师的捐书数量最少是______本.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 A A B B C D C D B D
二、填空题
11.【解】解:设数据的平均数为,
∴数据的方差为
,
∵,
∴,
∵,
∴,
∴,
∴,
∴的平均数,
∴的平均数为或,
故答案为:或.
12.【解】解:
这组数据的众数为分
中位数为分
第和个数据的平均数为分,前个数小于,
∴,即
为正整数且,,且
故答案为:.
13.【解】解:这位同学一周参加课外体育锻炼时长的平均数是:
(小时)
故答案为:.
14.【解】解:由方差计算公式可得,这组数据为,
∴,
∴,
故答案为:.
三、解答题
15.【解】(1)解:(人),
答:得6分的学生有25人.
(2)解:得5分的学生人数为(人),
由统计图可知,得4分和得7分的学生人数都为10人,
∴本次测试的平均分(分),
将50名女生测试的得分从小到大顺序排列,中位数为第25位和第26位的平均数,
∴中位数(分),
由统计图可知,得6分的学生人数最多,
∴众数是6分,
∴综上所述,本次测试的平均分是分,中位数是6分,众数是6分.
(3)解:由题意得,第二次测试中得5分的人数为(人),
设第二次测试中得6分的学生有人,则得7分的学生有人,
由题意得,,
解得:,
则,
答:第二次测试中得6分的学生有15人,得7分的学生有30人.
16.【解】(1)解:由折线统计图可知乙的5次数据分别为5、9、7、10、9(单位:环),
∴平均数为,
乙的5次数据从小到大排列为5、7、9、9、10,
∴中位数为,
由折线统计图发现甲的四次成绩分别为8、8、7、8,由表格可知其平均数为8,
∴,即第五次射击成绩为9,
∴8环次数最多,
∴众数,
补全折线统计图如下图,
故答案为:8,8,9;
(2)解:甲乙的平均数相同,但是甲的方差比乙的小,
说明甲的成绩更稳定,
故答案为:甲的成绩更稳定;
(3)解:因为第6次成绩等于平均数,根据方差定义可知分子多了个,
即分子不变,分母由5变成6,变大,
所以这个结果变小,即方差变小,
故答案为:变小;
(4)解:由(1)可知乙的前5次成绩为:5、7、9、9、10,
中位数为9,
要使中位数不变,则第6次成绩依然为9环即可,
故第6次射击成绩的最小值为9.
17.【解】(1)解: (人),
睡眠时间为小时的人数为:,
补全条形图如图所示:
(2)由图表可知,有人的睡眠时间为8小时,众数为小时,
中位数为小时,
故答案为8,8;
(3) (小时),
答:估计该校八年级学生平均每天的睡眠时间为小时.
18.【解】(1)解:甲的总分为522分,则甲的平均成绩是(分);
∵乙的总分为520分,,
∴甲的成绩好一些.
故答案为:87,甲;
(2)解:∵,,,
∴乙的各科成绩比较均衡,不偏科,
故答案为:乙;
(3)解:将乙的成绩从小到大排列:85,85,85,85,89,91,
∵第3个和第4个数据为85,85出现次数最多,
∴中位数为,众数为85.
故答案为:85,85;
(4)解:甲的总分:(分),
乙的总分:(分),
,
答:乙的成绩更好一些.
19.【解】(1)解:由图①可知,七年级管理的花圃中,评分B组的个数为,
故可补画条形统计图如下:
由图②可知,八年级班级管理的花圃中,评分C组的占比为,
故部分所占的圆心角为.
故答案为:;
(2)解:①由题意可知,B组得分的平均数为:,
故方差为;
②由题意可知,八年级20个花圃得分情况为
A组个,
若将20个数据按从大到小排列,其中中位数为第10、11两个分数的平均数,
则B组中87和88两个分数的平均数,
所以八年级20个花圃得分的中位数为.
故答案为:①;②;
20.【解】(1)解:人,
这个班有人,
故答案为:;
捐4本书的人有:人,
补全条形统计图:
(2)解:从图形看,这组数据中出现最多的是1,
这组数据的众数是1本;
把数据从小到大排列后,第,位数都是2,
这组数据的中位数是本,
故答案为:1,2;
(3)解:这60名学生捐书数量的平均数为:,
老师捐赠书之后平均数增大了,
老师的捐书数量最少是本,
故答案为:
21世纪教育网(www.21cnjy.com)
第三章数据的集中趋势与离散程度单元测试卷苏科版2025—2026学年九年级上册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题4分,满分40分)
题号 1 3 4 5 6 7 8 9 10
答案
1.在某次试验中,甲、乙两种水稻品种进行产量稳定试验,各选取了8块条件相同的试验田,同时播种并核定亩产,结果甲、乙两种水稻的平均产量均为1 200千克/亩, 为保证产量稳定,适合推广的品种为( )
A.甲 B.乙 C.甲、乙均可 D.无法确定
2.内厝中学初三某学习小组7位同学,为学校家庭困难学生捐款,捐款金额分别为5元,10元,6元,6元,7元,8元,9元,则这组数据的众数为( )
A.6 B.7 C.8 D.9
3.某商场进了一批橘子,每箱橘子的质量约为千克,进入仓库前,从中随机抽出箱称重,得到箱橘子的质量如下:(单位:千克),,,,,,,,,,这箱橘子质量的众数是( )
A. B. C. D.
4.某次八年级数学能力竞赛中,获得一等奖的5位同学得分由高到低依次为96,92,88,88,84,那么这组得分的中位数是( )
A.84 B.88 C.92 D.96
5.一组数据,,,,,,有唯一的众数,则为( )
A. B. C. D.
6.一组数据:0,1,2,2,5,若添加一个数据2,则下列刻画数据的指标发生变化的是( )
A.平均数 B.中位数 C.众数 D.方差
7.某中学校史展览馆要招募一名讲解员,小明经历了笔试和试讲两轮测试.他的笔试和试讲成绩分别为90分,98分.综合成绩中笔试占,试讲占,那么小明的综合成绩为( )
A.93.2分 B.94分 C.94.8分 D.95分
8.一组数据3,5,7,9,x的平均数为6,则x的值为( )
A.3 B.4 C.5 D.6
9.某公司要招聘一名职员,根据实际需要,从学历、专业技能、沟通能力和创新思维四个方面对应聘者进行打分,并按的比例确定每人最终得分.其中一名应聘者学历、专业技能、沟通能力和创新思维的得分依次是5分、8分、7分、9分,则他的最终得分是( )
A.分 B.分 C.分 D.分
10.A,B,C,D,E五位同学依次围成一个圆圈做益智游戏,规则是:每个人心里先想好一个实数,并把这个数悄悄地告诉相邻的两个人,然后每个人把与自己相邻的两个人告诉自己的数的平均数报出来.若A,B,C,D,E五位同学报出来的数恰好分别是1,2,3,4,5,则D同学心里想的那个数是( )
A.-3 B.4 C.5 D.9
二.填空题(每小题5分,满分20分)
11.已知一组数据的方差为,则关于数据的平均数为 ;
12.如图是某班体育成绩统计表,已知这组数据的众数为26分,中位数为27分,全班共有38人,则的值为 .
成绩(分) 23 24 25 26 27 28 29 30
人数(人) 2 3 5 6 4 3
13.某班体育老师为了解同学们一周参加课外体育锻炼的时长,随机调查了位同学,得到如表数据:这位同学一周参加课外体育锻炼时长的平均数是 小时.
时长(小时)
人数
14.求一组数据方差的算式为:,由算式提供的信息,则该组数据的方差 .
三.解答题(共6小题,总分60分,每题须有必要的文字说明和解答过程)
15.本学期开学初,九年级一名体育老师对自己所教班级的50名女生进行了仰卧起坐的测试(满分为7分),根据测试成绩制作了下面两个统计图.
根据统计图解答下列问题:
(1)本次测试的学生中,得6分的学生有多少人?
(2)本次测试的平均分是多少分?中位数是多少?众数是多少?
(3)通过一段时间的训练,体育老师对50名女生的仰卧起坐进行第二次测试,测得成绩的最低分为5分,且得6分和7分的人数共有45人,平均分比第一次提高了0.8分,问第二次测试中得6分、7分的学生各有多少人?
16.为了从甲乙两名运动员中选拔一人参加射击比赛,现对他们进行一次测验,两人在相同条件下各射击5次,成绩如下图表(成绩为整数,单位:环):
甲、乙两人射击成绩平均数、众数、中位数、方差如下表:
平均数 众数 中位数 方差
甲 8 b 8 0.4
乙 a 9 c 3.2
根据以上信息,回答下列问题:
(1)补全折线统计图, , , .(填数值)
(2)教练根据这5次的成绩,决定选择甲参加比赛,选择甲的理由是 .
(3)如果甲又射击一次命中了8环,那么甲射击成绩的方差_______(填“变大”、“变小”或“不变”)
(4)若乙又射击一次,且6次射击成绩的中位数不变,请写出第6次射击成绩的最小值.
17.某中学为了解八年级学生平均每天的睡眠时间(均保留整数),随机调查了该年级若干个学生,绘制了如下不完整的条形统计图和扇形统计图.请根据图中的信息解答下列问题:
(1)请补全条形统计图;
(2)这组数据的众数是 ;中位数是 ;
(3)根据调查统计结果,估计该校八年级学生平均每天的睡眠时间.
18.九年级甲、乙两名同学期末考试的成绩(单位:分)如表:
语文 数学 英语 历史 理化 体育
甲 75 93 85 84 95 90
乙 85 85 91 85 89 85
根据表格中的数据,回答下列问题:
(1)甲的总分为522分,则甲的平均成绩是_______分,乙的总分为520分,_______的成绩好一些.
(2)经计算知,,你认为_______不偏科;(填“甲”或者“乙”)
(3)乙的六科考试成绩的中位数是________分,众数是_________分.
(4)中考录取计算总分时,历史和体育科目的权重都是0.3,其它科的权重都是1,请问谁的成绩更好一些?
19.劳动课已正式成为中小学的一门独立课程,合肥市某中学提前尝试建立劳动教育实践基地,将劳动教育纳入日常教育教学中.某日,学校从七、八年级班级管理的花圃中,分别随机抽取了20个花圃对管理情况进行了评分(满分100分,数据分组为A组,,B组:,C组:,D组:,x表示评分的分数),现将评分情况绘制成了不完整的统计图:
(1)补全图1中的条形统计图,图2中C组所对应的圆心角为______;
(2)若八年级B组得分情况为89,88,87,87,86,85.
①八年级B组得分的方差为______;
②八年级20个花圃得分的中位数为______分.
20.为了丰富班级的“阅读角”,八年级某班发起图书征集活动,将同学们上交的书籍情况制成了如图所示尚不完整的统计图.请根据以下信息,解答下列问题:
(1)这个班级有______人,请你补全条形统计图;
(2)学生捐书数量的众数是______本,中位数是______本;
(3)为了丰富“阅读角”的书目类别,在统计完学生的捐书情况后,老师也参与了捐书.若学习委员将老师捐书的本数和原统计的捐书数量合并成一组新数据后,发现平均数增大了,则老师的捐书数量最少是______本.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 A A B B C D C D B D
二、填空题
11.【解】解:设数据的平均数为,
∴数据的方差为
,
∵,
∴,
∵,
∴,
∴,
∴,
∴的平均数,
∴的平均数为或,
故答案为:或.
12.【解】解:
这组数据的众数为分
中位数为分
第和个数据的平均数为分,前个数小于,
∴,即
为正整数且,,且
故答案为:.
13.【解】解:这位同学一周参加课外体育锻炼时长的平均数是:
(小时)
故答案为:.
14.【解】解:由方差计算公式可得,这组数据为,
∴,
∴,
故答案为:.
三、解答题
15.【解】(1)解:(人),
答:得6分的学生有25人.
(2)解:得5分的学生人数为(人),
由统计图可知,得4分和得7分的学生人数都为10人,
∴本次测试的平均分(分),
将50名女生测试的得分从小到大顺序排列,中位数为第25位和第26位的平均数,
∴中位数(分),
由统计图可知,得6分的学生人数最多,
∴众数是6分,
∴综上所述,本次测试的平均分是分,中位数是6分,众数是6分.
(3)解:由题意得,第二次测试中得5分的人数为(人),
设第二次测试中得6分的学生有人,则得7分的学生有人,
由题意得,,
解得:,
则,
答:第二次测试中得6分的学生有15人,得7分的学生有30人.
16.【解】(1)解:由折线统计图可知乙的5次数据分别为5、9、7、10、9(单位:环),
∴平均数为,
乙的5次数据从小到大排列为5、7、9、9、10,
∴中位数为,
由折线统计图发现甲的四次成绩分别为8、8、7、8,由表格可知其平均数为8,
∴,即第五次射击成绩为9,
∴8环次数最多,
∴众数,
补全折线统计图如下图,
故答案为:8,8,9;
(2)解:甲乙的平均数相同,但是甲的方差比乙的小,
说明甲的成绩更稳定,
故答案为:甲的成绩更稳定;
(3)解:因为第6次成绩等于平均数,根据方差定义可知分子多了个,
即分子不变,分母由5变成6,变大,
所以这个结果变小,即方差变小,
故答案为:变小;
(4)解:由(1)可知乙的前5次成绩为:5、7、9、9、10,
中位数为9,
要使中位数不变,则第6次成绩依然为9环即可,
故第6次射击成绩的最小值为9.
17.【解】(1)解: (人),
睡眠时间为小时的人数为:,
补全条形图如图所示:
(2)由图表可知,有人的睡眠时间为8小时,众数为小时,
中位数为小时,
故答案为8,8;
(3) (小时),
答:估计该校八年级学生平均每天的睡眠时间为小时.
18.【解】(1)解:甲的总分为522分,则甲的平均成绩是(分);
∵乙的总分为520分,,
∴甲的成绩好一些.
故答案为:87,甲;
(2)解:∵,,,
∴乙的各科成绩比较均衡,不偏科,
故答案为:乙;
(3)解:将乙的成绩从小到大排列:85,85,85,85,89,91,
∵第3个和第4个数据为85,85出现次数最多,
∴中位数为,众数为85.
故答案为:85,85;
(4)解:甲的总分:(分),
乙的总分:(分),
,
答:乙的成绩更好一些.
19.【解】(1)解:由图①可知,七年级管理的花圃中,评分B组的个数为,
故可补画条形统计图如下:
由图②可知,八年级班级管理的花圃中,评分C组的占比为,
故部分所占的圆心角为.
故答案为:;
(2)解:①由题意可知,B组得分的平均数为:,
故方差为;
②由题意可知,八年级20个花圃得分情况为
A组个,
若将20个数据按从大到小排列,其中中位数为第10、11两个分数的平均数,
则B组中87和88两个分数的平均数,
所以八年级20个花圃得分的中位数为.
故答案为:①;②;
20.【解】(1)解:人,
这个班有人,
故答案为:;
捐4本书的人有:人,
补全条形统计图:
(2)解:从图形看,这组数据中出现最多的是1,
这组数据的众数是1本;
把数据从小到大排列后,第,位数都是2,
这组数据的中位数是本,
故答案为:1,2;
(3)解:这60名学生捐书数量的平均数为:,
老师捐赠书之后平均数增大了,
老师的捐书数量最少是本,
故答案为:
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
