5.1 第1课时 直角三角形的性质和判定 课件(共18张PPT) 2025-2026学年度湘教版数学八年级上册
文档属性
| 名称 | 5.1 第1课时 直角三角形的性质和判定 课件(共18张PPT) 2025-2026学年度湘教版数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 707.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
第5章
直角三角形
八年级数学湘教版·上册
5.1 第1课时 直角三角形的性质和判定
授课人:XXXX
学习目标
1.理解和掌握直角三角形的性质和判定及斜边上中线的性质;(重点)
2.会运用直角三角形的性质和判定解决基本问题.(难点)
新课导入
三角形顶点与对边中点的连线段.
问题1 直角三角形的定义是什么?
问题2 三角形内角和的性质是什么?
有一个是直角的三角形叫直角三角形.
三角形内角和等于180°.
这节课我们一起探索直角三角形的判定与性质.
复习引入
问题3 三角形中线的定义是什么?
新知探究
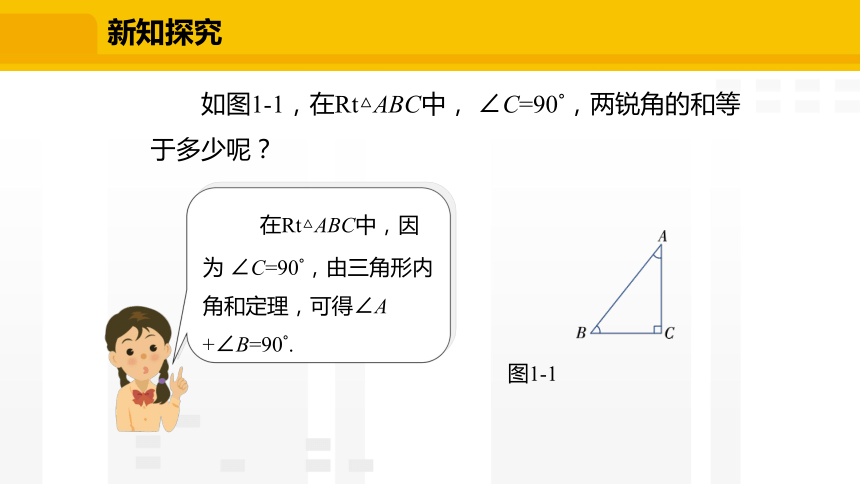
如图1-1,在Rt△ABC中, ∠C=90°,两锐角的和等于多少呢?
图1-1
在Rt△ABC中,因为 ∠C=90°,由三角形内角和定理,可得∠A +∠B=90°.
新知探究
结论
直角三角形的两个锐角互余.
由此得到:
新知探究
问题:有两个锐角互余的三角形是直角三角形吗?
如图1-2,在△ABC中, ∠A +∠B=90° , 那么△ABC
是直角三角形吗?
在△ABC中,因为 ∠A +∠B +∠C=180°, 又∠A +∠B=90°,所以∠C=90°. 于是△ABC是直角三角形.
图1-2
有两个锐角互余的三角形是直角三角形
二
新知探究
结论
有两个角互余的三角形是直角三角形.
由此得到:
新知探究
例 : 已知:如图,CD是△ABC的AB边上的中
线,且 .
求证:△ABC是直角三角形.
新知探究
证明:
因为 ,
所以 ∠1=∠A,(等边对等角)
∠2=∠B .
根据三角形内角和性质,有
∠A+∠B+∠ACB =180°,
即得∠A+∠B+∠1+∠2=180°,
2(∠A+∠B)=180°.
所以 ∠A+∠B =90°.
根据直角三角形判定定理,所以△ABC是直角三角形.
新知探究
问题: 如图1-3,画一个Rt△ABC, 并作出斜边AB上的中线CD,比较线段CD 与线段AB 之间的数量关系,你能得出什么结论?
图1-3
直角三角形斜边上的中线等于斜边的一半
三
新知探究
我测量后发现CD = AB.
线段CD 比线段AB短.
图1-3
新知探究
是否对于任意一个Rt△ABC,都有 CD = 成立呢?
图1-4
如图1-3, 如果中线CD = AB,则有∠DCA = ∠A .
由此受到启发,在图1-4 的Rt△ABC中,过直角顶点C作射线 交AB于点 ,使 ,
∠ = ∠A
则 .
图1-3
CD与 重合,且
从而
新知探究
∠A +∠B=90° ,
又∵
,
∴
∴
故得
∴ 点 是斜边上的中点,即 是斜边 的中线.
图1-4
新知探究
结论
直角三角形斜边上的中线等于斜边的一半.
由此得到:
课堂小结
直角三角形的两个锐角互余.
有两个角互余的三角形是直角三角形.
直角三角形斜边上的中线等于斜边的一半.
直角三角形的性质和判定:
课堂小测
1.在Rt△ABC中,斜边上的中线CD=2.5cm ,则斜边 AB的长是多少?
解:
AB=2CD=2×2.5=5(cm).
课堂小测
2.如图,AB∥CD,∠BAC和∠ACD的平分线相交于H点,E为AC的中点,EH=2. 那么△AHC是直角三角形吗?为什么?若是,求出AC的长.
解:
因为 AB∥CD,所以 ∠BAC+∠DCA=180°.
又 , ,
所以 ,
所以△AHC是直角三角形.
在Rt△AHC中,EH为斜边上的中线,
所以有 ,
由EH=2易知AC=4.
课堂小测
3.如图所示,在锐角三角形ABC中,CD,BE分别是AB,AC边上的高,且CD,BE交于一点P,若∠A=50°,求∠BPC的度数.
解:因为BE,CD是ABC的高,
所以∠BDP=90°,∠BEA=90°.
又∠A=50°,
所以∠ABE=90°-∠A=90°-50°= 40°.
所以∠BPC =∠ABE +∠BDP = 40°+ 90°= 130°.
A
D
B
E
P
C
第5章
直角三角形
八年级数学湘教版·上册
5.1 第1课时 直角三角形的性质和判定
授课人:XXXX
学习目标
1.理解和掌握直角三角形的性质和判定及斜边上中线的性质;(重点)
2.会运用直角三角形的性质和判定解决基本问题.(难点)
新课导入
三角形顶点与对边中点的连线段.
问题1 直角三角形的定义是什么?
问题2 三角形内角和的性质是什么?
有一个是直角的三角形叫直角三角形.
三角形内角和等于180°.
这节课我们一起探索直角三角形的判定与性质.
复习引入
问题3 三角形中线的定义是什么?
新知探究
如图1-1,在Rt△ABC中, ∠C=90°,两锐角的和等于多少呢?
图1-1
在Rt△ABC中,因为 ∠C=90°,由三角形内角和定理,可得∠A +∠B=90°.
新知探究
结论
直角三角形的两个锐角互余.
由此得到:
新知探究
问题:有两个锐角互余的三角形是直角三角形吗?
如图1-2,在△ABC中, ∠A +∠B=90° , 那么△ABC
是直角三角形吗?
在△ABC中,因为 ∠A +∠B +∠C=180°, 又∠A +∠B=90°,所以∠C=90°. 于是△ABC是直角三角形.
图1-2
有两个锐角互余的三角形是直角三角形
二
新知探究
结论
有两个角互余的三角形是直角三角形.
由此得到:
新知探究
例 : 已知:如图,CD是△ABC的AB边上的中
线,且 .
求证:△ABC是直角三角形.
新知探究
证明:
因为 ,
所以 ∠1=∠A,(等边对等角)
∠2=∠B .
根据三角形内角和性质,有
∠A+∠B+∠ACB =180°,
即得∠A+∠B+∠1+∠2=180°,
2(∠A+∠B)=180°.
所以 ∠A+∠B =90°.
根据直角三角形判定定理,所以△ABC是直角三角形.
新知探究
问题: 如图1-3,画一个Rt△ABC, 并作出斜边AB上的中线CD,比较线段CD 与线段AB 之间的数量关系,你能得出什么结论?
图1-3
直角三角形斜边上的中线等于斜边的一半
三
新知探究
我测量后发现CD = AB.
线段CD 比线段AB短.
图1-3
新知探究
是否对于任意一个Rt△ABC,都有 CD = 成立呢?
图1-4
如图1-3, 如果中线CD = AB,则有∠DCA = ∠A .
由此受到启发,在图1-4 的Rt△ABC中,过直角顶点C作射线 交AB于点 ,使 ,
∠ = ∠A
则 .
图1-3
CD与 重合,且
从而
新知探究
∠A +∠B=90° ,
又∵
,
∴
∴
故得
∴ 点 是斜边上的中点,即 是斜边 的中线.
图1-4
新知探究
结论
直角三角形斜边上的中线等于斜边的一半.
由此得到:
课堂小结
直角三角形的两个锐角互余.
有两个角互余的三角形是直角三角形.
直角三角形斜边上的中线等于斜边的一半.
直角三角形的性质和判定:
课堂小测
1.在Rt△ABC中,斜边上的中线CD=2.5cm ,则斜边 AB的长是多少?
解:
AB=2CD=2×2.5=5(cm).
课堂小测
2.如图,AB∥CD,∠BAC和∠ACD的平分线相交于H点,E为AC的中点,EH=2. 那么△AHC是直角三角形吗?为什么?若是,求出AC的长.
解:
因为 AB∥CD,所以 ∠BAC+∠DCA=180°.
又 , ,
所以 ,
所以△AHC是直角三角形.
在Rt△AHC中,EH为斜边上的中线,
所以有 ,
由EH=2易知AC=4.
课堂小测
3.如图所示,在锐角三角形ABC中,CD,BE分别是AB,AC边上的高,且CD,BE交于一点P,若∠A=50°,求∠BPC的度数.
解:因为BE,CD是ABC的高,
所以∠BDP=90°,∠BEA=90°.
又∠A=50°,
所以∠ABE=90°-∠A=90°-50°= 40°.
所以∠BPC =∠ABE +∠BDP = 40°+ 90°= 130°.
A
D
B
E
P
C
同课章节目录
