5.1 第2课时 含30°角的直角三角形的性质及其应用 课件(共12张PPT) 2025-2026学年度湘教版数学八年级上册
文档属性
| 名称 | 5.1 第2课时 含30°角的直角三角形的性质及其应用 课件(共12张PPT) 2025-2026学年度湘教版数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 504.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 22:21:52 | ||
图片预览





文档简介
(共12张PPT)
第5章
直角三角形
八年级数学湘教版·上册
5.1 第2课时 含30°角的直角三角形的
性质及其应用
授课人:XXXX
学习目标
1.理解和掌握有关30°角的直角三角形的性质和应用;(重点)
2.通过定理的证明和应用,初步了解转化思想,并培养学生
逻辑思维能力、分析问题和解决问题的能力.(难点)
新课导入
问题:回顾一下,上节课学了三角形的哪些性质和判定?
直角三角形的两个锐角互余.
有两个角互余的三角形是直角三角形.
直角三角形斜边上的中线等于斜边的一半.
新知探究
动手:用刻度尺测量含30°角的直角三角形的斜边和短直角边,比较它们之间的数量关系.
结论:短直角边=斜边
含30°角的直角三角形的性质
活动探究
新知探究
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
A
)
30°
B
C
几何语言:在Rt△ABC中,
∵∠A=30°,
∴BC= AC或AC=2BC.
归纳结论
新知探究
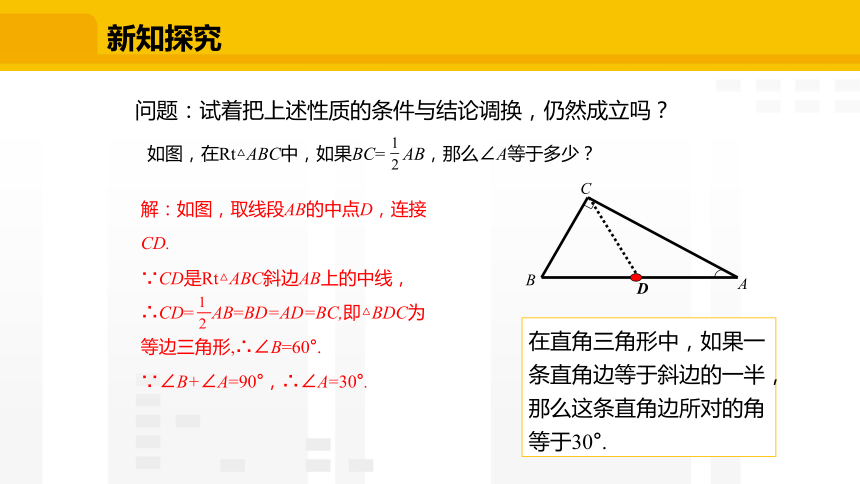
解:如图,取线段AB的中点D,连接CD.
∵CD是Rt△ABC斜边AB上的中线,
∴CD= AB=BD=AD=BC,即△BDC为等边三角形,∴∠B=60°.
∵∠B+∠A=90°,∴∠A=30°.
如图,在Rt△ABC中,如果BC= AB,那么∠A等于多少?
B
C
A
D
问题:试着把上述性质的条件与结论调换,仍然成立吗?
在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°.
新知探究
典例精析
例: 一艘船从A处出发,以每小时10海里的速度向正北航行,从A处测得一礁石C在北偏西30°的方向上.如果这艘轮船上午8:00从A处出发,10:00到达B处,从B处测得一礁石C在北偏西60°的方向上.
(1)画出礁石C的位置;
(2)求出B处到礁石C的距离.
B
C
30°
60°
A
D
解:(1)如图,以B为顶点,向北偏西60°作角,
这角一边与AM交于点C,
则C为礁石所在地.
M
北
新知探究
(2)∵∠DBC=∠BAC+∠ACB,
∠BAC=30 °, ∠DBC=60°,
∴∠ACB=30°,即∠BAC=∠ACB,
∴BC=AB ( 等角对等边) ,
即 BC=AB=10×2=20(海里).
答:B处到礁石C的距离为20海里.
B
C
30°
60°
A
D
M
北
课堂小结
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°.
直角三角形中30°角的性质定理:
课堂小测
1.如图,是屋架设计图的一部分,点D是斜梁AB的中点,BC为立柱,DE垂直于横梁AC,AB=7.4m, ∠A=30 ° ,求立柱BC,DE的长.
A
B
C
D
E
课堂小测
解:在△ABC中,
∵ BC⊥AC ,∠A=30°,
∴BC= AB= ×7.4=3.7(m).
∵ 点D是AB的中点 ,
∴ AD= AB=3.7(m).
在△ADE中,
∵ DE⊥AC ,∠A=30°,
∴DE= AD= ×3.7=1.85(m).
答:立柱BC的长是3.7m,DE的长是1.85m.
课堂小测
2.如图,要把一块三角形的土地均匀分给甲、乙、丙三家农户去种植作物.如果∠ C=90 °,∠ B=30 ° ,要使这三家农户所得土地的大小、形状都相同,请你试着分一分,在图上画出来.
B
A
C
解:如图所示.
第5章
直角三角形
八年级数学湘教版·上册
5.1 第2课时 含30°角的直角三角形的
性质及其应用
授课人:XXXX
学习目标
1.理解和掌握有关30°角的直角三角形的性质和应用;(重点)
2.通过定理的证明和应用,初步了解转化思想,并培养学生
逻辑思维能力、分析问题和解决问题的能力.(难点)
新课导入
问题:回顾一下,上节课学了三角形的哪些性质和判定?
直角三角形的两个锐角互余.
有两个角互余的三角形是直角三角形.
直角三角形斜边上的中线等于斜边的一半.
新知探究
动手:用刻度尺测量含30°角的直角三角形的斜边和短直角边,比较它们之间的数量关系.
结论:短直角边=斜边
含30°角的直角三角形的性质
活动探究
新知探究
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
A
)
30°
B
C
几何语言:在Rt△ABC中,
∵∠A=30°,
∴BC= AC或AC=2BC.
归纳结论
新知探究
解:如图,取线段AB的中点D,连接CD.
∵CD是Rt△ABC斜边AB上的中线,
∴CD= AB=BD=AD=BC,即△BDC为等边三角形,∴∠B=60°.
∵∠B+∠A=90°,∴∠A=30°.
如图,在Rt△ABC中,如果BC= AB,那么∠A等于多少?
B
C
A
D
问题:试着把上述性质的条件与结论调换,仍然成立吗?
在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°.
新知探究
典例精析
例: 一艘船从A处出发,以每小时10海里的速度向正北航行,从A处测得一礁石C在北偏西30°的方向上.如果这艘轮船上午8:00从A处出发,10:00到达B处,从B处测得一礁石C在北偏西60°的方向上.
(1)画出礁石C的位置;
(2)求出B处到礁石C的距离.
B
C
30°
60°
A
D
解:(1)如图,以B为顶点,向北偏西60°作角,
这角一边与AM交于点C,
则C为礁石所在地.
M
北
新知探究
(2)∵∠DBC=∠BAC+∠ACB,
∠BAC=30 °, ∠DBC=60°,
∴∠ACB=30°,即∠BAC=∠ACB,
∴BC=AB ( 等角对等边) ,
即 BC=AB=10×2=20(海里).
答:B处到礁石C的距离为20海里.
B
C
30°
60°
A
D
M
北
课堂小结
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°.
直角三角形中30°角的性质定理:
课堂小测
1.如图,是屋架设计图的一部分,点D是斜梁AB的中点,BC为立柱,DE垂直于横梁AC,AB=7.4m, ∠A=30 ° ,求立柱BC,DE的长.
A
B
C
D
E
课堂小测
解:在△ABC中,
∵ BC⊥AC ,∠A=30°,
∴BC= AB= ×7.4=3.7(m).
∵ 点D是AB的中点 ,
∴ AD= AB=3.7(m).
在△ADE中,
∵ DE⊥AC ,∠A=30°,
∴DE= AD= ×3.7=1.85(m).
答:立柱BC的长是3.7m,DE的长是1.85m.
课堂小测
2.如图,要把一块三角形的土地均匀分给甲、乙、丙三家农户去种植作物.如果∠ C=90 °,∠ B=30 ° ,要使这三家农户所得土地的大小、形状都相同,请你试着分一分,在图上画出来.
B
A
C
解:如图所示.
同课章节目录
