5.2 第1课时 勾股定理 课件(共15张PPT) 2025-2026学年度湘教版数学八年级上册
文档属性
| 名称 | 5.2 第1课时 勾股定理 课件(共15张PPT) 2025-2026学年度湘教版数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 873.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 22:21:40 | ||
图片预览



文档简介
(共15张PPT)
第5章
直角三角形
八年级数学湘教版·上册
5.2 第1课时 勾股定理
授课人:XXXX
学习目标
1.了解勾股定理的内容,理解并掌握直角三角形三边之间的数量关系.(重点)
2.能够运用勾股定理进行简单的计算.(难点)
新课导入
如图,这是一幅美丽的图案,仔细观察,你能发现这幅图中的奥秘吗?带着疑问我们来一起探索吧.
新知探究
勾股定理
一
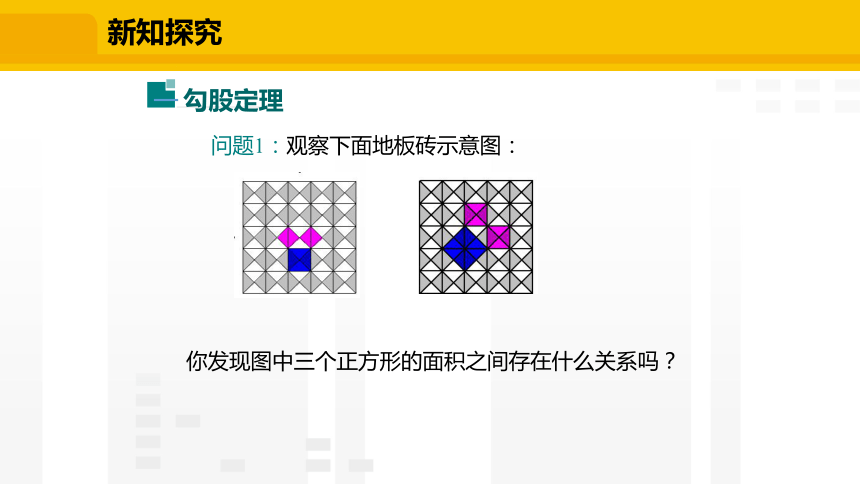
问题1:观察下面地板砖示意图:
你发现图中三个正方形的面积之间存在什么关系吗?
新知探究
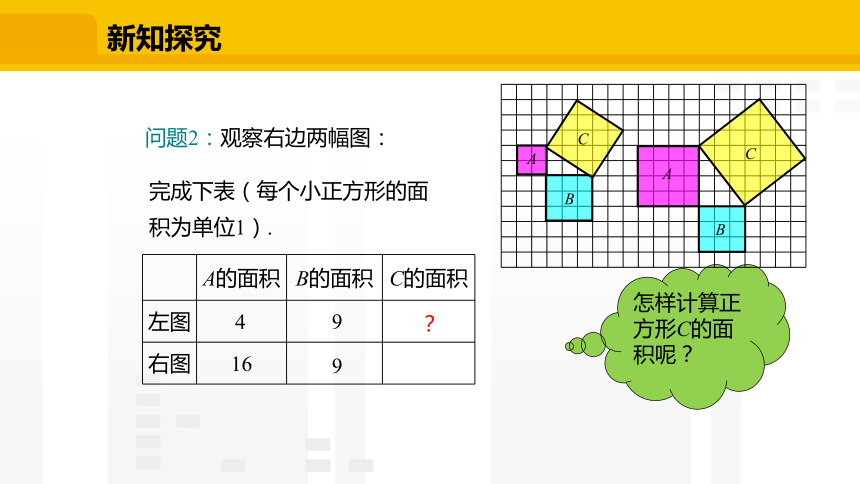
问题2:观察右边两幅图:
完成下表(每个小正方形的面积为单位1).
A的面积 B的面积 C的面积
左图
右图
4
?
怎样计算正方形C的面积呢?
9
16
9
A
B
C
A
B
C
新知探究
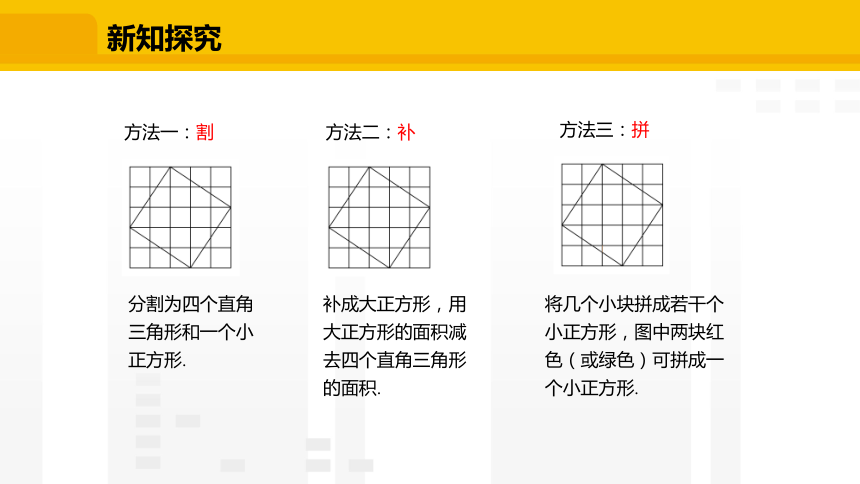
方法一:割
方法二:补
方法三:拼
分割为四个直角三角形和一个小正方形.
补成大正方形,用大正方形的面积减去四个直角三角形的面积.
将几个小块拼成若干个小正方形,图中两块红色(或绿色)可拼成一个小正方形.
新知探究
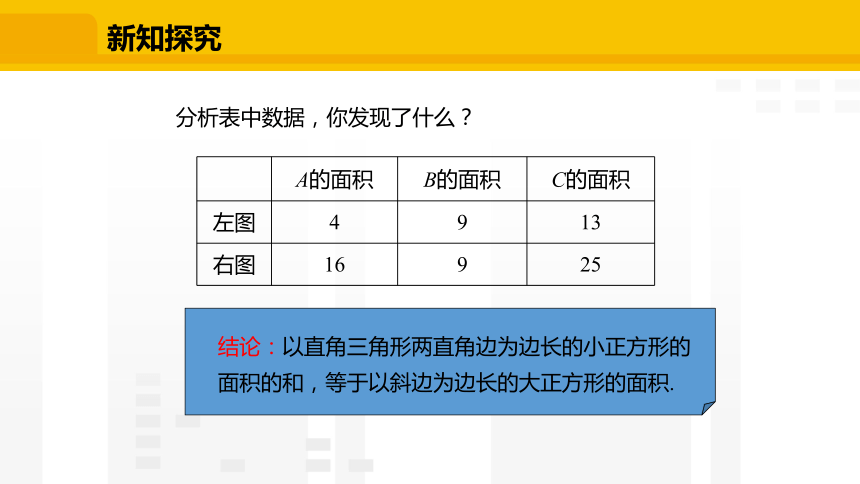
分析表中数据,你发现了什么?
A的面积 B的面积 C的面积
左图 4 9 13
右图 16 9 25
结论:以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的大正方形的面积.
新知探究
(1)你能用直角三角形的两直角边的长a,b和斜边长c来表示图中正方形的面积吗?根据前面的结论,它们之间又有什么样的关系呢?
想一想
a2+b2=c2
(2)以5 cm,12 cm为直角边作出一个直角三角形,并测量斜边的长度. (1)中的规律对这个三角形仍然成立吗?
新知探究
直角三角形两直角边的平方和等于斜边的平方.如果a,b和c分别表示直角三角形的两直角边和斜边,那么 a2+b2=c2.
勾股定理
要点归纳
新知探究
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦,“勾股定理”因此而得名.
名字的由来
在西方又称毕达哥拉斯定理
新知探究
例 : 求斜边长为17 cm、一条直角边长为15 cm的直角三角形的面积.
解:设另一条直角边长是x cm.由勾股定理得,
152+ x2 =172,x2=172-152=289–225=64,
解得 x=±8(负值舍去),
所以另一直角边长为8 cm,
故直角三角形的面积是
(cm2).
利用勾股定理进行计算
二
课堂小结
勾股定理
如果直角三角形两直角边长分别为a,b,斜边长为 c ,那么a2+b2=c2
利用勾股定理进行计算
课堂小测
1.图中阴影部分是一个正方形,则此正方形的面积
为 .
8 cm
10 cm
36 cm
课堂小测
2.判断题.
①△RtABC的两直角边AB=5,AC=12,则斜边BC=13 ( ) ②△ABC的两边a=6,b=8,则c=10 ( )
3.填空题.
在△ABC中,∠C=90°,AC=6,CB=8,则
△ABC的面积为_____,斜边上的高CD为______.
√
24
4.8
A
B
C
D
课堂小测
4.一高为2.5m 的木梯,架在高为2.4m 的墙上(如图),这时梯脚与墙的距离是多少
A
B
C
解:在Rt△ABC中,根据勾股定理,
得BC2=AB2-AC2
=2.52-2.42
=0.49,
所以BC=0.7 (m).
答:梯脚与墙的距离是0.7m.
第5章
直角三角形
八年级数学湘教版·上册
5.2 第1课时 勾股定理
授课人:XXXX
学习目标
1.了解勾股定理的内容,理解并掌握直角三角形三边之间的数量关系.(重点)
2.能够运用勾股定理进行简单的计算.(难点)
新课导入
如图,这是一幅美丽的图案,仔细观察,你能发现这幅图中的奥秘吗?带着疑问我们来一起探索吧.
新知探究
勾股定理
一
问题1:观察下面地板砖示意图:
你发现图中三个正方形的面积之间存在什么关系吗?
新知探究
问题2:观察右边两幅图:
完成下表(每个小正方形的面积为单位1).
A的面积 B的面积 C的面积
左图
右图
4
?
怎样计算正方形C的面积呢?
9
16
9
A
B
C
A
B
C
新知探究
方法一:割
方法二:补
方法三:拼
分割为四个直角三角形和一个小正方形.
补成大正方形,用大正方形的面积减去四个直角三角形的面积.
将几个小块拼成若干个小正方形,图中两块红色(或绿色)可拼成一个小正方形.
新知探究
分析表中数据,你发现了什么?
A的面积 B的面积 C的面积
左图 4 9 13
右图 16 9 25
结论:以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的大正方形的面积.
新知探究
(1)你能用直角三角形的两直角边的长a,b和斜边长c来表示图中正方形的面积吗?根据前面的结论,它们之间又有什么样的关系呢?
想一想
a2+b2=c2
(2)以5 cm,12 cm为直角边作出一个直角三角形,并测量斜边的长度. (1)中的规律对这个三角形仍然成立吗?
新知探究
直角三角形两直角边的平方和等于斜边的平方.如果a,b和c分别表示直角三角形的两直角边和斜边,那么 a2+b2=c2.
勾股定理
要点归纳
新知探究
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦,“勾股定理”因此而得名.
名字的由来
在西方又称毕达哥拉斯定理
新知探究
例 : 求斜边长为17 cm、一条直角边长为15 cm的直角三角形的面积.
解:设另一条直角边长是x cm.由勾股定理得,
152+ x2 =172,x2=172-152=289–225=64,
解得 x=±8(负值舍去),
所以另一直角边长为8 cm,
故直角三角形的面积是
(cm2).
利用勾股定理进行计算
二
课堂小结
勾股定理
如果直角三角形两直角边长分别为a,b,斜边长为 c ,那么a2+b2=c2
利用勾股定理进行计算
课堂小测
1.图中阴影部分是一个正方形,则此正方形的面积
为 .
8 cm
10 cm
36 cm
课堂小测
2.判断题.
①△RtABC的两直角边AB=5,AC=12,则斜边BC=13 ( ) ②△ABC的两边a=6,b=8,则c=10 ( )
3.填空题.
在△ABC中,∠C=90°,AC=6,CB=8,则
△ABC的面积为_____,斜边上的高CD为______.
√
24
4.8
A
B
C
D
课堂小测
4.一高为2.5m 的木梯,架在高为2.4m 的墙上(如图),这时梯脚与墙的距离是多少
A
B
C
解:在Rt△ABC中,根据勾股定理,
得BC2=AB2-AC2
=2.52-2.42
=0.49,
所以BC=0.7 (m).
答:梯脚与墙的距离是0.7m.
同课章节目录
