人教版2025—2026学年八年级上册数学期中考试仿真试卷(含答案)
文档属性
| 名称 | 人教版2025—2026学年八年级上册数学期中考试仿真试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 758.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 20:45:11 | ||
图片预览



文档简介
人教版2025—2026学年八年级上册数学期中考试仿真试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。笞卷前,考生务必
将自己的姓名、准考证号填写在答题卡上。
2.回答第I卷时,选出每小题答案后,把答案填写在答题卡上对应题目的位置
,填空题填写在答题卡相应的位置写在本试卷上无效。
3.回答第II卷时,将答案写在第II卷答题卡上。
4.考试结束后,将本试卷和答题卡一并交回。
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列组成冬奥会会徽的四个图案中是轴对称图形的是( )
A.B.C.D.
2.下列各组线段能组成一个三角形的是( )
A. B. C. D.
3.下列计算中正确的是( )
A. B. C. D.
4.如果,,则的度数是( )
A. B. C. D.
5.下面四个图形中,画出的边上的高正确的是( )
A. B. C. D.
6.下列条件中不可以判定两个直角三角形全等的是( )
A.两条直角边对应相等 B.斜边和直角边对应相等
C.一条边和一锐角对应相等 D.一条边和一个角对应相等
7.如图,△ABC中,∠BAC=100°,DF,EG分别是AB,AC的垂直平分线,则∠DAE等于( )
A.50° B.45° C.30° D.20°
8.如果(2x+m)与(x+3)的乘积中不含x的一次项,那么m的值为( )
A.﹣6 B.﹣3 C.0 D.1
9.下面四个式子中,不能表示图中阴影部分面积的是( )
A. B.
C. D.
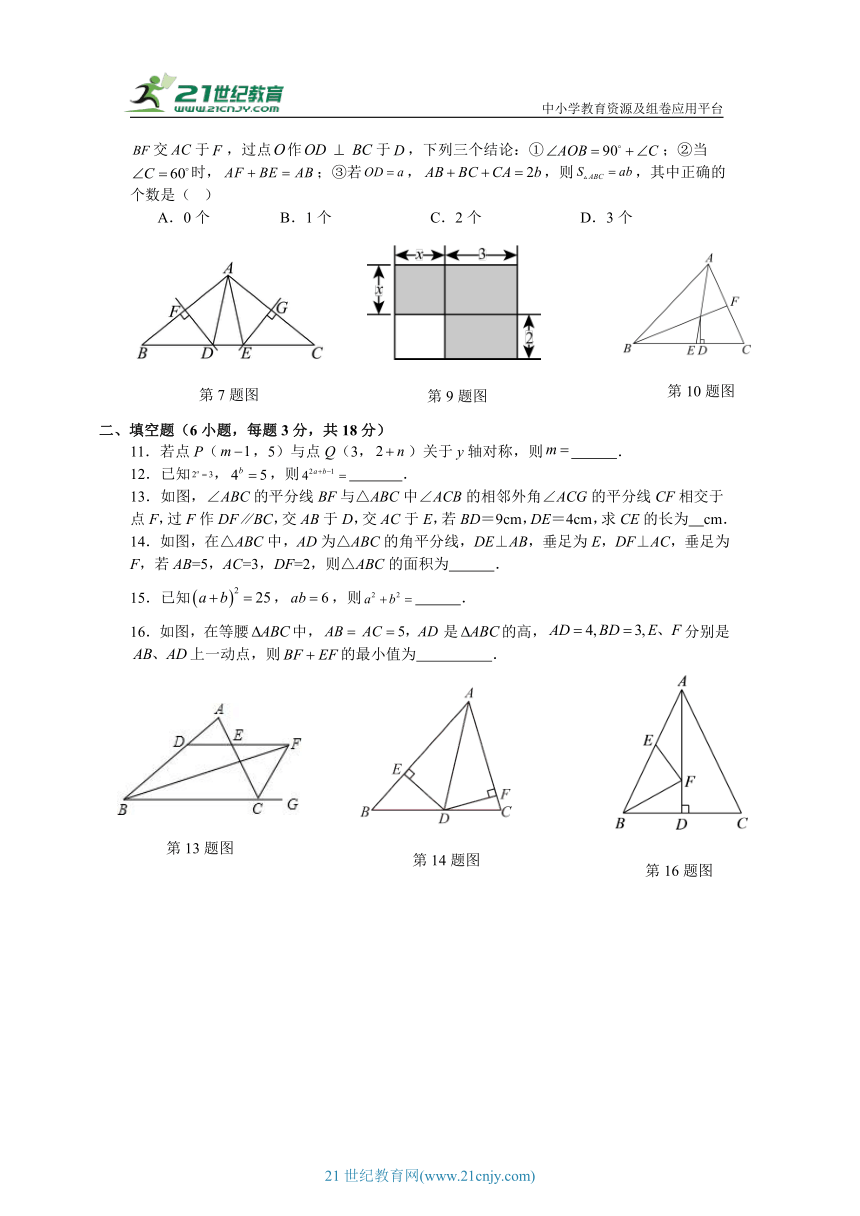
10.如图,在中,和的平分线,相交于点,交于,交于,过点作于,下列三个结论:①;②当时,;③若,,则,其中正确的个数是( )
A.0个 B.1个 C.2个 D.3个
二、填空题(6小题,每题3分,共18分)
11.若点P(,5)与点Q(3,)关于y轴对称,则 .
12.已知,,则 .
13.如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E,若BD=9cm,DE=4cm,求CE的长为 cm.
14.如图,在△ABC中,AD为△ABC的角平分线,DE⊥AB,垂足为E,DF⊥AC,垂足为F,若AB=5,AC=3,DF=2,则△ABC的面积为 .
15.已知,,则 .
16.如图,在等腰中,是的高,分别是上一动点,则的最小值为 .
第II卷
人教版2025—2026学年八年级上册数学期中考试仿真试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.化简:(1);
(2).
18.先化简,再求值:,其中.
19.如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=82°,∠C=40°,求∠DAE的度数.
20.两个大小不同的等腰直角三角形三角板如图所示放置,如图是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC.
(1)求证:①△ABE≌△ACD;
②DC⊥CE;
(2)若图2中的BE=3CE,CD=6,求△DCE的面积.
21.如图,在中,是边上的中线,,, 交的延长线于点.
(1)若,,求的长;
(2)求证:为等腰三角形.
22.已知:△A1B1C1三个顶点的坐标分别为A1(﹣3,4),B1(﹣1,3),C1(1,6),把△A1B1C1先向右平移3个单位长度,再向下平移3个单位长度后得到△ABC,且点A1的对应点为A,点B1的对应点为B,点C1的对应点为C.
(1)在坐标系中画出△ABC;
(2)求△ABC的面积;
(3)设点P在y轴上,且△APB与△ABC的面积相等,求点P的坐标.
23.如图,在ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,CE=DB.
(1)求证:DEF是等腰三角形;
(2)当∠A=50°时,求∠DEB+∠FEC的度数;
(3)当∠EDF=60°时,求∠A的度数.
24.如图,在△ABC中.AB=AC,点E在线段BC上,连接AE并延长到G,使得EG=AE,过点G作GD∥BA分别交BC,AC于点F,D.
(1)求证:△ABE≌△GFE;
(2)若GD=3,CD=1,求AB的长度;
(3)过点D作DH⊥BC于H,P是直线DH上的一个动点,连接AF,AP,FP,若∠C=45°,在(2)的条件下,求△AFP周长的最小值.
25.如图在直角坐标系中,四边形ABCO为正方形,A点的坐标为(a,0),D点的坐标为(0,b),且a,b满足(a﹣3)2+|b﹣|=0.
(1)求A点和D点的坐标;
(2)若∠DAE=∠OAB,请猜想DE,OD和EB的数量关系,说明理由.
(3)若∠OAD=30°,以AD为三角形的一边,坐标轴上是否存在点P,使得△PAD为等腰三角形,若存在,直接写出有多少个点P,并写出P点的坐标,选择一种情况证明.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D C D C C D D A C C
二、填空题
11.【解】解:∵点P(,5)与点Q(3,)关于y轴对称,
∴,
解得,
故答案为:.
12.【解】解:原式=,
∵,,
∴原式=,
故答案为:101.25.
13.【解】解:∵BF、CF分别平分∠ABC、∠ACG,
∴∠DBF=∠CBF,∠FCE=∠FCG,
∵DE∥BC,
∴∠DFB=∠CBF,∠EFC=∠FCG,
∴∠DBF=∠DFB,∠FCE=∠EFC,
∴BD=FD,EF=CE,
∵BD=9cm,DE=4cm,,
∴EF=DF﹣DE=BD﹣DE=9﹣4=5(cm),
∴EC=5cm,
故答案为:5.
14.【解】解:∵AD为△ABC的角平分线,DE⊥AB, DF⊥AC,
∴DE=DF=2,
∴△ABC的面积=×5×2+×3×2=8,
故答案侍:8.
15.【解】解:∵(a+b)2=a2+2ab+b2=25,
∴a2+b2=25-2ab,
∵
∴a2+b2=25-2×6=25-12=13
故答案为13.
16.【解】如图所示:点B关于AD的对称点是点C,
∴BF=CF,
∴BF+EF=CF+EF=CE,
当CE⊥AB时,线段的长度有最小值,
利用△ABC面积的两种表示方法,得:
,
∵BC=2BD=6,AD=4,AB=5,
∴,
解得:.
三、解答题
17.【解】(1)
;
(2)
.
18.【解】解:原式
,
,
原式.
19.【解】解:∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°-82°-40°=58°,
∵AE平分∠BAC,
∴∠BAE=∠BAC=29°;
∵AD⊥BC,
∴∠ADB=90°,
∴∠BAD=90°-∠B=8°,
∴∠DAE=∠BAE-∠BAD=29°-8°=21°.
∴∠DAE的度数为21°.
20.【解】(1)①是等腰直角三角形,
,,
即
△ABE≌△ACD
②
是等腰直角三角形,
DC⊥CE;
(2)△ABE≌△ACD
,
CD=6,BE=3CE,
DC⊥CE;
是直角三角形,
21.【解】(1)解:∵,
∴,
∵,
∴,
∵ ,
∴,,
∴是等边三角形,
∴;
(2)证明:过点作,,垂足为点;
∵平分,
∴.
又∵是边上的中线,
∴,
在和中,
,
∴,
∴,
∴,
∴为等腰三角形.
22.【解】解:(1)如图,△ABC即为所求.
(2)S△ABC=3×4﹣×2×4﹣×1×2﹣×2×3=4.
(3)设P(0,m),由题意, |m﹣1| 2=4,
解得,m=5或﹣3,
∴P(0,5)或(0,﹣3).
23.【解】证明:∵AB=AC,
∴∠ABC=∠ACB,
在DBE和CEF中,
,
∴DBE≌CEF(SAS),
∴DE=EF,
∴DEF是等腰三角形;
(2)∵DBE≌CEF,
∴∠BDE=∠CEF,∠DEB=∠EFC,
∵∠A+∠B+∠C=180°,
∴∠B=×(180°﹣50°)=65°,
∴∠BDE+∠CEF=115°,
∴∠DEB+∠FEC=115°,
∴∠DEB+∠FEC=115°,
(3)∵∠EDF=60°,DE=EF,
∴DEF是等边三角形,
∴∠DEF=60°,
∵DBE≌CEF,
∴∠BDE=∠CEF,∠DEB=∠EFC,
∵∠DEF+∠FEC=∠B+∠BDE,
∴∠B=∠DEF=60°,
∴∠C=60°,
∴∠A=180°﹣∠B﹣∠C=60°.
24.【解】(1)如图1中,
∵GD∥AB,
∴∠B=∠EFG,
在△ABE和△GFE中,
,
∴△ABE≌△GFE(AAS);
(2)∵AB=AC,
∴∠B=∠ACB,
∵DF∥AB,
∴∠DFC=∠B,
∴∠DFC=∠DCF,
∴DC=DF=1,
∵DG=3,
∴FG=DG﹣DF=2,
∵△ABE≌△GFE,
∴AB=GF=2;
(3)如图2中,
∵AB=AC=2,
∴∠B=∠C=45°,
∴∠BAC=90°,
∵AB∥FD,
∴∠FDC=∠BAC=90°,即FD⊥AC,
∵AC=AB=2,CD=1,
∴DA=DC,
∴FA=FC,
∴∠C=∠FAC=45°,
∴∠AFC=90°,
∴DF=DA=DC=1,
∴AF==,
∵DH⊥CF,
∴FH=CH,
∴点F与点C关于直线PD对称,
∴当点P与D重合时,△PAF的周长最小,
最小值为△ADF的周长:2+.
25.【解】(1)∵(a﹣3)2+|b﹣|=0,
∴a=3,b=,
∴D(0,),A(3,0);
(2)DE=OD+EB; 理由如下:
如图1,在CO的延长线上找一点F,使OF=BE,连接AF,
在△AOF和△ABE中, ,
∴△AOF≌△ABE(SAS),
∴AF=AE,∠OAF=∠BAE,
又∵∠OAB=90°,∠DAE=,
∴∠BAE+∠DAO=45°,
∴∠DAF=∠OAF+∠DAO=45°,
∴∠DAF=∠EAD,
在△AFD和△AED中, ,
∴△AFD≌△AED(SAS),
∴DF=DE=OD+EB;
(3)有3种情况共6个点:
①当DA=DP时,如图2,
Rt△ADO中,OD=,OA=3,
∴AD=,
∴P1(﹣3,0),P2(0,3),P3(0,﹣);
②当AP4=DP4时,如图3,
∴∠ADP4=∠DAP4=30°,
∴∠OP4D=60°,
Rt△ODP4中,∠ODP4=30°,OD=,
∴OP4=1,
∴P4(1,0);
③当AD=AP时,如图4,
∴AD=AP5=AP6=2,
∴P5(3+2,0),P6(3﹣2,0),
综上,点P的坐标为:∴P(﹣3,0)或(0,3)或(0,﹣)或(1,0)或(3+2,0)或(3﹣2,0).
证明:P5(3+2,0),
∵∠OAD=30°且△ADO是直角三角形,
又∵AO=3,DO=,
∴DA=2,
而P5A=|3+2﹣3|=2,
∴P5A=DA,
∴△P5AD是等腰三角形.
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。笞卷前,考生务必
将自己的姓名、准考证号填写在答题卡上。
2.回答第I卷时,选出每小题答案后,把答案填写在答题卡上对应题目的位置
,填空题填写在答题卡相应的位置写在本试卷上无效。
3.回答第II卷时,将答案写在第II卷答题卡上。
4.考试结束后,将本试卷和答题卡一并交回。
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列组成冬奥会会徽的四个图案中是轴对称图形的是( )
A.B.C.D.
2.下列各组线段能组成一个三角形的是( )
A. B. C. D.
3.下列计算中正确的是( )
A. B. C. D.
4.如果,,则的度数是( )
A. B. C. D.
5.下面四个图形中,画出的边上的高正确的是( )
A. B. C. D.
6.下列条件中不可以判定两个直角三角形全等的是( )
A.两条直角边对应相等 B.斜边和直角边对应相等
C.一条边和一锐角对应相等 D.一条边和一个角对应相等
7.如图,△ABC中,∠BAC=100°,DF,EG分别是AB,AC的垂直平分线,则∠DAE等于( )
A.50° B.45° C.30° D.20°
8.如果(2x+m)与(x+3)的乘积中不含x的一次项,那么m的值为( )
A.﹣6 B.﹣3 C.0 D.1
9.下面四个式子中,不能表示图中阴影部分面积的是( )
A. B.
C. D.
10.如图,在中,和的平分线,相交于点,交于,交于,过点作于,下列三个结论:①;②当时,;③若,,则,其中正确的个数是( )
A.0个 B.1个 C.2个 D.3个
二、填空题(6小题,每题3分,共18分)
11.若点P(,5)与点Q(3,)关于y轴对称,则 .
12.已知,,则 .
13.如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E,若BD=9cm,DE=4cm,求CE的长为 cm.
14.如图,在△ABC中,AD为△ABC的角平分线,DE⊥AB,垂足为E,DF⊥AC,垂足为F,若AB=5,AC=3,DF=2,则△ABC的面积为 .
15.已知,,则 .
16.如图,在等腰中,是的高,分别是上一动点,则的最小值为 .
第II卷
人教版2025—2026学年八年级上册数学期中考试仿真试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.化简:(1);
(2).
18.先化简,再求值:,其中.
19.如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=82°,∠C=40°,求∠DAE的度数.
20.两个大小不同的等腰直角三角形三角板如图所示放置,如图是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC.
(1)求证:①△ABE≌△ACD;
②DC⊥CE;
(2)若图2中的BE=3CE,CD=6,求△DCE的面积.
21.如图,在中,是边上的中线,,, 交的延长线于点.
(1)若,,求的长;
(2)求证:为等腰三角形.
22.已知:△A1B1C1三个顶点的坐标分别为A1(﹣3,4),B1(﹣1,3),C1(1,6),把△A1B1C1先向右平移3个单位长度,再向下平移3个单位长度后得到△ABC,且点A1的对应点为A,点B1的对应点为B,点C1的对应点为C.
(1)在坐标系中画出△ABC;
(2)求△ABC的面积;
(3)设点P在y轴上,且△APB与△ABC的面积相等,求点P的坐标.
23.如图,在ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,CE=DB.
(1)求证:DEF是等腰三角形;
(2)当∠A=50°时,求∠DEB+∠FEC的度数;
(3)当∠EDF=60°时,求∠A的度数.
24.如图,在△ABC中.AB=AC,点E在线段BC上,连接AE并延长到G,使得EG=AE,过点G作GD∥BA分别交BC,AC于点F,D.
(1)求证:△ABE≌△GFE;
(2)若GD=3,CD=1,求AB的长度;
(3)过点D作DH⊥BC于H,P是直线DH上的一个动点,连接AF,AP,FP,若∠C=45°,在(2)的条件下,求△AFP周长的最小值.
25.如图在直角坐标系中,四边形ABCO为正方形,A点的坐标为(a,0),D点的坐标为(0,b),且a,b满足(a﹣3)2+|b﹣|=0.
(1)求A点和D点的坐标;
(2)若∠DAE=∠OAB,请猜想DE,OD和EB的数量关系,说明理由.
(3)若∠OAD=30°,以AD为三角形的一边,坐标轴上是否存在点P,使得△PAD为等腰三角形,若存在,直接写出有多少个点P,并写出P点的坐标,选择一种情况证明.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D C D C C D D A C C
二、填空题
11.【解】解:∵点P(,5)与点Q(3,)关于y轴对称,
∴,
解得,
故答案为:.
12.【解】解:原式=,
∵,,
∴原式=,
故答案为:101.25.
13.【解】解:∵BF、CF分别平分∠ABC、∠ACG,
∴∠DBF=∠CBF,∠FCE=∠FCG,
∵DE∥BC,
∴∠DFB=∠CBF,∠EFC=∠FCG,
∴∠DBF=∠DFB,∠FCE=∠EFC,
∴BD=FD,EF=CE,
∵BD=9cm,DE=4cm,,
∴EF=DF﹣DE=BD﹣DE=9﹣4=5(cm),
∴EC=5cm,
故答案为:5.
14.【解】解:∵AD为△ABC的角平分线,DE⊥AB, DF⊥AC,
∴DE=DF=2,
∴△ABC的面积=×5×2+×3×2=8,
故答案侍:8.
15.【解】解:∵(a+b)2=a2+2ab+b2=25,
∴a2+b2=25-2ab,
∵
∴a2+b2=25-2×6=25-12=13
故答案为13.
16.【解】如图所示:点B关于AD的对称点是点C,
∴BF=CF,
∴BF+EF=CF+EF=CE,
当CE⊥AB时,线段的长度有最小值,
利用△ABC面积的两种表示方法,得:
,
∵BC=2BD=6,AD=4,AB=5,
∴,
解得:.
三、解答题
17.【解】(1)
;
(2)
.
18.【解】解:原式
,
,
原式.
19.【解】解:∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°-82°-40°=58°,
∵AE平分∠BAC,
∴∠BAE=∠BAC=29°;
∵AD⊥BC,
∴∠ADB=90°,
∴∠BAD=90°-∠B=8°,
∴∠DAE=∠BAE-∠BAD=29°-8°=21°.
∴∠DAE的度数为21°.
20.【解】(1)①是等腰直角三角形,
,,
即
△ABE≌△ACD
②
是等腰直角三角形,
DC⊥CE;
(2)△ABE≌△ACD
,
CD=6,BE=3CE,
DC⊥CE;
是直角三角形,
21.【解】(1)解:∵,
∴,
∵,
∴,
∵ ,
∴,,
∴是等边三角形,
∴;
(2)证明:过点作,,垂足为点;
∵平分,
∴.
又∵是边上的中线,
∴,
在和中,
,
∴,
∴,
∴,
∴为等腰三角形.
22.【解】解:(1)如图,△ABC即为所求.
(2)S△ABC=3×4﹣×2×4﹣×1×2﹣×2×3=4.
(3)设P(0,m),由题意, |m﹣1| 2=4,
解得,m=5或﹣3,
∴P(0,5)或(0,﹣3).
23.【解】证明:∵AB=AC,
∴∠ABC=∠ACB,
在DBE和CEF中,
,
∴DBE≌CEF(SAS),
∴DE=EF,
∴DEF是等腰三角形;
(2)∵DBE≌CEF,
∴∠BDE=∠CEF,∠DEB=∠EFC,
∵∠A+∠B+∠C=180°,
∴∠B=×(180°﹣50°)=65°,
∴∠BDE+∠CEF=115°,
∴∠DEB+∠FEC=115°,
∴∠DEB+∠FEC=115°,
(3)∵∠EDF=60°,DE=EF,
∴DEF是等边三角形,
∴∠DEF=60°,
∵DBE≌CEF,
∴∠BDE=∠CEF,∠DEB=∠EFC,
∵∠DEF+∠FEC=∠B+∠BDE,
∴∠B=∠DEF=60°,
∴∠C=60°,
∴∠A=180°﹣∠B﹣∠C=60°.
24.【解】(1)如图1中,
∵GD∥AB,
∴∠B=∠EFG,
在△ABE和△GFE中,
,
∴△ABE≌△GFE(AAS);
(2)∵AB=AC,
∴∠B=∠ACB,
∵DF∥AB,
∴∠DFC=∠B,
∴∠DFC=∠DCF,
∴DC=DF=1,
∵DG=3,
∴FG=DG﹣DF=2,
∵△ABE≌△GFE,
∴AB=GF=2;
(3)如图2中,
∵AB=AC=2,
∴∠B=∠C=45°,
∴∠BAC=90°,
∵AB∥FD,
∴∠FDC=∠BAC=90°,即FD⊥AC,
∵AC=AB=2,CD=1,
∴DA=DC,
∴FA=FC,
∴∠C=∠FAC=45°,
∴∠AFC=90°,
∴DF=DA=DC=1,
∴AF==,
∵DH⊥CF,
∴FH=CH,
∴点F与点C关于直线PD对称,
∴当点P与D重合时,△PAF的周长最小,
最小值为△ADF的周长:2+.
25.【解】(1)∵(a﹣3)2+|b﹣|=0,
∴a=3,b=,
∴D(0,),A(3,0);
(2)DE=OD+EB; 理由如下:
如图1,在CO的延长线上找一点F,使OF=BE,连接AF,
在△AOF和△ABE中, ,
∴△AOF≌△ABE(SAS),
∴AF=AE,∠OAF=∠BAE,
又∵∠OAB=90°,∠DAE=,
∴∠BAE+∠DAO=45°,
∴∠DAF=∠OAF+∠DAO=45°,
∴∠DAF=∠EAD,
在△AFD和△AED中, ,
∴△AFD≌△AED(SAS),
∴DF=DE=OD+EB;
(3)有3种情况共6个点:
①当DA=DP时,如图2,
Rt△ADO中,OD=,OA=3,
∴AD=,
∴P1(﹣3,0),P2(0,3),P3(0,﹣);
②当AP4=DP4时,如图3,
∴∠ADP4=∠DAP4=30°,
∴∠OP4D=60°,
Rt△ODP4中,∠ODP4=30°,OD=,
∴OP4=1,
∴P4(1,0);
③当AD=AP时,如图4,
∴AD=AP5=AP6=2,
∴P5(3+2,0),P6(3﹣2,0),
综上,点P的坐标为:∴P(﹣3,0)或(0,3)或(0,﹣)或(1,0)或(3+2,0)或(3﹣2,0).
证明:P5(3+2,0),
∵∠OAD=30°且△ADO是直角三角形,
又∵AO=3,DO=,
∴DA=2,
而P5A=|3+2﹣3|=2,
∴P5A=DA,
∴△P5AD是等腰三角形.
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
同课章节目录
