21.3 《二次函数与一元二次方程》小节复习题(含答案)沪科版数学九年级上册
文档属性
| 名称 | 21.3 《二次函数与一元二次方程》小节复习题(含答案)沪科版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 454.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 00:36:18 | ||
图片预览




文档简介
21.3 《二次函数与一元二次方程》小节复习题
【题型1 抛物线与x轴的交点】
1.已知二次函数(a为常数且).
(1)当函数图象经过,求该二次函数的表达式.
(2)若,判断该二次函数图象与x轴的交点个数并证明.
(3)若该函数图象上有两点,其中,若,.求证:.
2.若抛物线与x轴只有一个公共点,则a的值为 .
3.已知二次函数为常数的图象与轴有交点,当时,随的增大而增大,则的取值范围是( )
A. B. C. D.
4.二次函数(a为常数,).
(1)若该二次函数图象关于直线对称,求a的值;
(2)若该二次函数图象上点,满足,求a的范围;
(3)若该二次函数图象上两个不同的点,满足,求的取值范围
【题型2 利用二次函数的图象确定方程根的情况】
1.如图所示是二次函数的部分图象,该函数图象的对称轴是直线,图象与轴交点的纵坐标是2.则下列结论:①;②方程一定有一个根在和之间;③方程一定有两个不相等的实数根;④点,在抛物线上,且,当时,;⑤函数的最大值大于.其中正确结论的个数为( )
A.5个 B.4个 C.3个 D.2个
2.已知关于的一元二次方程的一个根是,且二次函数的对称轴是直线,则此方程的另一个根为 .
3.如图,抛物线与直线的两个交点坐标分别为,,则关于的方程的解为 .
4.若二次函数与x轴交于和,关于x的一元二次方程的两个根分别是和,则 .
【题型3 求x轴与抛物线的截线长】
1.在平面直角坐标系中,已知抛物线.
(1)当时,
①求抛物线的顶点坐标.
②将抛物线向下平移个单位,若平移后的抛物线过点,且与轴两交点之间的距离为6,求的值.
(2)已知点,在抛物线上,且,求的取值范围.
2.设二次函数 的图像与一次函数 的图像交于点 ,若函数 的图像与 轴仅有一个交点,则 的值是( )
A.6 B.8 C. D.7
3.已知关于的一元二次方程.
(1)求证:该方程总有两个实数根;
(2)若抛物线与轴交于点,,且,求的值.
4.已知,是抛物线上的两个不同点.
(1)若,两点都在直线上,求线段的长;
(2)若抛物线关于轴对称,直线过坐标原点,求的值;
(3)若点,在抛物线对称轴的左侧,,为整数,且,证明:为正值.
【题型4 利用二次函数的图象求一元二次方程的近似解】
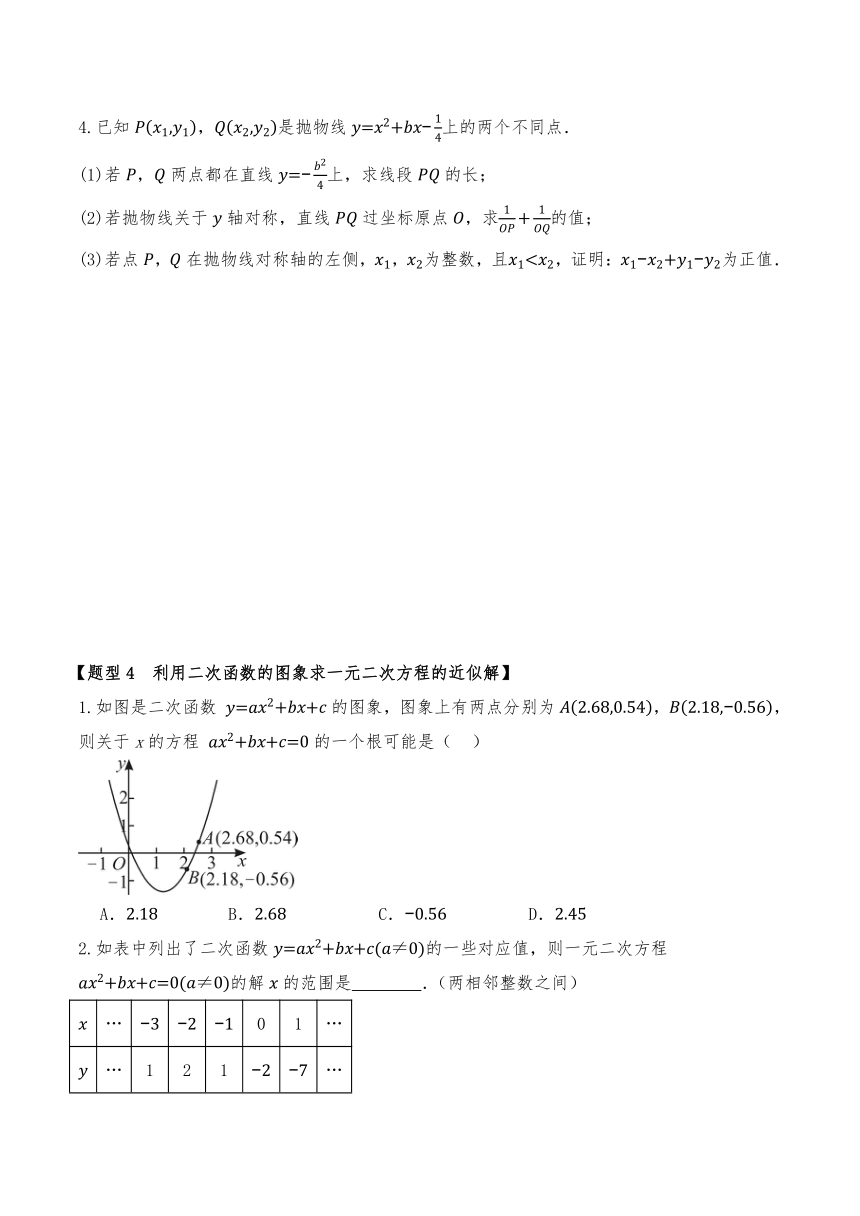
1.如图是二次函数 的图象,图象上有两点分别为,,则关于x的方程 的一个根可能是( )
A. B. C. D.
2.如表中列出了二次函数的一些对应值,则一元二次方程的解的范围是 .(两相邻整数之间)
… 0 1 …
… 1 2 1 …
3.小明用探索方程(、、为常数)的根,作出如图所示的图象,并求得一个近似根,则方程的另一个近似根(精确到)为( )
A. B. C. D.
4.在实际问题中往往需要求得方程的近似解,这个时候,我们通常利用函数的图象来完成.如,求方程x2﹣2x﹣2=0的实数根的近似解,观察函数y=x2﹣2x﹣2的图象,发现,当自变量为2时,函数值小于0(点(2,﹣2)在x轴下方),当自变量为3时,函数值大于0(点(3,1)在x轴上方).因为抛物线y=x2﹣2x﹣2是一条连续不断的曲线,所以抛物线y=x2﹣2x﹣2在2<x<3这一段经过x轴,也就是说,当x取2、3之间的某个值时,函数值为0,即方程x2﹣2x﹣2=0在2、3之间有根.进一步,我们取2和3的平均数2.5,计算可知,对应的数值为﹣0.75,与自变量为3的函数值异号,所以这个根在2.5与3之间任意一个数作为近似解,该近似解与真实值的差都不会大于3﹣2.5=0.5.重复以上操作,随着操作次数增加,根的近似值越来越接近真实值.用以上方法求得方程x2﹣2x﹣2=0的小于0的解,并且使得所求的近似解与真实值的差不超过0.3,该近似解为
【题型5 利用二次函数的图象求一元二次不等式的取值范围】
1.二次函数的图象如图所示,则不等式的解集是 .
2.二次函数的图象如图所示,则函数值时,自变量x的取值范围是( )
A. B. C. D.或
3.二次函数的图象如图,根据图象解答下列问题:
(1)直接写出方程的两个根;
(2)直接写出y随x的增大而减小时自变量x的取值范围;
(3)直接写出关于x的不等式的解集.
4.抛物线如图所示,抛物线与轴交于点,顶点坐标为,下列结论:①;②;③对于任意实数,都有;④当时,.其中正确的个数是( )
A.1 B.2 C.3 D.4
【题型6 利用不等式求自变量或函数值的取值范围】
1.抛物线的顶点纵坐标与抛物线的顶点纵坐标之和为4.
(1)求的值;
(2)已知为抛物线上一点,为抛物线上一点.
(i)若仅存在一个正数,使得,求的最大值;
(ii)若,且当时,总有,求的取值范围.
2.已知二次函数,当时,函数值;当时,.若点,都在函数上,且,则的取值范围是 .
3.已知二次函数,经过点.当时,x的取值范围为或.则如下四个值中有可能为m的是( )
A.1 B.2 C.3 D.4
4.在平面直角坐标系中,直线与抛物线交于点、,且,点是该抛物线上位于,两点之间的动点.
(1)当,时,求抛物线的解析式;
(2)在()的条件下,当面积最大时,求点的坐标;
(3)设抛物线顶点的横坐标为,当,且时,求证:.
【题型7 根据两函数交点确定不等式的解集】
1.已知抛物线经过两点,.
(1)求b,c值;
(2)当时,函数的函数值总大于函数的函数值,且函数的函数值总小于函数的函数值,直接写出满足题意的n的取值范围.
2.一次函数与二次函数的图象如图所示,则不等式的解集为( )
A. B. C. D.或
3.已知二次函数,则下列结论正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
4.定义:若函数和函数的图象关于直线对称,则称函数和关于直线互为“和睦函数”,函数和的图象交点叫做“和睦点”.
例如:函数关于直线的“和睦函数”为,“和睦点”为.下列说法不正确的序号为 .
①函数关于直线的“和睦函数”为,“和睦点”坐标为;
②函数关于直线的“和睦点”的纵坐标为,当时,则的取值范围是;
③函数关于直线的“和睦点”纵坐标d满足:,m的取值范围是或
④已知,,函数关于直线的“和睦函数”为,将函数与的图象组成的图形记为,若与线段只有2个公共点,则的取值范围是.
【题型8 抛物线与x轴交点上的四点问题】
1.已知抛物线,抛物线与x轴交于,两点(mA. B.
C. D.
2.已知抛物线的图象与x轴的两交点的横坐标分别,,而的两根为,则、、M、N的大小顺序为( )
A. B.
C. D.
3.在平面坐标系中,抛物线与轴交于,两点,其中.现将此抛物线向上平移,平移后的抛物线与轴交于,两点,且,下列结论正确的是( )
A., B.,
C., D.,
4.如图,在平面直角坐标系中,抛物线与轴交于A、B两点,抛物线与轴交于C、D两点,其中.若,则n的值为 .
参考答案
【题型1 抛物线与x轴的交点】
1.(1)解:将代入,
得,
解得,
∴该二次函数的表达式为.
(2)解:该二次函数图象与x轴无交点.
证明:令,
∵,
∴,
∴方程无实数解,
∴该二次函数图象与x轴无交点.
(3)证明:∵该函数图象上有两点,
∴,,,
∴,
∵,
∴,
∵,
∴,
∴,
即.
2.
【分析】本题考查了抛物线与轴的交点,理解函数与方程的关系是解题的关键.根据二次函数与一元二次方程的关系列方程求解.
【详解】解:由题意得:关于的方程有两个相等的实数根,
,
解得:,
故答案为:9.
3.A
【分析】本题考查了抛物线与x轴的交点,明确抛物线与x轴的交点个数与判别式的关系及二次函数的性质是解题的关键.
根据图象与x轴有交点,得出判别式,从而解得,然后求出抛物线的对称轴,结合抛物线开口向上,且当时,y随x的增大而增大,可得,从而得出选项.
【详解】解:∵二次函数(为常数)的图象与x轴有交点,
∴,
解得:,
∵抛物线对称轴为直线,抛物线开口向上,当时,y随x的增大而增大,
∴,
∴
∴m的取值范围是,
故选:A.
4.(1)解:二次函数的对称轴为直线,
∴,
解得:;
(2)解:∵点,在二次函数图象上,
∴,
,
∴,
∵,
∴,
解得:;
(3)解:点,在二次函数图象上,
∴,,
∵,
∴,
代入得 ,
∴
,
∵,,
∴.
【题型2 利用二次函数的图象确定方程根的情况】
1.B
【分析】本题考查抛物线与x轴的交点,根与系数的关系,二次函数的性质,二次函数图象上点的坐标特征,解题的关键是掌握二次函数的图象和性质,熟练运用数形结合的方法解决问题.根据二次函数的对称性,开口方向等来判断结论①②,根据二次函数与一元二次方程的关系来判断结论③,根据函数的增减性,函数值判断结论④⑤即可.
【详解】解:抛物线的对称轴为直线,
,
,即,故①正确;
抛物线的对称轴为直线,与x轴的一个交点的横坐标在2和3之间,
抛物线与x轴的另一个交点的横坐标在和0之间,
∴方程一定有一个根在和0之间,故②错误;
∵抛物线图象与轴交点的纵坐标是2,
,
,
,
令,得,
或,
,
,
∴方程一定有两个不相等的实数根,故③正确;
抛物线的开口向下,
抛物线上的点距离对称轴越远y值越小,距离对称轴越近y值越大,
,
,
,
,
,
点到对称轴的距离是,点到对称轴的距离是,
,故④正确;
如图,当时,,
,
,
,
当时,,
函数的最大值大于,故⑤正确,
综上所述,正确的结论有:①③④⑤,共4个,
故选:B.
2.
【分析】本题考查二次函数与一元二次方程的关系,以及抛物线的对称性,明确抛物线与x轴的两个交点关于对称轴对称是解题的关键.
根据抛物线的对称性,可知的图像与x轴的两个交点关于直线对称,两交点的横坐标即为方程的两根,根据对称性建立关系式即可求解.
【详解】解:设方程的另一根为,
∵二次函数的对称轴是直线,
∴,即,
解得,,
∴另一根为,
故答案为:.
3.,
【分析】本题考查抛物线与一次函数的交点、一元二次方程等知识,解题的关键是灵活运用所学知识,学会利用图象法解决实际问题,利用图象法即可解决问题,方程的解就是两个函数图象的交点的横坐标.
【详解】解:由图象可知,关于x的方程的解,就是抛物线与直线的两个交点坐标分别为,的横坐标,
即,.
故答案为:,.
4.
【分析】本题考查二次函数的性质,一元二次方程的根与系数的关系,根据二次函数的性质求得,,得到,,则方程可转化为,根据根与系数的关系,,再将整理得到,代入数据计算即可求解.
【详解】解:二次函数与x轴交于和,
∴,,
∴,,
∴一元二次方程为,
即,
∵关于x的一元二次方程的两个根分别是和,
∴,,
∴,
故答案为:.
【题型3 求x轴与抛物线的截线长】
1.(1)解:①∵,
∴
∴抛物线的顶点坐标为,
②∵将抛物线向下平移个单位,
∴平移后抛物线解析式为,
把代入,得,
∴
∴
设平移后的抛物线与轴两交点横坐标为,,
则,,
∴
∴
∵平移后的抛物线与轴两交点之间的距离为6,
∴
∴
∴
解得:
经检验,是分式方程的解,且符合题意,
∴.
(2)解:把,代入,得
,
∵,
∴,
∴,
把代入,得
,
∴,
∵,
∴,
∵,
∴,
∴.
2.A
【分析】此题主要考查了抛物线与轴的交点问题,以及曲线上点的坐标与方程的关系,要熟练掌握,解答此题的关键是判断出:函数与轴的交点为,.
首先根据一次函数 的图像交于点 ,可得,然后根据函数的图象与轴仅有一个交点,可得函数与轴的交点为,进而可得,再结合求解即可.
【详解】解:一次函数的图象经过点,
,解得:,
当时,,,
当时,,
∵函数 的图像与 轴仅有一个交点,
的图象与轴的交点为,
∴
又∵,
∴
,
∴,解得:
∴,
故选:A.
3.(1)解:∵
,
该方程总有两个实数根;
(2)解:令,得:,
∴,,
∴,
∵抛物线与轴交于点,,且,
∴,
∴,
化简为:,
解得:或.
4.(1)解:∵直线平行于轴,
∴令,即,
解得,
∴线段的长度为.
(2)解:∵抛物线关于轴对称,
∴
∴抛物线
若直线落在轴上,
∴当时,即
解得
∴
∴;
若直线不在轴上,
设直线的解析式为,联立方程,
得,
解得.
不妨设,
∴,,
∴.
(3)证明:
∵,且,为整数,
∴,即
∴,
又,
∴为正值.
【题型4 利用二次函数的图象求一元二次方程的近似解】
1.D
【分析】本题考查了抛物线和x轴交点,理解抛物线和一元二次方程的关系是解答关键.
观察函数图象可得的点对应的横坐标在和之间,进而求解.
【详解】解:从函数图象看,的点对应的横坐标在和之间,
而在和之间被选项中的数为,
∴的方程的一个根可能为.
故选:D.
2.或
【分析】本题考查图像法求一元二次方程的解,解题的关键是理解函数和方程的关系.据此解答即可.
【详解】解:∵,,
∴根据函数的连续性可得在之间,存在一个数,使得,
∵和的函数值相等,
∴对称轴为:,
∴根据对称性可得:在之间,也存在一个数,使得,
∴一元二次方程的解的范围是或,
故答案为:或.
3.C
【分析】本题考查了二次函数与一元二次方程,由二次函数的对称性可得抛物线与轴的另一个交点坐标为,据此即可求解,掌握二次函数的性质是解题的关键.
【详解】解:∵抛物线与轴的一个交点为,对称轴为直线,
∴抛物线与轴的另一个交点坐标为,
∴方程的另一个近似根为,
故选:.
4.﹣0.75
【分析】观察函数y=x2 2x 2的图象,发现,当自变量为0时,函数值小于0,当自变量为 1时,函数值大于0,求得 1和0的平均数 0.5,对应的数值为 0.75,与自变量为 1的函数值异号,再求 1和 0.5的平均数 0.75,对应的数值为0.0625,即可求得这个根在 0.75与 0.5之间任意一个数作为近似解,由 0.5 ( 0.75)=0.25<0.3,即可求得近似值.
【详解】解:观察函数y=x2﹣2x﹣2的图象,发现,当自变量为0时,函数值小于0,当自变量为﹣1时,函数值大于0,因为抛物线y=x2﹣2x﹣2是一条连续不断的曲线,所以抛物线y=x2﹣2x﹣2在﹣1<x<0这一段经过x轴,也就是说,当x取﹣1、0之间的某个值时,函数值为0,即方程x2﹣2x﹣2=0在﹣1、0之间有根.
我们取﹣1和0的平均数﹣0.5,计算可知,对应的数值为﹣0.75,与自变量为﹣1的函数值异号,所以这个根在﹣1与﹣0.5之间,取﹣1和﹣0.5的平均数﹣0.75,计算可知,对应的数值为0.0625,与自变量为﹣0.5的函数值异号,所以这个根在﹣0.75与﹣0.5之间任意一个数作为近似解,该近似解与真实值的差都不会大于﹣0.5﹣(﹣0.75)=0.25<0.3,该近似解为﹣0.75,
故答案为﹣0.75.
【题型5 利用二次函数的图象求一元二次不等式的取值范围】
1.或
【分析】本题考查了二次函数与不等式,根据对称轴为直线,可求出当时,或,再结合图象即可求解,掌握二次函数的性质,利用数形结合求不等式的解集是解题的关键.
【详解】解:由图象可知,二次函数的对称轴为直线,
当时,或,
∴通过图象可知:不等式的解集是或,
故答案为:或.
2.D
【分析】本题考查了二次函数与不等式的关系.根据题意,当函数值时,自变量x的取值范围,就是求当函数图象在x轴上方时,对应的x取值范围,由此得到答案.
【详解】观察图象知,当函数值时,自变量x的取值范围是或,
故选:D.
3.(1)解:由图象看,
∵二次函数与x轴交于点,
∴方程的两个根是,;
(2)解:从图象看,
当时,y随x的增大而增大;
(3)解:从图象看,
∵当或时,二次函数的图象在x轴
∴不等式的解集是:或.
4.C
【分析】本题主要考查了二次函数图象的性质、二次函数图象与系数的关系、二次函数图象与不等式的关系等知识点,灵活运用二次函数的性质成为解题的关键.
根据图象开口向上可知,与轴的交点在原点上方可知,据此可判断①;因为抛物线与轴交于,对称轴为直线,所以另一交点为,则、两式相减可得,可判断②;抛物线顶点坐标为,开口向下,则为最大值,对于任意实数,都有,据此可判断③;由图象可得当时,,据此可判定④.
【详解】解:∵抛物线的开口向上,
∴,
∵与轴的交点在原点上方可,
∴,
∴,即①正确;
∵抛物线与轴交于,对称轴为直线,
∴抛物线与x轴的另一交点为,
∴当时,;当时,,
∴两式相减可得,即②正确;
∵抛物线顶点坐标为,开口向下,
∴为最大值,
∴对于任意实数,都有,即③错误;
④由图象可得,当时,,即④正确.
综上,正确的有3个.
故选C.
【题型6 利用不等式求自变量或函数值的取值范围】
1.(1)解:∵,,
∴抛物线顶点坐标为,抛物线的顶点坐标为,
∵抛物线的顶点纵坐标与抛物线的顶点纵坐标之和为4,
∴,即;
(2)解:(i)由(1)知,
∴抛物线,
∵为抛物线上一点,
∴,
∵,即,
∴,即,
∵仅存在一个正数,使得,
∴关于的一元二次方程,有两个相等的正数根,
∴,即,
解得:,
当时,,解得:(舍去,不符合题意);
当时,,解得:(符合题意);
∴,
∴,
∵为抛物线上一点,
∴,
∴,
∵,
∴当时,有最大值;
(ii)∵,,且为抛物线上,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴.
2.
【分析】本题主要考查了二次函数的图象和性质.根据题意得到二次函数的对称轴为直线,再由当时,函数值;当时,,可得,且抛物线与x轴的交点的横坐标为5和1,然后分两种情况:若点,均在对称轴的右侧,若点,均在对称轴的两侧,结合二次函数的性质解答即可.
【详解】解:根据题意得:二次函数的对称轴为直线,
∴横坐标为5关于对称轴的对称点的横坐标为1,
∵当时,函数值;当时,,
∴,且抛物线与x轴的交点的横坐标为5和1,
∴当时,y随x的增大而增大,当时,y随x的增大而减小,
若点,均在对称轴的右侧,
此时,
∵抛物线与x轴的交点的横坐标为5和1,
∴当时,,
∴,即,
∴抛物线的解析式为,
当时,,
∴抛物线与y轴的交点为,
∴点关于对称轴的对称点为,
∵,
∴,
即,
此时;
若点,均在对称轴的两侧,则
,
即;
综上所述,的取值范围是.
故答案为:
3.A
【分析】本题主要考查了二次函数与不等式之间的关系,二次函数的性质,根据题意可得当时,或,且函数开口向上,即,则可求出对称轴为直线,则可得到,把代入解析式得到,据此求出m的取值范围即可得到答案.
【详解】解:∵当时,x的取值范围为或,
∴当时,或,且函数开口向上,即,
∴,为抛物线上的点,
∴抛物线对称轴为直线,
∴,
∴,
∴,
当时,,解得,
将代入解析式得,
∴,
∴,
∴,
∴或,
∵,
∴,
∴,
∴,
综上所述,m的可能取值为1,
故选:A.
4.(1)解:当时,,时,,
∴将,代入得
,解得,
∴;
(2)解:过点作轴交直线于点,
设点,则,
∴,
∵
,
∴当时,有最大值,
∴;
(3)解:当,,且,
将,代入得:
,,
得:,
∴,
∴,
∵,
∴,
∴,
∴,即.
【题型7 根据两函数交点确定不等式的解集】
1.(1)解:∵抛物线经过两点,.
∴
∴
(2)抛物线上,当时,,当时,;
函数的图象上,当,时,;
函数的图象上,当,时,
∵时,函数的函数值总大于函数的函数值,且函数的函数值总小于函数的函数值.
∴.
2.C
【分析】本题主要考查二次函数与一次函数的综合.观察图象得:当时,二次函数图象位于一次函数图象的上方,即可求解.
【详解】解:观察图象得:当时,二次函数图象位于一次函数图象的上方,
∴不等式的解集为,
即不等式的解集为.
故选:C.
3.B
【分析】本题二次函数的图象与性质、二次函数与不等式、二次函数图象与x轴的交点问题,理解并灵活运用相关知识是解答的关键.先构造差函数,再根据二次函数图象与性质,以及对应图象与x轴的交点问题求解即可.
【详解】解:设函数,
要使,只需恒成立,
当即时,函数是一次函数,显然不恒成立,
当即时,二次函数y的图象开口向下,
∴不恒成立,故选项C、D不符合题意;
∴只需,且恒成立,
当时,满足,但b值不确定,当b很大时,可能大于0,故选项A不符合题意;
当时,满足,,
∴恒成立,故选项B符合题意,
故选:B.
4.②④
【分析】本题主要考查了二次函数顶点式、二次函数点的坐标特征、二次函数交点问题等内容,利用数形结合是解题的关键.①根据“友好函数”的定义即可求解,②,再根据的取值范围即可得到的范围,③根据题意得出,解不等式,即可求解;④当过“和睦点”时,为临界点情况,当过的顶点时,此时与线段只有个公共点,找出临界值代入求解即可.
【详解】解:①,
顶点,它关于直线 的对称点为,
“和睦函数”为,
两个函数图象关于直线 对称,
其交点必在直线 上,将代入中,,
“和睦点”坐标为;故①正确;
②由题意得,
,
关于的函数图象是一条抛物线,开口向上,顶点为,
当 时,有最小值,
当 时,,当 时,,
;故②错误;
③依题意可得
∵,
∴
∴或
解得:或,故③正确
④如图,
当过“和睦点”时,为临界点情况,
当时,,
即,
解得:
则当时,与线段只有个公共点;
当过的顶点时,此时与线段只有个公共点,
当时,,
即,
解得:;
综上,的取值范围为:或,故④错误,
故答案为:②④.
【题型8 抛物线与x轴交点上的四点问题】
1.B
【分析】本题考查的是抛物线与x轴的交点,主要考查函数图象上点的坐标特征,设,而,即函数向下平移3个单位得到函数y,通过画出函数大致图象即可求解.
【详解】解:设,则、是函数和x轴的交点的横坐标,
而,
即函数向下平移3个单位得到函数y,
则两个函数的图象如图所示(省略了y轴),
从图象看,,
故选:B.
2.C
【分析】本题考查了二次函数与一元二次方程的关系,依题意画出函数和的图象草图,根据二次函数的图象可直接求解.
【详解】解:依题意,画出函的图象,如图所示.
函数图象为抛物线,开口向下,与x轴两个交点的横坐标分别为,
方程的两根是抛物线与直线的两个交点.
由,可知对称轴左侧交点横坐标为M,右侧为N.
由图象可知,,
故选:C.
3.C
【分析】本题考查抛物线与轴交点问题,解答涉及交点与对称轴的关系,会用数形结合思想是解题的关键.因为抛物线开口向下,所以抛物线向上平移,对称轴不变,与轴的两交点距离变长解答即可.
【详解】解:抛物线与轴相交于,两点,
抛物线的对称轴为直线,
将此抛物线向上平移,平移后的抛物线与轴相交于,两点,
抛物线的对称轴为直线,
抛物线向上平移对称轴不变,
,
即,
抛物线开口向下,
将此抛物线向上平移,平移后的抛物线与轴两交点间距离会变长,
,
故选:C.
4.3
【分析】本题主要考查了抛物线与轴的交点问题,根据题意用表示出,列出关于的方程是解题的关键.先求出抛物线与轴的交点,抛物线与轴的交点,然后根据,得出,列出关于的方程,解方程即可.
【详解】解:把代入得:,
解得:,,
把代入得:,
解得:,,
,
,
,即,
,
令,则,
解得:,,
当时,,解得:,
,
不符合题意,舍去;
当时,,解得:,
,
符合题意;
综上分析可知,的值为3,
故答案为:3.
【题型1 抛物线与x轴的交点】
1.已知二次函数(a为常数且).
(1)当函数图象经过,求该二次函数的表达式.
(2)若,判断该二次函数图象与x轴的交点个数并证明.
(3)若该函数图象上有两点,其中,若,.求证:.
2.若抛物线与x轴只有一个公共点,则a的值为 .
3.已知二次函数为常数的图象与轴有交点,当时,随的增大而增大,则的取值范围是( )
A. B. C. D.
4.二次函数(a为常数,).
(1)若该二次函数图象关于直线对称,求a的值;
(2)若该二次函数图象上点,满足,求a的范围;
(3)若该二次函数图象上两个不同的点,满足,求的取值范围
【题型2 利用二次函数的图象确定方程根的情况】
1.如图所示是二次函数的部分图象,该函数图象的对称轴是直线,图象与轴交点的纵坐标是2.则下列结论:①;②方程一定有一个根在和之间;③方程一定有两个不相等的实数根;④点,在抛物线上,且,当时,;⑤函数的最大值大于.其中正确结论的个数为( )
A.5个 B.4个 C.3个 D.2个
2.已知关于的一元二次方程的一个根是,且二次函数的对称轴是直线,则此方程的另一个根为 .
3.如图,抛物线与直线的两个交点坐标分别为,,则关于的方程的解为 .
4.若二次函数与x轴交于和,关于x的一元二次方程的两个根分别是和,则 .
【题型3 求x轴与抛物线的截线长】
1.在平面直角坐标系中,已知抛物线.
(1)当时,
①求抛物线的顶点坐标.
②将抛物线向下平移个单位,若平移后的抛物线过点,且与轴两交点之间的距离为6,求的值.
(2)已知点,在抛物线上,且,求的取值范围.
2.设二次函数 的图像与一次函数 的图像交于点 ,若函数 的图像与 轴仅有一个交点,则 的值是( )
A.6 B.8 C. D.7
3.已知关于的一元二次方程.
(1)求证:该方程总有两个实数根;
(2)若抛物线与轴交于点,,且,求的值.
4.已知,是抛物线上的两个不同点.
(1)若,两点都在直线上,求线段的长;
(2)若抛物线关于轴对称,直线过坐标原点,求的值;
(3)若点,在抛物线对称轴的左侧,,为整数,且,证明:为正值.
【题型4 利用二次函数的图象求一元二次方程的近似解】
1.如图是二次函数 的图象,图象上有两点分别为,,则关于x的方程 的一个根可能是( )
A. B. C. D.
2.如表中列出了二次函数的一些对应值,则一元二次方程的解的范围是 .(两相邻整数之间)
… 0 1 …
… 1 2 1 …
3.小明用探索方程(、、为常数)的根,作出如图所示的图象,并求得一个近似根,则方程的另一个近似根(精确到)为( )
A. B. C. D.
4.在实际问题中往往需要求得方程的近似解,这个时候,我们通常利用函数的图象来完成.如,求方程x2﹣2x﹣2=0的实数根的近似解,观察函数y=x2﹣2x﹣2的图象,发现,当自变量为2时,函数值小于0(点(2,﹣2)在x轴下方),当自变量为3时,函数值大于0(点(3,1)在x轴上方).因为抛物线y=x2﹣2x﹣2是一条连续不断的曲线,所以抛物线y=x2﹣2x﹣2在2<x<3这一段经过x轴,也就是说,当x取2、3之间的某个值时,函数值为0,即方程x2﹣2x﹣2=0在2、3之间有根.进一步,我们取2和3的平均数2.5,计算可知,对应的数值为﹣0.75,与自变量为3的函数值异号,所以这个根在2.5与3之间任意一个数作为近似解,该近似解与真实值的差都不会大于3﹣2.5=0.5.重复以上操作,随着操作次数增加,根的近似值越来越接近真实值.用以上方法求得方程x2﹣2x﹣2=0的小于0的解,并且使得所求的近似解与真实值的差不超过0.3,该近似解为
【题型5 利用二次函数的图象求一元二次不等式的取值范围】
1.二次函数的图象如图所示,则不等式的解集是 .
2.二次函数的图象如图所示,则函数值时,自变量x的取值范围是( )
A. B. C. D.或
3.二次函数的图象如图,根据图象解答下列问题:
(1)直接写出方程的两个根;
(2)直接写出y随x的增大而减小时自变量x的取值范围;
(3)直接写出关于x的不等式的解集.
4.抛物线如图所示,抛物线与轴交于点,顶点坐标为,下列结论:①;②;③对于任意实数,都有;④当时,.其中正确的个数是( )
A.1 B.2 C.3 D.4
【题型6 利用不等式求自变量或函数值的取值范围】
1.抛物线的顶点纵坐标与抛物线的顶点纵坐标之和为4.
(1)求的值;
(2)已知为抛物线上一点,为抛物线上一点.
(i)若仅存在一个正数,使得,求的最大值;
(ii)若,且当时,总有,求的取值范围.
2.已知二次函数,当时,函数值;当时,.若点,都在函数上,且,则的取值范围是 .
3.已知二次函数,经过点.当时,x的取值范围为或.则如下四个值中有可能为m的是( )
A.1 B.2 C.3 D.4
4.在平面直角坐标系中,直线与抛物线交于点、,且,点是该抛物线上位于,两点之间的动点.
(1)当,时,求抛物线的解析式;
(2)在()的条件下,当面积最大时,求点的坐标;
(3)设抛物线顶点的横坐标为,当,且时,求证:.
【题型7 根据两函数交点确定不等式的解集】
1.已知抛物线经过两点,.
(1)求b,c值;
(2)当时,函数的函数值总大于函数的函数值,且函数的函数值总小于函数的函数值,直接写出满足题意的n的取值范围.
2.一次函数与二次函数的图象如图所示,则不等式的解集为( )
A. B. C. D.或
3.已知二次函数,则下列结论正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
4.定义:若函数和函数的图象关于直线对称,则称函数和关于直线互为“和睦函数”,函数和的图象交点叫做“和睦点”.
例如:函数关于直线的“和睦函数”为,“和睦点”为.下列说法不正确的序号为 .
①函数关于直线的“和睦函数”为,“和睦点”坐标为;
②函数关于直线的“和睦点”的纵坐标为,当时,则的取值范围是;
③函数关于直线的“和睦点”纵坐标d满足:,m的取值范围是或
④已知,,函数关于直线的“和睦函数”为,将函数与的图象组成的图形记为,若与线段只有2个公共点,则的取值范围是.
【题型8 抛物线与x轴交点上的四点问题】
1.已知抛物线,抛物线与x轴交于,两点(m
C. D.
2.已知抛物线的图象与x轴的两交点的横坐标分别,,而的两根为,则、、M、N的大小顺序为( )
A. B.
C. D.
3.在平面坐标系中,抛物线与轴交于,两点,其中.现将此抛物线向上平移,平移后的抛物线与轴交于,两点,且,下列结论正确的是( )
A., B.,
C., D.,
4.如图,在平面直角坐标系中,抛物线与轴交于A、B两点,抛物线与轴交于C、D两点,其中.若,则n的值为 .
参考答案
【题型1 抛物线与x轴的交点】
1.(1)解:将代入,
得,
解得,
∴该二次函数的表达式为.
(2)解:该二次函数图象与x轴无交点.
证明:令,
∵,
∴,
∴方程无实数解,
∴该二次函数图象与x轴无交点.
(3)证明:∵该函数图象上有两点,
∴,,,
∴,
∵,
∴,
∵,
∴,
∴,
即.
2.
【分析】本题考查了抛物线与轴的交点,理解函数与方程的关系是解题的关键.根据二次函数与一元二次方程的关系列方程求解.
【详解】解:由题意得:关于的方程有两个相等的实数根,
,
解得:,
故答案为:9.
3.A
【分析】本题考查了抛物线与x轴的交点,明确抛物线与x轴的交点个数与判别式的关系及二次函数的性质是解题的关键.
根据图象与x轴有交点,得出判别式,从而解得,然后求出抛物线的对称轴,结合抛物线开口向上,且当时,y随x的增大而增大,可得,从而得出选项.
【详解】解:∵二次函数(为常数)的图象与x轴有交点,
∴,
解得:,
∵抛物线对称轴为直线,抛物线开口向上,当时,y随x的增大而增大,
∴,
∴
∴m的取值范围是,
故选:A.
4.(1)解:二次函数的对称轴为直线,
∴,
解得:;
(2)解:∵点,在二次函数图象上,
∴,
,
∴,
∵,
∴,
解得:;
(3)解:点,在二次函数图象上,
∴,,
∵,
∴,
代入得 ,
∴
,
∵,,
∴.
【题型2 利用二次函数的图象确定方程根的情况】
1.B
【分析】本题考查抛物线与x轴的交点,根与系数的关系,二次函数的性质,二次函数图象上点的坐标特征,解题的关键是掌握二次函数的图象和性质,熟练运用数形结合的方法解决问题.根据二次函数的对称性,开口方向等来判断结论①②,根据二次函数与一元二次方程的关系来判断结论③,根据函数的增减性,函数值判断结论④⑤即可.
【详解】解:抛物线的对称轴为直线,
,
,即,故①正确;
抛物线的对称轴为直线,与x轴的一个交点的横坐标在2和3之间,
抛物线与x轴的另一个交点的横坐标在和0之间,
∴方程一定有一个根在和0之间,故②错误;
∵抛物线图象与轴交点的纵坐标是2,
,
,
,
令,得,
或,
,
,
∴方程一定有两个不相等的实数根,故③正确;
抛物线的开口向下,
抛物线上的点距离对称轴越远y值越小,距离对称轴越近y值越大,
,
,
,
,
,
点到对称轴的距离是,点到对称轴的距离是,
,故④正确;
如图,当时,,
,
,
,
当时,,
函数的最大值大于,故⑤正确,
综上所述,正确的结论有:①③④⑤,共4个,
故选:B.
2.
【分析】本题考查二次函数与一元二次方程的关系,以及抛物线的对称性,明确抛物线与x轴的两个交点关于对称轴对称是解题的关键.
根据抛物线的对称性,可知的图像与x轴的两个交点关于直线对称,两交点的横坐标即为方程的两根,根据对称性建立关系式即可求解.
【详解】解:设方程的另一根为,
∵二次函数的对称轴是直线,
∴,即,
解得,,
∴另一根为,
故答案为:.
3.,
【分析】本题考查抛物线与一次函数的交点、一元二次方程等知识,解题的关键是灵活运用所学知识,学会利用图象法解决实际问题,利用图象法即可解决问题,方程的解就是两个函数图象的交点的横坐标.
【详解】解:由图象可知,关于x的方程的解,就是抛物线与直线的两个交点坐标分别为,的横坐标,
即,.
故答案为:,.
4.
【分析】本题考查二次函数的性质,一元二次方程的根与系数的关系,根据二次函数的性质求得,,得到,,则方程可转化为,根据根与系数的关系,,再将整理得到,代入数据计算即可求解.
【详解】解:二次函数与x轴交于和,
∴,,
∴,,
∴一元二次方程为,
即,
∵关于x的一元二次方程的两个根分别是和,
∴,,
∴,
故答案为:.
【题型3 求x轴与抛物线的截线长】
1.(1)解:①∵,
∴
∴抛物线的顶点坐标为,
②∵将抛物线向下平移个单位,
∴平移后抛物线解析式为,
把代入,得,
∴
∴
设平移后的抛物线与轴两交点横坐标为,,
则,,
∴
∴
∵平移后的抛物线与轴两交点之间的距离为6,
∴
∴
∴
解得:
经检验,是分式方程的解,且符合题意,
∴.
(2)解:把,代入,得
,
∵,
∴,
∴,
把代入,得
,
∴,
∵,
∴,
∵,
∴,
∴.
2.A
【分析】此题主要考查了抛物线与轴的交点问题,以及曲线上点的坐标与方程的关系,要熟练掌握,解答此题的关键是判断出:函数与轴的交点为,.
首先根据一次函数 的图像交于点 ,可得,然后根据函数的图象与轴仅有一个交点,可得函数与轴的交点为,进而可得,再结合求解即可.
【详解】解:一次函数的图象经过点,
,解得:,
当时,,,
当时,,
∵函数 的图像与 轴仅有一个交点,
的图象与轴的交点为,
∴
又∵,
∴
,
∴,解得:
∴,
故选:A.
3.(1)解:∵
,
该方程总有两个实数根;
(2)解:令,得:,
∴,,
∴,
∵抛物线与轴交于点,,且,
∴,
∴,
化简为:,
解得:或.
4.(1)解:∵直线平行于轴,
∴令,即,
解得,
∴线段的长度为.
(2)解:∵抛物线关于轴对称,
∴
∴抛物线
若直线落在轴上,
∴当时,即
解得
∴
∴;
若直线不在轴上,
设直线的解析式为,联立方程,
得,
解得.
不妨设,
∴,,
∴.
(3)证明:
∵,且,为整数,
∴,即
∴,
又,
∴为正值.
【题型4 利用二次函数的图象求一元二次方程的近似解】
1.D
【分析】本题考查了抛物线和x轴交点,理解抛物线和一元二次方程的关系是解答关键.
观察函数图象可得的点对应的横坐标在和之间,进而求解.
【详解】解:从函数图象看,的点对应的横坐标在和之间,
而在和之间被选项中的数为,
∴的方程的一个根可能为.
故选:D.
2.或
【分析】本题考查图像法求一元二次方程的解,解题的关键是理解函数和方程的关系.据此解答即可.
【详解】解:∵,,
∴根据函数的连续性可得在之间,存在一个数,使得,
∵和的函数值相等,
∴对称轴为:,
∴根据对称性可得:在之间,也存在一个数,使得,
∴一元二次方程的解的范围是或,
故答案为:或.
3.C
【分析】本题考查了二次函数与一元二次方程,由二次函数的对称性可得抛物线与轴的另一个交点坐标为,据此即可求解,掌握二次函数的性质是解题的关键.
【详解】解:∵抛物线与轴的一个交点为,对称轴为直线,
∴抛物线与轴的另一个交点坐标为,
∴方程的另一个近似根为,
故选:.
4.﹣0.75
【分析】观察函数y=x2 2x 2的图象,发现,当自变量为0时,函数值小于0,当自变量为 1时,函数值大于0,求得 1和0的平均数 0.5,对应的数值为 0.75,与自变量为 1的函数值异号,再求 1和 0.5的平均数 0.75,对应的数值为0.0625,即可求得这个根在 0.75与 0.5之间任意一个数作为近似解,由 0.5 ( 0.75)=0.25<0.3,即可求得近似值.
【详解】解:观察函数y=x2﹣2x﹣2的图象,发现,当自变量为0时,函数值小于0,当自变量为﹣1时,函数值大于0,因为抛物线y=x2﹣2x﹣2是一条连续不断的曲线,所以抛物线y=x2﹣2x﹣2在﹣1<x<0这一段经过x轴,也就是说,当x取﹣1、0之间的某个值时,函数值为0,即方程x2﹣2x﹣2=0在﹣1、0之间有根.
我们取﹣1和0的平均数﹣0.5,计算可知,对应的数值为﹣0.75,与自变量为﹣1的函数值异号,所以这个根在﹣1与﹣0.5之间,取﹣1和﹣0.5的平均数﹣0.75,计算可知,对应的数值为0.0625,与自变量为﹣0.5的函数值异号,所以这个根在﹣0.75与﹣0.5之间任意一个数作为近似解,该近似解与真实值的差都不会大于﹣0.5﹣(﹣0.75)=0.25<0.3,该近似解为﹣0.75,
故答案为﹣0.75.
【题型5 利用二次函数的图象求一元二次不等式的取值范围】
1.或
【分析】本题考查了二次函数与不等式,根据对称轴为直线,可求出当时,或,再结合图象即可求解,掌握二次函数的性质,利用数形结合求不等式的解集是解题的关键.
【详解】解:由图象可知,二次函数的对称轴为直线,
当时,或,
∴通过图象可知:不等式的解集是或,
故答案为:或.
2.D
【分析】本题考查了二次函数与不等式的关系.根据题意,当函数值时,自变量x的取值范围,就是求当函数图象在x轴上方时,对应的x取值范围,由此得到答案.
【详解】观察图象知,当函数值时,自变量x的取值范围是或,
故选:D.
3.(1)解:由图象看,
∵二次函数与x轴交于点,
∴方程的两个根是,;
(2)解:从图象看,
当时,y随x的增大而增大;
(3)解:从图象看,
∵当或时,二次函数的图象在x轴
∴不等式的解集是:或.
4.C
【分析】本题主要考查了二次函数图象的性质、二次函数图象与系数的关系、二次函数图象与不等式的关系等知识点,灵活运用二次函数的性质成为解题的关键.
根据图象开口向上可知,与轴的交点在原点上方可知,据此可判断①;因为抛物线与轴交于,对称轴为直线,所以另一交点为,则、两式相减可得,可判断②;抛物线顶点坐标为,开口向下,则为最大值,对于任意实数,都有,据此可判断③;由图象可得当时,,据此可判定④.
【详解】解:∵抛物线的开口向上,
∴,
∵与轴的交点在原点上方可,
∴,
∴,即①正确;
∵抛物线与轴交于,对称轴为直线,
∴抛物线与x轴的另一交点为,
∴当时,;当时,,
∴两式相减可得,即②正确;
∵抛物线顶点坐标为,开口向下,
∴为最大值,
∴对于任意实数,都有,即③错误;
④由图象可得,当时,,即④正确.
综上,正确的有3个.
故选C.
【题型6 利用不等式求自变量或函数值的取值范围】
1.(1)解:∵,,
∴抛物线顶点坐标为,抛物线的顶点坐标为,
∵抛物线的顶点纵坐标与抛物线的顶点纵坐标之和为4,
∴,即;
(2)解:(i)由(1)知,
∴抛物线,
∵为抛物线上一点,
∴,
∵,即,
∴,即,
∵仅存在一个正数,使得,
∴关于的一元二次方程,有两个相等的正数根,
∴,即,
解得:,
当时,,解得:(舍去,不符合题意);
当时,,解得:(符合题意);
∴,
∴,
∵为抛物线上一点,
∴,
∴,
∵,
∴当时,有最大值;
(ii)∵,,且为抛物线上,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴.
2.
【分析】本题主要考查了二次函数的图象和性质.根据题意得到二次函数的对称轴为直线,再由当时,函数值;当时,,可得,且抛物线与x轴的交点的横坐标为5和1,然后分两种情况:若点,均在对称轴的右侧,若点,均在对称轴的两侧,结合二次函数的性质解答即可.
【详解】解:根据题意得:二次函数的对称轴为直线,
∴横坐标为5关于对称轴的对称点的横坐标为1,
∵当时,函数值;当时,,
∴,且抛物线与x轴的交点的横坐标为5和1,
∴当时,y随x的增大而增大,当时,y随x的增大而减小,
若点,均在对称轴的右侧,
此时,
∵抛物线与x轴的交点的横坐标为5和1,
∴当时,,
∴,即,
∴抛物线的解析式为,
当时,,
∴抛物线与y轴的交点为,
∴点关于对称轴的对称点为,
∵,
∴,
即,
此时;
若点,均在对称轴的两侧,则
,
即;
综上所述,的取值范围是.
故答案为:
3.A
【分析】本题主要考查了二次函数与不等式之间的关系,二次函数的性质,根据题意可得当时,或,且函数开口向上,即,则可求出对称轴为直线,则可得到,把代入解析式得到,据此求出m的取值范围即可得到答案.
【详解】解:∵当时,x的取值范围为或,
∴当时,或,且函数开口向上,即,
∴,为抛物线上的点,
∴抛物线对称轴为直线,
∴,
∴,
∴,
当时,,解得,
将代入解析式得,
∴,
∴,
∴,
∴或,
∵,
∴,
∴,
∴,
综上所述,m的可能取值为1,
故选:A.
4.(1)解:当时,,时,,
∴将,代入得
,解得,
∴;
(2)解:过点作轴交直线于点,
设点,则,
∴,
∵
,
∴当时,有最大值,
∴;
(3)解:当,,且,
将,代入得:
,,
得:,
∴,
∴,
∵,
∴,
∴,
∴,即.
【题型7 根据两函数交点确定不等式的解集】
1.(1)解:∵抛物线经过两点,.
∴
∴
(2)抛物线上,当时,,当时,;
函数的图象上,当,时,;
函数的图象上,当,时,
∵时,函数的函数值总大于函数的函数值,且函数的函数值总小于函数的函数值.
∴.
2.C
【分析】本题主要考查二次函数与一次函数的综合.观察图象得:当时,二次函数图象位于一次函数图象的上方,即可求解.
【详解】解:观察图象得:当时,二次函数图象位于一次函数图象的上方,
∴不等式的解集为,
即不等式的解集为.
故选:C.
3.B
【分析】本题二次函数的图象与性质、二次函数与不等式、二次函数图象与x轴的交点问题,理解并灵活运用相关知识是解答的关键.先构造差函数,再根据二次函数图象与性质,以及对应图象与x轴的交点问题求解即可.
【详解】解:设函数,
要使,只需恒成立,
当即时,函数是一次函数,显然不恒成立,
当即时,二次函数y的图象开口向下,
∴不恒成立,故选项C、D不符合题意;
∴只需,且恒成立,
当时,满足,但b值不确定,当b很大时,可能大于0,故选项A不符合题意;
当时,满足,,
∴恒成立,故选项B符合题意,
故选:B.
4.②④
【分析】本题主要考查了二次函数顶点式、二次函数点的坐标特征、二次函数交点问题等内容,利用数形结合是解题的关键.①根据“友好函数”的定义即可求解,②,再根据的取值范围即可得到的范围,③根据题意得出,解不等式,即可求解;④当过“和睦点”时,为临界点情况,当过的顶点时,此时与线段只有个公共点,找出临界值代入求解即可.
【详解】解:①,
顶点,它关于直线 的对称点为,
“和睦函数”为,
两个函数图象关于直线 对称,
其交点必在直线 上,将代入中,,
“和睦点”坐标为;故①正确;
②由题意得,
,
关于的函数图象是一条抛物线,开口向上,顶点为,
当 时,有最小值,
当 时,,当 时,,
;故②错误;
③依题意可得
∵,
∴
∴或
解得:或,故③正确
④如图,
当过“和睦点”时,为临界点情况,
当时,,
即,
解得:
则当时,与线段只有个公共点;
当过的顶点时,此时与线段只有个公共点,
当时,,
即,
解得:;
综上,的取值范围为:或,故④错误,
故答案为:②④.
【题型8 抛物线与x轴交点上的四点问题】
1.B
【分析】本题考查的是抛物线与x轴的交点,主要考查函数图象上点的坐标特征,设,而,即函数向下平移3个单位得到函数y,通过画出函数大致图象即可求解.
【详解】解:设,则、是函数和x轴的交点的横坐标,
而,
即函数向下平移3个单位得到函数y,
则两个函数的图象如图所示(省略了y轴),
从图象看,,
故选:B.
2.C
【分析】本题考查了二次函数与一元二次方程的关系,依题意画出函数和的图象草图,根据二次函数的图象可直接求解.
【详解】解:依题意,画出函的图象,如图所示.
函数图象为抛物线,开口向下,与x轴两个交点的横坐标分别为,
方程的两根是抛物线与直线的两个交点.
由,可知对称轴左侧交点横坐标为M,右侧为N.
由图象可知,,
故选:C.
3.C
【分析】本题考查抛物线与轴交点问题,解答涉及交点与对称轴的关系,会用数形结合思想是解题的关键.因为抛物线开口向下,所以抛物线向上平移,对称轴不变,与轴的两交点距离变长解答即可.
【详解】解:抛物线与轴相交于,两点,
抛物线的对称轴为直线,
将此抛物线向上平移,平移后的抛物线与轴相交于,两点,
抛物线的对称轴为直线,
抛物线向上平移对称轴不变,
,
即,
抛物线开口向下,
将此抛物线向上平移,平移后的抛物线与轴两交点间距离会变长,
,
故选:C.
4.3
【分析】本题主要考查了抛物线与轴的交点问题,根据题意用表示出,列出关于的方程是解题的关键.先求出抛物线与轴的交点,抛物线与轴的交点,然后根据,得出,列出关于的方程,解方程即可.
【详解】解:把代入得:,
解得:,,
把代入得:,
解得:,,
,
,
,即,
,
令,则,
解得:,,
当时,,解得:,
,
不符合题意,舍去;
当时,,解得:,
,
符合题意;
综上分析可知,的值为3,
故答案为:3.
