北师大版六年级下册数学 圆锥的体积 课件(共23张PPT)
文档属性
| 名称 | 北师大版六年级下册数学 圆锥的体积 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 24.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 09:46:52 | ||
图片预览



文档简介
(共23张PPT)
北师大版六年级下册
圆锥的体积
这堆小麦的体积是多少呢?
想一想,如何得到圆锥的体积?
圆锥的体积是不是像长方体、圆柱那样,也和“底面积 × 高”有关系呢?
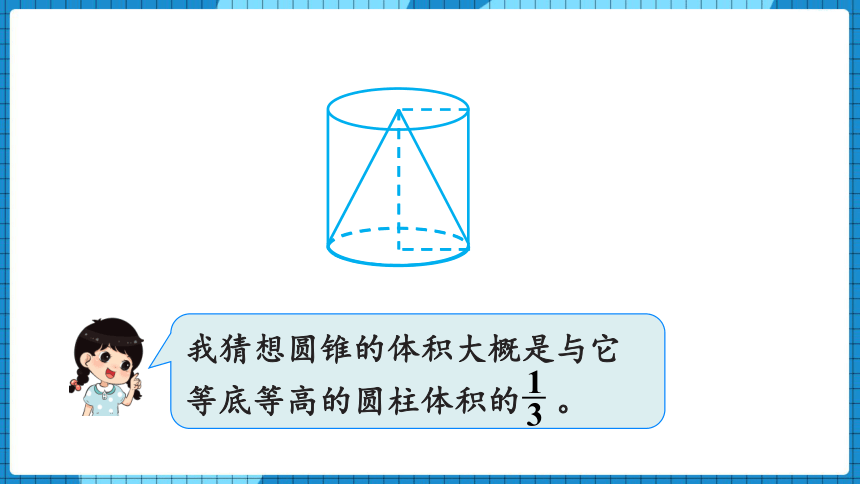
我猜想圆锥的体积大概是与它等底等高的圆柱体积的 。
1
3
活动探究:
① 拿出准备好的等底等高的圆柱形容器
和圆锥形容器各一个以及一些沙子。
② 将圆锥形容器装满沙子再倒入圆柱形
容器,看几次能倒满。
你发现圆锥的体积与同它等底、等高的圆柱的体积之间的关系了吗?
圆柱的体积是与它等底等高的圆锥的体积的3倍。
圆锥的体积是与它等底等高的圆柱的体积的 。
1
3
如果用V表示圆锥的体积,S表示底面积,h表示高,你能写出圆锥体积的计算公式吗?
S
h
圆锥的体积= ×底面积×高
1
3
V = Sh
1
3
=6.28(m3)
答:小麦堆的体积是6.28m3。
如果小麦堆的底面半径为2m,高为1.5m。小麦堆的体积是多少立方米?
1
3
×3.14×22×1.5
1.下图中,圆锥的体积与哪个圆柱的体积相等?
说说你是怎么想的。
答:圆锥的体积与第3个圆柱的体积相等。因为
圆锥与第3个圆柱等底,且高是圆柱高的3倍。
(教材P12 T1)
2.计算下面各圆锥的体积。
(教材P12 T2)
×9×3.6
=10.8(m3)
1
3
×3.14×32×8
=75.36(dm3)
1
3
×3.14×(8÷2)2×12
=200.96(cm3)
1
3
3.如图,测量中经常使用铅锤。这个铅锤的体积是
多少立方厘米?(结果保留2位小数)
答:这个铅锤的体积是16.75立方厘米。
(教材P12 T3)
×3.14×(4÷2)2×4
≈16.75(cm3)
1
3
通过这节课的学习活动,你有什么收获?
S
h
圆锥的体积= ×底面积×高
1
3
V = Sh
1
3
北师大版六年级下册
圆锥的体积
这堆小麦的体积是多少呢?
想一想,如何得到圆锥的体积?
圆锥的体积是不是像长方体、圆柱那样,也和“底面积 × 高”有关系呢?
我猜想圆锥的体积大概是与它等底等高的圆柱体积的 。
1
3
活动探究:
① 拿出准备好的等底等高的圆柱形容器
和圆锥形容器各一个以及一些沙子。
② 将圆锥形容器装满沙子再倒入圆柱形
容器,看几次能倒满。
你发现圆锥的体积与同它等底、等高的圆柱的体积之间的关系了吗?
圆柱的体积是与它等底等高的圆锥的体积的3倍。
圆锥的体积是与它等底等高的圆柱的体积的 。
1
3
如果用V表示圆锥的体积,S表示底面积,h表示高,你能写出圆锥体积的计算公式吗?
S
h
圆锥的体积= ×底面积×高
1
3
V = Sh
1
3
=6.28(m3)
答:小麦堆的体积是6.28m3。
如果小麦堆的底面半径为2m,高为1.5m。小麦堆的体积是多少立方米?
1
3
×3.14×22×1.5
1.下图中,圆锥的体积与哪个圆柱的体积相等?
说说你是怎么想的。
答:圆锥的体积与第3个圆柱的体积相等。因为
圆锥与第3个圆柱等底,且高是圆柱高的3倍。
(教材P12 T1)
2.计算下面各圆锥的体积。
(教材P12 T2)
×9×3.6
=10.8(m3)
1
3
×3.14×32×8
=75.36(dm3)
1
3
×3.14×(8÷2)2×12
=200.96(cm3)
1
3
3.如图,测量中经常使用铅锤。这个铅锤的体积是
多少立方厘米?(结果保留2位小数)
答:这个铅锤的体积是16.75立方厘米。
(教材P12 T3)
×3.14×(4÷2)2×4
≈16.75(cm3)
1
3
通过这节课的学习活动,你有什么收获?
S
h
圆锥的体积= ×底面积×高
1
3
V = Sh
1
3
