北师大版六年级数学上册第一单元应用圆的周长解决问题综合专项一(含解析)
文档属性
| 名称 | 北师大版六年级数学上册第一单元应用圆的周长解决问题综合专项一(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 559.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 00:00:00 | ||
图片预览




文档简介
北师大版六年级数学上册第一单元应用圆的周长解决问题综合专项一
一、解答题
1.三渡水大桥,古称三渡桥,位于温江区城西约7.5公里,横跨天府与永盛之间的金马河,曾经是川藏线上跨金马河的唯一大桥,也是连接川西平原东西地区的主要通道之一。淘气骑自行车从桥上经过,车轮滚动了230圈,已知自行车车轮直径60厘米(如图所示),三渡水大桥全长约多少米?(结果保留整数)
2.湛江海湾大桥全长3981米,一辆小汽车的轮胎外直径是80厘米,每分转300周。这辆小汽车通过这座桥大约需几分钟?(结果保留整数)
3.李叔叔家装修时,准备将一块周长为31.4厘米的圆形废旧木料加工成一块最大的正方形木板。这块正方形木板的面积是多少平方厘米?
4.第五套人民币中的1元硬币厚1.85毫米,圆形周长约是79毫米。如果要把1元硬币放进一个“开口是长3厘米、宽0.4厘米的长方形”储蓄罐中,能否放进去?请说明理由。(π取3.14,结果保留两位小数)
5.如图,圆形池塘的周长是157米,池塘周围(阴影部分)是一条5米宽的水泥路,在水泥路的外侧围一圈栅栏,栅栏至少长多少米?
6.伐木工人经常将圆木并排捆扎在一起,然后利用水的浮力从水路运输,从而节约成本。如果将10根直径约为0.5米的原木用铁丝紧紧地并排捆扎在一起(如下图)。捆一圈至少要用铁丝多少米(接口处不计)?
7.乐乐家距学校2.198千米,他每天骑自行车上学,已知自行车轮胎的外直径是70厘米。乐乐骑车从家到学校,自行车车轮一共转了多少周?
8.生态园计划用木料搭建一个舞台。工人师傅测得三棵树身周长分别是56.52厘米、50.24厘米、47.1厘米,请你根据下图的警示牌检验一下,有不能被砍伐的树吗?
9.喜迎元旦,畅想未来。为迎接元旦的到来,园艺工人沿着中心广场的圆形喷泉池的边沿每隔1.57米放一盆花,已知这个圆形喷泉池的半径为5.5米,园艺工人在这个喷泉池的边沿一共放了多少盆花?
10.如图,两个连在一起的滑轮,其中小轮的直径是4分米,当这个小轮转4周时,大轮刚好转1周,这个大轮的半径是多少分米?
11.将三根同样粗细的圆木像下图这样用铁丝在两头各捆一圈,如果每根圆木横截面的直径都是4分米,那么至少需要多长的铁丝?(接头处忽略不计)
12.一个圆形操场,外圈的周长是125.6米,沿操场的边有一条宽为4米的跑道(在操场内部)。淘气跑内圈一圈,你知道他跑了多少米吗?
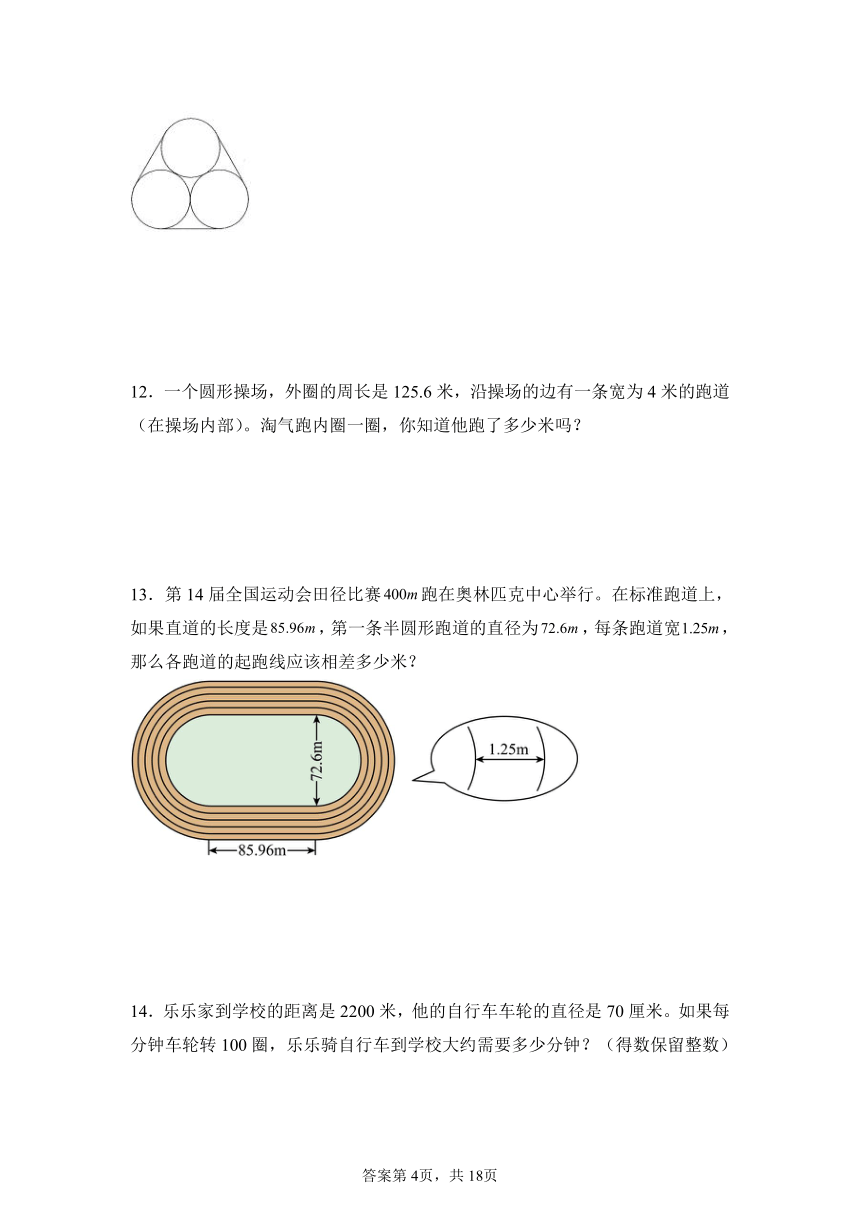
13.第14届全国运动会田径比赛跑在奥林匹克中心举行。在标准跑道上,如果直道的长度是,第一条半圆形跑道的直径为,每条跑道宽,那么各跑道的起跑线应该相差多少米?
14.乐乐家到学校的距离是2200米,他的自行车车轮的直径是70厘米。如果每分钟车轮转100圈,乐乐骑自行车到学校大约需要多少分钟?(得数保留整数)
15.共享单车有低碳环保、经济节能等优势,为人们的出行提供了诸多方便。一辆共享单车的轮胎直径是0.7米,如果每分钟转100圈,这辆共享单车的速度是多少千米/时?(得数保留整数)
16.李叔叔家距公司5千米,李叔叔每天7:30出发骑自行年去公司上班,自行车车轮直径约是60厘米。如果车轮平均每分转150圈,李叔叔7:50能到公司吗?
17.下图是田径跑道示意图,乐乐沿着这个跑道跑一周需要多长时间?
18.李星和李佳骑自行车经过一段长为628米的大桥,李星自行车车轮直径为0.8米、每分钟都转动50圈,需要用多长时间才能通过大桥?(自行车身长忽略不计)
19.彤彤家的小区有一个中心广场(如图),彤彤饭后绕中心广场走了一圈,她所走的路程是多少米?
20.一辆表演杂技用的独轮车,车轮的直径是0.3米,要骑过一条长9.42米的钢丝绳,车轮至少要转多少圈?
21.小涛骑自行车去上学,要通过一座长1256米的桥,他的自行车外轮直径是80厘米,平均每分钟转100周,他通过这座桥需要多少分钟?
22.淘气家客厅有一个圆形钟表,分针长8厘米,从上午9:00到上午9:30,分针的针尖走过了多少厘米?(π取3.14)
23.如下图,地面上平放着一个底面半径为0.5m的圆柱形油桶,如果将这个油桶滚到墙边,可以滚动几圈?
24.一种压路机的前轮直径是1.5米,每分钟可以转6圈。请问这种压路机每分钟前进多少米?(取3.14)
25.乐乐骑车来到白鹭洲湿地公园游玩,途中需要骑车通过一座长1601.4米的大桥,如果车轮平均每分转120圈,那么他通过这座大桥需要几分钟?
参考答案
1.433米
【分析】自行车车轮直径60厘米,先根据公式:圆的周长=圆周率×直径,求出车轮的周长;
车轮滚动了230圈,用车轮的周长乘转动的圈数,即可求三渡水大桥全长约多少米。
【详解】60×3.14×230
=188.4×230
=43332(厘米)
43332厘米=433.32米
433.32米≈433米
答:三渡水大桥全长约433米。
2.5分钟
【分析】先根据圆的周长公式:C=πd,据此求出自行车轮胎的周长,再乘轮胎每分钟转的圈数求出自行车每分钟行驶的路程,最后根据“时间=路程÷速度”求出自行车通过大桥需要的分钟数,注意结果要运用四舍五入法保留整数。
【详解】80厘米=0.8米
3.14×0.8×300
=2.512×300
=753.6(米)
3981÷753.6≈5(分钟)
答:这辆小汽车通过这座桥大约需5分钟。
3.50平方厘米
【分析】圆的周长C=πd,则d=C÷π,据此求出圆的直径,由于要把圆加工成一个最大的正方形,则圆的直径等于正方形的对角线长,再根据“正方形的面积等于对角线乘积的一半”计算正方形的面积即可。
【详解】31.4÷3.14=10(厘米)
10×10÷2
=100÷2
=50(平方厘米)
答:这块正方形木板的面积是50平方厘米。
【点睛】解答本题的关键是求出正方形的对角线长,知道“正方形的面积等于对角线乘积的一半”。
4.能;见详解
【分析】要把硬币放进储蓄罐中,需要满足两个条件,①硬币的厚度需要小于储蓄罐的宽;②利用圆的周长公式,求出硬币的直径,直径需要小于储蓄罐的长;如果满足这两个条件的话,就能放进去。
【详解】厚度:1.85毫米=0.185厘米<0.4厘米
直径:79÷3.14≈25.2(毫米)=2.52(厘米)<3(厘米)
答:可以放进去。因为硬币的厚度小于小于储蓄罐的宽,硬币的直径小于储蓄罐的长。
【点睛】此题主要考查圆的周长公式的灵活运用。
5.188.4米
【分析】根据圆的直径=周长÷圆周率,先求出池塘直径,池塘直径+路宽×2=大圆直径,再根据圆的周长=圆周率×直径,求出栅栏长度即可。
【详解】157÷3.14=50(米)
50+5×2
=50+10
=60(米)
3.14×60=188.4(米)
答:栅栏至少长188.4米。
【点睛】关键是掌握并灵活运用圆的周长公式。
6.10.57米
【分析】从图中可知,将10根原木用铁丝紧紧地捆绑一圈,最左边和最右边各有一个半圆,可以组成一个圆,根据圆的周长公式C=πd求出最左边和最右边铁丝的长度;上、下面的铁丝长度都等于(10-1)个直径的长度之和,再加上圆的周长,即是捆一圈至少要用铁丝的长度。
【详解】3.14×0.5=1.57(米)
(10-1)×0.5×2
=9×0.5×2
=9(米)
1.57+9=10.57(米)
答:捆一圈至少要用铁丝10.57米。
【点睛】本题考查圆的周长公式的运用,关键是从图中分析出铁丝是如何捆绑的。
7.1000周
【分析】先根据:C=πd,求出自行车车轮的周长,然后用乐乐家距学校的距离除以车轮的周长即可。
【详解】70厘米=0.7米
2.198千米=2198米
2198÷(3.14×0.7)
=2198÷2.198
=1000(周)
答:自行车车轮一共转了1000周。
【点睛】此题应根据求一个数里面有几个另一个数,用除法解答;用到的知识点:圆的周长的计算公式,注意单位要统一。
8.有不能砍的树
【分析】根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,分别求出三棵树的半径,再进行比较,如果半径都大于8厘米,就都能被砍伐,如果有半径小于8厘米,就有不能被砍伐的树,据此解答。
【详解】56.52÷3.14÷2
=18÷2
=9(厘米)
9厘米>8厘米,能被砍伐;
50.24÷3.14÷2
=16÷2
=8(厘米)
8厘米=8厘米,能被砍伐;
47.1÷3.14÷2
=15÷2
=7.5(厘米)
7.5厘米<8厘米,不能被砍伐。
答:有不能被砍伐的树。
【点睛】熟练掌握和灵活运用圆的周长公式是解答本题的关键。
9.22盆
【分析】根据题意知道,在封闭线路上植树,植树的棵数=间隔数;先求出圆形的周长,再除以间距即可。
【详解】3.14×(5.5×2)÷1.57
=3.14÷1.57×(5.5×2)
=2×11
=22(盆)
答: 园艺工人在这个喷泉池的边沿一共放了22盆花。
【点睛】本题主要考查了植树问题,解题的关键是明确:在封闭线路上植树,棵数与段数相等,即:棵数=间隔数。
10.8分米
【分析】由“小轮转4周时,大轮刚好转1周”可知:大轮周长是小轮周长的4倍,将小轮直径带入圆的周长公式求出小轮的周长,进而得出大圆的周长,再带入圆的周长公式求出半径即可。
【详解】3.14×4×4÷3.14÷2
=16÷2
=8(分米)
答:这个大轮的半径是8分米。
【点睛】本题主要考查圆的周长公式,理解“小轮转4周时,大轮刚好转1周”是解题的关键。
11.49.12分米
【分析】如图所示,捆圆木的铁丝分为线段和圆弧两部分,三条线段的长度相等,每条线段的长度等于一条直径的长度,三条圆弧的长度相等,圆弧合在一起刚好等于一个圆的周长,把圆弧的长度和直径的长度相加求和,因为需要捆圆木的两头,所以最后结果乘2,据此解答。
【详解】
(4×3+3.14×4)×2
=(12+12.56)×2
=24.56×2
=49.12(分米)
答:至少需要49.12分米的铁丝。
【点睛】利用圆的周长计算出铁丝圆弧部分的长度是解答题目的关键。
12.100.48米
【分析】根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,求出这个圆形操场的半径,沿操场的边有一条宽为4米的跑道(在操场内部),则内圈的半径为:外圈的半径-4米;再根据圆的周长公式,即可求出内圈的周长,也就是淘气跑的米数。
【详解】125.6÷3.14÷2
=40÷2
=20(厘米)
3.14×(20-4)×2
=3.14×16×2
=50.24×2
=100.48(米)
答:他跑了100.48米。
【点睛】解答本题的关键是求出内圈的半径,再利用圆的周长公式进行解答。
13.7.85米
【分析】根据题意,两个半圆和起来是一个圆,第二个圆的周长比第一个圆的周长长多少米,就是各跑道的起跑线相差的米数,第一个圆的直径是72.6米,半径是72.6÷2=36.3米,每条跑道宽是1.25米,第二个圆的半径为36.3+1.25=37.55米,根据圆的周长公式:π×2×半径,求出这两个圆的周长,再用第二个圆的周长-第一个圆的周长,据此解答。
【详解】72.6÷2=36.3(米)
3.14×2×(36.3+1.25)-3.14×2×36.3
=6.28×(36.3+1.25-36.3)
=6.28×1.25
=7.85(米)
答:各跑道的起点线应该相差7.85米。
【点睛】本题考查圆的周长公式的应用,关键明确各跑道的半圆合起来是一个圆,再进行解答。
14.10分钟
【分析】根据圆的周长公式:π×直径,求出自行车车轮的周长,再乘100圈,求出1分钟自行车行驶的距离即自行车的速度;再根据时间=距离÷速度;用乐乐家到学校的距离÷1分钟自行车行驶的距离,即可解答。
【详解】70厘米=0.7米
2200÷(3.14×0.7×100)
=2200÷(2.198×100)
=2200÷219.8
≈10(分钟)
【点睛】本题考查圆的周长公式的应用,以及距离、时间和速度三者的关系;注意单位名数的统一。
15.13千米/时
【分析】根据圆的周长公式:C=πd,把数据代入公式求出共享单车车轮的周长,用车轮的周长乘每分钟转的圈数,求出每分钟行驶的路程,再根据1小时=60分钟,再乘60就是这辆共享单车每小时的速度,据此解答。
【详解】0.7×3.14×100×60
=219.8×60
=13188(米/时)
13188米/时=13.188千米/时
13.188千米/时≈13千米/时
答:这辆共享单车的速度是13千米/时
【点睛】此题主要考查圆的周长公式的灵活运用。
16.能到公司
【分析】根据圆的周长公式:π×直径,代入数据,求出自行车车轮的周长,再成150圈,求出一分钟自行车行多少千米;7:30到7:50的时间是20分钟,20分钟李叔叔行驶的路程是多少千米,用一分钟行距离×20分钟,再和5千米进行比较,即可解答。
【详解】7时50分-7时30分=20(分)
5千米=5000千米
60厘米=0.6米
3.14×0.6×150×20
=1.884×150×20
=282.6×20
=5652(千米)
5652>5000
李叔叔7:50能到公司。
答:李叔叔7:50能到公司。
【点睛】本题考查圆的周长公式的应用,注意单位名数的统一。
17.56.4秒
【分析】先求出跑道的周长,包括左右两个半圆弧组成的整圆的周长和中间的长方形的两条长。根据圆的周长=πd求出整圆的周长,再加上长方形的两条长即可求出跑道的周长。最后除以乐乐的速度即可求出乐乐沿着这个跑道跑一周需要多长时间。
【详解】3.14×60+75×2
=188.4+150
=338.4(米)
338.4÷6=56.4(秒)
答:乐乐沿着这个跑道跑一周需要56.4秒。
【点睛】本题考查了组合图形的周长和简单的行程问题。明确跑道周长的组成是解题的关键。
18.5分钟
【分析】根据圆的周长公式:C=πd,求出车轮周长,再乘50求出骑自行车的速度。根据时间=路程÷速度,代入数据求出时间即可。
【详解】628÷(3.14×0.8×50)
=628÷125.6
=5(分钟)
答:需要5分钟才能通过大桥。
【点睛】本题主要考查圆的周长公式的实际应用。
19.714米
【分析】绕中心广场走了一圈,所走的路程是就是这个图形的周长,观察图形可知:这个图形的周长是下面长方形的一条长、2条宽和上面半圆弧的长度和,半圆弧的直径是200米,根据C=πd,求出圆的周长,再除以2就是半圆弧的长度,再加上1条长和2条宽进行即可求解。
【详解】3.14×200÷2+200+100×2
=314+200+200
=714(米)
答:她所走的路程是714米。
【点睛】解决本题根据周长的含义,找出这个图形的周长是由哪几部分组成的,分别求出后再相加。
20.10圈
【分析】根据圆的周长公式:C=πd,把数代入求出车轮转动一周走的长度,之后用钢丝绳的长度除以车轮一圈走的长度即可求出转多少圈。
【详解】9.42÷(3.14×0.3)
=9.42÷0.942
=10(圈)
答:车轮至少要转10圈。
【点睛】本题主要考查圆的周长公式,熟练掌握圆的周长公式并灵活运用。
21.5分钟
【分析】将数据带入圆的周长公式:C=πd,求出自行车外轮周长。乘100得出小涛骑自行车的速度,最后用桥长÷速度求出时间。
【详解】3.14×80×100
=3.14×8000
=25120(厘米)
25120厘米=251.2米
1256÷251.2=5(分钟)
答:他通过这座桥需要5分钟。
【点睛】本题主要考查圆的周长公式的实际应用,求出小涛的速度是解题的关键。
22.25.12厘米
【分析】根据题意可知,分针从上午9:00到上午9:30,分针尖走过的是半径为8厘米圆的周长的,根据圆的周长公式:π×半径×2,代入数据,即可解答。
【详解】3.14×8×2×
=25.12×2×
=50.24×
=25.12(厘米)
答:分针的针尖走过了25.12厘米。
【点睛】本题考查圆的周长公式的应用,关键明确分针的长度是圆的半径。
23.10圈
【分析】根据圆的周长公式C=2πr,求出油桶滚动一圈的距离,看图示可知油桶要滚过的路程是(32.4-0.5×2)米,再除以油桶滚动一圈的距离就是要求的答案。
【详解】(32.4-0.5×2)÷(3.14×0.5×2)
=31.4÷3.14
=10(圈)
答:可以滚动10圈。
【点睛】本题主要考查圆的周长公式的实际应用。
24.28.26米
【分析】根据圆的周长计算方法C=πd求出压路机前轮转动一周走的路程,进而求出每分钟行的路程,据此解答。
【详解】3.14×1.5×6
=4.71×6
=28.26(米)
答:这种压路机每分钟前进28.26米。
【点睛】此题主要考查圆的周长计算的计算方法,应根据题意,灵活运用,注意压路机转动一周走的路程等于直径是1.5米的圆的周长。
25.5分钟
【分析】已知自行车轮子的直径是85厘米,根据圆的周长公式C=πd,求出轮子的周长,即轮子转动一周行驶的距离;
已知车轮平均每分转120圈,用车轮的周长乘每分转的圈数,求出车轮每分钟行驶的距离,即自行车的速度;
已知需要骑车通过一座长1601.4米的大桥,先根据进率“1米=100厘米”,将1601.4米换算成160140厘米;再根据“路程÷速度=时间”,即可求出自行车通过这座桥需要的时间。
【详解】3.14×85=266.9(厘米)
266.9×120=32028(厘米)
1601.4米=160140厘米
160140÷32028=5(分钟)
答:他通过这座大桥需要5分钟。
答案第1页,共2页
答案第1页,共2页
一、解答题
1.三渡水大桥,古称三渡桥,位于温江区城西约7.5公里,横跨天府与永盛之间的金马河,曾经是川藏线上跨金马河的唯一大桥,也是连接川西平原东西地区的主要通道之一。淘气骑自行车从桥上经过,车轮滚动了230圈,已知自行车车轮直径60厘米(如图所示),三渡水大桥全长约多少米?(结果保留整数)
2.湛江海湾大桥全长3981米,一辆小汽车的轮胎外直径是80厘米,每分转300周。这辆小汽车通过这座桥大约需几分钟?(结果保留整数)
3.李叔叔家装修时,准备将一块周长为31.4厘米的圆形废旧木料加工成一块最大的正方形木板。这块正方形木板的面积是多少平方厘米?
4.第五套人民币中的1元硬币厚1.85毫米,圆形周长约是79毫米。如果要把1元硬币放进一个“开口是长3厘米、宽0.4厘米的长方形”储蓄罐中,能否放进去?请说明理由。(π取3.14,结果保留两位小数)
5.如图,圆形池塘的周长是157米,池塘周围(阴影部分)是一条5米宽的水泥路,在水泥路的外侧围一圈栅栏,栅栏至少长多少米?
6.伐木工人经常将圆木并排捆扎在一起,然后利用水的浮力从水路运输,从而节约成本。如果将10根直径约为0.5米的原木用铁丝紧紧地并排捆扎在一起(如下图)。捆一圈至少要用铁丝多少米(接口处不计)?
7.乐乐家距学校2.198千米,他每天骑自行车上学,已知自行车轮胎的外直径是70厘米。乐乐骑车从家到学校,自行车车轮一共转了多少周?
8.生态园计划用木料搭建一个舞台。工人师傅测得三棵树身周长分别是56.52厘米、50.24厘米、47.1厘米,请你根据下图的警示牌检验一下,有不能被砍伐的树吗?
9.喜迎元旦,畅想未来。为迎接元旦的到来,园艺工人沿着中心广场的圆形喷泉池的边沿每隔1.57米放一盆花,已知这个圆形喷泉池的半径为5.5米,园艺工人在这个喷泉池的边沿一共放了多少盆花?
10.如图,两个连在一起的滑轮,其中小轮的直径是4分米,当这个小轮转4周时,大轮刚好转1周,这个大轮的半径是多少分米?
11.将三根同样粗细的圆木像下图这样用铁丝在两头各捆一圈,如果每根圆木横截面的直径都是4分米,那么至少需要多长的铁丝?(接头处忽略不计)
12.一个圆形操场,外圈的周长是125.6米,沿操场的边有一条宽为4米的跑道(在操场内部)。淘气跑内圈一圈,你知道他跑了多少米吗?
13.第14届全国运动会田径比赛跑在奥林匹克中心举行。在标准跑道上,如果直道的长度是,第一条半圆形跑道的直径为,每条跑道宽,那么各跑道的起跑线应该相差多少米?
14.乐乐家到学校的距离是2200米,他的自行车车轮的直径是70厘米。如果每分钟车轮转100圈,乐乐骑自行车到学校大约需要多少分钟?(得数保留整数)
15.共享单车有低碳环保、经济节能等优势,为人们的出行提供了诸多方便。一辆共享单车的轮胎直径是0.7米,如果每分钟转100圈,这辆共享单车的速度是多少千米/时?(得数保留整数)
16.李叔叔家距公司5千米,李叔叔每天7:30出发骑自行年去公司上班,自行车车轮直径约是60厘米。如果车轮平均每分转150圈,李叔叔7:50能到公司吗?
17.下图是田径跑道示意图,乐乐沿着这个跑道跑一周需要多长时间?
18.李星和李佳骑自行车经过一段长为628米的大桥,李星自行车车轮直径为0.8米、每分钟都转动50圈,需要用多长时间才能通过大桥?(自行车身长忽略不计)
19.彤彤家的小区有一个中心广场(如图),彤彤饭后绕中心广场走了一圈,她所走的路程是多少米?
20.一辆表演杂技用的独轮车,车轮的直径是0.3米,要骑过一条长9.42米的钢丝绳,车轮至少要转多少圈?
21.小涛骑自行车去上学,要通过一座长1256米的桥,他的自行车外轮直径是80厘米,平均每分钟转100周,他通过这座桥需要多少分钟?
22.淘气家客厅有一个圆形钟表,分针长8厘米,从上午9:00到上午9:30,分针的针尖走过了多少厘米?(π取3.14)
23.如下图,地面上平放着一个底面半径为0.5m的圆柱形油桶,如果将这个油桶滚到墙边,可以滚动几圈?
24.一种压路机的前轮直径是1.5米,每分钟可以转6圈。请问这种压路机每分钟前进多少米?(取3.14)
25.乐乐骑车来到白鹭洲湿地公园游玩,途中需要骑车通过一座长1601.4米的大桥,如果车轮平均每分转120圈,那么他通过这座大桥需要几分钟?
参考答案
1.433米
【分析】自行车车轮直径60厘米,先根据公式:圆的周长=圆周率×直径,求出车轮的周长;
车轮滚动了230圈,用车轮的周长乘转动的圈数,即可求三渡水大桥全长约多少米。
【详解】60×3.14×230
=188.4×230
=43332(厘米)
43332厘米=433.32米
433.32米≈433米
答:三渡水大桥全长约433米。
2.5分钟
【分析】先根据圆的周长公式:C=πd,据此求出自行车轮胎的周长,再乘轮胎每分钟转的圈数求出自行车每分钟行驶的路程,最后根据“时间=路程÷速度”求出自行车通过大桥需要的分钟数,注意结果要运用四舍五入法保留整数。
【详解】80厘米=0.8米
3.14×0.8×300
=2.512×300
=753.6(米)
3981÷753.6≈5(分钟)
答:这辆小汽车通过这座桥大约需5分钟。
3.50平方厘米
【分析】圆的周长C=πd,则d=C÷π,据此求出圆的直径,由于要把圆加工成一个最大的正方形,则圆的直径等于正方形的对角线长,再根据“正方形的面积等于对角线乘积的一半”计算正方形的面积即可。
【详解】31.4÷3.14=10(厘米)
10×10÷2
=100÷2
=50(平方厘米)
答:这块正方形木板的面积是50平方厘米。
【点睛】解答本题的关键是求出正方形的对角线长,知道“正方形的面积等于对角线乘积的一半”。
4.能;见详解
【分析】要把硬币放进储蓄罐中,需要满足两个条件,①硬币的厚度需要小于储蓄罐的宽;②利用圆的周长公式,求出硬币的直径,直径需要小于储蓄罐的长;如果满足这两个条件的话,就能放进去。
【详解】厚度:1.85毫米=0.185厘米<0.4厘米
直径:79÷3.14≈25.2(毫米)=2.52(厘米)<3(厘米)
答:可以放进去。因为硬币的厚度小于小于储蓄罐的宽,硬币的直径小于储蓄罐的长。
【点睛】此题主要考查圆的周长公式的灵活运用。
5.188.4米
【分析】根据圆的直径=周长÷圆周率,先求出池塘直径,池塘直径+路宽×2=大圆直径,再根据圆的周长=圆周率×直径,求出栅栏长度即可。
【详解】157÷3.14=50(米)
50+5×2
=50+10
=60(米)
3.14×60=188.4(米)
答:栅栏至少长188.4米。
【点睛】关键是掌握并灵活运用圆的周长公式。
6.10.57米
【分析】从图中可知,将10根原木用铁丝紧紧地捆绑一圈,最左边和最右边各有一个半圆,可以组成一个圆,根据圆的周长公式C=πd求出最左边和最右边铁丝的长度;上、下面的铁丝长度都等于(10-1)个直径的长度之和,再加上圆的周长,即是捆一圈至少要用铁丝的长度。
【详解】3.14×0.5=1.57(米)
(10-1)×0.5×2
=9×0.5×2
=9(米)
1.57+9=10.57(米)
答:捆一圈至少要用铁丝10.57米。
【点睛】本题考查圆的周长公式的运用,关键是从图中分析出铁丝是如何捆绑的。
7.1000周
【分析】先根据:C=πd,求出自行车车轮的周长,然后用乐乐家距学校的距离除以车轮的周长即可。
【详解】70厘米=0.7米
2.198千米=2198米
2198÷(3.14×0.7)
=2198÷2.198
=1000(周)
答:自行车车轮一共转了1000周。
【点睛】此题应根据求一个数里面有几个另一个数,用除法解答;用到的知识点:圆的周长的计算公式,注意单位要统一。
8.有不能砍的树
【分析】根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,分别求出三棵树的半径,再进行比较,如果半径都大于8厘米,就都能被砍伐,如果有半径小于8厘米,就有不能被砍伐的树,据此解答。
【详解】56.52÷3.14÷2
=18÷2
=9(厘米)
9厘米>8厘米,能被砍伐;
50.24÷3.14÷2
=16÷2
=8(厘米)
8厘米=8厘米,能被砍伐;
47.1÷3.14÷2
=15÷2
=7.5(厘米)
7.5厘米<8厘米,不能被砍伐。
答:有不能被砍伐的树。
【点睛】熟练掌握和灵活运用圆的周长公式是解答本题的关键。
9.22盆
【分析】根据题意知道,在封闭线路上植树,植树的棵数=间隔数;先求出圆形的周长,再除以间距即可。
【详解】3.14×(5.5×2)÷1.57
=3.14÷1.57×(5.5×2)
=2×11
=22(盆)
答: 园艺工人在这个喷泉池的边沿一共放了22盆花。
【点睛】本题主要考查了植树问题,解题的关键是明确:在封闭线路上植树,棵数与段数相等,即:棵数=间隔数。
10.8分米
【分析】由“小轮转4周时,大轮刚好转1周”可知:大轮周长是小轮周长的4倍,将小轮直径带入圆的周长公式求出小轮的周长,进而得出大圆的周长,再带入圆的周长公式求出半径即可。
【详解】3.14×4×4÷3.14÷2
=16÷2
=8(分米)
答:这个大轮的半径是8分米。
【点睛】本题主要考查圆的周长公式,理解“小轮转4周时,大轮刚好转1周”是解题的关键。
11.49.12分米
【分析】如图所示,捆圆木的铁丝分为线段和圆弧两部分,三条线段的长度相等,每条线段的长度等于一条直径的长度,三条圆弧的长度相等,圆弧合在一起刚好等于一个圆的周长,把圆弧的长度和直径的长度相加求和,因为需要捆圆木的两头,所以最后结果乘2,据此解答。
【详解】
(4×3+3.14×4)×2
=(12+12.56)×2
=24.56×2
=49.12(分米)
答:至少需要49.12分米的铁丝。
【点睛】利用圆的周长计算出铁丝圆弧部分的长度是解答题目的关键。
12.100.48米
【分析】根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,求出这个圆形操场的半径,沿操场的边有一条宽为4米的跑道(在操场内部),则内圈的半径为:外圈的半径-4米;再根据圆的周长公式,即可求出内圈的周长,也就是淘气跑的米数。
【详解】125.6÷3.14÷2
=40÷2
=20(厘米)
3.14×(20-4)×2
=3.14×16×2
=50.24×2
=100.48(米)
答:他跑了100.48米。
【点睛】解答本题的关键是求出内圈的半径,再利用圆的周长公式进行解答。
13.7.85米
【分析】根据题意,两个半圆和起来是一个圆,第二个圆的周长比第一个圆的周长长多少米,就是各跑道的起跑线相差的米数,第一个圆的直径是72.6米,半径是72.6÷2=36.3米,每条跑道宽是1.25米,第二个圆的半径为36.3+1.25=37.55米,根据圆的周长公式:π×2×半径,求出这两个圆的周长,再用第二个圆的周长-第一个圆的周长,据此解答。
【详解】72.6÷2=36.3(米)
3.14×2×(36.3+1.25)-3.14×2×36.3
=6.28×(36.3+1.25-36.3)
=6.28×1.25
=7.85(米)
答:各跑道的起点线应该相差7.85米。
【点睛】本题考查圆的周长公式的应用,关键明确各跑道的半圆合起来是一个圆,再进行解答。
14.10分钟
【分析】根据圆的周长公式:π×直径,求出自行车车轮的周长,再乘100圈,求出1分钟自行车行驶的距离即自行车的速度;再根据时间=距离÷速度;用乐乐家到学校的距离÷1分钟自行车行驶的距离,即可解答。
【详解】70厘米=0.7米
2200÷(3.14×0.7×100)
=2200÷(2.198×100)
=2200÷219.8
≈10(分钟)
【点睛】本题考查圆的周长公式的应用,以及距离、时间和速度三者的关系;注意单位名数的统一。
15.13千米/时
【分析】根据圆的周长公式:C=πd,把数据代入公式求出共享单车车轮的周长,用车轮的周长乘每分钟转的圈数,求出每分钟行驶的路程,再根据1小时=60分钟,再乘60就是这辆共享单车每小时的速度,据此解答。
【详解】0.7×3.14×100×60
=219.8×60
=13188(米/时)
13188米/时=13.188千米/时
13.188千米/时≈13千米/时
答:这辆共享单车的速度是13千米/时
【点睛】此题主要考查圆的周长公式的灵活运用。
16.能到公司
【分析】根据圆的周长公式:π×直径,代入数据,求出自行车车轮的周长,再成150圈,求出一分钟自行车行多少千米;7:30到7:50的时间是20分钟,20分钟李叔叔行驶的路程是多少千米,用一分钟行距离×20分钟,再和5千米进行比较,即可解答。
【详解】7时50分-7时30分=20(分)
5千米=5000千米
60厘米=0.6米
3.14×0.6×150×20
=1.884×150×20
=282.6×20
=5652(千米)
5652>5000
李叔叔7:50能到公司。
答:李叔叔7:50能到公司。
【点睛】本题考查圆的周长公式的应用,注意单位名数的统一。
17.56.4秒
【分析】先求出跑道的周长,包括左右两个半圆弧组成的整圆的周长和中间的长方形的两条长。根据圆的周长=πd求出整圆的周长,再加上长方形的两条长即可求出跑道的周长。最后除以乐乐的速度即可求出乐乐沿着这个跑道跑一周需要多长时间。
【详解】3.14×60+75×2
=188.4+150
=338.4(米)
338.4÷6=56.4(秒)
答:乐乐沿着这个跑道跑一周需要56.4秒。
【点睛】本题考查了组合图形的周长和简单的行程问题。明确跑道周长的组成是解题的关键。
18.5分钟
【分析】根据圆的周长公式:C=πd,求出车轮周长,再乘50求出骑自行车的速度。根据时间=路程÷速度,代入数据求出时间即可。
【详解】628÷(3.14×0.8×50)
=628÷125.6
=5(分钟)
答:需要5分钟才能通过大桥。
【点睛】本题主要考查圆的周长公式的实际应用。
19.714米
【分析】绕中心广场走了一圈,所走的路程是就是这个图形的周长,观察图形可知:这个图形的周长是下面长方形的一条长、2条宽和上面半圆弧的长度和,半圆弧的直径是200米,根据C=πd,求出圆的周长,再除以2就是半圆弧的长度,再加上1条长和2条宽进行即可求解。
【详解】3.14×200÷2+200+100×2
=314+200+200
=714(米)
答:她所走的路程是714米。
【点睛】解决本题根据周长的含义,找出这个图形的周长是由哪几部分组成的,分别求出后再相加。
20.10圈
【分析】根据圆的周长公式:C=πd,把数代入求出车轮转动一周走的长度,之后用钢丝绳的长度除以车轮一圈走的长度即可求出转多少圈。
【详解】9.42÷(3.14×0.3)
=9.42÷0.942
=10(圈)
答:车轮至少要转10圈。
【点睛】本题主要考查圆的周长公式,熟练掌握圆的周长公式并灵活运用。
21.5分钟
【分析】将数据带入圆的周长公式:C=πd,求出自行车外轮周长。乘100得出小涛骑自行车的速度,最后用桥长÷速度求出时间。
【详解】3.14×80×100
=3.14×8000
=25120(厘米)
25120厘米=251.2米
1256÷251.2=5(分钟)
答:他通过这座桥需要5分钟。
【点睛】本题主要考查圆的周长公式的实际应用,求出小涛的速度是解题的关键。
22.25.12厘米
【分析】根据题意可知,分针从上午9:00到上午9:30,分针尖走过的是半径为8厘米圆的周长的,根据圆的周长公式:π×半径×2,代入数据,即可解答。
【详解】3.14×8×2×
=25.12×2×
=50.24×
=25.12(厘米)
答:分针的针尖走过了25.12厘米。
【点睛】本题考查圆的周长公式的应用,关键明确分针的长度是圆的半径。
23.10圈
【分析】根据圆的周长公式C=2πr,求出油桶滚动一圈的距离,看图示可知油桶要滚过的路程是(32.4-0.5×2)米,再除以油桶滚动一圈的距离就是要求的答案。
【详解】(32.4-0.5×2)÷(3.14×0.5×2)
=31.4÷3.14
=10(圈)
答:可以滚动10圈。
【点睛】本题主要考查圆的周长公式的实际应用。
24.28.26米
【分析】根据圆的周长计算方法C=πd求出压路机前轮转动一周走的路程,进而求出每分钟行的路程,据此解答。
【详解】3.14×1.5×6
=4.71×6
=28.26(米)
答:这种压路机每分钟前进28.26米。
【点睛】此题主要考查圆的周长计算的计算方法,应根据题意,灵活运用,注意压路机转动一周走的路程等于直径是1.5米的圆的周长。
25.5分钟
【分析】已知自行车轮子的直径是85厘米,根据圆的周长公式C=πd,求出轮子的周长,即轮子转动一周行驶的距离;
已知车轮平均每分转120圈,用车轮的周长乘每分转的圈数,求出车轮每分钟行驶的距离,即自行车的速度;
已知需要骑车通过一座长1601.4米的大桥,先根据进率“1米=100厘米”,将1601.4米换算成160140厘米;再根据“路程÷速度=时间”,即可求出自行车通过这座桥需要的时间。
【详解】3.14×85=266.9(厘米)
266.9×120=32028(厘米)
1601.4米=160140厘米
160140÷32028=5(分钟)
答:他通过这座大桥需要5分钟。
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
