22.3 实际问题与二次函数(喷水和其他问题) 过关练习 2025-2026学年上期初中数学人教版九年级上册
文档属性
| 名称 | 22.3 实际问题与二次函数(喷水和其他问题) 过关练习 2025-2026学年上期初中数学人教版九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 12:00:38 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
22.3 实际问题与二次函数(喷水和其他问题) 过关练习 2025-2026学年上期初中数学人教版九年级上册
一、单选题
1.如图,某数学小组发现滨江生态公园有一座假山的局部(阴影部分)的主视图呈现抛物线形状,以点O为原点建立平面直角坐标系(坐标系上1个单位长度表示),假山轮廓所在的抛物线的解析式为,其中垂直于水平地面,在点B处安装一喷水口,若向上喷出的水柱恰好为抛物线,落水点恰好为点C.下列说法不一定正确的是( )
A.假山上的点B到水平地面的距离为
B.水平方向上的长度为
C.
D.抛物线与的对称轴相同
2.如图,为了美化校园环境,学校计划在草坪中央修建一个直径为米的圆形喷水池,水池中心处立着一个圆柱形实心石柱,在圆形喷水池的四周安装了一圈喷头,喷射出的水柱呈抛物线型,水柱在距水池中心处到达最大高度为,从各方向喷出的水柱在石柱顶部的中心点处汇合,则要修建的高度是( )
A.米 B.米 C.米 D.米
3.如图1是某城市广场音乐喷泉,出水口A处的水流呈抛物线形,该水流喷出的高度与水平距离之间的关系如图2所示,点B为该水流的最高点,点C为该水流的落地点,且,垂足为点D,.若,,则的长为( )
A. B. C. D.
4.数学来源于生活,伞是生活中常见的一种工具.伞撑开后如图1所示,由此发现数学知识抛物线.如图2,以伞柄所在的直线为y轴,以伞骨,的交点O为坐标原点建立平面直角坐标系,C为抛物线上的点,点A,B在抛物线上,,关于y轴对称.已知抛物线的表达式为,若点A到x轴的距离是,则A,B两点之间的距离是( )
A. B. C. D.
5.冬季蔬菜大棚内某天的温度(单位:)与时间(单位:)满足函数关系式,其中.有下列结论:
①蔬菜大棚内当天的温度可以是;
②蔬菜大棚内当天的温度的最大值为;
③蔬菜大棚内当天的温度不低于19℃的时长为.
其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
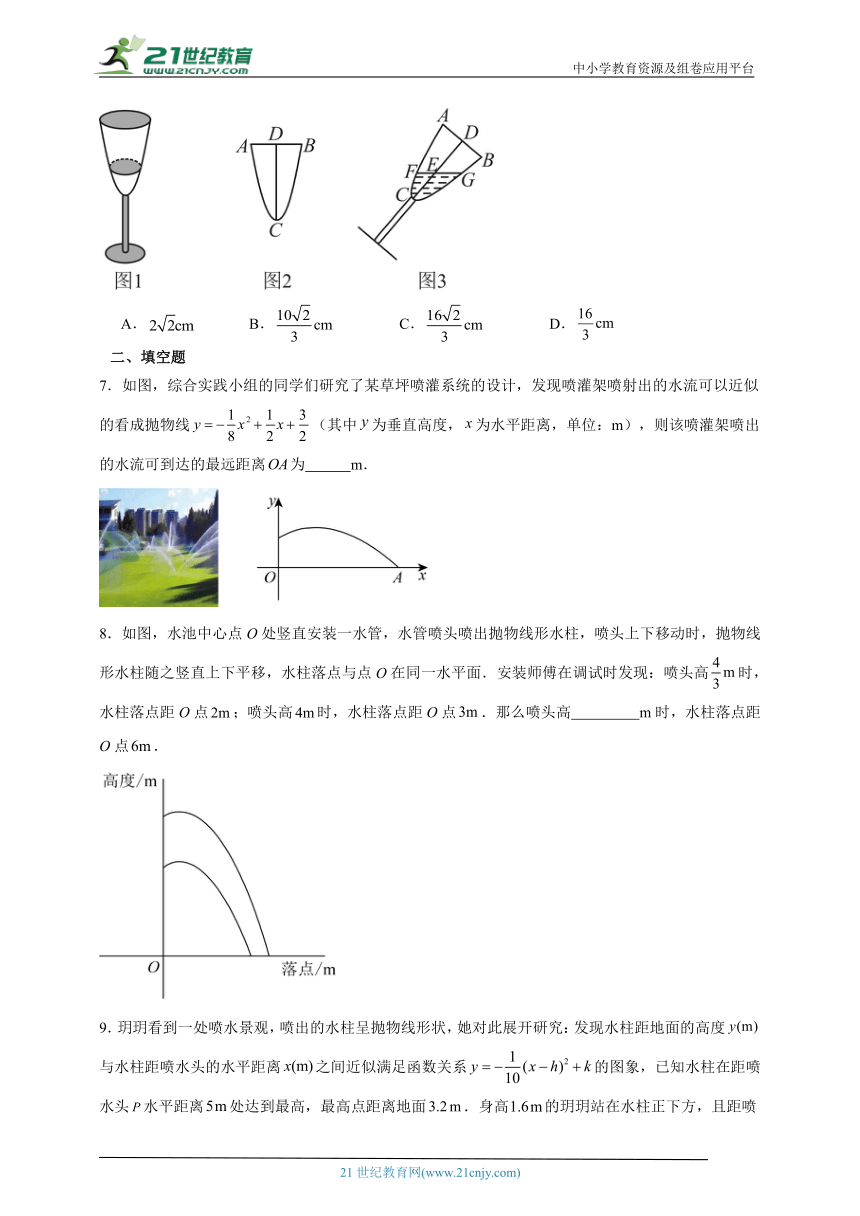
6.一种高脚杯如图1所示,其杯肚部分外轮廓线为抛物线的一部分,图2为其杯肚的截面图,已知杯口,杯深.如图3,若将盛有部分液体的高脚杯倾斜(即与液面所在直线相交,所夹较小角为),液面与交于点E,且点E距杯口的距离,则此时液面宽为( )
A. B. C. D.
二、填空题
7.如图,综合实践小组的同学们研究了某草坪喷灌系统的设计,发现喷灌架喷射出的水流可以近似的看成抛物线(其中为垂直高度,为水平距离,单位:m),则该喷灌架喷出的水流可到达的最远距离为 m.
8.如图,水池中心点O处竖直安装一水管,水管喷头喷出抛物线形水柱,喷头上下移动时,抛物线形水柱随之竖直上下平移,水柱落点与点O在同一水平面.安装师傅在调试时发现:喷头高时,水柱落点距O点;喷头高时,水柱落点距O点.那么喷头高 m时,水柱落点距O点.
9.玥玥看到一处喷水景观,喷出的水柱呈抛物线形状,她对此展开研究:发现水柱距地面的高度与水柱距喷水头的水平距离之间近似满足函数关系的图象,已知水柱在距喷水头水平距离处达到最高,最高点距离地面.身高的玥玥站在水柱正下方,且距喷水头水平距离的位置,她的头顶 碰到水柱.(填“能”或“不能”)
10.2023年5月28日,中国东方航空使用中国商飞全球首架交付的大型客机,执行航班,开启这一机型全球首次商业载客飞行,该航班标志若的“研发、制造、取证、投运”全面贯通.如果某型号飞机降落后滑行的距离s(单位:米)关于滑行的时间t(单位:秒)的函数表达式是,则该飞机着陆后滑行最长时间为 秒.
11.一般情况下,人体能够承受的安全电流为,电功率P(单位:)与电流I(单位:),电阻R(单位:)之间的公式为,已知人体电阻阻值约为,当一充电器电功率为时,若发生触电,则此时通过人体的电流 (填“已”或“未”)超过人体能承受的安全电流.
12.某足球运动员将足球沿与地面成一定角度的方向踢出,如果不考虑空气阻力,足球飞行的高度(单位:)与足球飞行的时间(单位:)之间具有二次函数关系,其部分图象如图所示,则足球从踢出到落地所需的时间是 .
13.“路亚”是一种钓鱼方法,用这种方法钓鱼时先把鱼饵通过鱼线收到鱼竿末端,然后用力将鱼饵甩向远处.如图,人站在离水面高度的位置,当鱼饵被抛出后,鱼竿所在的位置为直线,此时鱼线形成的图象近似的看成抛物线,若点C到y轴的距离为,则鱼线落在水面上的点到点A的水平距离 .
三、解答题
14.户太八号葡萄果肉柔软多汁,品质优良,深受广大消费者喜爱.如图①,在山坡上安装一个竖直喷水管向两侧喷水,浇灌葡萄园,喷出的水流呈抛物线状,且两侧水流关于喷水管所在的直线成轴对称,取图①的截面,建立如图②所示的平面直角坐标系,以喷水管底端点为坐标原点,喷头,水流落在山坡上的点和点处.
(1)求山坡和轴右侧抛物线的函数表达式;
(2)为了防治虫害,在葡萄树上露出地表的位置粘贴防虫胶带,若在坡段种植的葡萄树,则树上粘贴的胶带是否有被水流喷到的风险?请说明理由.
15.综合与实践
如图,这是一个直角三角形斜坡截面,,,,坡面上有一根标杆(标杆粗细忽略不计,点M在斜坡上且与点B不重合,),现在斜坡点A处安装一个喷水管(高度忽略不计),喷水管喷出的水流呈抛物线形状,建立如图所示的平面直角坐标系,喷水管喷出水流的水平距离x(单位:m)与水流的高度y(单位:m)的变化规律如表:
x 0 1 2 3 4 …
y 3 3 …
(1)求该抛物线的解析式,并写出其顶点坐标.
(2)若喷水管喷出的水流恰好经过标杆的顶部点N.
①求标杆的最大高度;
②若点A到M,N两点的距离相等,求点N的坐标.
16.一个可移动的喷灌架喷射出的水流可以看成抛物线,如图是喷灌架给坡地草坪喷水的平面示意图,喷灌架置于坡地草坪底部点处,喷水头的竖直高度为,当喷射出的水流与点的水平距离为时,达到最高,此时其与水平地面的竖直高度为.在直线坡地草坪上,点与点的水平距离为,与水平地面的竖直高度为.
(1)求水流抛物线的解析式;
(2)求水流抛物线与直线坡地草坪之间的竖直距离的最大值;
(3)已知在点处有一棵竖直高度为的小树.若将喷灌架沿直线坡地草坪向右移动,设其向右水平移动(其中),使其喷射出的水流不被小树遮挡,直接写出的取值范围.
17.某农庄计划在亩空地上全部种植蔬菜和水果,种植蔬菜面积大于种植水果面积,且均为正整数,菜农小张和果农小李分别承包了种植蔬菜和水果的任务.小张种植每亩蔬菜的工资(元)与种植面积x(亩)之间的函数关系为;小李种植水果所得报酬(元)与种植面积(亩)之间的函数关系为.
(1)若小张种植蔬菜为亩,用含的代数式表示下列各量:
①小李种植水果的面积为 亩;
②小张种植蔬菜所得的总工资为 元;
③小李种植水果所得的报酬为 元;
(2)若农庄支付小张和小李的总费用为元,求小张与小李种植的面积各为多少亩?
(3)直接写出农庄支付给小张和小李的总费用的最大值.
18.“碧玉妆成一树高,万条垂下绿丝绦.”垂柳观赏价值高,能稳固堤岸,防水土流失,且成本低廉,深受各地绿化工程的青睐.如图1是某园林湖旁的一棵垂柳,这棵垂柳中某一枝的形状如图2所示的抛物线,它距离地面的高度为,到树干的水平距离为,y与x之间满足关系式.已知这枝垂柳的始端到地面的距离,末端B恰好接触地面,且到始端的水平距离.
(1)求该抛物线的函数解析式;
(2)小聪坐在爸爸的肩头,已知小聪的头顶距离地面,他从点O出发向点B处走去,请计算小聪走出多远时,头顶刚好碰到这枝垂柳?
19.滑板是一项富有激情与挑战的极限运动,U型池则是它绽放魅力的重要舞台,滑手在连续的U型池滑道间展开挑战,这不仅能考验滑手的综合能力,也为观众带来极具观赏性的视觉盛宴.滑手在U型池之间转换时,脱离滑道起跳后的飞行路线可近似看作是抛物线的一部分.如图,某次挑战中,滑手小红尝试从滑道①转换到滑道②,已知小红从起跳到着陆的过程中,起跳点到滑道底部所在直线的距离为,当离起跳点水平距离为时,小红到滑道底部所在直线的距离达到了最大值,现以滑道底部所在直线为x轴,垂直于滑道底部所在直线且经过起跳点的直线为y轴建立平面直角坐标系(滑道①、②底部在一条直线上).
(1)求该抛物线的函数表达式;
(2)若滑手的着陆点位于下一个U型池滑道的内部,则视为滑手成功完成转换,已知滑道②与滑道①高度相同,两者水平距离为,请通过计算说明小红能否转换成功?
20.【问题背景】某体育社团开展跳大绳游戏活动,两个摇绳的同学手,之间相距,绳子在摇动过程中呈抛物线形状且轨迹保持不变,当手摇绳子到最上方时,绳子的最高点距地面,握绳的手距离地面,当摇绳两端的手更高时,绳子整体也会相应更高.
【模型抽象】以人站立的地面为轴,绳子最高点垂直于地面的直线为轴建立平面直角坐标系.
【问题解决】
(1)求抛物线解析式;
(2)若参加跳绳的人身高均为,人与人之间的距离为,最多能有多少人同时参与跳绳(除摇绳人外)?
(3)在(2)的条件下,由于还有1名同学没能同时参与跳绳,若加入这名同学,在不改变摇绳两端的水平距离和绳长的情况下,只需将两端向上移即可,则的值应满足什么条件?
参考答案
题号 1 2 3 4 5 6
答案 D B D D C C
1.D
【分析】本题考查了二次函数的应用,正确理解题意是解题的关键.
由假山所在抛物线的函数解析式为,分别令,,求出对应的,即可判断选项A、B,由,即可判断选项C,根据与的图象可判断D选项.
【详解】解:由假山所在抛物线的函数解析式为,
当时,,故假山上的点B到水平地面的距离为;
当时,或(舍去),故水平方向上的长度为,可知选项A、B正确;
由题意得,解得:,可知选项C正确;
由题图可知,喷出的水柱呈现的抛物线与的对称轴相同,故选项D不正确,符合题意.
故选:D.
2.B
【分析】本题考查了二次函数实际应用中的喷泉问题,选图中第一象限的抛物线,由题意得抛物线顶点坐标为,过点,则设抛物线解析式为,然后代入求出抛物线解析式为,然后令即可求解,正确求出二次函数解析式解题的关键.
【详解】解:选图中第一象限的抛物线,
由题意得,抛物线顶点坐标为,过点,
设抛物线解析式为,
∴,解得:,
∴抛物线解析式为,
当时,,
∴点,
∴,
故选:.
3.D
【分析】本题主要考查二次函数的应用,解题的关键是掌握待定系数法求函数解析式.
根据题意可得,设抛物线的表达式为.将代入,求出a的值,即可解答.
【详解】解:∵,,,
∴,
设抛物线的表达式为.
将代入,得,
解得.
抛物线的表达式为.
令,则.
解得,(不合题意,舍去).
的长为.
故选:D.
4.D
【分析】本题考查了二次函数的应用,轴对称的性质,先求出点到轴的距离为,再结合轴对称的性质即可得解,熟练掌握以上知识点并灵活运用是解此题的关键.
【详解】解:∵点A到x轴的距离是,
∴令,则,
解得:或(不符合题意,舍去),
∴点到轴的距离为,
∵点A,B在抛物线上,,关于y轴对称,
∴,
故选:D.
5.C
【分析】本题主要考查了二次函数的应用,依据题意得,,故当时,有最大值为19.4,且当时,随的增大而增大,进而逐个判断可以得解.解题时要熟练掌握并能灵活运用二次函数的性质是关键.
【详解】解:由题意得,,
当时,有最大值为19.4,且当时,随的增大而增大,故②错误.
,且当时,,
蔬菜大棚内当天的温度可以是,故①正确.
令,
.
或.
的图象开口向下,
蔬菜大棚内当天的温度不低于的时长为:小时,故③正确.
综上,正确的有①③,共2个.
故选:C.
6.C
【分析】本题考查的是二次函数的实际应用,建立如图所示平面直角坐标系,作于点H,作于点Q,则,求解二次函数解析式为,FG所在直线解析式为,再进一步求解即可.
【详解】解:建立如图所示平面直角坐标系,作于点H,作于点Q,
则,
则各点坐标为:,,,,.
设抛物线的表达式为,
把点A坐标代入解析式,得,
解得,
∴.
∵,E点坐标为,
∴直线与x轴的交点为.
设所在直线解析式为,
把点,代入解析式,得.
令,
得,
解得,.
∴,
∴.
故答案为:C.
7.6.
【分析】本题考查了二次函数的实际应用,读懂题意将问题转化为是解题的关键.
根据题意得到,解方程即可得到结论.
【详解】解:,
当时,即,
解得,(不合题意,舍去),
该喷灌架喷出的水流可到达的最远距离米.
故答案为:6.
8.20
【分析】本题主要考查了二次函数图象的性质,求二次函数的关系式,
由题意可知,在调整喷头高度的过程中,水柱的形状不发生变化,当喷头高2.5米时,可设,将代入关系式得出;当喷头高度为时,可设,将代入关系式得,联立求出a,b的值,设喷头高为h时,水柱落点距O点4m,此时的关系式为,将代入求出答案即可.
【详解】解:由题意可知,在调整喷头高度的过程中,水柱的形状不发生变化,对称轴也不变,
∴二次项系数和一次项系数都不变,
当喷头高时,可设,
将代入关系式,得;
当喷头高度为时,可设,
将代入关系式得.
联立,得,
解得.
设喷头高为h时,水柱落点距O点,
此时的关系式为,
将代入关系式,得,
解得.
当喷头高时,水柱落点距O点.
故答案为:20.
9.不能
【分析】本题考查了二次函数的实际应用,掌握顶点式求二次函数解析式是解题的关键.
根据顶点,得出抛物线的表达式,令,求得的值,与比较即可求解.
【详解】解:根据题意可知抛物线的顶点为,水柱距地面的高度与水柱距喷水头的水平距离之间近似满足函数关系,
则抛物线的解析式为,
令,则,
故她的头顶不能碰到水柱.
故答案为:不能.
10.18
【分析】本题考查了二次函数的应用,二次函数的最值.熟练掌握二次函数的应用是解题的关键.
由题意得,由可知当时,s有最大值,然后根据题意作答即可.
【详解】解:,
,
∴当时,s有最大值,
∵飞机滑行到最大距离时停下,此时滑行的时间最长,
∴该飞机着陆后滑行最长时间为18秒.
故答案为:18.
11.已
【分析】本题主要考查了二次函数的实际应用,根据题意把代入到中求出I的值即可得到答案.
【详解】解:在中,当时,,
∴或(舍去),
∵,
∴当一充电器电功率为时,若发生触电,则此时通过人体的电流已超过人体能承受的安全电流.
故答案为:已.
12.4
【分析】本题考查二次函数的应用,解答本题的关键是明确题意,利用二次函数的性质解答.
先确定抛物线的对称轴方程,再根据抛物线的对称性可得出结论.
【详解】解:根据函数的图象可得抛物线的对称轴方程为:,
因为抛物线与x轴的一个交点横坐标为0,
所以,抛物线与x轴的另一个交点横坐标为,
所以,足球从踢出到落地所需的时间是,
故答案为:4
13.10
【分析】根据题意,得,代入解析式,确定,得到解析式,根据,得到,代入解析式得到(舍去),解答即可.
【详解】解:根据题意,得,代入解析式,
解得,
故一次函数的解析式,
当时,
,
故点,
把代入解析式,
解得(舍去),
故抛物线的解析式为,
当时,
,
解得,
故鱼线落在水面上的点到点A的水平距离.
故答案为:10.
【点睛】本题考查了待定系数法求解析式,点到坐标轴的距离意义,解方程,抛物线的性质,熟练掌握待定系数法,抛物线的性质是解题的关键.
14.(1),
(2)粘贴的胶带没有被水流喷到的风险,理由见解析
【分析】本题主要考查了二次函数的应用,求一次函数解析式,二次函数解析式,解题的关键是熟练掌握待定系数法.
(1)用待定系数法求出直线和轴右侧抛物线的表达式即可;
(2)设水流所在的抛物线到山坡的竖直距离为,得出,求出,从而得出答案即可.
【详解】(1)解:设山坡的函数表达式为.
过点,
,解得.
山坡的函数表达式为.
点.
右侧拋物线上点的对称点为.
设轴右侧抛物线的函数表达式为.
解得
轴右侧抛物线的函数表达式为.
(2)解:粘贴的胶带没有被水流喷到的风险.
理由如下:
设水流所在的抛物线到山坡的竖直距离为,
粘贴的胶带没有被水流喷到的风险.
15.(1)抛物线的解析式为,顶点坐标为
(2)①的最大值为;②点的坐标为
【分析】本题主要考查了二次函数的应用,解题时要熟练掌握并能灵活运用二次函数的性质是关键.
(1)依据题意,结合表格数据可得,抛物线的对称轴是直线,则该抛物线的顶点坐标为,故可设该抛物线的解析式为,再将点代入得,解得,进而可以判断得解;
(2)①依据题意,设直线的解析式为,又将,代入得,可得直线的解析式为,又设点的坐标为,则的坐标为,故,进而可以判断得解;
②依据题意,过点作于点,连接,又设,则点的坐标为,由得为中点,即,又,则,可得,然后将点的坐标代入抛物线的解析式得,求出后即可判断得解.
【详解】(1)解:由题意可得该抛物线的顶点坐标为,
设该抛物线的解析式为.
将点代入得,解得,
该抛物线的解析式为,顶点坐标为.
(2)解:①设直线的解析式为.
将,代入得解得
即直线的解析式为.
设,则,
,
当时,的最大值为.
②如图,过点作于点,连接,设,则.
由得为中点,即.
,
,即.
将点坐标代入抛物线解析式得,
整理方程得,
解得(舍去),,
故点的坐标为.
16.(1)
(2)
(3)
【分析】本题考查了二次函数的应用.
(1)由顶点设抛物线的解析式为,将点代入求解即可;
(2)先求得直线的解析式为,计算,利用二次函数的性质求解即可;
(3)由题意得平移后的抛物线可表示为,将点代入,计算即可求解.
【详解】(1)解:由题意可知,水流抛物线的顶点坐标为,
设水流形成的抛物线的解析式为,
将点代入得,,
解得,
水流抛物线的解析式为;
(2)解:由题意可知点坐标为,
设直线的解析式为,把代入得,
∴,
∴直线的解析式为,
∴,
∵,抛物线开口向下,
∴当时,取最大值,最大值为;
(3)解: 设喷灌架沿直线坡地草坪向右水平移动,则向上移动,
则平移后的抛物线可表示为,
将点代入得,,
解得或.
∴结合图象可得,的取值范围为.
17.(1),,;
(2)小张种植的面积为18亩,小李种植的面积为12亩;
(3)当时,农庄支付给小张和小李的总费用的最大,最大值为4348元.
【分析】本题考查二次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,求出相应的函数关系式.
(1)根据题意列式即可得到结论;
(2)根据小张和小李的总费用为元列方程,解方程即可得到结论;
(3)设农庄支付给小张和小李的总费用为w元,根据题意列函数解析式,根据二次函数的性质即可得到结论.
【详解】(1)解:①小李种植水果的面积为亩;
②小张种植蔬菜所得的总工资为元;
③小李种植水果所得的报酬为元;
故答案为:,,;
(2)解:根据题意得,,
解得,,
∵种植蔬菜面积大于种植水果面积,即,即,
∴不符合题意,舍去;
小张种植蔬菜面积为18亩,小李种植的水果面积为亩;
答:小张种植蔬菜面积为18亩,小李种植的水果面积为12亩;
(3)解:设农庄支付给小张和小李的总费用为w元,
根据题意得,,
∵,且均为整数,
∴当时,农庄支付给小张和小李的总费用的最大,最大值为元.
18.(1)
(2)小聪走出时,头顶刚好碰到这枝垂柳
【分析】本题考查二次函数的应用、一元二次方程的应用.要求明确题意,找出所求问题需要的条件,并进行正确的计算.
(1)根据题意可得,,然后利用待定系数法进行计算,即可解答;
(2)利用(1)的结论进行计算,即可解答.
【详解】(1)解:∵,
∴,,
∵点 A,B 均在抛物线 上,
,
解得 ,
∴该抛物线的函数解析式为
(2)解:令,得
整理,得
解得 (不合题意,舍去),
故小聪走出 时,头顶刚好碰到这枝垂柳.
19.(1)
(2)能
【分析】此题考查了二次函数的应用,正确求出函数解析式是解题的关键.
(1)根据题意直接写出抛物线的顶点坐标,再利用待定系数法求出函数解析式即可;
(2)当时,,解方程比较后即可得到答案.
【详解】(1)解:由题知起跳点的坐标为,抛物线的顶点坐标为.
设该抛物线的函数表达式为,
把代入得,
解得,
设该抛物线的函数表达式为.
(2)当时,,
解得,(舍去),
因为,
所以小文能成功转换.
20.(1)
(2)9人
(3)的值应超过
【分析】本题主要考查了二次函数的应用,正确求得抛物线解析式是解题关键.
(1)由已知确定顶点,,设抛物线解析式为,利用待定系数法求解即可;
(2)令,解方程即可求出x的值;
(3)设出平移后的解析式为,然后求出绳高不低于的水平距离大于等于,求出t的取值范围.
【详解】(1)解:由题意可设抛物线解析式为,且抛物线过点和点,
则有:
解得:
抛物线解析式为
(2)解:当时有,解得:
当时,则有一个同学在原点处,其两侧均有4个同学,与最远端同学相距,
此时可有9个同学同时参加跳绳.
(3)解:由(2)可知,再增加1个同学即有10个同学,此时没有人能站在原点处,
故原点两侧的同学距原点,所以最远端到原点距离为,
解得
即的值应超过即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
22.3 实际问题与二次函数(喷水和其他问题) 过关练习 2025-2026学年上期初中数学人教版九年级上册
一、单选题
1.如图,某数学小组发现滨江生态公园有一座假山的局部(阴影部分)的主视图呈现抛物线形状,以点O为原点建立平面直角坐标系(坐标系上1个单位长度表示),假山轮廓所在的抛物线的解析式为,其中垂直于水平地面,在点B处安装一喷水口,若向上喷出的水柱恰好为抛物线,落水点恰好为点C.下列说法不一定正确的是( )
A.假山上的点B到水平地面的距离为
B.水平方向上的长度为
C.
D.抛物线与的对称轴相同
2.如图,为了美化校园环境,学校计划在草坪中央修建一个直径为米的圆形喷水池,水池中心处立着一个圆柱形实心石柱,在圆形喷水池的四周安装了一圈喷头,喷射出的水柱呈抛物线型,水柱在距水池中心处到达最大高度为,从各方向喷出的水柱在石柱顶部的中心点处汇合,则要修建的高度是( )
A.米 B.米 C.米 D.米
3.如图1是某城市广场音乐喷泉,出水口A处的水流呈抛物线形,该水流喷出的高度与水平距离之间的关系如图2所示,点B为该水流的最高点,点C为该水流的落地点,且,垂足为点D,.若,,则的长为( )
A. B. C. D.
4.数学来源于生活,伞是生活中常见的一种工具.伞撑开后如图1所示,由此发现数学知识抛物线.如图2,以伞柄所在的直线为y轴,以伞骨,的交点O为坐标原点建立平面直角坐标系,C为抛物线上的点,点A,B在抛物线上,,关于y轴对称.已知抛物线的表达式为,若点A到x轴的距离是,则A,B两点之间的距离是( )
A. B. C. D.
5.冬季蔬菜大棚内某天的温度(单位:)与时间(单位:)满足函数关系式,其中.有下列结论:
①蔬菜大棚内当天的温度可以是;
②蔬菜大棚内当天的温度的最大值为;
③蔬菜大棚内当天的温度不低于19℃的时长为.
其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
6.一种高脚杯如图1所示,其杯肚部分外轮廓线为抛物线的一部分,图2为其杯肚的截面图,已知杯口,杯深.如图3,若将盛有部分液体的高脚杯倾斜(即与液面所在直线相交,所夹较小角为),液面与交于点E,且点E距杯口的距离,则此时液面宽为( )
A. B. C. D.
二、填空题
7.如图,综合实践小组的同学们研究了某草坪喷灌系统的设计,发现喷灌架喷射出的水流可以近似的看成抛物线(其中为垂直高度,为水平距离,单位:m),则该喷灌架喷出的水流可到达的最远距离为 m.
8.如图,水池中心点O处竖直安装一水管,水管喷头喷出抛物线形水柱,喷头上下移动时,抛物线形水柱随之竖直上下平移,水柱落点与点O在同一水平面.安装师傅在调试时发现:喷头高时,水柱落点距O点;喷头高时,水柱落点距O点.那么喷头高 m时,水柱落点距O点.
9.玥玥看到一处喷水景观,喷出的水柱呈抛物线形状,她对此展开研究:发现水柱距地面的高度与水柱距喷水头的水平距离之间近似满足函数关系的图象,已知水柱在距喷水头水平距离处达到最高,最高点距离地面.身高的玥玥站在水柱正下方,且距喷水头水平距离的位置,她的头顶 碰到水柱.(填“能”或“不能”)
10.2023年5月28日,中国东方航空使用中国商飞全球首架交付的大型客机,执行航班,开启这一机型全球首次商业载客飞行,该航班标志若的“研发、制造、取证、投运”全面贯通.如果某型号飞机降落后滑行的距离s(单位:米)关于滑行的时间t(单位:秒)的函数表达式是,则该飞机着陆后滑行最长时间为 秒.
11.一般情况下,人体能够承受的安全电流为,电功率P(单位:)与电流I(单位:),电阻R(单位:)之间的公式为,已知人体电阻阻值约为,当一充电器电功率为时,若发生触电,则此时通过人体的电流 (填“已”或“未”)超过人体能承受的安全电流.
12.某足球运动员将足球沿与地面成一定角度的方向踢出,如果不考虑空气阻力,足球飞行的高度(单位:)与足球飞行的时间(单位:)之间具有二次函数关系,其部分图象如图所示,则足球从踢出到落地所需的时间是 .
13.“路亚”是一种钓鱼方法,用这种方法钓鱼时先把鱼饵通过鱼线收到鱼竿末端,然后用力将鱼饵甩向远处.如图,人站在离水面高度的位置,当鱼饵被抛出后,鱼竿所在的位置为直线,此时鱼线形成的图象近似的看成抛物线,若点C到y轴的距离为,则鱼线落在水面上的点到点A的水平距离 .
三、解答题
14.户太八号葡萄果肉柔软多汁,品质优良,深受广大消费者喜爱.如图①,在山坡上安装一个竖直喷水管向两侧喷水,浇灌葡萄园,喷出的水流呈抛物线状,且两侧水流关于喷水管所在的直线成轴对称,取图①的截面,建立如图②所示的平面直角坐标系,以喷水管底端点为坐标原点,喷头,水流落在山坡上的点和点处.
(1)求山坡和轴右侧抛物线的函数表达式;
(2)为了防治虫害,在葡萄树上露出地表的位置粘贴防虫胶带,若在坡段种植的葡萄树,则树上粘贴的胶带是否有被水流喷到的风险?请说明理由.
15.综合与实践
如图,这是一个直角三角形斜坡截面,,,,坡面上有一根标杆(标杆粗细忽略不计,点M在斜坡上且与点B不重合,),现在斜坡点A处安装一个喷水管(高度忽略不计),喷水管喷出的水流呈抛物线形状,建立如图所示的平面直角坐标系,喷水管喷出水流的水平距离x(单位:m)与水流的高度y(单位:m)的变化规律如表:
x 0 1 2 3 4 …
y 3 3 …
(1)求该抛物线的解析式,并写出其顶点坐标.
(2)若喷水管喷出的水流恰好经过标杆的顶部点N.
①求标杆的最大高度;
②若点A到M,N两点的距离相等,求点N的坐标.
16.一个可移动的喷灌架喷射出的水流可以看成抛物线,如图是喷灌架给坡地草坪喷水的平面示意图,喷灌架置于坡地草坪底部点处,喷水头的竖直高度为,当喷射出的水流与点的水平距离为时,达到最高,此时其与水平地面的竖直高度为.在直线坡地草坪上,点与点的水平距离为,与水平地面的竖直高度为.
(1)求水流抛物线的解析式;
(2)求水流抛物线与直线坡地草坪之间的竖直距离的最大值;
(3)已知在点处有一棵竖直高度为的小树.若将喷灌架沿直线坡地草坪向右移动,设其向右水平移动(其中),使其喷射出的水流不被小树遮挡,直接写出的取值范围.
17.某农庄计划在亩空地上全部种植蔬菜和水果,种植蔬菜面积大于种植水果面积,且均为正整数,菜农小张和果农小李分别承包了种植蔬菜和水果的任务.小张种植每亩蔬菜的工资(元)与种植面积x(亩)之间的函数关系为;小李种植水果所得报酬(元)与种植面积(亩)之间的函数关系为.
(1)若小张种植蔬菜为亩,用含的代数式表示下列各量:
①小李种植水果的面积为 亩;
②小张种植蔬菜所得的总工资为 元;
③小李种植水果所得的报酬为 元;
(2)若农庄支付小张和小李的总费用为元,求小张与小李种植的面积各为多少亩?
(3)直接写出农庄支付给小张和小李的总费用的最大值.
18.“碧玉妆成一树高,万条垂下绿丝绦.”垂柳观赏价值高,能稳固堤岸,防水土流失,且成本低廉,深受各地绿化工程的青睐.如图1是某园林湖旁的一棵垂柳,这棵垂柳中某一枝的形状如图2所示的抛物线,它距离地面的高度为,到树干的水平距离为,y与x之间满足关系式.已知这枝垂柳的始端到地面的距离,末端B恰好接触地面,且到始端的水平距离.
(1)求该抛物线的函数解析式;
(2)小聪坐在爸爸的肩头,已知小聪的头顶距离地面,他从点O出发向点B处走去,请计算小聪走出多远时,头顶刚好碰到这枝垂柳?
19.滑板是一项富有激情与挑战的极限运动,U型池则是它绽放魅力的重要舞台,滑手在连续的U型池滑道间展开挑战,这不仅能考验滑手的综合能力,也为观众带来极具观赏性的视觉盛宴.滑手在U型池之间转换时,脱离滑道起跳后的飞行路线可近似看作是抛物线的一部分.如图,某次挑战中,滑手小红尝试从滑道①转换到滑道②,已知小红从起跳到着陆的过程中,起跳点到滑道底部所在直线的距离为,当离起跳点水平距离为时,小红到滑道底部所在直线的距离达到了最大值,现以滑道底部所在直线为x轴,垂直于滑道底部所在直线且经过起跳点的直线为y轴建立平面直角坐标系(滑道①、②底部在一条直线上).
(1)求该抛物线的函数表达式;
(2)若滑手的着陆点位于下一个U型池滑道的内部,则视为滑手成功完成转换,已知滑道②与滑道①高度相同,两者水平距离为,请通过计算说明小红能否转换成功?
20.【问题背景】某体育社团开展跳大绳游戏活动,两个摇绳的同学手,之间相距,绳子在摇动过程中呈抛物线形状且轨迹保持不变,当手摇绳子到最上方时,绳子的最高点距地面,握绳的手距离地面,当摇绳两端的手更高时,绳子整体也会相应更高.
【模型抽象】以人站立的地面为轴,绳子最高点垂直于地面的直线为轴建立平面直角坐标系.
【问题解决】
(1)求抛物线解析式;
(2)若参加跳绳的人身高均为,人与人之间的距离为,最多能有多少人同时参与跳绳(除摇绳人外)?
(3)在(2)的条件下,由于还有1名同学没能同时参与跳绳,若加入这名同学,在不改变摇绳两端的水平距离和绳长的情况下,只需将两端向上移即可,则的值应满足什么条件?
参考答案
题号 1 2 3 4 5 6
答案 D B D D C C
1.D
【分析】本题考查了二次函数的应用,正确理解题意是解题的关键.
由假山所在抛物线的函数解析式为,分别令,,求出对应的,即可判断选项A、B,由,即可判断选项C,根据与的图象可判断D选项.
【详解】解:由假山所在抛物线的函数解析式为,
当时,,故假山上的点B到水平地面的距离为;
当时,或(舍去),故水平方向上的长度为,可知选项A、B正确;
由题意得,解得:,可知选项C正确;
由题图可知,喷出的水柱呈现的抛物线与的对称轴相同,故选项D不正确,符合题意.
故选:D.
2.B
【分析】本题考查了二次函数实际应用中的喷泉问题,选图中第一象限的抛物线,由题意得抛物线顶点坐标为,过点,则设抛物线解析式为,然后代入求出抛物线解析式为,然后令即可求解,正确求出二次函数解析式解题的关键.
【详解】解:选图中第一象限的抛物线,
由题意得,抛物线顶点坐标为,过点,
设抛物线解析式为,
∴,解得:,
∴抛物线解析式为,
当时,,
∴点,
∴,
故选:.
3.D
【分析】本题主要考查二次函数的应用,解题的关键是掌握待定系数法求函数解析式.
根据题意可得,设抛物线的表达式为.将代入,求出a的值,即可解答.
【详解】解:∵,,,
∴,
设抛物线的表达式为.
将代入,得,
解得.
抛物线的表达式为.
令,则.
解得,(不合题意,舍去).
的长为.
故选:D.
4.D
【分析】本题考查了二次函数的应用,轴对称的性质,先求出点到轴的距离为,再结合轴对称的性质即可得解,熟练掌握以上知识点并灵活运用是解此题的关键.
【详解】解:∵点A到x轴的距离是,
∴令,则,
解得:或(不符合题意,舍去),
∴点到轴的距离为,
∵点A,B在抛物线上,,关于y轴对称,
∴,
故选:D.
5.C
【分析】本题主要考查了二次函数的应用,依据题意得,,故当时,有最大值为19.4,且当时,随的增大而增大,进而逐个判断可以得解.解题时要熟练掌握并能灵活运用二次函数的性质是关键.
【详解】解:由题意得,,
当时,有最大值为19.4,且当时,随的增大而增大,故②错误.
,且当时,,
蔬菜大棚内当天的温度可以是,故①正确.
令,
.
或.
的图象开口向下,
蔬菜大棚内当天的温度不低于的时长为:小时,故③正确.
综上,正确的有①③,共2个.
故选:C.
6.C
【分析】本题考查的是二次函数的实际应用,建立如图所示平面直角坐标系,作于点H,作于点Q,则,求解二次函数解析式为,FG所在直线解析式为,再进一步求解即可.
【详解】解:建立如图所示平面直角坐标系,作于点H,作于点Q,
则,
则各点坐标为:,,,,.
设抛物线的表达式为,
把点A坐标代入解析式,得,
解得,
∴.
∵,E点坐标为,
∴直线与x轴的交点为.
设所在直线解析式为,
把点,代入解析式,得.
令,
得,
解得,.
∴,
∴.
故答案为:C.
7.6.
【分析】本题考查了二次函数的实际应用,读懂题意将问题转化为是解题的关键.
根据题意得到,解方程即可得到结论.
【详解】解:,
当时,即,
解得,(不合题意,舍去),
该喷灌架喷出的水流可到达的最远距离米.
故答案为:6.
8.20
【分析】本题主要考查了二次函数图象的性质,求二次函数的关系式,
由题意可知,在调整喷头高度的过程中,水柱的形状不发生变化,当喷头高2.5米时,可设,将代入关系式得出;当喷头高度为时,可设,将代入关系式得,联立求出a,b的值,设喷头高为h时,水柱落点距O点4m,此时的关系式为,将代入求出答案即可.
【详解】解:由题意可知,在调整喷头高度的过程中,水柱的形状不发生变化,对称轴也不变,
∴二次项系数和一次项系数都不变,
当喷头高时,可设,
将代入关系式,得;
当喷头高度为时,可设,
将代入关系式得.
联立,得,
解得.
设喷头高为h时,水柱落点距O点,
此时的关系式为,
将代入关系式,得,
解得.
当喷头高时,水柱落点距O点.
故答案为:20.
9.不能
【分析】本题考查了二次函数的实际应用,掌握顶点式求二次函数解析式是解题的关键.
根据顶点,得出抛物线的表达式,令,求得的值,与比较即可求解.
【详解】解:根据题意可知抛物线的顶点为,水柱距地面的高度与水柱距喷水头的水平距离之间近似满足函数关系,
则抛物线的解析式为,
令,则,
故她的头顶不能碰到水柱.
故答案为:不能.
10.18
【分析】本题考查了二次函数的应用,二次函数的最值.熟练掌握二次函数的应用是解题的关键.
由题意得,由可知当时,s有最大值,然后根据题意作答即可.
【详解】解:,
,
∴当时,s有最大值,
∵飞机滑行到最大距离时停下,此时滑行的时间最长,
∴该飞机着陆后滑行最长时间为18秒.
故答案为:18.
11.已
【分析】本题主要考查了二次函数的实际应用,根据题意把代入到中求出I的值即可得到答案.
【详解】解:在中,当时,,
∴或(舍去),
∵,
∴当一充电器电功率为时,若发生触电,则此时通过人体的电流已超过人体能承受的安全电流.
故答案为:已.
12.4
【分析】本题考查二次函数的应用,解答本题的关键是明确题意,利用二次函数的性质解答.
先确定抛物线的对称轴方程,再根据抛物线的对称性可得出结论.
【详解】解:根据函数的图象可得抛物线的对称轴方程为:,
因为抛物线与x轴的一个交点横坐标为0,
所以,抛物线与x轴的另一个交点横坐标为,
所以,足球从踢出到落地所需的时间是,
故答案为:4
13.10
【分析】根据题意,得,代入解析式,确定,得到解析式,根据,得到,代入解析式得到(舍去),解答即可.
【详解】解:根据题意,得,代入解析式,
解得,
故一次函数的解析式,
当时,
,
故点,
把代入解析式,
解得(舍去),
故抛物线的解析式为,
当时,
,
解得,
故鱼线落在水面上的点到点A的水平距离.
故答案为:10.
【点睛】本题考查了待定系数法求解析式,点到坐标轴的距离意义,解方程,抛物线的性质,熟练掌握待定系数法,抛物线的性质是解题的关键.
14.(1),
(2)粘贴的胶带没有被水流喷到的风险,理由见解析
【分析】本题主要考查了二次函数的应用,求一次函数解析式,二次函数解析式,解题的关键是熟练掌握待定系数法.
(1)用待定系数法求出直线和轴右侧抛物线的表达式即可;
(2)设水流所在的抛物线到山坡的竖直距离为,得出,求出,从而得出答案即可.
【详解】(1)解:设山坡的函数表达式为.
过点,
,解得.
山坡的函数表达式为.
点.
右侧拋物线上点的对称点为.
设轴右侧抛物线的函数表达式为.
解得
轴右侧抛物线的函数表达式为.
(2)解:粘贴的胶带没有被水流喷到的风险.
理由如下:
设水流所在的抛物线到山坡的竖直距离为,
粘贴的胶带没有被水流喷到的风险.
15.(1)抛物线的解析式为,顶点坐标为
(2)①的最大值为;②点的坐标为
【分析】本题主要考查了二次函数的应用,解题时要熟练掌握并能灵活运用二次函数的性质是关键.
(1)依据题意,结合表格数据可得,抛物线的对称轴是直线,则该抛物线的顶点坐标为,故可设该抛物线的解析式为,再将点代入得,解得,进而可以判断得解;
(2)①依据题意,设直线的解析式为,又将,代入得,可得直线的解析式为,又设点的坐标为,则的坐标为,故,进而可以判断得解;
②依据题意,过点作于点,连接,又设,则点的坐标为,由得为中点,即,又,则,可得,然后将点的坐标代入抛物线的解析式得,求出后即可判断得解.
【详解】(1)解:由题意可得该抛物线的顶点坐标为,
设该抛物线的解析式为.
将点代入得,解得,
该抛物线的解析式为,顶点坐标为.
(2)解:①设直线的解析式为.
将,代入得解得
即直线的解析式为.
设,则,
,
当时,的最大值为.
②如图,过点作于点,连接,设,则.
由得为中点,即.
,
,即.
将点坐标代入抛物线解析式得,
整理方程得,
解得(舍去),,
故点的坐标为.
16.(1)
(2)
(3)
【分析】本题考查了二次函数的应用.
(1)由顶点设抛物线的解析式为,将点代入求解即可;
(2)先求得直线的解析式为,计算,利用二次函数的性质求解即可;
(3)由题意得平移后的抛物线可表示为,将点代入,计算即可求解.
【详解】(1)解:由题意可知,水流抛物线的顶点坐标为,
设水流形成的抛物线的解析式为,
将点代入得,,
解得,
水流抛物线的解析式为;
(2)解:由题意可知点坐标为,
设直线的解析式为,把代入得,
∴,
∴直线的解析式为,
∴,
∵,抛物线开口向下,
∴当时,取最大值,最大值为;
(3)解: 设喷灌架沿直线坡地草坪向右水平移动,则向上移动,
则平移后的抛物线可表示为,
将点代入得,,
解得或.
∴结合图象可得,的取值范围为.
17.(1),,;
(2)小张种植的面积为18亩,小李种植的面积为12亩;
(3)当时,农庄支付给小张和小李的总费用的最大,最大值为4348元.
【分析】本题考查二次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,求出相应的函数关系式.
(1)根据题意列式即可得到结论;
(2)根据小张和小李的总费用为元列方程,解方程即可得到结论;
(3)设农庄支付给小张和小李的总费用为w元,根据题意列函数解析式,根据二次函数的性质即可得到结论.
【详解】(1)解:①小李种植水果的面积为亩;
②小张种植蔬菜所得的总工资为元;
③小李种植水果所得的报酬为元;
故答案为:,,;
(2)解:根据题意得,,
解得,,
∵种植蔬菜面积大于种植水果面积,即,即,
∴不符合题意,舍去;
小张种植蔬菜面积为18亩,小李种植的水果面积为亩;
答:小张种植蔬菜面积为18亩,小李种植的水果面积为12亩;
(3)解:设农庄支付给小张和小李的总费用为w元,
根据题意得,,
∵,且均为整数,
∴当时,农庄支付给小张和小李的总费用的最大,最大值为元.
18.(1)
(2)小聪走出时,头顶刚好碰到这枝垂柳
【分析】本题考查二次函数的应用、一元二次方程的应用.要求明确题意,找出所求问题需要的条件,并进行正确的计算.
(1)根据题意可得,,然后利用待定系数法进行计算,即可解答;
(2)利用(1)的结论进行计算,即可解答.
【详解】(1)解:∵,
∴,,
∵点 A,B 均在抛物线 上,
,
解得 ,
∴该抛物线的函数解析式为
(2)解:令,得
整理,得
解得 (不合题意,舍去),
故小聪走出 时,头顶刚好碰到这枝垂柳.
19.(1)
(2)能
【分析】此题考查了二次函数的应用,正确求出函数解析式是解题的关键.
(1)根据题意直接写出抛物线的顶点坐标,再利用待定系数法求出函数解析式即可;
(2)当时,,解方程比较后即可得到答案.
【详解】(1)解:由题知起跳点的坐标为,抛物线的顶点坐标为.
设该抛物线的函数表达式为,
把代入得,
解得,
设该抛物线的函数表达式为.
(2)当时,,
解得,(舍去),
因为,
所以小文能成功转换.
20.(1)
(2)9人
(3)的值应超过
【分析】本题主要考查了二次函数的应用,正确求得抛物线解析式是解题关键.
(1)由已知确定顶点,,设抛物线解析式为,利用待定系数法求解即可;
(2)令,解方程即可求出x的值;
(3)设出平移后的解析式为,然后求出绳高不低于的水平距离大于等于,求出t的取值范围.
【详解】(1)解:由题意可设抛物线解析式为,且抛物线过点和点,
则有:
解得:
抛物线解析式为
(2)解:当时有,解得:
当时,则有一个同学在原点处,其两侧均有4个同学,与最远端同学相距,
此时可有9个同学同时参加跳绳.
(3)解:由(2)可知,再增加1个同学即有10个同学,此时没有人能站在原点处,
故原点两侧的同学距原点,所以最远端到原点距离为,
解得
即的值应超过即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
