4.5 一元二次方程根的判别式 课件(共22张PPT) 2025-2026学年数学青岛版九年级上册
文档属性
| 名称 | 4.5 一元二次方程根的判别式 课件(共22张PPT) 2025-2026学年数学青岛版九年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1009.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-15 08:25:41 | ||
图片预览








文档简介
(共22张PPT)
第4章 一元二次方程
九年级上册
4.5 一元二次方程根的判别式
课前小测
1.一元二次方程的一般形式是什么?有哪些解法?
如果方程有括号,先不要去括号,看能否用直接开平方法,不能用再看能否用因式分解法,再不能用就去掉括号整理成一般式,用公式法或配方法.
ax2+bx+c = 0 (a≠0).直接开平方法,配方法,公式法,因式分解法.
2.一元二次方程按照什么顺序来选择方法会更简便?
课前小测
3.解方程x2+21x-22=0(用你认为最简便的方法):
解:(x+22)(x-1)=0,
x+22=0或x-1=0,
x1=-22,x2=1.
情境引入
问题:
求出方程的解:2x2-6x-1=0(公式法).
我们在运用公式法求解一元二次方程 ax2+bx+c = 0 (a≠0)时,总是要求b2-4ac≥0.这是为什么?
情境引入
b2-4ac值的正负与方程的根有什么关系呢?
合作探究
探究:一元二次方程根的判别式
探究:一元二次方程根的判别式
问题1: 解方程x 2 + 2x + 5 = 0.
方法一:因为 22 - 4× 1× 5 < 0,所以无法用公式法解这个方程.
方法二:把方程ax2+bx+c = 0 (a≠0)配方,得(x+1)2 = -4 .
因为任何实数的平方都不可能是负数,所以任何实数都不会是原方程的根.
合作探究
探究:一元二次方程根的判别式
问题2:b2 - 4ac的值的正负与一元二次方程的根有什么关系呢?
我们知道,任何一个一元二次方程
ax2+bx+c = 0(a≠0)
配方法
∵a≠0,∴ 4a2>0 ,
合作探究
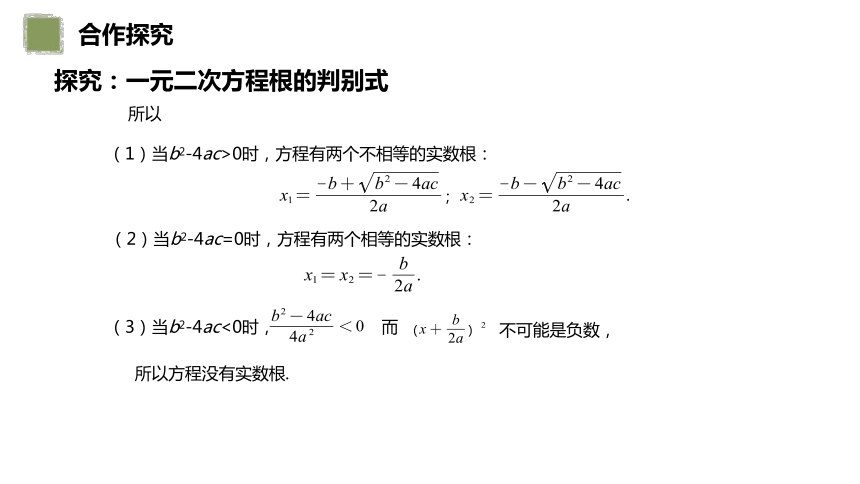
所以
(1)当b2-4ac>0时,方程有两个不相等的实数根:
(2)当b2-4ac=0时,方程有两个相等的实数根:
(3)当b2-4ac<0时,
而
不可能是负数,
所以方程没有实数根.
探究:一元二次方程根的判别式
合作探究
探究:一元二次方程根的判别式
一元二次方程 ax 2 + bx + c = 0 是否有实根,有实根时两个实根是否相等,均取决于一个含有该方程各项系数的代数式 b 2 - 4ac 的值的符号,因而把b 2 - 4ac叫做一元二次方程 ax 2 + bx + c = 0的根的判别式,通常用Δ表示,即Δ = b 2 - 4ac .
归纳小结
一元二次方程ax 2 + bx + c = 0
(1)当Δ > 0 时有两个不相等的实根;
一元二次方程ax 2+ bx + c = 0
(1)如果有两个不相等的实根,那么Δ > 0;
(2)如果有两个相等的实根,那么Δ = 0;
(3)如果没有实根,那么Δ < 0 .
上面结论的逆命题也是正确的. 你能说出它的逆命题吗?
(3)当Δ < 0 时没有实根.
(2)当Δ = 0 时有两个相等的实根;
典例分析
[例1]
不解方程,判断下列方程根的情况:
(1) 2x 2 + x - 4 = 0;
(2) 4y 2 + 9 = 12y;
(3) 5( t 2 + 1) - 6t = 0 .
解 :(1)这里 a = 2, b = 1, c = -4 .
∵Δ = b 2 - 4ac = 12 - 4× 2× -4) = 33 > 0,
∴ 方程有两个不相等的实根.
典例分析
不解方程,判断下列方程根的情况:
(1) 2x 2 + x - 4 = 0;
(2) 4y 2 + 9 = 12y;
(3) 5( t 2 + 1) - 6t = 0 .
(2)把原方程化为一般形式,得
4y 2 - 12y + 9 = 0 .
这里 a = 4, b = -12, c = 9 .
∵Δ = b 2 - 4ac =(-12)2 - 4× 4× 9 = 0,
∴ 原方程有两个相等的实根.
(3)把原方程化为一般形式,得
5t 2 - 6t + 5 = 0 .
这里 a = 5, b = -6, c = 5 .
∵Δ = b 2 - 4ac =(-6)2 - 4× 5× 5 = -64 < 0,
∴ 原方程没有实根.
[例1]
典例分析
[例2]
已知关于 x 的一元二次方程kx 2 - 3x + 1 = 0有两个不相等的实根.
(1)求 k 的取值范围;
(2)选择一个 k 的正整数值,并求出方程的根.
解 (1)∵ 关于 x 的一元二次方程kx 2 - 3x + 1 = 0有两个不相等的实根,
∴ Δ =(-3)2 - 4k > 0,即 9 - 4k > 0 .
解不等式,得k <
∵ kx 2 - 3x + 1 = 0 是一元二次方程,∴ k≠ 0 .
故 k 的取值范围是 k <
且 k≠ 0 .
典例分析
[例2]
已知关于 x 的一元二次方程kx 2 - 3x + 1 = 0有两个不相等的实根.
(1)求 k 的取值范围;
(2)选择一个 k 的正整数值,并求出方程的根.
(2)取不等式 k <
的一个正整数解 k = 2,则方程为2x 2 - 3x + 1 = 0 .
解这个方程,得x1 = 1 , x2=
.
例2中k是 一元二次方程kx 2 - 3x + 1 = 0的二次项系数,k的范围可以在数轴上表示出来,更加直观,范围内包含0,所以要强调不等于0.
挑战自我
有一边长为 3 的等腰三角形,它的另两边长分别是关于 x 的方程x 2 - 12x + k = 0的两根. 求 k 的值.
(2)若边长3为底边,则方程有两个相等的实数根. 由Δ =0,求得k=36.这时方程x 2 - 12x + 36 = 0的解为6,6.符合题意,故k=36.
(1)若边长3为等腰三角形的腰长,则3是方程x 2 - 12x + k = 0的一个根,代入求值得k=27.这时方程x 2 - 12x + k = 0的解为3和9,由于3,3,9不能构成三角形,所以舍去.
分析:分类讨论
随堂检测
一元二次方程根的判别式
课堂评价测试
同学们要认真答题哦!
随堂检测
1.一元二次方程2x2﹣3x+1=0的根的情况是( )
A.有两个相等的实数根 B.有两个不相等的实数根
C.只有一个实数根 D.没有实数根
2.下列一元二次方程没有实数根的是( )
A.x2+2x+1=0 B.x2+x+2=0 C.x2﹣1=0 D.x2﹣2x﹣1=0
3.若一元二次方程x2-ax+1=0的两实根相等,则 a 的值是( )
A. a=0 B. a=2或a=-2 C. a=2 D. a=2或a=0
A
B
B
随堂检测
4.当 k为何值时,关于 y 的方程(k - 1)y 2 - 2ky + k = 3,
(1)有两个不相等的实根;
(2)有两个相等的实根;
(3)没有实根.
解 :把方程化为一般形式,得(k - 1)y 2 - 2ky + k - 3=0.
这里,a= k – 1,b= - 2k,c= k – 3,
Δ = b 2 - 4ac=(-2k)2 – 4(k – 1)(k – 3)=16 k – 12.
∴当
时,方程有两个不相等的实数根;
(1)∵方程有两个不相等的实数根,
∴Δ =16 k – 12 > 0,解得
随堂检测
4.当 k为何值时,关于 y 的方程(k - 1)y 2 - 2ky + k = 3,
(1)有两个不相等的实根;
(2)有两个相等的实根;
(3)没有实根.
(2)∵方程有两个相等的实数根,
∴ Δ =16 k – 12 =0 解得
∴当
时,方程有两个不相等的实数根;
(3)∵方程没有实数根,
∴ Δ =16 k – 12<0 解得
∴当
时,方程没有实数根.
课堂小结
1. b 2 - 4ac叫做一元二次方程 ax 2 + bx+ c = 0 的根的判别式,
通常用Δ表示,即Δ = b 2 - 4ac .
2.一元二次方程ax 2 + bx + c = 0 (a≠0)
(1)当Δ > 0 时有两个不相等的实根;
(2)当Δ = 0 时有两个相等的实根;
(3)当Δ < 0 时没有实根.
反之,也成立.
作业布置
详见教材练习题
P145 T1-2
谢
谢
第4章 一元二次方程
九年级上册
4.5 一元二次方程根的判别式
课前小测
1.一元二次方程的一般形式是什么?有哪些解法?
如果方程有括号,先不要去括号,看能否用直接开平方法,不能用再看能否用因式分解法,再不能用就去掉括号整理成一般式,用公式法或配方法.
ax2+bx+c = 0 (a≠0).直接开平方法,配方法,公式法,因式分解法.
2.一元二次方程按照什么顺序来选择方法会更简便?
课前小测
3.解方程x2+21x-22=0(用你认为最简便的方法):
解:(x+22)(x-1)=0,
x+22=0或x-1=0,
x1=-22,x2=1.
情境引入
问题:
求出方程的解:2x2-6x-1=0(公式法).
我们在运用公式法求解一元二次方程 ax2+bx+c = 0 (a≠0)时,总是要求b2-4ac≥0.这是为什么?
情境引入
b2-4ac值的正负与方程的根有什么关系呢?
合作探究
探究:一元二次方程根的判别式
探究:一元二次方程根的判别式
问题1: 解方程x 2 + 2x + 5 = 0.
方法一:因为 22 - 4× 1× 5 < 0,所以无法用公式法解这个方程.
方法二:把方程ax2+bx+c = 0 (a≠0)配方,得(x+1)2 = -4 .
因为任何实数的平方都不可能是负数,所以任何实数都不会是原方程的根.
合作探究
探究:一元二次方程根的判别式
问题2:b2 - 4ac的值的正负与一元二次方程的根有什么关系呢?
我们知道,任何一个一元二次方程
ax2+bx+c = 0(a≠0)
配方法
∵a≠0,∴ 4a2>0 ,
合作探究
所以
(1)当b2-4ac>0时,方程有两个不相等的实数根:
(2)当b2-4ac=0时,方程有两个相等的实数根:
(3)当b2-4ac<0时,
而
不可能是负数,
所以方程没有实数根.
探究:一元二次方程根的判别式
合作探究
探究:一元二次方程根的判别式
一元二次方程 ax 2 + bx + c = 0 是否有实根,有实根时两个实根是否相等,均取决于一个含有该方程各项系数的代数式 b 2 - 4ac 的值的符号,因而把b 2 - 4ac叫做一元二次方程 ax 2 + bx + c = 0的根的判别式,通常用Δ表示,即Δ = b 2 - 4ac .
归纳小结
一元二次方程ax 2 + bx + c = 0
(1)当Δ > 0 时有两个不相等的实根;
一元二次方程ax 2+ bx + c = 0
(1)如果有两个不相等的实根,那么Δ > 0;
(2)如果有两个相等的实根,那么Δ = 0;
(3)如果没有实根,那么Δ < 0 .
上面结论的逆命题也是正确的. 你能说出它的逆命题吗?
(3)当Δ < 0 时没有实根.
(2)当Δ = 0 时有两个相等的实根;
典例分析
[例1]
不解方程,判断下列方程根的情况:
(1) 2x 2 + x - 4 = 0;
(2) 4y 2 + 9 = 12y;
(3) 5( t 2 + 1) - 6t = 0 .
解 :(1)这里 a = 2, b = 1, c = -4 .
∵Δ = b 2 - 4ac = 12 - 4× 2× -4) = 33 > 0,
∴ 方程有两个不相等的实根.
典例分析
不解方程,判断下列方程根的情况:
(1) 2x 2 + x - 4 = 0;
(2) 4y 2 + 9 = 12y;
(3) 5( t 2 + 1) - 6t = 0 .
(2)把原方程化为一般形式,得
4y 2 - 12y + 9 = 0 .
这里 a = 4, b = -12, c = 9 .
∵Δ = b 2 - 4ac =(-12)2 - 4× 4× 9 = 0,
∴ 原方程有两个相等的实根.
(3)把原方程化为一般形式,得
5t 2 - 6t + 5 = 0 .
这里 a = 5, b = -6, c = 5 .
∵Δ = b 2 - 4ac =(-6)2 - 4× 5× 5 = -64 < 0,
∴ 原方程没有实根.
[例1]
典例分析
[例2]
已知关于 x 的一元二次方程kx 2 - 3x + 1 = 0有两个不相等的实根.
(1)求 k 的取值范围;
(2)选择一个 k 的正整数值,并求出方程的根.
解 (1)∵ 关于 x 的一元二次方程kx 2 - 3x + 1 = 0有两个不相等的实根,
∴ Δ =(-3)2 - 4k > 0,即 9 - 4k > 0 .
解不等式,得k <
∵ kx 2 - 3x + 1 = 0 是一元二次方程,∴ k≠ 0 .
故 k 的取值范围是 k <
且 k≠ 0 .
典例分析
[例2]
已知关于 x 的一元二次方程kx 2 - 3x + 1 = 0有两个不相等的实根.
(1)求 k 的取值范围;
(2)选择一个 k 的正整数值,并求出方程的根.
(2)取不等式 k <
的一个正整数解 k = 2,则方程为2x 2 - 3x + 1 = 0 .
解这个方程,得x1 = 1 , x2=
.
例2中k是 一元二次方程kx 2 - 3x + 1 = 0的二次项系数,k的范围可以在数轴上表示出来,更加直观,范围内包含0,所以要强调不等于0.
挑战自我
有一边长为 3 的等腰三角形,它的另两边长分别是关于 x 的方程x 2 - 12x + k = 0的两根. 求 k 的值.
(2)若边长3为底边,则方程有两个相等的实数根. 由Δ =0,求得k=36.这时方程x 2 - 12x + 36 = 0的解为6,6.符合题意,故k=36.
(1)若边长3为等腰三角形的腰长,则3是方程x 2 - 12x + k = 0的一个根,代入求值得k=27.这时方程x 2 - 12x + k = 0的解为3和9,由于3,3,9不能构成三角形,所以舍去.
分析:分类讨论
随堂检测
一元二次方程根的判别式
课堂评价测试
同学们要认真答题哦!
随堂检测
1.一元二次方程2x2﹣3x+1=0的根的情况是( )
A.有两个相等的实数根 B.有两个不相等的实数根
C.只有一个实数根 D.没有实数根
2.下列一元二次方程没有实数根的是( )
A.x2+2x+1=0 B.x2+x+2=0 C.x2﹣1=0 D.x2﹣2x﹣1=0
3.若一元二次方程x2-ax+1=0的两实根相等,则 a 的值是( )
A. a=0 B. a=2或a=-2 C. a=2 D. a=2或a=0
A
B
B
随堂检测
4.当 k为何值时,关于 y 的方程(k - 1)y 2 - 2ky + k = 3,
(1)有两个不相等的实根;
(2)有两个相等的实根;
(3)没有实根.
解 :把方程化为一般形式,得(k - 1)y 2 - 2ky + k - 3=0.
这里,a= k – 1,b= - 2k,c= k – 3,
Δ = b 2 - 4ac=(-2k)2 – 4(k – 1)(k – 3)=16 k – 12.
∴当
时,方程有两个不相等的实数根;
(1)∵方程有两个不相等的实数根,
∴Δ =16 k – 12 > 0,解得
随堂检测
4.当 k为何值时,关于 y 的方程(k - 1)y 2 - 2ky + k = 3,
(1)有两个不相等的实根;
(2)有两个相等的实根;
(3)没有实根.
(2)∵方程有两个相等的实数根,
∴ Δ =16 k – 12 =0 解得
∴当
时,方程有两个不相等的实数根;
(3)∵方程没有实数根,
∴ Δ =16 k – 12<0 解得
∴当
时,方程没有实数根.
课堂小结
1. b 2 - 4ac叫做一元二次方程 ax 2 + bx+ c = 0 的根的判别式,
通常用Δ表示,即Δ = b 2 - 4ac .
2.一元二次方程ax 2 + bx + c = 0 (a≠0)
(1)当Δ > 0 时有两个不相等的实根;
(2)当Δ = 0 时有两个相等的实根;
(3)当Δ < 0 时没有实根.
反之,也成立.
作业布置
详见教材练习题
P145 T1-2
谢
谢
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
