4.6 一元二次方程根与系数的关系 课件(共20张PPT)2025-2026学年数学青岛版九年级上册
文档属性
| 名称 | 4.6 一元二次方程根与系数的关系 课件(共20张PPT)2025-2026学年数学青岛版九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 21:52:10 | ||
图片预览








文档简介
(共20张PPT)
第4章 一元二次方程
九年级上册
*4.6 一元二次方程根与系数的关系
课前小测
1.一元二次方程的一般形式是什么?
2.一元二次方程的求根公式是什么?
ax2+bx+c=0
3.一元二次方程的根的情况怎样确定?
一元二次方程ax 2 + bx + c = 0
(1)当Δ > 0 时有两个不相等的实根;
(2)当Δ = 0 时有两个相等的实根;
(3)当Δ < 0 时没有实根.
情境引入
问题:你能迅速求出下列方程的根吗?不用写步骤.
① x 2 + 3x + 2 = 0.
② x 2 - 5x + 6 = 0.
③ 3x 2 + x - 2 = 0.
④ 2x 2 - 4x + 1 = 0 .
x1= - 1 , x2= - 2
x1= 2, x2= 3
x1= - 1, x2=
情境引入
你知道一元二次方程的根与系数有什么关系吗
合作探究
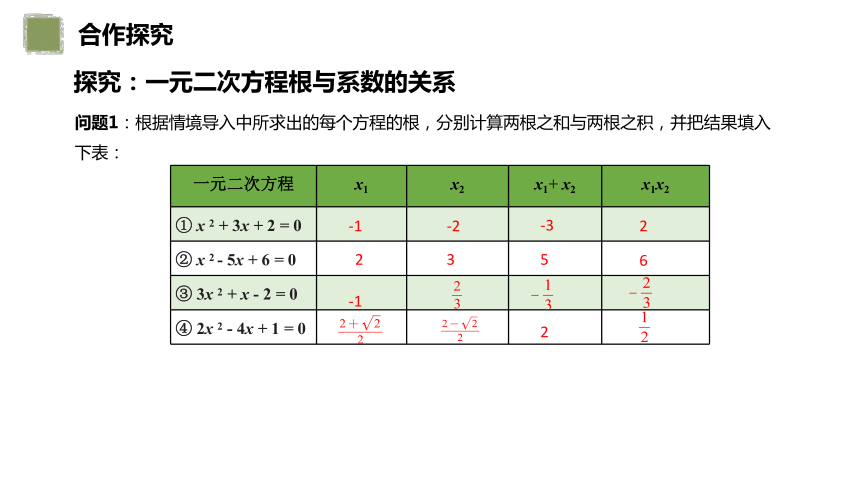
探究:一元二次方程根与系数的关系
问题1:根据情境导入中所求出的每个方程的根,分别计算两根之和与两根之积,并把结果填入下表:
一元二次方程 x1 x2 x1+ x2 x1x2
① x 2 + 3x + 2 = 0
② x 2 - 5x + 6 = 0
③ 3x 2 + x - 2 = 0
④ 2x 2 - 4x + 1 = 0
-1
-2
-3
2
2
3
5
6
-1
2
合作探究
探究:一元二次方程根与系数的关系
问题2:观察上表,你发现在上面的四个方程中,两根之和与两根之积的值分别与相应的方程的系数之间有怎样的关系?
方程③④的二次项系数不是 1 时,化成二次项系数是 1的情况后,可把上面的发现进一步推广.
发现方程①②的二次项系数为 1 时,一元二次方程的两根之和等于一次项系数的相反数,两根之积等于常数项.
合作探究
探究:一元二次方程根与系数的关系
问题3:由此你猜想一元二次方程 ax 2 + bx + c = 0 的两个根 x 1, x 2 与方程的系数 a, b, c 之间有什么关系?能证明你的猜想是正确的吗?与同学交流.
当 b 2 - 4ac ≥ 0 时,一元二次方程 ax 2 + bx + c = 0的两个实数根是
于是,两个根的和为
合作探究
探究:一元二次方程根与系数的关系
两个根的积为
归纳小结:一元二次方程的根与系数有以下的关系:
.
如果一元二次方程 ax 2 + bx + c = 0 的两个根是 x 1, x 2,那么
x1 x2 =
x 1 + x 2 =
典例分析
[例1]
关于 x 的方程 3x 2 + mx - 4 = 0有一个根是 2,求另一个根及 m 的值.
解 设方程的另一个根为x1 ,则由一元二次方程根与系数的关系,得
典例分析
[例1]
关于 x 的方程 3x 2 + mx - 4 = 0有一个根是 2,求另一个根及 m 的值.
对于例 1,你还有其他的解法吗?
分析:可以把已知的根2代入原方程先求出m,再把m代入原方程,解方程求根.
典例分析
[例2]
设 x 1, x 2 是方程 2x 2 + 5x + 1 = 0 的两个根,求下列各式的值:
(1)( x 1 + 1)( x 2 + 1); (2)
.
解: 由一元二次方程根与系数的关系,得
拓展
能利用例2求出 x12 + x22,( x1 - x2 )2 的值吗?
归纳小结
如果要求与一元二次方程的两个根有关系的代数式的值,可以先把要求的代数式转化
成含有 x 1 + x 2 和 x1 x2 的形式,再利用x 1 + x 2 =
和 x1 x2 =
求出值,代入计算
即可
随堂检测
一元二次方程根与系数的关系 课堂评价测试
同学们要认真答题哦!
随堂检测
3
1
0
16
D
随堂检测
4.已知x1,x2是关于x的一元二次方程x2-2(m+1)x+m2+5=0的两实数根.
(1)若(x1-1)(x2-1)=28,求 m 的值;
(2)已知等腰 △ABC 的一边长为7,若 x1,x2 恰好是△ABC 另外两边的边长,求这个三角形的周长.
解:(1)∵x1,x2是关于x的一元二次方程x2-2(m+1)x+m2+5=0的两个实数根,
∴x1+x2=2(m+1),x1·x2=m2+5,
∴(x1-1)(x2-1)=x1·x2-(x1+x2)+1.
即m2+5-2(m+1)+1=28,
解得:m=-4或m=6.
∵m=-4时原方程无解,
∴m=6;
随堂检测
(2)①当7为底边时,
此时方程x2-2(m+1)x+m2+5=0有两个相等的实数根,
∴Δ=4(m+1)2-4(m2+5)=0,
解得:m=2.
∴方程变为x2-6x+9=0,解得x1=x2=3.∵3+3<7,∴不能构成三角形;
②当7为腰时,
设x1=7,代入方程得:49-14(m+1)+m2+5=0,解得:m=10或4.
当m=10时,方程变为x2-22x+105=0,解得:x=7或15.
∵7+7<15,不能组成三角形;
当m=4时方程变为x2-10x+21=0,解得:x=3或7,
此时三角形的周长为7+7+3=17.
课堂小结
1.一元二次方程的根与系数有以下的关系:
如果一元二次方程 ax 2 + bx + c = 0 的两个根是 x 1, x 2,
那么x 1 + x 2 =
, x1 x2 =
.
2.常见的形式:
3.利用两根的和与积求一元二次方程ax 2 + bx + c = 0的字母系数的值,要在a≠0和Δ≥0的前提下.
作业布置
详见教材练习题
P149 T1-4
谢
谢
第4章 一元二次方程
九年级上册
*4.6 一元二次方程根与系数的关系
课前小测
1.一元二次方程的一般形式是什么?
2.一元二次方程的求根公式是什么?
ax2+bx+c=0
3.一元二次方程的根的情况怎样确定?
一元二次方程ax 2 + bx + c = 0
(1)当Δ > 0 时有两个不相等的实根;
(2)当Δ = 0 时有两个相等的实根;
(3)当Δ < 0 时没有实根.
情境引入
问题:你能迅速求出下列方程的根吗?不用写步骤.
① x 2 + 3x + 2 = 0.
② x 2 - 5x + 6 = 0.
③ 3x 2 + x - 2 = 0.
④ 2x 2 - 4x + 1 = 0 .
x1= - 1 , x2= - 2
x1= 2, x2= 3
x1= - 1, x2=
情境引入
你知道一元二次方程的根与系数有什么关系吗
合作探究
探究:一元二次方程根与系数的关系
问题1:根据情境导入中所求出的每个方程的根,分别计算两根之和与两根之积,并把结果填入下表:
一元二次方程 x1 x2 x1+ x2 x1x2
① x 2 + 3x + 2 = 0
② x 2 - 5x + 6 = 0
③ 3x 2 + x - 2 = 0
④ 2x 2 - 4x + 1 = 0
-1
-2
-3
2
2
3
5
6
-1
2
合作探究
探究:一元二次方程根与系数的关系
问题2:观察上表,你发现在上面的四个方程中,两根之和与两根之积的值分别与相应的方程的系数之间有怎样的关系?
方程③④的二次项系数不是 1 时,化成二次项系数是 1的情况后,可把上面的发现进一步推广.
发现方程①②的二次项系数为 1 时,一元二次方程的两根之和等于一次项系数的相反数,两根之积等于常数项.
合作探究
探究:一元二次方程根与系数的关系
问题3:由此你猜想一元二次方程 ax 2 + bx + c = 0 的两个根 x 1, x 2 与方程的系数 a, b, c 之间有什么关系?能证明你的猜想是正确的吗?与同学交流.
当 b 2 - 4ac ≥ 0 时,一元二次方程 ax 2 + bx + c = 0的两个实数根是
于是,两个根的和为
合作探究
探究:一元二次方程根与系数的关系
两个根的积为
归纳小结:一元二次方程的根与系数有以下的关系:
.
如果一元二次方程 ax 2 + bx + c = 0 的两个根是 x 1, x 2,那么
x1 x2 =
x 1 + x 2 =
典例分析
[例1]
关于 x 的方程 3x 2 + mx - 4 = 0有一个根是 2,求另一个根及 m 的值.
解 设方程的另一个根为x1 ,则由一元二次方程根与系数的关系,得
典例分析
[例1]
关于 x 的方程 3x 2 + mx - 4 = 0有一个根是 2,求另一个根及 m 的值.
对于例 1,你还有其他的解法吗?
分析:可以把已知的根2代入原方程先求出m,再把m代入原方程,解方程求根.
典例分析
[例2]
设 x 1, x 2 是方程 2x 2 + 5x + 1 = 0 的两个根,求下列各式的值:
(1)( x 1 + 1)( x 2 + 1); (2)
.
解: 由一元二次方程根与系数的关系,得
拓展
能利用例2求出 x12 + x22,( x1 - x2 )2 的值吗?
归纳小结
如果要求与一元二次方程的两个根有关系的代数式的值,可以先把要求的代数式转化
成含有 x 1 + x 2 和 x1 x2 的形式,再利用x 1 + x 2 =
和 x1 x2 =
求出值,代入计算
即可
随堂检测
一元二次方程根与系数的关系 课堂评价测试
同学们要认真答题哦!
随堂检测
3
1
0
16
D
随堂检测
4.已知x1,x2是关于x的一元二次方程x2-2(m+1)x+m2+5=0的两实数根.
(1)若(x1-1)(x2-1)=28,求 m 的值;
(2)已知等腰 △ABC 的一边长为7,若 x1,x2 恰好是△ABC 另外两边的边长,求这个三角形的周长.
解:(1)∵x1,x2是关于x的一元二次方程x2-2(m+1)x+m2+5=0的两个实数根,
∴x1+x2=2(m+1),x1·x2=m2+5,
∴(x1-1)(x2-1)=x1·x2-(x1+x2)+1.
即m2+5-2(m+1)+1=28,
解得:m=-4或m=6.
∵m=-4时原方程无解,
∴m=6;
随堂检测
(2)①当7为底边时,
此时方程x2-2(m+1)x+m2+5=0有两个相等的实数根,
∴Δ=4(m+1)2-4(m2+5)=0,
解得:m=2.
∴方程变为x2-6x+9=0,解得x1=x2=3.∵3+3<7,∴不能构成三角形;
②当7为腰时,
设x1=7,代入方程得:49-14(m+1)+m2+5=0,解得:m=10或4.
当m=10时,方程变为x2-22x+105=0,解得:x=7或15.
∵7+7<15,不能组成三角形;
当m=4时方程变为x2-10x+21=0,解得:x=3或7,
此时三角形的周长为7+7+3=17.
课堂小结
1.一元二次方程的根与系数有以下的关系:
如果一元二次方程 ax 2 + bx + c = 0 的两个根是 x 1, x 2,
那么x 1 + x 2 =
, x1 x2 =
.
2.常见的形式:
3.利用两根的和与积求一元二次方程ax 2 + bx + c = 0的字母系数的值,要在a≠0和Δ≥0的前提下.
作业布置
详见教材练习题
P149 T1-4
谢
谢
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
