4.7 一元二次方程的应用 课件(共43张PPT、2课时) 2025-2026学年数学青岛版九年级上册
文档属性
| 名称 | 4.7 一元二次方程的应用 课件(共43张PPT、2课时) 2025-2026学年数学青岛版九年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-15 08:26:39 | ||
图片预览











文档简介
(共43张PPT)
第4章 一元二次方程
九年级上册
4.7 一元二次方程的应用
第1课时 面积问题与利润问题
课前小测
1.一元二次方程的解法有___________、_________________、______________、________________.
2.一元二次方程ax2+bx+c=0,当b2-4ac____0时,有两个不相等的实数根;当b2-4ac____0时,有两个相等的实数根;当b2-4ac____0时,没有实数根.
3.如果一元二次方程ax2+bx+c=0的两根为x1,x2,则x1 +x2 =__________, x1x2=_________.
直接开平方法
因式分解法
公式法
配方法
>
=
<
情境引入
与我们学过的一元一次方程、二元一次方程组和分式方程一样,一元二次方程也是刻画现实生活与生产中数量关系的有效模型.本节课学习一元二次方程的应用.
合作探究
探究一:面积问题
一元二次方程应用题与一元一次方程应用题的步骤类似:
1审;2设;3列;4解;5答.
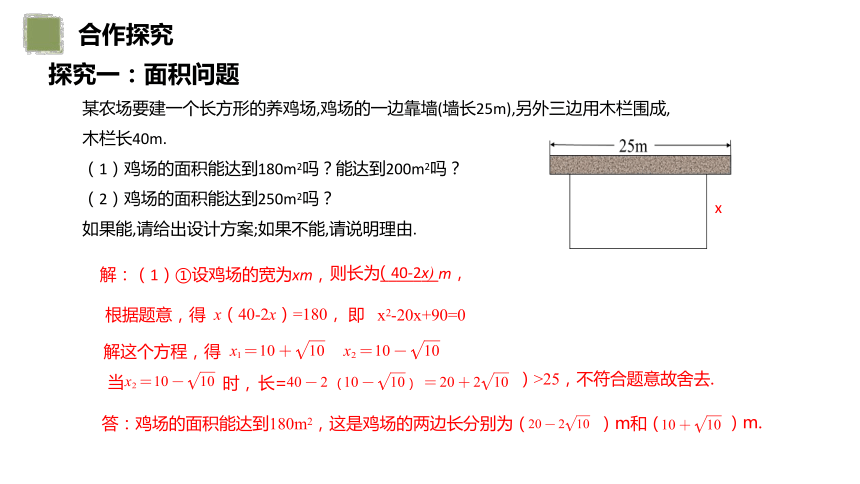
某农场要建一个长方形的养鸡场,鸡场的一边靠墙(墙长25m),另外三边用
木栏围成,木栏长40m.
(1)鸡场的面积能达到180m2吗?能达到200m2吗?
(2)鸡场的面积能达到250m2吗?
如果能,请给出设计方案;如果不能,请说明理由.
分析:可设鸡场的一边为x,另一边为_______
然后根据长方形的面积等于__________,
用含未知数的代数式表示出鸡场的面积.
x
典例分析
[例1]
要想知道鸡场的面积能否达到180平方米,只需要让鸡场的面积先等于180,然后看得出的方程有没有解,如果有,就证明可以达到180平方米,如果方程无解,说明不能达到.其他问题的方法一样
40-2x
长乘宽
40-2x
合作探究
探究一:面积问题
某农场要建一个长方形的养鸡场,鸡场的一边靠墙(墙长25m),另外三边用木栏围成,
木栏长40m.
(1)鸡场的面积能达到180m2吗?能达到200m2吗?
(2)鸡场的面积能达到250m2吗?
如果能,请给出设计方案;如果不能,请说明理由.
x
解:(1)①设鸡场的宽为xm,
解这个方程,得
x(40-2x)=180,
则长为_______m,
根据题意,得
(40-2x)
当
时,
即 x2-20x+90=0
)>25,不符合题意故舍去.
长=
答:鸡场的面积能达到180m2,这是鸡场的两边长分别为(
)m和(
)m.
合作探究
探究一:面积问题
②同理当面积为200m2时,根据题意,得
x(40-2x)=200
即 x2-20x+100=0
解这个方程,得 x1=x2=10.
当x=10时,长=20,符合题意.
(
答:鸡场的面积能达到180m2,这时鸡场的两边长分别为(
)m和
)m;当一边为10m时,另一边为20m时,鸡场的面积能达到200m2.
合作探究
探究一:面积问题
(2)同理当面积为250m2时,得
x(40-2x)=250.
整理,得 x2-20x+125=0.
∵△=(-20)2-4×125=-100<0
∴原方程无解,
∴鸡场的面积不能达到250m2.
试一试
MN是一面长10m的墙,用长24m的篱笆,围成一个一面是墙,中间隔着一道篱笆的矩形花圃ABCD,已知花圃的设计面积为45m2,花圃的宽应当是多少?
解:(1)设花圃的宽AB为xm,那么它的长BC是 _ _ _ _
当x1=3时,长=24-9=15>10,故舍去.
所以,花圃的宽是5m.
(24-3x)m
根据题意得
x(24-3x)=45.
即 x2-8x+15=0.
解这个方程,得 x1=3 , x2=5 .
归纳小结
靠墙建矩形,问怎样设计能使面积等于已知数的题型,跟下册的二次函数关系非常密切,是重点易考题型.要注意靠墙的一边的长度不能超过墙长,要注意检验.
合作探究
探究二:利润问题
每件的利润=每件的售价-进价;
销售量.
总利润=
每件的利润
典例分析
[例1]
某商场将每件进价为80元的某种商品原来按每件100元出售,每天可售出100件,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经过市场调查,发现这种商品售价每降低1元,商场销售量平均每天可增加10件,若商场经营该商品一天要获利润2160元,且让顾客得到实惠,则每件商品应降价多少元?
分析:设每件商品应降价x元,现在的总利润=现在每件的利润
现在的销售量.
利用现在每件的利润=现在每件的售价-进价,
表示出现在每件的利润为___________元
(100-x-80)
降低1元增加10件,可知降低x元增加______件,
10x
所以现在的销售量为___________
(100+10x),
则根据现在的总利润=现在每件的利润
现在的销售量列出方程解答即可.
典例分析
[例2]
某商场将每件进价为80元的某种商品原来按每件100元出售,每天可售出100件,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经过市场调查,发现这种商品售价每降低1元,商场销售量平均每天可增加10件,若商场经营该商品一天要获利润2160元,且让顾客得到实惠,则每件商品应降价多少元?
解 :设每件商品降价x元.根据题意,得
(100-x-80)×(100+10x)=2160,
解得:x1=2,x2=8,
由原题为了减少库存,应降价多点,故把x=2舍去,所以x=8,
答:每件商品应降价8元.
归纳小结
销售利润问题,是一元二次方程应用题的难点问题,也是重点.要正确理解销售量与利润的关系,能准确用未知数表示销售量和单件的利润是关键.
试一试
某商店准备进一批季节性小家电,单价40元,经市场预测,销售定价为52元时,可售出180个,定价每增加1元,销售量减少10个.因受库存影响,每批次进货个数不得超过180个.商店若准备获利2000元,则应进货多少个?定价多少元?
解:设每个小家电的定价是x元,
根据题意,得
答:商店若准备获利2000元,则应进货100个,定价60元.
∴ x=60元,则180﹣10·8=100(个).
∴x≥52.
∵180﹣10(x-52)≤180,
解得x1=50,x2=60.
随堂检测
面积问题与利润问题 课堂评价测试
同学们要认真答题哦!
随堂检测
1.如图,在宽为20 m、长为36 m的矩形草地上修建两条同样宽且互相垂直的道路,剩余草地的面积是540 m2.则道路的宽为 .
2.将一根长为 64 cm 的铁丝剪成两段,再将每段分别围成正方形(如图),如果两个正方形的面积的和等于 160 cm2,两个正方形的边长为______和_____.
4cm
12cm
随堂检测
3.某品牌服装专营店平均每天可销售该品牌服装20件,每件可盈利44元.若每件降价1元,则每天可多售出5件.若要平均每天盈利1600元且使顾客得到最大的实惠,则应降价________元.
36
随堂检测
4.如图,一个农户要建一个矩形猪舍ABCD,猪舍的一边AD利用长为12米的住房墙,另外三边用25米长的建筑材料围成.为了方便进出,在CD边留一个1米宽的小门.
(1)若矩形猪舍的面积为80平方米,求与墙平行的一边BC的长;
(2)若与墙平行的一边BC的长度不小于与墙垂直的一边AB的长度,问BC边至少应为多少米?
分析:(1)设BC的长为xm,则AB的长为
m.根据矩形的面积公式建立方程求出其解即可;
(2)根据“与墙平行的一边BC的长度不小于与墙垂直的一边AB的长度”列出关于x的不等式组,通过解不等式组求得x的取值范围即可.
X
随堂检测
解:(1)设BC的长为xm,依题意得:
解得x1=10,x2=16(舍去).
答:矩形猪舍的面积为80平方米,求与墙平行的一边BC的长为10m;
(2)依题意得:
解得
所以x最小为
.
答:若与墙平行的一边BC的长度不小于与墙垂直的一边AB的长度,问BC边至少应
米.
随堂检测
5.某商店如果将进价为8元的商品按每件10元售出,每天可销售200件,现采用提高售价,减小进货量的方法增加利润。已知这种商品每涨价0.5元,其每天销售量就减少10件,问应将售价定为多少元时,才能使每天所获利润为640元?
解:设将售价定为x元,根据题意,得
即
.
解这个方程得 x1=12,x2=16.
∵要提高售价,减少进货量,
∴x只取16 .
答: 售价为16元时,每天所获的利润为640元.
课堂小结
一元二次方程应用题与一元一次方程应用题的步骤类似:
1审;2设;3列;4解;5答.
一.面积问题
二.销售利润问题
注意:列方程解应用题,要验根,根的取值要满足题意.
作业布置
详见教材练习题
P152 T1-2
第4章 一元二次方程
九年级上册
4.7 一元二次方程的应用
第2课时 增长率问题与其他应用
课前小测
某品牌服装去年每套300元.(只列式子不计算结果)
(1)如果今年提价10%,今年的售价是多少元?
据说明年还要提价10%,那么明年的售价是多少元?
(2)如果今年降价10%,则今年的售价是多少元?
据说明年还要降价10%,那么明年的售价是多少元?
情境引入
某品牌服装去年每套300元
(1)今年增长率是x,则今年的售价是多少元?
(2)据说明年的增长率还是x ,那么明年的售价是多少元?
问题1:(只列式子不计算结果)
情境引入
某品牌服装去年每套300元,
(1)今年的降价率是x,则今年的售价是多少元?
(2)据说明年的降价率还是x,那么明年的售价是多少元?
问题2:(只列式子不计算结果)
合作探究
探究一:增长率问题
某养殖场 2010 年的产值为 500 万元, 2012 年的产值为 605 万元. 求
2010 2012 年该养殖场产值的年平均增长率.
你会解决这个问题吗?
可列方程______________________________.
而这2012年的年产值正好是605万元.
2012年的年产值为______________________________.
2011年的年产值为_____________________________,
分析:如果设该场2010-2012年产值的平均增长率为x,那么
500(1+x)
500(1+x)2
合作探究
探究一:增长率问题
解 设该场 2010 2012 年产值的年平均增长率为 x,根据题意,得
根据题意, 605 万元 > 500 万元,故年增长率 x > 0,而 x2= -2.1 < 0,因此
x2 = -2.1 不符合题意,应当舍去, x1= 0.1 符合题意.
所以,该养殖场 2010 2012 年产值的年平均增长率为 0.1,即 10% .
解这个方程,得
x1 = 0.1, x2 = -2.1 .
典例分析
[例1]
某种药品经过两次降价后,每盒售价为原售价的 64%,求该药品平均每次的降价率.
可列方程______________________________
而两次降价后的价格是
第二次降价后该药品每盒的售价为_________________,
那么第一次降价后该药品每盒的售价为______________,
分析:如果把降价之前的价格看作单位“1”.设该药品平均每次的降价率为x,
(1-x)
(1-x)2
请你把步骤写完整.
典例分析
[例1]
某种药品经过两次降价后,每盒售价为原售价的 64%,求该药品平均每次的降价率.
解 设该药品平均每次的降价率为 x,
根据题意,得
(1 - x)2 = 64% .
所以,该药品平均每次的降价率为 0.2,即 20% .
根据题意,降价率应满足 0 < x < 1,因而 x2 = 1.8 不符合题意,应当舍去,
而 x = 0.2 符合题意.
解这个方程,得
x1 = 0.2, x2 = 1.8 .
归纳小结
如果 a 表示原来的基数,m 表示平均增长率,n 表示增长的次数,A 为增长后的目标数,那么 a(1±m)2=A .本节课只研究n = 2 的情况.当m前面是“ - ”时表示负增长,即降低.
合作探究
探究二:数字问题
典例分析
[例2] 有一个两位数等于其各位数字之积的3倍,其十位数字比个位数字小2,求这个两位数.
分析:设个位数字为 x ,
则十位数字为 ___________,
这个两位数为______________ ;
(x-2)
10(x-2)+x
然后根据“这个两位数等于其各位数字之积的3倍”可列出关于x的方程.
[例2]
典例分析
当x=4时,x-2=2,
∴这个两位数是24.
解:设个位数字为x,则十位数字为(x-2),这个两位数是[10(x-2)+x].
根据题意,得10(x-2)+x=3x(x-2),
整理,得3x2-17x+20=0,5分
解得x1=4,x2=
(不合题意,舍去).
归纳小结
两位数= 十位数字乘以10 + 个位数字;
三位数= 百位数字乘以100 + 十位数字乘以10 + 个位数字;…….
要注意检验.
随堂检测
增长率问题与其他应用 课堂评价测试
同学们要认真答题哦!
随堂检测
B
B
随堂检测
3.某商品经过连续两次降价,销售单价由原来的125元降到80元,则平均每次降价的百分率为______.
4.在一次同学聚会时,大家一见面就相互握手.有人统计了一下,大家一共握了45次手,参加这次聚会的同学共有多少人?若参加聚会有x名同学,可列方程______________________.
20%
随堂检测
5. 电动自动车已成为市民日常出行的首选工具.据某市某品牌电动自行车经销商1至3月份统计,该品牌电动自行车1月份销售150辆,3月份销售216辆.
(1)求该品牌电动自行车销售量的月均增长率;
(2)若该品牌电动自行车的进价为2300元,售价为2800元,则该经销商1至3月共盈利多少元?
解:(1)设该品牌电动自行车销售量的月均增长率为x,
根据题意列方程:150(1+x)2=216,
解得x1=-220%(不合题意,舍去),x2=20%.
答:该品牌电动自行车销售量的月均增长率20%.
(2)二月份的销量是:150×(1+20%)=180(辆)
所以该经销商1至3月共盈利:(2800-2300)×(150+180+216)=500×546=273000(元)
答:1至3月共盈利273000元.
随堂检测
6. 有一个两位数,它们的十位数字与个位数字之和为5,如果把十位数字与个位数字调换后,所得的两位数乘以原来的两位数就得736,求原来的两位数.
解:设原两位数字的个位数字为x,则十位数字为﹙5-x﹚,
原两位数为10﹙5-x﹚+x,新两位数为10x+﹙5-x﹚
根据题意得:[10x+﹙5-x﹚] [10﹙5-x﹚+x] =736
解得x1=2,x2=3
当x=2时,5-x=3,符合题意,原来的两位数是23.
当x=3时,5-x=2,符合题意,原来的两位数是32
答:原来的两位数是23或32.
课堂小结
1.增长率问题
如果a表示原来的基数,m表示平均增长率,n表示增长的次数,A为增长后的目标数,那么a(1±m)2=A.本节课只研究n=2的情况.当m前面是“-”时表示负增长,即降低.
2.两位数= 十位数字乘以10 + 个位数字;三位数= 百位数字乘以100 + 十位数字乘以10 + 个位数字;…….要注意检验.
作业布置
详见教材练习题
P154 T1-4
谢
谢
第4章 一元二次方程
九年级上册
4.7 一元二次方程的应用
第1课时 面积问题与利润问题
课前小测
1.一元二次方程的解法有___________、_________________、______________、________________.
2.一元二次方程ax2+bx+c=0,当b2-4ac____0时,有两个不相等的实数根;当b2-4ac____0时,有两个相等的实数根;当b2-4ac____0时,没有实数根.
3.如果一元二次方程ax2+bx+c=0的两根为x1,x2,则x1 +x2 =__________, x1x2=_________.
直接开平方法
因式分解法
公式法
配方法
>
=
<
情境引入
与我们学过的一元一次方程、二元一次方程组和分式方程一样,一元二次方程也是刻画现实生活与生产中数量关系的有效模型.本节课学习一元二次方程的应用.
合作探究
探究一:面积问题
一元二次方程应用题与一元一次方程应用题的步骤类似:
1审;2设;3列;4解;5答.
某农场要建一个长方形的养鸡场,鸡场的一边靠墙(墙长25m),另外三边用
木栏围成,木栏长40m.
(1)鸡场的面积能达到180m2吗?能达到200m2吗?
(2)鸡场的面积能达到250m2吗?
如果能,请给出设计方案;如果不能,请说明理由.
分析:可设鸡场的一边为x,另一边为_______
然后根据长方形的面积等于__________,
用含未知数的代数式表示出鸡场的面积.
x
典例分析
[例1]
要想知道鸡场的面积能否达到180平方米,只需要让鸡场的面积先等于180,然后看得出的方程有没有解,如果有,就证明可以达到180平方米,如果方程无解,说明不能达到.其他问题的方法一样
40-2x
长乘宽
40-2x
合作探究
探究一:面积问题
某农场要建一个长方形的养鸡场,鸡场的一边靠墙(墙长25m),另外三边用木栏围成,
木栏长40m.
(1)鸡场的面积能达到180m2吗?能达到200m2吗?
(2)鸡场的面积能达到250m2吗?
如果能,请给出设计方案;如果不能,请说明理由.
x
解:(1)①设鸡场的宽为xm,
解这个方程,得
x(40-2x)=180,
则长为_______m,
根据题意,得
(40-2x)
当
时,
即 x2-20x+90=0
)>25,不符合题意故舍去.
长=
答:鸡场的面积能达到180m2,这是鸡场的两边长分别为(
)m和(
)m.
合作探究
探究一:面积问题
②同理当面积为200m2时,根据题意,得
x(40-2x)=200
即 x2-20x+100=0
解这个方程,得 x1=x2=10.
当x=10时,长=20,符合题意.
(
答:鸡场的面积能达到180m2,这时鸡场的两边长分别为(
)m和
)m;当一边为10m时,另一边为20m时,鸡场的面积能达到200m2.
合作探究
探究一:面积问题
(2)同理当面积为250m2时,得
x(40-2x)=250.
整理,得 x2-20x+125=0.
∵△=(-20)2-4×125=-100<0
∴原方程无解,
∴鸡场的面积不能达到250m2.
试一试
MN是一面长10m的墙,用长24m的篱笆,围成一个一面是墙,中间隔着一道篱笆的矩形花圃ABCD,已知花圃的设计面积为45m2,花圃的宽应当是多少?
解:(1)设花圃的宽AB为xm,那么它的长BC是 _ _ _ _
当x1=3时,长=24-9=15>10,故舍去.
所以,花圃的宽是5m.
(24-3x)m
根据题意得
x(24-3x)=45.
即 x2-8x+15=0.
解这个方程,得 x1=3 , x2=5 .
归纳小结
靠墙建矩形,问怎样设计能使面积等于已知数的题型,跟下册的二次函数关系非常密切,是重点易考题型.要注意靠墙的一边的长度不能超过墙长,要注意检验.
合作探究
探究二:利润问题
每件的利润=每件的售价-进价;
销售量.
总利润=
每件的利润
典例分析
[例1]
某商场将每件进价为80元的某种商品原来按每件100元出售,每天可售出100件,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经过市场调查,发现这种商品售价每降低1元,商场销售量平均每天可增加10件,若商场经营该商品一天要获利润2160元,且让顾客得到实惠,则每件商品应降价多少元?
分析:设每件商品应降价x元,现在的总利润=现在每件的利润
现在的销售量.
利用现在每件的利润=现在每件的售价-进价,
表示出现在每件的利润为___________元
(100-x-80)
降低1元增加10件,可知降低x元增加______件,
10x
所以现在的销售量为___________
(100+10x),
则根据现在的总利润=现在每件的利润
现在的销售量列出方程解答即可.
典例分析
[例2]
某商场将每件进价为80元的某种商品原来按每件100元出售,每天可售出100件,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经过市场调查,发现这种商品售价每降低1元,商场销售量平均每天可增加10件,若商场经营该商品一天要获利润2160元,且让顾客得到实惠,则每件商品应降价多少元?
解 :设每件商品降价x元.根据题意,得
(100-x-80)×(100+10x)=2160,
解得:x1=2,x2=8,
由原题为了减少库存,应降价多点,故把x=2舍去,所以x=8,
答:每件商品应降价8元.
归纳小结
销售利润问题,是一元二次方程应用题的难点问题,也是重点.要正确理解销售量与利润的关系,能准确用未知数表示销售量和单件的利润是关键.
试一试
某商店准备进一批季节性小家电,单价40元,经市场预测,销售定价为52元时,可售出180个,定价每增加1元,销售量减少10个.因受库存影响,每批次进货个数不得超过180个.商店若准备获利2000元,则应进货多少个?定价多少元?
解:设每个小家电的定价是x元,
根据题意,得
答:商店若准备获利2000元,则应进货100个,定价60元.
∴ x=60元,则180﹣10·8=100(个).
∴x≥52.
∵180﹣10(x-52)≤180,
解得x1=50,x2=60.
随堂检测
面积问题与利润问题 课堂评价测试
同学们要认真答题哦!
随堂检测
1.如图,在宽为20 m、长为36 m的矩形草地上修建两条同样宽且互相垂直的道路,剩余草地的面积是540 m2.则道路的宽为 .
2.将一根长为 64 cm 的铁丝剪成两段,再将每段分别围成正方形(如图),如果两个正方形的面积的和等于 160 cm2,两个正方形的边长为______和_____.
4cm
12cm
随堂检测
3.某品牌服装专营店平均每天可销售该品牌服装20件,每件可盈利44元.若每件降价1元,则每天可多售出5件.若要平均每天盈利1600元且使顾客得到最大的实惠,则应降价________元.
36
随堂检测
4.如图,一个农户要建一个矩形猪舍ABCD,猪舍的一边AD利用长为12米的住房墙,另外三边用25米长的建筑材料围成.为了方便进出,在CD边留一个1米宽的小门.
(1)若矩形猪舍的面积为80平方米,求与墙平行的一边BC的长;
(2)若与墙平行的一边BC的长度不小于与墙垂直的一边AB的长度,问BC边至少应为多少米?
分析:(1)设BC的长为xm,则AB的长为
m.根据矩形的面积公式建立方程求出其解即可;
(2)根据“与墙平行的一边BC的长度不小于与墙垂直的一边AB的长度”列出关于x的不等式组,通过解不等式组求得x的取值范围即可.
X
随堂检测
解:(1)设BC的长为xm,依题意得:
解得x1=10,x2=16(舍去).
答:矩形猪舍的面积为80平方米,求与墙平行的一边BC的长为10m;
(2)依题意得:
解得
所以x最小为
.
答:若与墙平行的一边BC的长度不小于与墙垂直的一边AB的长度,问BC边至少应
米.
随堂检测
5.某商店如果将进价为8元的商品按每件10元售出,每天可销售200件,现采用提高售价,减小进货量的方法增加利润。已知这种商品每涨价0.5元,其每天销售量就减少10件,问应将售价定为多少元时,才能使每天所获利润为640元?
解:设将售价定为x元,根据题意,得
即
.
解这个方程得 x1=12,x2=16.
∵要提高售价,减少进货量,
∴x只取16 .
答: 售价为16元时,每天所获的利润为640元.
课堂小结
一元二次方程应用题与一元一次方程应用题的步骤类似:
1审;2设;3列;4解;5答.
一.面积问题
二.销售利润问题
注意:列方程解应用题,要验根,根的取值要满足题意.
作业布置
详见教材练习题
P152 T1-2
第4章 一元二次方程
九年级上册
4.7 一元二次方程的应用
第2课时 增长率问题与其他应用
课前小测
某品牌服装去年每套300元.(只列式子不计算结果)
(1)如果今年提价10%,今年的售价是多少元?
据说明年还要提价10%,那么明年的售价是多少元?
(2)如果今年降价10%,则今年的售价是多少元?
据说明年还要降价10%,那么明年的售价是多少元?
情境引入
某品牌服装去年每套300元
(1)今年增长率是x,则今年的售价是多少元?
(2)据说明年的增长率还是x ,那么明年的售价是多少元?
问题1:(只列式子不计算结果)
情境引入
某品牌服装去年每套300元,
(1)今年的降价率是x,则今年的售价是多少元?
(2)据说明年的降价率还是x,那么明年的售价是多少元?
问题2:(只列式子不计算结果)
合作探究
探究一:增长率问题
某养殖场 2010 年的产值为 500 万元, 2012 年的产值为 605 万元. 求
2010 2012 年该养殖场产值的年平均增长率.
你会解决这个问题吗?
可列方程______________________________.
而这2012年的年产值正好是605万元.
2012年的年产值为______________________________.
2011年的年产值为_____________________________,
分析:如果设该场2010-2012年产值的平均增长率为x,那么
500(1+x)
500(1+x)2
合作探究
探究一:增长率问题
解 设该场 2010 2012 年产值的年平均增长率为 x,根据题意,得
根据题意, 605 万元 > 500 万元,故年增长率 x > 0,而 x2= -2.1 < 0,因此
x2 = -2.1 不符合题意,应当舍去, x1= 0.1 符合题意.
所以,该养殖场 2010 2012 年产值的年平均增长率为 0.1,即 10% .
解这个方程,得
x1 = 0.1, x2 = -2.1 .
典例分析
[例1]
某种药品经过两次降价后,每盒售价为原售价的 64%,求该药品平均每次的降价率.
可列方程______________________________
而两次降价后的价格是
第二次降价后该药品每盒的售价为_________________,
那么第一次降价后该药品每盒的售价为______________,
分析:如果把降价之前的价格看作单位“1”.设该药品平均每次的降价率为x,
(1-x)
(1-x)2
请你把步骤写完整.
典例分析
[例1]
某种药品经过两次降价后,每盒售价为原售价的 64%,求该药品平均每次的降价率.
解 设该药品平均每次的降价率为 x,
根据题意,得
(1 - x)2 = 64% .
所以,该药品平均每次的降价率为 0.2,即 20% .
根据题意,降价率应满足 0 < x < 1,因而 x2 = 1.8 不符合题意,应当舍去,
而 x = 0.2 符合题意.
解这个方程,得
x1 = 0.2, x2 = 1.8 .
归纳小结
如果 a 表示原来的基数,m 表示平均增长率,n 表示增长的次数,A 为增长后的目标数,那么 a(1±m)2=A .本节课只研究n = 2 的情况.当m前面是“ - ”时表示负增长,即降低.
合作探究
探究二:数字问题
典例分析
[例2] 有一个两位数等于其各位数字之积的3倍,其十位数字比个位数字小2,求这个两位数.
分析:设个位数字为 x ,
则十位数字为 ___________,
这个两位数为______________ ;
(x-2)
10(x-2)+x
然后根据“这个两位数等于其各位数字之积的3倍”可列出关于x的方程.
[例2]
典例分析
当x=4时,x-2=2,
∴这个两位数是24.
解:设个位数字为x,则十位数字为(x-2),这个两位数是[10(x-2)+x].
根据题意,得10(x-2)+x=3x(x-2),
整理,得3x2-17x+20=0,5分
解得x1=4,x2=
(不合题意,舍去).
归纳小结
两位数= 十位数字乘以10 + 个位数字;
三位数= 百位数字乘以100 + 十位数字乘以10 + 个位数字;…….
要注意检验.
随堂检测
增长率问题与其他应用 课堂评价测试
同学们要认真答题哦!
随堂检测
B
B
随堂检测
3.某商品经过连续两次降价,销售单价由原来的125元降到80元,则平均每次降价的百分率为______.
4.在一次同学聚会时,大家一见面就相互握手.有人统计了一下,大家一共握了45次手,参加这次聚会的同学共有多少人?若参加聚会有x名同学,可列方程______________________.
20%
随堂检测
5. 电动自动车已成为市民日常出行的首选工具.据某市某品牌电动自行车经销商1至3月份统计,该品牌电动自行车1月份销售150辆,3月份销售216辆.
(1)求该品牌电动自行车销售量的月均增长率;
(2)若该品牌电动自行车的进价为2300元,售价为2800元,则该经销商1至3月共盈利多少元?
解:(1)设该品牌电动自行车销售量的月均增长率为x,
根据题意列方程:150(1+x)2=216,
解得x1=-220%(不合题意,舍去),x2=20%.
答:该品牌电动自行车销售量的月均增长率20%.
(2)二月份的销量是:150×(1+20%)=180(辆)
所以该经销商1至3月共盈利:(2800-2300)×(150+180+216)=500×546=273000(元)
答:1至3月共盈利273000元.
随堂检测
6. 有一个两位数,它们的十位数字与个位数字之和为5,如果把十位数字与个位数字调换后,所得的两位数乘以原来的两位数就得736,求原来的两位数.
解:设原两位数字的个位数字为x,则十位数字为﹙5-x﹚,
原两位数为10﹙5-x﹚+x,新两位数为10x+﹙5-x﹚
根据题意得:[10x+﹙5-x﹚] [10﹙5-x﹚+x] =736
解得x1=2,x2=3
当x=2时,5-x=3,符合题意,原来的两位数是23.
当x=3时,5-x=2,符合题意,原来的两位数是32
答:原来的两位数是23或32.
课堂小结
1.增长率问题
如果a表示原来的基数,m表示平均增长率,n表示增长的次数,A为增长后的目标数,那么a(1±m)2=A.本节课只研究n=2的情况.当m前面是“-”时表示负增长,即降低.
2.两位数= 十位数字乘以10 + 个位数字;三位数= 百位数字乘以100 + 十位数字乘以10 + 个位数字;…….要注意检验.
作业布置
详见教材练习题
P154 T1-4
谢
谢
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
