28.2解直角三角形(2)
图片预览


文档简介
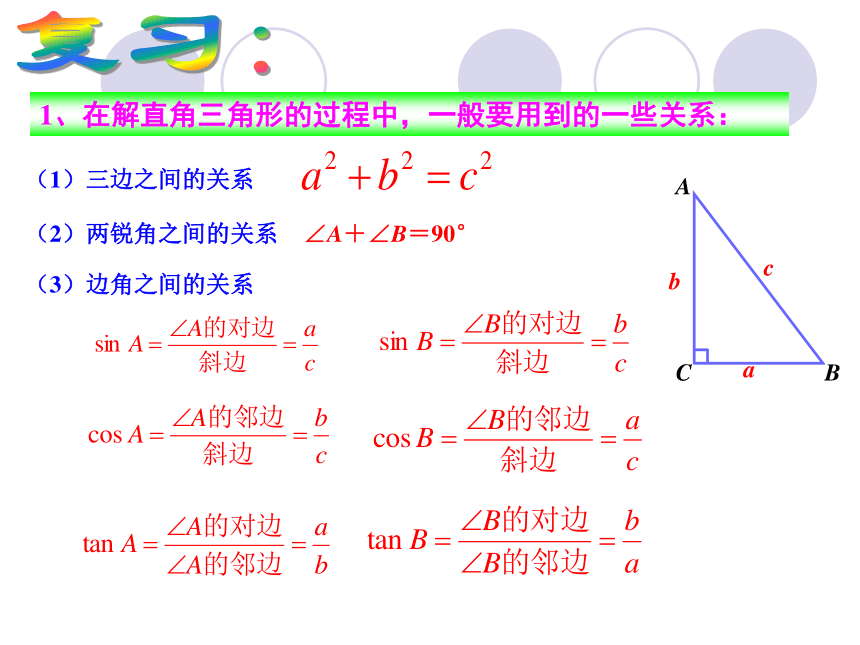
课件18张PPT。28.2 解直角三角形(第2课时)福州鼓山中学 潘钦(2)两锐角之间的关系∠A+∠B=90°(3)边角之间的关系(1)三边之间的关系 1、在解直角三角形的过程中,一般要用到的一些关系:复习:2. 解直角三角形.
在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三角形.复习:3、解直角三角形,只有下面两种情况:
(1)已知两条边
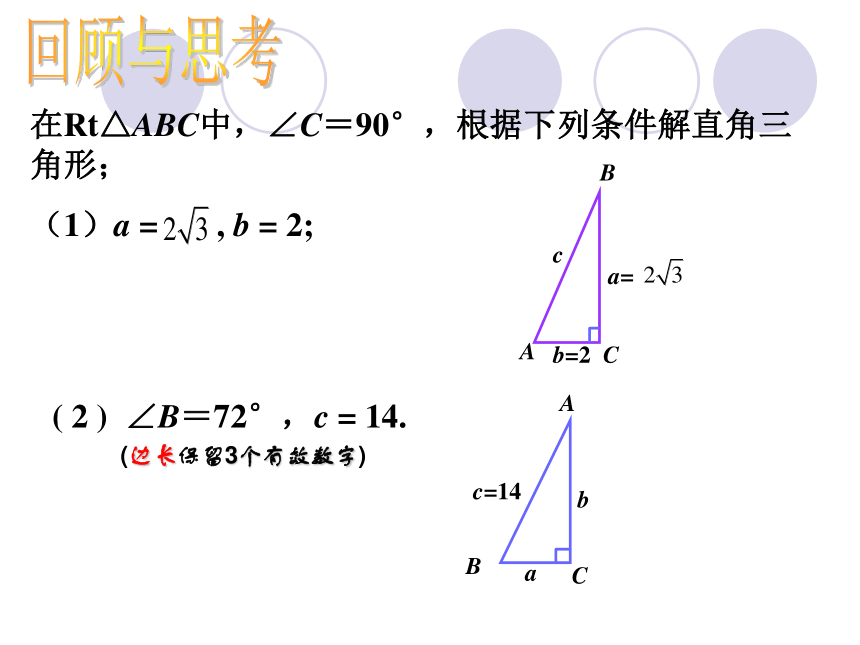
(2)已知一条边和一个锐角两直角边一直角边,一斜边一直角边,一锐角一斜边,一锐角回顾与思考在Rt△ABC中,∠C=90°,根据下列条件解直角三角形;
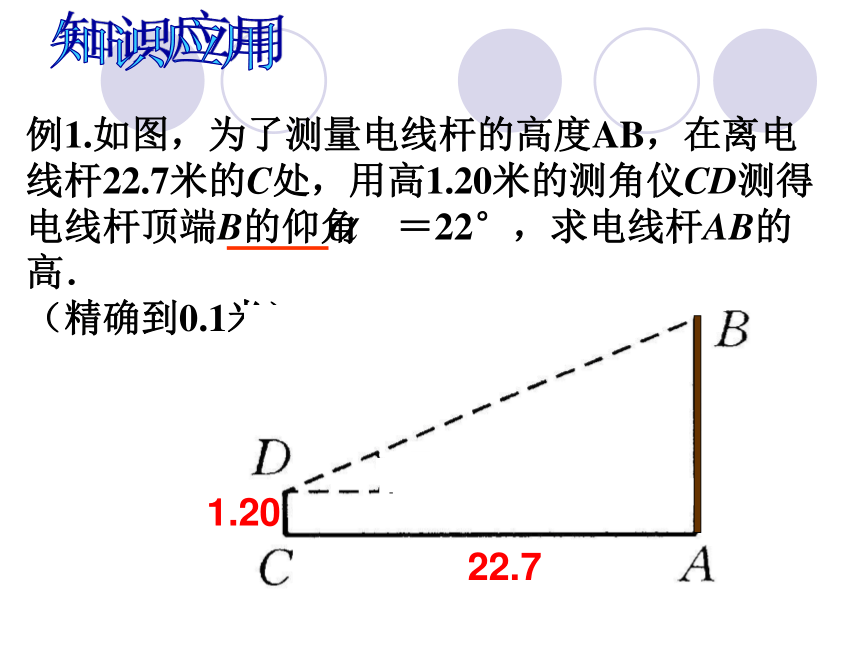
(1)a = , b = 2; ( 2 ) ∠B=72°,c = 14.(边长保留3个有效数字)例1.如图,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角 =22°,求电线杆AB的高.
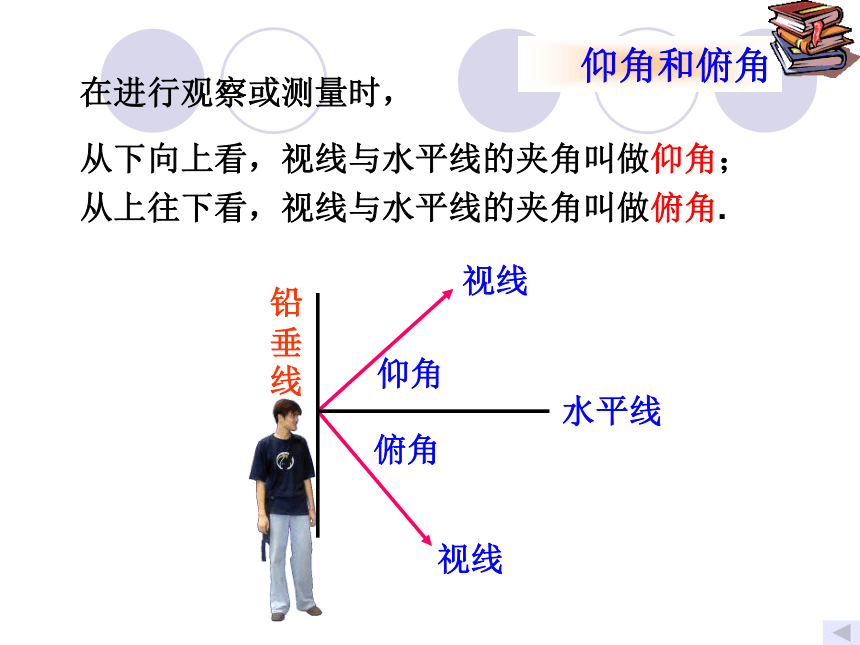
(精确到0.1米)1.2022.7知识应用视线视线仰角俯角在进行观察或测量时,从上往下看,视线与水平线的夹角叫做俯角.从下向上看,视线与水平线的夹角叫做仰角;1.2022.7 =22°知识应用E例1:如图,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角 =22°,求电线杆AB的高.(精确到0.1米)1.2022.7例2:热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高?(精确到0.1m)α=30°β=60°120ABCD解: 在Rt 中,
答:这栋楼高约为277.1m在Rt 中,如果其他条件不变,改120m为楼高,求热气球与高楼的水平距离 ?(精确到0.1m)
α=30°β=60°120ABCD拓展:?巩固练习建筑物BC上有一旗杆AB,由距BC 20m的D处观察旗杆顶部A的仰角为60°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m)建筑物BC上有一旗杆AB,由距BC20m的D处观察旗杆顶部A的仰角60°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m)解:在等腰三角形BCD中∠BCD=90°BC=DC=20m在Rt△ACD中答:棋杆的高度约为14.6m.即10m?试一试建筑物BC上有一旗杆AB,高度为10m,在D处观察旗杆顶部A的仰角60°,观察底部B的仰角为45°,求DC的长。(精确到0.1m)体会一下:这节课你有哪些收获?你能否用所学的知识去解决一些
实际问题吗? 某人在A处测得建筑物的仰角∠BAC为300 ,沿AC方向行20m至D处,测得仰角∠BDC 为450,求此建筑物的高度BC.AC挑战B____________________D名言: 聪明在于学习,天才在于积累。……所谓天才,实际上是依靠学习。_____华罗庚欢 迎 指 点
在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三角形.复习:3、解直角三角形,只有下面两种情况:
(1)已知两条边
(2)已知一条边和一个锐角两直角边一直角边,一斜边一直角边,一锐角一斜边,一锐角回顾与思考在Rt△ABC中,∠C=90°,根据下列条件解直角三角形;
(1)a = , b = 2; ( 2 ) ∠B=72°,c = 14.(边长保留3个有效数字)例1.如图,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角 =22°,求电线杆AB的高.
(精确到0.1米)1.2022.7知识应用视线视线仰角俯角在进行观察或测量时,从上往下看,视线与水平线的夹角叫做俯角.从下向上看,视线与水平线的夹角叫做仰角;1.2022.7 =22°知识应用E例1:如图,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角 =22°,求电线杆AB的高.(精确到0.1米)1.2022.7例2:热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高?(精确到0.1m)α=30°β=60°120ABCD解: 在Rt 中,
答:这栋楼高约为277.1m在Rt 中,如果其他条件不变,改120m为楼高,求热气球与高楼的水平距离 ?(精确到0.1m)
α=30°β=60°120ABCD拓展:?巩固练习建筑物BC上有一旗杆AB,由距BC 20m的D处观察旗杆顶部A的仰角为60°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m)建筑物BC上有一旗杆AB,由距BC20m的D处观察旗杆顶部A的仰角60°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m)解:在等腰三角形BCD中∠BCD=90°BC=DC=20m在Rt△ACD中答:棋杆的高度约为14.6m.即10m?试一试建筑物BC上有一旗杆AB,高度为10m,在D处观察旗杆顶部A的仰角60°,观察底部B的仰角为45°,求DC的长。(精确到0.1m)体会一下:这节课你有哪些收获?你能否用所学的知识去解决一些
实际问题吗? 某人在A处测得建筑物的仰角∠BAC为300 ,沿AC方向行20m至D处,测得仰角∠BDC 为450,求此建筑物的高度BC.AC挑战B____________________D名言: 聪明在于学习,天才在于积累。……所谓天才,实际上是依靠学习。_____华罗庚欢 迎 指 点
