3.1 圆的对称性 教案 (表格式)2025-2026学年数学青岛版九年级上册
文档属性
| 名称 | 3.1 圆的对称性 教案 (表格式)2025-2026学年数学青岛版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 200.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 00:00:00 | ||
图片预览




文档简介
3.1 圆的对称性
课题 3.1 圆的对称性 课时 第1课时 授课人
教学目标 1.经历探索圆的对称性及垂径定理和推论的过程. 2.理解圆的对称性及有关性质. 3.会用垂径定理解决有关问题.
教学重难点 教学重点:垂径定理. 教学难点:运用垂径定理进行有关的计算.
教学活动
教学流程 师生活动 设计意图
课前小测 1.圆是平面内到 定点 的距离等于 定长 的点的集合. 2.弦:圆上任意两点之间所连接的线段叫做 弦 ,圆中最长的弦是 直径 . 3.弧:圆上任意两点间的部分叫做 圆弧 ,简称弧.用符号“ ”表示. 弧的分类 如图,以A,B为端点的弧有 2 条,分别是 劣弧 和 优弧 . 复习圆、弦、直径等的定义,弧的分类和表示方法,为这一章的学习做好准备.
情境导入 这是北京天坛公园内圜丘坛的照片. 圜丘坛,俗称祭天台,高5米,直径23米,是一座由汉白玉石雕栏围绕的三层石造圆台. 观察这幅图片,思考下面的问题: (1)圆是轴对称图形吗 是中心对称图形吗 是轴对称图形,也是中心对称图形. (2)如果站在圜丘坛最上一层,你能准确找到它的圆心吗 怎么能准确找到圆心呢 等学完这一章,同学们就会有办法了. 以美丽的北京天坛导入圆,并提出问题,第(1)个问题较简单,根据已学知识可以回答,第(2)个问题有一定的挑战性,激发学习兴趣.
合作探究 探究一:圆是轴对称图形吗? 思考下面的问题,动手操作并与同学交流: (1)在一张半透明的纸片上画一个圆,标出它的圆心O,再任意作出一条直径AB.将☉O沿直径AB折叠,你发现了什么 折叠后两边完全重合. (2)再任意作一条直径,重复(1)中的操作,还有同样的结论吗 折叠后还是两边完全重合. 归纳小结: 圆是轴对称图形,每一条直径所在的直线都是它的对称轴. 1.让学生画图、折叠、观察、交流各自的发现,得出圆是轴对称图形的结论.
续表
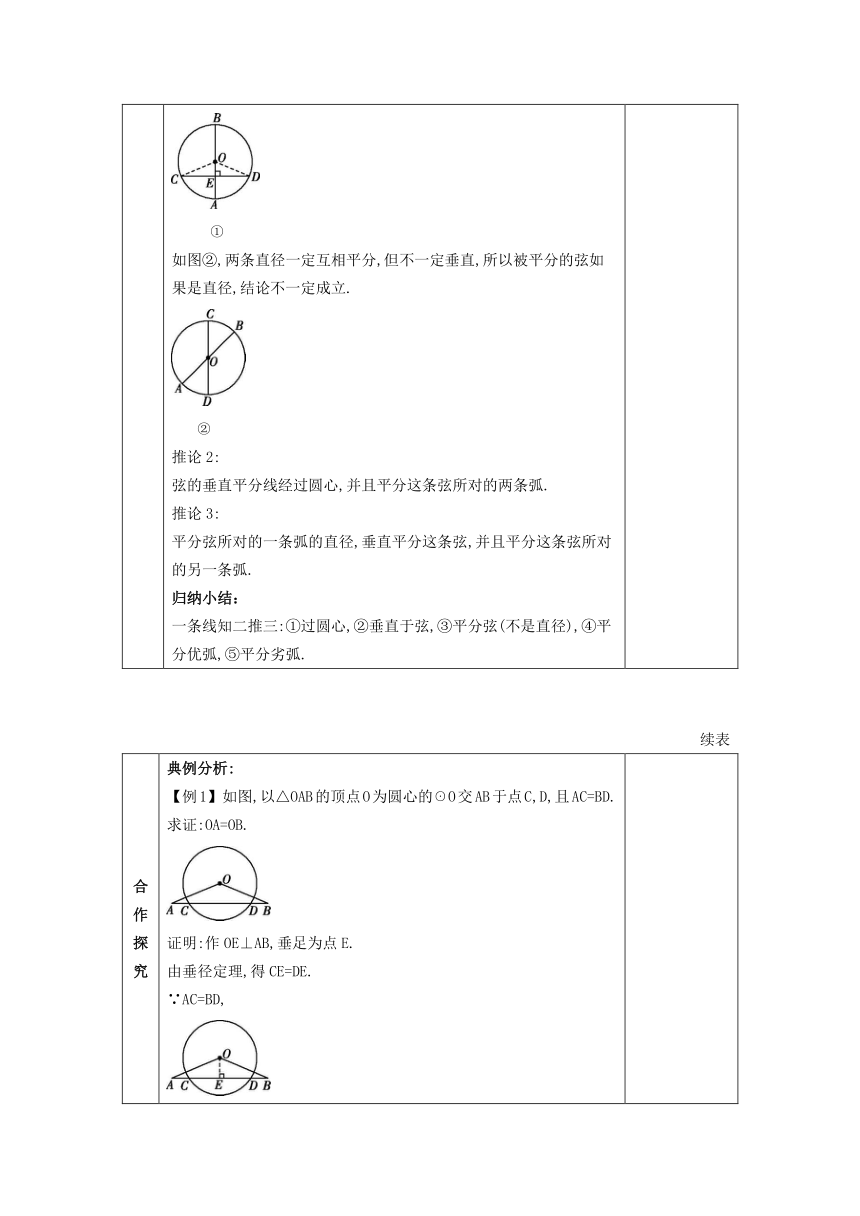
合作探究 探究二:垂径定理和推论 1.垂径定理 如图,CD是☉O的弦,AB是与CD垂直的直径,垂足为点E.将☉O沿直径AB折叠. (1)你发现线段CE与DE有什么关系 与有什么关系 与有什么关系 通过折叠发现CE=DE,=,=. (2)能不能通过推理得到结论呢 证明:连接OC,OD.∵OC=OD,OE⊥CD,OE=OE, ∴Rt△OCE≌Rt△ODE,∴CE=DE. ∴点C与点D关于直线AB对称. ∵直线AB是☉O的对称轴, ∴当☉O沿直线AB折叠时,点C与点D重合,与重合,与重合, ∴=,=. 归纳小结:垂径定理:垂直于弦的直径平分弦以及弦所对的两条弧. 已知:①AB是直径;②AB⊥CD. 结论:③CE=DE;④=,⑤=. 符号语言:∵AB是直径,AB⊥CD, ∴CE=DE, =, =. “垂直于弦的直径”可以是直径,也可以是半径(如图),甚至还可以是过圆心的直线或线段. 2.垂径定理的推论 由折叠或垂径定理的证明可知,下列推论成立. 推论1: 平分弦(不是直径)的直径,垂直这条弦,并且平分这条弦所对的两条弧. 几何语言:如图①,∵CE=DE,AB是直径, ∴AB⊥CD,=,=. ① 如图②,两条直径一定互相平分,但不一定垂直,所以被平分的弦如果是直径,结论不一定成立. ② 推论2: 弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧. 推论3: 平分弦所对的一条弧的直径,垂直平分这条弦,并且平分这条弦所对的另一条弧. 归纳小结: 一条线知二推三:①过圆心,②垂直于弦,③平分弦(不是直径),④平分优弧,⑤平分劣弧. 2.引导学生探索垂径定理,根据圆的对称性,通过操作发现结论,然后引导学生通过合情推理和演绎推理来得到垂径定理. 3.垂径定理是圆中一个重要的结论,要能与推论相互转化,形成整体.
续表
合作探究 典例分析: 【例1】 如图,以△OAB的顶点O为圆心的☉O交AB于点C,D,且AC=BD.求证:OA=OB. 证明:作OE⊥AB,垂足为点E. 由垂径定理,得CE=DE. ∵AC=BD, ∴AC+CE=BD+DE, 即AE=BE. ∴OE为线段AB的垂直平分线. ∴OA=OB. 圆心到弦的垂线段的长度称为这条弦的弦心距. 例如:OE是CD的弦心距. 归纳小结:在圆中,作弦心距是常用的辅助线,可以利用垂径定理得到的结论来推理. 【例2】 1400多年前,我国隋朝时期建造的赵州石拱桥(如图)的桥拱近似于圆弧形,它的跨度(弧所对的弦长)为37.02 m,拱高(弧的中点到弦的距离,也叫弓形的高)为7.23 m.求桥拱所在圆的半径(精确到0.1 m). 解:设桥拱所在圆的半径为R(m),如图,用表示桥拱,的圆心为O,经过点O作弦AB的垂线,垂足为点D,与交于点C. ∵OC⊥AB,∴D是线段AB的中点,C是的中点,CD就是拱高. ∵AB=37.02,CD=7.23, ∴AD=AB=×37.02=18.51, OD=OC-CD=R-7.23. 在Rt△ODA中,由勾股定理,得 OA2=AD2+OD2, 即R2=18.512+(R-7.23)2. 解这个方程,得R≈27.3. ∴赵州石拱桥桥拱所在圆的半径约为27.3 m. 归纳小结:作弦心距和连半径是圆中常见的辅助线,构造直角三角形,应用垂径定理,结合勾股定理来解决问题. 拓展: 设半径OC=r,弦心距OE=d,弦CD的一半CE(半弦)为a,拱高AE为m,在这四个量r,d,a,m中,知二推二. 4.例2是必考题型,作弦心距、连半径、和半弦构成直角三角形,利用勾股定理求解. 5.拓展的知二推二是求圆的半径、弦、弦心距和拱高常用的方法,学生应熟练掌握.
续表
随堂检测 1.如图,AB是☉O的直径,弦CD⊥AB,垂足为E,若AB=10,CD=8,则线段OE的长为( C ) A.5 B.4 C.3 D.2 2.如图,在☉O中,CD是直径,AB是弦,且CD⊥AB,已知AB=16,CM=4,求OA. 解:∵直径CD⊥AB,AB=16, ∴AM=AB=8. ∵OA=OC=OM+CM,CM=4, ∴OM=OA-CM=OA-4. 在Rt△AOM中,由勾股定理,得 OA2=AM2+OM2,即OA2=82+(OA-4)2, ∴OA=10.
课堂小结 1.圆具有怎样的对称性 2.垂径定理及其推论的内容是什么 3.在圆中,通常怎样构造直角三角形解决问题 内容相对较多且有一定难度,及时归纳总结,可让学生思维更清晰.
作业布置 请完成教材练习题P70T1-T2
板书设计
垂径定理 1.圆的对称性 2.垂径定理及其推论 一条线知二推三:①过圆心,②垂直于弦,③平分弦(不是直径),④平分优弧,⑤平分劣弧. 3.弦心距、半径、半弦、拱高知二推二 【例2】
教学反思
本节课是学生在学习了圆、弧、弦、等圆、等弧、扇形等概念的基础上来学习圆的其他性质,让学生在画图、折叠、思考、猜测和交流等活动中发现圆是轴对称图形,它有无数条对称轴,对称轴是任意一条直径所在的直线.垂径定理和推论是圆的重要性质,是证明圆内线段相等、角相等、弧相等的重要依据,要让学生熟练掌握其辅助线作法和解法.
课题 3.1 圆的对称性 课时 第2课时 授课人
教学目标 1.探索理解并掌握圆的旋转不变性,圆心角、弧、弦之间的关系. 2.认识弧的度数的概念,了解圆心角的度数与它所对弧的度数之间的关系.
教学重难点 教学重点:弧、弦、圆心角关系定理及弧的度数和圆心角度数的关系. 教学难点:定理的探索和应用.
教学活动
教学流程 师生活动 设计意图
课前小测 1.垂径定理及推论总结出的知二推三的内容是什么 一条线知二推三:①过圆心,②垂直于弦,③平分弦(不是直径), ④平分优弧,⑤平分劣弧. 2.如图,在☉O中,已知AB是直径,AB⊥CD. (1)若AB=10,OE=3,则CD= 8 ,AE= 2 . (2)若OE=3,CD=8,则AB= 10 ,AE= 2 . (3)若AE=2,CD=8,则OE= 3 ,AB= 10 . 复习垂径定理及推论,第2题是有关垂径定理的练习,考察知二推二的学习情况.
情境导入 1.任意画一个圆,将圆围绕圆心旋转任意角度,你有什么发现 围绕圆心旋转任何一个角度,都与原来的圆重合.因此圆具有旋转不变性. 2.圆是中心对称图形吗 哪个点是对称中心 圆是中心对称图形,圆心是它的对称中心. 3.什么是圆心角 如图,在☉O上任取两点A与B,连接OA,OB,得到∠AOB.像∠AOB这样,顶点在圆心的角叫做圆心角. 1.让学生动手画圆,通过围绕圆心旋转来观察、发现圆的旋转不变性. 2.直接给出圆心角的定义,为学习关系定理做好准备.
合作探究 探究一:圆心角、弧、弦的关系定理 任意画一个☉O,在☉O内画圆心角∠AOB=∠A'OB'.连接AB,A'B'. (1)以点O为旋转中心,逆时针旋转,旋转角为∠AOA',OA和OA'重合,这时OB和OB'重合吗 解:∵∠AOA'=∠AOB+∠BOA',∠BOB'=∠A'OB'+∠BOA',∠AOB=∠A'OB', ∴∠AOA'=∠BOB'. ∵旋转后半径OA与OA'重合, ∴半径OB与OB'重合. (2)这时,与重合吗 弦AB与A'B'重合吗 由此你能得到什么结论 解:∵在同一个圆中,点A与A'重合,点B与B'重合, ∴与重合,弦AB与A'B'重合. 1.探究一的问题,是运用圆的旋转不变性以及合情推理得出的,让学生通过探究发现结论,并说明理由.
续表
合作探究 归纳小结: 这就是说,在同圆中,如果两个圆心角相等,那么它们所对的弧相等,所对的弦也相等. 利用旋转的基本性质还可以得出:在同圆中,如果=,那么∠AOB=∠A'OB',弦AB=A'B';反之,如果弦AB=A'B',那么∠AOB=∠A'OB',=.这些结论在等圆中也成立. 定理 在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等. 典例分析: 【例1】 如图,AB与DE是☉O的两条直径,C是☉O上一点,AC∥DE.求证: (1)=;(2)BE=EC. 证明:(1)连接OC. ∵AC∥DE,∴∠AOD=∠OAC,∠COE=∠OCA. ∵OA=OC, ∴∠OAC=∠OCA. ∴∠AOD=∠COE. ∴=. (2)∵∠AOD=∠BOE, ∴∠BOE=∠COE. ∴BE=CE. 探究二:圆心角的度数与所对弧的度数的关系 问题1:把顶点在圆心的周角等分成360份,每一份圆心角的度数是多少 每一份圆心角的度数是1°. 问题2:把顶点在圆心的周角等分为360份时,整个圆被分成了多少份 每一份的弧是否相等 为什么 分析:整个圆被分成了360份,整个圆的叫做1°的弧.因此,1°的圆心角所对的弧是1°的弧;反之,1°的弧所对的圆心角是1°的角.一般地,n°的圆心角所对的弧是n°的弧;反之,n°的弧所对的圆心角是n°的角(如图). 由此可见,圆心角与它所对的弧有以下关系: 圆心角的度数与它所对弧的度数相等. 2.只有在同圆或等圆中才有等弧. 3.让学生回答问题1,2,经历“1°的弧”概念产生的过程,并理解合理性.
续表
合作探究 典例分析: 【例2】 如图,OA,OC是☉O中两条垂直的半径,D是☉O上的一点.连接AD并延长与OC的延长线相交于点B,∠B=25°.求,的度数. 解:连接OD. 由已知∠AOB=90°,∠B=25°,得∠A=65°. ∵OA=OD,∴∠ODA=∠A=65°. ∴∠DOA=180°-(∠ODA+∠A) =180°-(65°+65°) =50°. ∴的度数为50°. ∵的度数为90°, ∴的度数 =的度数-的度数 =90°-50° =40°. 【例3】 如图,在☉O中,弦AB所对的劣弧为圆的,圆的半径为2 cm,求AB的长. 解:连接OA,OB. 题意可知的度数为×360°=120°, ∴∠AOB=120°. 作OC⊥AB,垂足为点C. ∵OA=OB, ∴∠AOC=60°,AC=BC. 在Rt△AOC中, AC=OAsin∠AOC=2·sin 60°=2×=(cm). ∴AB=2AC=2 cm. 归纳小结:已知弧的度数,相当于知道圆心角的度数,所以连半径构造圆心角的同时也构造出等腰三角形,利用等腰三角形的性质、垂径定理、锐角的三角比、勾股定理等来求解. 4.例2、例3,可让学生先独立思考,交流思路.
续表
随堂检测 1.有下列四个命题:①顶点在圆心的角是圆心角;②两个圆心角相等,它们所对的弦也相等;③两条弦相等,它们所对的弧也相等;④等弧所对的圆心角相等.其中正确的有( C ) A.0个 B.1个 C.2个 D.3个 2.如图,AB,CD是☉O的直径,=,若∠AOE=32°,则∠COE的度数是 64° . 3.点A,C是半径为3的圆周上两点,点B为的中点,以线段BA,BC为邻边作菱形ABCD,顶点D恰在该圆直径的三等分点上,则该菱形的边长为 或2 . 4.如图,在 ABCD中,以A为圆心,AB的长为半径的圆分别交AD,BC于F,G,交BA的延长线于点E,求证:=. 证明:连接AG. ∵四边形ABCD是平行四边形,∴AD∥BC. ∴∠EAD=∠ABC,∠DAG=∠AGB. ∵AB=AG,∴∠ABC=∠AGB, ∴∠EAD=∠DAG.∴=.
课堂小结 1.圆是中心对称图形吗 它的对称中心是什么 2.圆心角、弧、弦之间有怎样的关系 应用的前提是什么 3.圆心角的度数与它所对弧的度数有怎样的关系 关系定理是圆中证明线段相等、角相等常用的方法,对定理要理解透彻.
作业布置 请完成教材练习题P72T1-T3,P74T1-T2
板书设计
弧、弦、圆心角之间的关系 1.圆是中心对称图形,圆心是它的对称中心. 2.定理:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等. 3.圆心角的度数与它所对弧的度数相等. 【例1】
教学反思
利用旋转的方法得到了圆的旋转不变性,由圆的旋转不变性,我们探究了圆心角、弧、弦之间的关系定理.例1是圆心角与所对弧和弦的关系定理的直接应用,例2和例3都是综合运用本节所学的圆的有关定理以及解直角三角形的知识解决有关圆心角、弧的度数及弦长的计算.通过例题,让学生感受不同数学知识之间的联系.
课题 3.1 圆的对称性 课时 第1课时 授课人
教学目标 1.经历探索圆的对称性及垂径定理和推论的过程. 2.理解圆的对称性及有关性质. 3.会用垂径定理解决有关问题.
教学重难点 教学重点:垂径定理. 教学难点:运用垂径定理进行有关的计算.
教学活动
教学流程 师生活动 设计意图
课前小测 1.圆是平面内到 定点 的距离等于 定长 的点的集合. 2.弦:圆上任意两点之间所连接的线段叫做 弦 ,圆中最长的弦是 直径 . 3.弧:圆上任意两点间的部分叫做 圆弧 ,简称弧.用符号“ ”表示. 弧的分类 如图,以A,B为端点的弧有 2 条,分别是 劣弧 和 优弧 . 复习圆、弦、直径等的定义,弧的分类和表示方法,为这一章的学习做好准备.
情境导入 这是北京天坛公园内圜丘坛的照片. 圜丘坛,俗称祭天台,高5米,直径23米,是一座由汉白玉石雕栏围绕的三层石造圆台. 观察这幅图片,思考下面的问题: (1)圆是轴对称图形吗 是中心对称图形吗 是轴对称图形,也是中心对称图形. (2)如果站在圜丘坛最上一层,你能准确找到它的圆心吗 怎么能准确找到圆心呢 等学完这一章,同学们就会有办法了. 以美丽的北京天坛导入圆,并提出问题,第(1)个问题较简单,根据已学知识可以回答,第(2)个问题有一定的挑战性,激发学习兴趣.
合作探究 探究一:圆是轴对称图形吗? 思考下面的问题,动手操作并与同学交流: (1)在一张半透明的纸片上画一个圆,标出它的圆心O,再任意作出一条直径AB.将☉O沿直径AB折叠,你发现了什么 折叠后两边完全重合. (2)再任意作一条直径,重复(1)中的操作,还有同样的结论吗 折叠后还是两边完全重合. 归纳小结: 圆是轴对称图形,每一条直径所在的直线都是它的对称轴. 1.让学生画图、折叠、观察、交流各自的发现,得出圆是轴对称图形的结论.
续表
合作探究 探究二:垂径定理和推论 1.垂径定理 如图,CD是☉O的弦,AB是与CD垂直的直径,垂足为点E.将☉O沿直径AB折叠. (1)你发现线段CE与DE有什么关系 与有什么关系 与有什么关系 通过折叠发现CE=DE,=,=. (2)能不能通过推理得到结论呢 证明:连接OC,OD.∵OC=OD,OE⊥CD,OE=OE, ∴Rt△OCE≌Rt△ODE,∴CE=DE. ∴点C与点D关于直线AB对称. ∵直线AB是☉O的对称轴, ∴当☉O沿直线AB折叠时,点C与点D重合,与重合,与重合, ∴=,=. 归纳小结:垂径定理:垂直于弦的直径平分弦以及弦所对的两条弧. 已知:①AB是直径;②AB⊥CD. 结论:③CE=DE;④=,⑤=. 符号语言:∵AB是直径,AB⊥CD, ∴CE=DE, =, =. “垂直于弦的直径”可以是直径,也可以是半径(如图),甚至还可以是过圆心的直线或线段. 2.垂径定理的推论 由折叠或垂径定理的证明可知,下列推论成立. 推论1: 平分弦(不是直径)的直径,垂直这条弦,并且平分这条弦所对的两条弧. 几何语言:如图①,∵CE=DE,AB是直径, ∴AB⊥CD,=,=. ① 如图②,两条直径一定互相平分,但不一定垂直,所以被平分的弦如果是直径,结论不一定成立. ② 推论2: 弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧. 推论3: 平分弦所对的一条弧的直径,垂直平分这条弦,并且平分这条弦所对的另一条弧. 归纳小结: 一条线知二推三:①过圆心,②垂直于弦,③平分弦(不是直径),④平分优弧,⑤平分劣弧. 2.引导学生探索垂径定理,根据圆的对称性,通过操作发现结论,然后引导学生通过合情推理和演绎推理来得到垂径定理. 3.垂径定理是圆中一个重要的结论,要能与推论相互转化,形成整体.
续表
合作探究 典例分析: 【例1】 如图,以△OAB的顶点O为圆心的☉O交AB于点C,D,且AC=BD.求证:OA=OB. 证明:作OE⊥AB,垂足为点E. 由垂径定理,得CE=DE. ∵AC=BD, ∴AC+CE=BD+DE, 即AE=BE. ∴OE为线段AB的垂直平分线. ∴OA=OB. 圆心到弦的垂线段的长度称为这条弦的弦心距. 例如:OE是CD的弦心距. 归纳小结:在圆中,作弦心距是常用的辅助线,可以利用垂径定理得到的结论来推理. 【例2】 1400多年前,我国隋朝时期建造的赵州石拱桥(如图)的桥拱近似于圆弧形,它的跨度(弧所对的弦长)为37.02 m,拱高(弧的中点到弦的距离,也叫弓形的高)为7.23 m.求桥拱所在圆的半径(精确到0.1 m). 解:设桥拱所在圆的半径为R(m),如图,用表示桥拱,的圆心为O,经过点O作弦AB的垂线,垂足为点D,与交于点C. ∵OC⊥AB,∴D是线段AB的中点,C是的中点,CD就是拱高. ∵AB=37.02,CD=7.23, ∴AD=AB=×37.02=18.51, OD=OC-CD=R-7.23. 在Rt△ODA中,由勾股定理,得 OA2=AD2+OD2, 即R2=18.512+(R-7.23)2. 解这个方程,得R≈27.3. ∴赵州石拱桥桥拱所在圆的半径约为27.3 m. 归纳小结:作弦心距和连半径是圆中常见的辅助线,构造直角三角形,应用垂径定理,结合勾股定理来解决问题. 拓展: 设半径OC=r,弦心距OE=d,弦CD的一半CE(半弦)为a,拱高AE为m,在这四个量r,d,a,m中,知二推二. 4.例2是必考题型,作弦心距、连半径、和半弦构成直角三角形,利用勾股定理求解. 5.拓展的知二推二是求圆的半径、弦、弦心距和拱高常用的方法,学生应熟练掌握.
续表
随堂检测 1.如图,AB是☉O的直径,弦CD⊥AB,垂足为E,若AB=10,CD=8,则线段OE的长为( C ) A.5 B.4 C.3 D.2 2.如图,在☉O中,CD是直径,AB是弦,且CD⊥AB,已知AB=16,CM=4,求OA. 解:∵直径CD⊥AB,AB=16, ∴AM=AB=8. ∵OA=OC=OM+CM,CM=4, ∴OM=OA-CM=OA-4. 在Rt△AOM中,由勾股定理,得 OA2=AM2+OM2,即OA2=82+(OA-4)2, ∴OA=10.
课堂小结 1.圆具有怎样的对称性 2.垂径定理及其推论的内容是什么 3.在圆中,通常怎样构造直角三角形解决问题 内容相对较多且有一定难度,及时归纳总结,可让学生思维更清晰.
作业布置 请完成教材练习题P70T1-T2
板书设计
垂径定理 1.圆的对称性 2.垂径定理及其推论 一条线知二推三:①过圆心,②垂直于弦,③平分弦(不是直径),④平分优弧,⑤平分劣弧. 3.弦心距、半径、半弦、拱高知二推二 【例2】
教学反思
本节课是学生在学习了圆、弧、弦、等圆、等弧、扇形等概念的基础上来学习圆的其他性质,让学生在画图、折叠、思考、猜测和交流等活动中发现圆是轴对称图形,它有无数条对称轴,对称轴是任意一条直径所在的直线.垂径定理和推论是圆的重要性质,是证明圆内线段相等、角相等、弧相等的重要依据,要让学生熟练掌握其辅助线作法和解法.
课题 3.1 圆的对称性 课时 第2课时 授课人
教学目标 1.探索理解并掌握圆的旋转不变性,圆心角、弧、弦之间的关系. 2.认识弧的度数的概念,了解圆心角的度数与它所对弧的度数之间的关系.
教学重难点 教学重点:弧、弦、圆心角关系定理及弧的度数和圆心角度数的关系. 教学难点:定理的探索和应用.
教学活动
教学流程 师生活动 设计意图
课前小测 1.垂径定理及推论总结出的知二推三的内容是什么 一条线知二推三:①过圆心,②垂直于弦,③平分弦(不是直径), ④平分优弧,⑤平分劣弧. 2.如图,在☉O中,已知AB是直径,AB⊥CD. (1)若AB=10,OE=3,则CD= 8 ,AE= 2 . (2)若OE=3,CD=8,则AB= 10 ,AE= 2 . (3)若AE=2,CD=8,则OE= 3 ,AB= 10 . 复习垂径定理及推论,第2题是有关垂径定理的练习,考察知二推二的学习情况.
情境导入 1.任意画一个圆,将圆围绕圆心旋转任意角度,你有什么发现 围绕圆心旋转任何一个角度,都与原来的圆重合.因此圆具有旋转不变性. 2.圆是中心对称图形吗 哪个点是对称中心 圆是中心对称图形,圆心是它的对称中心. 3.什么是圆心角 如图,在☉O上任取两点A与B,连接OA,OB,得到∠AOB.像∠AOB这样,顶点在圆心的角叫做圆心角. 1.让学生动手画圆,通过围绕圆心旋转来观察、发现圆的旋转不变性. 2.直接给出圆心角的定义,为学习关系定理做好准备.
合作探究 探究一:圆心角、弧、弦的关系定理 任意画一个☉O,在☉O内画圆心角∠AOB=∠A'OB'.连接AB,A'B'. (1)以点O为旋转中心,逆时针旋转,旋转角为∠AOA',OA和OA'重合,这时OB和OB'重合吗 解:∵∠AOA'=∠AOB+∠BOA',∠BOB'=∠A'OB'+∠BOA',∠AOB=∠A'OB', ∴∠AOA'=∠BOB'. ∵旋转后半径OA与OA'重合, ∴半径OB与OB'重合. (2)这时,与重合吗 弦AB与A'B'重合吗 由此你能得到什么结论 解:∵在同一个圆中,点A与A'重合,点B与B'重合, ∴与重合,弦AB与A'B'重合. 1.探究一的问题,是运用圆的旋转不变性以及合情推理得出的,让学生通过探究发现结论,并说明理由.
续表
合作探究 归纳小结: 这就是说,在同圆中,如果两个圆心角相等,那么它们所对的弧相等,所对的弦也相等. 利用旋转的基本性质还可以得出:在同圆中,如果=,那么∠AOB=∠A'OB',弦AB=A'B';反之,如果弦AB=A'B',那么∠AOB=∠A'OB',=.这些结论在等圆中也成立. 定理 在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等. 典例分析: 【例1】 如图,AB与DE是☉O的两条直径,C是☉O上一点,AC∥DE.求证: (1)=;(2)BE=EC. 证明:(1)连接OC. ∵AC∥DE,∴∠AOD=∠OAC,∠COE=∠OCA. ∵OA=OC, ∴∠OAC=∠OCA. ∴∠AOD=∠COE. ∴=. (2)∵∠AOD=∠BOE, ∴∠BOE=∠COE. ∴BE=CE. 探究二:圆心角的度数与所对弧的度数的关系 问题1:把顶点在圆心的周角等分成360份,每一份圆心角的度数是多少 每一份圆心角的度数是1°. 问题2:把顶点在圆心的周角等分为360份时,整个圆被分成了多少份 每一份的弧是否相等 为什么 分析:整个圆被分成了360份,整个圆的叫做1°的弧.因此,1°的圆心角所对的弧是1°的弧;反之,1°的弧所对的圆心角是1°的角.一般地,n°的圆心角所对的弧是n°的弧;反之,n°的弧所对的圆心角是n°的角(如图). 由此可见,圆心角与它所对的弧有以下关系: 圆心角的度数与它所对弧的度数相等. 2.只有在同圆或等圆中才有等弧. 3.让学生回答问题1,2,经历“1°的弧”概念产生的过程,并理解合理性.
续表
合作探究 典例分析: 【例2】 如图,OA,OC是☉O中两条垂直的半径,D是☉O上的一点.连接AD并延长与OC的延长线相交于点B,∠B=25°.求,的度数. 解:连接OD. 由已知∠AOB=90°,∠B=25°,得∠A=65°. ∵OA=OD,∴∠ODA=∠A=65°. ∴∠DOA=180°-(∠ODA+∠A) =180°-(65°+65°) =50°. ∴的度数为50°. ∵的度数为90°, ∴的度数 =的度数-的度数 =90°-50° =40°. 【例3】 如图,在☉O中,弦AB所对的劣弧为圆的,圆的半径为2 cm,求AB的长. 解:连接OA,OB. 题意可知的度数为×360°=120°, ∴∠AOB=120°. 作OC⊥AB,垂足为点C. ∵OA=OB, ∴∠AOC=60°,AC=BC. 在Rt△AOC中, AC=OAsin∠AOC=2·sin 60°=2×=(cm). ∴AB=2AC=2 cm. 归纳小结:已知弧的度数,相当于知道圆心角的度数,所以连半径构造圆心角的同时也构造出等腰三角形,利用等腰三角形的性质、垂径定理、锐角的三角比、勾股定理等来求解. 4.例2、例3,可让学生先独立思考,交流思路.
续表
随堂检测 1.有下列四个命题:①顶点在圆心的角是圆心角;②两个圆心角相等,它们所对的弦也相等;③两条弦相等,它们所对的弧也相等;④等弧所对的圆心角相等.其中正确的有( C ) A.0个 B.1个 C.2个 D.3个 2.如图,AB,CD是☉O的直径,=,若∠AOE=32°,则∠COE的度数是 64° . 3.点A,C是半径为3的圆周上两点,点B为的中点,以线段BA,BC为邻边作菱形ABCD,顶点D恰在该圆直径的三等分点上,则该菱形的边长为 或2 . 4.如图,在 ABCD中,以A为圆心,AB的长为半径的圆分别交AD,BC于F,G,交BA的延长线于点E,求证:=. 证明:连接AG. ∵四边形ABCD是平行四边形,∴AD∥BC. ∴∠EAD=∠ABC,∠DAG=∠AGB. ∵AB=AG,∴∠ABC=∠AGB, ∴∠EAD=∠DAG.∴=.
课堂小结 1.圆是中心对称图形吗 它的对称中心是什么 2.圆心角、弧、弦之间有怎样的关系 应用的前提是什么 3.圆心角的度数与它所对弧的度数有怎样的关系 关系定理是圆中证明线段相等、角相等常用的方法,对定理要理解透彻.
作业布置 请完成教材练习题P72T1-T3,P74T1-T2
板书设计
弧、弦、圆心角之间的关系 1.圆是中心对称图形,圆心是它的对称中心. 2.定理:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等. 3.圆心角的度数与它所对弧的度数相等. 【例1】
教学反思
利用旋转的方法得到了圆的旋转不变性,由圆的旋转不变性,我们探究了圆心角、弧、弦之间的关系定理.例1是圆心角与所对弧和弦的关系定理的直接应用,例2和例3都是综合运用本节所学的圆的有关定理以及解直角三角形的知识解决有关圆心角、弧的度数及弦长的计算.通过例题,让学生感受不同数学知识之间的联系.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
